Computational models of the pulmonary circulation: Insights and the move towards clinically directed studies

Abstract

Biophysically-based computational models provide a tool for integrating and explaining experimental data, observations, and hypotheses. Computational models of the pulmonary circulation have evolved from minimal and efficient constructs that have been used to study individual mechanisms that contribute to lung perfusion, to sophisticated multi-scale and -physics structure-based models that predict integrated structure-function relationships within a heterogeneous organ. This review considers the utility of computational models in providing new insights into the function of the pulmonary circulation, and their application in clinically motivated studies. We review mathematical and computational models of the pulmonary circulation based on their application; we begin with models that seek to answer questions in basic science and physiology and progress to models that aim to have clinical application. In looking forward, we discuss the relative merits and clinical relevance of computational models: what important features are still lacking; and how these models may ultimately be applied to further increasing our understanding of the mechanisms occurring in disease of the pulmonary circulation.

INTRODUCTION

The pulmonary circulation is comprised of several scales of biological complexity: the genes, molecules, cells, and tissues that–as in any other organ system–work in concert to determine resultant function. The main function of the pulmonary circulation is to optimize the exposure of blood to alveolar air whilst maintaining a low enough resistance to accommodate passage of the full cardiac output. Malfunctions of structural components of the lung at any spatial scale can result in pulmonary vascular disease, to the detriment of gas exchange and right heart function. Vast amounts of data emerge from studies at each of these biological scales–particularly with the development of genetic and proteomic databases. The question then becomes, how can scientists integrate this data and knowledge across all of the biological scales to build on each new discovery and provide a collaborative advancement of knowledge that is greater than can be provided by studies at the individual scales? This integration of data and knowledge motivates the development of biophysically-based computational models in physiology. A mathematical model is a description of the behavior of a system using mathematical equations that describe physical processes, often in a simplified manner. (In the context of this review, the terms “mathematical model,” “computational model,” and “model” are synonymous and are used interchangeably throughout the text.) The use of such models in the biological realm is crucial to enable the integration and useful interpretation of data that results from experimental studies, and to provide an increased understanding of physiology.

Computational models have been used to investigate problems across a wide range of disciplines. Computational modeling is well established in, for example, engineering and weather prediction; but its application to biomedicine is more recent. The two major initiatives in this field are the International Union of Physiological Sciences Physiome Project (IUPS: see www. physiome.org.nz) and the European Virtual Physiological Human initiative (VPH: see www. vph.noe.eu). The IUPS Physiome Project aims to construct integrative biophysically-based models across the range of biological organization within and organism (genes, molecules, cells, tissue, whole organ), to provide an understanding of the structure-function relationships within a living entity.[1,2] The VPH initiative is Europe's rendition of the Physiome Project and aims to develop predictive computational models of a living human body.[3] The ultimate drive of these initiatives is towards the clinical environment, to create personalized medicine aimed at increasing the efficiency of medical practice.

The pulmonary vasculature in a typical human lung includes on the order of hundreds of thousands of arterial and venous vessels.[4–6] Gas exchange occurs across the thin walls of the alveolar capillaries, of which there are billions. The sheer number of vessels in this circuit-let alone the number of interactions at a cellular and sub-cellular level-means that numerous simplifying assumptions are required to enable construction of computational models. What is important to bear in mind is that a mathematical or computational model does not seek to represent each and every feature of an organ system. Such “mathematical microscopy” would do little to enhance understanding of function in the integrative system. A well designed model includes only the minimum information that is necessary to interpret a set of experimental data, or to test a specific hypothesis-for example, a modeling study of the distribution of humidity in the airways would not benefit from including the pulmonary circulation or the distal airways in the model, but it could be improved by coupling to distributed models of fluid transport through the ciliated epithelial cell.[7] Mathematical modeling of lung function has historically provided an important contribution to the understanding of pulmonary health and disease. The lung is a complex organ that works dynamically and reacts rapidly to changes in posture, environment and disease. Yet understanding of its different functions has been improved by using simplistic qualitative and quantitative models to explain inhaled gas transport,[8,9] respiratory gas transfer,[10] and pulmonary blood distribution,[11] amongst others. The continued increase in computational capability and the advancement of knowledge in related areas such as mathematics, computer science, image processing, biology and medicine has led, and is leading, to the development of ever more complex computational models in biomedicine. These advancements have made possible the creation of detailed anatomically-based models of the pulmonary airway and vascular geometries.[12,13] This has enabled the solution of functional model equations within geometries that closely resemble the structure of a real lung, with the goal of understanding structure-function relationships, their spatial distribution, and inter-subject and inter-species variability. But how complex does a model need to be for it to provide useful information about physiology? The answer to this is dependent on the functional aspect of the pulmonary circulation that is being investigated. For example, do we want to investigate heterogeneity in lung function; or are we interested in whole lung measures? Are we modeling a diffuse or localized disease state? Are we interested in small- or large-scale function?

Models that use simple geometries and few equations are easier to understand intuitively than complex multi-physics and multi-scale models. The complex models also suffer from the perception that they have “too many free parameters” in comparison to the simple models. By and large, however, the situation is quite the reverse. The simple models rely on lumping together the detailed laws and principles that govern function in the lung, so these types of model often have to fit parameters that don’t have a specific physical meaning. An example is the Starling resistor model of the pulmonary circulation used by Mélot et al.[14] compared with their distensible vessel model, which is more strongly based on physical principles. In contrast, in the class of biophysically-based models, each functional equation is a physical law with parameters that have a specific physical meaning. The model parameters are either well defined (e.g., viscosity of blood in the major arteries), estimated from experimental studies as invariable throughout the model (e.g., arterial wall elasticity), or poorly defined but still with a physical meaning that can be easily interpreted and quantified when experimental measurements become available. While a complex model may include explicit representation of each artery and vein in the pulmonary circulation, only a small set of equations with exactly the same parameters govern function within them; that is, the equations for flow, pressure, and vessel elasticity are identical at all levels of the trees. It is therefore exceedingly difficult to simply modify parameters in this type of model to better fit some functional outcome. The insights from a biophysically-based model often come from identifying how the model doesn’t fit some data–this can indicate the importance of otherwise neglected mechanisms in contributing to the integrated function of the lung.

Structure-based modeling provides a non-invasive approach to investigation of function, particularly when intervention is not possible in clinical studies due to ill health. Predictive models are powerful tools for interpreting experimental measurements and forming new testable hypotheses. An example is the use of appropriate computational models in conjunction with imaging modalities, each method acting as a means to verify and guide the other. For example, functional imaging data can be compared with model predictions of flow in large arteries, thereby validating some of the function of the model. The model predictions can then be used to postulate the flow distribution in smaller vessels, which are not directly visible on clinical imaging, or to investigate conditions that are difficult to investigate using imaging alone, such as the differences in perfusion distribution in the upright posture compared with the more readily imaged prone and supine postures. A model may also be used to help interpret results from functional imaging studies, if the quantities being measured are uncertain. Computational models may also be used to obtain quick predictions of the functional consequences of certain changes in vascular geometry, for example the effect of pulmonary vasoconstriction, pulmonary embolism, or pulmonary hypertension, for individual subjects.

To understand pulmonary disease and abnormal function first requires a thorough understanding of the mechanisms contributing to function in the “normal” healthy pulmonary circulation. Therefore, constructing physiologically realistic models of the normal pulmonary circulation has been a priority. These models must be validated–that is, compared with clinical or experimental data–before they can be used to investigate how perturbations to normal function manifest in disease. Validation remains the central challenge with this type of model, because the specific data that would provide a robust validation are often inaccessible to measurement. Studies of the pulmonary circulation generally aim to gain increased understanding of the mechanisms impacting on pulmonary vascular resistance (PVR), blood flow distribution, or the impact of alterations in pulmonary blood flow on gas exchange efficiency. Here we describe examples of models of the normal pulmonary circulation that have been used to investigate baseline function. We then discuss an example of model application in a clinically motivated problem: understanding the redistribution of blood flow and development of pulmonary hypertension in pulmonary embolism.

USING COMPUTATIONAL MODELS TO DEVELOP NEW INSIGHTS INTO THE BASIC FUNCTION OF THE PULMONARY CIRCULATION

Predicting pulmonary vascular resistance and pulmonary blood pressures

In the healthy adult lung the pulmonary vascular resistance (PVR) is low, allowing delivery of the entire cardiac output with a relatively low right ventricular (RV) pressure (compared with left ventricular pressure). Total PVR can be calculated as the difference between mean pulmonary artery (PA) and mean left atrial (LA) pressure, divided by the cardiac output (where LA pressure is approximated by pulmonary wedge pressure). Because flow, pressure, and resistance are interrelated, elevation of PVR results in elevated RV pressure if the cardiac output is to be maintained. The lung has an in-built protective mechanism against elevation of PVR in the form of recruitment of capillaries and, to a smaller extent, distension of the elastic vessels comprising the circuit.[15] Under resting conditions a substantial portion of the capillary bed is un-recruited;[16] some or all of the de-recruited capillaries can open when cardiac output increases—and presumably under other conditions that elevate PA pressure—to increase the total cross-sectional area of capillary bed through which the blood traverses, and concomitantly decrease the PVR. The functional consequence is that during exercise in the healthy individual–when the cardiac output can increase six-fold–PA pressure increases only moderately.[17] When capillary recruitment is insufficient to prevent PVR rising above a critical level, this impacts on right heart function and capillary wall integrity, and potentially fluid filtration and edema formation will occur. Several modeling studies have investigated the relationship between vessel dimensions, vessel elasticity, and PVR. Most have taken a highly simplified approach to model geometry and fluid dynamics, which is sufficient for demonstrating the importance of vascular geometry and distensibility on pressure-flow relationships, and therefore on PVR.

Perhaps the simplest approach to modeling blood flow in a complex vascular network is to represent the fluid flow as analogous to a current in an electrical circuit: if flow is steady then the analogue of a direct current (DC) circuit is used, and if flow is pulsatile the analogue of an alternating current (AC) circuit is used. Using the DC circuit as an example, Ohm's Law states that the voltage drop (ΔV) across a circuit is equal to the current through the circuit (I) multiplied by the total resistance (R), so ΔV=IR. Similarly, in a steady fluid flow the pressure drop (ΔP) across a system of blood vessel ‘resistors’ is equal to the flow through the system (Q) multiplied by the total resistance (ΔP=QR). Most mathematical models of the pulmonary circulation use the electrical circuit analogy (e.g., references 18 through 22), but differ in two major features: (a) the structural representation of the blood vessels, which influences the estimation of the total resistance to blood flow; and (b) whether the model uses an AC or DC circuit analogy (so whether it includes or neglects the pulsatility of blood flow, respectively).

The most simplified approach to representing the vascular structure and hence estimating the distribution of vascular resistance is to assume that the pulmonary blood vessels are a symmetrically branching tree. Total resistance can then be calculated as the series and parallel summation of the individual vessels/resistors: because all blood vessels in a single generation of a symmetric tree are identical and act “in parallel,” their combined resistance is calculated as the individual resistance divided by the number of vessels in the generation; and the total resistance is simply the sum of the resistances of each generation. An advantage of the symmetric approximation is that because all pathways from the PA to the pulmonary veins are identical, the whole vasculature can in effect be treated as a single pathway. Dawson et al.[23] used this type of mathematical model of the pulmonary arterial tree to investigate the effect of vascular geometry and vessel mechanics on the mean pressure-flow relationship and longitudinal pressure profile. This study aimed to use the experimental data available at the time of the study to construct a range of possible hemodynamic outcomes. They found that hemodynamics were sensitive to both the elasticity of blood vessels (highlighting the possible role of disease in affecting elasticity) and the rate of change of vessel diameter from the main PA to distal blood vessels. While symmetric models are convenient and computationally inexpensive, they are very limited in the studies to which they can be applied. For example, any study in which the spatial distribution of a structural or functional property of the pulmonary circulation is important cannot use a symmetric tree model.

Zhuang et al.[22] considered more complex branching structures that statistically matched (the same) morphometric cat lung data and–by assuming that blood flow was equally divided through vessels of the same Strahler order (and so simplifying the resistance calculations)–they studied the pressure-resistance-flow relationships within two different geometric structures. They found that both of their model structures provided similar predictions, and their predicted pressure-flow relationships and the blood pressure distribution through the models had some consistency with experimental data. The distribution of pressure drop in the models is illustrated in Figure 1(a). The most significant decrease in pressure occurred across the capillary bed. However, they concluded that some important physiological data was lacking in areas where their model did not match the experimental data. For example they could not match the data well when the airway or pleural pressure was altered from its baseline value. In short, they concluded that an interaction between experiment and modeling was required to fully describe the pulmonary circulation. A non-symmetric extra-alveolar tree structure was considered by Bshouty et al.[24,25] (Fig. 2), with each blood vessel's resistance set independently. Their study differed from that of Zhuang et al. in its asymmetry within blood vessel generations as well as including an upper bound for vessel distensibility with pressure. The model asymmetry complicates the calculation of resistance, so this study restricted the vessel tree to only 4 Strahler orders (compared with Zhuang's 11-17). They investigated whether non-linearity in pressure-flow curves were a result of vessel distensibility or recruitment, and concluded that recruitment was likely the dominant factor.

Figure 1.

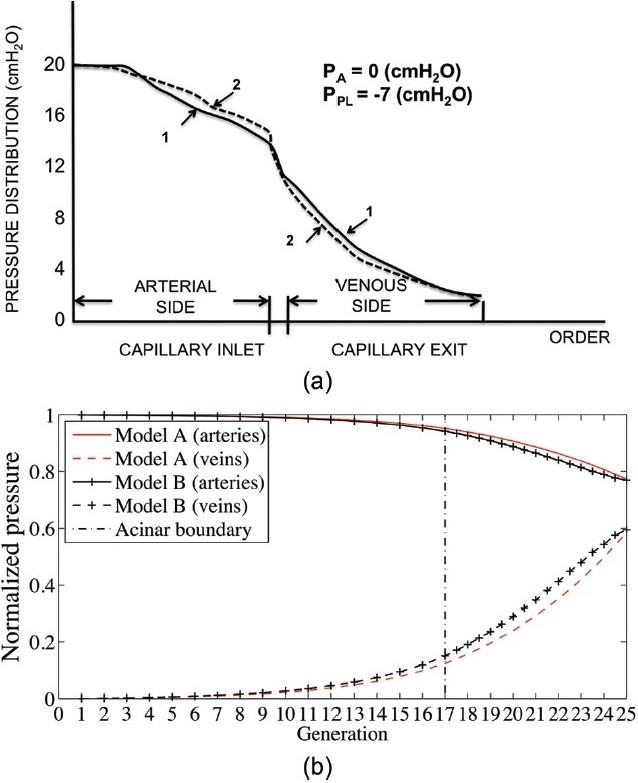
Blood pressure drop across four models with symmetric large vessels. [a] Zhuang et al.[22] Curves (1 and 2) show pressure drop across two models that statistically match the same morphometric data. Capillary beds join arteries and veins in parallel. [b] Clark et al.[29] Model A (red) joins large vessels similarly to Zhuang et al.; Model B (black) joins arteries and veins via a ladder model for combined series and parallel perfusion of capillary sheets. Figure sources: [a] redrawn from Zhuang et al.;[22] [b] from Clark et al.[29], used with permission.

Figure 2.

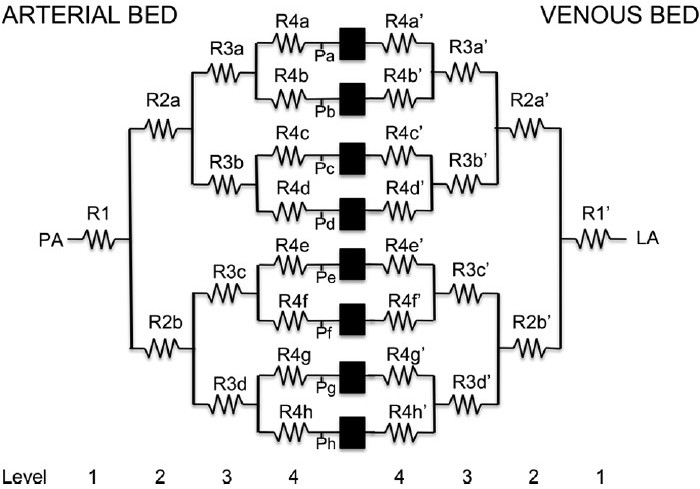
The DC circuit representation of the pulmonary blood vessels reproduced from Bshouty et al. Each blood vessel is represented by a “resistor” with a unique resistance adding heterogeneity to the flow through each order of blood vessels. However, computational constraints prevented the construction of a model with more than four orders of arteries and veins. Redrawn from Figure 1 in Bshouty et al.,[25] used with permission.

Each of these modeling studies assumed a steady blood flow (DC circuit analogue), which is considered a valid assumption in many models of the pulmonary circulation.[26] A class of pulsatile flow models also exists. The models are based on Zhuang's geometrical approach and an AC circuit analogy to describe blood flow[18,19,21] in dogs, cats and humans. These models give additional temporal information compared with steady models. This additional information may be useful in some studies, for example in estimating the rate of change of shear stress at the endothelium due to the pulsatile blood flow. However, to date they have not been used widely outside the context of normal pulmonary function.

The models described above take a simplifying approach to both fluid dynamics (the movement of blood through the lungs) and geometry. Therefore, they have the distinct advantage that they can be solved quickly and easily to study normal function or disease which manifests in a reasonably uniform manner throughout the vasculature. An alternative to this simplifying approach is three-dimensional computational fluid dynamics (3D CFD). This approach aims to solve the most accurate equations in the most anatomically correct model geometries possible. Unfortunately, the equations that govern fluid (blood) flow–the Navier-Stokes equations–are very difficult to solve, especially when the flow is turbulent. This means that application of 3D CFD to compute pulmonary blood flow requires substantial computing power, and model geometries are usually restricted to a small subsection of the vasculature. However, the accuracy of these models allows investigation into shear-stress distributions along vessel walls, and blood flow characteristics within a vessel itself. Tang et al.[27] used 3D CFD to model blood flow in the central pulmonary arteries and provided detailed predictions of wall shear stress and energy efficiency in these blood vessels at rest and in exercise. Their vessel structure was constructed from MRI images and so provided a very accurate geometrical description of the central blood vessels, compared with the simple cylinder (non-elastic) or tapered cylinder (elastic) representation of a blood vessel that is required in 1D models. They predicted a non-uniform blood flow distribution within these vessels and determined that there was a 10% reduction in energy efficiency between rest and exercise conditions, noting that this may have implications for the long term results of surgical procedures. In addition they predicted wall shear stress over the entire surface of these vessels–a finding that is interesting in the context of vasodilation, where shear stress acts as a mechanical stimulus for the release of nitric oxide (NO). The major limitation of this field of modeling is that only a small subset of pulmonary blood vessels could be explicitly included, resulting in major assumptions concerning the behavior of the downstream blood vessels. In other studies by this group,[28] they have proposed a morphometry-based boundary condition to mimic the impedance of the downstream vasculature. Each sub-tree appending a 3D discretized artery has its parameters "tuned" such that the whole model has impedance that is appropriate for the intact pulmonary circulation. This is an important step in acknowledging the contribution of the downstream vasculature is determining the distribution of blood through the largest vessels, however this cannot account for the interaction between tissue mechanics, gravity, and blood flow, and how this changes with posture or increased cardiac output.

The models that have been introduced so far have neglected the intricacy of structure in the pulmonary microcirculation. Whether symmetric or asymmetric, the arteries and veins were assumed to be joined by a capillary bed that was perfused strictly in parallel. That is, a unit of capillary sheet that was supplied by a symmetrically branching set of arterioles. This neglects the morphometric structure of the pulmonary microvasculature, where small pre-capillary blood vessels arise from Strahler ordered arteries with order as high as 8;[6] small arterioles feed into the capillary plexus, as well as supplying daughter arterioles. Recognizing the importance of the anatomical geometry in determining the distribution of intra-acinar flow and resistance, Clark et al.[29] developed a microcirculatory model with a “ladderlike” structure. As shown schematically in Figure 3(a), each “rung” on the ladder represents the alveolar septae at a separate generation of a symmetrically branching tree. One set of “posts” on the ladder are the feeding arterioles, and the matching set of posts are the draining venules. The ladder model therefore includes combined series and parallel perfusion, where blood can either progress to the next generation of arterioles, or enter the capillary bed and pass to the venules without having to traverse the entire length of the intra-acinar arteriole tree. Coupling the symmetric ladder model to symmetric models for the arteries and veins confirmed earlier experimental observations of a stratified acinar blood flow from proximal to distal capillary beds.[30,31] The model also demonstrated that the hierarchical structure of blood vessels within the acinar unit pathways significantly decreases PVR when compared with capillary beds that connect only the most distal blood vessels. Figure 1(b) shows the pressure drop predicted through the symmetric large vessel and ladder model, compared with pressure drop in a model with symmetric arterioles supplying only a single distal capillary sheet. The number and size of the arterioles can be modified to give a similar prediction of pressure drop between the two models; however, the dimensions and effective numbers of these intra-acinar arterioles is unrealistic. Clark et al.[32] extended the model to an asymmetric acinar structure, showing heterogeneity in blood flow even at the level of the intra-acinar blood vessels.

Figure 3.

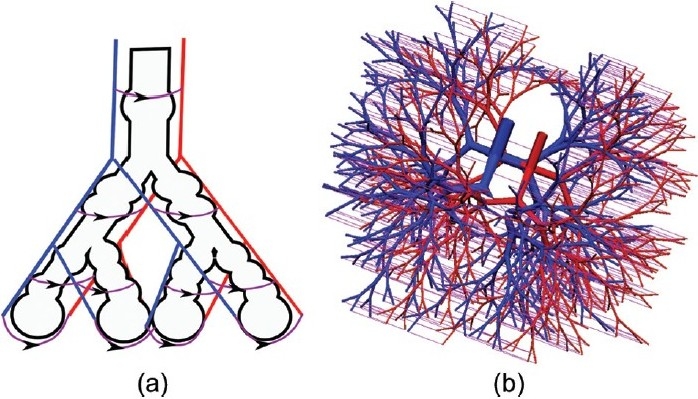
Ladder model by Clark et al. In this ladder model of Clark et al.,[29] arterioles are in blue, venules in red, and capillary beds in purple. Arrows show direction of capillary blood flow. The schematic in Panel A illustrates the concept of the ladder model. This was the first computational model to include the serial and parallel capillary pathways. Panel B illustrates the ladder model implemented over a multi-branching asymmetric model of the human pulmonary acinus, from Clark et al.[32] Figure source: Reprinted from Clark et al.,[32] with permission from Elsevier; Panel A from Clark et al.,[29] used with permission.

The resistance of individual vessels depends on their size, which in turn depends on their hierarchy within the pulmonary circulation, and their location within the lung. And because of the hydrostatic pressure gradient, blood pressures vary considerably depending on the vascular pathway that blood traverses from the right to the left heart. Clark et al.[33] developed a subject-specific anatomically-based model for the entire pulmonary circulation that can be used to predict the distribution of vascular resistances and the pressure fluctuations along individual pathways. The model geometry is anatomically-based in that it captures the branching asymmetry of the extra-acinar pulmonary blood vessels and the spatial relationship between blood vessels and lung parenchymal tissue. It is subject-specific in that it describes the lung shape, the distribution of the largest blood vessels and the regional tissue density measured from multi-row detector computed tomography (MDCT) data in an individual. Additional modeling methodology was used to supplement the model from the level at which the imaging data had insufficient resolution. The model includes anatomically-based geometry of the lung surface and central blood vessels; computationally-generated morphometrically-consistent models of the “accompanying” arterial and venous vessels (i.e., not including supernumerary vessels[34]) to the level of the acini;[13] a ladder model[29] attached to each of the ~32,000 acini, consisting of 9 symmetric branches of intra-acinar arteries and veins coupled in a serial and parallel arrangement through a ‘sheet’ flow representation of the pulmonary capillaries;[35] and a model of parenchymal tissue deformation,[36] to which the vascular networks are tethered. The anatomically-structured models for the pulmonary arteries and veins are illustrated in Fig. 4. Blood flow through the entire circuit of arteries, capillaries, and veins can be simulated after applying boundary conditions for pressure or flow at the level of the heart. Then by solving equations for Poiseuille resistance, conservation of mass, vessel elasticity, and a microcirculatory model–including gravity–predictions can be obtained for the regional distribution of blood flow, blood and transmural pressures, capillary recruitment, and vessel radius. Blood within the larger vessels is assumed to be Newtonian, however in the microcirculatory vessels the shear-thinning properties of blood are accounted for via an apparent viscosity parameter in the model equations.

Figure 4.

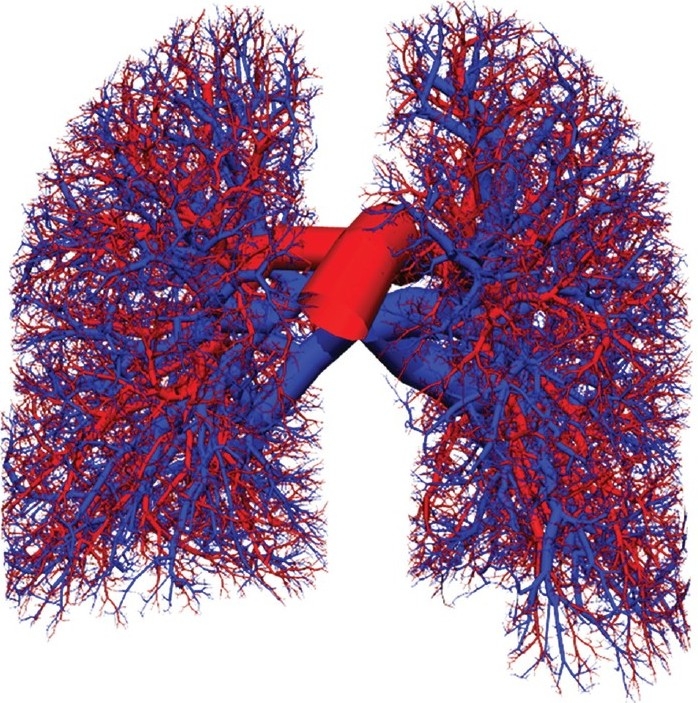
Anatomically structured model of the human pulmonary circulation by Burrowes et al. The pulmonary arteries are colored red, and the pulmonary veins are colored blue. The geometry of the first 10-12 generations was manually segmented from MDCT imaging. The remainder of the vascular trees were generated using a volume-filling branching algorithm. Figure source: Burrowes et al.[13] used with permission.

Figure 5 shows the pressure variation through three pathways in the spatially-distributed model. The capillary pressure in each pathway is inversely proportional to the location of the tissue with respect to gravity: blood pressure upon entering the capillary bed is least in the non-dependent lung and greatest in the dependent lung. This can be explained by the larger hydrostatic pressure in the most dependent tissue. In contrast to the single pathway (symmetric) models where blood pressure systematically decreases, the three pathways in Figure 5 illustrate a deviation from this, with increase in blood pressure in the arteries of the dependent pathway, and in the veins of the non-dependent pathway. This occurs again as a consequence of the hydrostatic pressure gradient, and is influenced by the orientation of the vessels as they traverse to the parenchymal tissue. Pathways that are oriented towards the non-dependent tissue experience pressure loss due to friction on the vessel walls (energy dissipation) plus decrease in the hydrostatic pressure; pathways that are oriented towards the dependent tissue experience the frictional pressure loss, but have added increase in hydrostatic pressure. The vessel sizes are determined by transmural pressure (the difference between blood pressure and external pleural pressure acting on the vessel); in regions where blood pressure is smallest, the magnitude of pleural pressure is greatest, and vice versa for locations where blood pressure is larger. Vessel size is therefore dependent on spatial location and the distance that the vessel sits along the flow pathway.

Figure 5.

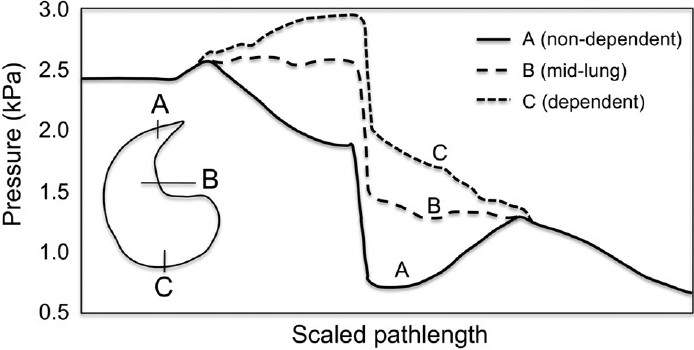
Variation in pathway blood pressure from right to left heart in the full-circuit model. Vertical lines show the capillary bed, where the greatest pressure drop occurs. Results differ substantially from previous models (Fig. 1), which show continuous blood pressure drop. In contrast this illustrates the influence of the hydrostatic pressure gradient, with pathways to non-dependent (A) tissue having decreasing arterial blood pressures and increasing venous pressure, while pathways to the dependent tissue (C) having increasing arterial pressures and decreasing venous pressures.

The spatial distribution of blood in the lung

Early experimental studies suggested that gravity was the primary determinant of blood flow distribution in the lung, due to the hydrostatic pressure gradient affecting the balance of forces at the capillary level and hence allowing or limiting flow.[11] The classic “zonal” description of blood flow distribution is therefore gravitationally dependent, with lung tissue in the non-dependent region (apices of the upright lung) receiving proportionately less of the cardiac output than tissue in the dependent region (base of the upright lung). The zonal model has persisted as the primary hypothesis for the distribution of pulmonary perfusion for over 30 years. More recent studies have highlighted irreversibility of the flow gradient with reversal of posture,[37] and large iso-gravitational heterogeneity of flow,[38] both of which are inconsistent with a purely gravitational theory for flow distribution. These and other studies[37–41] have suggested that other factors play as much of–or even more of–a role in determining pulmonary blood flow distributions than the hydrostatic effects of gravity. For example, recent imaging studies have suggested that the influence of gravity on the regional distribution of blood flow in the lung is largely through the deformation of the parenchymal tissue[40–42] (the lung acting as a Slinky^™), rather than via the balance of pressures at the microcirculatory level, as described by the classic zonal model. The anatomical geometry of the lung and vasculature have also been proposed to be important contributors.[38,43] The potential contribution of each mechanism has become a strongly debated issue.[44,45] What is clear is that reconciling data from different imaging or experimental studies is difficult-perhaps impossible-without a predictive, quantitative framework in which to test the different mechanisms that contribute to perfusion. Here we describe a fractal modeling approach that has been used to study an individual mechanism, and explain a recent physiologically-based computational model that seeks to reconcile data from different experimental studies, and to estimate the contribution of individual mechanisms when acting integratively in a single functioning lung.

An important feature of pulmonary blood flow distribution is the large degree of heterogeneity that is observed within isogravitational planes. This heterogeneity is accompanied by a spatial correlation in perfusion (high blood flow regions neighboring high blood flow regions and vice versa), which again occurs within isogravitational planes, suggesting a structural influence on pulmonary blood flow distribution. These observations have led to the construction of fractal models to describe pulmonary blood flow.[46] The fractal approach assumes that each vessel bifurcation (which includes a parent and two daughter branches) is a simple scaling of the previous bifurcation; that is, the fractal tree has self-similarity. The fractal branching models relate one aspect of structure to one aspect of function of the pulmonary vascular tree. The fractal model is sufficient for explaining how asymmetry in flow distribution at a bifurcation can result in perfusion heterogeneity at the tissue level. They also provide a mechanism to describe the spatially correlated distribution of flow and the gravity-independent heterogeneity of blood flow.[46–50] The interaction between theoretical fractal models and experimental validation has provided an insight into the importance of blood vessel structure to pulmonary blood flow distribution that was not attainable via experiment alone. However this is an examination of a single mechanism, without interaction with tissue mechanics or the constraint that is introduced by the microvasculature. A further limitation is the basis for the fractal models: the assumption of self-similarity may hold on average, but there is marked variability in parent to child diameter ratios at all levels of the vascular tree, spatial variability in vessel dimension due to the regional differences in transmural pressure, and potentially major differences in structure and function between the accompanying (conventional) vessels and the supernumerary vessels[34] that would violate the assumption of self-similarity.

An alternative to the fractal approach to modeling blood flow is to construct anatomically-based models of the pulmonary vasculature and to solve equations describing blood flow within these geometries.[13,28] This type of model captures the structural aspects of the lung that lead to blood flow heterogeneity, and can accurately represent the hydrostatic effects of gravity and deformation of parenchymal tissue–ultimately allowing the relative contribution of each to perfusion distribution to be assessed. Anatomically-based models suffer from a high computational cost (unlike fractal models). However, advances in computational power have allowed rapid progression from models of blood flow in the arterial tree alone,[51] through coupling to a model of lung tissue deformation under gravity,[52] to a model that can describe the distribution of pulmonary blood flow though the full pulmonary circuit coupled to deformed tissue.[33] Using this modeling approach, one can investigate the effects of structure alone (heterogeneity and a reduction in blood flow through high resistance paths), hydrostatics (inducing a gravitational gradient in blood flow) and tissue deformation (increasing/decreasing gravitational gradients depending on lung size and posture).[33] This is achieved by ‘switching’ model components on and off-a task that can be achieved far more easily in a computational model than in a biological organism. The contribution of each of these factors–as revealed by a computational modeling study–is considered below.

Clark et al.[33] developed an anatomically-based model of blood flow through the full pulmonary circuit of a single human subject coupled to a model of parenchymal tissue mechanics[36] to study the interdependence of structure, fluid transport, and mechanical behavior in perfusion of the lung. This complex multi-scale and multi-physics model is currently the only model in the literature that simultaneously includes all of the basic passive mechanisms that influence the distribution of blood flow in the lung. The model built upon previous structure-based models for perfusion[13,51–53] by coupling anatomically based pre-acinar geometries (representing the largest pulmonary arteries and veins) with the ladder model for perfusion in the pulmonary acinus,[29] as described in the previous section. Each artery, vein, or capillary is embedded within a model of the deforming parenchyma[36] such that the vessel-by-vessel transmural pressure has an appropriate dependence on vessel blood pressure and the local elastic recoil pressure of the tissue (elastic recoil pressure is approximately equal and opposite to pleural pressure), and in the case of the capillaries the additional dependence on local air pressure. The coupling of models describing the microcirculation in an anatomically-based large vessel structure enables application of readily measurable pressure and/or flow boundary conditions at the heart rather than at the micro-circulatory level as previous anatomically-based models had been constrained to do.[13,51–53] Previous modeling studies of the relative influence of gravity and structure[13,52,54] considered perfusion of the arterial tree in isolation from the structure of the capillary bed or veins, instead using a linear increase in acinar blood pressure with decrease in gravitational height, hence each acinus within a single isogravitational plane was assumed to have the same blood pressure. The full-circuit model removes the necessity for this simplifying assumption, which allows more meaningful predictions of pulmonary perfusion gradients and heterogeneity than has previously been possible from this type of computational model. That is, by including the structure of each level of vessel in the circulatory tree, simulations of perfusion only require setting cardiac output and LA pressure, and selecting the orientation of the lung with respect to gravity. The “full-circuit” model is a comprehensive tool for studying the integrated function of the pulmonary circulation, and provides the only tool for teasing apart the individual contributions of the various passive mechanisms that are at play. Clark et al.[33] specifically addressed whether tissue deformation is the major contribution of gravity to the pulmonary perfusion gradient in the human lung, whether the hydrostatic pressure gradient makes a quantifiable contribution, and whether the balance of pressures at the micro-circulatory level remains a significant feature in the presence of other mechanisms of gravitational origin.

The vascular trees are tethered to the parenchymal tissue, which is highly compliant and deforms readily in gravity due to its own weight. In the upright lung the gradient of deformation is in the cranial-caudal axis, with tissue near the base on average less expanded than tissue near the apices.[40,41] Note that the word “compression” is often misused in this context, with many authors and textbooks describing the lung tissue as “compressed” in the dependent region rather than “less expanded.” A material that is in compression has restoring forces that will act to return it to a more expanded state; in contrast the parenchyma in the dependent tissue is in tension, just to a lesser degree than the parenchyma in the non-dependent regions. Understanding this distinction is important when studying the mechanical deformation of the lung tissue. The study of Clark et al.[33] found that postural differences in perfusion gradients could be attributed largely to tissue deformation. Unlike previous findings in models of the ovine lung,[53] the orientation of the vascular structure with respect to gravity had little effect on perfusion gradients in the human lung. That is, the vascular structure did not contribute significantly to a persistence of the flow distribution pattern. Tissue deformation in the model supported experimental studies that describe the lung tissue as acting as a Slinky that deforms under gravity and hence changes the density of blood vessels and capillaries per unit volume,[40,41] but the model also added new insight into the individual contribution of each mechanism beyond the Slinky hypothesis. Each structural and gravitational feature of the pulmonary circulation was found to make a distinct contribution to the distribution of blood. Postural differences in perfusion gradients were explained by the combined effect of tissue deformation and extra-acinar blood vessel resistance to flow in the dependent tissue. The model also showed that gravitational perfusion gradients persisted when the effect of tissue deformation was eliminated, highlighting the importance of the hydrostatic effects of gravity acting directly on the weight of the blood (imagine a solid, non-deforming parenchyma with a vascular tree that contains blood). Heterogeneous large vessel resistance (due to geometric asymmetry of the vascular trees) was shown to cause variation in driving pressures across the microcirculation. This variation was amplified by the complex balance of pressures, distension, and flow at the micro-circulatory level. That is, the normal variation in resistance pathways of the vascular tree were found to result in isogravitational heterogeneity of flow and pressures at the entrance and exit of the microcirculation of each acinus. This heterogeneity was amplified by the zonal model, which considers the balance of arteriole, venule, and alveolar pressures, and the extent of local alveolar stretch. The influence of the vascular asymmetry combined with the zonal effect was enhancement of the isogravitational heterogeneity of tissue perfusion. The contribution of these mechanisms issummarized in the schematic in Fig. 6.

Figure 6.

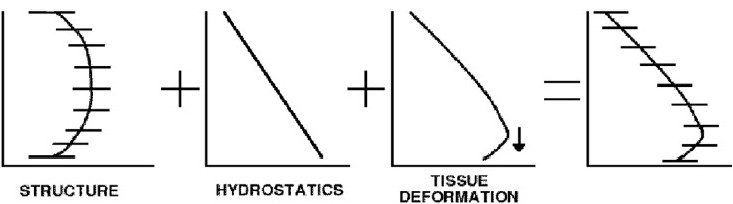
Schematic of contributions to distribution of blood. (A) Vascular asymmetry contributes to heterogeneity, and decrease in perfusion in the extremities; (B) hydrostatic pressure gradient acts directly on blood to drive it preferentially downwards, and introduces a constraint at the capillary level; (C) deformation of tissue establishes a gravitational gradient of vessels per unit tissue, enhancing the flow gradient; also contributes to reduction in flow in most dependent region; (D) combined result is a gravitational gradient and isogravitational heterogeneity, each affected by multiple mechanisms.

An important outcome of the modeling study was the ability to reconcile the experimental measurements that formed the basis of the zonal model with more recent studies using higher resolution (microsphere) techniques, and even more recent imaging studies that demonstrated the importance of tissue deformation. The model showed that each theory can co-exist within the same structure, and that each makes an important and distinct contribution to the distribution of blood flow. The model encapsulates each of the theories related to microcirculatory pressures, vascular geometry, and tissue deformation, and shows that these can be predicted on the basis of the physical behavior of the pulmonary circulation. This is only predicted however when structure and function are considered in parallel: a model with symmetric geometry (neglecting vascular asymmetry) or lacking a realistic spatial distribution of blood vessels (so neglecting the interaction with the deforming tissue) would only recognize the contribution of the hydrostatic pressure gradient.

Species differences in perfusion distribution

Experimental measurements of pulmonary perfusion are more easily obtained in animal studies than human. High resolution methods using microspheres are destructive, hence can only be used in animals, and MDCT imaging–which gives highest resolution for lung tissue–requires radiation exposure, so must be used minimally in humans. However humans have quite different vascular branching asymmetry to most other mammals, and this could influence the translation of outcomes from animal experiments to human physiology and pathophysiology. Species-specific branching and diameter asymmetry in the vascular trees of the lung has been well documented.[6,55] The quadruped pulmonary arteries and veins branch monopodially (a parent vessel gives rise to a major branch with relatively large diameter at a small branching angle to the parent, and a minor branch with relatively small diameter at a large branching angle). If the supernumerary arteries and veins are neglected, then the human pulmonary vascular trees are relatively more symmetric than in the quadruped lung. Various measurements of pulmonary perfusion gradients in animals and humans in different postures and at different lung volumes[38,40,41,47,56–60] have suggested differences between quadruped and human pulmonary perfusion gradients.[45] Burrowes et al.[53] used species-specific computational models of the pulmonary vasculature to study whether species differences in vascular asymmetry were sufficient to produce characteristic differences in pulmonary perfusion gradients in the human and ovine lung.

Species-specific models were derived from MDCT imaging, using the lung and lobe shapes as boundary conditions and the MDCT-segmented arteries as initial conditions for generating a volume-filling tree to represent the pulmonary vasculature of each species.[53] The governing equations, method for numerical solution, and parameters in the two species models were the same. The only difference was in the branching pattern and branch diameters. This meant that any predicted difference in flow distribution was due to species-specific pulmonary arterial geometry. The regional distribution of perfusion in the ovine model was consistent with microsphere measurements in supine pig[47] and dog[61] lungs. The microsphere measurements showed the same characteristic distribution as the model, with flow lowest near the ventral and dorsal surfaces, and maximum at about 40% (dorso-ventral) height. Perfusion gradients in both species were smaller than those measured via imaging, which was likely due to neglecting tissue deformation in the model. Importantly, in both the model (after exclusion of decreasing flow in zone 4) and in experimental studies, animal perfusion gradients were generally larger than in human. The model predicted only a modest change in flow gradient with posture (supine to prone), similar to measurements from Glenny et al.,[47] suggesting that the arterial structure has a persistent effect on regional perfusion regardless of posture. When the ovine model was supine there was large flow resistance in the dorsal pathways that acted to reduce the flow in this region; the human dorsal pathways provided relatively less resistance than those to the ventral tissue, so there was a smaller reduction in flow.

A species comparison such as this is clearly only possible using a structure-based model that accounts for the species-specific morphometry of the vascular trees. Sheep and other quadrupeds with monopodially branching pulmonary vasculature are more frequently used as experimental animals in studies of lung function than primates, whose lung geometry is most similar to human. Sheep, pigs, and dogs are variously described as having lungs that are ‘similar to human’. While this may be true of lung size, and distribution and density of some cell and receptor types, it is not correct with respect to the tree geometries of the airways and blood vessels. The monopodial animal vasculature has markedly greater asymmetry of child vessel diameters than in the human lung, so greater potential for the vasculature to contribute to flow heterogeneity. The animal pulmonary vasculature also has long wide vessels that extend to the dorsal-diaphragmatic region. The modeling study demonstrated the consequence of these geometric differences on distribution of blood flow. Important species differences were highlighted that need to be accounted for when interpreting animal measurements in the context of human lung physiology. One caution is that the modeling study of Burrowes et al.[53] did not explicitly couple the arterial tree to the geometries of the capillary bed and venous tree, as in the later study of Clark et al.[33]

Interesting future extensions to this work would be in considering smaller animals that are used as genetic models for disease, such as rats and mice. The same methodologies and governing equations apply, only now working with a smaller sized organ.

CLINICALLY DIRECTED MODELING STUDIES

Models describing pathophysiology in the pulmonary circulation are fewer in number than those describing normal physiology. However, they have been able to provide useful insights into disease and provide advances towards improving clinical practice. In 1999 Taylor et al.[62] proposed that surgical planning could be improved via predictive medicine. That is, that a simulation-based set of tools that could predict patient outcomes and test hypotheses would allow better surgical planning than diagnostic imaging and empirical data based on past treatments alone. The concept of predictive medicine is not restricted to the surgical arena; it can be–and should be–used in developing diagnostic procedures and treatment strategies for acute and chronic illnesses. Here we describe models that aim to advance understanding of the development of pulmonary hypertension (PH) in the presence of vascular obstruction.

Pulmonary embolism

Thromboembolic pulmonary embolism (PE) is a relatively common clinical condition that can result in acute or chronic elevation in PA pressure, thereby inducing secondary PH. Clinically, acute PE is poorly diagnosed and is responsible for many thousands of deaths each year.[63] If left untreated, chronic elevations in PA pressure may lead to RV hypertrophy (cor pulmonale) and ultimately to RV failure. PE is difficult to diagnose because of its range of symptoms and clinical features, and the response to acute PE is heterogeneous. The capability of stratifying risk amongst PE patients is therefore vital to enable optimal management.[64] PE is also often used to induce PH in animal models,[65] either by instilling inert beads, inflating a balloon catheter to obstruct an artery, or injecting autologous blood clots.

Arterial thromboembolic PE have been proposed to raise PA pressure by two mechanisms: first, by mechanical obstruction of the arterial tree, reducing the effective size of the vascular tree so elevating PVR; and, second, by release of vasoactive mediators (for example, serotonin and thromboxane A₂) from the blood clot, causing vasoconstriction and an increase in PVR.[66–68] There is some uncertainty as to the action of the second mechanism in the human pulmonary vasculature. It is clear clinically that while patients can tolerate occlusion of a major PA by a passive obstruction (such as a balloon catheter) or indeed removal of an entire lung, thromboembolic obstruction of a far smaller proportion of the vascular tree can result in RV failure via elevated PVR and PA pressure.[69,70] Many animal studies have demonstrated that PVR is far more sensitive to vascular occlusion by a thrombus than by a passive occlusion (e.g., references 65 through 67); others have demonstrated elevated levels of vasoactive mediators in the circulation in the presence of a blood clot in both animals and humans.[71–73] These studies have hence concluded that–more definitively, in animal lungs-vasoconstriction is an important mechanism for developing high PA pressure. The same amount of direct evidence for vasoconstriction in humans is not available, but the indirect evidence does suggest that ‘something other’ than mechanical obstruction must be contributing to the response to APE, and that this is likely to be vasoconstriction mediated by vascular interaction with the thrombus.

Despite the prevalence of clinical PE and numerous animal experimental studies to understand its mechanisms, it is still not clear precisely how it affects gas exchange on a patient-specific basis, and how the degree of hypoxemia and elevation of RV pressure varies according to embolus distribution and severity. There is also some lack of certainty concerning the development of PH in human APE. The aim when developing computational models is to include only as much detail as is necessary to address the specific question of the study. Examples of this in the area of PE are the models of Mélot et al.,[14] who were the first to propose theoretical models for PE, and Roselli et al.,[74] who used a rudimentary model to investigate the effect of embolization on measurement of capillary pressure via venous occlusion. Mélot et al.[14] adopted a simplified Starling resistor model (based on Mitzner et al.[75]) that included 100 parallel resistors (each representing a pulmonary vessel), each with a randomly generated critical closing pressure, and a distensible vessel model based on Haworth et al.[76] and Zhuang et al.,[22] to investigate which model best described the relationship between PA pressure and flow in embolic PH in dogs. They found that the distensible vessel model was able to reproduce blood pressure-flow curves measured in dogs with embolic PH (induced using 500-μm glass beads). Their simulations provided reasonably accurate predictions of experimentally-derived PA pressure-flow and PA pressure-LA pressure curves pre- and post-embolic occlusion. These early studies were designed to answer specific experimentally-led questions. At least part of the variable response to PE treatment is due to heterogeneity in embolus location. A structure-based model for PE is therefore essential to capture regionally-varying changes in the distribution of perfusion post-occlusion.

Burrowes et al.[77] presented a pilot study using the full-circuit model of Clark et al.[33] to investigate the extent to which RV dysfunction in PE can be attributed to mechanical obstruction of the vasculature, and whether the contribution of signaling from the embolus via vasoactive mediators can be estimated. Computed tomography pulmonary angiography (CTPA) from 10 patients acquired during routine clinical examination for PE was used to define the location of emboli in each subject. For each of the 10 subjects, the percentage of arterial occlusion in each artery from the main PA to the level of the segmental arteries was estimated from their CTPA, for use in post-occlusion simulations. Partial occlusions of individual arteries identified on the imaging were mapped onto the computational model, and their hemodynamic consequence was predicted by solving the functional flow model of Clark et al.[33] with application of boundary conditions for pressure and flow that assumed no increase in LA pressure or decrease in cardiac output. All but one subject demonstrated preferential redistribution of blood flow to non-dependent regions. This pattern of redistribution was because of increased potential for capillary recruitment in the non-dependent lung due to lower baseline capillary pressures and therefore lower recruitment at baseline.

In comparison to clinical data acquired in multiple patients with no prior cardiopulmonary disease and with variable levels of tissue obstruction,[70,78] the model showed far less increase in PA pressure with degree of tissue obstruction. All of the model results for mechanical obstruction in the absence of vasoconstriction predicted PA pressure at levels below the clinically defined hypertensive level (mean PA pressure >25 mmHg); this level of PA pressure was not reached until >65% of the vascular bed was occluded. This contrasts with the clinical data, in which PA pressure in most subjects with >30% of tissue occluded had reached this threshold.[70] The discrepancy between the model predictions and clinical reality cannot be explained by a simple mis-parameterization of the model: the model geometry is well founded in human pulmonary vascular morphometry,[13] is consistent with previous morphometric studies,[4,79] and was tailored to each patient for this study; the functional model is based largely on physical conservation laws, and where this isn’t the case the parameters in the functional equations come from experimental measurements. The modeling study therefore provided evidence that mechanical obstruction alone is insufficient to elevate PA pressure to hypertensive levels in the human lung, and this is because of the large reserve of unrecruited capillaries that open in the unobstructed tissue. Elevating PA pressure implies either increased cardiac output or increased PVR. Cardiac output is most likely to decrease in PE,[70] which leaves increase in PVR as the only possibility for increasing PA pressure. There are two means by which PVR could be elevated in the model: through a decrease in the radius of the vessels, which under acute conditions is most likely due to vasoconstriction; and by obstruction with smaller emboli that are usually unresolved on the imaging.

As proxies for vasoconstriction and/or increased vascular tone, further simulations were performed with vascular constriction enforced by setting all vessel radii to 80% of their baseline value, and a reduction in vessel elasticity to 80% of baseline. Neither mechanism was sufficient by itself to increase PA pressure to hypertensive levels for any volume of occluded tissue. PA pressure increased twice as much (~14%) as a result of vascular constriction compared to the reduction in vessel elasticity (PA pressure increased by ~7%). This result provides indirect evidence that the release of vasoactive mediators from emboli plays an important role in whole organ response to PE.[66–68]

Small sub-segmental emboli are not able to be assessed clinically (radiological examination of CTPA generally only identifies emboli down to the segmental level) and would be difficult, if not impossible, to assess experimentally. Inclusion of sub-segmental emboli in the full-circuit model (located one vessel downstream of a measured segmental partial occlusion) demonstrated that increases in PVR could be significant if sub-segmental vessels are occluded in addition to partial occlusion of larger vessels (for example due to the break off of part of a large embolus). This provides a possible explanation for heterogeneity in PE outcome, particularly when taken in combination with vasoconstriction. This new prediction of the model requires clinical and experimental validation.

The full-circuit model is a unique tool for this type of clinically relevant study. A model by itself cannot prove a hypothesis, but a model that is biophysically-based can disprove the physical possibility of certain hypotheses. In this case the model clearly demonstrated that it is physically impossible for a previously normal pulmonary circulation to develop high enough PVR to reach hypertensive levels of PA pressure via purely mechanical obstruction of <50% of the vascular bed. This is an example of the insight that a model can provide when it does not fit the experimental data.

Micro-emboli

Emboli can also develop within the micro-vasculature of the pulmonary circulation. Although this would rarely be diagnosed as a clinical condition, some cases of arterial PE show signs of small micro-emboli breaking off from larger clots, perhaps exacerbating symptoms. There is also the rare occurrence of cor pulmonale as a result of tumor micro-emboli, in which clusters of tumor cells occlude small pulmonary arterioles. Cor pulmonale often develops more quickly with tumor emboli than blood clot emboli due to differences in interactions between the arterioles and the embolus.[80] Experimentally, the occlusion of multiple arterioles at the intra-acinar level has been shown to have a significant impact on pulmonary function, and–for an equivalent proportion of vascular bed occlusion–this impact is often greater than for emboli in the larger extra-acinar vessels.[65,81] In contrast to emboli in the larger blood vessels, for small induced intra-acinar emboli (<170 μm in diameter) PH has been observed when less than 50% of the vascular bed is occluded.[81] Pulmonary micro-embolism using inert emboli is therefore a useful method for inducing hypertension and pulmonary edema in animal experiments.[65,82] To properly interpret results from these animal models, an understanding of the implications of micro-emboli is important. It has been suggested that the location of obstruction within the acinus (proximal or distal) may have a role in determining differences in response to intra- and extra-acinar emboli.[30] In addition, constriction or loss of elasticity in intra-acinar vessels may increase the severity of the response to embolization.[80,81] Finally, edema as a result of increased micro-vascular blood pressure, or mechanical injury to the vascular bed, may increase the severity of symptoms following embolus occlusion.[81]

Clark et al.[32] used the ladder model described in a previous section[29] distributed over an asymmetric intra-acinar branching geometry,[83] as illustrated in Fig. 3b, to investigate blood flow redistribution and changes in vascular resistance following arterial occlusion at the microcirculatory level. An important application of this type of model is the ability to differentiate between the behaviors of different types of embolus. For example, PE can be induced in experimental animals using materials such as balloons,[84] glass beads,[82] or blood clots.[85] An embolus may occur in vivo due to a blood clot or a tumor. Each provides a mechanical obstruction to perfusion. However, although different types of embolus may ultimately have the same effect on pulmonary function, their interactions with surrounding blood vessels differ and these differences must be well understood to properly interpret experimental and clinical data.[81]

The modeling study showed that with mechanical obstruction alone (without vasoconstriction), the size and location of emboli have an impact on the increase in PVR post-embolus occlusion, with larger or more proximally located emboli resulting in PH with a relatively small capillary bed occlusion. However, consistent with the studies of embolic obstruction in the larger arteries, the micro-circulatory model showed a rise in PVR, but not sufficient to increase PA pressure to PH levels until >50% of the capillary bed was occluded. This again was suggestive of other factors, such as vessel constriction or loss of elasticity, also contributing to observed hypertension.[65,81] Further simulations showed that proximally occluded vessels along with localized constriction has the potential to induce hypertension with <50% capillary occlusion. The model analysis further showed that it is possible for capillary blood pressures to be elevated to levels that may cause capillary damage at approximately the onset of PH, that in some cases red blood cell transit time across the capillary bed can be reduced to below that required for oxygen saturation in the non-occluded region, and that both a localized arteriole constriction or loss of compliance can have a significant effect on PVR post occlusion.

A structure-based model was necessary for study of micro-embolism in that the structure of acinar blood vessels leads to both heterogeneity and stratification in perfusion within the acinus, and this must be captured sufficiently for plausible predictions of intra-acinar occlusions with micro-emboli. The series and parallel arrangement of blood vessels within the acinus model, which is only captured in models of this type, allows for a redistribution of perfusion within the acinus itself following the introduction of micro-emboli. Because the model-like the real pulmonary acinus-has capacity for perfusion redistribution and recruitment of capillary blood volume, it allows for substantial portions of the acinus to be occluded before a significant rise in resistance occurs. If arterioles of a similar size to the embolus are occluded then the smaller the embolus, the less effect it has on PVR. But if the serial-parallel structure of the acinus is disrupted by occlusion of the proximal capillary beds, the effect of the loss of capillary surface area has a far greater effect on PVR. Proximally located smaller emboli have a more significant effect on PVR for the same percentage occlusion as larger emboli in the model due to a substantial shift in flow to the distal capillary beds which are at the end of the highest resistance vessel pathways.

The acinar micro-circulatory model that was used in this study is a more elaborate version of the original ladder model of Clark et al.[29] The difference between the models lies in their geometry. The ladder model is a sufficient representation of intra-acinar perfusion for coupling to structure-based models of the pulmonary circulation, where each of the ~32,000 acini and their circulation is modeled explicitly. The more geometrically accurate model was necessary for the study of intra-acinar flow redistribution. Accurate acinar geometry has also been shown necessary for modeling based studies of inert gas washing and mixing,[9] and the intra-acinar distribution of respiratory gas exchange.[86]

FUTURE DIRECTIONS

Mathematical models of the pulmonary circulation have evolved from convenient tools with which to explain some experimental observations, to a new class of structure-based models that are giving a greater depth of understanding of blood flow in the lung and how it relates to the other physical processes with which it interacts. One obvious limitation of the current structure-based models described here is that they only include the passive features of the pulmonary circulation: the vascular geometries, blood flow, pressure, and tissue mechanics. That is, they do not include any of the vasoactive components that are likely to be important under non-baseline conditions. In terms of mathematics the models described above for PE are relatively simple–with complexity being introduced in the geometry. They suggest some, but not all, aspects of the pathophysiology. Looking forward, and in the context of the IUPS Physiome and VPH projects, a link between micro-scale behaviors and whole lung function is lacking. For example, a large part of the response to PE is likely to happen via cellular level signaling, which results in active alterations in vessel dimensions and so to PVR and perfusion distributions.

The pulmonary vasculature is a dynamic system that responds rapidly to vasoactive mediators. Blood vessel dilation occurs in response to shear stress mediating production of NO by the endothelium, and its signaling for smooth muscle relaxation. Conversely the vessels are stimulated to constrict by hypoxia and circulating vasoconstrictive mediators. The smooth muscle in the vessel walls appears to operate under a fine balance of vasoconstrictive and vasodilatative stimuli. The next generation of computational models will play a role in understanding how these stimuli translate into smooth muscle contraction, and whether there is positive feedback that leads to excessive increase in PVR, or negative feedback that ensures system stability. An example of how such a model would be composed has recently been presented by Politi et al.[87] for the airway tree. In this multi-scale model the balance of forces acting on a stimulated airway is considered over spatial scales from the intra-cellular calcium dynamics, to development of force via a cross-bridge model, to a cross-section of a constricting airway that is embedded in a dynamically expanding and recoiling parenchyma. This study demonstrates the viability of creating a model that accounts for force development over such a wide range of scales. The additional complexity in the pulmonary vasculature is the sheer range of mediators to which the smooth muscle responds. And whereas smooth muscle activation in the airway tree is undesirable, in the pulmonary vasculature it seems to be a prevalent feature that is continually acting to–presumably–optimize the delivery of blood to the gas exchange tissue.

A multi-scale modeling approach which links cellular mechanisms to arterial dilation and contraction and in turn to pulmonary function may be the only way to link small scale interactions with emergence of whole organ function.