Abstract
Much diversity in animal morphology results from variation in the relative size of morphological traits. The scaling relationships, or allometries, that describe relative trait size can vary greatly in both intercept and slope among species or other animal groups. Yet within such groups, individuals typically exhibit low variation in relative trait size. This pattern of high intra- and low intergroup variation may result from natural selection for particular allometries, from developmental constraints restricting differential growth among traits, or both. Here we explore the relative roles of short-term developmental constraints and natural selection in the evolution of the intercept of the allometry between the forewing and hindwing of a butterfly. First, despite a strong genetic correlation between these two traits, we show that artificial selection perpendicular to the forewing–hindwing scaling relationship results in rapid evolution of the allometry intercept. This demonstrates an absence of developmental constraints limiting intercept evolution for this scaling relationship. Mating experiments in a natural environment revealed strong stabilizing selection favoring males with the wild-type allometry intercept over those with derived intercepts. Our results demonstrate that evolution of this component of the forewing–hindwing allometry is not limited by developmental constraints in the short term and that natural selection on allometry intercepts can be powerful.
Keywords: Allometry, complex phenotype, developmental constraint, genetic correlation, natural selection
Understanding the relative importance of internal developmental constraints and external natural selection in the evolution of complex phenotypes remains a central goal for evolutionary biology (Meagher and Futuyma 2001; Klingenberg 2005; Mezey and Houle 2005; Brakefield 2007). The scaling relationships, or allometries, among morphological traits represent a class of complex phenotype that is of interest in evolutionary, ecological, and developmental contexts. Allometries are described formally by two parameters: an intercept and a scaling exponent. Morphological variation among biological groups is reflected in variation in these parameters; differences among groups in allometry intercepts reflect variation in the average relative size of trait pairs among groups whereas differences in scaling exponents reflect among-group variation in the shape or slope of the scaling relationships. Allometries can be divided among three categories based on the kind of morphological variation they describe (Cock 1966). Ontogenetic allometries refer to the relative size of two traits during the growth of an individual. The growth trajectories described by ontogenetic allometries result in a static allometry, which is the scaling relationship among individuals within species, populations, sex, or other groups. Changes in ontogenetic allometries can affect the slope or intercept of static allometries to yield derived scaling relationships, called evolutionary allometries (see Klingenberg and Zimmermann 1992; Shingleton et al. 2007 for discussions). In sum, allometries describe patterns of morphological variation within and among animal groups, and the growth processes that give rise to those patterns. Hence, elucidating the roles of internal and external forces in the evolution of allometry intercepts or slopes will enhance our understanding of how complex morphologies are generated and how they diversify.
Insects derive much of their morphological diversity through exaggeration or reduction in the relative size of body segments, limbs, wings, and other appendages (Emlen and Nijhout 2000). The high diversity of evolutionary allometries exhibited by insects and other animals contrasts markedly with the low variation within animal groups in relative trait size, where individuals typically adhere tightly to group-specific static allometries (e.g., see Gould 1966; Burkhardt and de la Motte 1987; Stern and Emlen 1999; Emlen and Nijhout 2000). Despite a long history of interest in these intra- and intergroup patterns (e.g., Thompson 1917; Huxley 1932; Gould 1966), little has been learned about the pressures shaping allometry evolution (Maynard Smith et al. 1985; Stern and Emlen 1999; Emlen and Nijhout 2000). External natural selection on the relative size of functionally related traits is predicted to favor the evolution of genetic mechanisms that canalize phenotype expression against environmentally and genetically induced variation (Wagner 1996; Wagner et al. 1997). Such mechanisms will maintain low intragroup variation in relative trait size and may generate strong genetic correlations that are predicted to constrain the independent evolution of trait values (Cheverud 1984). Such constraints, however, must be overcome if scaling relationships are to diversify through natural selection.
The degree to which intra- and intergroup patterns in allometries reflect natural selection for particular size relationships among traits or developmental constraints (sensu Maynard Smith et al. 1985) limiting differential trait growth is largely unknown. In part, this is because the roles of internal and external constraints in allometry evolution are difficult to assess experimentally for two reasons. First, identifying developmental constraint is challenging because it requires the demonstration that intrinsic factors make a given phenotype difficult, if not impossible, to evolve. Developmental constraints can result from the lack of genetic variation for particular trait values or from the architecture of developmental or genetic hierarchies regulating and integrating trait expression (Maynard Smith et al. 1985; Hansen and Houle 2004; Klingenberg 2005). For example, pleiotropy can produce genetic covariation among traits that limits or impedes the multivariate response to selection for particular combinations of trait values, constraining the evolution of some complex phenotypes in both the short and the long term (Arnold 1992). Regardless of the cause of a putative developmental constraint on phenotype evolution, unequivocal demonstration of a such a negative is difficult. The second challenge for assessing constraints stems from the tendency of individuals in natural populations to adhere strongly to the group-specific static allometry (e.g., Eberhard and Gutierrez 1991; Baker and Wilkinson 2001; reviewed in Emlen and Nijhout 2000). Such low phenotypic variation prevents quantification of the shape and strength of selection in much of the surrounding phenotypic space (Endler 1986).
A two-step solution to these problems involves first testing for clearly defined developmental constraints by attempting to create novel scaling relationships through physiological manipulations or artificial selection (e.g., Weber 1990; Sinervo and Licht 1991; Beldade et al. 2002); production of a novel phenotype indicates an absence of constraint. Second, the artificially produced phenotypic variation is then used to estimate more completely the form of natural selection acting on the allometry (e.g., Sinervo et al. 1992; Wilkinson and Reillo 1994; Kingsolver 1999; approach reviewed in Sinervo and Basolo 1996). We have previously used this stepwise methodology to study the evolution of the intercept of the forewing–bodysize allometry in the model butterfly Bicyclus anynana (Frankino et al. 2005). Here, we apply the program to investigate evolution of the intercept of the scaling relationship between the size of the forewing and hindwing in the same system.
For several reasons, the scaling relationship between Lepidopteran fore- and hindwings represents a model well suited to study the evolution of allometries. First, the system is generalizable because wings develop from imaginal discs, discrete “modules” common to the development of most appendages in holometabolous insects. Second, internal developmental constraints are likely to affect evolution of this scaling relationship because fore- and hindwing imaginal discs are developmental homologues (Carroll et al. 2001) that have their growth regulated by the same body-wide signals (Nijhout 1994), exhibit congruent patterns of developmental gene expression (Carroll et al. 1994; Keys 1999), and show growth responses to experimental removal of adjacent, developing wing discs during larval ontogeny (Nijhout and Emlen 1998). Third, external constraints imposed by natural selection on locomotor performance (Dudley 2000) and mate acquisition (Wickman 1992) may favor particular within-group static allometries, perhaps accounting for the near-isometric relationship exhibited between fore- and hindwings across butterfly species, and the high among-lineage diversity in relative wing size (Strauss 1990, 1992). Hence, the forewing–hindwing allometries of Lepidopterans are ecologically relevant, developmentally generalizable, and likely to be subject to substantial developmental constraint and strong natural selection.
Below we present a series of experiments designed to determine the relative importance of developmental constraint and natural selection in the evolution of the intercept of the forewing–hindwing allometry in the butterfly B. anynana. The rapid evolution of intercepts we observe produced novel morphologies, and indicates at best a limited, indirect role for short-term developmental constraints. In addition, the very strong and consistent pattern of natural selection acting on the allometry we document suggests that natural selection plays a primary role in the evolution of this scaling relationship intercept.
Materials and Methods
GENERAL METHODS
All lineages were established from the same stock population, which was established from ~80 gravid females and has been in culture for ~90 generations (see Brakefield et al. 2001; Beldade et al. 2002). All rearing was at 27°C and 12:12 L:D. Unless noted otherwise, larvae were reared in groups not exceeding 450 larvae/cage and fed maize ad libitum. Adults were maintained on banana. In all experiments, forewing (FW) and hindwing (HW) areas were estimated by calculating the area within a polygon defined by four landmarks (Fig. 1A,B), measured by using a camera lucida attached to a digitizing tablet. Repeatabilities for both wing areas were estimated by measuring 45 females three times and dividing the among-individual mean squares for wing area by the within-individual mean squares for wing area (Lessels and Boag 1987; Becker 1992). Artificial selection was performed on females only. Consistently high egg hatching success in the stock population, the artificially selected lineages, and the control lineages (>90%), combined with high effective population size (Brakefield et al. 2001), indicate an absence of inbreeding in our laboratory B. anynana lineages.
Figure 1.
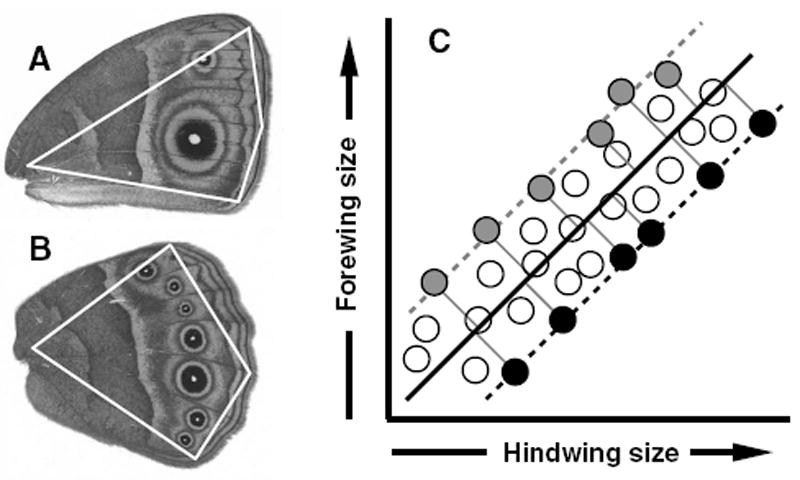
Methodology for estimation of wing areas and artificial selection on allometry intercepts. A and B, the right ventral views of fore- and hindwings of B. anynana, respectively. Wing sizes were estimated by calculating the area within the polygons (white lines), defined by four landmarks (vertices of polygons). (C) Selection for individuals with the most extreme FW/HW phenotypes. The dark solid line represents the static allometry describing the forewing–hindwing scaling relationship for this hypothetical population. Perpendicular deviations from this allometry are shown for the six most extreme observations in each direction as thin solid lines that connect to +FW/−HW phenotypes (gray circles) or −FW/+HW phenotypes (black circles). Static allometries for these subpopulations of individuals that would be selected in each direction are shown as gray or black dashed lines, respectively. Because this methodology selects individuals from across the full range of wing sizes, the expectation is that only the allometry intercept (not the slope) will respond to selection.
TESTS FOR DEVELOPMENTAL CONSTRAINTS
Estimation of phenotypic and genetic correlations between fore- and hindwing areas
We measured the FW and HW of ~700 stock population females to estimate the phenotypic correlation and wild-type allometry between the fore- and hindwing areas. As described below, we estimated the genetic correlation between FW and HW based on the direct and indirect response of lineages subjected to artificial selection for increased or decreased FW or HW areas. These single-trait selection lineages were established from ~3000 stock population eggs, from which FW and HW areas for 750 newly eclosed females were measured and ranked. Thirty females with the most extreme phenotypes were selected to found each of four unreplicated selection lines: large-FW (+FW), small-FW (−FW), large-HW (+HW), and small-HW (−HW). A control lineage was established by selecting 30 females randomly. In each subsequent generation, all females (approximately 150–220 per lineage each generation) were measured and the 30 with the most extreme phenotypes in each lineage were selected in the appropriate direction and crossed with 35–45 males selected haphazardly from the same lineage. In all experiments, realized heritabilities were calculated as twice the slope of the regression of the response to selection over the cumulative selective differential; this is an appropriate estimate as we artificially selected only females (Falconer and Mackay 1997). Genetic correlations (r) between fore- and hindwing areas were estimated for each selected direction by calculating the square root of the products of the ratios of the indirect and direct response of the traits to selection (eq. 19.7 in Falconer and Mackay 1997). A 95% confidence limit (2.5 and 97.5% quantiles) was estimated for each correlation by bootstrap resampling each population from the final generation of the experiment 5000 times in the following manner. First, all artificially selected populations and the control lineage were resampled and mean values for each resultant population calculated. Because of strong, stochastic environmental effects on absolute size each generation, comparing the unadjusted mean phenotypes across generations or experiments can be misleading. We therefore remove these environmental effects by analyzing artificially selected lineage means as deviations from the control lineage means generated by resampling. Our resampling was restricted to the final generation as data for all traits from all lineages were available for that generation only; consequently, our estimate is valid only for this generation and these environmental conditions. We calculated the genetic correlation between FW and HW as the mean of genetic correlations estimated for each artificially selected direction.
Artificial selection on allometry intercept
We performed artificial selection on FW area relative to HW area in an effort to shift the intercept, but not the slope, of the allometry (Fig. 1C). Using our previously established criterion (Frankino et al. 2005), we decided a priori that developmental constraints would be indicated by a failure of an artificially selected lineage to evolve a mean phenotype distinguishable from wild-type by the end of our experiment (12 generations of artificial selection).
Following our established protocol for artificially selecting on allometry intercepts (Frankino et al. 2005), we established two replicate lineages selected for large FW relative to HW (+FW/−HW; lineages A and B), and two for small FW relative to HW (−FW/+HW; lineages C and D). To identify females for selection, we used orthogonal regression, which fits a line by minimizing the deviations in both axes. This line represents the static allometry for females from a given replicate in that generation. We then quantified the deviation of all female’s relative wing sizes from the static allometry of the population by calculating the residual, perpendicular distance from the allometry to each datapoint in the replicate (Fig. 1C). Extreme residual values correspond to individuals with forewing–hindwing size combinations that are most divergent from the average in the population, and hence we used such extreme residuals to identify females for selection. In this manner, we identified and selected females to establish and perpetuate the +FW/−HW and −FW/+HW lineages. Because our approach selects females equally from across the full range of body sizes, we expected allometry intercept, but not the slope, to respond to selection (see similar approach and argument in Weber 1990). We also established an unreplicated control lineage for which we measured both traits, but from which females were selected randomly. For mating, all selected females were placed in a cage with 30–40 males collected haphazardly from the same replicate.
Under our selection design, the allometry intercept was free to evolve through changes in the value of the forewing, the hindwing, or both. We investigated the morphological basis of allometry evolution by examining the indirect responses of the individual traits to direct selection on their relative size. To quantify the indirect response of the individual fore- and hindwing sizes to direct selection on the intercept of their allometry, univariate means for each wing at each generation were plotted against the cumulative indirect selection differential each wing experienced. In our case, the indirect selection differential experienced by a wing is calculated as the difference between the bivariate mean of a lineage and the bivariate mean of selected females from that lineage in a given generation. This contrasts with the direct selection differential, which involves only the means of the perpendicular distance values and measures the difference between the intercept of the static allometry of a replicate lineage and the intercept of the static allometry of the females selected from that lineage in a given generation. Variation among replicates in the morphological basis of allometry evolution would indicate a lack of constraint whereas consistent pattern in the morphological basis of response would indicate developmental bias or constraint in how the allometry intercept can evolve in response to our selection regime.
TESTS FOR ABSENCE OF GENETIC VARIATION SELECTION −FW/+
We founded four new artificially selected lineages, two from each of the −FW/+HW lineages (lineages C and D), to determine if the cessation of response to direct selection in lineages C and D at around generation six (see Results) resulted from a lack of genetic variation in FW or HW. These new lineages were subject to selection to change absolute FW or HW areas in the same direction in which they had been previously selected jointly (i.e., −FW or +HW). To establish the new lines, 30 females from both lineages C and D that had the smallest FW and 30 more with the largest HW were selected. These new lineages were then selected for −FW or +HW as single-trait selection lineages (see above). We were also able to use these new lineages to determine if the genetic correlation between the wings had been altered during selection on the allometry intercept. We did this by estimating the genetic correlation from these lineages as outlined above. Again, because we resample data only from the final generation of this single-trait selection experiment, our estimates of the genetic correlation between wings is only valid for the conditions experienced by butterflies in that generation.
TEST FOR EXTERNAL CONSTRAINTS
Natural selection experiment
To estimate the strength and form of natural selection on the intercept of the FW/HW allometry, we divided males into three phenotype classes and compared their mating success and survival in a seminatural environment. We created two similarly outbred populations from which males could be drawn for the experiment by performing reciprocal crosses (five males and five females per cross) between each of the replicate lineages selected for novel allometry intercepts. FW/HW phenotypes of all hybrid males were quantified using the same methodology described above for females in the allometry-selected lineages (Fig. 1), and the 30 males with the most extreme FW/HW phenotypes were placed into one of two “treatment male” phenotype categories (+FW/−HW or −FW/+HW). Control-lineage males from the artificial selection experiments were measured and used to define the wild-type static allometry for male B. anynana. Fifteen males from each hybrid lineage possessing FW/HW phenotypes closest to that of this wild-type allometry were placed into a single “control male” phenotype category for the fitness tests. In this manner, we generated control-group males with genotypes drawn equally from the same genetic backgrounds as that of the treatment males (Frankino et al. 2005), thereby minimizing any effects of female preference for a particular genetic background (e.g., Joron and Brakefield 2003).
Phenotype classes were haphazardly assigned one of three fluorescent powder colors (blue, orange, or yellow), which was then applied to the genitalia of each male in that phenotype class. This powder is transferred during copulation and thus can be used to identify the phenotype class of male with which a female has mated (Joron and Brakefield 2003; Frankino et al. 2005). After marking, 90 males were released at 0700 h (Day 0) into a spacious, naturally planted tropical greenhouse (~15-m2 flight area with a high, open space over a central pond) containing six regularly spaced feeding stations of water and banana. Butterflies interact in this patchy, heterogeneous environment as if they are in the wild (Joron and Brakefield 2003; Frankino et al. 2005). In particular, males engaged each other in prolonged aerial chases, sometimes involving up to six males in a single group (W. A. Frankino, pers. obs.). Ninety unmated females from the control lineage were released into the greenhouse at 0700 h on Day 1, and an additional 30 females were released at 0700 h on Day 2. As females are unlikely to mate twice over the time period of our study (Joron and Brakefield 2003; and see Results), release of females in two waves achieved a realistic butterfly density (Windig et al. 1994) but in a manner that promoted competition among males for access to females. All butterflies were recaptured on the afternoon of Day 3 and the morning of Day 4. Butterflies were frozen at capture and inspected under a black light to identify the phenotype class of recaptured males and the phenotype class with which individual females had mated (Joron and Brakefield 2003; Frankino et al. 2005). Survival (recapture frequency) and fitness (proportions of mating) were compared among phenotype classes by G-test with the expectation of no differences among groups, however, estimates of male phenotype fitness include correction for male phenotype survival rate. The experiment was replicated once and dust colors assignment was made such that the same male phenotype category differed in color between replicates.
Results
TESTS FOR DEVELOPMENTAL CONSTRAINTS
As described above, we remove environmental effects on absolute size in each generation by analyzing and presenting artificially selected lineage means as deviations from control lineage means where appropriate. We also standardize values using the phenotypic variation in the starting population. This allows meaningful comparison of trait values across generations or experiments. All calculations and analyses on wing areas were performed on pixel values and converted to square millimeters only for presentation. Owing to rounding errors during conversion, in some cases slight discrepancies result in the precise values of calculations based on pixel values or on standardized square millimeters.
Estimation of phenotypic and genetic correlations between fore- and hindwing areas
Our estimates of wing area exhibited acceptable repeatabilities (FW = 0.91, HW = 0.87). FW and HW areas adhere tightly to a nearly isometric relationship and exhibit a strong, positive, phenotypic correlation (Fig. 2A; Pearson’s r = 0.95; slope of orthogonal regression = 0.94, upper and lower bounds of 95% confidence interval 0.92, 0.96; N = 698 stock population females). Mean wing areas were very similar (mean area in square mm, SD, SE for each is in parentheses; FW 112.0 (0.5), 13.0 (0.4); HW 116.9 (0.5), 13.8 (0.4) and had low variation in the perpendicular deviations from the static allometry (SD around the allometry was 3.0 mm2). Over the course of the experiment, both wings responded similarly to selection in each direction (Fig. 2B; Table 1). To calculate the realized heritabilities for absolute wing size and estimate the genetic correlation between fore- and hindwing size, we standardized the data by dividing the standard deviation of the starting stock population and by expressing all transformed means as deviations from standardized control lineage means. Realized heritabilities were very similar for each wing in a given direction (h2: +FW = 0.38, +HW = 0.36, −FW = 0.16, −HW = 0.16; Fig. 2B). The confidence intervals around these realized heritabilities were reasonably small, except for the +FW lineage that was affected strongly by extreme FW values in generation four (Fig. 2B). Genetic correlations (r) between wings selected for increased area was estimated as 1.05 (upper and lower bounds of estimate, 95% confidence limits: 1.00, 1.10), and was 0.95 (0.77, 1.09) for decreased wing area. The mean genetic correlation between FW and HW was estimated as 1.0.
Figure 2.
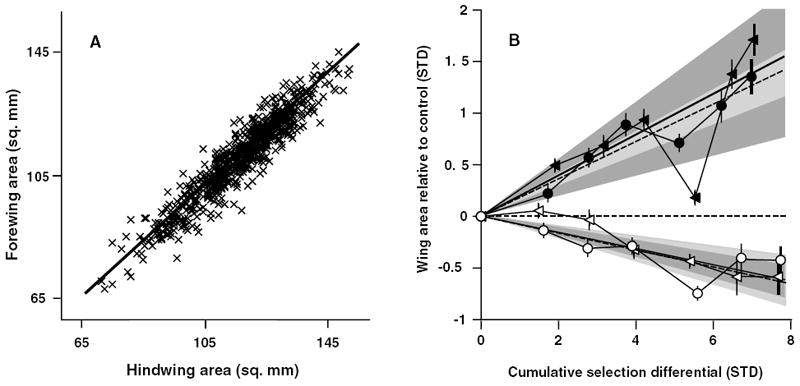
Forewing–hindwing static allometry and the evolution of absolute wing areas. (A) The static allometries for FW and HW for several hundred stock females. (B) The response to selection of females selected for increased (filled) or decreased (open) FW (triangles) and HW (circles) areas. Lineage means ± 2 SE are shown relative to the control-lineage mean (horizontal dashed line). Realized heritabilities for FW and HW are shown as solid and dashed lines, respectively. Dark gray regions represent 95% confidence intervals around the realized FW heritabilities and lighter gray regions show confidence intervals around HW heritabilities; these are for the slope of the regression only as the intercept was forced through the origin. Cumulative selection differentials are shown as absolute values to facilitate comparison between selected directions.
Table 1.
Mean fore- and hindwing sizes following five generations of artificial selection on absolute wing area. Lineage means are presented in categories based on selection for increased or decreased wing size and whether the wing was the direct target of artificial selection or the trait exhibiting a correlated response. Mean wing areas are given in square millimeters and are followed by SD. Standard errors for the means and SD are given in parentheses.
| Increased wing size
|
Decreased wing size
|
|||
|---|---|---|---|---|
| Direct target | Correlated trait | Direct target | Correlated trait | |
| Forewing | ||||
|
| ||||
| Mean | 132.7 (1.9) | 135.0 (2.3) | 102.9 (1.7) | 104.9 (1.8) |
|
| ||||
| SD | 11.1 (1.3) | 13.5 (1.6) | 11.9 (1.2) | 13.0 (1.3) |
|
| ||||
| Hindwing | ||||
|
| ||||
| Mean | 131.5 (2.0) | 131.4 (2.3) | 106.7 (1.9) | 105.1 (1.7) |
|
| ||||
| SD | 13.7 (1.5) | 15.8 (1.7) | 12.7 (1.3) | 11.6 (1.2) |
Artificial selection on scaling relationships and investigations of genetic variation
After 12 generations of selection, the intercept of the forewing–hindwing allometry had diverged ~ 2 SD in each direction from that of the unselected control lineage, producing distinct phenotypes (Fig. 3A,B; discriminant function analysis correctly classified 94.8% of females from generation 13; N = 849, replicates pooled). The bivariate means (through which the static allometry of the population passes) and (mm2) for each lineage at the end of the experiment are given in Table 2. Standard deviations of the perpendicular distances (mm2) of all females in each lineage was as follows; +FW/−HW, lineage A 3.6, lineage B 3.1; −FW/+HW, lineage C 2.5, lineage D 2.8; control lineage 3.6. The +FW/−HW lineages responded steadily to selection whereas both −FW/+HW replicates ceased to evolve at about generation six (Fig 3B; lineages C and D), producing asymmetry in how the allometry intercepts diverged. Before this plateau in response, the allometry intercepts (or the bivariate mean) had comparable average realized heritabilities between selected directions (−FW/+HW h2 = 0.34 and +FW/−HW h2 = 0.22).
Figure 3.
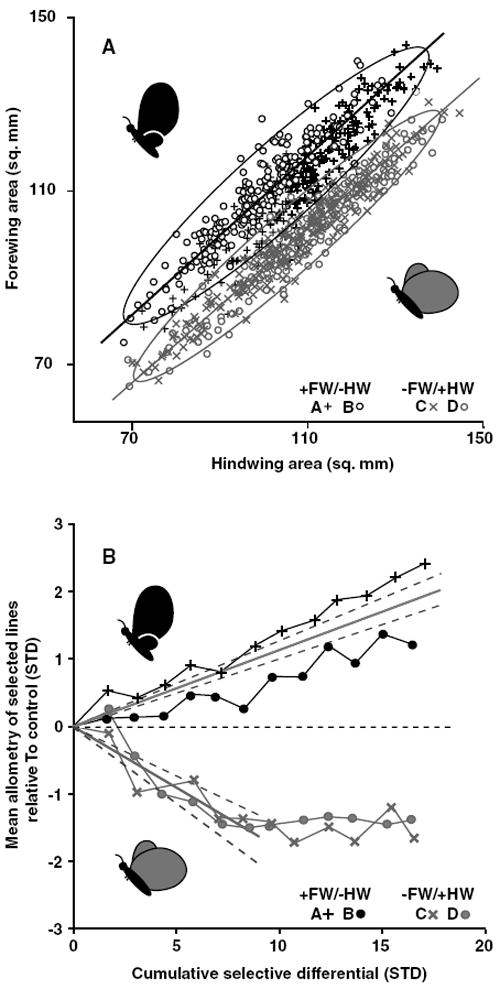
Forewing–hindwing allometries after 12 generations of artificial selection and evolution of allometry intercepts. (A) The phenotype distributions of lineages selected for changes in forewing–hindwing scaling. Each selected population is shown as a different symbol, replicates of a selection direction share colors. The static allometry of each selected direction (replicates combined) is shown as the orthogonal regression through the points and are enclosed by 95% confidence ellipses. (B) Realized heritabilities of the allometry intercepts. Bivariate mean phenotype (through which the allometry of each replicate passes) is shown relative to control value (horizontal dashed line) as a function of the absolute value of the cumulative selection differential. Mean heritabilities (solid gray lines) are fitted to each selected direction and are bordered by 95% confidence intervals (gray dashed lines). Note that heritability of the allometry is calculated only through generation six for the −FW/+HW direction because of a cessation in the response to selection around that point. Target phenotypes are represented by cartoons in both panels.
Table 2.
Mean forewing and hindwing areas for generation 13 females from the control lineage and lineages selected for increased (+FW/−HW, replicates A and B) or decreased (−FW/+HW, replicates C and D) allometry intercept. Means are in square millimeters and followed by SD. Standard errors for the means and SD are given in parentheses.
| +FW/−HW
|
−FW/+HW
|
||||
|---|---|---|---|---|---|
| Lineage | Control | A | B | C | D |
| Forewing | |||||
|
| |||||
| Mean | 107.8 (0.1) | 121.2 (1.2) | 116.9 (1.1) | 107.8 (1.0) | 108.2 (1.1) |
|
| |||||
| SD | 1.2 (0.1) | 13.1 (0.8) | 12.2 (0.8) | 13.3 (0.7) | 13.5 (0.8) |
|
| |||||
| Hindwing | |||||
|
| |||||
| Mean | 109.7 (0.1) | 117.9 (1.1) | 107.2 (1.1) | 116.9 (1.2) | 118.6 (1.2) |
|
| |||||
| SD | 1.3 (0.1) | 12.0 (0.8) | 12.1 (0.8) | 15.2 (0.8) | 15.0 (0.9) |
We tested the hypothesis that the plateau in the response to selection in the −FW/+HW lineages (Fig. 3B) resulted from an absence of appropriate genetic variation by using females from lineages C and D to establish four new single-trait selection lineages at generation eight. In this experiment, FW size decreased whereas HW failed to respond (Fig. 4), providing mixed support for the hypothesis (but see Discussion). Using the same procedure outlined above, we estimated the genetic correlation between FW and HW using the direct and indirect response to selection in these newly founded lineages. However, an acute larval food shortage in the final generation (five) of the experiment produced atypical size differences and eclosion asynchrony between the selected lineages and the control lineage. Consequently, the control lineage was uncharacteristically small for that generation and was therefore not useful for correction of environmental effects on body size. Hence, the inclusion of the control lineage means as a correction for stochastic environmental effects on body size is biologically misleading in this experiment. We therefore estimated the genetic correlation without performing standardization using the control lineage as described previously. Instead, we estimated the genetic correlation using only the unadjusted bivariate means, which are technically all that are required to calculate r (Falconer and Mackay 1996). The genetic correlation between wings remained strong in the single-trait selection lineages (−FW, +HW) derived from both lineages C (r = 1.0; upper and lower bounds of estimate, 95% confidence limits 0.99 and 1.0) and D (r = 1.0; upper and lower bounds of estimate, 95% confidence limits 0.98 and 1.0) lines. Means from generation five for all single-trait selected lineages are provided in Table 3. In sum, the very similar estimates of the genetic correlation across our selection experiments suggest that the genetic correlation between the size of the fore- and hind wings is stable across the range of environments present in our study.
Figure 4.
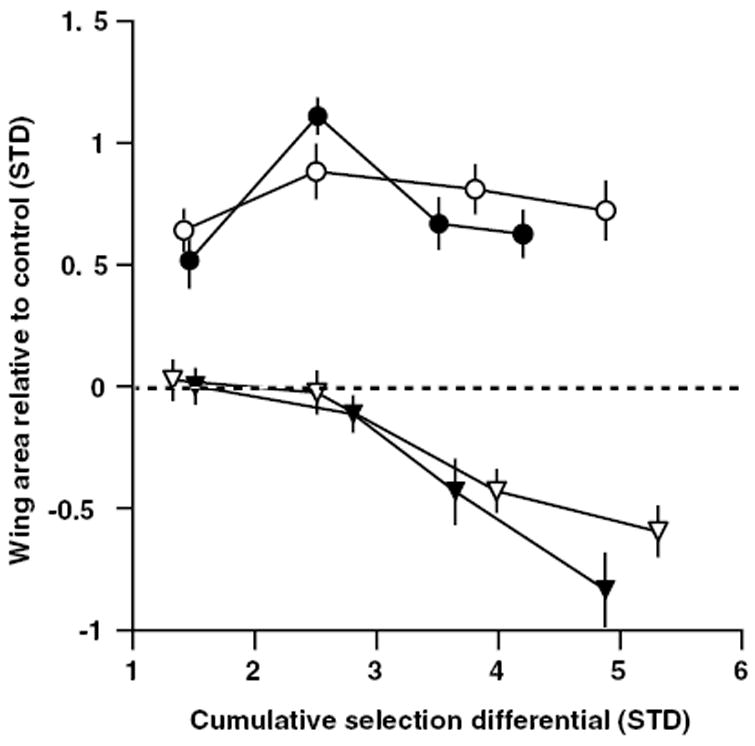
Response to selection on individual wing areas in lineages established from the −FW/+HW allometry selected lineages. Females from lineages C (filled symbols) and D (open symbols) were used to establish lineages selected for increased HW (circles) or decreased FW (triangles) area. Points are lineage means relative to control values (horizontal dashed line) and are shown ± 1 SE Cumulative selection differentials are shown as absolute values to facilitate comparison between selected directions. Means from the final generation (five) are not shown owing to problems with the control lineage for that generation (see text), but are provided in Table 3.
Table 3.
Mean forewing and hindwing areas for females from the single-trait selection lineages derived from the −FW/+HW lineages (replicates C and D). Females in these new lineages were selected for decreased forewing (−FW) or increased hindwing (+HW) for four generations. Presented means are for generation five, are given in square millimeters and followed by SD. Standard errors for the means and SD are given in parentheses.
| Lineages derived from C
|
Lineages derived from D
|
|||
|---|---|---|---|---|
| −FW | +HW | −FW | +HW | |
| Forewing | ||||
|
| ||||
| Mean | 101.2 (0.1) | 109.7 (0.1) | 104.3 (0.1) | 111.0 (0.1) |
|
| ||||
| SD | 0.8 (0.1) | 1.0 (0.1) | 0.8 (0.1) | 1.1 (0.1) |
|
| ||||
| Hindwing | ||||
|
| ||||
| Mean | 110.3 (0.1) | 120.8 (0.1) | 113.4 (0.1) | 122.1 (0.1) |
|
| ||||
| SD | 0.8 (0.1) | 1.1 (0.1) | 0.9 (0.1) | 1.2 (0.1) |
Indirect response to selection
Fore- and hindwings showed variability in how they responded indirectly to direct selection on the intercept of their scaling relationship (Fig. 5). In the +FW/−HW replicates, both FW and HW were subject to similar amounts of indirect selection pressure, and the allometry intercepts evolved via changes in both traits to different degrees. By contrast, FW was subject to lower indirect selection pressure in the −FW/+HW lineages, and evolution of the allometry intercept in these replicates was due entirely to changes in HW.
Figure 5.
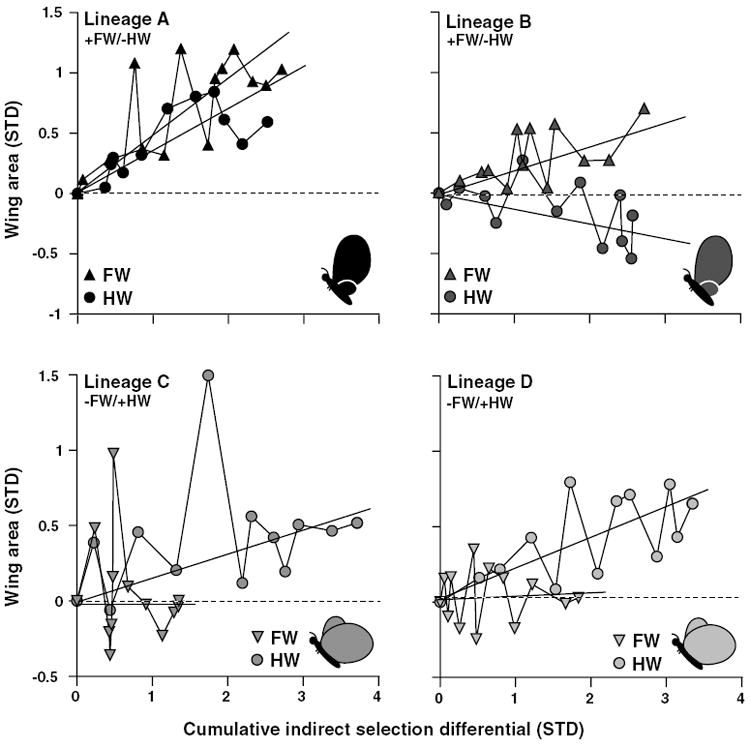
Indirect response to selection for each replicate of the allometry-intercept selected lineages. Mean forewing (FW) and hindwing (HW) areas relative to control values (dashed line) as a function of the absolute value of the cumulative indirect selection on each trait. Mean indirect response of each trait is shown by individual regressions for that trait over the absolute value of the cumulative indirect selection differential. Cartoons represent the selected target phenotypes.
TEST FOR EXTERNAL CONSTRAINTS
Natural selection experiment
The intercept of the forewing–hindwing allometry control class males fell along the same allometry as control-lineage males and differed in intercept from the allometry extreme phenotype classes by ~ 3 SD in each direction (Fig. 6A). Ninety (75%) and 101 (84%) females were recaptured in Trials 1 and 2 respectively, 81% of which had mated in each trial. Recapture rates differed among male phenotype classes in Trial 1 (G = 7.604, P = 0.022) but not in Trial 2 (G = 3.243, P = 0.198). In both trials, the mating success of wild-type phenotype males was three times higher than that of either phenotype class with divergent wing allometry (Fig. 6B); differences in mating success remained after survival of males in each phenotype class was taken into account (Trial 1, G = 29.6, P < 0.001; Trial 2, G = 17.83, P < 0.001). These results demonstrate strong stabilizing selection favoring the natural allometry between fore- and hindwings of B. anynana.
Figure 6.

Distributions and relative mating success of three male phenotype classes. (A) The distributions of individual males with +FW/−HW, wild-type, and −FW/+HW phenotypes included in the experiment. Solid circles represent novel phenotype classes and open circles indicate wild-type controls. The regression line shows the static allometry for males from the control lineage, which represents the wild-type allometry for that generation and was used to identify hybrid males for inclusion in the control group (see Methods). (B) The mating success of each male phenotype class. Columns indicate percentage of recaptured females that mated with males in each class and are shown with 95% confidence intervals based on a bimodal distribution. Numbers in the columns indicate the number of males recaptured in each phenotype class. Similar shading indicates data from replicate trials and are shared between panels. Cartoons represents male phenotype in each class.
Discussion
Determining the relative roles of internal and external constraints in the evolution of complex phenotypes is a critical, albeit challenging, goal for evolutionary biology (Mezey and Houle 2005). We used artificial selection to test for the presence of developmental constraints limiting the evolution of the forewing–hindwing allometry intercept in a butterfly. We then used the resultant phenotypic variation to estimate the form and strength of natural selection on this aspect of the allometry. Below we discuss our results from these experiments and then use them and the results of other investigators to infer the relative importance of developmental constraints and natural selection in the evolution of the complex phenotypes represented by scaling relationships among morphological traits in insects.
DEVELOPMENTAL CONSTRAINTS ON FOREWING–HINDWING EVOLUTION
Bicyclus anynana FW and HW areas exhibit tight adherence to a nearly isometric relationship within and beyond the natural range of body size (Fig. 2A; Frankino et al. 2005). This pattern results from a stable genetic correlation between wings that cannot be distinguished statistically from unity in our experiments, and the narrow confidence intervals around our estimates suggest that the correlation is indeed very high if not precisely 1.0. Such a strong genetic correlation is predicted to constrain the independent evolution of traits (Lande 1979; Falconer and Mackay 1997), inhibiting phenotype evolution in directions other than that of maximum genetic covariance (Schluter 1996). It is therefore surprising that in only 12 generations of artificial selection, the allometry evolved along an axis perpendicular to that of the maximum genetic covariance, changing in intercept to produce lineages with novel, discrete forewing–hindwing phenotypes (Fig. 3A). By our a priori criterion, we can therefore reject the hypothesis that the strong genetic correlation between wings imposes a developmental constraint on the short-term evolution of their allometry intercept. However, developmental processes may have influenced how the allometry intercept evolved by introducing sources of evolutionarily important variation not captured in our estimates of the genetic correlation, or by introducing developmental bias (Maynard Smith et al. 1985; Arthur 2002). Such variation or bias could have caused the eventual cessation in response of the −FW/+HW allometry intercept to direct selection (Fig. 3B) and the interesting patterns of indirect responses to selection (Fig. 5). In the next sections, we discuss the evidence for these developmental effects, and then return to their general importance for the evolution of complex phenotypes such as allometries toward the end of the Discussion.
The +FW/−HW lineages responded steadily to selection on their intercept whereas the intercept in both −FW/+HW replicates ceased to evolve in the longer term, beginning at about generation six (Fig 3B). Asymmetries in the response to selection can have a variety of causes, including differences among lineages in selection differentials, inbreeding depression, variation in the frequency of key alleles, variable indirect responses to selection caused by different correlations with other traits in each selected direction, etc. (e.g., Bohren et al. 1966; Falconer and Mackay 1997). In our case, the similarity in the cessation of response in the two −FW/+HW replicates suggests a common underlying cause. Although we cannot identify the cause(s) of the asymmetry in the response of the +FW/−HW and −FW/+HW directions, based on our data we can reject some possibilities and gather support for others. Mechanical constraints might limit the evolution of the −FW/+HW phenotype (e.g., extreme −FW/+HW allometry could cause unsuccessful pupation, eclosion, or wing unfurling). However, there were no differences in the rate of successful eclosion from the pupal case among treatments in generations eight (G = 0.350, P = 0.840, N = 1776) or nine (G = 1.165, P = 0.559, N = 2050). Consequently, we consider such physical constraints to be an unlikely explanation for the plateau in the response to selection exhibited by the −FW/+HW lineages. Genetic correlations between the FW and HW themselves or between the individual wings and some unmeasured third trait (e.g., body size) might have inhibited the response to selection (Burger 1986; Hansen et al. 2003). Although the genetic correlation, as estimated by the single-trait selection experiments (Tables 1 and 3, Figs. 2, 4) did not change during the experiments (at least in one direction), the initially rapid evolutionary response of the allometry intercept in lineages C and D suggests that the genetic correlation between the wings probably did not cause the cessation in the response (see below also). Assessing the likelihood that correlations with other traits imposed unexpected limits to the response to selection is difficult as the set of candidate traits is potentially large and only FW and HW were measured. Instead, a lack of appropriate genetic variation at loci contributing to the size of the individual fore- and hind wings, or at loci that specifically mediate the allometry between wings, may be responsible. We tested for the presence of genetic variation at loci regulating individual wing sizes by selecting for changes in the absolute size (−FW or +HW) in new lineages founded from the −FW/+HW lineages. The overall trend was for HW to remain unchanged and for FW to decrease (Fig. 4), suggesting that the depletion of the genetic variation for HW may be responsible in part for the cessation in the response to selection.
The asymmetrical pattern of indirect responses of FW and HW to the direct selection on the intercept of their scaling relationship (Fig. 5) also suggests developmental bias that may be related to the genetic variation underlying the individual wings or loci controlling their relative size. The degree to which FW or HW size contributed to the evolution of the scaling relationship was dependent on the direction of selection (Fig. 5). This among-lineage variation was unexpected because the individual wings exhibited similar patterns of phenotypic variation through the experiment and nearly identical realized heritabilities in each direction (Fig. 2B), indicating that they should have responded similarly to selection in a given direction. Moreover, we found a more consistent pattern in our companion study of the evolution of forewing–body size allometry in B. anynana (Frankino et al. 2005), in which changes in FW were responsible for nearly all of the response to artificial selection on the intercept of that scaling relationship. These patterns of indirect responses of the wings to direct selection on their allometry intercept, and the results from the experiments described above regarding the asymmetrical response of the allometry intercept to direct selection, are consistent with results expected from selection on a limited pool of alleles that can contribute independently to, or uncouple, growth of the two wings
Together, these results demonstrate the absence of strong developmental constraints on the short-term evolution of the allometry between the fore- and hindwings. They also suggest the existence of an interesting bias, perhaps rooted in patterns of genetic variation underlying the individual traits and their scaling relationship, that affects how this allometry intercept evolves in the short and longer terms. Classical quantitative genetic models predict that genetic correlations can influence the evolutionary trajectory of a population during adaptation, constraining a population from reaching some adaptive peaks or biasing it toward others (e.g., Phillips and Arnold 1989; Arnold 1992; Price et al. 1993). Recent theory, however, suggests that the diversification of complex morphologies may draw upon developmental variation that can remain hidden until revealed by changes in patterns of selection (Rice 1998) and that the developmental bases of genetic correlations are more important than the strength of the correlation in determining the response to selection (Gromko 1995; Wolf et al. 2001, 2004; see also Klingenberg 2005). Both here and in our previous study of morphological allometries in B. anynana (Frankino et al. 2005), estimates of the genetic correlations between traits were based on reciprocal single-trait selection experiments and so should be interpreted with caution for a few reasons. Single-trait selection experiments may confound genetic variation underlying these individual traits with that contributing to the intercept of their allometries. Moreover, selection in the single-trait selection experiments may sort alleles at different loci than the selection experiments targeting components of their allometries directly. For example, selection for changes in absolute trait size may draw primarily on variation in body size rather than on variation in the focal trait (Weber 1990). Such a notion is supported by the variable responses of FW to direct selection on absolute wing size (Figs. 2B, 4) and indirect response to selection on relative wing size (Fig. 5 and Frankino et al. 2005). In sum, these complications mean that genetic correlations calculated from single-trait selection experiments may underestimate the evolutionary independence of the individual traits, generating inaccurate predictions of their response to selection. Several potential physiological processes rooted in the regulation of wing disc growth are potential targets of selection on relative wing size. For example, evolution of the allometry intercept could occur through changes in the sizes of the fore- and hindwing discs at the start of their exponential growth phases, through alterations of the relative timing and duration of these growth phases, the relative rates of wing disc growth, or the pattern of apoptosis within the wing (for recent reviews, see Emlen and Nijhout 2000; Emlen and Allen 2004; Frankino and Raff 2004; Shingleton et al. 2007). More information regarding the physiology and genetic architecture of absolute and relative wing size variation is required to fully elucidate the proximate basis of allometric changes in this system.
EXTERNAL SELECTIVE CONSTRAINTS ON FOREWING–HINDWING EVOLUTION
To examine the form and strength of natural selection on the intercept of the FW/HW allometry, we measured the relative fitness of competing wild-type and extreme-phenotype males in a spacious, naturally planted, tropical greenhouse. In both trials, males with the wild-type phenotype had three times higher mating success than did males from either phenotype class with divergent wing allometry intercepts (Fig. 6B), demonstrating strong stabilizing selection on the scaling relationship intercept. There are at least three possible explanations for the higher mating success of wild-type males. First, males with deviations from the wild-type phenotype could have lower survival, which in turn would reduce their mating success. Survival (percent males recaptured) differed among phenotype classes in one of the two trials, but the much higher fitness of wild-type males remained even after survival was taken into account. Second, females may choose wild-type males on the basis of superior signals produced during flight or courtship (Joron and Brakefield 2003). Any female preference for male phenotype must be largely unrelated to genetic background or inbreeding effects in our study, because males of wild-type phenotype were drawn from the same outcrossed populations as those with the extreme phenotypes (see Methods). We cannot exclude, however, some contribution of higher numbers of alleles for wild-type allometry in the males of the control class. Third, deviations from wild-type scaling relationships may adversely affect male locomotor performance, thereby reducing access to females in the presence of normally performing wild-type males. It is noteworthy that the strength and pattern of natural selection we document here is the same as that demonstrated for natural selection acting on the intercept of the forewing–body size allometry intercept in male B. anynana (Frankino et al. 2005). In both cases, determining the selective forces acting on the allometry intercepts should prove interesting as they may touch on the relative importance of inter- versus intrasexual selection in the evolution of these complex phenotypes.
Conclusions
The strong natural selection on the intercept of the allometry we demonstrate is consistent with that found for other scaling relationships in insect morphology (e.g., Wilkinson and Reillo 1994; Emlen 1997; Moczek and Emlen 2002; Frankino et al. 2005). Similarly, the lack of short-term constraints we demonstrate for the intercepts of the FW/HW (this study) and FW-body size allometries in B. anynana (Frankino et al. 2005) is consistent with the results from other studies showing rapid scaling relationship evolution in response to novel selection regimes (e.g., Weber 1990; Wilkinson 1993; Emlen 1996; Moczek et al. 2002; Frankino et al. 2005). Despite the differences in developmental and genetic mechanisms that presumably regulate the growth and differentiation of the diverse traits comprising these allometries, in no case yet studied experimentally does it appear that internal developmental constraints impose short-term limits on the evolution of scaling relationships in insect morphology. This is true even when the relative size of traits shows low variation within large taxonomic groups (e.g., Hansen and Houle 2004; Mezey and Houle 2005). The pattern emerging from these studies suggests that natural selection may be the primary determinant of allometry shape and distribution in morphological space. However, development may influence which evolutionary pathways are taken as allometries evolve, affecting both evolutionary trajectories in complex adaptive landscapes over the longer term (Burger 1986; Zeng 1988; Price et al. 1993), and how individual traits respond indirectly to selection for novel scaling relationships. Emerging theoretical treatments posit that the developmental basis of coupling or “entanglement” among traits affects the symmetry and rates of trait evolution, the evolution of heritabilities, the impact of correlations on evolutionary trajectories across different time scales, and the evolutionary relationship among trait means, variances, and covariances (Wolf et al. 2001, 2004; Rice 2002, 2004); such models may offer important insights into the evolution of complex phenotypes such as the scaling relationships among ecologically integrated trait suites (Rice 2004). In sum, predicting how morphologies will diversify through changes in allometry intercepts or slopes may require knowing how proximate mechanisms regulate and integrate the absolute and relative growth rates of traits. Future work should focus in part on elucidating these mechanisms, and quantifying how variation in them influences how allometries evolve under different patterns of selection.
Acknowledgments
K. Koops provided essential assistance in rearing caterpillars, with N. Wurzer and colleagues providing maize plants. C. Allen, P. Beldade, C. Klingenberg, R. Repasky, A. Shingleton, and two anonymous reviewer and Associate Editor T. F. Hansen made helpful comments on previous versions of the manuscript. R. Repasky and A. Buerkle helped with statistics and computer code. We thank the Hortus Botanicus, Leiden for access to the tropical greenhouse. This work was supported by Leiden University, and by a 2001 Bioinformatics Postdoctoral Fellowship from the National Science Foundation to W.A.F.
LITERATURE CITED
- Arnold SJ. Constraints on phenotypic evolution. Am Nat. 1992;140:S85–S107. doi: 10.1086/285398. [DOI] [PubMed] [Google Scholar]
- Arthur W. The interaction between developmental bias and natural selection: from centipede segments to a general hypothesis. Heredity. 2002;89:239–246. doi: 10.1038/sj.hdy.6800139. [DOI] [PubMed] [Google Scholar]
- Baker RH, Wilkinson GS. Phylogenetic analysis of sexual dimorphism and eye-span allometry in stalk-eyed flies (Diopsidae) Evolution. 2001;55:1373–1385. doi: 10.1111/j.0014-3820.2001.tb00659.x. [DOI] [PubMed] [Google Scholar]
- Becker WA. Manual of quantitative genetics. Academic Enterprises; Pullman, WA: 1992. [Google Scholar]
- Beldade P, Koops K, Brakefield PM. Developmental constraints versus flexibility in morphological evolution. Nature. 2002;416:844–847. doi: 10.1038/416844a. [DOI] [PubMed] [Google Scholar]
- Brakefield PM. Evo-devo and constraints on selection. Trends Ecol Evol. 2007;21:362–368. doi: 10.1016/j.tree.2006.05.001. [DOI] [PubMed] [Google Scholar]
- Brakefield PM, El Filali E, Van Der Laan R, Breuker CJ, Saccheri IJ, Zwaan BJ. J Evol Biol. 2001;14:148–156. doi: 10.1046/j.1420-9101.2001.00248.x. [DOI] [PubMed] [Google Scholar]
- Bohren BB, Hill WG, Robertson A. Some observations on asymmetrical correlated responses to selection. Genet Res. 1966;7:44–57. doi: 10.1017/s0016672300009460. [DOI] [PubMed] [Google Scholar]
- Burger R. Constraints for the evolution of functionally coupled characters: a nonlinear analysis of a phenotypic model. Evolution. 1986;40:182–193. doi: 10.1111/j.1558-5646.1986.tb05729.x. [DOI] [PubMed] [Google Scholar]
- Burkhardt D, de la Motte I. Physiological, behavioral, and morphometric data elucidate the evolutive significance of stalked eyes in Diopsidae (Diptera) Entomol Gener. 1987;12:221–233. [Google Scholar]
- Carroll SB, Gates J, Keys DN, Paddock SW, Panganiban GEF, Selegue JE, Williams JA. Pattern formation and eyespot determination in butterfly wings. Science. 1994;265:109–114. doi: 10.1126/science.7912449. [DOI] [PubMed] [Google Scholar]
- Carroll SB, Grenier JK, Weatherbee SD. From DNA to diversity: molecular genetics and the evolution of animal design. Blackwell Science; Malden, MA: 2001. [Google Scholar]
- Cheverud JM. Quantitative genetics and developmental constraints on evolution by selection. J Theor Biol. 1984;110:155–171. doi: 10.1016/s0022-5193(84)80050-8. [DOI] [PubMed] [Google Scholar]
- Cock AG. Genetical aspects of metrical growth and form in animals. Q Rev Biol. 1966;41:131–190. doi: 10.1086/404940. [DOI] [PubMed] [Google Scholar]
- Dudley R. The biomechanics of insect flight: form, function, evolution. Princeton Univ. Press; Princeton, NJ: 2000. [Google Scholar]
- Eberhard WG, Gutierrez EE. Male dimorphisms in beetles and earwigs and the question of developmental constraints. Evolution. 1991;45:18–28. doi: 10.1111/j.1558-5646.1991.tb05262.x. [DOI] [PubMed] [Google Scholar]
- Emlen DJ. Artificial selection on horn length-body size allometry in the horned beetle Onthophagus acuminatus (Coleoptera:Scarabaeidae) Evolution. 1996;50:1219–1230. doi: 10.1111/j.1558-5646.1996.tb02362.x. [DOI] [PubMed] [Google Scholar]
- Emlen DJ. Alternative reproductive tactics and male-dimorphism in the horned beetle Onthophagus acuminatus (Coleoptera: Scarabaeidae) Behav Ecol Sociobiol. 1997 Nov;41:335–341. [Google Scholar]
- Emlen DJ, Allen CE. Genotype to phenotype: physiological control of trait size and scaling in insects. Integr Comp Biol. 2004;43:617–634. doi: 10.1093/icb/43.5.617. [DOI] [PubMed] [Google Scholar]
- Emlen DJ, Nijhout HF. The development and evolution of exaggerated morphologies in insects. Ann Rev Entomol. 2000;45:661–708. doi: 10.1146/annurev.ento.45.1.661. [DOI] [PubMed] [Google Scholar]
- Endler JA. Natural selection in the wild. Princeton Univ. Press; Princeton, NJ: 1986. [Google Scholar]
- Falconer DS, Mackay TFC. Introduction to quantitative genetics. Addison Wesley Longman Limited; Essex, U.K: 1997. [Google Scholar]
- Frankino WA, Raff RA. Evolutionary importance and pattern of phenotypic plasticity: insights gained from development. In: De Witt TJ, Scheiner SM, editors. Phenotypic plasticity, functional and conceptual approaches. Oxford Press; Cambridge UK: 2004. pp. 64–81. [Google Scholar]
- Frankino WA, Zwaan BJ, Stern DL, Brakefield PM. Natural selection and developmental constraints in the evolution of allometries. Science. 2005;307:718–720. doi: 10.1126/science.1105409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gromko MH. Unpredictability of correlated response to selection: pleiotropy and sampling interact. Evolution. 1995;49:685–693. doi: 10.1111/j.1558-5646.1995.tb02305.x. [DOI] [PubMed] [Google Scholar]
- Gould SJ. Allometry and size in ontogeny and phylogeny. Biol Rev. 1966;41:587–640. doi: 10.1111/j.1469-185x.1966.tb01624.x. [DOI] [PubMed] [Google Scholar]
- Hansen TF, Ambruster WS, Carlson ML, Pelabon C. Evolvability and genetic constraint in Dalechampia blossoms: genetic correlations and conditional evolvability. J Exp Zool. 2003;296B:23–39. doi: 10.1002/jez.b.14. [DOI] [PubMed] [Google Scholar]
- Hansen TF, Houle D. Evolvability, stabilizing selection, and the problem of stasis. In: Pigliucci M, Preston K, editors. Phenotypic integration: studying the ecology and evolution of complex phenotypes. Oxford Univ. Press; New York: 2004. pp. 130–150. [Google Scholar]
- Huxley JS. Problems of relative growth. Methuen & Co.; London: 1932. [Google Scholar]
- Joron M, Brakefield PM. Captivity masks inbreeding effects on male mating success in butterflies. Nature. 2003;424:191–194. doi: 10.1038/nature01713. [DOI] [PubMed] [Google Scholar]
- Keys DN, Lewis DL, Selegue JE, Pearson BJ, Goodrich LV, Johnson RL, Gates J, Scott MP, Carroll SB. Recruitment of a hedgehog regulatory circuit in butterfly eyespot evolution. Science. 1999;283:532–534. doi: 10.1126/science.283.5401.532. [DOI] [PubMed] [Google Scholar]
- Kingsolver JG. Experimental analyses of wing size, flight, and survival in the western white butterfly. Evolution. 1999;53:1479–1490. doi: 10.1111/j.1558-5646.1999.tb05412.x. [DOI] [PubMed] [Google Scholar]
- Klingenberg CP. Developmental constraints, modules, and evolvability. In: Hallgrimsson B, Hall BK, editors. Variation. Elsevier Academic Press; Burlington, MA: 2005. pp. 219–247. [Google Scholar]
- Klingenberg CP, Zimmermann M. Static, ontogenetic, and evolutionary allometry: a multivariate comparison in nine species of water striders. Am Nat. 1992;140:601–620. [Google Scholar]
- Lande R. Quantitative genetic analysis of multivariate evolution, applied to brain body size allometry. Evolution. 1979;33:402–416. doi: 10.1111/j.1558-5646.1979.tb04694.x. [DOI] [PubMed] [Google Scholar]
- Lessels CM, Boag PT. Unrepeatable repeatabilities: a common mistake. Auk. 1987;104:116–121. [Google Scholar]
- Maynard Smith J, Burian R, Kauffman S, Alberch P, Campbell J, Goodwin B, Lande R, Raup D, Wolpert L. Developmental constraints and evolution. Q Rev Biol. 1985;60:265–287. [Google Scholar]
- Meagher TR, Futuyma DJ. Executive document: evolution, science, and society. Am Nat. 2001;158(S1):1–45. [Google Scholar]
- Mezey JG, Houle D. The dimensionality of genetic variation for wing shape in Drosophila melanogaster. Evolution. 2005;59:1027–1038. [PubMed] [Google Scholar]
- Moczek AP, Emlen DJ. Male horn dimorphism in the scarab beetle, Onthophagus taurus: do alternative reproductive tactics favour alternative phenotypes? Anim Behav. 2002;59:459–466. doi: 10.1006/anbe.1999.1342. [DOI] [PubMed] [Google Scholar]
- Moczek AP, Hunt J, Emlen DJ, Simmons LW. Threshold evolution in exotic population of a polyphenic beetle. Evol Ecol Res. 2002;4:587–601. [Google Scholar]
- Nijhout HF. Insect hormones. Princeton Univ. Press; Princeton, NJ: 1994. [Google Scholar]
- Nijhout HF, Emlen DJ. Competition among body parts in the development and evolution of insect morphology. Proc Natl Acad Sci USA. 1998;95:3685–3689. doi: 10.1073/pnas.95.7.3685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips PC, Arnold SJ. Visualizing multivariate selection. Evolution. 1989;43:1209–1222. doi: 10.1111/j.1558-5646.1989.tb02569.x. [DOI] [PubMed] [Google Scholar]
- Price T, Turelli M, Slatkin M. Peak shifts produced by correlated response to selection. Evolution. 1993;47:280–290. doi: 10.1111/j.1558-5646.1993.tb01216.x. [DOI] [PubMed] [Google Scholar]
- Rice SH. The evolution of canalization and the breaking of von Baer’s laws: modeling the evolution of development with epistasis. Evolution. 1998;52:647–656. doi: 10.1111/j.1558-5646.1998.tb03690.x. [DOI] [PubMed] [Google Scholar]
- Rice SH. A general population genetic theory for the evolution of developmental interactions. Proc Natl Acad Sci USA. 2002;99:15518–15523. doi: 10.1073/pnas.202620999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice SH. Developmental associations between traits: covariance and beyond. Genetics. 2004;166:513–526. doi: 10.1534/genetics.166.1.513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schluter D. Adaptive radiation along genetic lines of least resistance. Evolution. 1996;50:1766–1774. doi: 10.1111/j.1558-5646.1996.tb03563.x. [DOI] [PubMed] [Google Scholar]
- Shingleton AW, Frankino WA, Flatt T, Nijhout HF, Emlen DJ. Size and shape: the regulation of static allometry in insects. BioEssays. 2007;29:536–548. doi: 10.1002/bies.20584. [DOI] [PubMed] [Google Scholar]
- Sinervo B, Basolo AL. Testing adaptation using phenotypic manipulations. In: Rose MJ, Lauder GV, editors. Adaptation. Academic Press; San Diego, CA: 1996. pp. 149–185. [Google Scholar]
- Sinervo B, Doughty P, Huey RB, Zamudio K. Allometric engineering: a causal analysis of natural selection on offspring size. Science. 1992;258:1927–1930. doi: 10.1126/science.258.5090.1927. [DOI] [PubMed] [Google Scholar]
- Sinervo B, Licht P. Proximate constraints on the evolution of egg size, egg number, and total clutch mass in lizards. Science. 1991;252:1300–1302. doi: 10.1126/science.252.5010.1300. [DOI] [PubMed] [Google Scholar]
- Stern DL, Emlen DJ. The developmental basis of allometry in insects. Development. 1999;126:1091–1101. doi: 10.1242/dev.126.6.1091. [DOI] [PubMed] [Google Scholar]
- Strauss RE. Patterns of quantitative variation in lepidopteran wing morphology: the convergent groups heliconiinae and ithomiinae (Papilionoidea: Nymphalidae) Evolution. 1990;44:86–103. doi: 10.1111/j.1558-5646.1990.tb04281.x. [DOI] [PubMed] [Google Scholar]
- Strauss RE. Lepidopteran wing morphology: the multivariate analysis of size, shape, and allometric scaling. In: Sorensen JT, Foottit R, editors. Ordination in the study of morphology, evolution, and systematics of insects: applications and quantitative genetic rationales. Elsevier Science Publishers; Amsterdam: 1992. pp. 157–179. [Google Scholar]
- Thompson DW. On growth and form. Cambridge Univ. Press; Cambridge: 1917. [Google Scholar]
- Wagner GP. Homologues, natural kinds, and the evolution of modularity. Am Zool. 1996;36:36–43. [Google Scholar]
- Wagner GP, Booth G, Bagheri-Chaichian H. A population genetic theory of canalization. Evolution. 1997;51:329–347. doi: 10.1111/j.1558-5646.1997.tb02420.x. [DOI] [PubMed] [Google Scholar]
- Weber KE. Selection on wing allometry in Drosophila melanogaster. Genetics. 1990;126:975–989. doi: 10.1093/genetics/126.4.975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wickman P. Sexual selection and butterfly design—a comparative study. Evolution. 1992;46:1525–1536. doi: 10.1111/j.1558-5646.1992.tb01142.x. [DOI] [PubMed] [Google Scholar]
- Wilkinson GS. Artificial selection alters allometry in the stalk-eyed fly Cyrtodiopsis dalmanni (Diptera:Diopsidae) Genet Res. 1993;62:213–222. [Google Scholar]
- Wilkinson GS, Reillo PR. Female choice response to artificial selection on an exaggerated male trait in a stalk-eyed fly. Proc Biol Sci. 1994;255:1–6. [Google Scholar]
- Windig JJ, Brakefield PM, Reitsma PM, Wilson JGM. Seasonal polyphenism in the wild: survey of wing patterns in five species of Bicyclus butterflies in Malawi. Ecol Entomol. 1994;19:285–298. [Google Scholar]
- Wolf JB, Allen CE, Frankino WA. Multivariate phenotypic evolution in developmental hyperspace. In: Pigliucci M, Preston K, editors. Phenotypic integration: studying the ecology and evolution of complex phenotypes. Oxford Univ. Press; New York: 2004. pp. 366–389. [Google Scholar]
- Wolf JB, Frankino WA, Agrawal AF, Brodie ED, III, Moore AJ. Developmental interactions and the constituents of quantitative variation. Evolution. 2001;55:232–245. doi: 10.1111/j.0014-3820.2001.tb01289.x. [DOI] [PubMed] [Google Scholar]
- Zeng Z. Long-term correlated response, interpopulation covariation, and interspecific allometry. Evolution. 1988;42:363–374. doi: 10.1111/j.1558-5646.1988.tb04139.x. [DOI] [PubMed] [Google Scholar]


