Integrating Biological Knowledge with Gene Expression Profiles for Survival Prediction of Cancer

Abstract

Due to the large variability in survival times between cancer patients and the plethora of genes on microarrays unrelated to outcome, building accurate prediction models that are easy to interpret remains a challenge. In this paper, we propose a general strategy for improving performance and interpretability of prediction models by integrating gene expression data with prior biological knowledge. First, we link gene identifiers in expression dataset with gene annotation databases such as Gene Ontology (GO). Then we construct “supergenes” for each gene category by summarizing information from genes related to outcome using a modified principal component analysis (PCA) method. Finally, instead of using genes as predictors, we use these supergenes representing information from each gene category as predictors to predict survival outcome. In addition to identifying gene categories associated with outcome, the proposed approach also carries out additional within-category selection to select important genes within each gene set. We show, using two real breast cancer microarray datasets, that the prediction models constructed based on gene sets (or pathway) information outperform the prediction models based on expression values of single genes, with improved prediction accuracy and interpretability.

1. Introduction

Gene expression profiles have been used extensively in diagnostic and prognostic predictions of various cancers (Alizadeh et al., 2000; Beer et al., 2002; Golub et al., 1999; Perou et al., 2000; Ramaswamy et al., 2003; Rosenwald et al., 2002; Shipp et al., 2002; van't Veer et al., 2002). Typically, to predict tumor subtype or patient survival time, a prediction model is constructed based on expression values of single genes. Some commonly used methods include the Lasso (Gui and Li, 2005; Segal, 2006), principal component analysis (PCA) (Tan et al., 2005), Supervised principal component analysis (Bair and Tibshirani, 2004), partial least squares (Ngyen and Rocke, 2002), support vector machine (Furey et al., 2000), among others.

However, due to the large variability in survival times between cancer patients and the plethora of genes on the microarrays unrelated to outcome, building accurate prediction models that are easy to interpret remains a challenge. In this paper, we propose a general strategy for improving performance and interpretability of prediction models by integrating gene expression data with prior biological knowledge. For simplicity, we use the terms “gene categories,” “pathways,” and “gene sets” interchangeably, although they may not be strictly equivalent. The idea is simple: first, we link gene identifiers in expression dataset with gene annotation databases such as Gene Ontology (GO) (Ashburner et al., 2000). Then we construct “supergenes” for each pathway by summarizing information from genes related to outcome using a modified PCA method. Finally, instead of using genes as predictors, we use these supergenes representing information from each pathway as predictors to predict survival outcome.

We hypothesize that prediction models constructed based on pathway information will have improved prediction performance and better interpretability for several reasons: (1) As suggested by Hanahan and Weinberg (2000), the underlying disease process for cancer may be dependent on perturbations of different pathways, so prediction models based on pathways may approximate the true disease process more closely than gene-based models; moreover, because the lists of significant pathways are more stable over different datasets compared to lists of significant genes (Manoli et al., 2006), information based on pathways may be more robust to outlying samples or artifacts from sample handlings, thus serving as better predictors with improved prediction accuracy. (2) The feature list comprised of significant pathways will help delineate more clearly the underlying biological processes that are predictive of variations in outcome; by borrowing strength across genes in the same pathway, pathway-based methods (Subramanian et al., 2005; Wang et al., 2008) allow one to identify patterns that are too subtle to discern at single gene level. For example, Mootha et al. (2003) showed that the oxidative phosphorylation genes are significantly associated with diabetes as a group, while none of the genes in the pathway showed significant change individually. Segal et al. (2004, 2005) identified combinations of activated and deactivated gene sets that characterize different tumor stages and types of cancer to obtain a global view underlying human cancer.

Some discussion of related approaches and comparisons of them with the proposed method are in order. Tai and Pan (2007) proposed a method to incorporate prior knowledge of predictors into penalized classifiers with multiple penalty terms. Wei and Li (2007) proposed a modified boosting method, called “nonparametric pathway-based regression.” While the method of Tai and Pan (2007) applies only to penalized classifiers and the method of Wei and Li (2007) applies only to boosting, our proposal is a more general strategy that can be applied to a wide variety of prediction methods. Ma et al. (2007) proposed the supervised group Lasso method, and Park et al. (2007) proposed using averaged gene expressions for regression-based prediction models. However, the gene groupings for these methods are based on statistically derived clusters, not on biological knowledge. In contrast, the gene annotation databases we use provide an automatic way of grouping genes that are less dependent on the particular dataset being analyzed; therefore, models based on these a priori defined gene sets will be more stable across different datasets and will have better interpretability. Chuang et al. (2007) proposed using protein interaction networks for classification of breast cancer metastasis status for patients. Instead of choosing a cut-off such as 5-year-survival, which converts time-dependent survival outcomes to binary outcomes, we study models for predicting right censored survival outcome such as time to metastasis. Censoring occurs, for example, when patients survived over the entire study period or were lost to follow-up; in these cases, we only know partial information on the outcome. We model survival outcomes with Cox proportional hazard regression models.

In summary, our goal is to improve prediction accuracy and interpretability of models based on single gene expression values for prediction of survival outcomes, by combining gene expression data with prior biological knowledge on groups of genes. In the next section, we provide a more in-depth discussion of the proposed method. By incorporating information from a priori defined gene sets, this method not only models but also selects pathways and genes that are predictive of variations in survival outcome, which could in turn shed light on the underlying mechanisms of the disease. We show, using two real breast cancer microarray datasets, that when the proposed strategy is applied to the prediction methods of Lasso and Supervised PCA, the model with pathway information as predictors has both improved prediction accuracy and better interpretability compared to a gene-based prediction model. The details of the prediction algorithms, software implementations, and performance evaluation criterion for the prediction methods are presented in Methods.

2. Results and Discussion

An overview of pathway-based prediction models

Biologically, a subset of genes from an a priori defined gene set, each contributing a different amount, work together to bring about changes in a cellular process, and this cellular process then relates to variations in phenotype. Therefore, for each pathway, our objective is to select the subset of relevant genes, estimate the latent variable associated with underlying cellular process and then construct prediction model based on these latent variables. The selection of genes is especially important for gene sets with large number of genes, therefore, a successful prediction method would need to be able to select pertinent genes in addition to model variations in outcome.

When using gene sets from databases such as GO, one challenge is that some genes are not yet assigned to a definite gene category. Rather than discarding these genes, we perform K-means clustering on these genes to divide them into subgroups with similar expression patterns. To this end, we used the method of Tibshirani et al. (2001), where the optimal number of clusters was estimated using the Gap statistics. The resulting clusters or the pseudo gene categories were then combined with other gene sets from GO for subsequent analysis.

There are two steps for building prediction models based on pathways: (1) for each gene set, select genes associated with outcome and summarize information from these selected genes by estimating the underlying latent variable, which are the “super genes;” and (2) construct prediction model using relevant super genes as predictors. In this paper, we study pathway-based versus gene-based prediction models using Supervised PCA (Bair and Tibshirani, 2004; Bair et al., 2006) and Lasso because of their simplicity and popularity, but the proposed strategy can be easily adapted to other prediction models as well.

In the first step, PCA is a good strategy for data reduction and summarization of high-dimensional data from expressions of multiple genes. However, because PCA is an unsupervised approach, the estimated principal component (PC) score is often unrelated to outcome. To help ensure that estimated PC is driven by sources of variations associated with outcome, we used the Supervised PCA method to summarize information from genes in each pathway. This method selects subset of genes that are most associated with outcome, with largest log likelihood using cross-validation first and then estimate principal component using only the selected genes. Because outcome information is used in the gene selection step, this method is supervised, thus called the “Supervised PCA model.” We call the latent variable (or the first PC score explaining the largest proportion of variations in outcome) the “super gene” for the pathway. Note that when evaluating performance of prediction models, only outcomes of training data should be used in cross-validation to select genes.

In the second step, we apply the SPCA method again, to select supergenes (representing pathways) that are most significantly associated with outcome. With selected supergenes, principal component regression model can be constructed, with the first PC scores estimated from selected supergenes (or pathways) as predictors; this is then the pathway-based prediction model. Similarly, Lasso constructs a linear model based on pathways by shrinking some of the coefficients of supergenes in the linear regression model to exactly zero.

Pathway-based prediction models improve prediction accuracy

We compared the pathway-based versus gene-based SPCA and Lasso prediction models using two breast cancer microarray datasets. The pathway-based models used supergenes, or the first principal component scores estimated from genes in each pathway as predictors, whereas the gene-based models used expression values of single genes as predictors.

Wang et al. (2005) studied gene expression profiles from 286 lymph-node-negative breast cancer patients using Affymetrix U133a GeneChip (GEO accession no. GSE2034). These patients were treated with surgery or radiotherapy over an 11-year period, but they had not received adjuvant systemic treatment. As another example, Miller et al. (2005) studied gene expression profiles from 251 Sweden patients using Affymetrix U133a and U133b platforms (GEO accession no. GSE3494). Among these patients, 236 samples with follow-up information on time and event of disease-specific survival were used for this analysis.

To estimate prediction accuracy of gene-based versus pathway-based prediction models, for each dataset, we randomly split the samples into training and testing samples with a 2:1 ratio. So, for the Wang et al. (2005) dataset, there were 190 training samples and 96 testing samples, and for the Miller et al. (2005) dataset, there were 156 training samples and 80 testing samples. We next constructed gene-based and pathway-based prediction models using training samples and estimated prediction accuracy using testing samples. Note that, in order to achieve an unbiased evaluation, the models were completely specified using only the training data; the test samples were never used in any aspect of any model building process.

When evaluating the performances of prediction models for survival outcomes, because of the presence of censoring, the standard mean-squared-error or misclassification rate criteria are not appropriate. Here, to account for censoring, we used the method described in Heagerty et al. (2000) for the calculation of time-dependent operating characteristics curves (ROC) for survival outcome, where the bivariate distribution function of predictors and survival time were estimated using a nearest neighbor estimator.

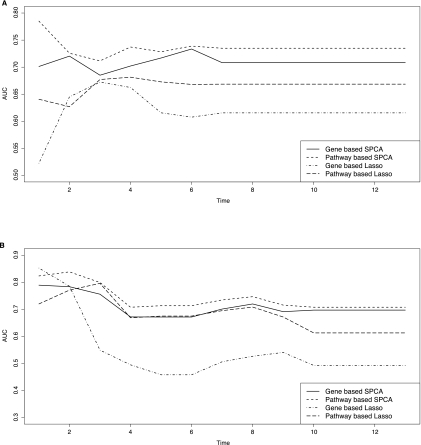
Because the survivals of patients change with time, we examined performances of the models over the entire range of time. In Figure 1, we plotted area under ROC curves (AUC) over time for each model. At each follow-up time t, we calculated a time-dependent ROC curve, ROC(t), and an overall measure, AUC(t). The ROC curve shows that the trade-off between sensitivity and 1-specificity as threshold for declaring disease status is varied; the AUC measures the overall discriminative abilities of the prediction model over all thresholds. Figure 1 shows the AUCs for the four models over time for the Wang et al. (2005) dataset and the Miller et al. (2005) dataset. Pathway-based SPCA model consistently outperformed the gene-based SPCA model over the entire range of time with higher AUC. Similarly, the pathway-based Lasso model consistently outperformed the gene-based Lasso model, except by a small margin at year 2. To examine performance of the models more closely, Figure 2 shows the ROC curves estimated at 5-year follow-up for gene-based and pathway-based models for the two datasets. Note that we accounted for censoring in the estimation of ROC, so the result is different from ROC calculated from the binary outcome with 5-year survival as the cut-off. Compared to the gene-based models, the pathway-based models had better sensitivity across all levels of specificity. For the Wang et al. (2005) dataset, at 5-year follow-up, the estimated AUCs for pathway-based SPCA and Lasso models were 0.735 and 0.669, respectively, indicating improved performances over gene-based SPCA and Lasso models, with AUCs of 0.708 and 0.616, respectively. Similarly, for the Miller et al. (2005) data, the AUCs of pathway-based SPCA and Lasso models at 5-year follow-up were 0.713 and 0.675, again outperforming gene-based SPCA and Lasso models, with AUCs of 0.672 and 0.458, respectively.

FIG. 1.

Time-dependent AUCs (area under ROC curve) for pathway-based and gene-based survival prediction models using Wang et al. (2005) dataset (A) and Miller et al. (2005) dataset (B). The AUC measures the overall discriminative abilities of the prediction model over all thresholds. To account for censoring in survival outcome, the method of Heagerty et al. (2000) was used for estimation of AUC.

FIG. 2.

ROC curves for pathway-based and gene-based prediction models at 5-year follow-up for Wang et al. (2005) dataset (A) and Miller et al. (2005) dataset (B). The ROC curves show the trade-off between sensitivity and 1-specificity as threshold for declaring disease status is varied. To account for censoring in survival outcome, the method of Heagerty et al. (2000) was used for estimation of ROC.

In addition to time-dependent ROC curves, we also compared the gene-based and pathway-based prediction models using two other measures: p-value and R² statistic. The p-values were calculated from likelihood ratio test comparing null model (intercept only) with a model with intercept and the linear predictor (used in the last step of SPCA or Lasso model to predict survival outcome); therefore, a small p-value indicates that the linear predictor from a given model is a good predictor for survival outcome. In the SPCA model, the linear predictor is the supervised principal component score; in the Lasso model, the linear predictor is the linear combination of predictors after applying shrinkage. The R² statistic, which ranges from 0 to 1, represents the proportion of variation in outcome explained by prediction model. Table 1 shows that results of comparison for the four models using p-value and R² were consistent with results using survival ROC curves. For both the Wang et al. (2005) and Miller et al. (2005) datasets, pathway-based models performed better with larger R² and smaller p-values.

Table 1.

Comparison of Different Methods Using p-Value and R²

	Methods	R2	p-value
Wang et al. (2005) data set	Gene-based SPCA	0.284	4.94 × 10−7
	Pathway-based SPCA	0.304	1.33 × 10−7
	Gene-based Lasso	0.060	1.51 × 10−2
	Pathway-based Lasso	0.146	9.83 × 10−5
Miller et al. (2005) data set	Gene-based SPCA	0.115	2.09 × 10−2
	Pathway-based SPCA	0.160	2.97 × 10−3
	Gene-based Lasso	0.003	0.646
	Pathway-based Lasso	0.093	5.26 × 10−2

The p-values were calculated from likelihood ratio test comparing null model (intercept only) with a model with intercept and the linear predictor (used in last step of SPCA or Lasso model to predict survival outcome). The R² statistic, which ranges from 0 to 1, represents the proportion of variation in outcome explained by prediction model.

Factors contributing to improved performance of pathway-based prediction models

We conducted additional study to assess contributions of the following factors for the improved prediction performance in pathway-based prediction models:

• 1. Gene screening (feature selection) within each GO category

• 2. Supergene screening at the pathway level

• 3. K-means clustering for genes not assigned to any gene category

For each of these contributing factors, we re-run pathway-based SPCA model for both the Wang et al. (2005) and Miller et al. (2005) datasets, eliminating steps in the model corresponding to each factor, but keeping all other steps unchanged. More specifically, in model 1, instead of using first Supervised PC score as supergenes, we used PC score as supergenes in the model re-fitting; in model 2, all supergenes were used to estimate the first principal component score in the final step of SPCA model; and in model 3, the genes not assigned to any gene category were removed.

The results in Table 2 show that the within-category feature selection is the most critical step for the superior prediction performance of pathway-based models. For both datasets, when all genes in each category were used to estimate supergene values, R² dropped substantially (0.304 vs. 0.122; 0.160 vs. 0.111), and p-values increased considerably (1.33 × 10⁻⁷ vs. 5.79 × 10⁻²; 2.97 × 10⁻³ vs. 2.42 × 10⁻²). In contrast, selection of supergenes affected prediction performance only slightly, and dropping genes not assigned to a definite gene category had little impact on prediction performance.

Table 2.

Factors Contributing to Improved Performance of Pathway-Based Prediction Models

	Methods	R2	p-value
Wang et al. (2005) data set	Pathway-based SPCA	0.304	1.33 × 10−7
	(1) No gene screening in GO	0.122	5.79 × 10−2
	(2) No supergene screening	0.261	2.15 × 10−6
	(3) No K-means clusters	0.300	1.66 × 10−7
Miller et al. (2005) data set	Pathway-based SPCA	0.16	2.97 × 10−3
	(1) No gene screening in GO	0.111	2.42 × 10−2
	(2) No supergene screening	0.158	3.12 × 10−3
	(3) No K-means clusters	0.160	3.01 × 10−3

For each of the contributing factors (1)–(3), pathway-based SPCA model was re-run, eliminating steps in the model corresponding to each factor, but keeping all other steps unchanged. In (1), instead of using first Supervised PCA score as supergenes, we used PCA score as supergenes in the model re-fitting; in (2), all supergenes were used to estimate the first principal component score in the final step of the Supervised PCA model; in (3), the genes not assigned to any gene category were removed. The results show that the within-category feature selection is the most critical step for the superior prediction performance of pathway-based models. In contrast, selection of supergenes affected prediction performance only slightly, and dropping genes not assigned to a definite gene category had little impact on prediction performance.

These results suggest that within each category, only a subset of genes may be related to outcome; therefore, without a gene screening step, when all genes from an a priori defined gene set are used to estimate principal components, performance of pathway-based prediction model would be adversely affected by noisy signals from irrelevant genes, especially when the gene-set size is large (Chen et al., 2008). This is because the estimated supergene (first principal component) is often driven by sources of variation unrelated to outcome. In contrast, Supervised PCA removes irrelevant genes before extracting the desired principal component, thus improving prediction performance in pathway-based models.

Pathway-based models identify biological processes and genes that play important roles in tumorigenesis

Using all samples, we next constructed SPCA model which had the best prediction performance. Although datasets in both Wang et al. (2005) and Miller et al. (2005) were from breast cancer patients, different biological processes were identified because only samples from Wang et al. (2005) were lymph-node-negative primary breast cancer.

For the dataset in Wang et al. (2005), we estimated supergenes (first principal component score) for each gene set and constructed the final prediction model with 252 supergenes representing different biological processes selected by the SPCA algorithm. To rank the selected gene sets, we next computed correlations between supergene values and the first principal component score estimated from all 252 selected supergenes in the final model. Table 1 shows the 10 supergenes with the highest absolute correlations. These gene sets are involved in different biological processes such as immune response, ion transport, protein phosphorylation, and neuron development that are known to play important roles in tumorigenesis and metastasis. For example, axon-guidance genes have been shown to be genetically and epigenetically inactivated in human cancers, implying their roles as tumor suppressor genes.

In addition to identifying supergenes representing different biological processes associated with cancer survival, the pathway-based SPCA model also identified important genes within each gene set. In Table 3, we list the selected genes used to estimate supergene values. There were a total of 41 genes selected to estimate supergene values in these 10 gene sets. The relations between these genes and cancer are also supported by experimental results in the literature. For example, EFNB1 encodes a member of the ephrin family of transmembrane ligands for Eph receptor tyrosine kinases, and the expression of EFNB1 gene is regulated by p53 directly (Arakawa, 2005); the product of TGFB2 is transforming growth factor–β, which has dual roles in beast cancer development; in the early tumor formation stage, TGFβ is a potent inhibitor of epithelial cell proliferation, but in the later stages the overexpression of TGFB can accelerate metastases (Dumont and Arteaga, 2000; Muraoka-Cook et al., 2005).

Table 3.

Ten Most Significant Predictors for Predicting Survival Outcome in Lymph-Node-Negative Primary Breast Cancer Dataset (Wang et al. 2005) Using Pathway-Based Supervised PCA Model

Gene set	Description	Set size	No. of selected genes	Gene symbols
GO:0007411	Axon guidance	46	5	EFNB1, NRXN3, NTN2L, TGFB2, ATOH1
GO:0006826	Iron ion transport	18	3	LTF, SLC11A1, SLC25A28
GO:0000187	Activation of MAPK activity	30	3	TDGF1, IGHM, SHC1
GO:0006879	Cellular iron ion homeostasis	16	6	LTF, MYC, ABCB6, TFRC, TF, IREB2
GO:0008150	Biological process	503	6	TNFRSF17, C18orf1, IGHM, BTN3A2, ABO, EPB41L4A
GO:0030890	Positive regulation of B cell proliferation	5	3	IL7, IL4, IGHM
GO:0050371	Positive regulation of peptidyl-tyrosine phosphorylation	10	6	CD81, CD4, TDGF1, CD80, TNFRSF17, IGHM
GO:0006811	Ion transport	375	10	LTF, TRPC1, GABRG2, KCNS1, SCN5A, P2RX3, TRPA1, SLC39A4, SLC25A28, SLC22A7
GO:0050853	B cell receptor signaling pathway	5	3	CD79A, IGHM, PTPRC
GO:0007275	Multicellular organismal development	668	5	MMP11, TNFRSF17, RECQL4, GREM1, CDX4

“Set size” refers to the number of genes in the GO category. In addition to identifying gene categories associated with outcome, the pathway-based Supervised PCA model also carries out additional within-category selection to select important genes within each gene set. “No. of selected genes” refers to the number of selected genes in each gene set that were used to estimate principal component score or supergene. Gene symbols for the selected genes are listed in the last column.

We next assessed the likelihood of these genes being included in gene-based prediction models. First, for each gene on the array, we fit univariate Cox proportional hazard regression model with survival outcome and single gene value as predictor. Next, we ranked p-values from Cox model for all genes. The mean and median rankings of the 41 genes selected by Supervised PCA algorithm were 1161 and 401, respectively. Among these 41 genes, several well-known cancer prognostic genes, such as TGFB2 (ranking 401), and MYC (ranking 3582) are unlikely to pass the gene screening step to be included in the gene-based prediction model. Therefore, the pathway-based SPCA model allows one to select genes that may not be differentially expressed itself, but are significantly associated with the biological process predictive of survival outcome.

Another feature of the pathway-based SPCA algorithm is that genes that play important roles in multiple biological processes predictive of survival outcome are automatically assigned more weight. In Table 3, among the top 10 gene sets, several genes such as IGHM, TNFRSF17, and LTF were selected multiple times in different gene sets. Among these genes, IGHM and TNFRSF17 are related to immune responses. IGHM has been shown to have a key prognostic impact in node-negative breast cancer (Schmidt et al., 2008). This is reasonable since all samples in this dataset were from node-negative patients. In addition, TNFRSF17 has also been shown to be a good prognosis marker in estrogen-receptor-negative breast cancer (Teschendorff et al., 2007).

For the Miller et al. (2005) dataset, Table 4 shows the 10 most significant gene sets from pathway-based SPCA model and 85 selected genes from these gene sets. Most of these gene sets are related to signal transduction and response to stimulus. Among them, estrogen receptor signaling pathway is most directly related to breast cancer, since estrogen receptors are overexpressed in around 70% of breast cancer.

Table 4.

Ten Most Significant Predictors for Predicting Survival Outcome in Sweden Breast Cancer Dataset (Miller et al., 2005) Using Pathway-Based Supervised PCA Model

Gene set	Description	Set size	No. of selected genes	Gene symbols
GO:0019233	Sensory perception of pain	5	4	NPY1R, NGF, NDN, PENK
GO:0007193	G-protein signaling, adenylate cyclase inhibiting pathway	10	6	RGS1, EDG1, NPY1R, 0PRD1, CORT, GPR44
GO:0030520	Estrogen receptor signaling pathway	9	8	TAF7, RBM14, ESR1, NC0A6, ARID1A, ESR2, RBM9, DDX54
GO:0050729	Positive regulation of inflammatory response	5	3	STAT5A, FABP4, STAT5B
GO:0007631	Feeding behavior	20	12	NPY1R, BDNF, AGRP, HTR2C, HCRTR1, HCRT CCKBR, CCKAR, GALR2 PYY, FYN, MCHR1
GO:0001816	Cytokine production	8	7	CD4, FABP4, PTAFR, CD226, MAF, NFATC2IP, N0D2
GO:0007026	Negative regulation of microtubule depolymerization	10	4	MAP4, MAPT, CLASP2, MID1IP1
GO:0007626	Locomotory behavior	17	13	SEPP1, HEXA, HEXB, GNA01, NPY1R, C1QL1, N0VA1, PGDS, GRM1, ADRA1B, NRG1, DRD1, CELSR1
GO:0007187	G-protein signaling, coupled to cyclic nucleotide second messenger	37	29	VIPR1, NPY1R, MC1R, PTHR1, NPY, CNR2, HTR6, HTR1E, HTR, 0PRD1, HTR7, SSTR1, MTNR1B, MC5R, HTR1B, CALCRL, 0PRM1, CNR1, SSTR4, DRD1, CCL2, SSTR2, HRH3, HRH2, EDG7, MTNR1A, MC3R, HTR1F, XCR1
GO:0032012	Regulation of ARF protein signal transduction	13	6	PSD4, PSD3, PSD, IQSEC3, ARFGEF2, PSCD4

“Set size” refers to the number of genes in the GO category. In addition to identifying gene categories associated with outcome, the pathway-based Supervised PCA model also carries out additional within-category selection to select important genes within each gene set. “No. of selected genes” refers to the number of selected genes in each gene set that were used to estimate principal component score or supergene. Gene symbols for the selected genes are listed in the last column.

Among the 85 selected genes, NPY1 is the most interesting one since it was selected five times in the top 10 gene sets, but its single gene ranking is 4599. Another interesting gene is Neuropeptide Y (NPY), a 36-amino acid peptide neurotransmitter found in the brain and autonomic nervous system, which plays important roles in food intake, obesity, memory, and anxiety. It had never been linked to cancer development, until recent findings which showed that the NPY Y1 receptor (NPY1R) subtype is expressed in 85% of the primary human breast cancer carcinomas (Reubi et al., 2001). Finally, estrogen was also found to up-regulate NPY1R expression, which is coupled to both cAMP and calcium signaling pathway to reduce the proliferative activity of estrogen in breast cancer (Amlal et al., 2006). Again, the mean and median of rankings of Cox model p-values for the 85 genes in the univariate gene list were 5829 and 5650, respectively, suggesting they are unlikely to be included as predictors in traditional gene-based prediction models.

3. Conclusion

In this paper, we have described a general strategy for constructing survival prediction models by integrating biological knowledge with gene expression data. We have shown that these pathway-based models have improved prediction accuracy and interpretability over gene-based prediction models. In addition to identifying gene categories associated with outcome, the proposed approach also carries out additional within-category selection to select important genes within the gene sets. These genes can provide starting points for carrying out additional experiments to understand the disease processes. The power and potential of the proposed strategy will increase as the coverage and quality of gene annotation databases improve. Although a comprehensive comparison of pathway-based versus gene-based models is beyond the scope of this paper, we believe that many other gene-based prediction models will also benefit from the proposed strategy.

4. Methods

Supervised PCA method

The details of the Supervised PCA method were described in Bair and Tibshirani (2004) and Bair et al. (2006). The idea behind the Supervised PCA method is that there is an underlying latent variable U that is possibly associated with the outcome. For the i th subject, we have model 1:

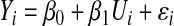(1)

Here, U represents the underlying biological process. We assume only a subset of genes from all the genes on each array is related to U. Our objective is then to select these relevant genes, estimate U, and fit model 1.

We follow these detailed steps:

• 1. Compute association measure between each gene with outcome.

• 2. Select genes most associated with outcome using cross-validation.

• 3. Estimate principle component scores using only the selected genes.

• 4. Fit regression with outcome using model 1.

In step 1, an association measure with outcome is computed for each gene separately. This can be obtained by fitting linear, logistic, or proportional hazards models for continuous, binary or survival outcomes respectively with a single gene as the predictor and take the score statistics for the predictor (gene) as the association measure. For linear regression, this measure is simply the standardized regression coefficient.

In step 2, a cross-validation procedure is used to select relevant genes by fitting model 1 to leave-out samples. Specifically,

• a. Pre-determine a set of threshold values.

• b. For a given threshold value, select only genes with association measure above it. For each cross-validation (CV) fold, compute PCA scores using training data and save coefficients of the PCA scores (these are the eigenvectors).

• c. Apply these coefficients to leave-out samples to obtain PCA scores for leave-out samples. Fit model 1 to leave-out sample, calculate log-likelihood ratio statistics (LRT) associated with first PCA score.

• d. Do this for each CV fold, and average LRTs over all folds. Select threshold value to be the one corresponding to largest average LRT for leave-out samples in CV.

In step 3, the estimation of PC scores for selected genes can be computed using Singular Value Decomposition. Briefly, let X be an N × p matrix with columns corresponding to standardized gene expression values (with mean 0 and variance 1) of selected genes, so there are N samples and p genes. Let r = rank(X), the kth PC score is z_k = Xα_k where α_k is unit length eigenvector of covariance matrix S = X^t X/(N − 1) corresponding to kth largest eigenvalue λ_k, and var(z_k) = λ_k.

The singular value decomposition (SVD) of X is

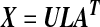(2)

where 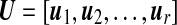is an N × r matrix where 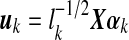is scaled kth principal component score, these are linear combinations of gene expression values corresponding to columns of matrix X. 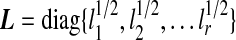is an r × r diagonal matrix where l_k is kth eigenvalue of 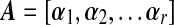is a p× r matrix where α_k is eigenvector of covariance matrix S, which are also coefficients for defining PC scores. Note that since kth eigenvalue of covariance matrix S is λ_k = l_k/(N − 1), we have var(u_k) = 1/(N − 1). Therefore, SVD provides not only the coefficients and standard deviations for the PCs with L and A matrices, but also the PC scores of each observation with matrix UL.

L₁-regularized Cox proportional hazard models

The Cox proportional hazard model for survival model has the form

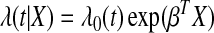(3)

where λ₀(t) is baseline hazard function and β is the coefficients vector for predictors X (Cox, 1972). The parameter β is the maximum likelihood estimate from partial likelihood

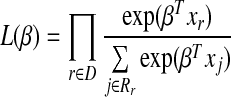(4)

where D is the set of indices for the failures and R_r is the set of indices for patients at risk at time t_r.

For general linear regression, Tibshirani (1996) proposed the “Lasso” method as a variable selection strategy using L₁ penalty. This method is attractive in the high-dimensional problem setting, because it can shrink coefficients for some of the predictors to exactly zero. For survival analysis, a similar strategy was proposed for L₁-penalized Cox regression model to estimate β with regularization:

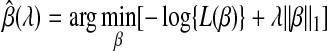(5)

where L(β) is the partial likelihood and λ > 0 is the regularization parameter (Tibshirani, 1997). To increase computational efficiency of the iteratively reweighted least squares (IRLS)-based linearization optimization method used in Tibshirani (1997), especially for large p and small n situation, a more efficient algorithm was recently developed by Park and Hastie (2007) for generalized linear models and Cox models. This algorithm uses the predictor-corrector method to determine the entire path of coefficient estimates as parameter λ varies. The optimal λ value is chosen by cross-validation.

In this paper, we used the method of Park and Hastie (2007) for fitting the L₁-regularized Cox proportional hazard models for simulation data and real data (for simplicity, we called this method “Lasso”). For gene level analysis, the Lasso was fitted using single gene expression values as predictors. For pathway-based model, the supergenes (estimated from Supervised PCA) from each gene category were used as predictors for Lasso regression models. The R package glmpath was used for fitting Lasso models.

K-means clustering method and the Gap statistic

The K-means clustering method is a simple but very useful unsupervised data partition algorithm. To apply this method, first, the number of clusters k is pre-determined for n data points. Next, k-clusters are obtained by minimizing the squared error function

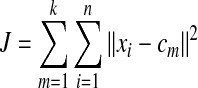(6)

where x_i is the i th data point and c_m is the centroid of cluster m. Initially, the data points are randomly assigned to each cluster and centroids are calculated for each cluster, then the data points are assigned to the closest cluster by measuring the distance between the data point and centroids. These procedures are iterated until the assignments of all data points do not change.

To avoid arbitrariness for the number k, the Gap statistic (Tibshirani, 2001) was proposed to estimate the optimal number of clusters for expression values of genes not assigned to any pathway. In our data, each observation is represented by x_ij for 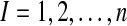genes and 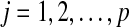individuals. Suppose all non-annotated gene expression data has been grouped into k clusters, 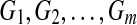, using K-means method, and let the sample size for each cluster be n_m. The within-cluster dispersion measure is then defined as

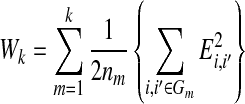(7)

where 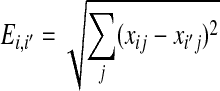is the Euclidean distance for two observations in the same cluster. To determine the optimal cluster number, we followed these steps:

• 1. Group the data into k clusters by K-means method and calculate W_k.

• 2. Permute the gene expression observations to generate the new data set B times and repeat step 1 to have 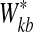each time.

• 3. Compute the Gap statistic

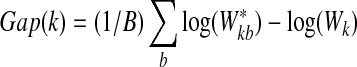(8)

and the standard deviation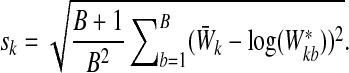

• 4. Choose the smallest number 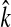that satisfies the condition

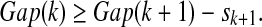
We used the R package SLmics for k-means clustering and the determination of the optimal number of clusters.

Pathway-based prediction models

Given a collection of gene sets from gene annotations databases such as GO and a gene expression dataset from a microarray experiment with survival outcome, there are several steps involved for the construction of pathway-based prediction models:

(1) Add grouping information to genes in expression data set. For the Wang et al. (2005) dataset, to integrate gene expression data with gene annotation database GO, we first mapped the 22283 transcripts from Affymetrix U133A gene chip to EntrezGene IDs and then associated each gene with the GO “Biological Process” (GO-BP) categories that include it as a member. When multiple probe sets for a gene were present, the median of all probe sets values was used for further analysis. After these steps, we were left with 13,441 genes, of which 9983 genes belong to 848 GO categories with gene set size more than 4, the remaining 3458 genes were divided into 4 groups with similar gene expression pattern using k-means clustering. The optimal number of clusters, which is 4 in this example, was determined by the Gap statistic (Tibshirani et al., 2001). Similarly, for the Miller et al. (2005) dataset, we mapped 848 GO categories, and the remaining 3558 genes were divided into seven clusters. The R packages hgu133a and SLmics were used for mapping and K-means clustering.

(2) Summarize information from each pathway. For each pathway, we applied the Supervised PCA method to select a subset of genes that are most associated with outcome. The supergenes or the principal component scores associated with largest eigenvalue were then estimated using only the selected genes. The first PC score is the linear combination of gene expression values with the largest sample variance among all unit-length linear combinations of gene expression values. For simple models, it can be shown that the PC scores provide an optimal approximation to the original variables (Bair and Tibshirani, 2006). The R package superpc was used for selection of relevant genes and estimation of PC score.

(3) Construct prediction model based on pathway information. For the Lasso model, the algorithm in Park and Hastie (2007) was used for fitting L₁ regularized Cox proportional hazard models. With estimated supergenes for each pathway, the R package glmpath was used for constructing pathway-based Lasso model.

For the Supervised PCA model, the number of principal component scores for the final prediction model was determined by cross-validation using training data only. The rankings of gene sets in Tables 3 and 4 were determined by absolute correlation between values of supergenes and the first principal component score in the final pathway-based prediction model. The R package superpc was used for constructing the pathway-based Supervised PCA model.

For gene-based prediction models, gene expression values from single genes were used as predictors, and the R packages glmpath and superpc were used for the Lasso and Supervised PCA models, respectively.

Performance evaluation for predicting survival outcomes

The time-dependent ROC method for censored survival outcomes was developed by Heagerty et al. (2000). For survival time prediction, let f (x) be the predictive model based on genes x, let D(t) = 1 or 0 be disease status for patient at time t. The time-dependent sensitivity and specificity at time t for cut-off point c, are defined as

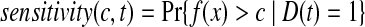(9)

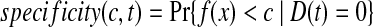(10)

and these conditional probabilities can be estimated using a nearest neighbor estimator for the bivariate distribution function of (x, T), where T is survival time. The time-dependent ROC curve at time t, ROC(t | f (x)), is a plot of sensitivity(c, t | f(x)) versus 1-specificity(c, t | f(x)) with all possible cut-off values c. The area under the time-dependent ROC curve is defined as time-dependent AUC(t). We used the R package survivalROC for the calculation and graphing of time-dependent ROC curves.

Acknowledgments

X.C. was supported in part by NHLBI SCCOR grant 1-P50-HL-077107. L.W. was supported in part by NICHD grant 5P30-HD015052-25 and NIH grant 1P50-MH078028-01A1.

Disclosure Statement

No competing financial interests exist.