Abstract
The effects of solvation and entropy play a critical role in determining the binding free energy in protein-ligand interactions. Despite the good balance between speed and accuracy, no current knowledge-based scoring functions account for the effects of solvation and configurational entropy explicitly due to the difficulty in deriving the corresponding pair potentials and the resulting double counting problem. In the present work, we have included the solvation effect and configurational entropy in the knowledge-based scoring function by an iterative method. The newly developed scoring function has yielded a success rate of 91% in identifying near-native binding modes with Wang et al.’s benchmark of 100 diverse protein-ligand complexes. The results have been compared with the results of 15 other scoring functions for validation purpose. In binding affinity prediction, our scoring function has yielded a correlation of R2 = 0.76 between the predicted binding scores and the experimentally measured binding affinities on the PMF validation sets of 77 diverse complexes. The results have been compared with R2 of four other well-known knowledge-based scoring functions. Finally, our scoring function was also validated on the large PDBbind database of 1299 protein-ligand complexes and yielded a correlation coefficient of 0.474. The present computational model can be applied to other scoring functions to account for solvation and entropic effects.
Keywords: scoring function, ligand-protein interactions, knowledge-based, desolvation, entropy
1 Introduction
Scoring functions that are used to rank putative protein-ligand complexes are crucial in structure-based drug design.1–5 Despite the developments of the past two decades, the scoring problem remains to be a challenge. There are three types of scoring functions: force-field, empirical, and knowledge-based scoring functions. Force-field based scoring functions use force field parameters to measure the binding energy between the protein and the ligand.6–8 Despite its lucid physical meaning, rigorous force field-based scoring functions are normally computationally expensive and sometimes involve empirical weighting coefficients that are difficult to be generalized.4,5 Empirical scoring functions are based on a set of weighted energy terms whose coefficients are derived by reproducing the binding affinity data of a training set of protein-ligand complexes with known three-dimensional structures.9–16 Although the empirical scoring function is computationally efficient because of its simple energy forms, its general applicability is training set-dependent.
The knowledge-based scoring functions offer a good compromise between the accuracy/general applicability and the computational speed.17–33 The principle behind knowledge-based scoring functions is simple, and its pairwise potentials are directly converted from the the occurrence frequency of atom pairs in a database by an inverse Boltamann relation34–37
| (1) |
where kB is the Boltzmann constant, T is the absolute temperature of the system, ρ(r) is the number density of the protein-ligand atom pair at distance r, and ρ*(r) is the pair density in a reference state where the interatomic interactions are zero. Because the potentials in eq 1 are extracted from the structures rather than reproducing the known affinities by fitting and because the training structural database can be very large and diverse, the knowledge-based scoring functions are robust and insensitive to the training set.24,25,38,39 Their pairwise feature also enables the scoring process to be as fast as the empirical scoring functions.
Despite significant progress, there exist limitations in knowledge-based scoring functions. One major limitation arises from the inaccessible reference state associated with ρ*(r) defined in eq 1.36 Most of the current knowledge-based scoring functions approximate ρ*(r) with an atom-randomized state by ignoring the effects of excluded volume, interatomic connectivity, etc.36 Researchers have introduced useful approximations of the reference state (e.g. refs 24 and 31). Yet, the reference state problem remains unsolved. A second limitation is that existing knowledge-based scoring functions do not explicitly include the contributions from solvation and entropy. One of the reasons may be due to the difficulty in determining the reference states for solvents and entropy. Another challenge may be from the parameterization of pairwise potentials, solvation and entropy, which belong to different energetic categories. Therefore, despite the importance of solvation and entropy in ligand binding,40–52 little effort has been made to account for their effects in the knowledge-based scoring functions.
In the present work, we have developed a new computational model that explicitly includes the contributions from solvation and entropy in the knowledge-based scoring functions. We chose ITScore as an example for illustration. The pair potentials of ITScore were recently developed using a novel iterative extraction method for protein-ligand interactions.38,39 The iterative method circumvents the long-standing reference state problem. The basic idea of the method is to iteratively improve the pair potentials by comparing the calculated and predicted pair distribution functions until the predicted pair distribution function converges to the experimentally observed one. ITScore has been extensively validated using diverse test sets on binding mode identification, binding affinity prediction, and virtual database screening.39,53–55 The good performance of ITScore makes it a nice candidate to assess the feasibility and necessity of including solvation and entropy in the knowledge-based scoring functions. The newly developed scoring function, named as ITScore/SE, was tested with three important benchmarks of diverse protein-ligand complexes. The results showed that the performance of ITScore/SE was significantly improved compared to ITScore and 14 other published scoring functions in both binding mode and affinity predictions.
2 Materials and Methods
2.1 Inclusion of the Solvation Effect
2.1.1 Formalism to account for the solvation effect
Ligand binding is a desolvation process, in which water plays two roles:46,49 strongly screening the electrostatic interactions among charged atoms, and causing hydrophobic effect for nonpolar atoms/groups and hydrophilic effect for polar atoms/groups. The dielectric screening effect is implicitly accounted for in the knowledge-based pair potentials during their derivations. The hydrophobic/hydrophilic effect has been proposed to be accounted for by a simple solvent-accessible surface area (SASA)-based energy term.56 Thus, the binding energy score of a protein-ligand complex can be expressed as follows
| (2) |
where uij(r) is the pair potential between the protein atom of type i and the ligand atom of type j at the interatomic distance r, σi is the solvation parameter of the atom of type i, and ΔSAi is the change of the SASA for the atoms of type i from the unbound state to the bound state.
In the present study, the SASA of an atom was calculated by using the algorithm of uniform atom-based spherical grids by Zou et al.46 The probe radius was set 1.4 Å. The van der Waals (VDW) radii for polar atoms O and N were reduced by 0.2 Å to account for a potential involvement in hydrogen bonding.57
2.1.2 The iterative method to extract the effective potentials and atomic solvation parameters
The effective potentials uij(r) and σi defined in eq 2 were simultaneously derived using a novel iteration method. The iterative method circumvents the long-standing reference state problem.34,38,55,58 The basic idea of the method is to improve the trial potentials iteratively by comparing the experimental and predicted structures until the potentials can reproduce the experimentally observed pair distribution functions for the training set of protein-ligand complexes.38 The detailed derivation of the effective pair potentials uij(r) and atomic solvation parameters σi are described as follows.
The iterative procedure for the pairwise potentials uij(r) can be expressed as follows38
| (3) |
where n stands for the iterative step, kB is the Boltzmann constant, and T denotes the system temperature. Without loss of generality, kBT was set to 1 during the iteration. λ is a parameter to control the convergence speed and was set to be 1/2 in this work.38,58 are the experimentally observed pair distribution functions in the native structures of the training database, and are the predicted pair distribution functions at the n-th iterative step that are calculated by using a Boltzmann-weighted average over the ensemble of native and decoy structures. The details about the calculations of the pair distribution functions are referred to our previous study.38
Similar to the pair potential uij(r), the atomic solvation parameter σi in eq 2 can be obtained by the following iterative equation
| (4) |
where is the SASA change of the atoms of type i divided by the total SASA change of all the atoms in the experimentally observed native structures between the bound and unbound state, and is calculated as follows:
| (5) |
where is the total SASA change of the atoms of type i in the native structure of the m-th complex in the training database, and M is the number of the complexes in the training set.
The is the the SASA change of the atoms of type i divided by the total SASA change of all the atoms for the lowest-energy modes predicted by the current potentials defined in eq 2 at the n-th iterative step, which is calculated by a Boltzmann-weighted average over the decoy structures as
| (6) |
where β = 1/kBT and is set to 1 as aforementioned. is the total SASA change of the atoms of type i for the l-th ligand orientation/decoy of the m-th complex in the training database at the n-th iterative step. is the binding energy score of this orientation calculated by eq 2 with the current potentials. L is the total number of ligand orientations/decoys generated for each complex (including the native structure).
Thus, given a guess of initial , the effective pair potentials uij(r) and atomic solvation parameters σi can be improved iteratively using Eqs. (3)–(6) until the convergence criterion is satisfied. In the present study, the initial were set to be a weighted combination of the potential of mean force and Lennard-Jones VDW potential,38 and the initial value of every σi was set to zero. The convergence criterion was set as for all i and j, in which S is the number of the divided shells for the reference sphere in the calculation of pair distribution functions38 and η is set to be 10−4 in this study. Our iterative method converges rapidly, usually within 50 steps.
2.1.3 The Training Database for the Iterations
In the present iterative procedure, the same training set was used as the set used in our previous study,38 which consists of 786 diverse protein-ligand complex structures from the Protein Data Bank (PDB)59. They are all crystal structures under near-neutral pH conditions (i.e. 6.5 < pH < 7.5) with resolution better than 2.5 Å. The training set also excludes nonconventional ligands such as RNA, DNA, covalently bound ligands, peptide inhibitors, or ligands with less than 5 or more than 66 heavy atoms. For each complex structure, up to 200 putative ligand orientations were generated by one-time calculation using the molecular docking program DOCK 4.0,60 serving as the decoy ensemble of the training set. The decoy structures were then used for the iterative extractions. Details of the preparation of the training set and the corresponding PDB entries are described in our previous work.38
In the training set, water molecules and hydrogen atoms were removed from the complexes. A total of 27 atom types were used to represent non-hydrogen atoms in the proteins and ligands, based on the definitions provided by the SYBYL software (Tripos, Inc.). The 27 atom types with their corresponding VDW radii are listed in Table 1.
Table 1.
List of 27 atom types and their corresponding van der Waals (VDW) radii used for the guess of initial pair potentials.
| atom type | description | VDW radii (Å) |
|---|---|---|
| sp/sp2 Carbon (C.1, C.2, C.ar and C.cat) | ||
| C2+ | carbon bonded to a positively charged nitrogen | 1.85 |
| C2− | carbon bonded to a negatively charged oxygen | 1.85 |
| C2N | carbon in amide groups | 1.85 |
| C2O | carbon bonded to O.2, but not belonging to C2+, C2− or C2N | 1.85 |
| C2F | carbon only bonded to carbon or hydrogen | 1.85 |
| C2X | other sp/sp2 carbon | 1.85 |
| sp3 Carbon (C.3) | ||
| C3F | carbon only bonded to carbon or hydrogen | 2.00 |
| C3X | carbon other than C3F | 2.00 |
| sp2 Nitrogen (N.2, N.ar, N.am and N.pl3) | ||
| N2N | nitrogen in amide groups | 1.75 |
| N2+a/NC | positively charged nitrogen | 1.75 |
| N21 | nitrogen bonded to one non-hydrogen atom | 1.75 |
| N22 | nitrogen bonded to two non-hydrogen atoms | 1.75 |
| N2X | nitrogen except N2N, N2+, N21 and N22 | 1.75 |
| sp Nitrogen (N.1) | ||
| N1 | all sp nitrogen | 1.75 |
| sp3 Nitrogen (N.3 and N.4) | ||
| N3+a/NC | N.4 or nitrogen bonded to one or two non-hydrogen atoms | 1.75 |
| N3X | sp3 nitrogen except N3+ | 1.80 |
| sp2 Oxygen (O.2) | ||
| O2 | all sp2 oxygen | 1.60 |
| sp3 Oxygen (O.3) | ||
| O31 | oxygen bonded to one non-hydrogen atom | 1.65 |
| O32 | oxygen bonded to two non-hydrogen atoms | 1.65 |
| negatively charged Oxygen (O.co2) | ||
| OC | all negatively charged oxygen | 1.60 |
| Sulfur (S.2, S.3, S.O, S.O2, etc.) | ||
| S1 | sulfur single-bonded to one non-hydrogen atom | 2.00 |
| SO | sulfur bonded to sp2 oxygen | 2.00 |
| SX | sulfur except S1 and SO | 2.00 |
| Phosphorus (P.3) | ||
| P | all phosphorus | 2.10 |
| Halogan (F, Cl, Br and I) | ||
| F | all fluorine | 1.55 |
| Cl | all chlorine | 2.03 |
| Brb | all bromine | 2.18 |
| Ib | all iodine | 2.35 |
| Metal ions | ||
| MET | metal ions (MG, ZN, CA etc.) | 1.20 |
The atom types ‘N2+’ and ‘N3+’ are grouped as the charged nitrogen ‘NC’ because they normally carry a positive charge.
The atom types ‘Br’ and ‘I’ are grouped as one atom type because of their low occurrences.
2.2 Inclusion of the Entropic Contributions
In addition to the solvation effect, we also added two additional energy terms to the derived knowledge-based scoring function defined in eq 2 to account for the ligand configurational entropy, which is partitioned into a conformational component and a vibrational component:52
| (7) |
2.2.1 Calculation of the ligand conformational entropy ΔGconf
The energy term for ligand conformational entropy arises from the loss of the torsional degrees of freedom for a flexible ligand upon binding. This entropic contribution can be crudely approximated by an empirical term proportional to the number of rotatable bonds in the molecule (Nrot):61,62
| (8) |
where ΔSconf stands for the loss of ligand conformational entropy upon binding and Wconf is a weighting coefficient to balance the entropic and VDW/electrostatic terms. As shown in the scoring function of AutoDock4, the weighting coefficients for ligand conformational entropy, van der Waals (VDW) and electrostatic energy terms are 0.298, 0.166 and 0.141 for the native complexes, respectively.62 In other words, in their formalism, the weighting coefficient for the ligand conformational entropy is about 1 ~ 2 times of the coefficient for the other two energy terms. Considering that the knowledge-based potentials defined in eq 2 roughly represents an overall contribution from VDW and electrostatic interactions, for simplicity, a mean value of 1.5 between 1.0 and 2.0 was used for the weighting coefficient Wconf in the present study. Namely,
| (9) |
2.2.2 Calculation of the ligand vibrational entropy ΔGvib
ΔGvib results from the loss of ligand translational and rotational degrees of freedom upon binding (i.e. vibrational entropy loss). It is thought that there exist multiple minima on the ligand binding energy landscape. The vibrational entropy in a specific energy minimum can be approximately proportional to the probability of a ligand binding mode found in the local minimum.63–65 Therefore, given clustered ligand modes generated by an appropriate docking program, the vibrational entropy contribution for the l-th mode can be approximated by
| (10) |
where Nnb is the number of the neighboring ligand modes within a rmsd cutoff from the l-th ligand binding mode. Here, the rmsd cutoff was set to 2.0 Å, same as the criterion for defining the success of binding mode prediction. Wvib is a scaling factor. It was estimated that the the vibrational entropy and the true binding energy have about the same order of magnitude.63,64 Therefore, in the present study, Wvib was set to 9.0, same as the scaling factor that roughly relates measured affinities (or true binding energies) to the binding scores calculated with our knowledge-based scoring function in eq 2. At T = 300K, kBT = 0.596 kcal/mol. Thus, the vibrational entropic contribution for the l-th ligand binding mode can be approximated by
| (11) |
2.3 Test sets for Validation
Three benchmarks of protein-ligand complexes were used to test the new iterative knowledge-based scoring function with explicit inclusion of solvation and ligand entropy, ITScore/SE. The first benchmark was the test set of 100 diverse protein-ligand complexes constructed by Wang et al., which includes 43 different proteins and covers a range of binding affinities spanning nearly 9 orders of magnitudes.66 For each complex in this set, 100 putative ligand binding conformations were generated using the docking program AutoDock.61,66 The second benchmark was the test set prepared by Muegge and Martin to validate their PMF, which consists of 77 protein-ligand complexes.24 The set covers five diverse classes: 16 serine protease complexes, 15 metalloprotease complexes, 18 L-arabinose binding protein complexes, 11 endothiapepsin complexes, and 17 different protein-ligand complexes. These two benchmarks were widely used to evaluate many different knowledge-based, force field-based, and empirical scoring functions, which facilitates our comparative evaluation of ITScore/SE. The third benchmark was the PDBbind database constructed by Wang et al.67,68 We downloaded the latest version (v2007) of the database that includes a total of 1300 protein-ligand complexes in its general set. After removing an inappropriate complex (PDB code: 1FO069), we obtained a large test set of 1299 protein-ligand complexes.
3 Results
3.1 Extracted Pairwise Potentials and Solvation Parameters
Using the iterative procedure and the training set described in the Methods section, the effective pair potentials uij(r) and atomic solvation parameters σi defined in eq 2 were simultaneously derived according to Eqs. (3) and (4). The extracted parameters were able to reproduce the experimentally observed pair distribution functions of the training set at the 41-th step, indicating the efficacy of our iterative method.
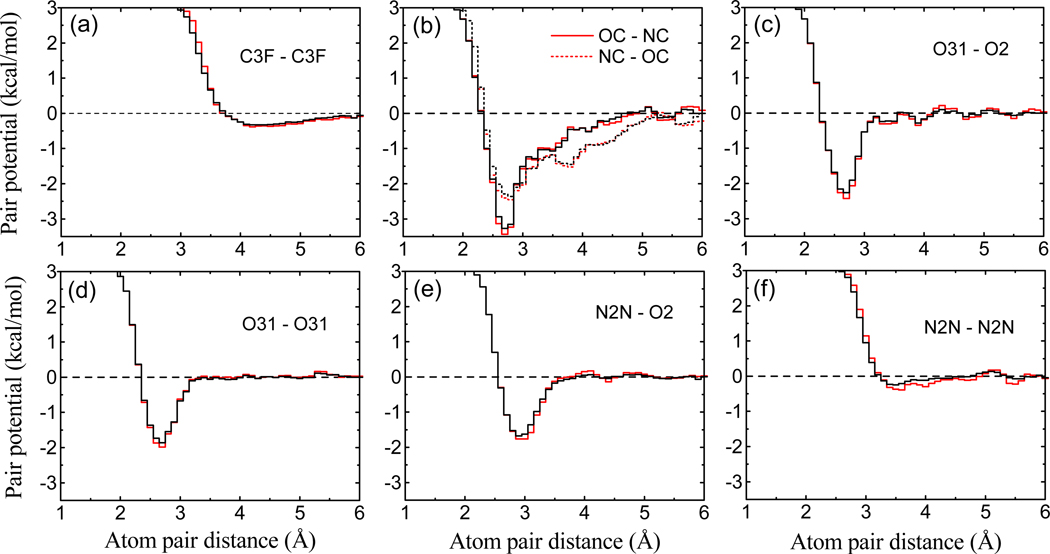
Figure 1 shows a selected set of derived pair potentials uij(r). For comparison, we also show the corresponding pair potentials from ITScore, which does not explicitly account for the solvation and entropic effect.38,39 It can be seen from the figure that the two sets of pair potentials are close, suggesting our iterative method is robust and yields consistent pair potentials for these two cases. Several notable characteristics can been observed from Figure 1, showing consistency with the experimental findings.38 Namely, the potential minimum around 4 Å for C3F-C3F corresponds to hydrophobic interactions between the atom pair. The valleys between 2.7 Å and 2.9 Å on OC-NC (or NC-OC), O31-O2, O31-O31, and N2N-O2 curves are consistent with hydrogen bond interactions between these atom types.70 The stronger interaction for the OC-NC (or NC-OC) pair than the other three pairs is due to the involvement of an additional favorable salt bridge, as OC and NC are oppositely charged. The weak interaction for N2N-N2N reflects that being both hydrogen bond donors they cannot form hydrogen bonds and repulse each other in electrostatics because of carrying the same type of partial charges.
Figure 1.
Comparison of six selected pair potentials for ITScore/SE (red lines) and ITScore (black lines). The first atom-type label refers to the protein atom, and the second to the ligand atom. The dashed line (y = 0) is plotted for reference.
Table 2 lists the derived atomic solvation parameters σi for the 27 atom types. Here, the parameter σi is a characteristic measure of an atom type on its favorableness of being desolvated, reflecting the hydrophobic/hydrophilic property of the atom type. Normally, the solvation parameter σi has a negative value for a hydrophilic atom type and a positive value for a hydrophobic atom type. For example, the non-polar atom types such as C3F and C3X have positive solvation parameters, indicating their preference in the buried/binding state resulting from their hydrophobicity. In contrast, the polar atom types such as OC, O2, O31, NC and N21 have negative solvation parameters, reflecting their hydrophilic features. In addition, unlike the individual atom ions, in the present ligand binding case, each atom type is part of a chemical group of ligand or protein. Therefore, the atomic solvation parameters actually reflect an overall effect of the associated functional group and depend not only on the atom type itself but also on the connecting atoms in the group.71–73. In other words, in such cases the sign of σi may alter the common rule. For example, the non-polar atom types C2− and C2+ have negative solvation parameters, unlike aforementioned C3F even though they are all carbon atoms. A second example is O32 (positive) vs OC (negative) despite both being oxygen atoms. The solvation parameters of C2− and C2+ are negative because their connecting atoms (OC and NC) are highly hydrophilic, which alter their hydrophobicity. Vice versa for O32, because its connecting atoms are often hydrophobic (e.g. C3X). These features of the solvation parameters are consistent with experimental findings.71–73
Table 2.
Solvation parameters σi of 27 atom types in the derived ITScore/SE. Some solvation parameters are not available because of the lack of the atom types or their low statistics.
| atom type | σi (kcal·mol−1 · Å−2) |
|---|---|
| C2+ | −0.048 |
| C2− | −0.010 |
| C2N | −0.002 |
| C2O | 0.020 |
| C2F | −0.001 |
| C2X | 0.002 |
| C3F | 0.017 |
| C3X | 0.018 |
| N2N | 0.020 |
| NC | −0.029 |
| N21 | −0.043 |
| N22 | −0.031 |
| N2X | N/A |
| N1 | N/A |
| N3X | N/A |
| O2 | −0.010 |
| O31 | −0.023 |
| O32 | 0.039 |
| OC | −0.027 |
| S1 | 0.038 |
| SO | 0.066 |
| SX | −0.065 |
| P | −0.008 |
| F | −0.068 |
| Cl | 0.005 |
| Br/I | 0.039 |
| MET | N/A |
In summary, the resulted scoring function (referred to as ITScore/SE) is expressed as
| (12) |
where the first term on the right side is the knowledge-based pairwise potential, the second term represents the desolvation energy of the protein and the ligand, and the last two terms are the ligand conformational and vibrational entropy, respectively (see Materials and Methods).
3.2 Validation of ITScore/SE Scoring Function
ITScore/SE was tested for its ability of identifying native-like binding modes and predicting experimentally measured binding affinities by using three benchmarks. The details are described as follows.
3.2.1 Test on the benchmark constructed by Wang et al
The first benchmark was the test set constructed by Wang et al., which consists of 100 diverse protein-ligand complexes and each complex has been generated 100 putative ligand conformations.66
Specifically, first, ITScore/SE was used to calculate the binding energy scores of the 101 ligand conformations (100 decoys plus one native structure) for each complex. These ligand conformations were then ranked from low to high according to their calculated scores. In the present work, the native binding mode of a complex was defined to be successfully identified if the rmsd value of the best-scored ligand conformation is ≤ 2.0 Å from the experimentally observed native structure, which is the default criterion unless otherwise specified.
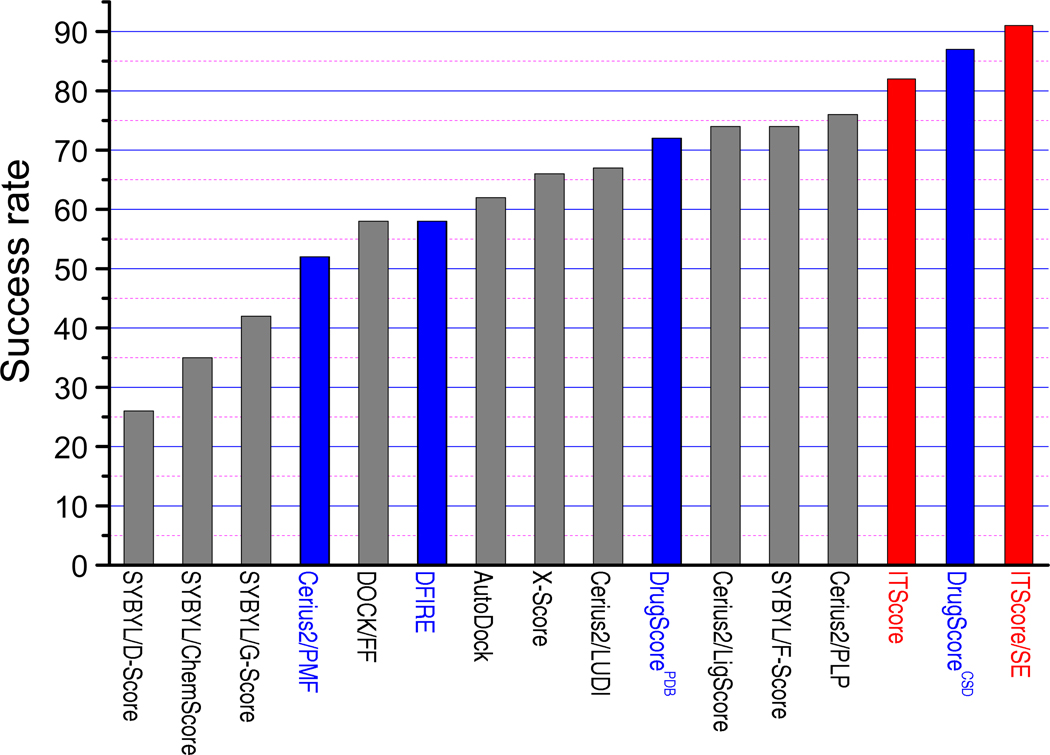
Table 3 and Figure 2 show the success rates of ITScore/SE with the criteria set from rmsd ≤ 1.0 Å to rmsd ≤ 3.0 Å. For comparison, the success rates of 15 other scoring functions extracted from the literature are also listed.27,31,39,66 It can be seen from the table that ITScore/SE achieved significant improvement in identifying native binding modes and yielded success rates of 80%, 86%, 91%, 95% and 95% for the rmsd criteria ranging from 1.0 to 3.0 Å, respectively, compared to 72%, 79%, 82%, 85% and 88% for ITScore which consists of the pair potentials only. Overall, ITScore/SE, DrugScoreCSD, and ITScore performed better than the other 13 scoring functions listed in the table, yielding success rates of 91%, 87% and 82%, respectively, when the commonly-used criterion of rmsd ≤ 2.0 Å was adopted (see Table 3 and Figure 2). The other three knowledge-based scoring functions, DrugScorePDB, DFIRE, and Cerius2/PMF, yielded success rates of 72%, 58%, and 52%, ranking at the 7-th, 11-th, and 13-th places, respectively.
Table 3.
Success rates of ITScore/SE, ITScore, and 14 other scoring functions for Wang et al.’s test set of 100 diverse protein-ligand complexes under different rmsd criteria.
| success rateb (%) | ||||||
|---|---|---|---|---|---|---|
| scoring functiona | function type | rmsd ≤ 1.0Å |
rmsd ≤ 1.5Å |
rmsd ≤ 2.0Å |
rmsd ≤ 2.5Å |
rmsd ≤ 3.0Å |
| ITScore/SE | iterative score | 80 | 86 | 91 | 95 | 95 |
| DrugScoreCSD27 | knowledge-based | 83 | 85 | 87 | – | – |
| ITScore39 | iterative score | 72 | 79 | 82 | 85 | 88 |
| Cerius2/PLP14, 15 | empirical | 63 | 69 | 76 | 79 | 80 |
| SYBYL/F-Score83 | empirical | 56 | 66 | 74 | 77 | 77 |
| Cerius2/LigScore84 | empirical | 64 | 68 | 74 | 75 | 76 |
| DrugScorePDB26 | knowledge-based | 63 | 68 | 72 | 74 | 74 |
| Cerius2/LUDI12,13 | empirical | 43 | 55 | 67 | 67 | 67 |
| X-Score16 | empirical | 37 | 54 | 66 | 72 | 74 |
| AutoDock61 | semiempiricalc | 34 | 52 | 62 | 68 | 72 |
| DFIRE31 | knowledge-based | 37 | 52 | 58 | 61 | 64 |
| DOCK/FF6 | force-field-based | 37 | 47 | 58 | 66 | 69 |
| Cerius2/PMF24 | knowledge-based | 40 | 46 | 52 | 54 | 57 |
| SYBYL/G-Score85 | force-field-based | 24 | 32 | 42 | 49 | 56 |
| SYBYL/ChemScore11 | empirical | 12 | 26 | 35 | 37 | 40 |
| SYBYL/D-Score6 | force-field-based | 8 | 16 | 26 | 30 | 41 |
The scoring functions are ranked by their success rates at rmsd ≤ 2.0 Å.
The results of the scoring functions other than ITScore/SE were obtained from literature.27, 31, 39, 66 There are no available data for DrugScoreCSD for the criteria of rmsd ≤ 25 Å and rmsd ≤ 3.0 Å.
Two important energy terms in the AutoDock scoring function are typical force field terms (VDW and electrostatic energies), but the weighting parameters are empirical61.
Figure 2.
Success rates of ITScore/SE, ITScore, and 14 other well-known scoring functions for Wang et al’s test set of 100 protein-ligand complexes under the criterion of rmsd ≤ 2.0 Å when the best-scored conformation was considered (see Table 3).
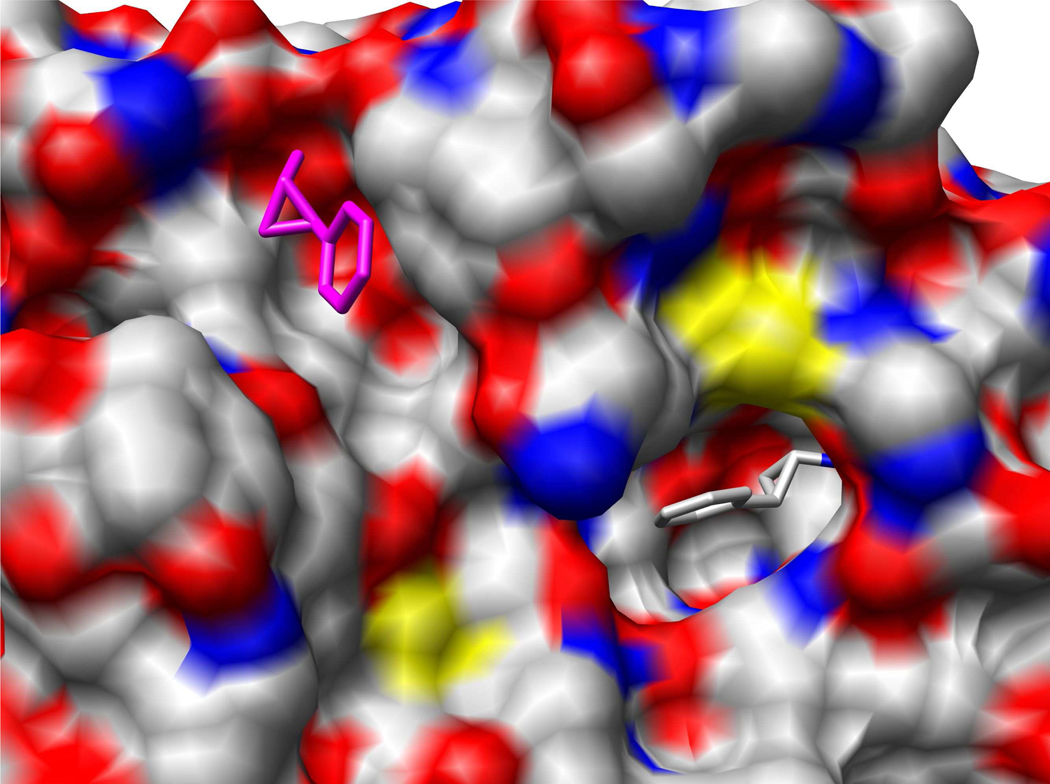
To show the important role of solvation effect in determining ligand binding modes, an example (PDB code: 1TNL) is displayed in Figure 3. In this case, ITScore/SE was able to predict the correct native binding mode, but ITScore failed with an rmsd of 15.5 Å for the top-ranked mode. 1TNL is a trypsin bound with a hydrophobic inhibitor, tranylcypromine.74 Because of the effect of solvation, the hydrophobic ligand tends to be buried in the protein rather than exposed to water.51 As predicted by ITScore/SE, which accounts for the desolvation effect, the ligand is embedded in a well-defined pocket (Figure 3). In contrast, lack of desolvation in a scoring function is expected to lead to a wrong prediction with this hydrophobic ligand. Indeed, as shown in Figure 3, the original ITScore without explicit desolvation predicted a wrong mode which is exposed on a cleft of the protein surface.
Figure 3.
The ligand binding modes predicted by ITScore/SE and ITScore for the complex 1TNL, respectively. The protein is represented by molecular surface and colored by atom types (i.e. C: gray, O: red, N: blue, S: yellow). The ligand is represented in stick mode. The ligand binding mode predicted by ITScore/SE (i.e., the native binding mode) is colored by atom type. The binding mode predicted by ITScore is colored in magenta. The figure was prepared by UCSF Chimera.82
To investigate the relative contributions of ITScore, solvation, and entropy, we also calculated the success rates of ITScore with the solvation term alone (ITScore/Solvation) and ITScore with the entropy term alone (ITScore/Entropy). The results are listed in Table 4 for comparison. It can be seen from the table that the improvement of the success rate due to including solvation is less than the improvement due to including entropy. Compared to ITScore (82%), ITScore/solvation improves the success rate by 4% (from 82% to 86%), whereas ITScore/entropy improves the success rate by 7% (from 82% to 89%). The reason may be explained as follows: The entropic effect is a global property of the ligand and the binding pocket (size and shape), and is therefore much less accounted for by atom type-dependent pairwise potentials in ITScore than the solvation effect. The solvation effect of each atom depends on the local environment of the atom and therefore can be better accounted for by atom type-dependent pairwise potentials. Thus, the explicit inclusion of entropy is expected to have more impact on the accuracy than the explicit inclusion of solvation for ITScore. Table 4 also shows that the inclusion of both solvation and entropy yielded the highest success rate of 91%.
Table 4.
Success rates of ITScore and ITScore with solvation (S) and/or entropy (E) for Wang et al.’s test set of 100 diverse protein-ligand complexes under different rmsd criteria.
| success rate (%) | |||||
|---|---|---|---|---|---|
| function type | rmsd ≤ 1.0Å |
rmsd ≤ 1.5Å |
rmsd ≤ 2.0Å |
rmsd ≤ 2.5Å |
rmsd ≤ 3.0Å |
| ITScore | 72 | 79 | 82 | 85 | 88 |
| ITScore/Solvation | 79 | 81 | 86 | 90 | 91 |
| ITScore/Entropy | 79 | 85 | 89 | 93 | 93 |
| ITScore/SE | 80 | 86 | 91 | 95 | 95 |
ITScore/SE was further examined for its ability of predicting binding affinities with the same benchmark, which was measured by the correlation coefficient between the calculated energy scores and the experimentally measured binding affinities as75
| (13) |
where N is the number of tested complexes, xk and yk are the experimental binding data and calculated energy scores for the k-th complex, and 〈 〉 is an arithmetic average over all the complexes.
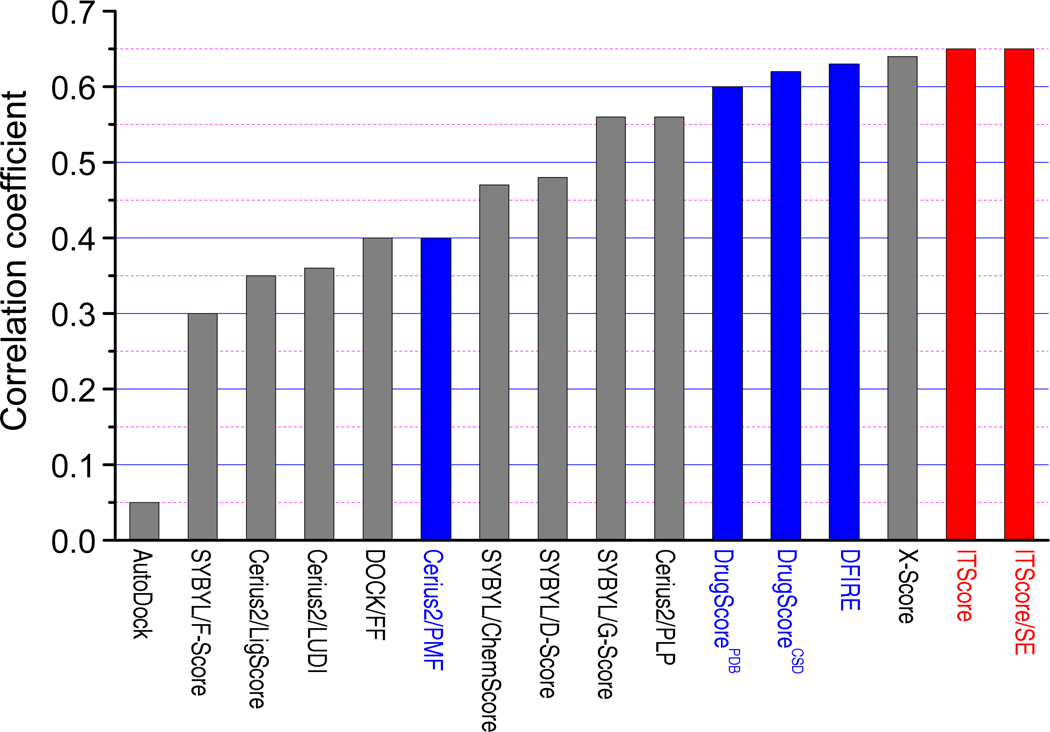
Table 5 and Figure 4 show the calculated correlation coefficients for ITScore/SE and 15 other scoring functions with Wang et al’s test set of 100 protein-ligand complexes. It can be seen that ITScore/SE and ITScore both yielded a good correlation coefficient of R = 0.65 and performed better than the other 14 scoring functions.
Table 5.
Correlation coefficients between the experimentally determined binding energies and the calculated binding scores using ITScore/SE, ITScore, and 14 other scoring functions for Wang et al.’s test set of 100 complexes.
| scoring functiona | function type | correlation (R) |
|---|---|---|
| ITScore/SE | iterative score | 0.65 |
| ITScore | iterative score | 0.65 |
| X-Score | empirical | 0.64 |
| DFIRE | knowledge-based | 0.63 |
| DrugScoreCSD | knowledge-based | 0.62 |
| DrugScorePDB | knowledge-based | 0.60 |
| Cerius2/PLP | empirical | 0.56 |
| SYBYL/G-Score | force-field-based | 0.56 |
| SYBYL/D-Score | force-field-based | 0.48 |
| SYBYL/ChemScore | empirical | 0.47 |
| Cerius2/PMF | knowledge-based | 0.40 |
| DOCK/FF | force field | 0.40 |
| Cerius2/LUDI | empirical | 0.36 |
| Cerius2/LigScore | empirical | 0.35 |
| SYBYL/F-Score | empirical | 0.30 |
| AutoDock | semiempirical | 0.05 |
Figure 4.
Correlation coefficients (R) of binding affinity prediction for ITScore/SE, ITScore, and 14 other well-known scoring functions with Wang et al’s test set of 100 protein-ligand complexes (see Table 5).
3.2.2 Test on the benchmark constructed by Muegge and Martin
ITScore/SE was next evaluated on its ability of binding affinity prediction using the PMF validation sets prepared by Muegge and Martin, which consists of 77 diverse protein-ligand complexes from five protein classes.24 The test sets have been commonly used to evaluate knowledge-based scoring functions.24,29,39,76,77
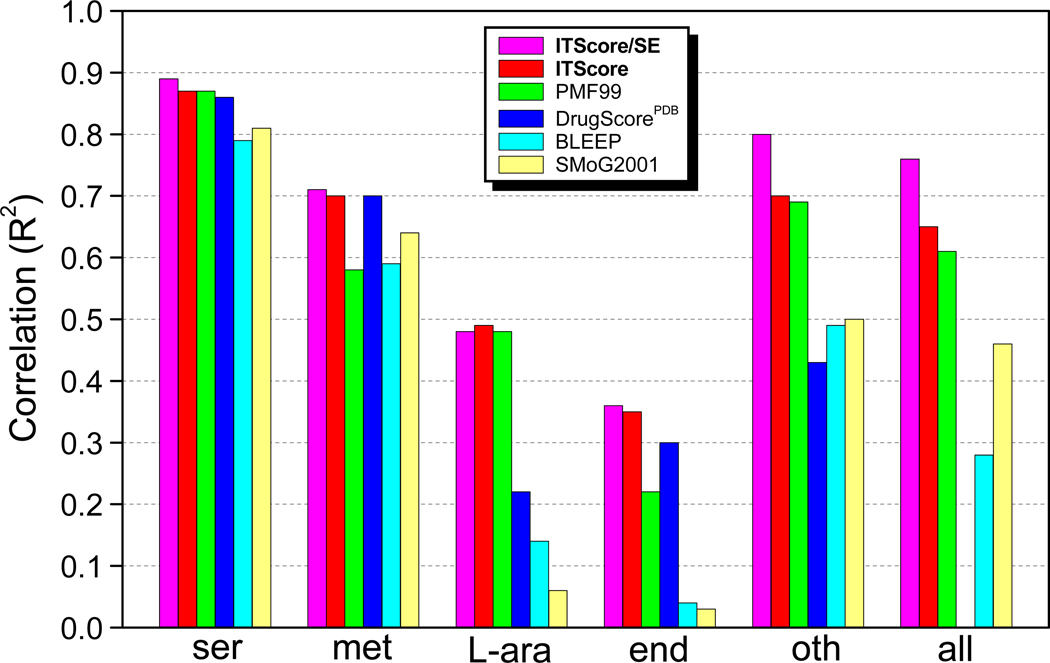
Table 6 and Figure 5 show the correlations of affinity prediction for ITScore/SE, ITScore, and four other well-known knowledge-based scoring functions: PMF by Muegge and Martin,24 DrugScorePDB by Gohkle et al.,76 BLEEP by Mitchell et al.,28 and SMoG2001 by Ishchenko and Shakhnovich.29 Table 6 and Figure 5 show a significant improvement in the performance of ITScore/SE (R2 = 0.76) over ITScore (R2 = 0.65).
Table 6.
Correlations of binding affinity prediction for ITScore/SE, ITScore, and four well-known knowledge-based scoring functions with the PMF validation sets of 77 diverse protein-ligand complexes constructed by Muegge and Martina.
| no. | set | no. of complexes |
correlationb (R2) | |||||
|---|---|---|---|---|---|---|---|---|
| ITScore/SE | ITScore | PMF99 | DrugScorePDB | BLEEP | SMoG2001 | |||
| 1 | serine protease | 16 | 0.89 | 0.87 | 0.87 | 0.86 | 0.79 | 0.81 |
| 2 | metalloprotease | 15 | 0.71 | 0.70 | 0.58 | 0.70 | 0.59 | 0.64 |
| 3 | L-arabinose binding prot. | 18(9)c | 0.48 | 0.49 | 0.48 | 0.22 | 0.14 | 0.06 |
| 4 | endothiapepsin | 11 | 0.36 | 0.35 | 0.22 | 0.30 | 0.04 | 0.03 |
| 5 | others | 17 | 0.80 | 0.70 | 0.69 | 0.43 | 0.49 | 0.50 |
| 6 | sets 1–5 | 77 | 0.76 | 0.65 | 0.61 | n/a | 0.28 | 0.46 |
The results for the scoring functions other than ITScore/SE were extracted from their original papers.24,29,39,76,77
Note that the correlation parameter in this table is the square of correlation coefficient (R2) rather than correlation coefficient itself (R) to keep consistency with the original data.
The crystal structures of the nine L-arabinose complexes that contain two ligand conformations were treated separately.
Figure 5.
Correlations of binding affinity predictions for ITScore/SE, ITScore, and four other well-known knowledge-based scoring functions (PMF99, DrugScorePDB, BLEEP, and SMoG2001) with the PMF test sets listed in Table 6.
Detailed examinations of the performance on each of Muegge and Martin’s test sets showed that ITScore/SE yielded significantly higher correlation than ITScore (R2 = 0.80 vs. 0.70) for set 5, which consists of 15 different protein-ligand complexes. This set is diverse, showing the robustness of the affinity predictions of ITScore/SE compared to ITScore. ITScore/SE did slightly better than ITScore on the 16 serine protease complexes (set 1, R2 = 0.89 vs. 0.87), 15 metalloprotease complexes (set 2, R2 = 0.71 vs. 0.70), and 11 endothiapepsin complexes (set 4, R2 = 0.36 vs. 0.35), and slightly less satisfactory on the 18 L-arabinose binding protein complexes (set 3, R2 = 0.48 vs. 0.49) (Table 6 and Figure 5).
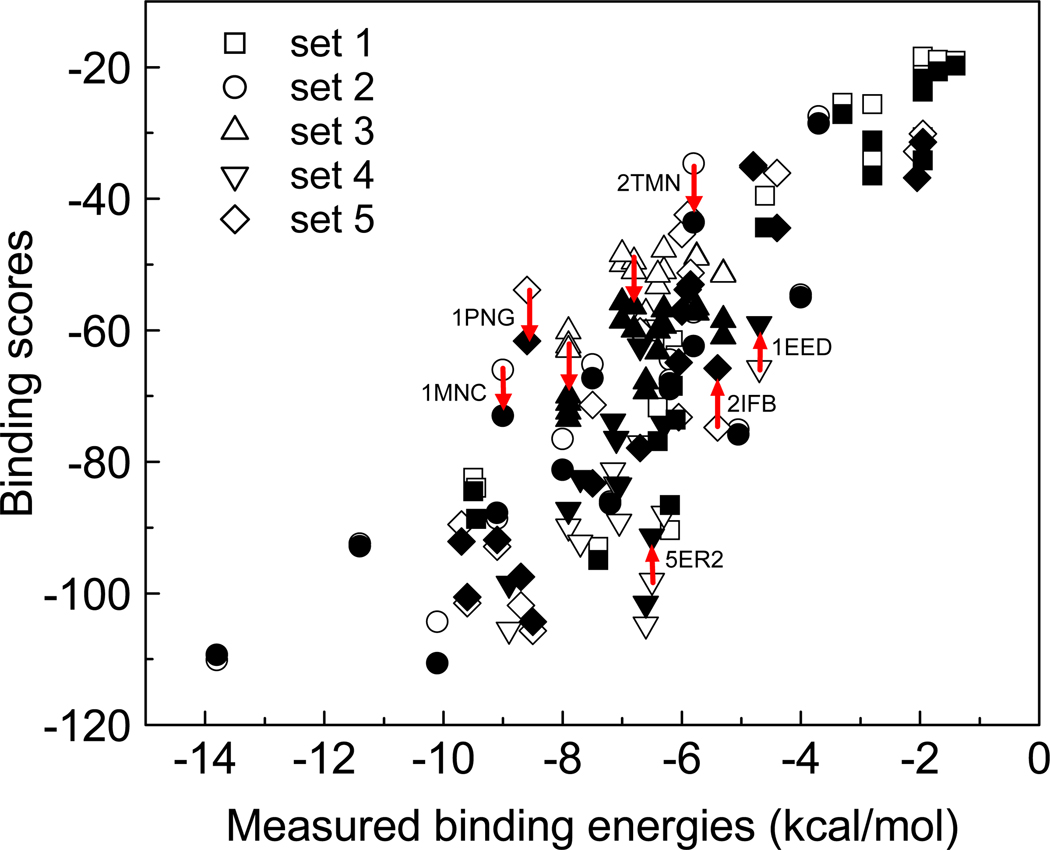
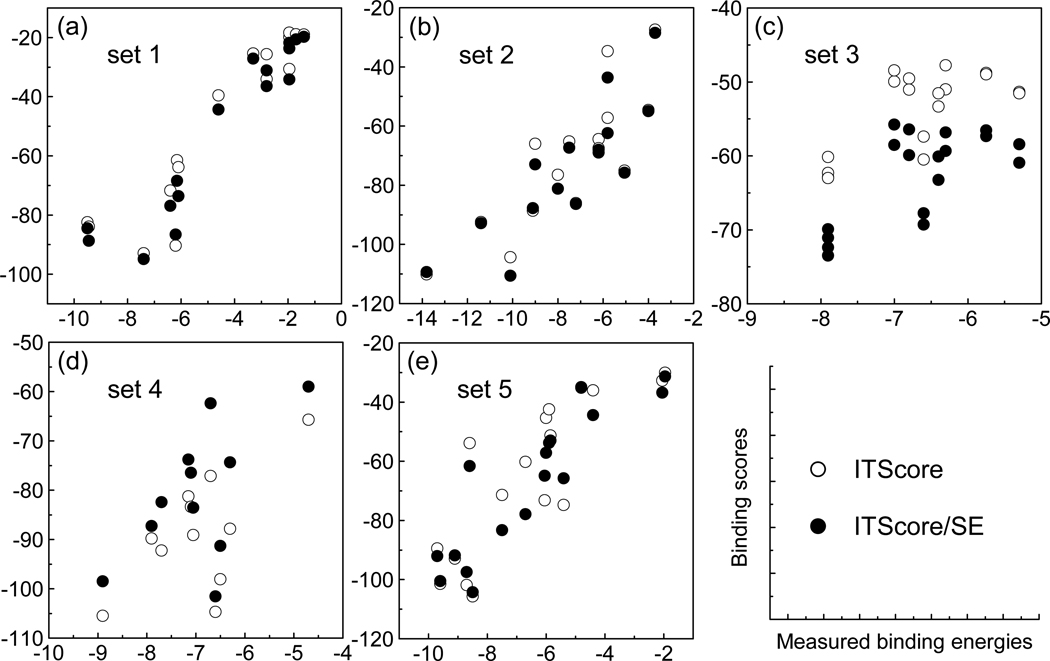
To further investigate how including solvation and entropy improved the affinity prediction, Figures 6 and 7 plot the calculated ITScore/SE scores vs the measured binding data for the 77 protein-ligand complexes. The results for ITScore are also displayed for comparison. It can be seen from Figure 6 that the better performance of ITScore/SE may benefit from the elimination of some outliers due to the inclusion of solvation and entropy. For example, ITScore/SE decreases the binding scores of some complexes such as 1MNC, 1PNG and 2TMN compared to the ITScore, whereas increases the binding scores of complexes like 1EED, 2IFB and 5ER2. Examining the five individual sets of the benchmark in more detail reveals that the set 4 of 11 endothiapepsin complexes benefit from the newly introduced energy penalty for ligand conformational entropy, which increases the ITScore/SE scores of the flexible ligands with many rotatable bonds in those complexes [Figure 7, (d)]. The lower ITScore/SE scores for set 2 (15 metalloprotease complexes) and set 3 (18 L-arabinose binding protein complexes) are largely due to the newly introduced desolvation energies [Figure 7, (b) and (c)]. Set 1 (16 serine protease complexes) and set 5 (17 other protein-ligand complexes) may attribute their higher correlation to the overall contributions of both desolvation and entropy [Figure 7, (a) and (e)].
Figure 6.
ITScore/SE (filled symbols) and ITScore (open symbols) scores vs the measured binding energies with the PMF validation sets of 77 diverse protein-ligand complexes constructed by Muegge and Martin. The arrows indicate several particularly beneficial changes in scoring between ITScore/SE and ITScore. Five different symbols stand for five different sets of protein-ligand complexes that are defined in Table 6.
Figure 7.
ITScore/SE and ITScore scores vs the measured binding energies for the five individual sets of the PMF benchmark (see Table 6). The legend applies to all the panels in this figure.
3.2.3 Test on the PDBbind database
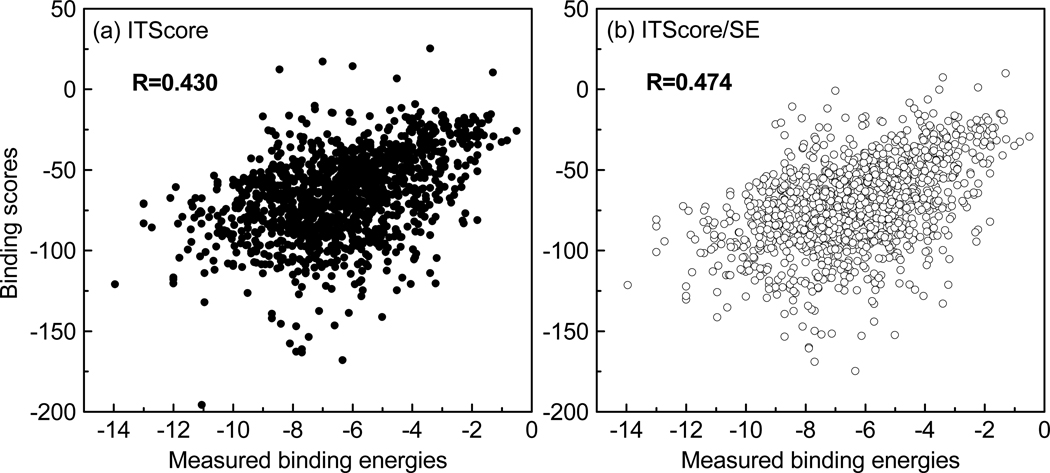
In addition, we also test the ability of ITScore/SE in binding affinity prediction on the large and challenging PDBbind database of 1299 protein-ligand complexes.67,68 Figure 8 shows the correlation between the calculated energy scores and the measured binding affinities for ITScore and ITScore/SE. It can be seen from the figure that compared to ITScore (R = 0.430), ITScore/SE shows a tighter distribution of points with a higher correlation coefficient of 0.474.
Figure 8.
ITScore/SE and ITScore energy scores vs the measured binding energies for the PDB-bind database of 1299 protein-ligand complexes.
4 Discussion
It is well-known that the solvation and entropic effects play a critical role in determining the binding free energy between protein and ligand. Failure to include the contributions of solvation and entropy may result in a wrong prediction in the ligand binding mode and a poor ranking of different protein-ligand complexes in binding affinity prediction. These effects are not explicitly accounted for in current knowledge-based scoring functions because of the difficulties in deriving the corresponding potentials for solvents and entropy. In the present study we have presented a computational model to include the solvation and entropic effects in ITScore—an iterative knowledge-based scoring function recently developed by our group.38,39 In the newly developed scoring function ITScore/SE, the solvation effect was included by using an atom-based solvent accessible surface area (SASA) term, and the entropic contribution was estimated by two empirical energy terms. Despite the simple forms of the solvation and entropic energy terms, ITScore/SE achieved significant improvement over ITScore in binding mode and affinity predictions on two widely-used benchmarks of diverse protein-ligand complexes.
The physics basis for adding the solvation and entropy terms to ITScore is as follows. Indeed, ITScore implicitly accounts for part of the solvation and entropy effects, because they are converted from the structural information of native protein-ligand complexes which result from the sum effect of all natural interactions including the solvation and entropy effects. However, desolvation depends on the local environment, and cannot be fully accounted by pair potentials. For example, an embedded salt bridge formed between the protein and the ligand would be much stronger than the salt bridge with the same separation distance that is exposed to the solvent. A second SASA-based energy term (referred to as a singlet potential term in ref 26) is needed to better characterize the solvation and hydrophobicity/hydrophilicity effects. The entropy effect is not a pairwise effect, and cannot be fully accounted for by the protein-ligand pairwise potentials. For example, the ligand conformational entropy depends on the ligand rotatable bonds and vibrational entropy depends on the size and shape of the binding pocket.
The next question that should be addressed about ITScore/SE is the possibility of double counting. It is expected that conventional knowledge-based pair potentials implicitly include part of the solvation and entropy effects, because they are converted from the structural information of native protein-ligand complexes which result from the sum effect of all natural interactions including the solvation and entropy effects.24 Therefore, explicit consideration of solvation or entropy in a knowledge-based scoring function could result in a double counting problem. However, a detailed analysis of individual energy terms in ITScore/SE suggests that double counting may be much less significant in this scoring function than in conventional knowledge-based scoring functions because of the following reasons. First, there is no double counting between the pair potentials and the solvation term because they were simultaneously adjusted/extracted from the native protein-ligand structures through our novel iterative procedure. Second, the conformational entropy loss is particularly important for large, highly flexible ligands, which are unlikely to form complexes with proteins in most cases and therefore are rare in the training database. Thus, the corresponding entropic energy information is missing in the training set and cannot be extracted when deriving the pair potentials, resulting in insignificant double counting effect between the pair potential terms and the ligand conformational entropy term. In addition, the conformational entropy defined in eq 8 does not affect ligand binding modes, and is therefore expected to be excluded from the pair potentials, which are derived from discerning ligand binding modes. Third, the vibrational entropic effect depends mainly on binding pocket dimensions and ligand geometric properties. Its little dependance on atom types suggests that the vibrational entropic effect may be largely excluded from the atom type-dependent pair potentials.
Another important issue is whether or not the potentials in ITScore/SE were overtrained due to some homologous proteins between the training database of 786 complexes and the test sets. To answer this question, we excluded 76 homologous protein-ligand complexes in the original training set that have λ 60% protein sequence identities with the 100 complexes in Wang et al’s benchmark or the 77 complexes in the PMF test set, and re-derived the potential parameters of ITScore/SE. The results for two ITScore/SE versions for Wang et al’s test set and the pmf sets are listed in Table 7. It can be seen from the table that there is no significant difference between the correlations of two ITScore/SE versions. The ITScore/SE from the training set of 786 complexes obtained sightly higher correlations for sets 1, 3, 6 and 7, while the ITScore/SE from the training set of 710 complexes yielded better performances for sets 2 and 4. The two ITScore/SE versions tied on set 5. The overall slightly lower correlation for the ITScore/SE from 710 complexes might be due to fewer protein-complexes in the training database, which may provide less statistics in structural information for potential extraction. Future training set would include additional non-homologous protein-ligand complexes in the abundant Protein Data Bank. The results suggest that our ITScore/SE potentials are not overtrained by the database of 786 protein-ligand complexes.
Table 7.
Correlation coefficients of binding affinity prediction for ITScore/SE derived from the training databases with and without the highly homologous proteins, using the pmf sets (Sets 1–6) and Wang, et al’s set (Set 7).
| No. | Set | No. of complexes |
Correlation coefficient (R) | |
|---|---|---|---|---|
| ITScore/SEa | ITScore/SEb | |||
| 1 | serine protease | 16 | 0.94 | 0.93 |
| 2 | metalloprotease | 15 | 0.84 | 0.85 |
| 3 | L-arabinose binding prot. | 18(9)c | 0.69 | 0.66 |
| 4 | endothiapepsin | 11 | 0.60 | 0.61 |
| 5 | others | 17 | 0.89 | 0.89 |
| 6 | sets 1–5 (Muegge and Martin’s set) | 77 | 0.87 | 0.85 |
| 7 | Wang et al’s set | 100 | 0.65 | 0.61 |
The results for ITScore/SE derived from the training database of 786 protein-ligand complexes.
The results for ITScore/SE derived from the training database of 710 protein-ligand complexes after excluding 76 homologous protein-ligand complexes.
Although the conformational entropic term defined in eq 8 does not affect the ligand binding mode prediction, the inclusion of the conformational entropy in a scoring function is important for binding affinity prediction, which is especially crucial in virtual database screening that ranks hundreds of thousands of different ligands against a protein target. Without considering the conformational entropy, docking programs have a bias toward large ligands, which can easily have favorable VDW energies. Introducing ligand conformational entropy term results in an energy penalty for large flexible ligands that have many rotatable bonds, thereby reducing false positives. Indeed, as shown in Figure 5, ITScore/SE significantly improves the correlation between predicted binding scores and measured affinities with the benchmark of 77 diverse complexes compared to ITScore.
Despite the present success, there exist limitations in ITScore/SE that need further investigation. In the present study, we used the number of the neighbors for a ligand mode defined in eq 10 to estimate ligand vibrational entropy. This fast empirical method can be regarded as a simplified version of a much more computationally expensive integral approach52,63,64,78–81 by taking advantage of the multiple ligand binding modes generated from docking programs, which are assumed to fully sample the binding site. From the physics implied in the configurational integral,52,78–81 the generated ligand modes would follow a Boltzmann distribution according to their binding scores. Therefore, a reliable estimation of eq 10 requires the use of a set of well-sampled ligand modes with Boltzmann distribution, which means that the accuracy of eq 10 may be docking program-dependent, even though the present study was validated by using AutoDock to generate appropriate ligand poses61. For docking programs that generate Boltzmann distribution-like ligand sampling, there will be no significant difference for the contribution of the ligand vibrational entropy of eq 10 to the success rate in binding mode prediction. Otherwise, the difference would be significant and could make the success rate worse. In this case, it would be better to remove the ligand vibrational entropy of eq 10 from eq 12 when implementing ITScore/SE, which can still yield a high success rate, e.g. 86% as in Table 4. To overcome this limitation, future studies would require a general method that does not depend on a specific docking program for the calculation of the ligand vibrational entropy.
To summarize, due to the importance of desolvation and entropy in ligand binding and the nature that the pairwise potentials cannot fully account for their effects, explicit inclusion of desolvation and entropy into the knowledge-based scoring function is needed. Predictions are improved especially for Muegge and Martin’s sets (affinity prediction) and Wang et al’s set (mode prediction). The much larger PDBbind set is a challenging set, and future studies would include how to achieve a high correlation coefficient in affinity prediction for this set.
5 Conclusion
We have presented a new iterative knowledge-based scoring function to explicitly include the contributions of solvation and entropy. The scoring function, referred to as ITScore/SE, was evaluated using three well-known benchmarks of diverse protein-ligand complexes. Despite the simplicity of the forms for desolvation and entropic energies, ITScore/SE achieved significant improvement in its performance over ITScore — an iterative knowledge-based scoring function that consists of the pair potentials only. For binding mode prediction, ITScore/SE yielded a success rate of 91% compared to ITScore (82%) for Wang et al.’s test set of 100 protein-ligand complexes, if the criterion of rmsd ≤ 2.0 Å was used. For binding affinity prediction, ITScore/SE yielded a correlation of R2 = 0.76 between the calculated binding scores and measured binding energies for Muegge and Martin’s test sets of 77 protein-ligand complexes, compared to R2 = 0.65 for ITScore and R2 = 0.28 ~ 0.61 for four other well-known knowledge-based scoring functions. In addition, ITScore/SE yielded an improved correlation coefficient of R = 0.474 with the large PDBbind database of 1299 protein-ligand complexes, compared to ITScore (R = 0.430). The improvement of ITScore/SE over ITScore suggests the necessity of including desolvation and entropy in the knowledge-based scoring functions. The present method is applicable to other knowledge-based scoring functions to account for solvation and entropy effects.
Acknowledgments
Support to XZ from OpenEye Scientific Software Inc. (Santa Fe, NM) and Tripos, Inc. (St. Louis, MO) is gratefully acknowledged. XZ is supported by NIH grant GM088517, Cystic Fibrosis Foundation grant ZOU07I0, and the Research Board Award of the University of Missouri RB-07-32. The work is also supported by Federal Earmark NASA Funds for Bioinformatics Consortium Equipment and additional financial support from Dell, SGI, Sun Microsystems, TimeLogic, and Intel.
References
- 1.Brooijmans N, Kuntz ID. Molecular recognition and docking algorithms. Annu. Rev. Biophys. Biomol. Struct. 2003;32:335–373. doi: 10.1146/annurev.biophys.32.110601.142532. [DOI] [PubMed] [Google Scholar]
- 2.Shoichet BK, McGovern SL, Wei B, Irwin JJ. Lead discovery using molecular docking. Curr. Opin. Chem. Biol. 2002;6:439–446. doi: 10.1016/s1367-5931(02)00339-3. [DOI] [PubMed] [Google Scholar]
- 3.Böhm HJ, Stahl M. The use of scoring functions in drug discovery applications. Rev. Comput. Chem. 2002;18:41–87. [Google Scholar]
- 4.Wang W, Donini O, Reyes CM, Kollman PA. Biomolecular simulations: Recent developments in force fields, simulations of enzyme catalysis, protein-ligand, protein-protein, and protein-nucleic acid noncovalent interactions. Annu. Rev. Biophys. Biomol. Struct. 2001;30:211–243. doi: 10.1146/annurev.biophys.30.1.211. [DOI] [PubMed] [Google Scholar]
- 5.Reddy MR, Erion MD. Free Energy Calculations in Rational Drug Design. New York: Kluwer Academic; 2001. [Google Scholar]
- 6.Meng EC, Shoichet BK, Kuntz ID. Automated docking with grid-based energy approach to macromolecule-ligand interactions. J. Comput. Chem. 1992;13:505–524. [Google Scholar]
- 7.Weiner SJ, Kollman PA, Case DA. A new force field for molecular mechanical simulation of nucleic acids and proteins. J. Am. Chem. Soc. 1984;106:765–784. [Google Scholar]
- 8.Weiner SJ, Kollman PA, Nguyen DT, Case DA. An all atom force field for simulations of proteins and nucleic acids. J. Comput. Chem. 1986;7:230–252. doi: 10.1002/jcc.540070216. [DOI] [PubMed] [Google Scholar]
- 9.Jain AN. Scoring noncovalent protein-ligand interactions: A continuous differentiable function tuned to compute binding affinities. J. Comput.-Aided Mol. Des. 1996;10:427–440. doi: 10.1007/BF00124474. [DOI] [PubMed] [Google Scholar]
- 10.Head RD, Smythe ML, Oprea TI, Waller CL, Green SM, Marshall GR. Validate a new method for the receptor-based prediction of binding affinities of novel ligands. J. Am. Chem. Soc. 1996;118:3959–3969. [Google Scholar]
- 11.Eldridge MD, Murray CW, Auton TR, Paolini GV, Mee RP. Empirical scoring functions: I. The development of a fast empirical scoring function to estimate the binding affinity of ligands in receptor complexes. J. Comput.-Aided Mol. Des. 1997;11:425–445. doi: 10.1023/a:1007996124545. [DOI] [PubMed] [Google Scholar]
- 12.Böhm HJ. The development of a simple empirical scoring function to estimate the binding constant for a protein-ligand complex of known three-dimensional structure. J. Comput.-Aided Mol. Des. 1994;8:243–256. doi: 10.1007/BF00126743. [DOI] [PubMed] [Google Scholar]
- 13.Böhm HJ. Prediction of binding constants of ptotein ligands: A fast method for the polarization of hits obtained from de novo design or 3D database search programs. J. Comput.-Aided Mol. Des. 1998;12:309–323. doi: 10.1023/a:1007999920146. [DOI] [PubMed] [Google Scholar]
- 14.Gehlhaar DK, Verkhivker GM, Rejto PA, Sherman CJ, Fogel DB, Freer ST. Molecular recognition of the inhibitor AG-1343 by HIV-1 Protease: Conformationally flexible docking by evolutionary programming. Chem. Biol. 1995;2:317–324. doi: 10.1016/1074-5521(95)90050-0. [DOI] [PubMed] [Google Scholar]
- 15.Gehlhaar DK, Bouzida D, Rejto PA. In: Rational Drug Design: Novel Methodology and Practical Applications. Parrill L, Reddy MR, editors. Vol. 719. Washington, DC: American Chemical Society; 1999. pp. 292–311. [Google Scholar]
- 16.Wang R, Lai L, Wang S. Further development and validation of empirical scoring functions for structure-based binding affinity prediction. J. Comput.-Aided Mol. Des. 2002;16:11–26. doi: 10.1023/a:1016357811882. [DOI] [PubMed] [Google Scholar]
- 17.Tanaka S, Scheraga HA. Medium- and long-range interaction parameters between amino acids for predicting three-dimensional structures of proteins. Macromolecules. 1976;9:945–950. doi: 10.1021/ma60054a013. [DOI] [PubMed] [Google Scholar]
- 18.Miyazawa S, Jernigan RL. Estimation of effective interresidue contact energies from protein crystal structures: quasi-chemical approximation. Macromolecules. 1985;18:534–552. [Google Scholar]
- 19.Sippl MJ. Calculation of conformational ensembles from potentials of mean force. J. Mol. Biol. 1990;213:859–883. doi: 10.1016/s0022-2836(05)80269-4. [DOI] [PubMed] [Google Scholar]
- 20.Vajda S, Sippl M, Novotny J. Empirical potentials and functions for protein folding and binding. Curr. Opin. Struct. Biol. 1997;7:222–228. doi: 10.1016/s0959-440x(97)80029-2. [DOI] [PubMed] [Google Scholar]
- 21.Verkhivker G, Appelt K, Freer ST, Villafranca JE. Empirical free energy calculations of ligand-protein crystallographic complexes. I. Knowledge-based ligand-protein interaction potentials applied to the prediction of human immunodeficiency virus 1 protease binding affinity. Protein Eng. 1995;8:677–691. doi: 10.1093/protein/8.7.677. [DOI] [PubMed] [Google Scholar]
- 22.Wallqvist A, Jernigan RL, Covell DG. A preference-based free-energy parameterization of enzyme-inhibitor binding. Applications to HIV-1-protease inhibitor design. Protein Sci. 1995;4:1881–1903. doi: 10.1002/pro.5560040923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.DeWitte RS, Shakhnovich EI. SMoG: de Novo design method based on simple, fast, and accutate free energy estimate. 1. Methodology and supporting evidence. J. Am. Chem. Soc. 1996;118:11733–11744. [Google Scholar]
- 24.Muegge I, Martin YC. A general and fast scoring function for protein-ligand interactions: A simplified potential approach. J. Med. Chem. 1999;42:791–804. doi: 10.1021/jm980536j. [DOI] [PubMed] [Google Scholar]
- 25.Muegge I. PMF scoring revisited. J. Med. Chem. 2006;49:5895–5902. doi: 10.1021/jm050038s. [DOI] [PubMed] [Google Scholar]
- 26.Gohlke H, Hendlich M, Klebe G. Knowledge-based scoring function to predict protein-ligand interactions. J. Mol. Biol. 2000;295:337–356. doi: 10.1006/jmbi.1999.3371. [DOI] [PubMed] [Google Scholar]
- 27.Velec HFG, Gohlke H, Klebe G. DrugScoreCSD-knowledge-based scoring function derived from small molecule crystal data with superior recognition rate of near-native ligand poses and better affinity prediction. J. Med. Chem. 2005;48:6296–6303. doi: 10.1021/jm050436v. [DOI] [PubMed] [Google Scholar]
- 28.Mitchell JBO, Laskowski RA, Alex A, Thornton JM. BLEEP – Potential of mean force describing protein-ligand interactions: I. Generating potential. J. Comput. Chem. 1999;20:1165–1176. [Google Scholar]
- 29.Ishchenko AV, Shakhnovich EI. Small molecule growth 2001 (SMoG2001): An improved knowledge-based scoring function for protein-ligand interactions. J. Med. Chem. 2002;45:2770–2780. doi: 10.1021/jm0105833. [DOI] [PubMed] [Google Scholar]
- 30.Ozrin VD, Subbotin MV, Nikitin SM. PLASS: protein-ligand affinity statistical score-a knowledge-based force-field model of interaction derived from the PDB. J. Comput.-Aided Mol. Des. 2004;18:261–270. doi: 10.1023/b:jcam.0000046819.20241.16. [DOI] [PubMed] [Google Scholar]
- 31.Zhang C, Liu S, Zhu Q, Zhou Y. A knowledge-based energy function for protein-ligand, protein-protein, and protein-DNA complexes. J. Med. Chem. 2005;48:2325–2335. doi: 10.1021/jm049314d. [DOI] [PubMed] [Google Scholar]
- 32.Mooij WTM, Verdonk ML. General and targeted statistical potentials for protein-ligand interactions. Proteins. 2005;61:272–287. doi: 10.1002/prot.20588. [DOI] [PubMed] [Google Scholar]
- 33.Yang CY, Wang RX, Wang SM. M-score: a knowledge-based potential scoring function accounting for protein atom mobility. J. Med. Chem. 2006;49:5903–5911. doi: 10.1021/jm050043w. [DOI] [PubMed] [Google Scholar]
- 34.Thomas PD, Dill KA. An iterative method for extracting energy-like quantities from protein structures. Proc. Natl. Acad. Sci. USA. 1996;93:11628–11633. doi: 10.1073/pnas.93.21.11628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Koppensteiner WA, Sippl MJ. Knowledge-based potentials – Back to the roots. Biochemistry (Moscow) 1998;63:247–252. [PubMed] [Google Scholar]
- 36.Thomas PD, Dill KA. Statistical potentials extracted from protein structures: How accurate are they? J. Mol. Biol. 1996;257:457–469. doi: 10.1006/jmbi.1996.0175. [DOI] [PubMed] [Google Scholar]
- 37.McQuarrie DA. Statistical Mechanics. New York: Harper Collins Publishers; 1976. [Google Scholar]
- 38.Huang S-Y, Zou X. An iterative knowledge-based scoring function to predict protein-ligand interactions: I. Derivation of interaction potentials. J. Comput. Chem. 2006;27:1866–1875. doi: 10.1002/jcc.20504. [DOI] [PubMed] [Google Scholar]
- 39.Huang S-Y, Zou X. An iterative knowledge-based scoring function to predict protein-ligand interactions: II. Validation of the scoring function. J. Comput. Chem. 2006;27:1876–1882. doi: 10.1002/jcc.20505. [DOI] [PubMed] [Google Scholar]
- 40.Reddy MR, Singh UC, Erion MD. Development of a quantum mechanics-based free-energy perturbation method: Use in the calculation of relative solvation free energies. J. Am. Chem. Soc. 2004;126:6224–6225. doi: 10.1021/ja049281r. [DOI] [PubMed] [Google Scholar]
- 41.Rocchia W, Sridharan S, Nicholls A, Alexov E, Chiabrera A, Honig B. Rapid grid-based construction of the molecular surface and the use of induced surface charge to calculate reaction field energies: Applications to the molecular systems and geometric objects. J. Comput. Chem. 2002;23:128–137. doi: 10.1002/jcc.1161. [DOI] [PubMed] [Google Scholar]
- 42.Grant JA, Pickup BT, Nicholls A. A smooth permittivity function for Poisson-Boltzmann solvation methods. J. Comput. Chem. 2001;22:608–640. [Google Scholar]
- 43.Baker NA, Sept D, Joseph S, Holst MJ, McCammon JA. Electrostatics of nanosystems: Application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wei BQ, Baase WA, Weaver LH, Matthews BW, Shoichet BK. A model binding site for testing scoring functions in molecular docking. J. Mol. Biol. 2002;322:339–355. doi: 10.1016/s0022-2836(02)00777-5. [DOI] [PubMed] [Google Scholar]
- 45.Still WC, Tempczyk A, Hawley RC, Hendrickson T. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc. 1990;112:6127–6129. [Google Scholar]
- 46.Zou X, Sun Y, Kuntz ID. Inclusion of solvation in ligand binding free energy calculations using the generalized-Born model. J. Am. Chem. Soc. 1999;121:8033–8043. [Google Scholar]
- 47.Srinivasan J, Miller J, Kollman PA, Case DA. Continuum solvent studies of the stability of RNA hairpin loops and helices. J. Biomol. Struct. Dyn. 1998;16:671–682. doi: 10.1080/07391102.1998.10508279. [DOI] [PubMed] [Google Scholar]
- 48.Lee MR, Duan Y, Kollman PA. Use of MM-PB/SA in estimating the free energies of proteins: application to native, intermediates, and unfolded villin headpiece. Proteins. 2000;39:309–316. [PubMed] [Google Scholar]
- 49.Liu H-Y, Kuntz ID, Zou X. Pairwise GB/SA scoring function for structure-based drug design. J. Phys. Chem. B. 2004;108:5453–5462. [Google Scholar]
- 50.Liu H-Y, Zou X. Electrostatics of ligand binding: Parametrization of the generalized born model and comparison with the Poisson-Boltzmann approach. J. Phys. Chem. B. 2006;110:9304–9313. doi: 10.1021/jp060334w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Feig M, Brooks CL. Recent advances in the development and application of implicit solvent models in biomolecule simulations. Curr. Opin. Struct. Biol. 2004;14:217–224. doi: 10.1016/j.sbi.2004.03.009. [DOI] [PubMed] [Google Scholar]
- 52.Chang CEA, Chen W, Gilson MK. Ligand configurational entropy and protein binding. Proc. Nat. Acad. Sci. USA. 2007;104:1534–1539. doi: 10.1073/pnas.0610494104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Huang S-Y, Zou X. Ensemble docking of multiple protein structures: Considering protein structural variations in molecular docking. Proteins. 2007;66:399–421. doi: 10.1002/prot.21214. [DOI] [PubMed] [Google Scholar]
- 54.Huang S-Y, Zou X. Efficient molecular docking of NMR structures: Application to HIV-1 protease. Protein Sci. 2007;16:43–51. doi: 10.1110/ps.062501507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Huang S-Y, Zou X. An iterative knowledge-based scoring function for protein-protein recognition. Proteins. 2008;72:557–579. doi: 10.1002/prot.21949. [DOI] [PubMed] [Google Scholar]
- 56.Eisenberg D, McLachlan A. Solvation energy in protein folding and binding. Nature. 1986;319:199–203. doi: 10.1038/319199a0. [DOI] [PubMed] [Google Scholar]
- 57.Li A-J, Nussinov R. A set of van der Waals and coulombic radii of protein atoms for molecular and solvent-accessible surface calculation, packing evaluation, and docking. Proteins. 1998;32:111–127. [PubMed] [Google Scholar]
- 58.Almarza NG, Lomba E. Determination of the interaction potential from the pair distribution function: An inverse Monte Carlo technique. Phys. Rev. E. 2003;68:1–6. doi: 10.1103/PhysRevE.68.011202. 011202. [DOI] [PubMed] [Google Scholar]
- 59.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Ewing TJA, Makino S, Skillman AG, Kuntz ID. DOCK 4.0: Search strategies for automated molecular docking of flexible molecule database. J. Comput.-Aided Mol. Des. 2001;15:411–428. doi: 10.1023/a:1011115820450. [DOI] [PubMed] [Google Scholar]
- 61.Morris GM, Goodsell DS, Halliday RS, Huey R, Hart WE, Belew RK, Olson AJ. Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function. J. Comput. Chem. 1998;19:1639–1662. [Google Scholar]
- 62.Huey R, Morris GM, Olson AJ, Goodsell DS. A semiempirical free energy force field with charge-based desolvation. J. Comput. Chem. 2007;28:1145–1152. doi: 10.1002/jcc.20634. [DOI] [PubMed] [Google Scholar]
- 63.Ruvinsky AM. Role of binding entropy in the refinement of protein-ligand docking predictions: Analysis based on the use of 11 scoring functions. J. Comput. Chem. 2007;28:1364–1372. doi: 10.1002/jcc.20580. [DOI] [PubMed] [Google Scholar]
- 64.Ruvinsky AM. Calculations of protein-ligand binding entropy of relative and overall molecular motions. J. Comput.-Aided Mol. Des. 2007;21:361–370. doi: 10.1007/s10822-007-9116-0. [DOI] [PubMed] [Google Scholar]
- 65.Chang MW, Belew RK, Carroll KS, Olson AJ, Goodsell DS. Empirical entropic contributions in computational docking: Evaluation in APS reductase complexes. J. Comput. Chem. 2008;29:1753–1761. doi: 10.1002/jcc.20936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Wang R, Lu Y, Wang S. Comparative evaluation of 11 scoring functions for molecular docking. J. Med. Chem. 2003;46:2287–2303. doi: 10.1021/jm0203783. [DOI] [PubMed] [Google Scholar]
- 67.Wang R, Fang X, Lu Y, Yang C-Y, Wang S. The PDBbind database: Methodologies and updates. J. Med. Chem. 2005;48:4111–4119. doi: 10.1021/jm048957q. [DOI] [PubMed] [Google Scholar]
- 68.Wang R, Fang X, Lu Y, Wang S. The PDBbind database: Collection of binding affinities for protein-ligand complexes with known three-dimensional structures. J. Med. Chem. 2004;47:2977–2980. doi: 10.1021/jm030580l. [DOI] [PubMed] [Google Scholar]
- 69.Reiser JB, Darnault C, Guimezanes A, Grégoire C, Mosser T, Schmitt-Verhulst AM, Fontecilla-Camps JC, Malissen B, Housset D, Mazza G. Crystal structure of a T cell receptor bound to an allogeneic MHC molecule. Nat. Immunol. 2000;1:291–297. doi: 10.1038/79728. [DOI] [PubMed] [Google Scholar]
- 70.Davis AM, Teague SJ. Hydrogen bonding, hydrophobic interactions, and failure of the rigid receptor hypothesis. Angew. Chem. Int. Ed. Engl. 1999;38:736–749. doi: 10.1002/(SICI)1521-3773(19990315)38:6<736::AID-ANIE736>3.0.CO;2-R. [DOI] [PubMed] [Google Scholar]
- 71.Wang JM, Wang W, Huo SH, Lee M, Kollman PA. Solvation model based on weighted solvent accessible surface area. J. Phys. Chem. B. 2001;105:5055–5067. [Google Scholar]
- 72.Hou TJ, Qiao XB, Zhang W, Xu XJ. Empirical aqueous solvation models based on accessible surface areas with implicit electrostatics. J. Phys. Chem. B. 2002;106:11295–11304. [Google Scholar]
- 73.Pei JF, Wang Q, Zhou JJ, Lai LH. Estimating protein-ligand binding free energy: Atomic solvation parameters for partition coefficient and solvation free energy calculation. Proteins. 2004;57:651–664. doi: 10.1002/prot.20198. [DOI] [PubMed] [Google Scholar]
- 74.Kurinov IV, Harrison RW. Prediction of new serine proteinase inhibitors. Nat. Struct. Biol. 1994;1:735–743. doi: 10.1038/nsb1094-735. [DOI] [PubMed] [Google Scholar]
- 75.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in Fortran 77: The Art of Scientific Computing. 2nd ed. New York: Cambridge University Press; 1992. [Google Scholar]
- 76.Gohlke H, Hendlich M, Klebe G. Predicting binding modes, binding affinities and ‘hot spots’ for protein-ligand complexes using a knowledge-based scoring function. Perspect. Drug Discov. Des. 2000;20:115–144. [Google Scholar]
- 77.Nobeli I, Mitchell JBO, Alex A, Thornton JM. Evaluation of a knowledge-based potential of mean force for scoring docked protein-ligand complexes. J. Comput. Chem. 2001;22:673–688. [Google Scholar]
- 78.Finkelstein AV, Janin J. The price of lost freedom: entropy of bimolecular complex formation. Protein Eng. 1989;3:1–3. doi: 10.1093/protein/3.1.1. [DOI] [PubMed] [Google Scholar]
- 79.Ajay, Murcko MA. Computational methods to predict binding free energy in ligand-receptor complexes. J. Med. Chem. 1995;38:4953–4967. doi: 10.1021/jm00026a001. [DOI] [PubMed] [Google Scholar]
- 80.Gilson MK, Given JA, Bush BL, McCammon JA. The statistical-thermodynamic basis for computation of binding affinities: A critical review. Biophys. J. 1997;72:1047–1069. doi: 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Swanson JM, Henchman RH, McCammon JA. Revisiting free energy calculations: a theoretical connection to MM/PBSA and direct calculation of the association free energy. Biophys. J. 2004;86:67–74. doi: 10.1016/S0006-3495(04)74084-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF Chimera – A visualization system for exploratory research and analysis. J. Comput. Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 83.Rarey M, Kramer B, Lengauer T, Klebe G. A fast flexible docking method using an incremental construction algorithm. J. Mol. Biol. 1996;261:470–489. doi: 10.1006/jmbi.1996.0477. [DOI] [PubMed] [Google Scholar]
- 84.Cerius2, version 4.6. Accelrys Inc.; http://www.accelrys.com/ [Google Scholar]
- 85.Jones G, Willett P, Glen RC, Leach AR, Talor R. Development and validation of a genetic algorithm for flexible docking. J. Mol. Biol. 1997;267:727–748. doi: 10.1006/jmbi.1996.0897. [DOI] [PubMed] [Google Scholar]