SUMMARY
Beta oscillations (12-30Hz) in local field potentials are prevalent in the motor system, yet their functional role within the context of planning a movement is still debated. In this study, a human participant implanted with a multi-electrode array in the hand area of primary motor cortex (MI) was instructed to plan a movement using either the second or fourth of five sequentially presented instruction cues. The beta amplitude increased from the start of the trial until the informative (second or fourth) cue, and was diminished afterwards. Moreover, the beta amplitude peaked just prior to each instruction cue and the delta frequency (0.5-1.5Hz) entrained to the interval between the cues - but only until the informative cue. This result suggests that the beta amplitude and delta phase in MI reflect the subject’s engagement with the rhythmically-presented cues and work together to enhance sensitivity to predictable and task-relevant visual cues.
INTRODUCTION
Local field potential oscillations in the beta frequency range (12-30Hz) are prevalent throughout the primate motor system, including the primary motor cortex (MI), the basal ganglia and the cerebellum (Courtemanche, Pellerin, & Lamarre, 2002; Kuhn et al., 2008; Kuhn, Kempf et al., 2008; Murthy & Fetz, 1992; Sanes & Donoghue, 1993) and yet little is known about their functional relevance. When researchers first observed beta oscillations in MI, they speculated that the transient increases in beta amplitude during tactile exploration might be related to some form of attention (Bouyer, Montaron, Vahnee, Albert, & Rougeul, 1987; Murthy & Fetz, 1992). However, most subsequent studies of LFP beta activity primarily focused on the relationship between beta oscillations and external cues or movement execution, without considering their relationship to internal states (O’Leary & Hatsopoulos, 2006; Roux, Mackay, & Riehle, 2006; Rubino, Robbins, & Hatsopoulos, 2006).
For example, it is well known that in humans and other primates, the strength of motor cortical oscillations in the beta frequency range (12-30Hz) varies in a characteristic way with reaching behaviors. Specifically, oscillations are enhanced during initial stationary hold and instruction periods, are attenuated during movement, and display an increase in power (“beta rebound”) during the post-movement period (Donoghue, Sanes, Hatsopoulos, & Gaal, 1998; Pfurtscheller & Lopes da Silva, 1999; Sanes & Donoghue, 1993; Williams, Soteropoulos, & Baker, 2009; Zhang, Chen, Bressler, & Ding, 2008). Some researchers have speculated that the increase in beta amplitude during instruction periods is linked to increases in attention level but there is currently little direct evidence supporting this view (Donoghue, Sanes, Hatsopoulos, & Gaal, 1998; Roux et al., 2006; Sanes & Donoghue, 1993). However, in other cortical areas, there is increasing evidence that beta oscillations are related to some aspect of attention. In human frontal eye fields (FEF), beta oscillations are suppressed during periods of spatial attention (Siegel, Donner, Oostenveld, Fries, & Engel, 2008). In the monkey prefrontal and posterior parietal cortices, features of beta oscillations are correlated with serial covert shifts of attention in a visual search paradigm (Buschman & Miller, 2007; Buschman & Miller, 2009). In mouse olfactory cortex, beta amplitude increases during a more difficult odor discrimination task (Kay et al., 2009; Martin, Beshel, & Kay, 2007).
Higher-frequency oscillations in the gamma frequency band (40-95Hz) have been even more robustly linked to attention in sensory areas (Fell, Fernandez, Klaver, Elger, & Fries, 2003; Fries, Womelsdorf, Oostenveld, & Desimone, 2008b; Vidal, Chaumon, O’Regan, & Tallon-Baudry, 2006). Many studies in visual cortex have shown that gamma frequency oscillations are enhanced during attentive periods (Fries, Schroder, Roelfsema, Singer, & Engel, 2002; Fries, Womelsdorf, Oostenveld, & Desimone, 2008a; Mitchell, Sundberg, & Reynolds, 2007; Sundberg, Mitchell, & Reynolds, 2009). In auditory cortex, ECoG gamma amplitude increases while humans attend to an auditory cue (Ray, Niebur, Hsiao, Sinai, & Crone, 2008); a similar phenomenon has been observed in human somatosensory cortex (Bauer, Oostenveld, Peeters, & Fries, 2006; Bauer, Oostenveld, & Fries, 2009).
Recently, lower frequency oscillations in the delta (1-4Hz) band in visual cortex have been shown to entrain to the rhythm of attended cues in a task where audio and visual cues are presented in alternating sequence (Lakatos, Karmos, Mehta, Ulbert, & Schroeder, 2008a). Peaks in the delta oscillations are aligned in time with periods of increased gamma power. This suggests that the entrainment of the delta oscillation to the rhythm of the task enhances gamma oscillations around the attended cues (Schroeder & Lakatos, 2009). Such cross-frequency effects are reported in other areas of cortex and may play a role in increasing sensitivity to incoming attended stimuli (Isler, Grieve, Czernochowski, Stark, & Friedman, 2008; Palva, Palva, & Kaila, 2005; Sauseng, Klimesch, Gruber, & Birbaumer, 2008; Steriade, Nunez, & Amzica, 1993).
In this study, we test the hypothesis that the strength of beta oscillations in primary motor cortex varies with attention around task-relevant instructive cues. Specifically, we hypothesize that if beta amplitude varies with attention, we should find that beta oscillations are enhanced around the presentation of task-relevant cues, and are attenuated when the same cues are irrelevant. Furthermore, if these cues are presented in a predictable, rhythmic fashion, we expect to see evidence that the nervous system can take advantage of this predictability and modulate the beta activity in a “top-down” fashion prior to the arrival of the informative cue. In this case, we expect low-frequency oscillations in the delta range to entrain to the rhythm of attended, but not unattended, cues.
RESULTS
We had the unique opportunity to test these hypotheses in the knob area of the primary motor cortex of a tetraplegic individual with a BrainGate neuroprosthetic implant (Hochberg et al., 2006). The participant performed an instructed-delay, center-out task in which he executed a chin movement from a central position to one of eight peripherally positioned targets. During the instructed-delay period, a sequence of 5 potential instructive cues were presented with a fixed inter-stimulus interval (ISI), and at the subsequent “GO” cue, the participant was instructed to move to the target indicated by the 2nd or 4th instruction (we refer to these two conditions as “Count 2” , and. “Count 4”, respectively). This design required the participant to attend to the task (in order to keep track of the number of cues) until the informative cue appeared. In addition to varying the serial position of the informative cue, we also varied the cognitive load; in the simpler, “spatial” version of the task, the location of the informative cue directly indicated the target to be reached. In the “associative” version of the task, the participant had to locate the peripheral target with the same color as the central target in order to know which target to acquire at the go cue (Figure 1). In what follows, we first describe the results for this associative task and then report the differences between the associative and spatial tasks.
Figure 1.
Two versions of the 5-instruction, 8-direction, center-out task with an instructed delay. Each task is separated into 4 different periods: the hold period, the instructed delay period, the reaction period and the movement period. Our study focuses on beta oscillation activity in the instructed delay period, where beta oscillations are most prevalent. The task in row A (Spatial Task) presents 5 sequential instructions to the participant, each flashing for 150ms followed by 500ms intervals during which the instruction disappeared. The participant was instructed to use the 2nd or the 4th instruction as the relevant cue (Count 2 or Count 4 conditions). For the task in row B (Associative task), the participant was instructed to match the color of the center target with one of the peripheral targets.
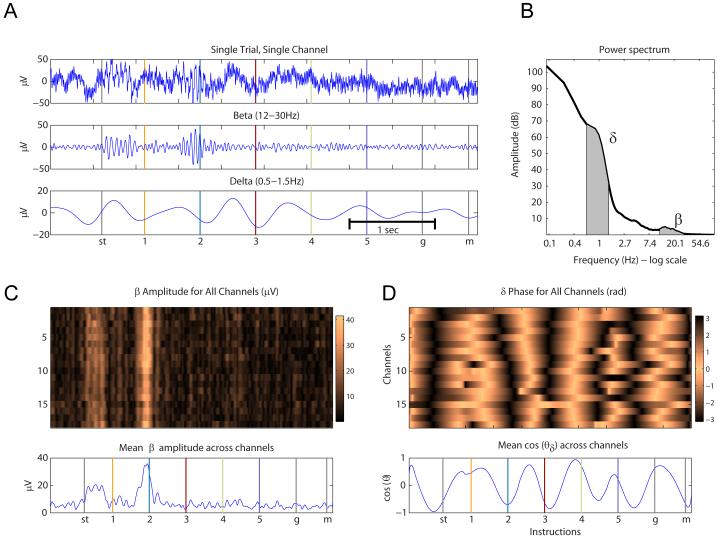
Using a multi-electrode array implanted in the arm area of the primary motor cortex, we recorded multiple local field potential signals (LFP) while the human subject performed the task. Single-trial LFP traces during the instructed-delay period (Figure 2A, top panel) reveal fast oscillations in the beta frequency range (Figure 2A, middle panel) as well as slower oscillations in the delta frequency range (Figure 2A, bottom panel). Power spectra measured around the onset of the informative cue demonstrate local peaks in the delta frequency band, around 0.5-1.5Hz, and in the beta frequency band, between 12-30Hz (Figure 2B). Although the amplitude of the beta oscillation (Figure 2C, upper panel), and the phase of the slower delta oscillation (Figure 2D, upper panel) vary with features of the task, these LFP features are highly redundant across different electrodes within the same trial (mean pair-wise correlation coefficients >0.76), and so they are averaged across electrodes in order to improve the signal-to-noise ratio (Figure 2C-D, lower panels).
Figure 2.
Beta and delta oscillations in local field potentials. (A) Single trial trace extracted from the Count 2 condition during the associative task for one channel (top), filtered between 12-30Hz (middle), and filtered between 0.5-1.5Hz (bottom). (B) Power spectrum from one channel, computed across 2 second windows and averaged over all trials, recorded during the Count 2 condition. Delta and beta frequency bands are highlighted in black. (C top) Amplitude of the signal (in μvolts) in the beta frequency band (12-30Hz) for a single trial in the Count 2 condition, for all channels. (C bottom) Mean beta amplitude, in μV, across all channels. (D top) Phase of the signal in the delta frequency band (0.5-1.5Hz), for all channels. (D bottom) The mean of the cosine of the phase of the delta cycle.
Variation in beta amplitude around the instructive cues
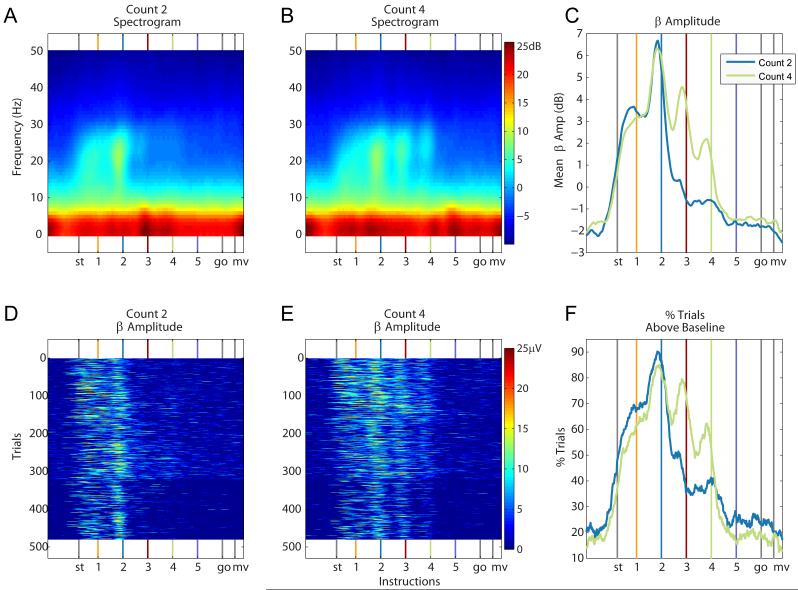
The averaged spectrograms (across trials, channels and experiments) for the Count 2 and Count 4 condition are shown in Figures 3A and 3B. Beta oscillations in the MI local field potential are prevalent throughout the hold and instructed delay periods, but are primarily concentrated between the first and the informative instruction cues. We refer to this period as the attended period. In the attended period, the amplitude of the beta oscillations (average 12-30Hz power) peaks 50ms before each instruction (Figure 3C). From the onset of the informative cue to the end of the movement period, the amplitude of the beta oscillations is diminished. The beta amplitude in the Count 4 condition is significantly higher at the third and fourth (informative) instruction cues than it is in the Count 2 condition, where the second cue is informative (T958, p<0.001 for third and fourth instructions; Table 1).
Figure 3.
Beta Amplitude under the Count 2 and 4 task conditions. (A) Spectrogram for the beta (12-30Hz) and delta (0.5-1.5Hz) frequency range for the Count 2 and (B) Count 4 conditions in the associative task. Beta amplitude increases before the onset of the instructions, leading up to the informative cue. The delta amplitude does not follow such a pattern. (C) Mean beta amplitude, in dB, for both task conditions. (D-E) Trial by trial beta amplitude in μVolts, for the Count 2 and Count 4 conditions, respectively. (F) Percent trials with mean amplitude significantly above the mean amplitude across a trial. The beta amplitude displays local peaks around each instruction until and including the informative instruction cue.
Table 1.
Beta amplitude analysis results for all tasks. C2A, C4A, C2S, C4S are the Count 2 Associative, Count 4 Associative, Count 2 Spatial and Count 4 Spatial tasks respectively. C4A-C2A shows the results of a paired t-test comparing beta amplitudes in the Count 4 condition to beta amplitudes in the Count 2 condition. C4A Peak shows p-values for a significance test comparing beta amplitude sampled 300ms before an instruction to the beta amplitude sampled 50ms before the same instruction (see Methods). P-values are only reported if they are smaller than 0.05. Beta amplitude was suppressed from the go cue to the end of the trial so we omitted the results at the start of movement.
| start of trial | Instructions | go cue | |||||
|---|---|---|---|---|---|---|---|
| Task | 1 | 2 | 3 | 4 | 5 | ||
| C2A | |||||||
| % trials above mean Mean amplitude ±standard error (dB) |
49% 1.32±0.26 |
68% 3.43±0.26 |
87% 5.26±0.23 |
36% −0.62±0.16 |
41% −0.62±0.16 |
26% −1.62±0.15 |
23% −1.81±0.14 |
| C4A | |||||||
| % trials above mean Mean amplitude ±standard error (dB) |
38% 0.69±0.24 |
62% 3.17±0.26 |
82% 5.83±0.24 |
73% 3.74±0.21 |
52% 1.27±0.17 |
16% −1.48±0.12 |
19% −1.47±0.13 |
| C2S | |||||||
| % trials above mean Mean amplitude ±standard error (dB) |
21% −2.45±0.12 |
32% −1.37±0.15 |
89% 7.80±0.28 |
56% 0.60±0.19 |
46% −0.45±0.16 |
29% −1.77±0.14 |
29% −1.70±0.12 |
| C4S | |||||||
| % trials above mean Mean amplitude ±standard error (dB) |
10% −2.34±0.11 |
24% −1.25±0.15 |
86% 7.20±0.28 |
81% 5.01±0.24 |
65% 2.48±0.20 |
21% −1.36±0.14 |
19% −1.67±0.12 |
| C4A-C2A : T479, p-value | n.s. | n.s. | n.s. | p<0.001 | p<0.001 | p=0.040 | n.s. |
| C4S-C2S : T479, p-value | n.s. | n.s. | n.s. | p<0.001 | p < 0.001 | p=0.031 | n.s. |
| C4A Peak: T479, p-value | - | 0.0143 | 0 | 0 | n.s. | n.s. | - |
| C4S Peak: T479, p-value | - | 0.0182 | 0 | n.s. | n.s. | n.s. | - |
| C2A Peak: T479, p-value | - | n.s. | 0 | n.s. | n.s. | n.s. | - |
| C2S Peak : T479, p-value | - | n.s. | 0 | n.s. | n.s. | n.s. | - |
This characteristic temporal profile of beta amplitude modulation is visible even in single trials (Figure 3D-E). For each 1ms time point, we report the percentage of trials (out of a total of 480 trials gathered over 3 experiments) that show significantly more power than the mean power across the entire trial (z-test, p<0.001; Figure 3F). In the Count 2 condition, the sharpest drop in this percentage occurs between the second and third instructions (87% to 36%), whereas in the Count 4 condition, the sharpest drop occurs later, between the fourth and fifth instructions (52% to 16%; Table 1). Similarly, a local peak in beta power 50ms before each instruction is also visible in single trials (Figure 3D-3E).
In addition to the sharp drop in beta amplitude after the informative cue, there is also a gradual decay in beta amplitude during the attended period. The mean amplitude of the local peaks, computed in 200ms windows around each instruction cue, decreases significantly from the 2nd to the 5th instructions (ANOVA, p<0.001; post hoc paired t-test between sequential cues, T479, p<0.001 in all three cases; Figure 3C).
Entrainment of delta phase
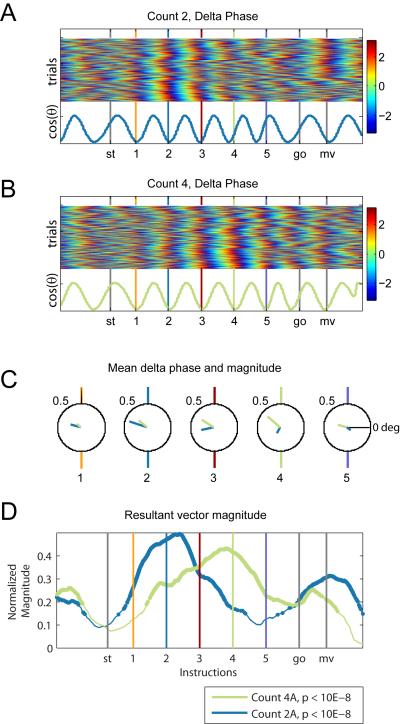
Delta oscillations in the MI local field potential are entrained to the rhythm of the task-relevant instruction cues. Since the power spectrum displays a peak at 1Hz (Figure 2B), we bandpass filtered the signal between 0.5Hz and 1.5Hz, and calculated the instantaneous Hilbert phase for all trials. The phase distribution across trials is significantly non-uniform around most of the cues (Rayleigh test; Table 2), and the mean resultant vector magnitude, a measure of phase entrainment, increases from the start of the trial to the informative cue and drops afterwards (C2A and C4A, Resultant Magnitude and p-value, Table 2).
Table 2.
Delta phase analysis results for all tasks. C2A, C4A, C2S and C4S are the Count 2 Associative, Count 4 Associative, Count 2 Spatial and Count 4 Spatial tasks respectively. For each task, we report the mean resultant vector magnitude at the cues and its significance (see Methods section for calculation of significance level). We also report the mean phase at the cues and the significance level of the Rayleigh test (see Methods section). P-values are reported if they are smaller than 0.05.
| Instructions | ||||||||
|---|---|---|---|---|---|---|---|---|
| Task | start of trial |
1 | 2 | 3 | 4 | 5 | go cue | mv |
| C2A | ||||||||
| Mean Resultant Vector Magnitude |
0.10 | 0.26 | 0.47 | 0.32 | 0.17 | 0.13 | 0.21 | 0.31 |
| p-value | 0.001 | 1.8E-12 | 7.36E-69 | 2.32E-13 | 4.13E-03 | 1.32E-05 | 2.42E-09 | 3.25E-21 |
| Mean phase | 298 | 165 | 162 | 193 | 242 | 324 | 265 | 148 |
| Rayleigh, p-value | 0.008 | 2.12E-15 | 6.84E-50 | 2.02E-22 | 8.37E-07 | 4.95E-04 | 5.22E-10 | 6.15E-21 |
| C4A | ||||||||
| Mean Resultant Vector Magnitude |
0.08 | 0.13 | 0.28 | 0.35 | 0.42 | 0.23 | 0.19 | 0.21 |
| p-value | 0.049 | 2.87E-05 | 1.40E-11 | 3.55E-29 | 7.81E-62 | 1.51E-07 | 2.50E-08 | 5.27E-08 |
| Mean Phase | 304 | 137 | 141 | 148 | 139 | 165 | 230 | 176 |
| Rayleigh, p-value | 0.045 | 4.78E-04 | 7.86E-17 | 8.51E-28 | 1.77E-38 | 1.79E-11 | 1.44E-08 | 5.59E-10 |
| C2S | ||||||||
| Mean Resultant Vector Magnitude |
0.05 | 0.15 | 0.11 | 0.05 | 0.14 | 0.20 | 0.32 | 0.26 |
| p-value | n.s. | 2.94E-09 | 1.25E-03 | 2.68E-01 | 3.46E-04 | 5.12E-10 | 1.69E-18 | 2.29E-15 |
| Mean Phase | 159 | 213 | 165 | 188 | 181 | 69 | 6 | 155 |
| Rayleigh, p-value | n.s. | 2.07E-05 | 2.99E-03 | 2.41E-01 | 7.82E-05 | 2.56E-09 | 5.78E-23 | 1.35E-14 |
| C4S | ||||||||
| Mean Resultant Vector Magnitude |
0.03 | 0.23 | 0.27 | 0.17 | 0.03 | 0.03 | 0.14 | 0.13 |
| p-value | n.s. | 1.19E-16 | 1.75E-16 | 5.93E-07 | 8.14E-01 | 7.45E-01 | 9.18E-12 | 3.11E-06 |
| Mean Phase | 14 | 224 | 226 | 168 | 61 | 101 | 14 | 153 |
| Rayleigh, p-value | n.s. | 1.50E-11 | 2.03E-16 | 1.52E-06 | 6.91E-01 | 7.25E-01 | 6.98E-05 | 4.02E-04 |
While the mean phase of the delta frequency oscillation is not identical across all five cues in either condition (Watson-Williams multi-sample test for equal means (WWm), p < 0.001), a post-hoc pairwise comparison reveals that the phase values are consistent during the attended period for each condition (Figure 4A-C; Table 2, Phase): in the Count 2 Associative task the mean phase is consistent at the 1st and 2nd instruction (Watson-Williams pairwise test (WWp), p=0.6309), and in the Count 4 Associative task, the mean phase is consistent from the 1st to the 4th instruction (WWp, p>0.1122).
Figure 4.
Delta phase in the Count 2 and 4 task conditions. Delta phase measured in radians in the Count 2 (A) and Count 4 (B) task conditions in the associative task across 480 trials, collected in three sessions. The cosine of the mean phase, for each time point, is displayed in the bottom rows. (C) Mean delta phase and mean resultant vector magnitude at each instruction, for the Count 2 (blue) and Count 4 (green) task conditions. For both conditions, the mean phases at the instructions are not significantly different from each other (Watson-Williams multi-sample test, p>0.1 see Table 2). However, the mean phases at the instructions following the informative cue are significantly different from the mean phases at the informative cue (D) Mean resultant vector magnitude, a measure of phase locking, for the Count 2 and Count 4 conditions. For the Count 2 condition, the mean resultant vector magnitude drops after the second instruction and for the Count 4 condition, the mean resultant vector magnitude drops after the fourth instruction.
To test whether the effects we describe above are specific to the 0.5-1.5Hz frequency range, we computed the mean resultant vector magnitude of the signal filtered in different 1Hz frequency windows, ranging from 0.5Hz to 5Hz. For frequencies larger than 1.5Hz, the mean resultant vector magnitude is not significant (z-test, p > 0.05; see Delta Phase in methods) and the distribution of phases at the instruction cues are not significantly different from uniform (Rayleigh test, p>0.05; see Supplemental Figure 1). Finally, we examined the variations in the amplitude of the delta-frequency oscillation to look for a similar relationship with the instruction cues across the various conditions. Unlike the phase effects we describe here, the delta amplitude does not appear to exhibit any consistent relationship with the instruction cues (see Figure 3A-B).
Spatial vs associative tasks
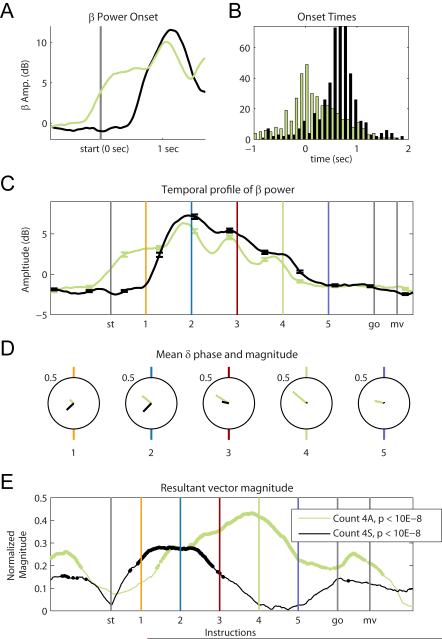
The spatial task is designed to require less of a cognitive load compared to the associative task. Consistent with this interpretation, response latencies after the go cue are significantly shorter in the spatial task (T479, p<0.001), with a mean reaction time of 325±102ms in the spatial task versus a mean reaction time of 542±207ms in the associative task. The timing of beta amplitude fluctuations is notably different between the spatial and associative task. In both the Count 2 and Count 4 conditions, the mean beta amplitude increases earlier for the more difficult associative task than it does for the spatial task (Figure 5A for Count 4 condition). The beta onset times (defined as an increase of two standard deviations above the 1.5 s pre-trial baseline) for all trials (Figure 5B) occur significantly earlier for the associative task than for the spatial task (T479, p<0.001). For the associative task, the mean beta onset occurs 172±508ms before the start of the trial whereas, for the spatial task, the mean onset time occurs 685±742ms after the start of the trial.
Figure 5.
Spatial versus associative tasks for Count 4 condition. (A) Mean beta amplitude for the Count 4 condition, around the start of the trial, for the associative (green) and the spatial (black) tasks. (B) Distribution of onset times for the two tasks. The onset of power is determined by finding the first timestamp at which the power is significantly higher than the baseline for more than three consecutive points, where the baseline is calculated in a 1.5s window prior to the start of a trial. The associative task’s onset times occur significantly earlier than the onset times for the spatial task for the Count 4 condition. (C) Mean beta amplitude as a function of time in both tasks. For the 1st to the 4th instructions only in the associative task, the mean amplitude at 50ms before all these instructions is significantly higher than at the mean amplitude sampled 300ms before (Table 1, C4A Peak). The spatial task does not exhibit peaks around these instruction cues. (D) Mean delta phase for each instruction for the spatial and associative tasks. See Table 2 for p-values for Rayleigh test at each instruction. (E) Mean resultant vector magnitude for spatial and associative tasks, Count 4 condition. The spatial task shows a larger mean resultant vector magnitude only around the first and second instructions. The associative task shows significant phase locking up to the 4th instruction. P-values were lower than 10E-8 for all points that are highlighted in black and green.
The overall temporal profile of the beta amplitude is similar for the spatial and associative tasks (Figure 5C), but while the associative task has local peaks around 50ms before the onset of the attended instruction cues, the spatial task elicits more of a sustained increase in beta amplitude during the attended period (Figure 5C; Table 2). However, the gradual decrease in power between sequential cues from the second to fifth instruction is maintained in the spatial task (paired t-test between sequential cues,T479, p<0.001 in all cases). Interestingly, the mean beta amplitude during the attended period is significantly higher in the spatial task than it is in the associative task (count 2 T479, p < 0.001; count4 T479, p<0.001).
The precise delta phase entrainment we observed in the associative task is not apparent in the spatial task. In the spatial task, the mean resultant vector magnitudes are generally lower and in the Count 4 condition, they drop before the informative instruction (Figure 5E; Table 2). Unlike the associative task, the mean phase values are not consistent across all the task-relevant instruction cues (WWm, p<0.001 for all instruction in the attended period).
DISCUSSION
Our results show that beta oscillations in the human primary motor cortex are enhanced during the attended period of an instructed delay task. Furthermore, we show that in a more difficult task, with longer reaction times, beta oscillations peak just before the onset of the task-relevant instruction cues and delta oscillations entrain to the rhythm of these cues. We speculate that this low frequency entrainment may act to change the gain of the beta oscillations so as to increase their amplitude around the onset of the task-relevant cues (Schroeder & Lakatos, 2009).
Beta oscillations in primary motor cortex
Experimental findings have lead to two common interpretations of the functional relevance of beta oscillations. The first is that they are related to maintaining a stable posture by inhibiting movement (Baker, Kilner, Pinches, & Lemon, 1999; Kuhn, Kempf et al., 2008) and the second that they are related to some aspect of movement planning or attention (Donoghue, Sanes, Hatsopoulos, & Gaal, 1998a; Murthy & Fetz, 1992; Murthy & Fetz, 1996a; Roux et al., 2006; Sanes & Donoghue, 1993; Schwartz et al., 2005).
Previous reports showed that the beta power increases during an instructed delay period (Donoghue, Sanes, Hatsopoulos, & Gaal, 1998a; O’Leary & Hatsopoulos, 2006), but did not test for the task-relevance of the instruction. Our study dissociates the activity related to task-relevant and task-irrelevant cues by displaying 5 sequential potential instruction cues and informing the participant to use to the 2nd or the 4th instruction to guide his future movement. Our findings are consistent with recent studies in prefrontal and parietal cortices that link the enhancement of synchronous beta-frequency band oscillations during visual search paradigms to top-down attention (Buschman & Miller, 2007; Buschman & Miller, 2009).
We find evidence that the amplitude of beta oscillations varies with attention; while the participant engaged in the task and attended to the number of cues that were presented, beta oscillations increased around the task-relevant instruction cues. However, beta oscillations were significantly suppressed after the appearance of the informative instruction cue (i.e., in the Count 2 condition, beta amplitude decreased sharply after the 2nd instruction, and in the Count 4 condition, the amplitude decreased sharply after the 4th instruction). The fact that the elevated beta amplitude didn’t persist throughout the entire instructed delay period (during which time, the participant was instructed to hold the cursor on the center target), conflicts with the view that beta oscillations are simply related to the maintenance of a stable posture or to the inhibition of a movement. Instead, it supports the view that beta oscillations may be related to the anticipation of task-relevant cues, as they are enhanced just prior to the onset of these cues.
Delta oscillations in primary motor cortex
In the associative task, the delta frequency is entrained to the rhythm of the task-relevant instruction cues throughout the attended period. Our findings support the view that entrained delta oscillations may act as an “internal metronome” for the appearance of task-relevant cues and are linked to the enhancement of the beta amplitude around each cue. In all associative tasks, the mean resultant vector magnitude increases from the first to the informative cue, and then decreases at the next cue indicating greater phase variability across trials. After the informative cue and along with this decrease in mean resultant vector magnitude, the mean phase of the delta frequency wanders away from the tightly-locked phase that we observe around the task-relevant cues (Figure 4C, Table 2). Although studies in nonhuman primates have shown that oscillations < 10Hz (perhaps involving the delta frequency) phase lock to single instruction cues and contain information about the movement direction in their amplitude (O’Leary & Hatsopoulos, 2006), our study focuses on a restricted lower frequency band (0.5-1.5Hz), and shows that the delta oscillation is phase-locked at all attended instruction cues but not at instruction cues following the informative cue. This suggests that the effects are not just visually evoked responses to instructive cues. Whereas previous studies demonstrate that delta oscillations phase lock to informative cues, this study shows that delta oscillations phase lock to all task-relevant cues, ie. to cues that are relevant in their timing and to a cue that is informative about movement direction. Together, these results suggest that delta oscillations entrain to the timing of the cues.
Although delta frequency oscillations are typically associated with slow wave sleep (Steriade, 2006), they have also been suggested to play a mechanistic role in the amplification of sensory inputs due to cross-frequency interactions (Contreras, Timofeev, & Steriade, 1996; Handel & Haarmeier, 2009; Sanchez-Vives & McCormick, 2000; Steriade et al., 1993). In primary sensory cortices, low frequency oscillations entrain to attended rhythmic cues and modulate the power of gamma frequencies (Kay et al., 2009; Lakatos, Chen, O’Connell, Mills, & Schroeder, 2007; Lakatos, Karmos, Mehta, Ulbert, & Schroeder, 2008b). The coupling of delta phase and beta power may be an example of a more general mechanism that enhances attention around predictable, periodic cues (Lakatos, Karmos, Mehta, Ulbert, & Schroeder, 2008b).
Effect of cognitive load
To vary the cognitive load of the task, we either directly indicated the target location (see Figure 1A), or required that the participant associate a color to a spatial cue in order to identify the instructed target location (see Figure 1B) (Treisman & Gelade, 1980). The participant reported having a more difficult time executing this associative task and took significantly longer to respond after the go cue compared to his performance during the spatial version of the task. Concomitant with the increased effort required in the associative task, the beta amplitude increases earlier with respect to the start of each trial, and shows more defined local peaks just prior to each task-relevant cue. In the associative task, the amplitude starts to increase around 100ms before the start of the trial whereas for the spatial task, it starts 600ms after the start of the trial. In the Count 4 associative task, the beta amplitude peaks just prior to the onset of the task-relevant cues whereas in the spatial task, the beta amplitude exhibits a more sustained elevation during the attended period.
In the associative task, the delta phase is consistent and phase-locked across trials at all task-relevant instruction cues, whereas in the spatial task, the phase is more variable after the second instruction, even in the Count 4 condition. It is interesting to note that in the attended period of the spatial task – along with a lack of sustained entrainment of the delta phase to the periodic cues – the beta oscillations do not exhibit well-defined local peaks (Figure 5C). This finding is consistent with the view that the delta phase-locking may be linked to the peaks in beta amplitude exhibited in the associative task. The differences we observe between the spatial and associative tasks appear to correspond to proposed distinction between “sustained” and “periodic” attention (Schroeder & Lakatos, 2009).
One potential confound in interpreting these phenomenon in terms of task difficulty is the fact that the participant performed the spatial task several months before he learned the associative task. It is therefore possible that we did not allot enough of an initial training period for the delta frequency to entrain to the periodic cues in the spatial task (i.e. for the participant to “learn the rhythm” of the five cues).
Decay in peak beta power
After the second cue, the local peak in beta power significantly decreases from one instruction to the next in both the spatial and associative tasks. This phenomenon is visible even in single trials. PET, fMRI and EEG studies have shown that cortical signals habituate in response to repeating stimuli (Fischer, Furmark, Wik, & Fredrikson, 2000; Fischer et al., 2003; Ravden & Polich, 1998). We speculate that this decay function reflects the habituation of the beta oscillations in response to the repeating instruction stimuli.
Relationship to attention
In order to perform the task successfully, the participant had to internally count the number of instruction cues so as to determine the informative cue (i.e. Count 2 or Count 4). By counting, a task that requires significant attentional resources (Wilder, Kowler, Schnitzer, Gersch, & Dosher, 2009), the patient could use the rhythm of the task to build up an expectancy of the timing of the task-relevant cues. We interpret the observed effects in the beta amplitude and delta phase as reflections of top-down, attentional processes that enhance sensitivity to incoming, task-relevant cues.
There are, however, alternate interpretations that must be considered. First, these effects could be a reflection of general arousal. Arousal has a variety of meanings. Arousal can be viewed as a transition in physiological state (e.g. from sleep to wakefulness) which affects the nervous system globally and is presumably temporally sluggish. According to this definition, it would be difficult to interpret the effects we observed as reflecting arousal because both the beta amplitude modulation and the delta phase entrainment are temporally precise with respect to the occurrence of the instruction cues. Arousal also has a more cognitive meaning which refers to an increased alertness in response to sensory cues, typically concomitant with increases in EEG beta and gamma amplitudes and increases in spike synchrony in sensory and motor areas of cortex (Pfaff, 2006; Munk, Roelfsema, Konig, Engel, & Singer, 1996; Roelfsema, Engel, Konig, & Singer, 1997; Steriade, 1996; Steriade, Contreras, Amzica, & Timofeev, 1996). This conception of arousal is actually quite consistent with our interpretation of enhanced sensitivity to task-relevant cues with the exception that our observed effects do not occur in response to sensory cues but in their anticipation. In our task, the participant could take advantage of the rhythm of the task and anticipate or expect the sensory cues. Though beta oscillations in MI have not been shown to increase with respect to the expectancy of a cue, spikes in MI have been shown to synchronize with respect to the expectancy of a task-relevant cue (Riehle, A. 1997) and spike synchrony is often associated to increased oscillatory activity in local field potentials (Roelfsema, Engel, Konig, & Singer, 1997; Munk, Roelfsema, Konig, Engel, & Singer, 1996).
An alternative interpretation is that the observed effects represent a general programming of a motor response. If this were the case, we might expect the increase in beta amplitude to occur only around the informative cue (i.e. 2nd or 4th instruction) because a motor response is only associated with this instruction. In fact, the beta amplitude is enhanced from the 1st to the informative instruction ie. for all task-relevant instruction cues. One could argue that a motor program is initiated automatically around each instruction whether or not it is task-relevant. However, one would then expect the same beta amplitude increase for the instruction cues that followed the informative cue, and we don’t observe this. Therefore, this is an unlikely interpretation. If the transient increase in beta amplitude signals the suppression of a just programmed motor response, we would expect to see this effect around every instruction cue, even those that follow the informative cue. Again this is not what we observed, and, therefore, not a likely explanation of our findings.
This study provides some insight into the functional role of beta oscillations in primary motor cortex and introduces their relationship to the phase of the delta oscillation, when the delta oscillation entrains to the rhythm of a task. It remains to be tested if the effects are particular to visual cues or apply to any attended sensory modality (Schroeder & Lakatos, 2009). Future studies that can take advantage of current source density analyses may yield more insight into the cross-frequency effects we describe in this paper and how they differ from those observed in sensory cortical areas. Our participant was involved in the BrainGate feasibility clinical study, which aims to provide a means for participants to control a computer cursor via a decoding algorithm that interprets spiking activity from multiple neurons recorded during intended arm movements. Beta oscillations may serve as a means to detect the participant’s readiness to make a movement – when the instruction is selected - in single trials, by monitoring when the power in the beta band is diminished.
EXPERIMENTAL PROCEDURES
Behavioral tasks
The participant was instructed to perform an instructed delay, center-out task by moving a cursor with his end effector to one of eight peripheral targets, positioned at 45 degree increments starting at 0 degrees, subtending a visual angle of 11.88° (12cm) from the center of the screen. The distance from the screen center to the participant’s eyes was 57cm. During the instructed-delay period, a sequence of five instruction cues were presented, one of which was informative about the movement direction while the others were not. The Count 2 condition refers to the task where the informative cue was the second instruction and the Count 4 condition refers to the task where the informative cue was the fourth instruction. The timing of the instructions preceding the informative cue could be used to predict the onset of the informative cue. As such, all instruction cues leading up to the informative cue were task-relevant. At the start of a trial, the participant was instructed to hold the cursor on the center target (hold period). After 500ms, five instruction cues were sequentially shown to the participant. Each instruction cue was flashed for 150ms followed by a blank screen for 500 ms for a total of 650 ms between instruction cue onsets. After the fifth cue, the center target turned green which acted as a go cue instructing the participant to initiate the movement.
Two versions of the task were used in the study to alter the cognitive load on the participant: a spatial and associative task. Each task version under either the Count 2 and Count 4 conditions was repeated on three separate experimental sessions on different days. In each experimental session, 20 trials were collected for each of the eight targets yielding a total of 160 trials for each task condition.
Spatial Task
Each instruction cue was composed of eight peripherally-positioned targets, one of which was a different color (see Figure 1A). The location of the differently colored target in the relevant instruction cue (i.e. the 2nd or 4th cue in the sequence) determined the target that the participant needed to attain after the instructed-delay period. The participant was instructed not to move the cursor away from the center target until the go cue turned on (reaction period, followed by movement period). If the target was acquired before 5 seconds expired, the trial was considered a success. The next trial started after the participant brought the cursor back to the center target.
Associative Task
The basic task design was the same as that for spatial task. However, each instruction cue was composed of 8 differently-colored targets (see Figure 1B) and a colored center-hold target. After the instructed-delay period, the participant was required to move to the target whose color matched that of the center-hold in the relevant instruction cue (i.e. 2nd or 4th cue in the sequence).
Surgery and Data collection
Local field potentials (LFPs) were collected using 100-electrode “Utah” arrays (Blackrock™ Microsystems Inc.), implanted in the hand area of the primary motor cortex (Hochberg et al., 2006). LFP signals on each of the 96 channels were recorded continuously at 1 kHz, amplified using a gain of 5000, and band-pass filtered from 0.30 Hz to 250 Hz. The standard deviation of the LFP signal on each channel was calculated over the entire recording session, in order to identify outlier channels. Outlier channels, containing significant noise, were identified by visual inspection and excluded from analysis. The task was programmed using custom software (TheGame2), which also synchronized its event timestamps with the local field potentials. The following events’ timestamps were recorded: the start of a trial, the timing of the instruction cues, go cue, and target acquisition.
Analysis
All algorithms were implemented in MATLAB. The power spectrum was computed using the multitaper method (time-bandwidth product TW=3, K=2 tapers,; Chronux.Analysis Software, http:// chronux.org) across 2048ms windows around the relevant instruction, and then averaged across trials to produce the power spectrum for the instruction period.
To obtain the signal in the beta frequency, the local field potential was band-pass filtered between 12-30Hz using an 8th order Butterworth filter. For the delta frequency, we used a 4th order, band-pass Butterworth filter between 0.5-1.5Hz. To avoid phase distortion, filters were applied forward and backward in time. For each task, the filtered signal was averaged across channels. We applied the Hilbert transform to extract the instantaneous phase (for delta frequency) and amplitudes (for beta frequency) of the signals (Rubino et al., 2006).
Beta amplitude
We tabulated the time points for which the beta power was above the mean power for each trial and report the percentage of trials, per time point, with a power value above the mean. We tested whether the beta power at each instruction was significantly different between the Count 2 and Count 4 conditions using a t-test at alpha = 0.001. We also tested whether the power in the 12-30Hz frequency band, 200ms around an instruction, was significantly larger than the power calculated at the following instruction using a paired t-test at alpha = 0.001. Using the mean amplitudes across trials, we also computed the lag between the local peaks in beta amplitude and the instruction cues. To test for the occurrence of peaks around the instruction cues, we computed the mean beta amplitude 50ms before each instruction and compared it to the mean beta amplitude sampled 300ms before the instruction. We used a paired t-test across trials to assess if the beta amplitude was larger at 50ms before the instruction. The results are reported in Table 1.
For viewing purposes, we also computed the spectrograms using 12 to 30Hz multi-taper spectra from (time-bandwidth product TW=3, K=2 tapers, padding to 1024 points) (Chronux.Analysis Software, http://chronux.org) over a 384ms window, with a 10ms sliding step.
Delta phase
The MATLAB circular statistics toolbox was used for all analyses involving the delta phase (Berens, 2009). For each instruction, we computed the mean phase of the signal in the delta frequency band. To assess whether the phase distributions around the instruction cues are significantly different from a uniform distribution, we used the Rayleigh test for circular uniformity. We also computed the mean resultant vector – a measure of phase locking, which is a vector sum of all the magnitudes of the phases across trials. To test whether the mean resultant vector magnitude is significant, we generated 20 test data sets, where the resultant vector magnitudes was computed on the same trials, though phase shifted by a random value between 0-180°. We used a right-tailed z-test to test whether the mean resultant vector magnitude was significantly higher than the mean resultant vector magnitudes computed on the phase-shifted test data. To assess whether the mean phase values were significantly different from each other, we used the Watson-Williams multi-sample and pair-wise test for equal means depending on how many distributions were being compared.
Supplementary Material
Supplementary Figure 1. (Top) Mean resultant vector magnitude for different delta frequencies at the 5 instructions, for the Count 2 Associative (blue) and Count 4 Associative (green) tasks. Between 0.5 and 1.5Hz, the mean resultant vector magnitudes are higher, indicating that phase locking is maximal for those frequencies. In the Count 2 condition, the phase locking decreases after the second instruction. In the Count 4 condition, phase locking persists until the 4th instruction. (Bottom) Mean phase at the 5 instructions for a delta frequency of 1Hz for the Count 2 (blue) and Count 4 (green) tasks. For the rest of the analyses, we chose a center frequency of 1Hz, with a bandwidth of 1Hz, because phase locking at the attended cues was maximal for this center frequency.
ACKNOWLEDGMENTS
We thank the clinical trial participant for his willingness to contribute to this research and all the employees formerly at Cyberkinetics Neurotechnology Systems inc. for manufacturing and clinical trial management. We would also like to thank L. Kay and D. Freedman for their useful comments on the manuscript.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Baker SN, Kilner JM, Pinches EM, Lemon RN. The role of synchrony and oscillations in the motor output. Experimental Brain Research.Experimentelle Hirnforschung.Experimentation Cerebrale. 1999;128(1-2):109–117. doi: 10.1007/s002210050825. [DOI] [PubMed] [Google Scholar]
- Bauer M, Oostenveld R, Fries P. Tactile stimulation accelerates behavioral responses to visual stimuli through enhancement of occipital gamma-band activity. Vision Research. 2009;49(9):931–942. doi: 10.1016/j.visres.2009.03.014. [DOI] [PubMed] [Google Scholar]
- Bauer M, Oostenveld R, Peeters M, Fries P. Tactile spatial attention enhances gamma-band activity in somatosensory cortex and reduces low-frequency activity in parieto-occipital areas. The Journal of Neuroscience : The Official Journal of the Society for Neuroscience. 2006;26(2):490–501. doi: 10.1523/JNEUROSCI.5228-04.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berens P. CircStat: A MATLAB toolbox for circular statistics. Journal of Statistical Software. 2009;31(10) [Google Scholar]
- Bouyer JJ, Montaron MF, Vahnee JM, Albert MP, Rougeul A. Anatomical localization of cortical beta rhythms in cat. Neuroscience. 1987;22(3):863–869. doi: 10.1016/0306-4522(87)92965-4. [DOI] [PubMed] [Google Scholar]
- Buschman TJ, Miller EK. Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices. Science (New York, N.Y.) 2007;315(5820):1860–1862. doi: 10.1126/science.1138071. [DOI] [PubMed] [Google Scholar]
- Buschman TJ, Miller EK. Serial, covert shifts of attention during visual search are reflected by the frontal eye fields and correlated with population oscillations. Neuron. 2009;63(3):386–396. doi: 10.1016/j.neuron.2009.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Contreras D, Timofeev I, Steriade M. Mechanisms of long-lasting hyperpolarizations underlying slow sleep oscillations in cat corticothalamic networks. The Journal of Physiology. 1996;494(Pt 1):251–264. doi: 10.1113/jphysiol.1996.sp021488. (Pt 1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Courtemanche R, Pellerin JP, Lamarre Y. Local field potential oscillations in primate cerebellar cortex: Modulation during active and passive expectancy. Journal of Neurophysiology. 2002;88(2):771–782. doi: 10.1152/jn.2002.88.2.771. [DOI] [PubMed] [Google Scholar]
- Donoghue JP, Sanes JN, Hatsopoulos NG, Gaal G. Neural discharge and local field potential oscillations in primate motor cortex during voluntary movements. Journal of Neurophysiology. 1998a;79(1):159–173. doi: 10.1152/jn.1998.79.1.159. [DOI] [PubMed] [Google Scholar]
- Donoghue JP, Sanes JN, Hatsopoulos NG, Gaal G. Neural discharge and local field potential oscillations in primate motor cortex during voluntary movements. Journal of Neurophysiology. 1998b;79(1):159–173. doi: 10.1152/jn.1998.79.1.159. [DOI] [PubMed] [Google Scholar]
- Fell J, Fernandez G, Klaver P, Elger CE, Fries P. Is synchronized neuronal gamma activity relevant for selective attention? Brain Research.Brain Research Reviews. 2003;42(3):265–272. doi: 10.1016/s0165-0173(03)00178-4. [DOI] [PubMed] [Google Scholar]
- Fischer H, Furmark T, Wik G, Fredrikson M. Brain representation of habituation to repeated complex visual stimulation studied with PET. Neuroreport. 2000;11(1):123–126. doi: 10.1097/00001756-200001170-00024. [DOI] [PubMed] [Google Scholar]
- Fischer H, Wright CI, Whalen PJ, McInerney SC, Shin LM, Rauch SL. Brain habituation during repeated exposure to fearful and neutral faces: A functional MRI study. Brain Research Bulletin. 2003;59(5):387–392. doi: 10.1016/s0361-9230(02)00940-1. [DOI] [PubMed] [Google Scholar]
- Fries P, Schroder JH, Roelfsema PR, Singer W, Engel AK. Oscillatory neuronal synchronization in primary visual cortex as a correlate of stimulus selection. The Journal of Neuroscience : The Official Journal of the Society for Neuroscience. 2002;22(9):3739–3754. doi: 10.1523/JNEUROSCI.22-09-03739.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fries P, Womelsdorf T, Oostenveld R, Desimone R. The effects of visual stimulation and selective visual attention on rhythmic neuronal synchronization in macaque area V4. The Journal of Neuroscience : The Official Journal of the Society for Neuroscience. 2008a;28(18):4823–4835. doi: 10.1523/JNEUROSCI.4499-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fries P, Womelsdorf T, Oostenveld R, Desimone R. The effects of visual stimulation and selective visual attention on rhythmic neuronal synchronization in macaque area V4. The Journal of Neuroscience : The Official Journal of the Society for Neuroscience. 2008b;28(18):4823–4835. doi: 10.1523/JNEUROSCI.4499-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handel B, Haarmeier T. Cross-frequency coupling of brain oscillations indicates the success in visual motion discrimination. NeuroImage. 2009;45(3):1040–1046. doi: 10.1016/j.neuroimage.2008.12.013. [DOI] [PubMed] [Google Scholar]
- Hochberg LR, Serruya MD, Friehs GM, Mukand JA, Saleh M, Caplan AH, et al. Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature. 2006;442(7099):164–171. doi: 10.1038/nature04970. [DOI] [PubMed] [Google Scholar]
- Isler JR, Grieve PG, Czernochowski D, Stark RI, Friedman D. Cross-frequency phase coupling of brain rhythms during the orienting response. Brain Research. 2008;1232:163–172. doi: 10.1016/j.brainres.2008.07.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen O, Colgin LL. Cross-frequency coupling between neuronal oscillations. Trends in Cognitive Sciences. 2007;11(7):267–269. doi: 10.1016/j.tics.2007.05.003. [DOI] [PubMed] [Google Scholar]
- Kay LM, Beshel J, Brea J, Martin C, Rojas-Libano D, Kopell N. Olfactory oscillations: The what, how and what for. Trends in Neurosciences. 2009;32(4):207–214. doi: 10.1016/j.tins.2008.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhn AA, Brucke C, Schneider GH, Trottenberg T, Kivi A, Kupsch A, et al. Increased beta activity in dystonia patients after drug-induced dopamine deficiency. Experimental Neurology. 2008 doi: 10.1016/j.expneurol.2008.07.023. [DOI] [PubMed] [Google Scholar]
- Kuhn AA, Kempf F, Brucke C, Doyle L. Gaynor, Martinez-Torres I, Pogosyan A, et al. High-frequency stimulation of the subthalamic nucleus suppresses oscillatory beta activity in patients with parkinson’s disease in parallel with improvement in motor performance. The Journal of Neuroscience : The Official Journal of the Society for Neuroscience. 2008;28(24):6165–6173. doi: 10.1523/JNEUROSCI.0282-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakatos P, Chen CM, O’Connell MN, Mills A, Schroeder CE. Neuronal oscillations and multisensory interaction in primary auditory cortex. Neuron. 2007;53(2):279–292. doi: 10.1016/j.neuron.2006.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakatos P, Karmos G, Mehta AD, Ulbert I, Schroeder CE. Entrainment of neuronal oscillations as a mechanism of attentional selection. Science (New York, N.Y.) 2008a;320(5872):110–113. doi: 10.1126/science.1154735. [DOI] [PubMed] [Google Scholar]
- Lakatos P, Karmos G, Mehta AD, Ulbert I, Schroeder CE. Entrainment of neuronal oscillations as a mechanism of attentional selection. Science (New York, N.Y.) 2008b;320(5872):110–113. doi: 10.1126/science.1154735. [DOI] [PubMed] [Google Scholar]
- Martin C, Beshel J, Kay LM. An olfacto-hippocampal network is dynamically involved in odor-discrimination learning. Journal of Neurophysiology. 2007;98(4):2196–2205. doi: 10.1152/jn.00524.2007. [DOI] [PubMed] [Google Scholar]
- Mitchell JF, Sundberg KA, Reynolds JH. Differential attention-dependent response modulation across cell classes in macaque visual area V4. Neuron. 2007;55(1):131–141. doi: 10.1016/j.neuron.2007.06.018. [DOI] [PubMed] [Google Scholar]
- Munk MH, Roelfsema PR, Konig P, Engel AK, Singer W. Role of reticular activation in the modulation of intracortical synchronization. Science (New York, N.Y.) 1996;272(5259):271–274. doi: 10.1126/science.272.5259.271. [DOI] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE. Coherent 25- to 35-hz oscillations in the sensorimotor cortex of awake behaving monkeys. Proceedings of the National Academy of Sciences of the United States of America. 1992;89(12):5670–5674. doi: 10.1073/pnas.89.12.5670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE. Oscillatory activity in sensorimotor cortex of awake monkeys: Synchronization of local field potentials and relation to behavior. Journal of Neurophysiology. 1996a;76(6):3949–3967. doi: 10.1152/jn.1996.76.6.3949. [DOI] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE. Oscillatory activity in sensorimotor cortex of awake monkeys: Synchronization of local field potentials and relation to behavior. Journal of Neurophysiology. 1996b;76(6):3949–3967. doi: 10.1152/jn.1996.76.6.3949. [DOI] [PubMed] [Google Scholar]
- O’Leary JG, Hatsopoulos NG. Early visuomotor representations revealed from evoked local field potentials in motor and premotor cortical areas. Journal of Neurophysiology. 2006;96(3):1492–1506. doi: 10.1152/jn.00106.2006. [DOI] [PubMed] [Google Scholar]
- Palva JM, Palva S, Kaila K. Phase synchrony among neuronal oscillations in the human cortex. The Journal of Neuroscience : The Official Journal of the Society for Neuroscience. 2005;25(15):3962–3972. doi: 10.1523/JNEUROSCI.4250-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfaff D. Brain arousal and information theory : Neural and genetic mechanisms. 2006.
- Pfurtscheller G, da Silva F. H. Lopes. Event-related EEG/MEG synchronization and desynchronization: Basic principles. Clinical Neurophysiology : Official Journal of the International Federation of Clinical Neurophysiology. 1999;110(11):1842–1857. doi: 10.1016/s1388-2457(99)00141-8. [DOI] [PubMed] [Google Scholar]
- Posner MI, Petersen SE. The attention system of the human brain. Annual Review of Neuroscience. 1990;13:25–42. doi: 10.1146/annurev.ne.13.030190.000325. [DOI] [PubMed] [Google Scholar]
- Ray S, Niebur E, Hsiao SS, Sinai A, Crone NE. High-frequency gamma activity (80-150Hz) is increased in human cortex during selective attention. Clinical Neurophysiology : Official Journal of the International Federation of Clinical Neurophysiology. 2008;119(1):116–133. doi: 10.1016/j.clinph.2007.09.136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ravden D, Polich J. Habituation of P300 from visual stimuli. International Journal of Psychophysiology : Official Journal of the International Organization of Psychophysiology. 1998;30(3):359–365. doi: 10.1016/s0167-8760(98)00039-7. [DOI] [PubMed] [Google Scholar]
- Riehle A, Grun S, Diesmann M, Aertsen A. Spike synchronization and rate modulation differentially involved in motor cortical function. Science (New York, N.Y.) 1997;278(5345):1950–1953. doi: 10.1126/science.278.5345.1950. [DOI] [PubMed] [Google Scholar]
- Robertson IH, Manly T, Andrade J, Baddeley BT, Yiend J. ‘Oops!’: Performance correlates of everyday attentional failures in traumatic brain injured and normal subjects. Neuropsychologia. 1997;35(6):747–758. doi: 10.1016/s0028-3932(97)00015-8. [DOI] [PubMed] [Google Scholar]
- Roelfsema PR, Engel AK, Konig P, Singer W. Visuomotor integration is associated with zero time-lag synchronization among cortical areas. Nature. 1997;385(6612):157–161. doi: 10.1038/385157a0. [DOI] [PubMed] [Google Scholar]
- Roux S, Mackay WA, Riehle A. The pre-movement component of motor cortical local field potentials reflects the level of expectancy. Behavioural Brain Research. 2006;169(2):335–351. doi: 10.1016/j.bbr.2006.02.004. [DOI] [PubMed] [Google Scholar]
- Rubino D, Robbins KA, Hatsopoulos NG. Propagating waves mediate information transfer in the motor cortex. Nature Neuroscience. 2006;9(12):1549–1557. doi: 10.1038/nn1802. [DOI] [PubMed] [Google Scholar]
- Sanchez-Vives MV, McCormick DA. Cellular and network mechanisms of rhythmic recurrent activity in neocortex. Nature Neuroscience. 2000;3(10):1027–1034. doi: 10.1038/79848. [DOI] [PubMed] [Google Scholar]
- Sanes JN, Donoghue JP. Oscillations in local field potentials of the primate motor cortex during voluntary movement. Proceedings of the National Academy of Sciences of the United States of America. 1993;90(10):4470–4474. doi: 10.1073/pnas.90.10.4470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sauseng P, Klimesch W, Gruber WR, Birbaumer N. Cross-frequency phase synchronization: A brain mechanism of memory matching and attention. NeuroImage. 2008;40(1):308–317. doi: 10.1016/j.neuroimage.2007.11.032. [DOI] [PubMed] [Google Scholar]
- Schroeder CE, Lakatos P. Low-frequency neuronal oscillations as instruments of sensory selection. Trends in Neurosciences. 2009;32(1):9–18. doi: 10.1016/j.tins.2008.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz S, Vuilleumier P, Hutton C, Maravita A, Dolan RJ, Driver J. Attentional load and sensory competition in human vision: Modulation of fMRI responses by load at fixation during task-irrelevant stimulation in the peripheral visual field. Cerebral Cortex (New York, N.Y.: 1991) 2005;15(6):770–786. doi: 10.1093/cercor/bhh178. [DOI] [PubMed] [Google Scholar]
- Siegel M, Donner TH, Oostenveld R, Fries P, Engel AK. Neuronal synchronization along the dorsal visual pathway reflects the focus of spatial attention. Neuron. 2008;60(4):709–719. doi: 10.1016/j.neuron.2008.09.010. [DOI] [PubMed] [Google Scholar]
- Steriade M. Grouping of brain rhythms in corticothalamic systems. Neuroscience. 2006;137(4):1087–1106. doi: 10.1016/j.neuroscience.2005.10.029. [DOI] [PubMed] [Google Scholar]
- Steriade M, Nunez A, Amzica F. A novel slow (< 1 hz) oscillation of neocortical neurons in vivo: Depolarizing and hyperpolarizing components. The Journal of Neuroscience : The Official Journal of the Society for Neuroscience. 1993;13(8):3252–3265. doi: 10.1523/JNEUROSCI.13-08-03252.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steriade M. Arousal: Revisiting the reticular activating system. Science (New York, N.Y.) 1996;272(5259):225–226. doi: 10.1126/science.272.5259.225. [DOI] [PubMed] [Google Scholar]
- Steriade M, Contreras D, Amzica F, Timofeev I. Synchronization of fast (30-40 hz) spontaneous oscillations in intrathalamic and thalamocortical networks. The Journal of Neuroscience : The Official Journal of the Society for Neuroscience. 1996;16(8):2788–2808. doi: 10.1523/JNEUROSCI.16-08-02788.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sundberg KA, Mitchell JF, Reynolds JH. Spatial attention modulates center-surround interactions in macaque visual area v4. Neuron. 2009;61(6):952–963. doi: 10.1016/j.neuron.2009.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treisman AM, Gelade G. A feature-integration theory of attention. Cognitive Psychology. 1980;12(1):97–136. doi: 10.1016/0010-0285(80)90005-5. [DOI] [PubMed] [Google Scholar]
- Vidal JR, Chaumon M, O’Regan JK, Tallon-Baudry C. Visual grouping and the focusing of attention induce gamma-band oscillations at different frequencies in human magnetoencephalogram signals. Journal of Cognitive Neuroscience. 2006;18(11):1850–1862. doi: 10.1162/jocn.2006.18.11.1850. [DOI] [PubMed] [Google Scholar]
- Weissman DH, Roberts KC, Visscher KM, Woldorff MG. The neural bases of momentary lapses in attention. Nature Neuroscience. 2006;9(7):971–978. doi: 10.1038/nn1727. [DOI] [PubMed] [Google Scholar]
- Wilder JD, Kowler E, Schnitzer BS, Gersch TM, Dosher BA. Attention during active visual tasks: Counting, pointing, or simply looking. Vision Research. 2009;49(9):1017–1031. doi: 10.1016/j.visres.2008.04.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams ER, Soteropoulos DS, Baker SN. Coherence between motor cortical activity and peripheral discontinuities during slow finger movements. Journal of Neurophysiology. 2009 doi: 10.1152/jn.90996.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Chen Y, Bressler SL, Ding M. Response preparation and inhibition: The role of the cortical sensorimotor beta rhythm. Neuroscience. 2008;156(1):238–246. doi: 10.1016/j.neuroscience.2008.06.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figure 1. (Top) Mean resultant vector magnitude for different delta frequencies at the 5 instructions, for the Count 2 Associative (blue) and Count 4 Associative (green) tasks. Between 0.5 and 1.5Hz, the mean resultant vector magnitudes are higher, indicating that phase locking is maximal for those frequencies. In the Count 2 condition, the phase locking decreases after the second instruction. In the Count 4 condition, phase locking persists until the 4th instruction. (Bottom) Mean phase at the 5 instructions for a delta frequency of 1Hz for the Count 2 (blue) and Count 4 (green) tasks. For the rest of the analyses, we chose a center frequency of 1Hz, with a bandwidth of 1Hz, because phase locking at the attended cues was maximal for this center frequency.