A 3D Wavelet Fusion Approach for the Reconstruction of Isotropic-Resolution MR Images from Orthogonal Anisotropic-Resolution Scans

Abstract

Hardware constraints, scanning time limitations, patient movement, and SNR considerations, restrict the slice-selection and the in-plane resolutions of MRI differently, generally resulting in anisotropic voxels. This non-uniform sampling can be problematic, especially in image segmentation and clinical examination. To alleviate this, the acquisition is divided into (two or) three separate scans, with higher in-plane resolutions and thick slices, yet orthogonal slice-selection directions. In this work, a non-iterative wavelet-based approach for combining the three orthogonal scans is adopted, and its advantages compared to other existing methods, such as Fourier techniques, are discussed, including the consideration of the actual pulse response of the MRI scanner, and its lower computational complexity. Experimental results are shown on simulated and real 7T MRI data.

INTRODUCTION

Three-dimensional (3D) MRI can achieve high-resolution isotropic voxels via 3D Fourier encoding. Subject motion while using 3D encoding, however, affects the entire volume, thereby making such true 3D acquisitions clinically challenging and often impractical. 3D MR volumes are therefore typically acquired as tomographic sets of two-dimensional (2D) image slices, selected using radio frequency pulses. (See (1) for a comparison between the two acquisition techniques.) Since a different strategy is used for the in-plane encoding (i.e. frequency and phase encoding), it is not surprising that the hardware and timing limitations on the slice-selection and the in-plane resolutions are not the same. The trade-off imposed by these limitations, being principally more restrictive on the slice-selection resolution, generally results in thicker acquisition slices and therefore anisotropic voxels. This non-uniform sampling can be problematic, especially in image segmentation and clinical examination, since the image will be missing high frequencies in the slice-selection direction.

In case there is no time constraint, voxels may be chosen to be isotropic by matching the slice thickness with the in-plane resolution. However, acquiring such a high-resolution MR volume may require the subject to be motionless for a (clinically) unreasonably long time, otherwise increasing the risk of motion artifacts. This can be alleviated by dividing the acquisition into (two, or as considered here) three separate scans in orthogonal slice-selection directions, with thicker slices yet complementary resolutions, each containing a considerable proportion of the high frequencies, in two out of the three directions, but missing them in the other direction. This technique, which has also been exploited for motion correction (2), reduces the acquisition time of each scan and, in consequence, the chance of motion-related distortion. Global misalignment between the scans can be corrected by employing a variety of available registration techniques, and the high-resolution image should eventually be reconstructed from these scans.

Different approaches to combining the three orthogonal scans have been proposed in the literature. Simply averaging the volumes, (3,4), introduces artificial blurring and a decrease in the contrast. To avoid this, the authors of (5)-(8) have suggested a selective combination scheme in the Fourier domain, which is principally averaging the information where it comes from multiple scans, and zero padding where no information is available. This method, however, would only be mathematically accurate when assuming that the point spread function (PSF) of the MR scanner in the slice-selection direction is a sinc function (e.g. in true 3D acquisitions), which is different from the actual rectangular-window (RW) function often considered in the literature (e.g., in (1), (9)-(11)). A super-resolution based method has been proposed in (10), where the RW (or potentially any other) kernel can be considered as the system response of the MR scanner, and the orthogonal scans are combined by iteratively minimizing a cost function. In addition, the authors of (12) suggested reconstructing the high-resolution image iteratively by assuming it to be a linear combination of low-resolution images. Finally, a level-set segmentation algorithm for such multi-scan data has been introduced in (13).

In this work, we adopt a non-iterative and fast wavelet-based approach, which takes into account the actual PSF of the MR scanner. Wavelet fusion techniques, (14)-(29), are commonly used to combine multiple images into a single one, retaining important features from each, and providing a more accurate description of the object. In our case, ideally, we would like to collect all the meaningful information from the input images (i.e. the low frequencies and in-plane high frequencies), while discarding the parts bearing no information (i.e. missing high frequencies in the slice-selection direction). The wavelet transform, (30,31), simplifies this procedure by splitting the image into blocks of low and high frequencies in different directions, enabling us to easily pick the desired (available) blocks from each image. We will show how, assuming the RW-PSF,¹ the proposed wavelet-based approach strives to divide the image into all-information and no-information blocks, whereas the Fourier transform fails to accurately carry out such a separation, resulting in loss of information while combining the images. In addition, the wavelet transform has a lower computational complexity than the Fourier transform, and is non-iterative as opposed to (10,12).²

METHODS

Wavelet vs. Fourier

Each input image, having a low resolution in a unique Cartesian direction, lacks some high-frequency information compared to the desired high-resolution isotropic-voxel image, which we wish to reconstruct. The main challenge in image fusion lies in how to selectively extract information from the input images, to avoid relying on seemingly genuine yet information-free parts of the data. To achieve this, we need a tool that transforms every input image into two distinguishable parts: an all-information (AI) block to be used and a no-information (NI) block to be discarded. Ideally, the AI block of each input image will be identical to the same block of the desired high-resolution image, and the NI block will bear no useful information regarding the same block of the ground-truth image. Provided that this transform is invertible, the output image can be reconstructed in the transform domain by combining only the AI blocks of the input images, and then performing the inverse transform. We now show that by considering the standard RW-PSF in the slice-selection direction of the MR scanner, the one-dimensional (1D) wavelet transform with the Haar basis³ theoretically achieves such an ideal partition, whereas the performance of the 1D Fourier transform is suboptimal. This is of course in addition to the fact that the computational complexity of the Fast Wavelet Transform (FWT), $\mathcal{O}\left(N\right)$, is also lower than that of the Fast Fourier Transform (FFT), $\mathcal{O}\left(N\log N\right)$.

To demonstrate the proposed approach, we first simulate a row of 2×1×1-mm³ voxels. We consider a discrete 1D signal (representing isotropic 1-mm³ voxels) which has been blurred by the RW kernel of length 2 and then downsampled by a factor of 2. Generalization of the following to 3D is straightforward.

The Fourier transform decomposes a discrete signal x_n into its frequency elements, representing them as the function X(Ω), Ω ∈ [−π, π]. According to Nyquist-Shannon theorem, sampling the signal with the rate of 1 out of 2 voxels, results in aliasing unless the signal is band-limited, X(Ω) = 0, |Ω| > π/2, which is not guaranteed for the MR images due to the existing sub-voxel structures and edges. Only if the PSF of the MR scanner were an ideal low-pass filter for the Fourier transform (i.e. the sinc function), those high frequencies would be eliminated and no aliasing would occur. Then, in this unrealistic scenario, the low-frequency region |Ω| < π/2 of the (upsampled) signal would represent exactly the same region of the desired signal (AI block), and its high-frequency region |Ω| > π/2 would carry no information regarding the same region of the signal (NI block). However, the RW-PSF of the scanner in the slice-selection direction, although a low-pass filter, is far from an ideal one. Thus, aliasing does occur, distorting the low-frequency region of |Ω| < π/2 and making it inappropriate as an AI block.⁴ Likewise, the high-frequency region of |Ω| > π/2 contains some information about that region of the original signal, since the RW-PSF does not remove those frequencies. Therefore, this region cannot be considered as an NI block either. We hence conclude that the Fourier transform cannot separate an input image into AI and NI blocks. We will now see how this is solved by the wavelet transform.

In its simplest form (first decomposition level), the Haar wavelets are used to transform the sequence (signal) x₁,x₂, … , x_N into two separate sequences (L, H) a low-pass one L = l₁,l₂, … , l_N/2 and a high-pass one H = h₁,h₂, … , h_N/2, with $l_i=(x_{2i-1}+x_{2i})∕\sqrt{2}$ and $h_i=(x_{2i-1}-x_{2i})∕\sqrt{2}$. Since the signal $x_i^{\prime }$ acquired on the scanner is obtained after blurring x_i with the two-tap RW-PSF, {1/2, 1/2}, and then downsampling it with the factor of 2, one can easily verify that $x_i^{\prime }=l_i∕\sqrt{2}$. Therefore, an upsampled version of this signal (e.g. the inverse wavelet transform of the zero-padded $(L^{\prime },H^{\prime })=(\sqrt{2}{x}_i^{\prime },0)$) will have an L’ exactly equal to L corresponding to the desired high-resolution signal (AI block), and an information-free H’ = 0 (NI block). Thus, the Haar wavelet transform splits the blurred signal into a pair of AI (L) and NI (H) blocks, as desired.⁵

Volumetric Wavelet Image Fusion

Extended to higher dimensions, the simplest wavelet transform of a d-dimensional image consists of 2^d different blocks, each containing either the low- or high-frequency information corresponding to a unique Cartesian dimension of the image. The 3D wavelet transform of an MR image (with “XYZ” coordinates) has eight blocks, often denoted as “LLL,” “LLH,” “LHL,” …, “HHH” (Fig. 1), where, for instance, LHH stands for the block containing low-, high-, and high-frequency information in the X, Y, and Z directions, respectively. Now suppose that the three orthogonal scans have voxel sizes proportional to 2×1×1, 1×2×1, and 1×1×2.⁶ Then, as a generalization of the previous section, we can assume that the wavelet transform of, e.g., the first scan, has useful information in its four L## (AI) blocks, but virtually no information in its H## (NI) blocks (“#” stands for both H and L). Similarly, the informative (AI) blocks of the second and third volumes would be the four #L# and the four ##L blocks, respectively.

Fig. 1.

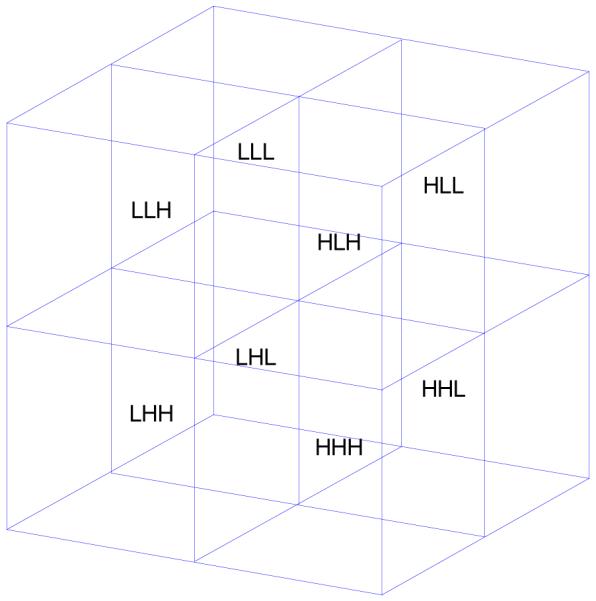
The eight blocks of the 3D wavelet transform at the first decomposition level.

It now becomes apparent why simply averaging the three scans produces artificial blurring, as a low-pass filter does, and thus is an inaccurate reconstruction of the object. Given the linearity of the wavelet transform, averaging the scans would be block-wise averaging the three images in the wavelet domain. This would mean including both the signal-containing AI blocks and the zero NI blocks while computing the mean (destructive superposition), resulting in an artificial attenuation of the high-frequency blocks (by the factors of ⅓ or ⅔).

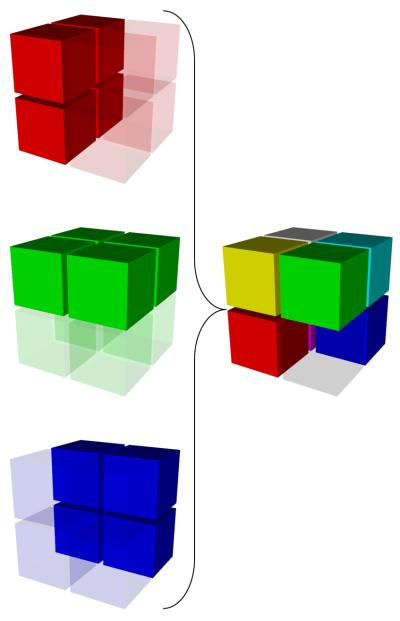
We proceed with the reconstruction of the desired high-resolution image – in the wavelet domain – by using as many AI blocks as available from the datasets (Fig. 2). For example, the reconstructed LLL block will be the average of the LLL blocks of all the three scans (all AI), the LLH will be the average of the LLH blocks of the first two scans, and the LHH will be the LHH of the first scan. The HHH block is the only one missing in all the three scans, which we handle by zero-padding, similarly to how the Fourier techniques do. Performing an inverse wavelet transform will then produce the isotropic-voxel high-resolution image, containing the maximal information from the three available scans.

Fig. 2.

The AI blocks are selected from the wavelet domain of the three anisotropic-voxel scans (left) and combined to make the high-resolution isotropic-voxel image (right).

Since the wavelet transform is performed using the FWT algorithm with the complexity of $\mathcal{O}\left(N\right)$ (N being the number of voxels) (31), the entire process is done directly (at once), as opposed to the iterative methods proposed in (10,12), and also faster than the direct FFT-based techniques which have the complexity of $\mathcal{O}\left(N\log N\right)$.

Data Acquisition

Three orthogonal T2-weighted images were acquired at 7T with a 2D turbo spin echo sequence using the following parameters: 18 slices of 2-mm thickness, FOV = 205×205 mm², matrix size = 512×512 (0.402×0.402 mm²), TR/TE = 5000/57 msec, flip angle = 120°, BW = 220 Hz/pixel, with an acceleration factor of 2 (GRAPPA) along the phase-encoding direction.

With this slice thickness, acquiring each orthogonal scan takes 80% shorter (40% overall) than an equivalent isotropic-voxel volume. Although the combined image is not quite as sharp as the equivalent (longer-acquisition) isotropic-voxel volume (since high-frequency blocks are missing), the risk of the major distortions due to the subject motion is significantly reduced.

RESULTS AND DISCUSSIONS

Results on Artificial Data

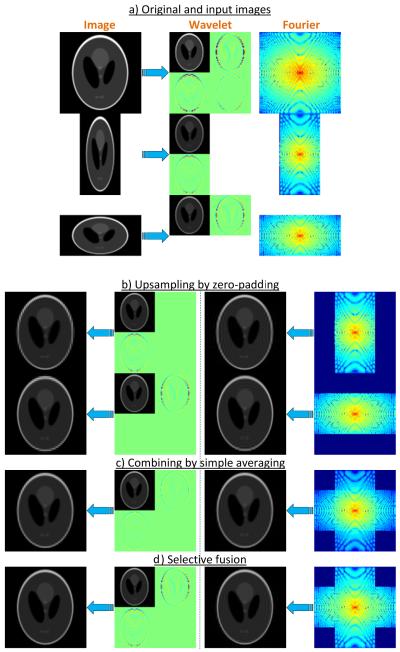
We first demonstrate experimental results on 2D artificial data.⁷ To simulate a realistic RF pulse profile, we used the Gaussian functions to generate the data, where the full width at half maximum (FWHM) was the slice width. This PSF was reported in (1) to well approximate typical slice profiles. Shepp-Logan phantom of the size 1000×1000 pixels was generated as the ground-truth image. To produce the two input images of sizes 100×50 and 50×100 pixels, it was blurred with the Gaussian filter and downsampled (Fig. 3a). The images were then upsampled by zero-padding in both the wavelet and the Fourier domains (Fig. 3b), and were eventually combined using both simple averaging (Fig. 3c), and the selective fusion technique (Fig. 3d).

Fig. 3.

Experimental results on a simulated phantom. a) The original and the subsampled data in the image, wavelet and Fourier domains. b) Upsampling of the input images by zero-padding. Note how aliasing artifacts are produced when zero-padding is performed in the Fourier, as opposed to the wavelet domain. c) Simple mean of the upsampled images. Note the artificial blurring resulting from the combination by simple averaging. d) Selective fusion using the proposed wavelet method and the Fourier method.

Visible ripple-shaped aliasing artifacts are produced when zero-padding is performed in the Fourier, as opposed to the wavelet domain. These artifacts are propagated to the fusion level, thereby remaining in the final results obtained from the Fourier technique. In addition, simply averaging the upsampled images, in wavelet or Fourier domain, results in extra blurring due to the fact that the same weight has been given to high frequencies of all images. By comparing the results with the original high-resolution image, we found the mean squared error of the proposed wavelet-fused image to be the smallest among those of all the other techniques (Table 1), particularly almost three times smaller than that of the Fourier-fused image.

Table 1.

Mean squared error when compared to the ground truth.

MSE (×10−3)	Wavelet	Fourier
Selective fusion	5.31	14.65
Simple mean	6.69	15.19

Results on Real Data

Next, we tested our method on real MRI data collected at our center (see the “Data Acquisition” section). The three orthogonal datasets were resampled in Amira (Visage Imaging Inc, San Diego, CA, USA) using the Lanczos filter, and then combined using the proposed wavelet fusion, the Fourier fusion, and the simple mean.

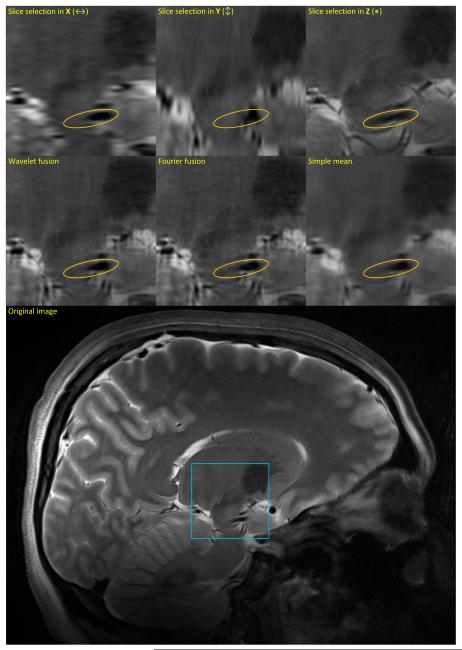
As Fig. 4 demonstrates, the selective fusion techniques (wavelet and Fourier) result in images sharper than the simple mean and the three input images. This is nicely demonstrated for the input images with the slice-selection in the X or Y direction, where the anisotropic blur is visible in the raw data. As for the input image with the slice-selection in the Z direction, its slice thickness results in an averaging and blurring of objects across the slice, e.g., blood vessels that appear more oval, as opposed to the sharp cross-sections observed in the results by the wavelet and the Fourier methods (regions marked by the orange ellipses in Fig. 4).

Fig. 4.

Experimental results on a real MRI dataset, shown on a sagittal slice. The first row shows the three orthogonal scans, and the second row demonstrates the results of three different methods of image fusion. The original sagittal slice is depicted at the bottom, with the blue square indicating the zoomed region. Orange ellipses indicate regions with vessel cross-sections, which have the correct size in the wavelet- and Fourier-based fused images, but are much more oval in the input image when the slice-selection is in the Z direction (due to the thicker slices).

While both wavelet and Fourier techniques produce clear and sharp images, those obtained with the Fourier technique seem noisier than those with the proposed wavelet technique, most probably due to the aliasing artifact. Nevertheless, the difference between the two results is not as obvious as that in the case of the artificial data (Fig. 3), which might be an outcome of the less-than-perfect alignment of the three scans. In the absence of the ground truth, we estimated the SNR of the images as the ratio of the variance of the entire image to that of a structure-free region, and found the SNR of the wavelet-fused image to be 0.5 dB higher than that of the Fourier-fused image, and about the same as that of the simple mean.⁸

CONCLUSIONS

In this work, an image fusion technique based on the wavelet transform was introduced to combine MR images that have orthogonal (low-resolution) slice-selection directions, to produce high-resolution isotropic-voxel images. Obtaining superior tissue contrast and smaller voxels (33) can provide invaluable information for a variety of clinical applications. As higher-field magnets (3T and 7T) are becoming more widely available, capitalizing on their enhanced capabilities should be met with clinically applicable acquisition protocols, such as shorter acquisition times. The advantages of the proposed algorithm over other commonly used methods were demonstrated, and experimental results on simulated and real 7T MRI data were shown. Extending this approach to wavelet bases other than Haar, to consider various MR pulse responses, is the subject of future research.