Comparison between end-tidal CO₂ and respiration volume per time for detecting BOLD signal fluctuations during paced hyperventilation

Abstract

Respiratory motion and capnometry monitoring were performed during blood oxygen level dependent (BOLD) functional magnetic resonance imaging (FMRI) of the brain while a series of paced hyperventilation tasks were performed that caused significant hypocapnia. Respiration volume per time (RVT) and end-tidal carbon dioxide (ETCO₂) were determined and compared for their ability to explain BOLD contrast changes in the data. A 35% decrease in ETCO₂ was observed along with corresponding changes in RVT. A best-fit ETCO₂ response function, with an average initial peak delay time of 12 s, was empirically determined. ETCO₂ data convolved with this response function was more strongly and prevalently correlated to BOLD signal changes than RVT data convolved with the corresponding respiration response function. The results suggest that ETCO₂ better models BOLD signal fluctuations in FMRI experiments with significant transient hypocapnia. This is due to hysteresis in the ETCO₂ response when moving from hypocapnia to normocapnia, compared to moving from normocapnia to hypocapnia.

Introduction

Blood oxygen level dependent (BOLD) functional magnetic resonance imaging (FMRI) is widely used to map neuronal activity in the brain based on localized fluctuations in blood oxygenation [1]. These oxygenation changes are not strictly metabolic in nature, but involve some combination of increased blood flow and increased venous volume [2]. As a result, BOLD contrast is susceptible to non-neuronally mediated changes in blood flow, the magnitude and timing of which are heterogeneous across the brain [3], most likely due to differing types of microvasculature in a given voxel [4].

The arterial carbon dioxide (CO₂) concentration is a well-known variable affecting cerebral blood flow (CBF) and volume [5,6] due to the direct vasodilatory effects of CO₂ on cerebral vasculature [7]. In healthy subjects, circulatory CO₂ equilibrates with the air in the lungs, which has two important implications. The first is that indirect control of arterial CO₂ can be achieved by changing the alveolar CO₂ concentration through changing minute ventilation or by inhaling CO₂-enriched air. Second, an estimate of the arterial CO₂ level can be obtained non-invasively from exhaled air at end-expiration, called the end-tidal CO₂ (ETCO₂) value. ETCO₂ has been shown to be well-correlated to arterial CO₂ with normal breathing at rest [8,9].

In healthy resting subjects, fluctuations in ETCO₂ of ± 5% occur and induce corresponding changes in middle cerebral artery (MCA) blood velocity [10,11], indicating changes in blood flow in these large arteries supplying the brain. These periodic variations in ETCO₂ at rest are also correlated to BOLD signal changes throughout the brain [11]. Hypercapnia induced by either breath holding or hypoventilation has been shown to increase the BOLD signal [12–14]. Increasing the inhaled CO₂ concentration has also been shown to increase the baseline BOLD signal and decrease the BOLD signal change in response to functional tasks performed during hypercapnia [15–19]. Conversely, hypocapnia due to hyperventilation causes decreases in the BOLD signal [20,21] and also affects functional task activation [21–23]. These results show that both natural and experimentally-induced changes in ETCO₂ level have a significant effect on BOLD-weighted FMRI data and suggest the importance of quantifying such changes.

The relationship between CO₂, CBF, and BOLD images has been used to normalize FMRI both across subjects using breath-holding [14] and across field strength and pulse sequence using inhaled hypercarbic gas [24]. Another potential optimization would be to include ETCO₂ fluctuations as a noise regressor in addition to standard physiologic noise correction with RETROICOR [25]. However, because CO₂ sampling is technically challenging, the benefits of directly determining ETCO₂ compared to modeling these changes from the respiratory motion tracing have been explored. The respiration volume per time (RVT) is calculated for each breath as a ratio of tidal volume to respiration period [26]. RVT performs similarly to another measure, respiration variation, calculated as the standard deviation of the respiratory waveform over a 6 s sliding window [27].

Because changes in BOLD signal do not immediately follow changes in either respiration or ETCO₂, a transfer function is needed to relate the physiologic change to signal fluctuations in the dataset. The respiration response function (RRF) is the transfer function derived for RVT [28]. For an RVT increase, the RRF describes a BOLD signal increase with peak effect at 3 s and larger negative BOLD signal change manifesting between 9 and 26 s, with a peak effect at 15 s [28]. The RVT timecourse convolved with the RRF (RVT*RRF) was shown to explain BOLD signal changes from several respiratory paradigms: breath holding, breathing rate and depth changes, as well as quiet breathing [28]. When comparing the ability to explain BOLD changes in resting-state FMRI, RVT*RRF performed similarly to ETCO₂ data implemented with an appropriate delay [29]. An optimized ETCO₂ transfer function analogous to the RRF has not been described, and its derivation may be complicated by large variability across subjects and heterogeneity of delay times across the brain [29]. Such a response function is determined and presented here.

In this study, respiratory and capnometry monitoring were performed during BOLD FMRI imaging of an experiment involving task periods of free breathing and several paced hyperventilation breathing paradigms. Both RVT and ETCO₂ measures were calculated for the duration of the experiment. Because of the redundancy shown between correcting for both ETCO₂ and end-tidal oxygen [29] and the 60-fold greater cerebrovascular reactivity to CO₂ compared to oxygen [30], end-tidal oxygen concentration was not examined in this study. It was recently shown [29] that ETCO₂ and RVT data were highly correlated to one another and displayed overlapping spatial patterns of correlation to BOLD signal changes in resting state FMRI data. This study compares the ability of RVT and ETCO₂ data convolved with optimized response functions to explain BOLD signal changes when imaging before and after a period of significant hypocapnia induced by paced hyperventilation. The primary hypothesis of this study was that ETCO₂ would more strongly correlate to the BOLD fluctuations seen throughout this experiment. It was also hypothesized that performing the breathing paradigm would cause significant, but different changes in both ETCO₂ and RVT between paced breathing conditions. It was predicted that RVT values would track ventilation throughout the paced breathing experiment, but that ETCO₂ changes would track ventilation during periods of increasing minute ventilation and lag significantly behind during periods of decreasing minute ventilation.

Methods

Subjects and breathing tasks

Nine healthy adult subjects participated in this study, which was approved by the Biomedical Institutional Review Board of The Ohio State University. The pace and depth of breathing were controlled throughout the experiment using computer-generated graphical cues which changed in size, representing the volume and timing of respiration that subjects were to model. Prior to entering the scanner, all subjects had underwent a training session with the same graphical cues and were able to consistently perform the required breathing tasks. The experiment consisted of nine task periods over 10.5 minutes, as listed in Table 1. During the first task condition, labeled FREE1, subjects paced their own breathing rate and depth. This was followed by NORMAL1, in which the rate was paced at 15/min, but subjects should maintain their resting tidal volume. Similarly, the same tidal volume was paced at 24/min in RAPID1. DEEP1 followed, in which subjects reduced their rate to 12/min and were cued to double their tidal volume. The fifth condition, called RAPID&DEEP, had subjects continue breathing at double their resting tidal volume but increase their rate to 25/min. The rest of the experiment was a reverse order of the previous tasks: DEEP2, RAPID2, and NORMAL2. The last condition, FREE2, was a 2.5 min free-breathing recovery period.

Table 1. Experimental design of the breathing conditions employed during scanning.

Condition Name	Tidal Volume	Respiratory Rate (min−1)	Length (min)	Condition Description
FREE1	-	-	1	Free breathing
NORMAL 1	1x	15	1	Paced normal breathing
RAPID1	1x	24	1	Paced rapid breathing
DEEP1	2x	12	1	Paced deep breathing
RAPID&DEEP	2x	25	1	Paced rapid and deep breathing
DEEP2	2x	12	1	Paced deep breathing
RAPID2	1x	24	1	Paced rapid breathing
NORMAL2	1x	15	1	Paced normal breathing
FREE2	-	-	2.5	Free breathing

Data acquisition

BOLD-weighted images were acquired with a Philips 3 Tesla Intera scanner (Philips Medical Systems, The Netherlands) using a gradient echo sequence with echo-planar readout. Whole brain coverage was achieved with 35 contiguous axial slices acquired in an interleaved fashion. The in-plane image matrix size was 64 × 64, with a final acquired voxel dimension of 3.75 × 3.75 × 4 mm. Repeat time (TR) was 3 s, echo time was 30 ms, the flip angle was 90°, the phase encode direction was anterior-posterior, and each dataset consisted of 210 volumes. An 8-channel receiver head coil was used with sensitivity encoding at a reduction factor of 2, to reduce the echo train length and minimize image distortion [31,32]. Four volumes were acquired and discarded prior to the acquisition of data used for analysis. Image reconstruction was performed on the scanner console.

Physiologic monitoring data from each subject was recorded for retrospective data correction as well as determining compliance with the paced breathing task. A respiratory belt (RB) gave a voltage signal directly proportional to changes in thoracoabdominal circumference. A pulse plethysmograph (PPG) sensor was placed on one of the subject’s fingers to measure the peripheral pulse waveform. Each subject wore a combined oral/nasal sampling device (Smart MAC-line Plus, Oridion, Needham, MA) that allowed simultaneous sampling of air expired through either the mouth or nose. The MAC-line was connected to a Datex Capnomac Ultima clinical gas monitor (GE Healthcare, Waukesha, WI) located outside the magnet room by nine meters of sampling tubing that was continuously sampled at 200 mL/min. The Datex monitor gave an analog voltage output reflecting the expired CO₂ waveform for each subject.

The analog output of each of these sensors was digitized at 500 Hz with a BIOPAC MP-30 data acquisition unit (BIOPAC Systems, Goleta, CA). The BIOPAC also captured a trigger signal from the scanner at the beginning of each brain volume acquisition such that the amplitude of each physiologic parameter during image acquisition could be determined. The RB and PPG data were low-pass filtered with a cutoff frequency of 2 Hz using AcqKnowledge version 3.5.7 (BIOPAC Systems) to remove high frequency interference from the rapid switching of the gradient magnets.

Physiologic data processing and analysis

The three physiologic waveforms were processed with custom code in MATLAB (MathWorks, Natick, MA). The RB and PPG timecourses were formatted for input to a slice-specific version of the RETROICOR physiologic noise correction algorithm [25] that was modified to account for the 500 Hz physiologic data sampling rate, as previously described [33].

The acquired capnograph was time-shifted to account for the constant 8.2 s time delay for expired air to traverse the sampling tubing and reach the gas monitor. The peak value at the end of each expiration, the ETCO₂ value, was determined using a two-second window. The resulting ETCO₂ timecourse was parsed for incomplete breaths in which the peak value did not reflect a full expiration, and these values were replaced with the average value of the previous and subsequent ETCO₂ value. The timing of these ETCO₂ values relative to each TR was determined and the values were interpolated to the beginning of each TR interval, giving one value per image volume.

For each breath in the respiratory timecourse, the RVT value was calculated as previously described [28]. The peak and trough of the RB timecourse for each breath was determined, along with the peak-to-peak respiratory period. These values were independently interpolated to the beginning of each TR interval, and RVT was calculated for each TR as the difference in respiration amplitude (peak minus trough) divided by the peak-to-peak respiratory period. As part of this processing, the respiration amplitude and period of each breath were also stored for later comparison of changes in respiratory rate and relative tidal volume during each breathing task period.

The values of ETCO₂ and RVT during each paced breathing condition were compared to assess which paced breathing conditions caused significant ETCO₂ and RVT changes. Analysis of variance was performed using a linear mixed effects model with subject number as a random factor and breathing task condition as a fixed factor. The measured ETCO₂ or RVT values for each subject during each breathing condition were treated as temporally dependent repeated measurements. Nine comparisons of interest were analyzed for ETCO₂ and RVT with null hypotheses as follows: FREE1 = RAPID&DEEP, FREE1 = FREE2, NORMAL1 = NORMAL2, RAPID1 = RAPID2, DEEP1 = DEEP2, FREE1 = NORMAL1, NORMAL1 = RAPID1, RAPID1 = DEEP1, and DEEP1 = RAPID&DEEP. In determining whether each null hypothesis was rejected, the Holm-Bonferroni method to correct for multiple comparisons was used, in which the p-value required for significance is divided by the number of comparisons being performed to keep the total family-wise error rate at α = 0.05.

ETCO₂ and respiration response functions

The average ETCO₂ response function was optimized empirically by iterative regression in MATLAB. Beginning with the shape of the classic hemodynamic response function [34], each parameter in the double gamma function was systematically varied. These candidate response functions were convolved with the ETCO₂ timecourse and regressed against the MRI data. The mean R² and mean F-statistic averaged across all voxels in all subjects were maximized, and the parameters from the best-fit response function were used for subsequent ETCO₂ analysis. The timing and amplitude parameters previously derived for the RRF [28] were used to model the BOLD response model to RVT changes.

MRI data processing and analysis

Image data were preprocessed using the FMRIB Software Library (FSL) version 4.1.1 [35], including brain extraction [36], spatial smoothing using a Gaussian kernel of full-width at half-maximum (FWHM) of 7 mm, and high-pass filtering with a cutoff period of 60 s. Slice-timing correction and pre-whitening were not used. Linear registration was used to correct for motion [37], and datasets were excluded from further analysis if the detected displacement exceeded half the in-plane voxel dimension, which was 1.875 mm. RETROICOR using first and second order harmonics was performed on the preprocessed image data before further analysis.

Statistical analysis was performed with FILM [38] in FEAT version 5.98 (part of FSL 4.1.1). General linear modeling was performed with either RVT or ETCO₂ as the model input. Flexible regressor response functions were created using the FMRIB Linear Optimal Basis Set (FLOBS) utility, which is also part of FSL [39]. For both ETCO₂ and RVT, a set of three basis functions was created based on the shape of the corresponding response function, but allowing a ± 2 s range of peak times. Convolution of the RVT and ETCO₂ data with the appropriate basis set models the shape of the known average response functions, while effectively allowing for flexibility in timing across voxels.

Individual subject images were registered to the Montreal Neurological Institute (MNI) standard space brain. Group average maps were created using FLAME [40,41] and were thresholded using a cluster threshold of Z > 3.0 and a corrected cluster significance threshold of p < 0.05 [42].

Results

Initial registration analysis of the data from subject 3 showed excessive motion, with a maximum displacement of 2.5 mm. Since this was greater than half the voxel dimension, this dataset was thus excluded from further analysis. The remaining eight subjects showed motion of, at most, 1.5 mm translation and 1.7 degrees rotation. In processing the expired CO₂ waveform, incomplete breaths were detected in three subjects’ data in which the peak value did not reflect the CO₂ concentration at end-expiration. These mid-tidal CO₂ values were replaced by interpolation of the surrounding ETCO₂ values. These aberrations were infrequent, affecting less than 2% of the ETCO₂ values in those datasets, with no consecutive occurrences. The analyzed subject pool consisted of three males and five females with mean ± standard deviation age of 29.3 ± 10.2 and age range 23 to 53 years. All subjects’ respiratory patterns changed appropriately in response to the experimental cues, as shown in Table 2.

Table 2. Measured respiratory parameters during each of the breathing conditions in Table 1.

All values are average ± standard deviation across subjects. Respiration amplitude ratio is calculated relative to the FREE1 condition; RVT = respiration volume per time; ETCO2 = end-tidal carbon dioxide.

Condition	Respiration Amplitude Ratio	Respiratory Rate (min−1)	RVT (arb. units)	ETCO2 (mmHg)
FREE1	1.00 ±0	15.5 ± 3.35	2.5 ± 0.68	37.4 ± 2.78
NORMAL1	1.11 ± 0.27	15.4 ± 0.85	2.8 ± 0.75	35.9 ± 3.40
RAPID1	1.07 ± 0.31	22.0 ± 0.30	3.9 ± 1.19	31.9 ± 2.42
DEEP1	1.50 ± 0.59	13.7 ± 2.78	3.0 ± 0.66	29.8 ± 2.46
RAPID&DEEP	1.24 ± 0.57	25.5 ± 3.71	4.8 ± 2.11	23.9 ± 2.07
DEEP2	1.59 ± 0.61	13.8 ± 1.05	3.2 ± 0.78	26.7 ± 2.78
RAPID2	1.11 ± 0.38	22.2 ± 0.34	3.9 ± 1.39	25.8 ± 2.63
NORMAL2	1.11 ± 0.26	15.6 ± 0.61	2.7 ± 0.87	28.5 ± 3.16
FREE2	0.88 ± 0.25	14.1 ± 2.55	2.0 ± 0.77	32.0 ± 3.59

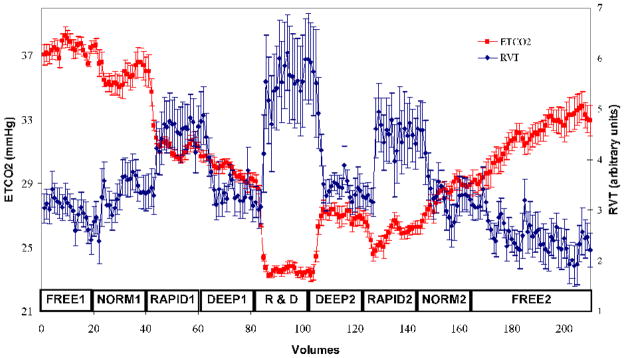
The average ETCO₂ and RVT timecourses were inversely correlated to one another (r = −0.61) and both showed significant average changes between the different breathing conditions of the experiment, as shown in Fig. 1. Compared to the baseline levels during the initial free breathing period, a 35% ETCO₂ decrease was seen during RAPID&DEEP. The ETCO₂ levels during the RAPID1, DEEP1, and RAPID&DEEP conditions were significantly lower than those in the immediately preceding condition. Also, the ETCO₂ levels during each breathing condition following RAPID&DEEP were significantly lower than in the first occurrence of the corresponding condition. Thus, for ETCO₂, NORMAL1 > NORMAL2, RAPID1 > RAPID2, and DEEP1 > DEEP2. In contrast, the average RVT timecourse showed no significant differences between the first and second occurrences of the FREE, NORMAL, RAPID, and DEEP breathing conditions, which parallels the identical breathing cues during these conditions. However, the RVT timecourse did significantly change between different breathing tasks. The largest change was a 105% increase in RVT between FREE1 and RAPID&DEEP. Looking at consecutive conditions, the RVT significantly differed between NORMAL1 and RAPID1 and between DEEP1 and RAPID&DEEP.

Fig. 1.

Plot of average end-tidal carbon dioxide (ETCO₂, red) and respiration volume per time (RVT, blue) timecourses for all subjects throughout the experiment. Error bars represent standard error of the mean. The labels immediately above the x-axis refer to the different breathing conditions in Table 1. NORM = NORMAL, R&D = RAPID&DEEP.

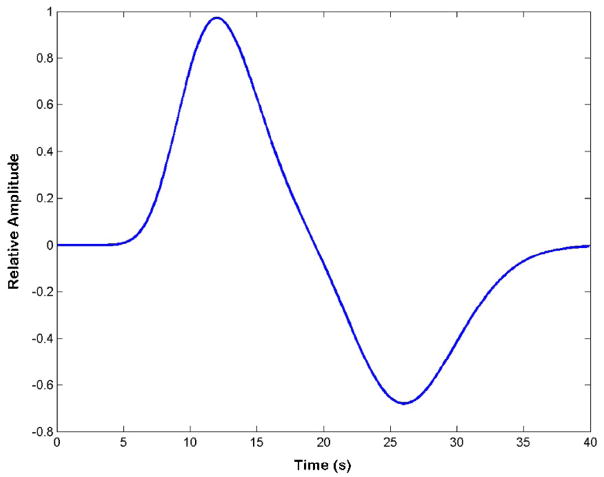
The iterative analysis used to empirically determine the ETCO₂ response function found a best-fit double gamma function, shown in Fig. 2. The first peak was at 12 s with FWHM = 7 s, while the second peak had opposite polarity, occurred at 26 s with FWHM = 9s, and had a relative amplitude of 0.7 times the first peak. Considerable variability across subjects was seen in strength of correlation between the MRI data and ETCO₂ convolved with this average response function, as shown in Table 3.

Fig. 2.

Plot of the determined average ETCO₂ response function.

Table 3. Individual subject average results for regression against the image data of the end-tidal carbon dioxide (ETCO2) timecourse convolved with the determined ETCO2 response function.

Voxel count is the number of voxels in which the regression was statistically significant (p < 0.05). Max = maximum; F-stat is the F-statistic. R² is the coefficient of multiple determination.

Subject Number	Voxel Count	Max F-stat	Mean F-stat	Max R2	Mean R2
1	24143	85.15	18.20	0.2905	0.0782
2	13709	61.25	10.20	0.2275	0.0460
4	13662	90.48	10.22	0.3031	0.0460
5	4902	30.09	6.87	0.1264	0.0318
6	2223	19.87	6.00	0.0872	0.0279
7	22643	98.89	20.20	0.3222	0.0851
8	10474	38.50	9.42	0.1562	0.0428
9	15580	47.64	11.00	0.1864	0.0495
Average	13417	58.98	11.52	0.2124	0.0509

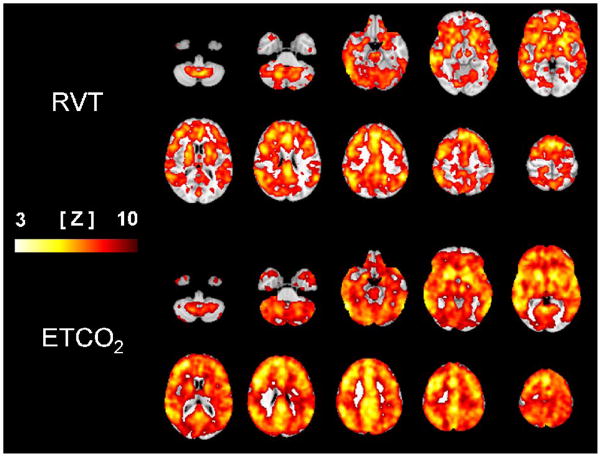
Figure 3 shows the group average FSL maps for ETCO₂ and RVT overlaid on the MNI standard brain. The top panel shows voxels correlated to RVT, which had a maximum Z-score of 7.02, with 144,733 significant voxels. A stronger and more widespread pattern of correlation to ETCO₂ changes was seen with maximum Z = 9.7 over 225,095 significant voxels, shown in the bottom panel.

Fig. 3.

Selected slices of the average maps showing significant correlation to the respiration volume per time (RVT, top) and end-tidal carbon dioxide (ETCO₂, bottom) regressors overlaid on the standard brain. The color scale shows the Z-score for each voxel.

Discussion

It is the arterial CO₂ concentration that actually drives blood vessel diameter, which controls CBF. Thus, a misestimation of arterial CO₂ levels could confound the ability to detect correlation between ETCO₂ and BOLD signal changes. Though ETCO₂ may underestimate arterial CO₂ at rest, misestimations are not typically seen during hypocapnia [9]. This implies that the actual maximum change in arterial CO₂ level in this study may have been greater than the measured change in ETCO₂, but this change is not likely to have been underestimated. Furthermore, MCA blood flow velocity, and thus CBF, is correlated to changes in ETCO₂ throughout the range of 20 to 50 mmHg [43]. This range includes, with wide margins, the values observed in this study, indicating that the ETCO₂ data should be a reliable predictor of CBF changes.

In addition to the CO₂-mediated changes in CBF, respiration has an instantaneous effect on the BOLD signal through susceptibility shifts due to tidal volume changes [44,45]. However, since this mechanism operates at a frequency equal to the respiratory rate, RETROICOR correction should reduce signal noise of this etiology [28]. Another mechanism has also been postulated for RVT to be a more direct predictor of BOLD changes than ETCO₂ [29], in that intrathoracic pressure changes with respiration may have a delayed effect on heart rate and stroke volume [29,46]. These changes could induce low-frequency fluctuations in CBF independent of the vasodilatory mechanism linked to hypercapnia. In a previous study, however, including RVT in the model for BOLD signal changes in addition to ETCO₂ did not appreciably increase the strength of correlation compared to ETCO₂ alone [29]. Furthermore, this study has demonstrated a stronger correlation of ETCO₂ to BOLD signal changes when imaging a period of hypocapnia induced by paced hyperventilation. This suggests that the predominant mechanism by which changes in minute ventilation cause low-frequency changes in CBF is CO₂-mediated changes in blood vessel caliber.

As part of this study, a reasonable transfer function between induced ETCO₂ variations and BOLD signal changes was determined, and this ETCO₂ response function is shown in Fig. 2. The seminal work on BOLD response to ETCO₂ changes [11] found the delay between CO₂ changes and MCA blood velocity to be 6.3 s. Using a gamma variate function with that delay to model BOLD changes in the brain parenchyma, the authors found many areas of significant correlation. The same group later found that a BOLD signal increase followed an ETCO₂ increase after 12 ± 4 s, when averaged across the brains of all subjects, and a much stronger and more widespread pattern of correlation was demonstrated with this longer latency [47]. Recently, an average latency of 10 ± 1.6 s was found [29], which contrasts with an older study reporting average delays of 15 to 18 s for gray and white matter, respectively [48]. Taken together, these findings suggest that an increase in ETCO₂ induces a BOLD signal increase occurring between 10 to 18 seconds later. This matches the first, positive peak of the derived average ETCO₂ response function described in the results and shown in Fig. 2. The second, negative peak in the average ETCO₂ response function describes a later, smaller amplitude BOLD signal change that is opposite in magnitude to the primary ETCO₂ change. Further analysis showed a reduced strength of correlation to the FMRI data when ETCO₂ was applied using an identical response function with the second peak removed or reduced in amplitude. This phenomenon has previously been unreported for the BOLD response to CO₂ changes, but may occur by mechanisms similar to the well-known BOLD post-stimulus undershoot seen with task FMRI [49]. It should be noted that variability in latency across brain regions and across subjects has been reported in the literature [29,47,48] and was observed in this study. Nonetheless, the widespread pattern of strong correlation seen in Fig. 3 when implementing the determined ETCO₂ response function demonstrates its efficacy. This extensive pattern generally agrees with previous maps for BOLD changes modeled by ETCO₂ data implemented with a similar delay time [29,47].

Changes in RVT are inversely correlated to changes in ETCO₂ as increased ventilation, reflected by an RVT increase, decreases ETCO₂. Thus, compared to the RRF, the ETCO₂ transfer function is expected to have the opposite polarity of its major peak. It is the second portion of the RRF, with negative peak occurring at 15.4 s, that has the larger amplitude of 1.12 times the first peak and is broader, representing a greater impact on BOLD signal. This second portion of the RRF corresponds to the first peak in the ETCO₂ response function, occurring at 12 s. The difference between the average response to ETCO₂ at 12 s and the RRF response at 15 s likely represents the delay for respiration changes to affect ETCO₂, which is an intermediate variable in the events linking breathing to CBF. Additional differences between the two response functions are in the timing and width of their lesser amplitude components. For an RVT increase, an early and short-lived BOLD signal increase is modeled by the minor RRF peak at 3.1 s with FWHM = 4.2 s. For an ETCO₂ increase, a late BOLD signal decrease is modeled by the lesser peak of the ETCO₂ response function at 26 s with FWHM = 9 s. The overall duration of effect for the RRF is greater than 50 s, whereas the ETCO₂ response function returns to baseline by 40 s. It is possible that the fit of the ETCO₂ response function would be further improved by including a third component analogous to the RRF peak at 3.1 s. However, such optimization was beyond the scope of this study in which a reasonably optimized two- component ETCO₂ transfer function was found to be adequate.

The iterative analysis in this study showed large variability in the optimum timing for the ETCO₂ response across subjects, which is consistent with the variability in BOLD response time reported for ETCO₂ fluctuations [29,47,48], as well as breath holding and cued deep breathing tasks [28,50]. The use of flexible response functions during model fitting was intended to account for these differences across subjects as well as across-voxel heterogeneity in the brain. The FLOBS utility in FSL [39] allows for a varying response at each voxel by modeling the transfer function as a set of basis functions that can be combined to create a response function that varies in shape within defined parameters. The response function estimates are constrained to have two peaks of opposite polarity, which can accommodate the shape of both the RRF and ETCO₂ response functions. In this study, timing variations of ± 2 s for the peak timings of the response functions were allowed, rather than applying the average best-fit response function to all brain regions in every subject. This method is analogous to optimizing the response function for each voxel independently, but is available in pre-packaged software, rather than requiring custom analysis.

Respiration is related to ETCO₂ by a bi-directional feedback control system, such that changes in breathing induce changes in ETCO₂, and any deviation of ETCO₂ away from its physiologic set-point stimulates changes in respiration to compensate. Because the rate and depth of breathing were paced in this experiment, RVT was effectively uncoupled from ETCO₂ feedback control. Nonetheless, since changing breathing was the sole mechanism used to manipulate the ETCO₂ level, it is reasonable to assume that RVT changes would effectively model changes in ETCO₂. However, the hypocapnia induced by the end of the RAPID&DEEP condition impacted the relationship between RVT and CO₂ for the remainder of the experiment. When comparing the first to the second occurrence of the NORMAL, RAPID, and DEEP conditions, lower ETCO₂ levels accompany similar RVT values, as shown in Fig. 1. In effect, hysteresis is seen in the ETCO₂ response to the paced breathing conditions when comparing the transition from normocapnia to hypocapnia with the transition from hypocapnia to normocapnia. This discrepancy results from a slow rate of metabolic CO₂ production, relative to the rate of CO₂ reduction with hyperventilation. This uncoupling creates a disparity between changes in RVT and the arterial CO₂ level it normally models. The result is greater correlation to the FMRI data of ETCO₂ compared to RVT, which is visually apparent in Fig. 3.

This work, in no way, contradicts previous studies in which RVT successfully modeled BOLD changes during experiments of a cognitive task [51], cued breathing [28], or breath holding [51]. In fact, the patterns of RVT-correlated voxels throughout the gray matter demonstrated in previous studies [28,29,51] roughly match the results for RVT shown in Fig. 3. However, this study demonstrated that ETCO₂ better models BOLD signal fluctuations in FMRI experiments that induce significant transient hypocapnia. This occurs not only with paced hyperventilation, as shown here, but may also confound experimental pain studies, which are known to have task-induced breathing increases [52, 53].

Conclusions

This study demonstrated a paced breathing experimental design that induced transient hypocapnia and effectively uncoupled respiration from CO₂. This resulted in a disparity between calculated RVT and ETCO₂ values. When both were implemented with average transfer functions incorporating flexibility across voxels and subjects, ETCO₂ was more robustly correlated to the BOLD data than RVT. This demonstrates that ETCO₂ monitoring and correction may be preferred in FMRI experiments that include episodes of significant hypocapnia amidst periods of relative normocapnia.