Compression of fiber supercontinuum pulses to the Fourier-limit in a high-numerical-aperture focus

Abstract

A multiphoton intrapulse interference phase scan (MIIPS) adaptively and automatically compensates the combined phase distortion from a fiber supercontinuum source, a spatial light modulator pulse shaper, and a high-NA microscope objective, allowing Fourier-transform-limited compression of the supercontinuum pulses at the focus of the objective. A second-harmonic-generation-based method is employed to independently validate the transform-limited compression. The compressed pulses at the focus of the objective have a tunable duration of 10.8–38.9 fs (FWHM), a central wavelength of ~1020 nm, an average power of 18–70 mW, and a repetition rate of 76 MHz, permitting the application of this source to nonlinear optical microscopy and coherently controlled microspectroscopy.

In nonlinear microscopy, efforts have been devoted to the pulse compression of fiber supercontinuum (SC) centered at ~800 nm through the combination of a photonic crystal fiber (PCF) and a Ti:sapphire laser oscillator (~80 MHz) producing 100–250 fs pulses [1-3]. However, similar efforts have been lacking for the increasingly popular Yb-based ultrafast lasers producing 100–500 fs pulses. Here we employ the multiphoton intrapulse interference phase scan (MIIPS) technique [4] to compress a Yb-oscillator-induced fiber SC. We demonstrate the in situ capability of this source for coherently controlled microscopy and microspectroscopy applications [5] by delivering transform-limited (TL) 10.8 fs pulses or shaped pulses at the focus of a high-NA microscope objective. Also, we validate the TL compression and the pulse shaping by a simple method that is applicable to all ultrashort pulse measurements using thin second-harmonic-generation (SHG) crystals.

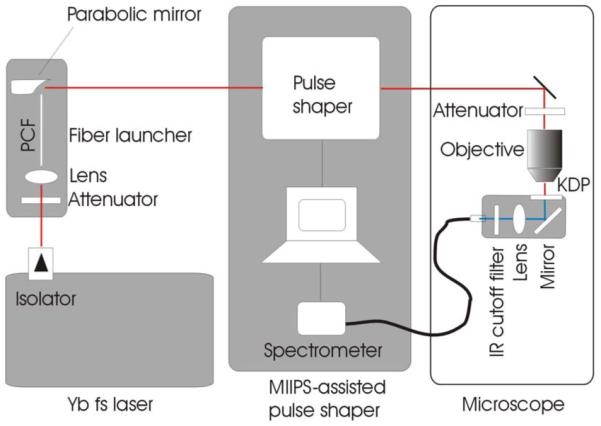
The polarized fiber SC source in the spectral range of 850–1200 nm is generated by coupling the 229 fs pulses of a solid-state Yb:KYW laser oscillator (FemtoTrain, High-Q Laser GmbH) into a 9 cm all-normal dispersion PCF (NL-1050-NEG-1, NKT Photonics, Denmark) [6]. The SC beam is first collimated by a parabolic mirror and sent to a MIIPS-assisted 4f pulse shaper (Box640, BioPhotonicSolutions Inc.) designed for broadband (700–1350 nm) operation on a 640 pixel spatial light modulator (SLM), corresponding to a spectral resolution of ~1 nm=pixel (Fig. 1). The exiting SC beam is then sent to a microscope and focused by a 60 × /0.9 NA aberration-corrected (600–1200 nm) objective (LUMPlanFL/IR, Olympus Inc.) onto a thin (10 μm) KDP crystal, while the resulting SHG signal is collected by a lens and sent into a spectrometer. The KDP crystal, the lens, the fiber port of the spectrometer, and an IR cutoff filter have been integrated into a compact (7.6 cm × 2.5 cm × 2.5 cm) and easily removable unit (MDU, BioPhotonicSolutions, Inc.) optimized for SHG collection (Fig. 1). The SHG signal is used as the real-time feedback for MIIPS operation.

Fig. 1.

(Color online) TL compression of fiber SC pulses in a high-NA focus.

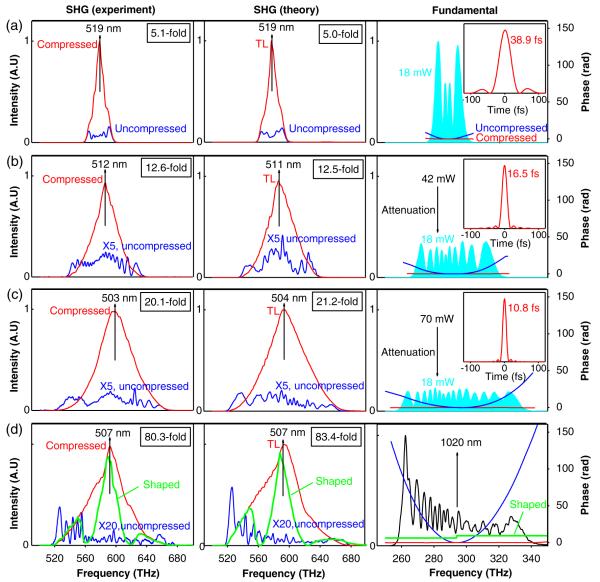
The power throughput of the SC generation, the pulse shaper, and the objective were ~55%, ~30%, and ~70%, respectively. The total throughput, measured as the ratio of the SC power at the focus of the objective to the attenuated Yb laser power incident on the PCF (Fig. 1), is therefore ~11%, and is relatively independent on the attenuation. By varying this attenuation at the output of the Yb laser alone, three SC spectra and powers at the focus of the objective were measured by an optical spectrum analyzer and a powermeter [Figs. 2(a)–2(c), right column], with the highest power (70 mW) corresponding to the broadest spectrum. The wavelength-dependent throughput of the pulse shaper and the objective slightly modified the reported spectra of the fiber SC [6]. To directly compare the SHG results among different incident SC spectra, the SC powers at the focus of the objective were further attenuated to a constant 18 mW [i.e., equal area of the shaded spectra in Figs. 2(a)–2(c), right column] by a neutral-density attenuator inserted in front of the objective (Fig. 1).

Fig. 2.

(Color online) (a)–(d) Comparison of the experimental SHG spectra (left column) and theoretical SHG spectra (middle column) corresponding to the spectral phases of four SC fundamentals (right column) for compressed (or TL) SC pulses (thin red), uncompressed SC pulses (thin blue), and shaped SC pulses (thick green). The spectral phases of the uncompressed pulses correspond to the retrieved spectral phases from MIIPS measurements. The shaded regions (or thin black curve) in the right column show the spectra of the four SC fundamentals, and the insets show the temporal profiles of the compressed SC pulses. SHG enhancement factors due to pulse compression are indicated in the left and middle columns.

The spectral phase of each focusing SC was then retrieved by standard MIIPS procedures and subsequently compensated by the pulse shaper, resulting in an uncompensated residual phase that approximates zero across the SC spectrum [Figs. 2(a)–2(c), right column]. The retrieved spectral phase is rather smooth, consistent with the simulation reported previously [6]. The reconstructed temporal intensity profile of the phase-compensated (compressed) pulse corresponding to this uncompensated residual phase [Figs. 2(a)–2(c), insets] differs little from that of the TL pulse (with zero spectral phase) calculated directly from the SC spectrum, while the FWHM width of the compressed pulse is only slightly larger (<3%, typically) than that of the TL pulse. These data have been consistently acquired in repeated measurements with statistical errors comparable to the reported values [4], despite the spiky spectra of the fiber SC source. In a review article [4], the pulse measurement by MIIPS has been justified to be as reliable as frequency-resolved optical gating (FROG) or spectral interferometry for direct electric-field reconstruction (SPIDER).

Similar near-TL ultrashort (~10 fs) Ti:sapphire-laser-based pulse compression in high NA (>0.65) foci have been demonstrated for the 4f pulse shaper using FROG/two-beam SPIDER [2,3], MIIPS [7], and single-beam SPIDER [8], all of which employ a thin SHG crystal as the nonlinear medium. Because the measurements by FROG and two-beam SPIDER may be affected by imperfect collinear alignment, while those by MIIPS and single-beam SPIDER by imperfect SLM calibration, cross validation has been performed between FROG and two-beam SPIDER [2,3], between MIIPS and autocorrelation [7], and between MIIPS and single-beam SPIDER [8].

This cross-validation procedure strongly ensures the correct pulse measurements but adds considerable complexity. A validation method independent of these pulse measurement methods is to compare the SHG signals immediately before and after the phase compensation (driven electronically by the pulse shaper) without varying any optical parameter(s) [Figs. 2(a)–2(c), left column]. To quantitatively understand these results, we calculate frequency-dependent SHG intensity of the SC pulse from $S\left(2\omega \right)={\mid \int \mid E(\omega +\Omega )\mid \mid E(\omega -\Omega )\times \mid e^{i\psi (\omega +\Omega )}{e}^{i\psi (\omega -\Omega )}d\Omega \mid }^2$, where Ω is integrated over the SC spectrum [4]. The amplitudes in the integral are derived from the SC spectrum scaled by the average power [i.e., equal area among the shaded spectra in Figs. 2(a)–2(c), right column], while the exponentials in the integral are either treated as unity for the TL pulse or calculated according to the retrieved spectral phase of the corresponding uncompressed pulse [Figs. 2(a)–2(c), middle column].

The comparison between the experimental and the theoretical SHG results [Figs. 2(a)–2(c), left and middle columns] validates the TL pulse compression by MIIPS. First, the theoretical SHG spectrum corresponding to each of the three TL SC pulses has a smooth profile and a well-defined central wavelength that approximate their experimental counterparts of the compressed SC pulse, despite the highly structured spectra of the SC fundamentals that produce the unsmooth SHG spectra of the uncompressed pulses. Second, the same average power of the three SC fundamentals under the same SHG acquisition condition allows direct comparison of the integrated SHG intensities (over frequency) among Figs. 2(a)–2(c). The theoretical ratio of the integrated SHG intensities among the three TL SC pulses is 1:2.4:3.7, which is in excellent agreement with the experimental ratio of 1:2.2:3.5 among the three compressed SC pulses. Consistently, the inverse of the calculated FWHM pulse width [Figs. 2(a)–2(c), right column] results in a ratio of 1:2.4:3.6.

The validation of the TL compression justifies the phase compensation, and therefore validates the retrieved spectral phases. Another indicator to validate the retrieved spectral phase is the enhancement factor of the integrated SHG intensities before and after the phase compensation, which highlights the effectiveness of the pulse compression. The theoretical enhancement factors of the three SC fundamentals are calculated to be 5.0, 12.5, and 21.2, matching the experimental values of 5.1, 12.6, and 20.1 [Figs. 2(a)–2(c), left column].

Each retrieved spectral phase in Figs. 2(a)–2(c) represents the combined phase distortion from the fiber SC itself and the dispersive optics transmitting the SC (i.e., pulse shaper, objective). The adaptive phase compensation of the fiber SC by MIIPS has been demonstrated in Figs. 2(a)–2(c). To demonstrate the adaptive phase compensation of the transmitting optics, the pulse shaper was replaced with another pulse shaper consisting of a similar 640 pixel SLM and grating, and the compression was performed with the same conditions as those in Fig. 2(c). In this case, the significantly enlarged phase distortion did not affect the spectral phase retrieval and the TL compression by MIIPS, as validated by the accurate prediction of the spectrum/central-wavelength of the SHG signal and the large (approximately eightyfold) enhancement factor of the phase compensation [Fig. 2(d)]. The results in Figs. 2(c) and 2(d) exhibit the surprisingly large variation of the intrinsic phase distortion from the pulse shapers, which may be attributed to the large variation of the dispersion among the 640 pixel SLMs. Similar adaptive phase compensation by MIIPS has also been demonstrated for the microscope objective.

The theory–experiment discrepancy in the SHG results of the uncompressed pulses [Figs. 2(b)–2(d)] is likely due to the oversimplified modeling of the spatiotemporal fields in the high NA focus [9]. However, this discrepancy is rather small in Fig. 2(a), suggesting that accurate coherent control can be attained at small phase distortions. As a confirmation, a flat phase mask, except for a stepwise jump of π at the center SC frequency, is superimposed on the compressed pulse [Fig. 2(d)] through the SLM. The obtained experimental SHG spectrum agrees with the theoretically calculated spectrum corresponding to the phase mask, indicating the applicability of this source to coherently controlled microspectroscopy.

The applicability of a fiber SC source to nonlinear optical microscopy and coherently controlled microspectroscopy has been demonstrated. This source can adaptively accommodate application-dependent modifications in transmitting optics, and is useful when long excitation wavelengths (>800 nm) are preferred. It is the starting point to develop compact fiber-based coherently controlled sources for portable applications.