NMR Data Processing using Iterative Thresholding and Minimum l₁-norm Reconstruction

Abstract

Iterative thresholding algorithms have a long history of application to signal processing. Although they are intuitive and easy to implement, their development was heuristic and mainly ad hoc. Using a special form of the thresholding operation, called soft thresholding, we show that the fixed point of iterative thresholding is equivalent to minimum l₁-norm reconstruction. We illustrate the method for spectrum analysis of a time series. This result helps to explain the success of these methods and illuminates connections with maximum entropy and minimum area methods, while also showing that there are more efficient routes to the same result. The power of the l₁-norm and related functionals as regularizers of solutions to underdetermined systems will likely find numerous useful applications in NMR.

Introduction

The computation of NMR spectra from short, noisy data records has long been a challenging problem. Procedures adopted from fields outside of NMR have proven to be superior to the discrete Fourier transform (DFT)[1, 2]; examples include maximum entropy (MaxEnt) [3, 4] and minimum-area[5] reconstruction, maximum likelihood reconstruction (MLM)[6, 7], and matrix methods such as LPSVD[8] and HSVD[9]. A method that is conceptually simpler and easier to implement than these methods is iterative thresholding[10-12]. This and related thresholding algorithms are widely used in the fields of image processing and fMRI. Iterative thresholding is a fixed-point technique; an operation is repeatedly applied until it no longer results in a change. The repeated operation has a particularly simple form: it involves setting all values below a threshold τ (in absolute value) to zero, while leaving values above τ unchanged.

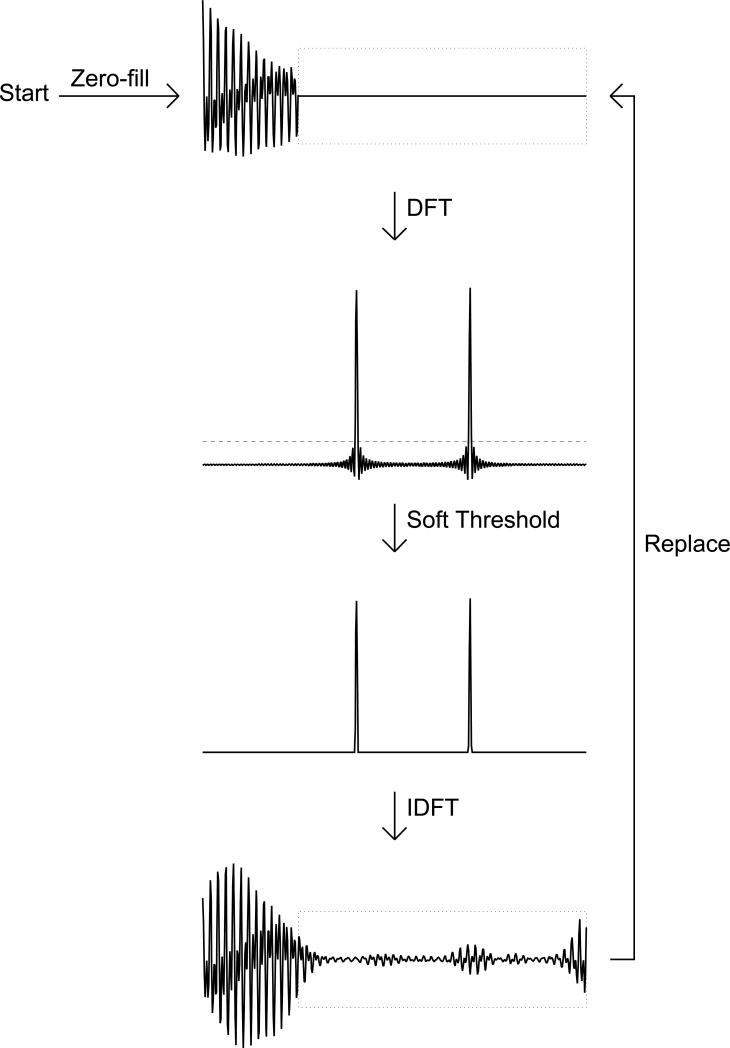
Iterative thresholding algorithms applied to spectrum analysis have a strong heuristic appeal. Consider a free induction decay (FID) containing several exponentially decaying sinusoids with similar amplitudes, in which the length of the FID is short compared to the decay time of the sinusoids. A high-resolution estimate of the spectrum can be obtained by zero-filling the FID prior to discrete Fourier transformation, but the DFT spectrum will contain truncation artifacts. Choose a threshold value τ that is smaller than the peak maxima, but larger than any truncation artifacts, and set every point in the DFT spectrum that is below τ to zero, leaving the others unchanged. The inverse DFT of the thresholded spectrum will not agree very well with the input FID. However, if we consider only the part that extends the measured data, we may find that it is a more realistic extension than extending the data with zeros. Thus a better spectral estimate may be obtained by extending the FID with values from the inverse DFT of the thresholded spectrum, or equivalently, replacing the initial part of the inverse DFT with the original FID. This process of inverse Fourier transformation, replacement, Fourier transformation, and thresholding (Fig. 1) is repeated until there is no change in the spectrum, that is, until the fixed-point is reached.

1.

A schematic diagram of IST. The initial trial spectrum is the DFT of the zero-filled data. Subsequent trial spectra are computed by applying the soft thresholding operation: setting points below a threshold to zero, and subtracting the threshold from all other points. The result is inverse Fourier transformed, the “tail” is used to extend the measured data, and the augmented data is forward Fourier transformed and thresholded.

We refer to the thresholding operation in which values above τ are unchanged as hard thresholding. By contrast, in the soft thresholding operation, data with absolute values above τ are reduced by τ (with no change in complex phase). We show in the Appendix (Supplementary Material) that the fixed-point of iterative soft thresholding (IST) is also a minimum l₁-norm reconstruction (defined below). This equivalence has several implications. (1) Formal results on the properties of minimum l₁-norm reconstructions have been derived; no comparable results on the properties of the fixed-points of iterative thresholding procedures are available; (2) Logan's theorem [13] shows that under certain circumstances l₁-norm reconstruction is able to perfectly reconstruct the spectrum of a noisy signal; (3) The equivalence demonstrates how IST can be generalized to incorporate deconvolution and modified to improve convergence; (4) The equivalence illuminates similarities between IST and methods such as MaxEnt and minimum-area reconstruction. The power of the l₁-norm for regularizing reconstructions from sparse or noisy data has received considerable attention in the statistical and applied mathematics communities[13-16], and helps to explain the success of iterative thresholding methods.

We also note that fixed thresholding has been applied to the wavelet domain as a means for “denoising” NMR spectra[17-19]. While we consider thresholding in the frequency or Fourier domain in this work, similar results (the equivalence of iterative soft thresholding and l₁-norm regularization) apply to wavelet thresholding.

Minimum l₁-norm reconstruction

The l₁-norm of a spectrum f is defined as

$$L\left(\mathbf{f}\right)={\parallel \mathbf{f}\parallel }_1\equiv \sum _{\omega =0}^{N-1}\mid f_{\omega }\mid$$ [1]

where N is the number of points in the complex vector f. The goal of minimum l₁-norm reconstruction is to find the spectrum f which minimizes L(f) subject to the constraint that f is consistent with the experimental data. This constraint is expressed by the formula

$$C\left(\mathbf{f}\right)\equiv \frac{1}{2}\sum _{k=0}^{M-1}{\mid \mathrm{IDFT}{\left(\mathbf{f}\right)}_k-d_k\mid }^2\le C_0$$ [2]

where M is the number of points in the complex FID d and C₀ is an estimate of the experimental error; IDFT is the inverse DFT. Minimum l₁-norm reconstruction is similar to minimum area reconstruction, proposed by Newman[5], the only difference being that Newman's “area” amounts to ${\sum }_{\omega }\mid \mathrm{Re}\left(f_{\omega }\right)\mid +\mid \mathrm{Im}\left(f_{\omega }\right)\mid$, which is not invariant under changes of phase. As we shall see later, minimum l₁-norm also bears a resemblance to MaxEnt.

The properties of minimum l₁-norm reconstruction were extensively studied by Logan[20]. One of his most striking results is that under certain conditions, having to do with the relative sparsity of the noise in the FID and the peaks in the spectrum, minimum l₁-norm reconstruction can result in a perfect spectrum, with no residual noise. Unfortunately, Logan's conditions do not apply to real NMR data, but this result indicates the potential power of the technique.

The problem of determining the minimum l₁-norm reconstruction can be converted to an unconstrained optimization problem by introducing a Lagrange multiplier τ. Let the objective function Q(f) be given by

$$Q\left(\mathbf{f}\right)\equiv \tau L\left(\mathbf{f}\right)+C\left(\mathbf{f}\right).$$ [3]

As we show in the Appendix (Supplementary Material), if f is a minimum l₁-norm reconstruction, then f is a minimum of Q. One technique for finding this minimum is to perform a gradient search. The gradient of Q is

$$\nabla Q\left(\mathbf{f}\right)=\tau \nabla L\left(\mathbf{f}\right)+\nabla C\left(\mathbf{f}\right).$$ [4]

Computing the gradient of L is straightforward. Expanding Eq. [1], and writing $f_{\omega }^r$ and $f_{\omega }^i$ for the real and imaginary parts of f_ω, we obtain

$$L\left(f\right)=\sum _{\omega =0}^{N-1}\mid f_{\omega }\mid ,$$ [5]

$$\frac{\partial L}{\partial f_{\omega }^r}=\frac{f_{\omega }^r}{\mid f_{\omega }\mid },\frac{\partial L}{\partial f_{\omega }^i}=\frac{f_{\omega }^i}{\mid f_{\omega }\mid }$$ [6]

We will adopt the convention that ∂L / ∂f_ω is $\partial L∕\partial f_{\omega }^r+i\partial L∕\partial f_{\omega }^i$, which yields

$$\frac{\partial L}{\partial f_{\omega }}=\nabla L{\left(\mathbf{f}\right)}_{\omega }=\frac{f_{\omega }}{\mid f_{\omega }\mid }.$$ [7]

The derivation of ∇C(f) is more laborious; we simply state the result (details are given in (14)). Let F be the (N × N) unitary matrix corresponding to the DFT, and let K be the (M × N) projection matrix which shortens an N-element vector to its first M elements. Then

$$C\left(\mathbf{f}\right)=\frac{1}{2}{\parallel {\mathbf{KF}}^{†}\mathbf{f}-\mathbf{d}\parallel }^2$$ [8]

and

$$\nabla C\left(\mathbf{f}\right)={\mathbf{FK}}^{†}({\mathbf{KF}}^{†}\mathbf{f}-\mathbf{d}),$$ [9]

where † denotes the Hermitian transpose; F^† corresponds to the IDFT and K^† corresponds to zero-filling.

Relationship of IST to minimum l₁-norm reconstruction

The somewhat opaque expression in Eq. [9] belies the simplicity of the underlying operations. Re-writing Eq. [9] in operator notation,

$$\nabla C(\mathbf{f})=\mathrm{DFT}\left\{\text{zerofill}(\text{shorten}(\mathrm{IDFT}\left(\mathbf{f}\right))-\mathbf{d})\right\}=\mathrm{DFT}\{\text{trunc}(\mathrm{IDFT}\left(\mathbf{f}\right))-\text{zerofill}\left(\mathbf{d}\right)\}$$ [10]

where trunc(x) = zerofill(shorten(x)) is the operation of setting the elements x_M, ..., x_N-1 to zero. Now we are in a position to see the unexpected relationship between the gradient of Q and the operations of IST. Soft thresholding by τ is expressed by

$${\text{thresh}}_{\tau }{\left(\mathbf{f}\right)}_{\omega }=\{\begin{array}{cc}{f}_{\omega }-\tau f_{\omega }∕\mid f_{\omega }\mid ,\hfill & \text{if}\mid f_{\omega }\mid >\tau \hfill \\ 0,\hfill & \text{if}\mid f_{\omega }\mid \le \tau .\hfill \end{array}\phantom{\}}$$ [11]

So for indices ω at which |f_ω| > τ , soft thresholding is the same as subtracting τ∇L. The replacement step of IST is expressed by

$$\mathbf{f}\to \mathrm{DFT}\{[\mathrm{IDFT}\left(\mathbf{f}\right)-\text{trunc}\left(\mathrm{IDFT}\left(\mathbf{f}\right)\right)]+\text{zerofill}\left(\mathbf{d}\right)\}=\mathbf{f}-\mathrm{DFT}\left\{\text{trunc}(\mathrm{IDFT}\left(\mathbf{f}\right)-\text{zerofill}\left(\mathbf{d}\right)\right\}.$$ [12]

Comparison with Eq. [10] shows that replacement is the same as subtracting ∇C. So combining the replacement operation and the thresholding operation, we see that one iteration of IST corresponds to motion opposite the gradient of Q, and a fixed point of IST corresponds to a minimum of Q.

This description is not quite complete, since ∇L is not defined for f_ω = 0 and soft thresholding is not the same as subtracting τf_ω/|f_ω| if |f_ω| < τ. Nevertheless, the description does suggest the relationship between IST and minimum l₁-norm reconstruction; the formal proof of their equivalence is given in the Appendix.

This equivalence shows how IST can be generalized to perform deconvolution. Deconvolving a decay w involves reconstructing a spectrum whose IDFT, when weighted by w, agrees with the experimental FID. This weighting can be incorporated into Eq. [2] by setting

$$C\left(\mathbf{f}\right)\equiv \frac{1}{2}\sum _{k=0}^{M-1}{\mid w_k\mathrm{IDFT}{\left(\mathbf{f}\right)}_k-d_k\mid }^2.$$ [13]

The corresponding modification to Eqs. [8] and [9] simply involve setting the diagonal elements of the matrix K equal to w. The only change needed in IST is to adjust the replacement operation so that it coincides with motion opposite the gradient of the revised constraint. In operator notation, this becomes

$$\mathbf{f}\to \mathbf{f}+\mathrm{DFT}\left\{\text{zerofill}\left[\text{weight}[\mathbf{d}-\text{weight}\left(\text{shrink}\left(\mathrm{IDFT}\left(\mathbf{f}\right)\right)\right)]\right]\right\}$$ [14]

where the weight operator corresponds to pointwise multiplication by the decay w.

IST is capable of reconstructing spectra for non-linearly sampled data (15). Indeed, this can be viewed as a special case of deconvolution: the weights for points not sampled are simply set to zero.

Relationship of IST to MaxEnt

The equivalence of IST and minimum l₁-norm reconstruction also makes clear the similarity to MaxEnt. The basic aim of MaxEnt reconstruction is the same as that of minimum l₁-norm reconstruction, except the regularization functional is the entropy, rather than the l₁-norm. The entropy functional S is approximately given by

$$S\left(\mathbf{f}\right)=-\sum _{\omega =0}^{N-1}\mid f_{\omega }\mid \log \mid f_{\omega }\mid .$$ [15]

The main difference between the entropy and the l₁-norm is the opposite sign; consequently maximizing the entropy is very similar to minimizing the l₁-norm. It has been shown that under certain circumstances, the action of MaxEnt reconstruction is equivalent to a nonlinear scaling of the DFT spectrum[21]. The nonlinear scaling reduces the absolute value of each point in the spectrum; small values are scaled down proportionally more than large values. The similarity to soft thresholding is clear.

Convergence of IST

While the formal results presented in the appendix show that the fixed-point of IST is the minimum l₁-norm reconstruction, they say nothing about how quickly IST converges. Indeed, the finite precision of computer arithmetic makes it entirely possible that the step size may reach machine zero — a value smaller than the smallest non-zero number that can be represented — well before the minimum of Q has been reached. Should this happen, the algorithm would appear to have converged, but it would not produce the correct result. In testing for convergence, therefore, it is important that we monitor not only the step size, defined by

$$Stepsize={\left[\frac{1}{N}\sum _{\omega =0}^{N-1}{\mid f_{\omega }(i+1)-f_{\omega }\left(i\right)\mid }^2\right]}^{1∕2},$$ [16]

where f_ω(i) is the ω^th element of f at iteration i, but also the quantity

$$Test=\mid \frac{\nabla L}{\mid \nabla L\mid }\mid -\mid \frac{\nabla C}{\mid \nabla C\mid }\mid ,$$ [17]

which is equal to zero only at a minimum of Q. (At indices ω for which f_ω=0, the gradient of L is not defined; these indices can simply be ignored in calculating Test.)

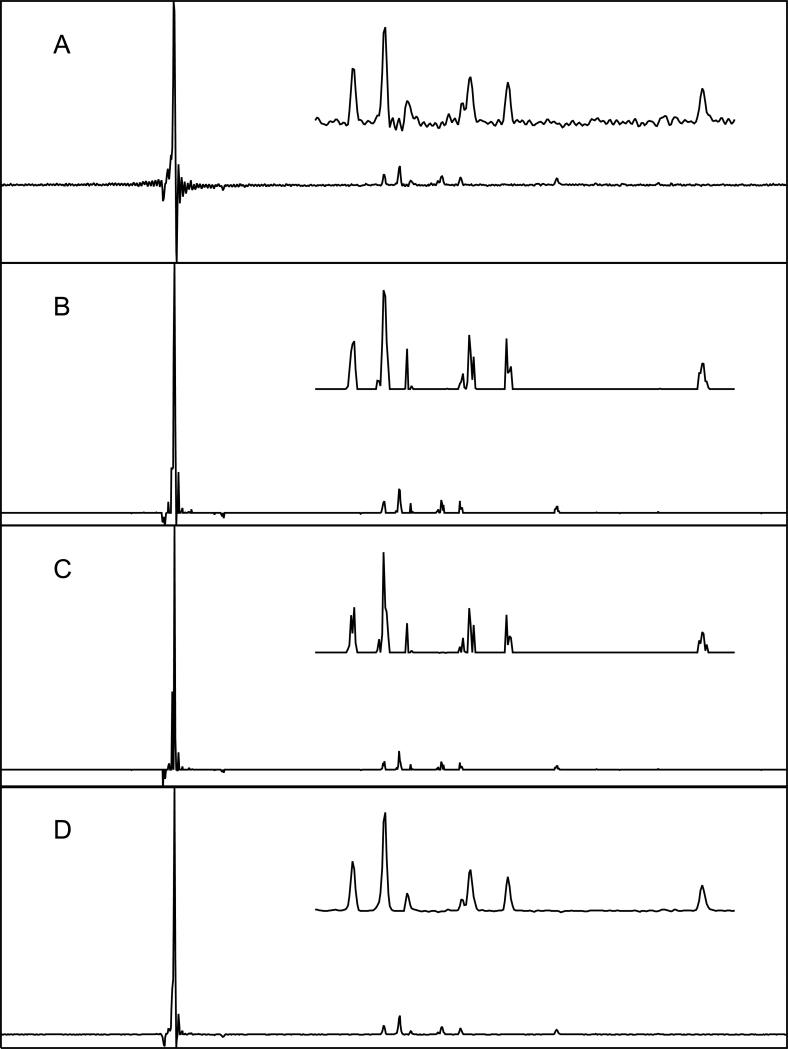
Figure 2 shows various spectrum reconstructions of a f₁ column from a NOESY data set (following processing in f₂) in which the diagonal resonance is about 10 times more intense than the off-diagonal resonances. Row A is the unapodized, zero-filled DFT. The result of IST applied for 800 steps is shown in row B; Stepsize became negligibly small, but not zero. Row C shows the results of a modified algorithm in which the change during each iteration is −β(i)∇Q, instead of −∇Q, where β(i) is a scale factor chosen to minimize Q at iteration i; it can be found by a simple line search (we refer to this algorithm as line-search IST, as opposed to simple IST).

2.

Spectral reconstructions of an f₁ column from NOESY data for a 66-residue protein. Row A is the unapodized zero-filled DFT spectrum; rows B and C show the results of 800 iterations of simple and line-search IST, respectively. D is the result of 40 iterations of MaxEnt reconstruction.

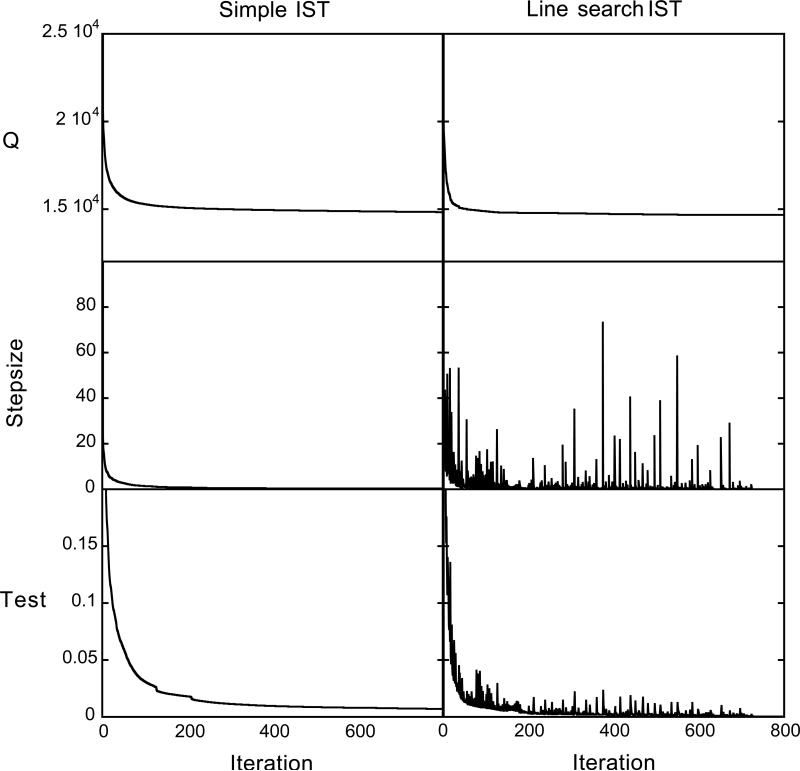
Figure 3 shows Q, Test, and Stepsize as a function of i. Since IST moves opposite ∇Q, the value of Q always decreases monotonically, in contrast to Test and Stepsize. The non-monotonic behavior of Stepsize and Test for line-search IST reflects well-known deficiencies of gradient descent[22]. Figure 3 also shows that merely monitoring Stepsize is not a safe way to test for convergence, since it becomes very small for simple IST even while Q is still changing. Test has not converged to zero for simple IST even after 800 iterations. In contrast, Test converges to zero for line-search IST at about the time that Stepsize becomes very small. The final values for Q are 14830 and 14665 for simple IST and line-search IST, respectively.

3.

Testing for convergence of IST by plotting the values of the objective function Q, Test, and Stepsize. Note that for simple IST, Q and Test continue to decrease even after Stepsize has approached zero.

Robustness of Minimum l₁-norm Reconstruction

Figure 2 illustrates that IST is capable of suppressing the truncation artifacts typical of zero-filled DFT spectra. For comparison, row D of Figure 2 shows a MaxEnt reconstruction. The most striking difference is that minimum l₁-norm reconstruction apparently “resolves” fine structure in the peaks that is not evident at all in the MaxEnt reconstruction. A simple test demonstrates that the additional structure in the minimum l₁-norm reconstruction is not correct. Figure 4 contains IST and MaxEnt reconstructions for the same data as Figure 3, except that a single synthetic decaying sinusoid has been added to the time domain data prior to reconstruction. Row A shows that IST yields an artifactual split line, while MaxEnt (row B) correctly yields a single peak. The reconstructions agree equally well with the time domain data: they have identical values of C(f).

4.

Reconstructions of the same data shown in Figure 2, except that a single decaying sinusoid was added to the time domain data. The artificial peak is indicated by the arrow. A) 800 iterations of IST. B) MaxEnt reconstruction.

In addition to proving more robust, MaxEnt reconstruction is more efficient. The modified Cambridge algorithm used to compute the MaxEnt reconstruction (14, 18) involves 8 discrete Fourier transformations during each iteration (except the first), plus several other matrix operations. Line-search IST requires two DFT's per iteration. IST typically requires on the order of ten times as many iterations as MaxEnt; the reconstructions in Fig. 4 used 800 iterations of line-search IST and 40 iterations of MaxEnt, and the MaxEnt processing required approximately one-sixth the computer time of IST. The difference in efficiency can be attributed mainly to the sophisticated optimizer used in the Cambridge algorithm, which incorporates elements of conjugate-gradient and variable metric optimizers, in contrast to the simple gradient-descent of line-search IST. In principle, computation of minimum l₁-norm reconstructions could be made comparably efficient to MaxEnt reconstruction by the use of more sophisticated search techniques.

Concluding Remarks

Iterative thresholding algorithms have proven to be popular because of their simplicity. We have shown that iterated soft thresholding leads to the computation of the minimum l₁-norm reconstruction, and is closely related to MaxEnt and minimum-area reconstruction. Although simple implementations of minimum l₁-norm reconstruction and MaxEnt reconstruction based on more powerful optimization techniques can yield strikingly different results, the differences appear to be due to the relative robustness of the optimizers employed, and not the objective functions. The relationship among thresholding, minimum l₁-norm reconstruction, and MaxEnt reconstruction demonstrated here provides an avenue for unifying these different approaches to the problem of spectrum reconstruction and deconvolution.