A computational statistics approach for estimating the spatial range of morphogen gradients

Abstract

A crucial issue in studies of morphogen gradients relates to their range: the distance over which they can act as direct regulators of cell signaling, gene expression and cell differentiation. To address this, we present a straightforward statistical framework that can be used in multiple developmental systems. We illustrate the developed approach by providing a point estimate and confidence interval for the spatial range of the graded distribution of nuclear Dorsal, a transcription factor that controls the dorsoventral pattern of the Drosophila embryo.

INTRODUCTION

In one of the most widely studied tissue patterning mechanisms, locally produced proteins establish signaling gradients that provide spatial and temporal control of gene expression within the tissue (Tabata and Takei, 2004; Ashe and Briscoe, 2006). Also known as morphogen gradients, spatially distributed inductive signals can establish multiple gene expression boundaries within the patterned field. Although some transcriptional effects of morphogens can be direct, other effects may be mediated by combinatorial strategies, based on regulatory cascades and tissue pre-patterning. As a first step in assessing the contributions of direct and indirect effects of morphogen gradients, it is necessary to quantify their spatial range: the distance over which they can act as spatial regulators of gene expression. Here, we present a straightforward statistical approach for estimating this important parameter.

Far from the source of ligand production, a signaling gradient decays to some basal value that corresponds to the ‘off’ state of the pathway. If a gene expression boundary is directly controlled by the signal, then this boundary must be located within the part of the tissue where the spatial distribution of the signal is graded, i.e. before it decays to the basal level. Although this is not a sufficient, but only a necessary condition for the regulatory connection between a signal and its target, it holds true for any gene expression boundary that is controlled by the signal. Based on this argument, we define the range of the signal as a part of the system where the signal level is different from the basal value.

To illustrate how this definition works in practice, we characterize the range for the nuclear localization gradient of Dorsal (Dl), a Rel-family transcription factor that controls the dorsoventral (DV) pattern of the Drosophila embryo (Roth et al., 1989; Rushlow et al., 1989; Steward, 1989). This gradient is established by the localized activation of Toll receptors on the ventral side of the embryo (reviewed by Morisato and Anderson, 1995). In the absence of Toll activation, Dl is located predominantly in the cytoplasm, in a complex with its binding protein Cactus (Govind and Steward, 1993). Toll activation leads to degradation of Cactus, enabling import of Dl into the nucleus, where it binds the regulatory regions of its target genes. Among these targets are transcription factors and signaling molecules that work together with Dl in gene regulation (Zeitlinger et al., 2007).

Several lines of evidence support a model in which Dl is directly involved in positioning multiple gene expression boundaries along the DV axis (reviewed by Hong et al., 2008). If this is indeed the case, then the spatial pattern of nuclear Dl must be graded over the region that contains all of these boundaries. We describe a statistical approach that can be used to test this condition. We quantified the gradient of nuclear Dl using a recently developed microfluidic device, which allows us to vertically orient large numbers of embryos and image nuclear Dl along the entire DV axis (Chung et al., 2011). To analyze the resulting dataset, we used a non-parametric statistical approach, which is based on empirical distribution of signal intensity across the tissue. This yields both the point estimate and the confidence interval for the spatial range of the Dl gradient.

Based on this estimate, we conclude that the spatial pattern of nuclear Dl is sufficiently graded over two-thirds of the DV axis, consistent with the model where this signal plays a direct role in specifying gene expression borders throughout the tissue. A similar approach is readily applicable to other experimental systems (e.g. Affolter and Basler, 2007; Dessaud et al., 2008; Schier, 2009; Porcher and Dostatni, 2010; Umulis et al., 2010).

MATERIALS AND METHODS

Flies, immunostaining and in situ hybridization

OreR flies were used as the wild-type strain for all experiments. Antibody staining was performed as described previously (Coppey et al., 2008). Mouse anti-Dl (1:100 Monoclonal Ab from Developmental Studies Hybridoma Bank) was used as the primary antibody, DAPI (1:10,000, Vector Laboratories) was used to stain the nuclei and Alexa Fluor conjugates (1:500, Invitrogen) were used as secondary antibodies. To visualize the sog transcript, fluorescence in situ hybridization (FISH) was used as described previously (Perry et al., 2010). Embryos were hybridized with digoxigenin (DIG)-labeled antisense probe to sog introns overnight at 60°C. Sheep anti-DIG (1:125; Roche) was used as primary antibody and Alexa Fluors (1:500) were used as secondary antibodies.

Microscopy

Imaging was performed on a Zeiss LSM 510 confocal microscope. Zeiss 20× [numerical aperture (NA) 0.6] A-plan objective was used for Dl gradient quantification. sog FISH staining was imaged with Zeiss 40× (NA 1.2) C-Apo water-immersion objective. High-resolution images (1024 × 1024 pixels, 12-bit depth for Dl experiments and 512×512 pixels, 12-bit depth for sog experiments) were obtained. All images were obtained from the focal plane ∼70 μm from either the anterior or posterior pole. Embryos were imaged in 90% glycerol solution.

Dl gradient quantification in 2D

Protein gradients were extracted from confocal images by using a previously described Matlab (MathWorks) program (Coppey et al., 2008). DAPI staining provided nuclear masks, which were then used to quantify the ventral-to-dorsal nuclear concentration gradient of Dl. To orient the extracted gradients, the raw nuclear Dl gradient was fitted to a Gaussian curve. These fits were not an accurate representation of the raw data itself. Therefore, the fits were used only to find the ventralmost position of the Dl gradient, whereas the entire analysis was based on the original raw measurements itself. After finding the ventralmost position of the gradient, the intensity was interpolated onto a uniform grid of 100 points, which is roughly equal to the average number of nuclei along the DV axis in a single cross-section. Since the embryo has bilateral symmetry, the measurement from one embryo provided two gradients of nuclear Dl from the ventral to the dorsal end. The ventralmost point is denoted as x=0 and the dorsal-most point as x=1.

3D quantification of the Dl gradient

Two-color 3D images of entire Drosophila embryos, containing signals for α-Dl and Histone, were acquired with scanned light sheet-based microscopy (Keller et al., 2010), using a z-step size of 2 μm between the 2D planes in each 3D image stack. A custom analysis pipeline was implemented to calculate dorsoventral gradients of α-Dl signal as a function of AP axis position. In the first step, the nuclear channel was used, which labels all of the nuclei, to generate an embryonic cellular mass shell by Gaussian smoothening, followed by application of a global threshold. The AP axis was then determined by identifying those pairs of points on the shell that were maximally separated. The anterior-posterior coordinates were calculated by averaging the coordinates of the top 100 pairs. Furthermore, thin planar slabs (2% of AP length), perpendicular to the AP axis, were generated such that (1) the normal surface vector coincided with AP axis direction and (2) the AP axis went through the middle plane of the slab at a pre-defined position. Intersecting the shell and the planar slabs resulted in approximate planar rings, which were further subdivided into non-overlapping cuboids (Fig. 1C) such that the lines connecting centers of two neighboring sub-regions and the geometric center of the ring were arranged at an angle of 5°. Finally, the second channel, which contained the α-Dl signal, was super-imposed onto these cuboids to calculate mean intensities.

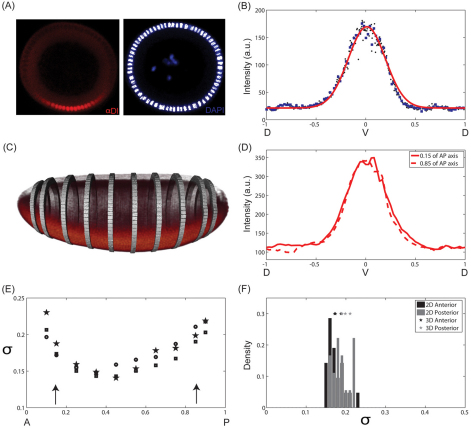
Fig. 1.

Data collection. (A) End-on imaging: DV cross-section of a Drosophila embryo stained using antibody against Dl (left) and DAPI (right). Ventral side is at the bottom and dorsal side is at the top. The nuclear mask (white) was established based on the DAPI signal. (B) Representative spatial pattern of nuclear Dl (black dots) as a function of DV position. The gradient is interpolated onto a uniform grid (blue squares). As the nuclei are spaced very tightly, linear interpolation does not introduce any artifact to the gradient. Solid red line represents the Gaussian fit that is used to find the ventralmost position along the DV axis. (C) 3D imaging of a Drosophila embryo stained with α-Dl antibody using scanned light sheet-based microscopy. The bands correspond to positions along the AP axis of the embryo where the DV pattern of nuclear Dl was quantified. (D) DV profile of nuclear Dl at 15% (solid) and 85% (dashed) of the AP axis from the anterior pole in one embryo. (E) Gaussian width (σ) of nuclear Dl profile as a function of position along the AP axis for three independent embryos. Arrows indicate the depth at which cross-sectional views are imaged using the microfluidic device. (F) Comparison of the estimated Gaussian widths of nuclear Dl profiles, measured 15% from anterior and posterior poles, obtained by scanned light sheet-based microscopy (3D) with those obtained by end-on imaging in a microfluidic device (2D).

Quantification of FISH images

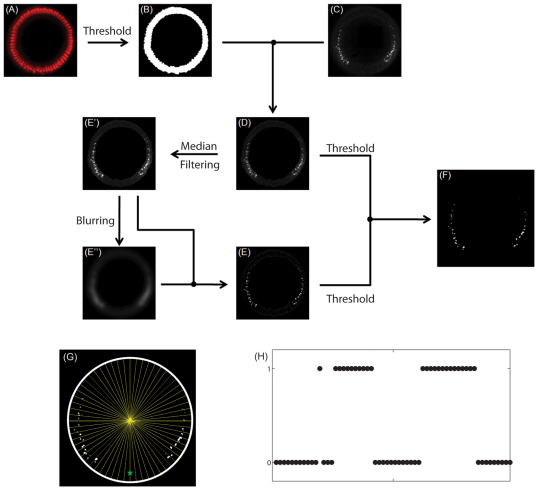
DAPI staining was used to extract nuclei close to the surface of the embryo (Fig. 4A). This was carried out by choosing a cutoff threshold for DAPI signal intensity. All pixels above the threshold were considered to be in the nuclear layer (Fig. 4B). sog introns were identified based on the three criteria (Fig. 4C). They should be present within the nuclear layer in the FISH staining, they should be bright and they should have sharp features. Specifically, the intronic signal was extracted by applying a cutoff threshold to intensity of the sog staining (Fig. 4D). As a result, only the blobs above a certain level of brightness were detected. A cutoff threshold was also applied to the nonlinearly filtered image of the staining (Fig. 4E). The purpose of this operation is to identify blobs with sharp features (Bretzner and Lindeberg, 1998; Lindeberg, 1998; Lindeberg, 2010). Non-linear filtering involved two steps. First, median filtering was used to reduce the noise in the image (Fig. 4E′). The MATLAB command ‘ordfilt2’ with order ‘9’ and domain ‘ones(3,3)’ is used for the purpose. The median filtered image was then Gaussian filtered (blurred) with a width of about 25 pixels to create an image that served as a proxy for the background (Fig. 4E″ ). The MATLAB command ‘imfilter’ was used for the purpose. Subtraction of the blurred image from the median filtered image resulted in an image with reduced noise and enhanced sharp features (Fig. 4E). Finally, those pixels that were above the cutoff thresholds in the original and filtered image were identified as those originating from sog introns (Fig. 4F).

Fig. 4.

Quantification of sog expression. (A) Nuclear staining using DAPI. (B) Nuclear layer close to the embryo surface, obtained by applying a cutoff threshold for intensity in A. (C) Fluorescent in situ hybridization staining for sog intronic probe. (D) sog signal within the nuclear layer. (E) Non-linear filtering of the image in D. E′ is obtained from D using median filtering. E″ is obtained from E′ using Gaussian blurring. (F) Identified sog probes in the embryo, obtained by applying cutoff thresholds for the images in D and E simultaneously. (G) Binning the expression of sog intronic probes along the DV axis. (H) Binary vector resulting from image processing of data from a single embryo.

In order to orient the image along the DV axis, each image was simultaneously stained with Dl and the position of peak nuclear Dl intensity was chosen as the ventral-most position. The DV position of intronic spots is given by the angle between the ventral-most point and the sog intronic probe with respect to the center of the embryo. The measurements for angular positions are then distributed into 100 equivalent bins along the circumference (Fig. 4G). Each bin contains a binary entry – 0 or 1 – where 0 corresponds to the case that there is no sog staining within the bin and 1 corresponds to the case where there is at least one non-zero pixel within the bin (Fig. 4H). Similar to the analysis of the Dl gradients, due to bilateral symmetry, each image provides two samples of sog expression along the DV axis.

Statistical methods

All calculations were carried out using MATLAB (MathWorks) functions. Empirical densities of Dl intensity at two positions were compared using ‘matched two sample t-test’ where the two points from the same gradient are paired. MATLAB function ‘ttest’ was used for the purpose. This test takes into account the dependence of the observations at two positions along the same gradient.

We calculated a 99% confidence interval (CI) for probability of sog expression P(i) at each DV position using a Bayesian approach (Wasserman, 2003). We took this approach because some of the intervals showed no instances of expression, thereby making the frequentist CIs nonsensical (i.e. the CI is [0,0] when no expression is observed in all n observations in an interval). We took a standard approach and placed a Uniform (0,1) prior on P(i) (Wasserman, 2003). This implies that the posterior distribution for a given interval is distributed Beta (1+x(i), 1+n-x(i)) where x(i) is the number of instances of expression observed in interval i and n is the total number of observations (n=68). This distribution yields a posterior expectation of E[P(i)|x(i)]=(1+x(i))/(2+n), which provides a point estimate of P(i). Next, we calculated the 99% Bayesian ‘credible interval’ based on Pr(P(i)|x(i)) by obtaining the 0.5% and 99.5% percentiles of the distribution. As the lowest possible posterior expectation is 1/(2+n) when x(i)=0, we called an interval estimated to be not expressed whenever the Bayesian CI did not overlap with this value. This occurred whenever x(i)≥4. The 99% Bayesian CI for sog expression shown in Fig. 5 is shown by the dashed curves in Fig. 5B. We found that the Bayesian and usual frequentist CIs largely agreed when x(i)≥7, particularly at the qualitative level.

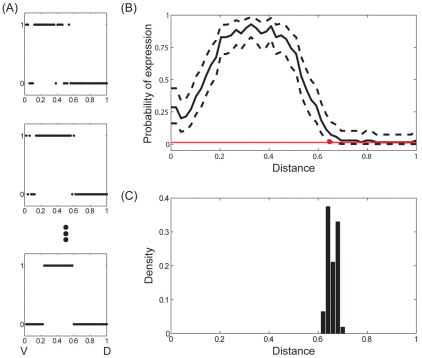
Fig. 5.

Spatial range of sog expression. (A) Examples of sog expression profiles in different embryos (n=68). (B) Mean sog expression profile during nuclear cycle 14 of embryogenesis. 0/1 corresponds to the ventral/dorsal sides of the embryo, respectively. Dashed curves indicate the 99% Bayesian confidence interval for probability of transcription at each point. From x=0 to x=0.66, the 99%CI for probability of transcription does not include the expected value of P(i) when there are no instances of expression. Therefore, we estimate the range of sog expression to be 0.66. (C) Probability distribution for the estimated range of sog expression.

The frequency distribution of the spatial ranges of the Dl gradient and sog expression pattern was estimated using the bootstrap technique (Efron and Tibshirani, 1993; Wasserman, 2003). Ten-thousand bootstrap datasets were generated from the original datasets by sampling with replacement. For each of the bootstrap datasets, the spatial range was estimated as described in the main text. Increasing the number of resampling times did not affect the estimated frequency distributions.

RESULTS

Data collection: end-on and multi-view imaging

Immunofluorescence techniques have been successfully used to quantify patterns along the anteroposterior (AP) axis of the Drosophila embryo (Jaeger et al., 2004; Gregor et al., 2005; Janssens et al., 2005; Coppey et al., 2008; He et al., 2008). Quantitative analysis of DV patterns has been less extensive, owing to the difficulties associated with imaging the distributions of protein and transcripts throughout the entire DV axis. This goal can be achieved by an ‘end-on’ approach, in which embryos are aligned with the optical axis of the microscope (Witzberger et al., 2008; Kanodia et al., 2009; Belu et al., 2010). The applicability of the end-on approach has been limited by the need to orient individual embryos manually. To enable large scale end-on imaging studies, we have recently developed a microfluidics platform for rapid and robust orientation of hundreds of embryos in a single experiment (Chung et al., 2011). Within this framework, a suspension of embryos is introduced into a microfluidic chip that has the dimensions of a regular microscope slide.

For this study, fixed embryos were stained with the anti-Dl antibody and DAPI, which marks the nuclei, providing a mask for gradient quantification (Fig. 1A). Multiple embryos, vertically oriented on a single microfluidic chip, were imaged using a confocal microscope, at a depth of ∼70 μm from the embryonic poles. Beyond this depth, the quality of images obtained in a single-photon confocal microscope deteriorates. Here, we focus on the analysis of the nuclear Dl gradients during the last nuclear division cycle in the syncytial blastoderm (nuclear cycle 14), a time interval of ∼45 minutes (Foe and Alberts, 1983).

Fig. 1B provides an example of the pattern of nuclear Dl, quantified by microfluidic-based end-on imaging. This figure also shows a Gaussian fit, used to locate the position that corresponds to the maximum of the gradient, which acts as a proxy for the ventralmost point along the DV axis (Fig. 1B). The anterior/posterior orientation of embryos loaded into a microfluidic device is essentially random. We found no significant differences in the widths of the gradients collected from the anteriorly and posteriorly oriented embryos (P>0.01). Based on this, we combine all the gradients from a single experiment into a common dataset. Furthermore, owing to the bilateral symmetry of the embryo, one image provides two gradients of Dl from the ventral to the dorsal side of the embryo.

To verify the quantification of Dl gradient using the microfluidic device, we used a multi-view imaging approach that measures the Dl intensity levels in the entire embryo. Briefly, anti-Dl and nuclear signals are measured in 3D using scanned light sheet-based microscopy (Keller et al., 2010). Fig. 1C presents a reconstructed 3D view of the spatial pattern of nuclear Dl, along with specific positions along the AP axis where this gradient was quantified. Representative examples of measured nuclear Dl gradient at different positions along the AP axis in one embryo are shown in Fig. 1D. Fig. 1E shows that the width of the nuclear Dl gradient decreases slightly from the pole towards the center of the embryo.

The multi-view approach provides information about the Dl gradient at arbitrary positions along the AP axis (Fig. 1C,D). However, owing to the considerable amount of time required for sample preparation and instrument alignment in whole-embryo imaging, multi-view light sheet microscopy is not yet suitable for high throughput analyses of signaling patterns. Thus, we used the light sheet-based imaging approach mainly to verify the measurements made in 2D in a whole-embryo context and to test our assumption of the AP symmetry of the gradients visualized by end-on imaging.

In the microfluidic device, the Dl gradient was measured at ∼70 μm from the pole; about 15% of AP axis. The histogram of fitted nuclear Dl gradient widths for measurements using the microfluidic device is superimposed with the fitted gradient widths for 3D measurements (Fig. 1F). The width of the Dl gradient measured by light sheet microscopy agrees well with the corresponding width obtained from end-on imaging. Furthermore, light sheet imaging reveals that estimated widths of nuclear Dl gradients at a distance of 15% from either pole are similar. Based on this, we conclude that the high throughput measurements in a microfluidic device do not introduce systematic biases owing to imaging, shape of the embryo or choice of the embryonic pole at which the measurement is performed.

Point estimate and confidence interval for the spatial range

Once the ventralmost position is defined, we interpolate the raw intensity levels onto a uniform grid with 100 points, which corresponds to the average number of nuclei along the circumference of the DV cross-section. Repeating this process for all embryos imaged in a single experiment and extracting the fluorescence intensity measurements at each position along the grid, we construct the empirical distribution for the nuclear levels of Dl at all positions along the DV axis (Fig. 2). These empirical distributions form the basis for our statistical analysis of the spatial range of the nuclear Dl gradient.

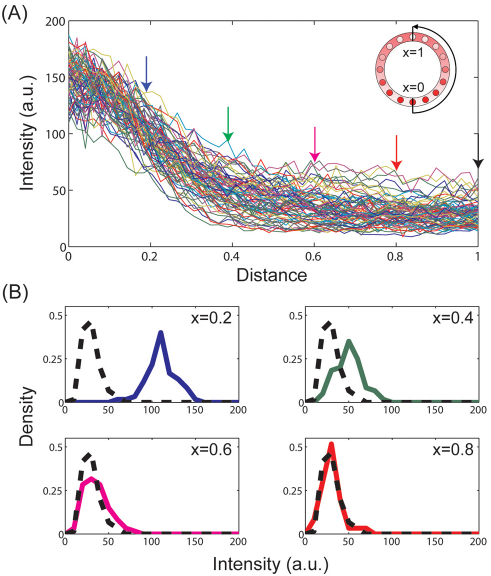
Fig. 2.

Empirical distributions. (A) Raw intensity measurements of nuclear Dl (36 embryos, 72 nuclear Dl gradients from ventral to dorsal end). 0/1 corresponds to the ventral/dorsal sides of the embryo, respectively. Colored arrows indicate the specific positions at which the empirical distribution functions are shown in B. (B) Empirical distributions of fluorescence intensities at x=0.2, 0.4, 0.6, 0.8 (solid line) compared with the basal level at x=1 (broken black line).

As already discussed, we define the spatial range of the signal as that part of the system where the signal is statistically different from the baseline level. For the spatial pattern of nuclear Dl, the fluorescence intensity level at the dorsalmost position provides a natural baseline value, as this position is most distant from the maximum of Toll receptor activation. To estimate the spatial range, we used a pairwise t-test to compare the means of the distributions between the dorsalmost position and all other grid points along the DV axis. For example, for x=0.2, which corresponds to the boundary of presumptive mesoderm (the boundary of Snail expression), the t-test comparing intensity levels at x=0.2 and x=1 leads to a P-value of 10^–50, indicating that the intensity level at x=0.2 is clearly different than the basal level. For more dorsal locations (x=0.4, 0.6, 0.8), the P-values are higher, indicating the fact that the fluorescence intensity levels become closer to the baseline value (Fig. 3A).

Fig. 3.

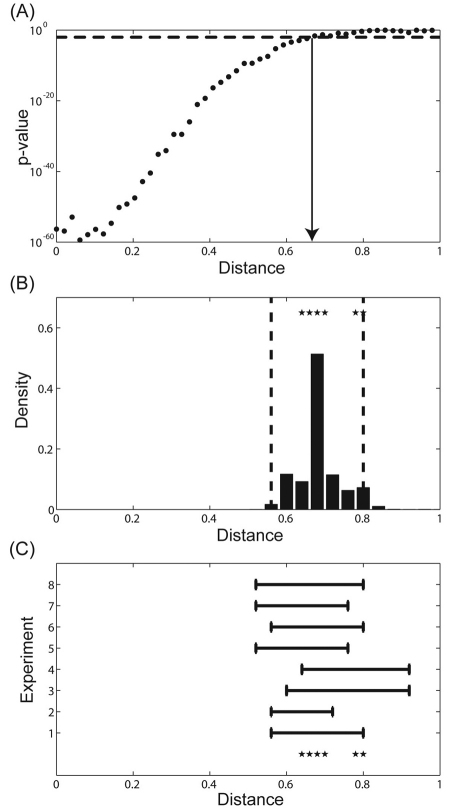
Point estimate and associated confidence interval. (A) P-value for pairwise comparison of the means of the signal intensities at a given position along the DV axis (x) and a baseline value (x=1). Dotted line indicates the cut-off chosen for level of significance. The estimated range of nuclear Dl gradient is indicated by the solid arrow. (B) Probability distribution for the estimated spatial range. Dotted lines indicate the 95% confidence interval. Stars represent the estimated range of Dl for eight independent experiments using the pairwise t-test. Sample sizes for the experiments are as follows n₁=72, n₂=76, n₃=50, n₄=72, n₅=78, n₆=74, n₇=74, n₈=80. (C) 95% confidence interval estimated by each independent experiment. Stars represent the estimated range of Dl for all experiments using pairwise t-test.

As a final step in quantifying the spatial range of a graded signal, we select a threshold P-value, above which the two means are considered indistinguishable. Choosing the threshold P-value provides a point estimate for the spatial range of a graded signal. For the set of data presented in Fig. 2A, the spatial range is relatively insensitive to threshold P-value between 0.001 and 0.05, and so we chose P=0.01 as a threshold. This yields x=0.68 as a point estimate for the spatial range (Fig. 3A). In other words, the fluorescence intensity levels are statistically different from the baseline level for all x<0.68.

We used two approaches to analyze the accuracy of our point estimate for the spatial range of the Dl gradient. First, we used a standard bootstrap method to computationally obtain the frequency distribution for the point estimates (Efron and Tibshirani, 1993; Wasserman, 2003). Briefly, starting with a collection of N gradients, we generated multiple data sets of the same size by sampling from this collection with replacement. For each of these bootstrap resampling data sets, we calculated the point estimate for the spatial range as described above. The frequency distribution for the point estimates, obtained from the t-test, is shown in Fig. 3B. Based on this distribution, one can easily obtain the confidence intervals (CI) for the point estimates. For example, the 95% CI for the data shown in Fig. 2A is given by [0.56-0.8]. This interval covers the true parameter value with 95% confidence.

As an independent way to assess the variability of our point estimates, we analyzed the results of seven additional experiments, each of which led to collection of several dozen gradients imaged during the last nuclear division in the syncytial blastoderm. The point estimates computed based on the results of these experiments are compared in Fig. 3B. Importantly, we found that estimates from replicate experiments lie well within the CI estimated from the first collection of gradients. We calculated the 95% CIs for each of these estimates and found that the point estimates obtained from each independent experiment lie close to each of the independent estimated CIs (Fig. 3C). Thus, the combined results obtained from eight independent repeats of nuclear Dl gradient quantification establish the robustness and reliability of the results obtained from a single experiment.

The uncertainty in our estimates reflects the combined effect of multiple factors contributing to the variability of fluorescence intensity profiles in our data. One of these factors is the dynamics of the Dl gradient, which increases in amplitude throughout the DV axis during nuclear cycle 14. Based on the published accounts of the Dl gradient dynamics, we expect that this factor alone contributes ∼30% to the variability at the ventralmost position. Quantitative contributions of other sources of variability are difficult to assess at this time.

Comparing the range of the Dl gradient with the spatial extent of Dl-dependent gene expression

In order to compare our estimate for the spatial range of the Dl gradient with the spatial range of Dl-dependent transcriptional effects, we quantified the spatial pattern of the expression of short gastrulation (sog). This gene encodes a secreted inhibitor of Bone Morphogenetic Protein signaling and is essential for patterning of the presumptive neural ectoderm and dorsal ectoderm tissues (O’Connor et al., 2006). sog is expressed in two lateral stripes, reflecting its broad activation by Dl and ventral repression by Snail (Sna). Based on the previously published in situ hybridization images, the dorsal extent of sog expression is one of the largest among all known transcriptional targets of the Dl gradient (Stathopoulos and Levine, 2002). Thus, analysis of the sog expression pattern can be used to probe the spatial extent of Dl-dependent gene expression. We quantified this pattern using FISH with a probe that hybridizes to the sog intronic sequence. Because introns are rapidly degraded, FISH stainings with this probe provide a snapshot of the transcriptional activity of the sog locus.

Fig. 4 outlines the data processing pipeline for the FISH data (also see Materials and methods). Briefly, processing of images from a single embryo generates a vector with binary components (Fig. 4H). Each component of this vector corresponds to a specific position along the DV axis. The value of the i-th vector component (0 or 1) corresponds to the absence or presence of sog introns at this position. Thus, the value of this component can be viewed as a realization of a Bernoulli random variable. A Bernoulli random variable takes only two values: 1, with probability P; and 0 with probability (1-P). Based on this, we use P(i) to denote the probability of sog expression at a specific position along the DV axis.

To estimate P(i), we use data from multiple embryos that were stained together and imaged on the same microfluidic device (Fig. 5A). The result, based on data from 34 embryos, is shown in Fig. 5B. In addition to estimating P(i), we calculated the corresponding Bayesian confidence intervals, also called credible intervals (see Materials and methods for details), which were used to quantify the spatial extent of sog expression. We defined this extent based on the largest index of the bin for which the 99% confidence interval for P(i) does not contain the expected value of P(i) when there are no instances of expression. This implies that the extent of sog expression is the region of the tissue where the probability of expression has posterior probability of not overlapping with the case of no expression equal to 99% or more. For the dataset that led to the spatial pattern of P(i) shown in Fig. 5B, the spatial range of sog expression is equal to 0.66. A distribution function for this estimate, based on bootstrapping, is shown in Fig. 5C. The spatial extent of sog expression is in a good agreement with our estimates for the spatial range of the Dl gradient. Indeed, the distribution function for the range of sog expression is localized around our estimate for the spatial range of the graded distribution of nuclear Dl.

DISCUSSION

As a practical definition for the spatial range of morphogen gradient, we propose to use the part of the system over which the level of signal is statistically different from the baseline level. Using the nuclear Dl gradient as an illustrative example, we presented a systematic computational approach for evaluating both the point estimate and confidence intervals for the range defined in this way. Our analysis of multiple independent experiments suggests that an accurate estimate for the range can be based on data from 50-70 gradients. This is within the reach of current experimental approaches, which means that our approach can be readily applied to multiple systems regulated by graded chemical signals (Mizutani et al., 2006; Affolter and Basler, 2007; Dessaud et al., 2008; Kicheva and Gonzalez-Gaitan, 2008; Porcher and Dostatni, 2010; Umulis et al., 2010).

Our results suggest that the spatial pattern of nuclear Dl is graded over two-thirds of the DV axis, which includes the presumptive mesoderm and neuroectoderm territories. This conclusion is based on comparing the nuclear levels of Dl at a given location along the DV axis with the level at the dorsalmost position. The estimate for the range of the Dl gradient agrees very well with the spatial extent of the expression of sog, a gene that is expressed in broad lateral pattern and is a direct transcriptional target of Dl. Based on this, we suggest that the dorsal limit of sog expression is determined by diminishing levels of nuclear Dl. At this point, there is no doubt that Dl is not the only signal that regulates the DV pattern of the fly embryo (Chopra and Levine, 2009). The spatial patterns of other regulators can be spatially uniform, which is the case for Zelda, the activator of the early zygotic transcription (Liang et al., 2008; Liberman and Stathopoulos, 2009), or graded, which is the case for Twist and phosphorylated Mad, established by cascades that act downstream of Dl (Ip et al., 1992; Dorfman and Shilo, 2001). The spatial ranges of these graded signals can be estimated using the presented approach.

Our approach is based on statistical analysis of an ensemble of gradients collected from multiple embryos. The variability of this dataset reflects combined effects of stochastic processes in a given embryo, embryo-to-embryo variations, as well as the variability of sample manipulation and imaging procedures. Because all of these effects increase the variability within the analyzed ensemble, our estimate for the spatial range is conservative. In other words, the spatial range we estimate is lower than the true spatial range. Gradients analyzed in this study were collected over a relatively wide time window, ∼45 minutes during the last nuclear division cycle in the syncytial blastoderm. The Dl gradient changes during this time, increasing in amplitude throughout the DV axis (Kanodia et al., 2009; Liberman et al., 2009). Therefore, a fraction of the variability in our estimate for the spatial range reflects the dynamics of the Dl gradient. In the future, our approach can be extended to gradients collected with higher temporal resolution. These measurements should clarify the differential effects of the dynamics of Dl and other regulatory factors in the DV patterning system.

The presented approach is not restricted to gradients of transcription factors in the Drosophila embryo and can be readily applied to morphogens in other developmental contexts, such as the gradients that pattern the vertebrate neural tube (De Robertis, 2008; Dessaud et al., 2008). As more molecular readouts of patterning events appear, the presented statistical framework can be used to analyze the range of other spatially distributed chemical, mechanical and electrical signals that organize pattern formation and tissue morphogenesis. In all of these cases, the estimated ranges must be interpreted with caution. For systems with small sample size, the sample mean can be different as compared with the true mean gradient. Thus, the point estimate for the spatial range must always be interpreted along with the corresponding confidence interval. Our study describes a straightforward computational approach for doing this systematically.