Abstract
The conformational behavior of a series of linear and cyclic oligo-(1→6)-β-D-glucosamines and their N-acetylated derivatives, which are related to fragments of natural poly-N-acetylglucosamine, was studied by theoretical molecular modeling and experimental determination of transglycosidic vicinal coupling constants 3JC,H and 3JH,H. Molecular dynamics simulations were performed under several types of conditions varying in the consideration of ionization of amino groups, solvent effect and temperature. Neural network clustering and asphericity calculations were performed on the basis of molecular dynamics data. It was shown that disaccharide fragments in the studied linear oligosaccharides were not rigid, and tended to have several conformers, thus determining the overall twisted shape with helical elements. In addition, it was found that the behavior of C5–C6 bond depended significantly upon the simulation conditions. The cyclic di-, tri-, and tetrasaccharides mostly had symmetrical ring-shaped conformations. The larger cycles tended to adopt more complicated shapes, and the conformational behavior of their disaccharide fragments was close to that in the linear oligosaccharides.
Keywords: Cyclic oligosaccharides, Glucosamine, Conformation analysis, MM3, SASA, Transglycosidic coupling constants
1. Introduction
Poly-N-acetylglucosamine (PNAG) represents the core component of biofilms formed by Staphylococcus aureus1 and other pathogens.2–6 Biofilms are important for bacterial virulence and environmental survival. The elucidation of PNAG’s secondary structure may help understand the organization of the whole biofilm and possible means to disrupt it to reduce the consequences of bacterial infections. Therefore, determination of the conformational properties of PNAG and its oligosaccharide fragments is an important goal in the chemistry of natural compounds.
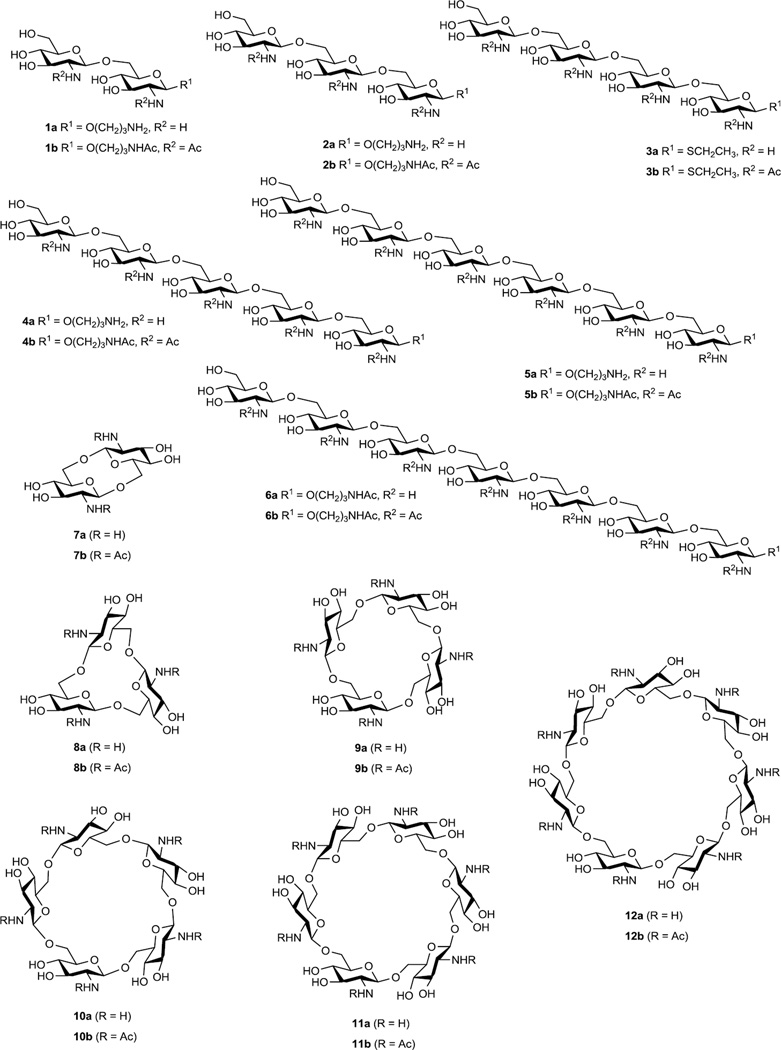
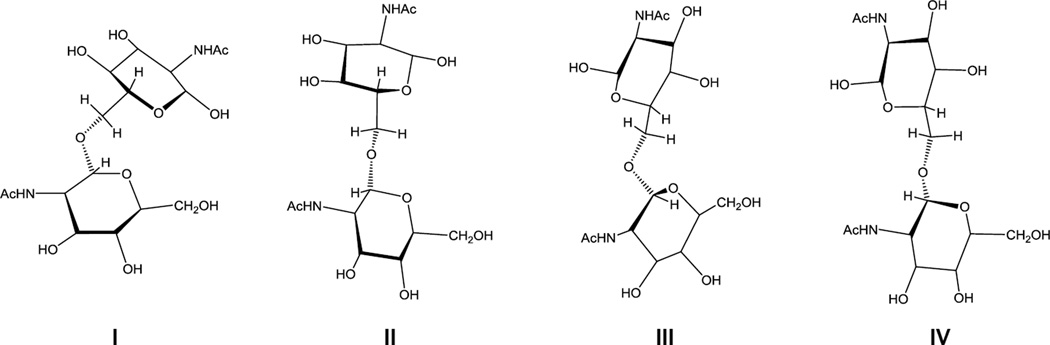
In this article we report on the results of NMR and theoretical conformational investigations of a large group of synthetic oligosaccharides related to the fragments of PNAG. These are linear 1a–6a and cyclic 7a–12a (Fig. 1) oligoglucosamines and their corresponding N-acetylated derivatives 1b–12b. Synthesis of these compounds has been described7–9 and some of them have been documented to induce formation of protective antibodies in animals when conjugated to carrier proteins.10 These oligosaccharides differ from each other by a number of structural factors such as the presence of N-acetyl groups, cyclization and elongation of the oligosaccharide chains which may drastically influence the biological activity in relation to biofilm formation and vaccine potential.10 The conformational analysis of oligosaccharides was based on the comparison of homo- (3JH,H) and heteronuclear (3JC,H) spin-spin coupling constants (SSCC) experimentally measured by NMR and calculated by Karplus equations using data from molecular dynamic (MD) simulations. This approach previously gave good results for elucidation of the conformations of a number of oligosaccharide groups related to natural polysaccharides.11,12
Figure 1.
Studied linear 1a,b–6a,b and cyclic 7a,b–12a,b oligoglucosamines. Non-N-acetylated oligosaccharides were obtained in the form of acetate salts.
Preliminary results from the conformational study of the cyclic glucosamines was reported previously;9 herein these compounds are investigated in more detail and in comparison with corresponding linear oligosaccharides. Their study is of special interest due to the structural relationship between cycloglucosamines and cyclodextrins. The latter are widely known for the ability to form inclusion complexes with various compounds.13 The presence of amino groups along with the central cavity in the studied oligosaccharides provides the possibility to modify and possibly extend their ability to form complex structures. Apart from our own previous publication9, only one work14 is known to us that describes the conformational analysis of (1→6)-linked oligosaccharides that consist of three or more monosaccharide residues.
2. Results and Discussion
2.1. NMR Spectroscopy Study
The structures of the synthesized oligoglucosamines 1a,b–4a,b and 6a,b–12a,b were determined by various NMR spectroscopy techniques (hexasaccharides 5a and 5b were not synthesized). Particularly, the NMR investigation included analysis of one-dimensional 1H and 13C and two-dimensional homonuclear 1H/1H COSY, TOCSY, NOESY and ROESY and heteronuclear 1H/13C HSQC, HSQC-TOCSY and HMBC spectra for solutions of the compounds in D2O. Analysis of COSY and TOCSY spectra permitted us to assign signals for protons in coupled spin systems of monosaccharide residues in 1H NMR spectra (Table 1). Analysis of 2D heteronuclear spectra HSQC and HSQC-TOCSY led to the assignment of all signals in one-dimensional 13C NMR spectra (Table 2) based on the 1H chemical shifts thus completing the analysis of monomeric compositions of the oligoglucosamines. The sequence of monosaccharide units in oligosaccharide chains is traditionally determined by the analysis of the nuclear Overhauser effect (NOE) values between pairs of protons in neighboring monosaccharide units. The values of the Overhauser effects were measured by means of NOE and ROE NMR experiments. However, for most of the oligoglucosamines examined in the present work this approach was not applicable due to the overlap of the signals both in 1D and 2D NOE and ROE spectra, as well as to the absolute values of NOE being close to zero in the large oligosaccharides.
Table 1.
1H NMR dataa for linear oligosaccharides 1a,b – 4a,b and 6a,b (D2O, 500.13 or 600.13 MHz, 300–307 Kb).
| R = H | R = Ac | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Residue | ||||||||||||||||
| # | H-1 | H-2 | H-3 | H-4 | H-5 | H-6R | H-6S | # | H-1 | H-2 | H-3 | H-4 | H-5 | H-6R | H-6S | |
| →6)-D-GlcNHR-β-aglycona | 1a | 4.74 | 3.03 | 3.67 | 3.57 | 3.70 | 3.97 | 4.24 | 1b | 4.48 | 3.65 | 3.52 | 3.38 | 3.55 | 3.73 | 4.2 |
| D-GlcNHR-β-(1→ | 4.76 | 3.05 | 3.67 | 3.48 | 3.52 | 3.78 | 3.94 | 4.54 | 3.72 | 3.55 | 3.45 | 3.45 | 3.75 | 3.93 | ||
| →6)-D-GlcNHR-β-aglycona | 4.71 | 3.01 | 3.65 | 3.52 | 3.66 | 3.90 | 4.22 | 4.46 | 3.64 | 3.52 | 3.38 | 3.55 | 3.70 | 4.15 | ||
| →6)-D-GlcNHR-β-(1→ | 2a | 4.74 | 3.02 | 3.65 | 3.54 | 3.66 | 3.93 | 4.22 | 2b | 4.51 | 3.69 | 3.54 | 3.40 | 3.56 | 3.75 | 4.19 |
| D-GlcNHR-β-(1→ | 4.74 | 3.02 | 3.65 | 3.44 | 3.47 | 3.74 | 3.90 | 4.55 | 3.73 | 3.55 | 3.44 | 3.44 | 3.74 | 3.92 | ||
| →6)-D-GlcNHR-β-aglycona | 3a | 4.76 | 3.14 | 3.63 | 3.49 | 3.68 | 3.84 | 4.22 | 3b | 4.61 | 3.72 | 3.53 | 3.4 | 3.58 | 3.67 | 4.14 |
| →6)-D-GlcNHR-β-(1→ | 4.75 | 3.04 | 3.63 | 3.52 | 3.67 | 3.91 | 4.22 | 4.51 | 3.7 | 3.53 | 3.4 | 3.56 | 3.74 | 4.14 | ||
| →6)-D-GlcNHR-β-(1→ | 4.75 | 3.04 | 3.63 | 3.52 | 3.67 | 3.91 | 4.22 | 4.53 | 3.7 | 3.56 | 3.4 | 3.56 | 3.76 | 4.19 | ||
| D-GlcNHR-β-(1→ | 4.74 | 3.03 | 3.65 | 3.46 | 3.48 | 3.74 | 3.90 | 4.54 | 3.73 | 3.55 | 3.45 | 3.45 | 3.75 | 3.92 | ||
| →6)-D-GlcNHR-β-aglycona | 4.65 | 2.96 | 3.62 | 3.47 | 3.62 | 3.85 | 4.18 | 4.48 | 3.65 | 3.54 | 3.38 | 3.55 | 3.68 | 4.15 | ||
| →6)-D-GlcNHR-β-(1→ | 4a | 4.72 | 3.00 | 3.63 | 3.49 | 3.63 | 3.87 | 4.20 | 4b | 4.52 | 3.70 | 3.55 | 3.40 | 3.56 | 3.75 | 4.17 |
| →6)-D-GlcNHR-β-(1→ | ±0.01 | ±0.01 | ±0.02 | ±0.01 | ±0.02 | ±0.02 | ±0.01 | ±0.01 | ±0.01 | ±0.02 | ±0.02 | |||||
| →6)-D-GlcNHR-β-(1→ | ||||||||||||||||
| D-GlcNHR-β-(1→ | 4.70 | 3.00 | 3.62 | 3.42 | 3.45 | 3.71 | 3.87 | 4.55 | 3.73 | 3.55 | 3.45 | 3.45 | 3.75 | 3.93 | ||
| →6)-D-GlcNHR-β-aglycona | 4.62 | 2.92 | 3.58 | 3.50 | 3.64 | 3.88 | 4.24 | |||||||||
| →[6)-D-GlcNHR-β-(1→]5c | 6a | 4.63 | 3.00 | 3.54 | 3.49 | 3.66 | 3.88 | 4.24 | 6bd | |||||||
| ±0.02 | ±0.02 | ±0.02 | ±0.02 | ±0.02 | ±0.02 | ±0.02 | ||||||||||
| D-GlcNHR-β-(1→ | 4.67 | 2.93 | 3.58 | 3.48 | 3.48 | 3.76 | 3.93 | |||||||||
Signals of the aglycon (in ppm): for 1a, 2a, 4a OCH2CH2CH2NH3Ac δ 3.66–4.01; OCH2CH2CH2NH3Ac δ 1.82–1.98; OCH2CH2CH2NH3Ac δ 3.10–3.38; OCH2CH2CH2NH3Ac δ 1.87–1.91; for 1b, 2b, 4b, 6b and 6a OCH2CH2CH2NHAc δ 3.57–3.94; OCH2CH2CH2NHAc δ 1.75–1.82; OCH2CH2CH2NHAc δ 3.14–3.30; OCH2CH2CH2NHAc δ 1.97–2.05; for 3a, 3b SCH2CH3 δ 2.68–2.75; SCH2CH3 δ 1.23–1.25.
The NMR spectra were acquired at the temperature of 300–307 K. For each compound the temperature was chosen so that to exclude the overlap of the solvent signal (HOD) with signals of the anomeric protons in 1H NMR spectrum.
The signals of all internal glucosamine residues.
The full assignment of signals in 1H and 13C NMR spectra of heptasaccharide 6b by 2D spectroscopy was not made. This compound was characterized by 1H NMR and MS spectra.8
Table 2.
13C NMR dataa for linear oligosaccharides 1a,b – 4a,b and 6a,b (D2O, 125.75 or 150.90 MHz, 300–307 Kb).
| R = H | R = Ac | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Residue | |||||||||||||||||
| # | C-1 | C-2 | C-3 | C-4 | C-5 | C-6 | # | C-1 | C-2 | C-3 | C-4 | C-5 | C-6 | ||||
| →6)-D-GlcNHR-β-aglycona | 1a | 101.0 | 57.2 | 73.8 | 71.0 | 76.1 | 69.8 | 1b | 102.5 | 57.0 | 75.2 | 71.4 | 76.0 | 70.0 | |||
| D-GlcNHR-β-(1→ | 101.0 | 57.2 | 73.7 | 71.2 | 77.7 | 61.8 | 102.9 | 57.0 | 75.2 | 71.4 | 77.3 | 62.2 | |||||
| →6)-D-GlcNHR-β-Agla | 2a | 100.5 | 56.9 | 73.3 | 70.7 | 76.0e | 69.6f | 2b | 102.5 | 57.0 | 75.2g | 71.4 | 75.9 | 69.9 | |||
| →6)-D-GlcNHR-β-(1→ | 101.0 | 56.9 | 73.4 | 70.7 | 75.9e | 69.7f | 102.9 | 57.0 | 75.2g | 71.4 | 76.1 | 69.9 | |||||
| D-GlcNHR-β-(1→ | 100.7 | 56.9 | 73.4 | 70.9 | 77.4 | 61.6 | 102.9 | 57.0 | 75.3g | 71.4 | 77.3 | 62.2 | |||||
| →6)-D-GlcNHR-β-Ag1a | 3a | 83.3 | 56.0 | 74.8 | 70.8 | 79.9 | 70.1 | 3b | 85.4 | 56.2 | 76.7 | 71.4 | 79.9 | 70.1 | |||
| →6)-D-GlcNHR-β-(1→ | 100.6 | 56.9 | 73.3 | 70.8 | 76.0g | 69.8 | 102.8 | 56.9 | 75.3 | 71.4 | 76.1 | 69.9 | |||||
| →6)-D-GlcNHR-β-(1→ | 100.9 | 56.9 | 73.3 | 70.8 | 76. 1g | 69.6 | 103 | 56.9 | 75.2 | 71.4 | 76.1 | 70 | |||||
| D-GlcNHR-β-(1→ | 100.6 | 56.9 | 73.4 | 70.9 | 77.5 | 61.6 | 103 | 57.0 | 75.2 | 71.4 | 77.3 | 62.2 | |||||
| →6)-D-GlcNHR-β-Agla | 100.6 | 57.1 | 73.4 | 71.0 | 76.2 | 69.8 | 102.5 | 56.9 | 75.2 | 71.5 | 76.1 | 69.9 | |||||
| →6)-D-GlcNHR-β-(1→ | 4a | 101.1 ±0.2 |
57.1 | 73.6 | 71.0 | 76.3 ±0.1 |
69.9 ±0.1 |
4b | 103.0 ±0.1 |
56.9 | 75.2 | 71.5 ±0.1 |
76.0 | 70.0 ±0.1 |
|||
| →6)-D-GlcNHR-β-(1→ | |||||||||||||||||
| →6)-D-GlcNHR-β-(1→ | |||||||||||||||||
| D-GlcNHR-β-(1→ | 100.9 | 57.1 | 73.6 | 71.1 | 77.6 | 61.8 | 102.9 | 56.9 | 75.2 | 71.4 | 77.3 | 62.2 | |||||
| →6)-D-GlcNHR-β-Agla | 101.7 | 57.4 | 74.4 | 71.0 | 76.3 | 70.0 | |||||||||||
| →[6)-D-GlcNHR-β-(1→]5c | 6a | 102.8 ±0.1 |
57.1 | 75.0 ±0.1 |
71.0 | 76.3 ±0.1 |
70.1 ±0.1 |
6bd | |||||||||
| D-GlcNHR-β-(1→ | 102.3 | 57.4 | 74.8 | 71.2 | 77.6 | 61.9 | |||||||||||
Signals of the aglycon (in ppm): for 1a, 2a, 4a OCH2CH2CH2NH3Ac δ 68.9–69.4; OCH2CH2CH2NH3Ac δ 27.9–30.0; OCH2CH2CH2NH3Ac δ 37.4–38.4; OCH2CH2CH2NH3Ac δ 24.2–24.7; for 1b, 2b, 4b, and 6a OCH2CH2CH2NHAc δ 69.1–69.3; OCH2CH2CH2NHAc δ 29.6–29.9; OCH2CH2CH2NHAc δ 37.6–37.8; OCH2CH2CH2NHAc δ 23.3–23.8; and 175.6–175.9; for 3a, 3b SCH2CH3 δ 25.9; SCH2CH3 δ 15.8.
The NMR spectra were acquired at the temperature of 300–307 K. For each compound the temperature was chosen so that to exclude the overlap of the solvent signal (HOD) with signals of the anomeric protons in 1H NMR spectrum.
The signals of all internal glucosamine residues.
The full assignment of signals in 1H and 13C NMR spectra of heptasaccharide 6b by 2D spectroscopy was not made. This compound was characterized by 1H NMR and MS spectra.8
e, f, g The assignment may be reversed.
NMR experiments based on the observation of inter-unit interactions between hydrogen and carbon atoms linked by long-range SSCCs were used for the determination of monosaccharide sequences in the oligoglucosamines 1a,b–12a,b. The techniques employed were J-HMBC15,16 and J-resolved,17,18 that allowed for the quantitative measurement of SSCC values. The obtained constant values were later used in the conformational analysis of oligoglucosamines 1a,b–12a,b.
Oligoglucosamines 1a–4a and 6a–12a were synthesized as acetic acid salts.7–9 Analysis of integral intensities in 1H NMR spectra of these compounds showed that in the case of cyclic oligosaccharides 7a–12a the stoichiometric salts were formed with one molecule of acetic acid per each amino group. In the case of linear di- (1a), tri- (2a) and tetrasaccharide (3a) acetate ions were also present in stoichiometric ratio to amino groups, while in penta- (4a) and heptasaccharide (6a) only four acetates were present. It was supposed that partial hydrolysis of oligoglucosamine acetic salts occurred in water solution with formation of free amino-groups and some amount of acetic acid evaporated during the sample preparation (pH of resulting solutions was about 5.5). Protonated amino groups in oligosaccharides 1a–4a and 6a–12a were randomly distributed and protons may exchange the positions between them.
The introduction of N-acetyl groups into the oligoglucosamines was accompanied by significant changes in chemical shift values (Tables 1–4). In 1H NMR spectra, chemical shifts of protons H-2 in glucosamine residues, which were directly connected to C-2 (α-carbons) bearing amino groups, were affected most greatly (the average value of Δδ(H-2) was 0.67 ppm; spectral N-acetylation effects are given in Supplementary Materials). The effects on β-protons (H-1 and H-3) were considerably smaller (the average values of Δδ(H-1) and Δδ(H-3) were −0.19 and −0.09 ppm, respectively). The effects on other protons of glucosamine residues were also small. Analysis of 13C NMR spectra showed that chemical shifts of α-carbons (C-2) did not change upon N-acetylation. In this case the biggest effects were observed on β-carbons (C-1 and C-3), the average values of Δδ(C-1) and Δδ(C-3) being 2.0 ppm and 1.7 ppm, correspondingly.
Table 4.
| R = H | R = Ac | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Residue | ||||||||||||||||
| # | C-1 | C-2 | C-3 | C-4 | C-5 | C-6 | # | C-1 | C-2 | C-3 | C-4 | C-5 | C-6 | |||
| →6)-D-GlcNHR-β-(1→ | 7a | 100.1 | 60.1 | 71.8 | 67.6 | 79.4 | 70.0 | 7b | 103.3 | 59.9 | 74.3 | 67.9 | 78.1 | 71.3 | ||
| →6)-D-GlcNHR-β-(1→ | 8a | 99.6 | 57.3 | 73.6 | 70.7 | 75.7 | 68.8 | 8b | 101.4 | 57.0 | 75.2 | 70.6 | 75.8 | 69.7 | ||
| →6)-D-GlcNHR-β-(1→ | 9a | 100.5 | 56.9 | 73.4 | 70.1 | 76.0 | 69.7 | 9B | 102.3 | 56.7 | 75.0 | 70.5 | 75.9 | 69.5 | ||
| →6)-D-GlcNHR-β-(1→ | 10a | 100.9 | 56.9 | 73.4 | 70.6 | 76.2 | 69.8 | 10b | 102.8 | 56.8 | 74.8 | 71.0 | 76.2 | 69.9 | ||
| →6)-D-GlcNHR-β-(1→ | 11a | 100.8 | 56.8 | 73.5 | 70.8 | 75.7 | 69.5 | 11b | 102.6 | 56.9 | 74.7 | 71.3 | 75.7 | 70.2 | ||
| →6)-D-GlcNHR-β-(1→ | 12a | 100.8 | 56.8 | 73.2 | 70.8 | 75.9 | 69.5 | 12b | 102.7 | 56.8 | 74.9 | 71.3 | 75.9 | 69.8 | ||
Signal of the Ac- δ24.0–24.6 and 181.8–182.7 for 7a–12a; signal of the Ac δ 23.3–23.6 and 175.6–175.9 for 7b-12b.
The NMR spectra were acquired at the temperature of 303–310 K. For each compound the temperature was chosen so that to exclude the overlap of the solvent signal (HOD) with signals of the anomeric protons in 1H NMR spectrum.
The comparison of the 1H and 13C spectra of linear N-acetylated oligoglucosamines 1b–6b showed that all monosaccharide residues in these molecules could be divided into three groups according to the characteristic features in their 1H and 13C chemical shifts (Tables 1 and 2). These were terminal residues at the non-reducing ends, middle residues and the residues at the reducing ends. All middle residues regardless of the length of oligosaccharide chain had very close chemical shifts.
1H and 13C spectra of cyclic N-acetylated oligoglucosamines 7b–12b contained a set of signals corresponding to a single monosaccharide residue (Tables 3 and 4) indicating that conformational states of all monosaccharide residues within a molecule were averaged during molecular motion. In the case of small cycles (di-, tri-, and tetrasacharide 7b–9b) the chemical shifts changed significantly upon the cycle enlargement, but in the case of larger cycles (penta-, hexa-, and heptasaccharide 10b–12b) they were not affected by the change of the molecular size and became close to those in internal units of linear oligoglucosamines 2b–4b, 6b (Tables 1 and 2).
Table 3.
| R = H· | R = Ac | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Residue | ||||||||||||||||
| # | H-1 | H-2 | H-3 | H-4 | H-5 | H-6R | H-6S | # | H-1 | H-2 | H-3 | H-4 | H-5 | H-6R | H-6S | |
| →6)-D-GlcNHR-β-(1→ | 7a | 4.95 | 3.33 | 3.72 | 4.17 | 3.85 | 3.73 | 4.12 | 7b | 4.68 | 3.94 | 3.62 | 4.32 | 3.72 | 4.17 | 3.61 |
| →6)-D-GlcNHR-β-(1→ | 8a | 4.79 | 3.03 | 3.65 | 3.56 | 3.56 | 4.01 | 4.22 | 8b | 4.60 | 3.64 | 3.49 | 3.46 | 3.48 | 4.09 | 3.90 |
| →6)-D-GlcNHR-β-(1→ | 9a | 4.74 | 3.03 | 3.67 | 3.72 | 3.60 | 4.07 | 4.14 | 9b | 4.57 | 3.67 | 3.53 | 3.52 | 3.51 | 3.94 | 4.02 |
| →6)-D-GlcNHR-β-(1→ | 10a | 4.77 | 3.04 | 3.65 | 3.58 | 3.61 | 4.03 | 4.13 | 10b | 4.59 | 3.67 | 3.55 | 3.46 | 3.53 | 3.90 | 4.07 |
| →6)-D-GlcNHR-β-(1→ | 11a | 4.73 | 3.02 | 3.64 | 3.55 | 3.68 | 3.97 | 4.21 | 11b | 4.54 | 3.63 | 3.59 | 3.40 | 3.54 | 3.77 | 4.10 |
| →6)-D-GlcNHR-β-(1→ | 12a | 4.79 | 3.06 | 3.67 | 3.60 | 3.66 | 3.96 | 4.20 | 12b | 4.58 | 3.70 | 3.57 | 3.47 | 3.57 | 3.82 | 4.13 |
Signal of the Ac− δ1.90–1.91 for 7a–12a; signal of the Ac δ 2.02–2.05 for 7b-12b.
The NMR spectra were acquired at the temperature of 303–310 K. For each compound the temperature was chosen so that to exclude the overlap of the solvent signal (HOD) with signals of the anomeric protons in 1H NMR spectrum.
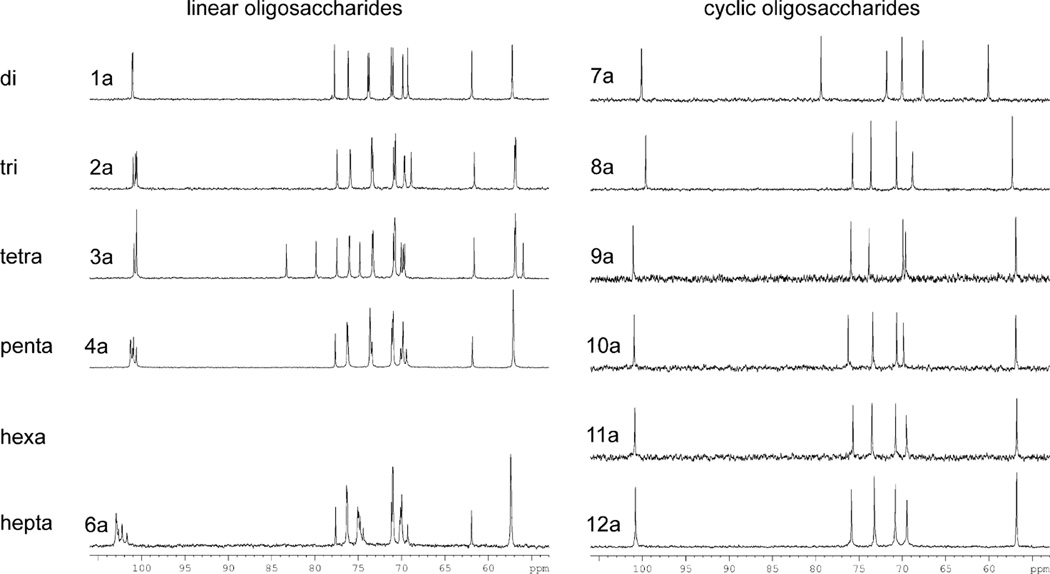
In oligoglucosamines 1a–4a and 6a–12a the tendencies in chemical shift values were almost the same as in the case of N-acetylated oligosaccharides 1b–4b and 6b–12b (Tables 1–4, Fig. 2). The only exception were linear disaccharide 1a and heptasaccharide 6a, where the chemical shifts of C-1 and C-3 (β-carbons relative to amino groups) differed from those in tri- (2a), tetra- (3a) and pentasaccharide 4a. Most likely this difference in chemical shifts is explained by the difference in ionization and solvation of oligosaccharides that was discussed above.
Figure 2.
13C NMR spectra (carbohydrate regions) of linear 1a–4a, 6a and cyclic 7a–12a oligoglucosamines.
Conformations of pyranoside rings in common carbohydrates change only slightly during molecular motion and are considered to have little influence on the conformational changes of the whole saccharide molecule.19,20 This also applied to most of the oligoglucosamines in this investigation as confirmed by the large values of intra-unit vicinal constants 3JH,H shown in Supplementary Materials, that obviously corresponded to glucopyranose residues in 4C1 conformation.19 The only exception were cyclic disaccharides 7a and 7b, where the coupling constants 3JH,H within the glucosamine residues had values atypical for the 4C1 conformation (Table 3 in Supplementary Materials). This could be explained by conformational distortions of the pyranose rings in these compounds occurring due to their strained structure.9 Similar distortions had already been observed for cyclogentiobioside.21,22
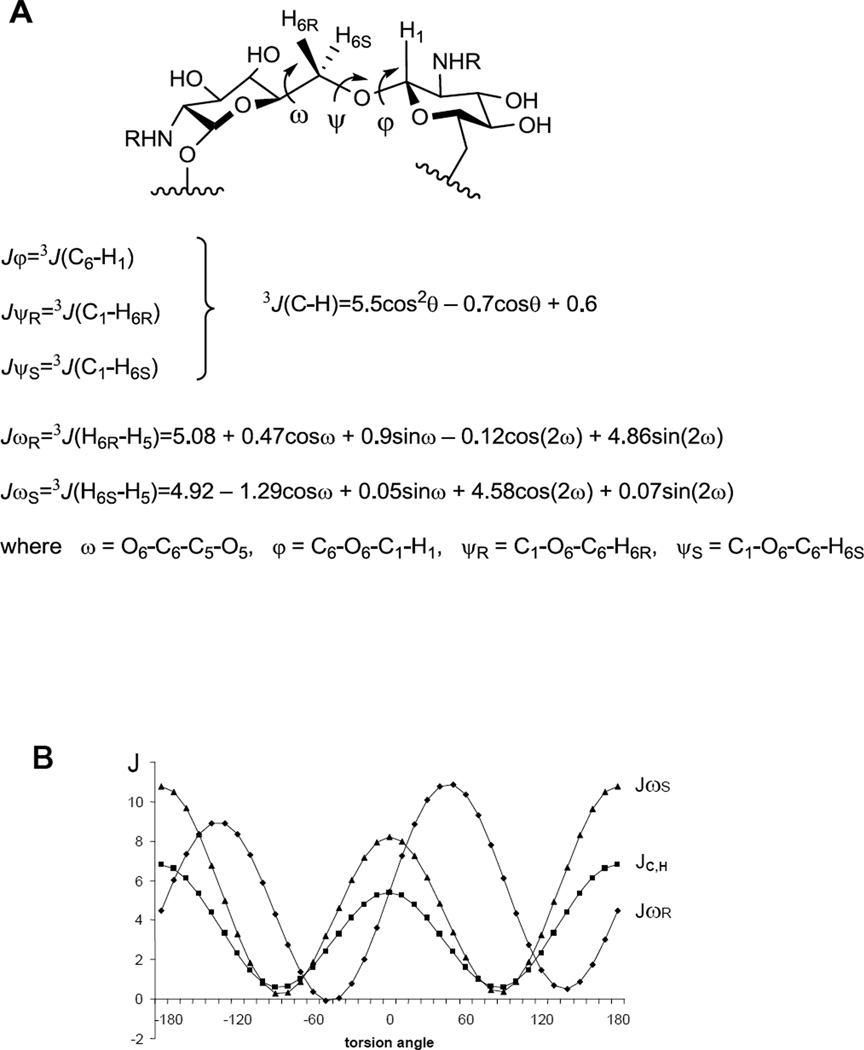
Spatial structures of (1→6)-linked pyranosides are primarily determined by the conformations of glycosidic bonds between monosaccharide residues which are described in terms of dihedral angles φ, ψ, and ω (Fig. 3). The values of these angles are connected with experimentally measured values of 3JC,H and 3JH,H coupling constants around the glycosidic linkages through the Karplus equations23,24 (Fig. 3). Hence, to investigate the conformational properties of oligoglucosamines 1a,b–4a,b and 6a,b–12a,b, the experimental values of transglycosidic constants 3JC,H and 3JH,H. were analyzed
Figure 3.
Dihedral angles and the Karplus equations for the coupling constants 3JC,H23 and 3JH,H24 describing the conformation of the (1→6)-linkage (A) and the graphs of Karplus functions (B).
J-HMBC15,16 is one of the most powerful methods for the detection of long-range carbon-proton SSCCs (nJC,H, where n≥2). This experiment was used to determine the values of constants Jψ (Fig. 3) in the studied oligoglucosamines. However, the determination of constants Jφ by J-HMBC experiment was not always possible due to the overlap of the correlation peaks in the spectra. Therefore, a selective 2D J-resolved17,18 experiment was employed for the determination of Jφ in these cases. The detailed description of the NMR technique for the measurement of transglycosidic coupling constants 3JC,H in oligosaccharides was provided in our previous work11 and can also be found in the experimental section of this article. The values of 3JH,H (JωR и JωS, Fig. 3) were measured directly from one-dimensional 1H NMR spectra as the difference between peak maxima in multiplets. Many of the Jω constants in the studied oligoglucosamines had small values, not exceeding 2 Hz (Tables 5 and 6). Their precise determination by the direct measurement as described above was impossible due to the influence of signal shapes of all multiplet components on the whole multiplet shape. The bigger value of the multiplet component width drastically increases the error during Jω measurement, which in some cases may reach 70%. Therefore, the full line shape analysis approach was used25 for the determination of small constants. Unfortunately, it was still impossible to measure 3JC,H and 3JH,H constants in linear penta- (4a and 4b) and heptasaccharides (6a and 6b) due to the strong overlap of signals.
Table 5.
Experimentala and calculated values of transglycosidic 3J (Hz) coupling constants (Fig. 3) for middle unitsb of linear oligoglucosamines 1a–6b.
| Method | Non-N-acetylated oligoglucosamines | N-acetylated oligoglucosamines | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Jφ | JψR | JψS | JωS | JωS | # | Jφ | JψR | JψS | JωR | JωS | |
| experiment | 1a | 3.0 | 2.9 | 3.0 | 5.0 | 2.0g | 1b | 4.2 | 2.8 | 3.1 | 6.1 | 1.9g |
| calc.c(ε = 81) | 3.4 | 2.3 | 2.3 | 8.5 | 3.1 | 3.3 | 2.2 | 2.0 | 2.3 | 1.9 | ||
| calc.d(SASA) | 3,6 | 1,8 | 2,1 | 9,4 | 1,6 | 3.7 | 2.7 | 2.3 | 6.8 | 1.7 | ||
| calc.e (NH3) | 3.4 | 2.3 | 2.3 | 6.6 | 2.2 | |||||||
| experiment | 2a | 3.5 | 3.0 | 2.3 | -f | 2.0g | 2b | 4.3 | 3.0 | 2.9 | -f | 2.1g |
| calc. (ε = 81) | 3.3 | 2.3 | 2.3 | 6.7 | 2.4 | 3.4 | 2.4 | 2.1 | 6.4 | 3.5 | ||
| calc. (SASA) | 3,7 | 2,1 | 2,1 | 9,4 | 1,8 | 3.1 | 2.3 | 2.1 | 3.6 | 2.2 | ||
| calc. (NH3) | 3.4 | 2.0 | 2.3 | 5.4 | 2.3 | |||||||
| experiment | 3a | 3.8 | 2.9 | 2.8 | -f | 2.0g | 3b | 4.2 | 2.7 | 2.6 | -f | 2.0g |
| calc. (ε = 81) | 3.3 | 2.4 | 2.6 | 5.5 | 2.0 | 3.5 | 3.1 | 2.9 | 7.9 | 1.9 | ||
| calc. (SASA) | 3,9 | 2,0 | 2,3 | 8,4 | 3,0 | 3.1 | 2.5 | 2.0 | 4.8 | 1.7 | ||
| calc. (NH3) | 3.3 | 2.4 | 2.5 | 6.2 | 2.0 | |||||||
| experiment | 4a | -f | -f | -f | -f | -f | 4b | ≈3.8h | ≈2.9h | ≈2.7h | -f | 2.0g |
| calc. (ε = 81) | 3.2 | 2.8 | 2.4 | 5.8 | 2.1 | 3.4 | 2.6 | 2.4 | 4.4 | 2.2 | ||
| calc. (SASA) | 3,5 | 2,2 | 2,1 | 6,1 | 2,7 | 3.1 | 2.7 | 1.9 | 7.2 | 1.8 | ||
| calc. (NH3) | 3.3 | 2.6 | 2.3 | 5.0 | 2.0 | |||||||
| experiment | 5a | -j | -j | -j | -j | -j | 5b | -j | -j | -j | -j | -j |
| calc. (ε = 81) | 3.3 | 2.9 | 2.6 | 6.3 | 2.7 | 3.3 | 2.5 | 2.2 | 3.7 | 2.0 | ||
| calc. (SASA) | 3,5 | 2,3 | 2,0 | 6,1 | 2,5 | 3.3 | 2.7 | 2.1 | 7.7 | 1.8 | ||
| calc. (NH3) | 3.2 | 2.1 | 2.4 | 4.1 | 3.5 | |||||||
| experiment | 6a | -f | -f | -f | -f | -f | 6b | -f | -f | -f | -f | -f |
| calc. (ε = 81) | 3.4 | 2.7 | 2.7 | 4.4 | 2.1 | 3.4 | 3.2 | 2.8 | 6.4 | 2.7 | ||
| calc. (SASA) | 3,7 | 2,2 | 2,1 | 7,0 | 2,5 | 3.2 | 2.6 | 1.8 | 5.3 | 2.1 | ||
| calc. (NH3) | 3.2 | 2.4 | 2.4 | 6.8 | 2.2 | |||||||
The NMR spectra were acquired at the temperature of 300–307 K. For each compound the temperature was chosen so that to exclude the overlap of the solvent signal (HOD) with signals of the anomeric protons in 1H NMR spectrum.
The data for all disaccharide units of oligoglucosamines are presented in Supplementary Materials.
The values of constants calculated for solvation model ε = 81 at TE = 300K.
The values of constants calculated for SASA implicit solvation model at TE = 300K.
The values of constants calculated for NH3-model of free oligoglucosamines 1a–6a at ε = 81 and TE = 300K.
Not determined due to the peak overlaps.
The value of constant was obtained by the curve-fitting algorithm25 which was applied for analysis of multiplet due to the small value of the interesting constant and the broad lines in multiplet.
The value of the coupling constant could not be measured exactly because the peaks overlap in the spectra.
Not measured.
Table 6.
Experimentala and averaged calculatedb values of transglycosidic 3J (Hz) coupling constants (Fig. 3) for cyclic oligoglucosamines 7a – 12b.
| Method | Non-N-acetylated oligoglucosamines | N-acetylated oligoglucosamines | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Jφ | JψR | JψS | JωR | JωS | # | Jφ | JψR | JψS | JψR | JψS | |
| experiment | 7a | 4.3 | 2.2 | 6.0 | 2.6g | ≈1.0h | 7b | 3.4 | 2.3 | 6.4 | 2.4g | -f |
| calc.c(ε = 81) | 4.7 | 4.1 | 4.4 | 5.4 | 1.6 | 4.8 | 4.0 | 4.5 | 5.1 | 1.4 | ||
| calc.d(SASA) | 4.8 | 4.1 | 4.4 | 5.4 | 1.5 | 4.4 | 3.8 | 3.9 | 5.3 | 1.6 | ||
| calc.e (NH3) | 4.6 | 3.8 | 4.3 | 5.0 | 1.5 | |||||||
| experiment | 8a | 3.4 | 2.3 | 6.5 | 2.1g | 0.9g | 8b | 3.7 | 2.7 | 6.1 | 4.1g | 1.4g |
| calc. (ε = 81) | 3.4 | 1.5 | 4.1 | 2.2 | 1.7 | 3.4 | 1.6 | 4.1 | 2.3 | 1.7 | ||
| calc. (SASA) | 3.5 | 2.1 | 4.1 | 3.3 | 1.6 | 3.6 | 2.4 | 4.0 | 3.7 | 1.8 | ||
| calc. (NH3) | 3.5 | 1.5 | 4.1 | 2.3 | 1.7 | |||||||
| experiment | 9a | 4.4 | 2.3 | 2.4 | 3.0 | 1.6g | 9b | 4.8 | 2.5 | 3.2 | 2.7g | 1.2g |
| calc. (ε = 81) | 3.8 | 2.3 | 2.7 | 3.5 | 2.0 | 3.7 | 2.3 | 2.8 | 3.5 | 2.1 | ||
| calc. (SASA) | 3.9 | 2.4 | 2.8 | 4.2 | 2.0 | 3.8 | 2.6 | 2.9 | 4.5 | 2.2 | ||
| calc. (NH3) | 3.8 | 1.5 | 3.2 | 2.5 | 1.5 | |||||||
| experiment | 10a | 3.8 | 2.7 | 2.8 | 4.0 | 1.7g | 10b | 4.4 | 3.6 | 2.8 | 4.9 | 1.8g |
| calc. (ε = 81) | 3.5 | 2.8 | 2.8 | 5.0 | 3.2 | 3.5 | 2.7 | 2.8 | 4.9 | 3.4 | ||
| calc. (SASA) | 3.6 | 2.7 | 2.7 | 4.9 | 3.2 | 3.6 | 2.8 | 2.8 | 5.0 | 3.0 | ||
| calc. (NH3) | 3.5 | 2.7 | 2.8 | 5.0 | 3.5 | |||||||
| experiment | 11a | 3.9 | 3.9 | 2.5 | 4.9 | 2.1g | 11b | 3.5 | 3.8 | 2.4 | 6.0 | 1.9g |
| calc. (ε = 81) | 3.5 | 2.7 | 2.7 | 5.2 | 3.4 | 3.4 | 2.6 | 2.6 | 4.8 | 3.5 | ||
| calc. (SASA) | 3.5 | 2.7 | 2.6 | 4.7 | 3.3 | 3.5 | 2.8 | 2.6 | 4.8 | 3.0 | ||
| calc. (NH3) | 3.5 | 2.7 | 2.6 | 5.0 | 3.6 | |||||||
| experiment | 12a | 3.8 | 3.5 | 3.2 | 4.0 | 2.0g | 12b | 3.9 | 3.5 | 2.8 | 5.2 | 2.0g |
| calc. (ε = 81) | 3.5 | 2.7 | 2.7 | 5.5 | 3.4 | 3.4 | 2.6 | 2.6 | 5.1 | 3.5 | ||
| calc. (SASA) | 3.5 | 2.7 | 2.5 | 4.9 | 3.4 | 3.5 | 2.7 | 2.5 | 4.9 | 3.1 | ||
| calc. (NH3) | 3.5 | 2.6 | 2.6 | 5.3 | 3.5 | |||||||
The NMR spectra were acquired at the temperature of 300–307 K. For each compound the temperature was chosen so that to exclude the overlap of the solvent signal (HOD) with signals of the anomeric protons in 1H NMR spectrum.
The calculated values for every disaccharide units of oligoglucosamines are presented in Supplementary Materials.
The values of constants calculated for solvation model ε = 81 at TE = 700K.
The values of constants calculated for SASA implicit solvation model at TE = 700K.
The values of constants calculated for NH3-model of free oligoglucosamines 7a–12a at ε = 81 and TE = 700K.
Not determined due to the peak overlaps.
The value of constant was obtained by the curve-fitting algorithm25 which was applied for analysis of multiplet due to the small value of the interesting constant and the broad lines in multiplet.
The value of the coupling constant could not be measured exactly because the peaks overlap in the spectra.
Analysis of the available experimental values for constants measured for linear oligoglucosamines 1a–3a revealed that they did not depend neither upon the oligosaccharide chain length nor the position of a linkage in the chain, contrary to the case in the previously studied β-(1→3)-linked oligofucosides.12 For cyclic structures with more than five residues 10a–12a SSCCs showed the same tendency, and their absolute values were close to those in linear molecules 1a–3a; the difference between the corresponding constants did not exceed 1.2 Hz. In small cyclic molecules 7a–9a, however, SSCCs changed considerably upon the enlargement of the molecule (Table 6). This indicated that the dominating conformations of glycosidic linkages in these cycles differed greatly from those in the cyclic penta-, hexa- and heptasaccharides.9 Similar conclusions could be achieved during the analysis of 1H and 13C chemical shifts (Tables 1–4). Changes in the spectra occurred because chemical shifts in carbohydrates are peculiarly dependent on the conformations of these molecules.26
In case of N-acetylated derivatives 1b–4b and 6b–12b the 3JC,H and 3JH,H values were generally similar to those of the corresponding fragments in free amines 1a–4a and 6a–12a. The exception was observed in the case of Jφ constants in the linear molecules, which in 1b–3b slightly exceeded the corresponding SSCC values in 1a–3a (Table 5).
2.2. Molecular Modeling
To elucidate conformational properties of glucosamines 1a,b–12a,b, molecular dynamics (MD) calculations were performed. They were carried out using MM3 force field (TINKER program suit). Although the MM3 was originally developed as a general purpose force field, it is now known to reproduce structural characteristics of carbohydrates among other parameter sets.27,28
One problem that arose during the studies of oligoglucosamines 1a–12a was the possibility of the dissociation of the ammonium salts with the formation of free amines. Therefore MD calculations for these molecules were carried out both for ammonium model (−NH3+) and deprotonated amine model (−NH2). In the latter case, solvent effects were considered using the continual Solvent Accessible Surface Area model (SASA) and a more rough approach based on the value of dielectric permittivity constant (81 for water). In the case of ammonium salts the SASA model cannot be applied without careful consideration of atomic charges and counter ions which is difficult to carry out on a molecular mechanics level, hence an approach based on the value of the dielectric permittivity constant was used. Both approaches (SASA and dielectric permittivity constant) were tried and compared in the case of N-acetylated oligoglucosamines 1b–12b. Besides, different temperatures were used to investigate the possibility of crossing internal barriers. Aglycon moieties were not considered in the simulation.
Simulation time was 50 ns for cyclic glucosamines 7a,b–12a,b. For linear oligosaccharides 1a,b–6a,b, adiabatic conformational maps were built first using a dihedral driving algorithm for each linkage.29 After that, several 10 ns trajectories were simulated starting from the global minima found on each map. Snapshot structures were written every 5 ps and then used for further analysis. This yielded 10000 conformations for cyclic oligosaccharides and 2000×N conformations for the linear structures, where N is the number of glycosidic linkages in the molecule.
In the beginning, the calculations were performed at a temperature of 300 K. However, the results obtained for cyclic structures 7a,b–12a,b were contradictory to the experimental data independently on the solvation model used. In particular, the values of transglycosidic SSCC 3JC,H and 3JH,H calculated by Karplus equations (Fig. 3) differed strongly from each other across the glycosidic linkages, while experiments showed all linkages to behave equally. For example, in 1H and 13C NMR spectra there were sets of signals corresponding to a single monosaccharide unit.
It was suggested that this problem might arise from the overestimation of conformational barriers in the MM3 calculations which makes the temperature of 300 K insufficient for the molecules to cross all barriers to obtain averaged conformations for each glycosidic linkage. A higher temperature of 700 K provided satisfactory results. The calculated values of constants (700 K) are shown in Table 6 (see also Table 5 in Supplementary Materials).
Alteration of the solvation model both in the case of linear and cyclic structures (Tables 5 and Table 6) mostly influenced the values of proton coupling constants 3JH,H (JωR and JωS) which were determined by the value of ω torsion, while the values of carbon-proton constants 3JC,H (Jφ, JψR and JψS) changed by not more than 1 Hz, which is within the experimental accuracy of these SSCC measurement. We explain such behavior by the difference in slopes of Karplus functions for 3JH,H and 3JC,H (Fig. 3) which leads to greater changes of 3JH,H values upon the equal changes in torsions. Besides, the alteration of the solvation model obviously changed the energy difference of rotamers resulting from the rotation of ω torsion.30 In the case of cyclic oligoglucosamines 7a,b–12a,b these torsions depended much less upon the solvation model used due to the conformational restrictions.
The comparison of the calculated SSCC values with those measured experimentally for the linear and cyclic oligosaccharides showed good coincidence for heteronuclear constants 3JC,H (for most of them the difference did not exceed 1 Hz). For 3JH,H constants the coincidence was expectedly worse, especially for the linear oligosaccharides 1a,b–6a,b.
The greatest deviation of the calculated hetero- and homonuclear SSCCs from the experimental ones was observed in the case of cyclic disaccharides 7a and 7b. These molecules are very constrained and suffer from monosaccharide ring deformations (see above in the NMR Spectroscopy Study section and Table 3 in the Supplementary Materials), that probably imply some torsional or van-der-Waals interactions unusual for saccharides, which are not considered correctly by molecular mechanics.
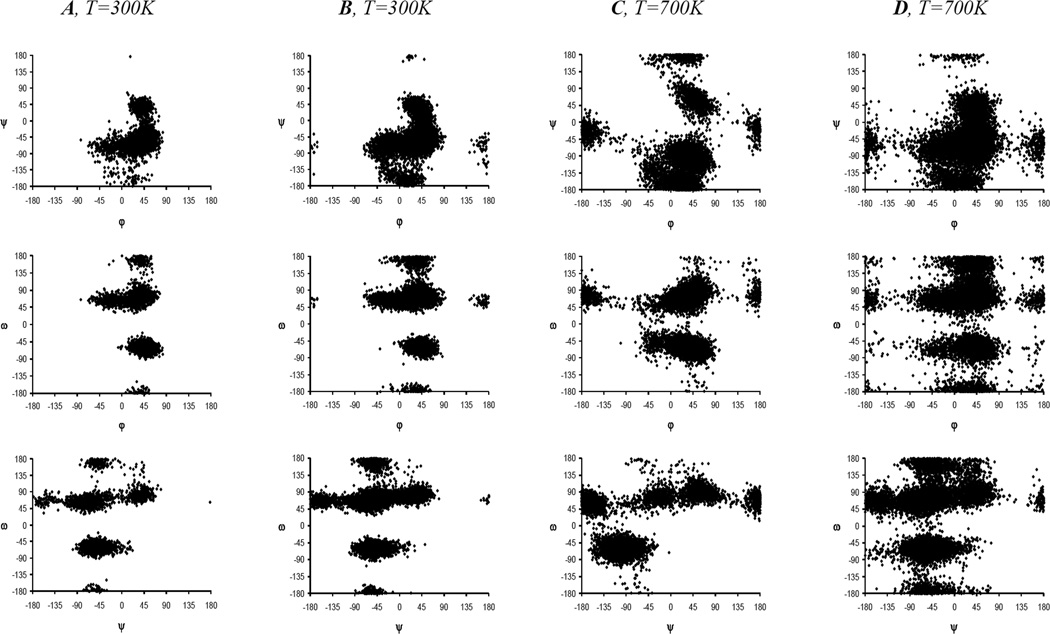
We performed the analysis and visualization of the results of molecular modeling, including the torsions values φ, ψ and ω (Fig. 3). In our case almost all molecules contained more than one such a linkage. This required that 3N variables be used to describe the conformation of the whole molecule. Such a huge data array was difficult to visualize directly, hence we employed two approaches for the analysis of MD trajectories. The scatter plots were built for pairs of angles (φ, ψ), (φ, ω) and (ψ, ω) (Fig. 4). Analysis of these plots showed that all disaccharide fragments in the studied oligoglucosamines 1a,b–12a,b (both linear and cyclic) were characterized by the presence of multiple conformational minima allowing the conclusion that they were not rigid. The scatter plots of linear oligosaccharides within the same coordinates (φ, ψ), (φ, ω) and (ψ, ω) were similar to each other (Fig. 4) for different disaccharide fragments and molecules suggesting the similarity of conformational behavior. In the case of cyclic oligosaccharides 7a,b–12a,b the number of accessible conformational states was greater than in the linear ones which apparently resulted from the higher temperature (700 K) used during MD simulations of cycles (see above). The areas corresponding to these states in the larger cyclic oligosaccharides were to be found at the scatter plots around points which were close to those corresponding to the linear molecules, but for the small cycles (di-, tri-, and tetrasaccharide) a considerable difference in the positions of conformational minima was observed. It is explained by the restricted flexibility of the small-sized cyclic saccharides, which confirms the observations made during the analysis of experimental chemical shifts and SSCC values. The scatter plots of non-N-acetylated oligoglucosamines 1a–12a (see Fig. 1 in Supplementary Materials) did not differ significantly from those of their N-acetylated counterparts 1b–12b (Fig. 4).
Figure 4.
Scatter plots for pairs of angles (φ, ψR), (φ, ω) and (ψR, ω) for internal disaccharide fragments of linear trisaccharide 2b (A) and heptasaccharide 6b (B) and their cyclic analogs 8b (C) and 12b (D). These scatter plots were built up with the use of SASA MD-simulation data at the temperature T=300 K for linear molecules 2b and 6b and T=700 K for cycles 8b and 12b.
The second approach to the analysis of MD data was based on their clustering by means of artificial neural networks (ANN) of ART2 (Adaptive Resonance Theory) topology implemented in the Stuttgart Neural Network Simulator (SNNS v4.2).31–33 This permitted the analysis of the regions in the conformational space accessible during MD simulations using all three torsions for each linkage. Furthermore, it allowed the analysis of the conformation of the studied molecules as a whole, using all torsions for all linkages. However, this only showed not unexpectedly that each linkage behaved independently, except for those in small cyclic structures (2–3 units) where MD simulations likely failed to provide all the available conformations due to high rigidity. Therefore we focused on the analysis of separate linkages. The torsional angles were represented in terms of corresponding coupling constants 3JC,H and 3JH,H (Fig. 3). ANN assisted clustering was performed for the MD trajectories obtained without the solvation model with dielectric constant of 81, and for those obtained using SASA model.
Five clusters in the space of (φ, ψR, ψS) angles were found for every linkage in the linear oligosaccharides, two of them tending to occupy over 70% of the whole array. They were characterized with (φ, ψR, ψS) torsions being around (40°, −60°, 60°) and (40°, −160°, −55°). It correlated with one or two big clouds to be found on (φ, ψ) scatter plots, which represented two conformers, sometimes without distinct border. Torsional angle ω had preferable values of −60° or +60° independent of the (φ, ψ) values. Conformations corresponding to these clusters are shown in Fig. 5. The molecules constructed from the preferable conformations of glycosidic linkages are characterized by twisted shapes in which the substituents at C-2 mostly protrude into the outer space and did not encounter any spatial hindrances, hence their acetylation did not lead to a considerable conformational change. This explains the similarity between free amines and their N-acetylated counterparts established during NMR investigation (See above in NMR Spectroscopy Study section).
Figure 5.
Four main conformations of (1→6)-β-linkage in the studied saccharides. Conformer I (φ, ψR, ψS, ω)=(40°, −140°, −25°, −60°); conformer II: (φ, ψR, ψS, ω)= (40°, −60°, 60°, −60°); conformer III: (φ, ψR, ψS, ω)= (40°, −140°, −25°, 60°); conformer IV: (φ, ψR, ψS, ω)= (40°, −60°, 60°, 60°).
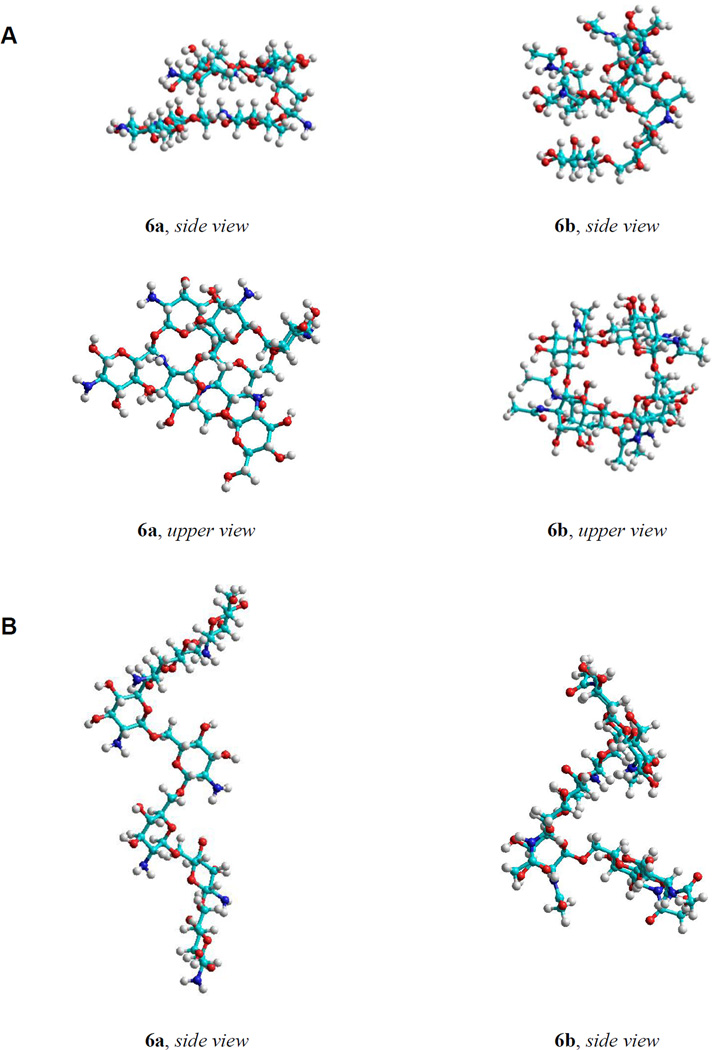
A global minima search was attempted via geometry optimization of the snapshot structures of the linear oligosaccharides. The shape corresponding to the energy minima of the large linear oligosaccharides calculated without taking into account the solvent effects tended to be a right-hand helix (Fig. 6A). Minima found using the SASA model had rather complicated twisted shapes with some helical elements maintained both for the acetylated and free amines (Fig. 6B). This correlated with MD results and suggested that these conformations may be regarded as adequate models of the studied molecules in water solution.
Figure 6.
The shapes corresponding to the energy minima of heptaglucosaminide 6a and per-N-acetylated heptaglucosaminide 6b calculated without the account of solvent effects (tending to be a right-hand helix) (A) and calculated with SASA solvent model (rather complicated twisted shape with some helical elements) (B).
It is noteworthy that the conformers of C5–C6 bond found during the calculations corresponded mainly to gt rotamers of ω with comparable amounts of the gg rotamer. The amount of the tg rotamer was significantly smaller although still observable. Ratios of gt and gg conformers changed slightly in different disaccharide fragments of the studied molecules. This is contradictory to the general opinion in which the relative weights of these rotamers in (1→6)-linked diglucoside fragment are 29:70:1 (gt:gg:tg).28
The large cyclic structures were also characterized by the similar clusters indicating that with increase in the monosaccharide residue number in the cycle, the conformational properties of the disaccharide fragments became similar to those in the linear structures. Thus, the large cyclic oligosaccharides have conformational shapes that can be described as a twisted ring. In the small cycles the number of clusters was less than five and there presented clusters with average values of coupling constants that deviated greatly from those calculated over the whole trajectory. On the whole, the conformations of the small cycles are rather restrained flattened rings.
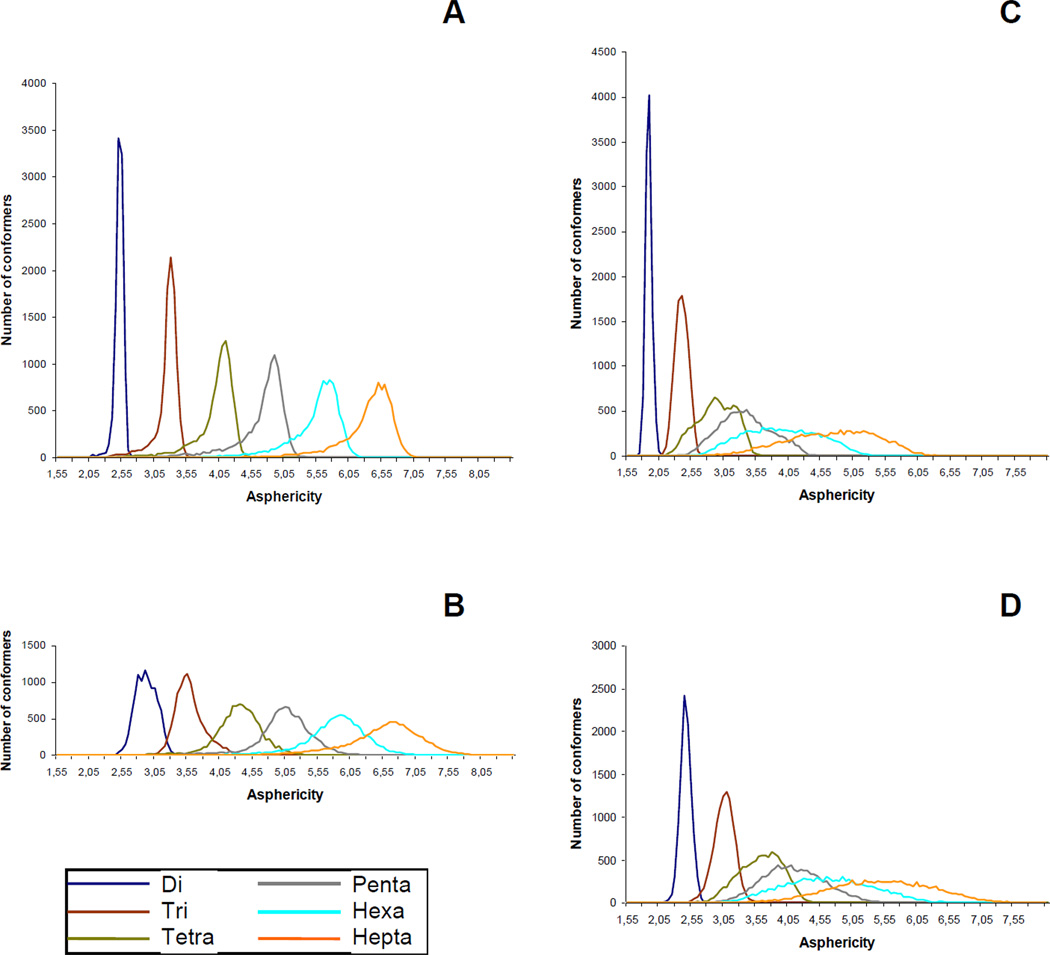
Another parameter that was used to analyze the behavior of the studied molecules during MD simulation were so called asphericity values,34 which can be calculated according to formula A3/36πV2, where A – is the molecular surface and V – molecular volume. Bigger values of this parameter indicate a greater deviation of the molecular shape from an ideal sphere. In our study, the distributions of asphericities were calculated over all MD trajectories computed under SASA conditions: the obtained results are presented in Fig. 7. The area under each graph is normalized to an equal value, thus the differences in the broadness of these distributions can be interpreted as the difference in total molecular flexibility. It can be seen that it increases upon the enlargement of the molecules, both linear and cyclic, but in the latter the increase is dramatic from the di- to the heptasaccharide. This also suggests that the rigidity present in smaller cycles falls upon the increase in the monosaccharide unit quantity and when it reaches the values of 6–7, the conformational behavior of the cyclic oligosaccharides actually becomes similar to that of the linear chains.
Figure 7.
Asphericity distributions calculated from SASA MD-simulations for linear oligoglucosamines 1a–6a (A), linear oligo-N-acetylglucosamines 1b–6b (B), cyclic oligoglucosamines 7a–12a (C) and cyclic oligo-N-acetylglucosamines 7b–12b (D).
In the case of the N-acetylated glucosamines the shapes of the asphericity distributions are similar but their maxima are slightly shifted towards the range of larger values. This supports the finding that the introduction of N-acetates does not affect the whole conformational shape of the studied compounds.
2.3. Conclusions
In this paper we have discussed the conformational properties of linear 1a,b–6a,b and cyclic 7a,b–12a,b oligo-(1→6)-β-D-glucosamines investigated by means of NMR spectroscopy and theoretical modeling. The experimental values of homo- (3JH,H) and heteronuclear (3JC,H) SSCC were used to characterize conformational state of the studied oligosaccharides in water solution. They were compared to SSCCs calculated using the data of MD simulations. The simulations were performed under several types of conditions used for the consideration of ionization of free amines, solvent effect and temperature. For cyclic structures 7a,b–12a,b the obtained results at 300 K were contradictory to the experiment, thus the higher temperature of 700 K was employed leading to an interpretable outcome.
The comparison of the calculated SSCC values with those measured experimentally for linear and cyclic oligosaccharides showed good coincidence for heteronuclear constants 3JC,H: in the most cases the difference did not exceed 1 Hz. In the case of homonuclear SSCCs the match between the experimental and the calculated values was worse. It was found that the simulated behavior of the C5–C6 bond depended strongly on the solvation model used, especially for the linear oligosaccharides. For cyclic disaccharides 7a and 7b the greatest overall SSCCs mismatch was observed possibly due to high straints and monosaccharide ring deformations, which are not considered correctly by molecular mechanics. On the other hand, experimental study by SSCCs measurement was impossible for some molecules due to the overlaps of the signals in NMR spectra. Therefore the final conclusion about the conformational state of C5–C6 bonds in the (1→6)-glycosidic linkages in these molecules is yet uncertain.
According to MD simulations, disaccharide fragments in the studied linear oligosaccharides were not rigid making their shapes twisted with some helical elements. The conformational shape of the cyclic di-, tri-, and tetrasaccharides was found to be symmetrical flattened ring. The larger cycles tended to adopt more complicated shapes, such as twisted rings, and the conformational behavior of their disaccharide fragments is close to that in linear oligosaccharides.
It was shown that conformational behavior of the N-acetylated compounds is similar to that of the non-N-acetylated oligoglucosamines. According to the results, the substituents at C-2 of the studied compounds protruded into the outer space and did not encounter any spatial hindrance. Hence, the introduction of N-acetyl groups did not lead to considerable conformational changes. This opens the possibility for further N-functionalization of these oligosaccharides without the loss of their spatial organization.
3. Experimental
Preparation of linear 1a,b–4a,b and 6a,b7,8 and cyclic 7a,b–12a,b9 oligoglucosamines was described previously.
Computer simulations: Details are given in the Molecular Modeling section (2.3.). Transglycosidic coupling constants were calculated for each structure in the MD trajectories according to the Karplus equations and then averaged. Neural network clustering was performed in Stuttgardt Neural Network Simulator, SNNS (v. 4.2) with the use ART2 ANN. The following options were used: ART2_Weights initialization function with parameters (0.9, 2); ART2 learning function with parameters (0.95, 10, 10, 0.1, 0.9) and ART2_Stable update function with the same parameters.
The NMR spectra of oligofucosides 1a,b–4a,b (10–15 mg) were recorded in D2O (99.98% D, Merck, 0.5 ml) solutions on Bruker spectrometers DRX-500 and AV-600 with 0.05% acetone as reference (1H 2.225 ppm, 13C 31.45 ppm). The pH of solutions was about 5.5, the temperature was chosen so that the signal of residual protons of HOD in 1H NMR spectra did not overlap with the signals of protons of oligoglucosamines. Thus, the spectra were acquired at the temperature of 300–310 K. Microtubes (Shigemi, Inc.) were sometimes used for sensitivity enhancement. The resonance assignment in 1H and 13C NMR spectra was performed by gradient enhanced 2D gCOSY, gNOESY, gHSQC, gJ-HMBC and gHSQC-TOCSY experiments as well as TOCSY and ROESY experiments.
Experimental 3JC,H constants were measured using J-HMBC15,16 and J-resolved17,18 techniques. The 2D J-HMBC experiment was performed in the constant-time version.15 The spectral widths were about 2 ppm for 1H region and 46 ppm for 13C region and did not include resonances of aglycon groups. The data were collected in the echo/anti-echo mode. For echo selection the two sinusoidal field gradients in a ratio of 5:−3 were applied, and for anti-echo selection the ratio was −3:5. The length of gradients was 1 ms, and the recovery time was 100 µs. The spectra were acquired with 60–110 t1 increments and 64–700 scans per increment. 512 points were collected during the acquisition time t2. The HMBC preparation delay Δ for the reliable measurement of a coupling constants should be taken at least 60% of inversed values of smallest coupling of interest (Δ=0.6/JC,Hmin).16 Smaller values of Δ lead to the overestimation of J because of the antiphase character of the peaks. Δ=300 ms was used that corresponded to JC,Hmin=2.0 Hz. The upscaling coefficient k was 30–60. The relaxation delay was 1s. Thus, resulting acquisition time was 1–15 hr. The third order low-pass J-filter16 was introduced for the suppression of one bond constants (1JC,H) in the range from 125 Hz to 180 Hz. Sinusoidal field gradient sequence with the ratio +7:−4:−2:−1 was applied during low-pass J-filter. The forward linear prediction to 1024 points was used in F1 that corresponded to resolution 5–6 Hz, and zero-filling to 1024 points was used in F2. The processing was performed with π/2 shifted sine square function in both dimensions.
J-resolved experiments were performed in direct 13C-detecting mode with the PENDANTE preparation sequence for the enhancement of the sensitivity of carbon atoms. The spectral widths were about 46 ppm for 13C dimensional and 14 Hz for J dimensional. The spectra were acquired with 44 t1 increments and 500–740 scans per increment. 2048 points were collected during the acquisition time t2 giving a spectral resolution of about 2.3 Hz in 13C dimension. The relaxation time between each individual scan was 1s. The resulting acquisition time was 10–15 hr. A Gauss shaped pulse was used, its duration τ was 20–50 ms corresponding to the required selectivity of 50–20 Hz. Zero-filling to 128 points was used for the J dimension prior to Fourier transformation, giving a spectral resolution of about 0.3 Hz. The 2D spectra were processed with π/2 shifted sine square function in 13C-dimension and in the J dimension.
Supplementary Material
Acknowledgments
We thank Dr. Yu. A. Strelenko for helpful discussions of NMR experiments. This work was supported by the grants of the President of the Russian Federation to Young Scientists MK-5544.2010.3 (A. A. Grachev) and the Russian Foundation for Basic Research 10-03-01012-a (A. G. Gerbst).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Supplementary data
Supplementary data associated with this article can be found, in the online version, at doi:......
References
- 1.Cerca N, Jefferson KK, Maira-Litran T, Kelly-Quintos C, Goldmann DA, Azeredo J, Pier GB. Infect. Immun. 2007;75:3406–3413. doi: 10.1128/IAI.00078-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Itoh Y, Wang X, Hinnebusch BJ, Preston JF, 3rd, Romeo T. J. Bacteriol. 2005;187:382–387. doi: 10.1128/JB.187.1.382-387.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Izano EA, Sadovskaya I, Vinogradov E, Mulks MH, Velllyagounder K, Ragunath C, Kher WB, Ramasubbu N, Jabbouri S, Perry MB, Kaplan JB. Microb. Pathogenesis. 2007;43:1–9. doi: 10.1016/j.micpath.2007.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mack D, Fischer W, Krokotsch A, Leopold K, Hartmann R, Egge H, Laufs R. J. Bacteriol. 1996;178:175–183. doi: 10.1128/jb.178.1.175-183.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sloan GP, Love CF, Sukumar N, Mishra M, Deora R. J. Bacteriol. 2007;189:8270–8276. doi: 10.1128/JB.00785-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wang X, Preston JF, 3rd, Romeo T. J. Bacteriol. 2004;186:2724–2734. doi: 10.1128/JB.186.9.2724-2734.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gening ML, Tsvetkov YE, Pier GB, Nifantiev NE. Russ. J. Bioorgan. Chem. 2006;32:389–399. [Google Scholar]
- 8.Gening ML, Tsvetkov YE, Pier GB, Nifantiev NE. Carbohydr. Res. 2007;342:567–575. doi: 10.1016/j.carres.2006.08.010. [DOI] [PubMed] [Google Scholar]
- 9.Gening ML, Titov DV, Grachev AA, Gerbst AG, Yudina ON, Shashkov AS, Chizhov AO, Tsvetkov YE, Nifantiev NE. Eur. J. Org. Chem. 2010;13:2465–2475. [Google Scholar]
- 10.Gening ML, Maira-Litran T, Kropec A, Skurnik D, Grout M, Tsvetkov YE, Nifantiev NE, Pier GB. Infect. Immun. 2010;78:764–772. doi: 10.1128/IAI.01093-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Grachev AA, Gerbst AG, Ustyuzhanina NE, Khatuntseva EA, Shashkov AS, Usov AI, Nifantiev NE. J. Carbohydr. Chem. 2005;24:85–100. [Google Scholar]
- 12.Grachev AA, Gerbst AG, Ustuzhanina NE, Krylov VB, Shashkov AS, Usov AI, Nifantiev NE. Mendeleev Commun. 2007;17:57–62. [Google Scholar]
- 13.Douhal A, editor. Chemical, Physical and Biological Aspects of Confined Systems. Volume 1. Amsterdam: Elsevier Science; 2006. Cyclodextrin Materials Photochemistry, Photophysics and Photobiology. [Google Scholar]
- 14.Bonas G, Vignon MR, Pérez S. Carbohydr. Res. 1991;211:191–205. doi: 10.1016/0008-6215(91)80091-z. [DOI] [PubMed] [Google Scholar]
- 15.Gotfredsen CH, Meissner A, Duus JØ, Sørensen OW. Magn. Reson. Chem. 2000;38:692–695. [Google Scholar]
- 16.Meissner A, Sørensen OW. Magn. Reson. Chem. 2001;39:49–52. [Google Scholar]
- 17.Bax A, Freeman R. J. Am. Chem. Soc. 1982;104:1099–1100. [Google Scholar]
- 18.Liu M, Farant RD, Gillam JM, Nicholson JK, Lindon JC. J. Magn. Reson. Series B. 1995;109:275–283. [Google Scholar]
- 19.Grachev AA, Gerbst AG, Shashkov AS, Nifantiev NE. Russ. Chem. Rev. 2009;78:717–736. [Google Scholar]
- 20.Olsson U, Sáwén E, Stenutz R, Widmalm G. Chem. Eur. J. 2009;15:8886–8894. doi: 10.1002/chem.200900507. [DOI] [PubMed] [Google Scholar]
- 21.Gagnaire D, Tran V, Vignon M. J. Chem. Soc. Chem. Commun. 1976;1:6–7. [Google Scholar]
- 22.Gagnaire D, Vignon M. Carbohydr. Res. 1976;51:140–144. doi: 10.1016/s0008-6215(00)84233-0. [DOI] [PubMed] [Google Scholar]
- 23.Mulloy B, Frenkiel TA, Davies DB. Carbohydr. Res. 1988;184:39–46. doi: 10.1016/0008-6215(88)80004-1. [DOI] [PubMed] [Google Scholar]
- 24.Stenutz R, Carmichael I, Widmalm G, Serianni AS. J. Org. Chem. 2002;67:949–958. doi: 10.1021/jo010985i. [DOI] [PubMed] [Google Scholar]
- 25.Popov AI, Hallenga K. Modern NMR techniques and their application in chemistry. New York: Marcel Dekker, Inc; 1991. [Google Scholar]
- 26.Lipkind GM, Shashkov AS, Knirel YA, Vinogradov EV, Kochetkov NK. Carbohydr. Res. 1988;175:59–75. doi: 10.1016/0008-6215(88)80156-3. [DOI] [PubMed] [Google Scholar]
- 27.Pérez S, Imberty A, Engelsen SB, Gruza J, Mazeau K, Jimenez-Barbero J, Poveda A, Espinosa J-F, van Eyck BP, Johnson G, French AD, Kouwijzer MLCE, Grootenuis PDJ, Bernardi A, Raimondi L, Senderowitz H, Durier V, Vergoten G, Rasmussen K. Carbohydr. Res. 1998;314:141–155. [Google Scholar]
- 28.Rosen J, Robobi A, Nyholm P-G. Carbohydr. Res. 2002;337:1633–1640. doi: 10.1016/s0008-6215(02)00089-7. [DOI] [PubMed] [Google Scholar]
- 29.Stortz CA. Carbohydr. Res. 1999;322:77–86. doi: 10.1016/s0008-6215(99)00207-4. [DOI] [PubMed] [Google Scholar]
- 30.Kirschner KN, Woods RJ. PNAS. 2001;98:10541–10545. doi: 10.1073/pnas.191362798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Carpenter GA, Grossberg S. Comput. Vision Graph. 1987;37:54–115. [Google Scholar]
- 32.Grossberg S. Biol. Cybern. 1976;23:121–134. doi: 10.1007/BF00344744. [DOI] [PubMed] [Google Scholar]
- 33.Grossberg S. Biol. Cybern. 1976;23:187–202. doi: 10.1007/BF00340335. [DOI] [PubMed] [Google Scholar]
- 34.Najdoo KJ, Kuttel M. J. Comput. Chem. 2001;22:445–456. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.