Volumetric Quantitative Computed Tomography Measurement Precision for Volumes and Densities of Tarsal and Metatarsal Bones

Abstract

Diabetic foot diseases, such as ulcerations, infections, and neuropathic (Charcot’s) arthropathy are major complications of diabetes mellitus and peripheral neuropathy and may cause osteolysis (bone loss) in foot bones. The purposes of our study were to make computed tomography (CT) measurements of foot-bone volumes and densities and to determine measurement precision (percent coefficients of variation for root mean square-standard deviations) and least significant changes in these percentages that could be considered biologically real with 95% confidence. Volumetric quantitative CT scans were performed and repeated on 10 young, healthy subjects and 13 subjects with diabetes mellitus and peripheral neuropathy. Two raters used the original- and repeat-scan data sets to make measurements of volumes and bone mineral densities (BMDs) of the tarsal and metatarsal bones of the two feet (24 bones). Precisions for the bones ranged from 0.1% to 0.9% for volume measurements and from 0.6% to 1.9% for BMD measurements. The least significant changes ranged from 0.4% to 2.5% for volume measurements and from 1.5% to 5.4% for BMD measurements. Volumetric quantitative CT provides precise measurements of volume and BMD for metatarsal bones and tarsal bones where diabetic foot diseases commonly occur.

INTRODUCTION

Diabetic foot disease [such as ulceration, infection, neuropathic (Charcot’s) arthropathy (NCA)] is a major complication of diabetes mellitus (DM) and peripheral neuropathy (PN) [1]. Inflammatory osteolysis (bone loss) in the small foot bones is an unappreciated consequence of diabetic foot disease [2]. Although the pathogenesis of inflammatory osteolysis remains poorly understood, there is accumulating evidence that neuropathy-induced osteopenia in the tarsal and metatarsal bones of the foot plays a pivotal role in diabetic, neuropathic pathogenesis and clinical outcome [3–7]. Currently, it is not known how tarsal and metatarsal bone volumes and bone mineral densities (BMDs) are affected by diabetic foot disease.

Imaging technologies such as dual energy x-ray absorptiometry (DXA) and quantitative ultrasonography are limited to the measurement of BMD in the calcaneus. Much of the destruction associated with diabetic foot disease occurs in the mid-foot bones, particularly the navicular bone [8]. Single-slice quantitative computed tomography (QCT) has been used to study the spine, proximal femur, forearm, and tibia [9]. Although single-slice QCT could be used to study the foot bones, it has three major limitations: (1) for serial measurements of treatment outcome, disease progression, or disease remission, it is difficult to accurately position feet within CT scanners so that serial CT slices are of the same anatomical areas, (2) multiple slices need to be acquired if all tarsal and metatarsal bones are to be studied, and (3) a single slice does not provide information about BMD in all regions of a bone.

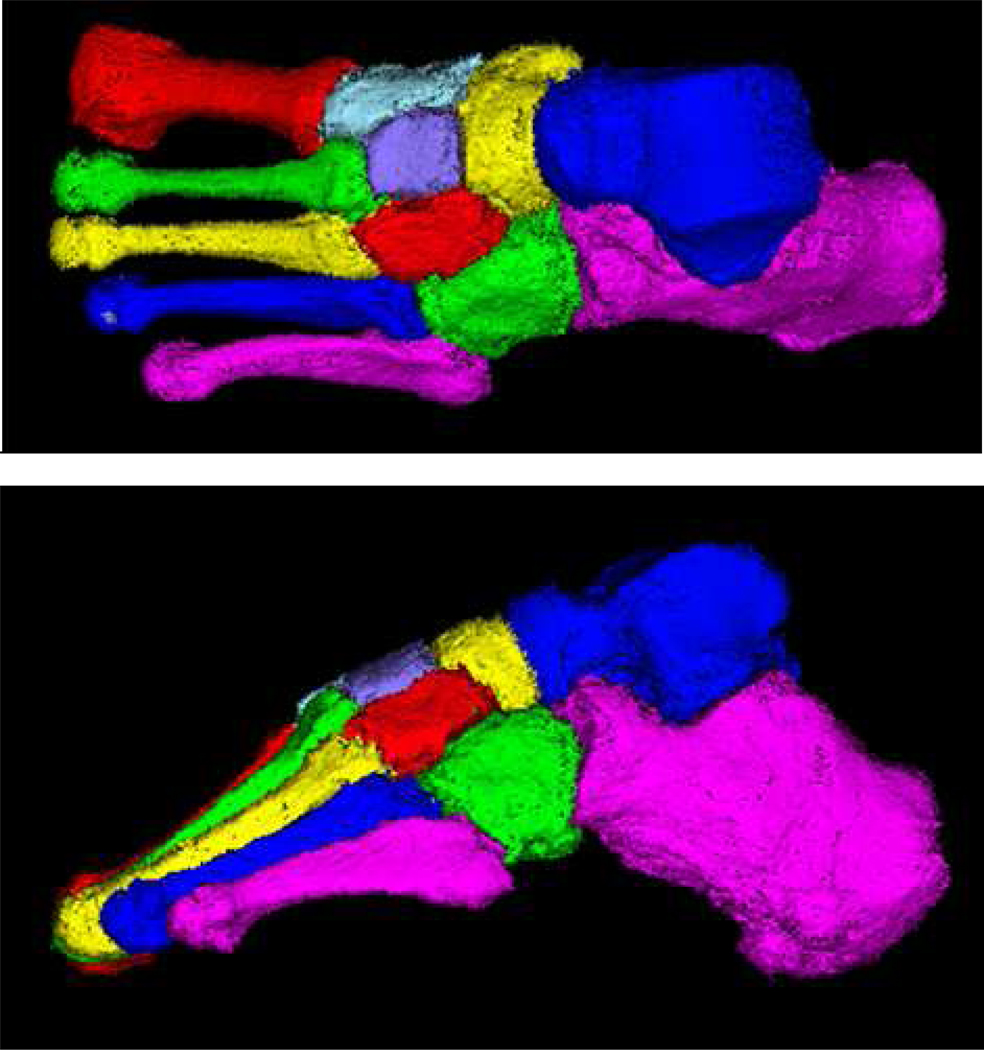
The major limitations associated with DXA, quantitative ultrasonography, and single-slice QCT for acquiring foot bones are overcome with volumetric QCT (vQCT). From the spiral CT scanner, a volume of data (a contiguous stack of slices) is obtained for the entire foot, and from the volume, individual bones can be segmented and measured as shown in Figure 1 [10]. For vQCT to be useful in tracking patients through time, it is necessary to know the precision and the least significant change (LSC) in each vQCT foot-bone measurement. The LSC is the smallest change that can be considered a true biological change and not measurement error.

Figure 1.

Volume-rendered QCT images of segmented tarsal and metatarsal bones of a healthy subject: (a) top view (top), and (b) side view.

The purpose of our study was to determine the precision of vQCT measurements of volumes and BMDs of tarsal and metatarsal bones of young healthy control subjects and older subjects with DM and PN. Specifically, we determined: (1) measurement precision, measured as the root mean square-standard deviation-% coefficient of variances (RMS-%CVs), (2) the LSCs in RMS-%CVs, and (3) the percentage of the total measurement variance within raters, between-raters, between feet (right and left), and between groups (young healthy or older subjects with DM and PN).

MATERIALS AND METHODS

Subjects

Our study protocol was approved by the Washington University School of Medicine’s Institutional Review Board, and prior to testing, informed consent was obtained from each subject. Ten young healthy adult control subjects and 13 older adult subjects with DM and PN without foot deformity or history of NCA or plantar ulceration were recruited for participation in the study. The healthy subjects were recruited from the students and staff members at Washington University Medical Center and were assumed to have peak bone masses. Advertisements were used to help recruit subjects who had DM and PN and lived in St. Louis, MO area. For each foot, PN was assessed using previously described, reliable methods [11]. In brief, we used a single-thickness (5.07/10-gr) Semmes-Weinstein monofilament to assess 7 locations on the plantar surface of each foot (dorsal mid-foot, first, third, and fifth metatarsal heads; medial and lateral mid-foot and central hind-foot). Subjects who were unable to accurately sense the 5.07 monofilament at any one of the 7 locations on either foot were graded as diminished or absent protective sensation and were considered to have PN. The demographics for the two groups of subjects are shown in Table 1.

Table 1.

Physical characteristics of groups of subjects.

	Healthy Subjects (n =10)		DM-PN (n = 13)*
	Mean (s.d.)†	n	Mean (s.d.)	n
Age (years)
Female	25.2 (4.4)	5	55.0 (7.6)	7
Male	27.0 (3.4)	5	64.3 (13.1)	6
Height (cm)
Female	169.4 (8.9)	5	165.8 (7.4)	7
Male	177.8 (6.2)	5	177.1 (3.2)	6
Weight (kg)
Female	67.4 (10.5)	5	71.5 (19.3)	7
Male	84.7 (16.2)	5	103.0 (20.2)	6
Body mass index
Female	23.4 (2.9)	5	25.7 (5.3)	7
Male	26.8 (4.9)	5	32.8 (6.0)	6

^*DMPN= Subjects with diabetes mellitus and peripheral neuropathy,

^†s.d. = standard deviation

Image Acquisition

A Siemens Definition 64-Slice CT dual-source scanner (Siemens Medical Systems, Inc, Malvern, PA, USA) was used to acquire foot images. Only one radiation source was used for this study. The spiral CT images of each foot were acquired separately while the subject was lying supine on the CT scanner table with his or her foot resting on the table. The table was positioned at approximately 120 mm from the iso-center (rotation center) of the gantry with the center of the foot (talus) approximately in the iso-center of the scan volume and the foot angled at approximately 45 degrees to the table surface (toes pointed away from the body). Scan volumes extended from beyond the toes to beyond the talus so that all tarsals, metatarsals, and phalanges were included. The right foot was scanned, followed by the left foot. The feet were re-positioned, re-aligned, and the scans repeated. The following CT acquisition parameters were used: 38.4 mm table increment per gantry rotation (64 slices × 0.6mm collimation = 38.4mm), 220 mAs, 120 kVp, pitch of 1, rotation time of 0.5 seconds, and a 512 × 512 matrix. With software available on the CT scanner console, the CT data were reconstructed with a B70f kernel at 0.6 mm slice reconstruction intervals (no gaps) to create vQCT images.

Apparent BMD Calibration

A solid QCT-Bone Mineral™ phantom (Image Analysis, Inc., Columbia, Kentucky, Serial No. 4225) was aligned parallel to the table and scanned in series with each foot scan (foot scanned first then the phantom). The phantom with dimensions of approximately 300 mm × 152 mm × 32 mm consisted of 3 rods (20mm in diameter) with different concentrations of calcium hydroxyapatite embedded in a water equivalent polymer. For each foot CT scan, the phantom data were used to calculate a calibration curve to convert the mean CT Hounsfield Units (HUs) to apparent BMD (mg/cm3 calcium hydroxyapatite). Although we use the term “BMD” throughout this article, our noninvasive vQCT method measures “apparent” BMD [12, 13]. Our “apparent” BMD measure not only includes bone mineral content (calcium hydroxyapatite), but also includes marrow. Thus the accuracy of our measurement of the concentration of calcium hydroxyapatite is subject to error due to the variable amount of marrow fat included in the measure. As is customary in the literature, we have dropped the term “apparent” for brevity.

Whole Bone Segmentation Using Semi-automatic Methods

The reconstructed vQCT images of each foot were loaded into Analyze software [14, 15] to create image volumes. The voxel size for each subject was approximately 0.6 mm × 0.6 mm × 0.6 mm. To avoid unnecessary density measurement errors, the image data were not interpolated to isotropic voxels. Edge detection methods were used to segment foot bones from the surrounding soft-tissues [10]. More specifically, foot bones contain high density cortical shell regions and are separated from each other by lower density soft-tissues (such as, muscle, fat, and joint spaces). An edge-detection method implemented using ImageJ 1.40g [16], was used to identify simultaneously the cortical-shell boundaries of the tarsals and metatarsals [10]. The resulting images were loaded into Analyze to produce binary maps in which voxels on the edges between two tissue types were set to values of 1 and voxels that were not on edges were set to values of 0.

We used a graph-cut method developed by our group to allow easy separation of the tarsal and metatarsal bones into individual objects [17]. In brief, an operator places one or multiple seeds on each bone. Based on the seeds, the algorithm performs a multi-way cut on a weighted graph constructed from the segmented binary volume of all of the bones to achieve bone separations. Using only a single seed point for each bone, the resulting cuts in the graph can usually be placed accurately at bone-interfaces. In cases where the joint spaces are not clearly defined, additional seeds are necessary to separate the bones. The graph-cut method was implemented with an interactive, graphical user interface to allow easy placement of the seeds and inspection of the separation results (Figure 1).

After each bone was separated, a program (developed by our group) employing morphology operators (dilation and erosion) was used to automatically fill holes and gaps in each bone. The gaps were typically small (i.e. 2 to 4 voxels). Occasionally, large gaps were caused by extremely thin cortical shells and required manual filling. After hole-filling, the segmented bones were converted to object maps that were overlaid with the original grayscale volumetric data so that bone volumes and BMDs could be automatically measured.

Bone Measurement

Two doctoral students in physical therapy served as raters (JAK, KAB). They had neither prior experience with bone segmentation tools nor with using Analyze to measure foot bones. Each rater received approximately 8 to 10 hours of training and learned to identify, segment, and measure foot bones. The two raters measured volumes and BMDs of the bones in the original and repeated vQCT images. The time between making original and repeat measurements was ≥ five days.

Statistical Analysis

There were 2,208 volumes and 2,208 BMD measurements performed [23 subjects (10 healthy subjects, and 13 subjects with DM and PN) × 2 feet (right and left) × 12 bones × 2 raters × 2 measurements (original scan plus repeat scan)]. To determine measurement precision, original and repeat measurements were used to calculate root-mean-square standard deviation (RMS-SD), root-mean-square coefficient of variation (RMS-CV), and root-mean-square percent coefficient of variation (RMS-%CV) [18–20]. The RMS-SDs and RMS-%CVs were used to calculate least significant changes (LSCs) as follows:

$$\text{LSC}=\text{RMS}-\text{SD}\times 2.77$$ Equation 1

$$\%\text{LSC}=\text{RMS}-\%\text{CV}\times 2.77$$ Equation 2

LSCs represent the magnitudes of changes in measurements needed to indicate that true biological changes have occurred and that the changes are not attributable to measurement errors (that is, the inability to reproduce measurements) [18]. For the determination of LSC, the 95% statistical confidence level was used and was based on one baseline measurement and one follow-up measurement being made. Separate calculations were performed for each rater for the foot bones (tarsals and metatarsals) of the right and left feet. In reporting measurement precision, it is customary to pool values [21, 22]. To justify pooling, a repeated measures analysis of variance was used to test for differences among original and repeat BMD measurements made by the two raters (that is, four sets of repeated measurements were compared). Forty-eight tests were performed (2 groups × 12 bones × 2 feet). Our multiple comparisons corrected (Bonferroni) p value for these comparisons was p < 0.001. This was followed by repeated measures analysis of variance between left and right feet with the measurements for the two raters averaged. Twenty-four tests were performed for this comparison (two groups of patients X twelve bones). A p value < 0.001 was also used as our criterion for significance for these tests. Similar testing was performed for volume measurements. Data for any tests that had p values below the criterion value were examined further with paired t tests (after assuring that differences were normally distributed).

Data were also entered into a mixed-model nested analysis of variance with two fixed effects [(1) Group (healthy subjects or subjects with diabetes mellitus and peripheral neuropathy), and (2) Gender (female or male)] and four random effects [(1) Subjects (10 healthy subjects, and 13 subjects with diabetes mellitus and peripheral neuropathy), (2) Foot (right and left) nested within subjects, (3) Rater (n =2) nested within foot, nested within subjects, (4) Measurement (original and repeat) nested within rater, nested within foot, nested within subjects]. The restricted/residual maximum likelihood (REML) method was used to perform a variance components analysis. Nested analysis of variance (hierarchical analysis of variance) is used when subordinate classifications (which must be random) are nested within higher levels of classification [23]. With this analysis, a variance components analysis is performed to determine the amount of variation that occurs at various levels (that is, intra- and inter-rater variation). The intraclass correlation coefficient is determined with such an analysis and in the case of repeated measurements by a single observer represents the proportion of variation attributable to subjects versus that attributable to repeat measurements.

RESULTS

Volume and BMD Measurement Precision

For repeated measures analysis of variance testing for the two raters, only BMD measurements for the right calcaneus of control patients resulted in a p < 0.001, but with further testing with paired t tests, the criterion value was not exceeded. Values for the two readers were, therefore, pooled. There was also no difference detected between feet; so values for right and left feet were also pooled. Tables 2–3 contain the pooled precision results for rater 1 and 2s’ volume and BMD measurements for the healthy subjects and the subjects with DM and PN.

Table 2.

Measurement precision for volumes (cm³) in healthy control subjects and subjects with DM-PN with pooled rater results.

	Bone*
	Cal	Cub	Cun1	Cun2	Cun3	Met1	Met2	Met3	Met4	Met5	Nav	Tal
Healthy Controls
Both Feet Combined
Mean Volume	67.4	12.4	9.6	3.8	5.4	15.2	7.7	6.3	6.3	7.2	10.3	35.5
RMS-SD† (LSC)**	0.10 (0.27)	0.03 (0.09)	0.03 (0.08)	0.03 (0.09)	0.02 (0.06)	0.06 (0.16)	0.04 (0.12)	0.03 (0.07)	0.02(0.06)	0.03 (0.08)	0.03 (0.08)	0.09 (0.25)
RMS-%CV§ (%LSC)#	0.1 (0.4)	0.3 (0.7)	0.3 (0.9)	0.9 (2.5)	0.4 (1.2)	0.4(1.0)	0.5 (1.5)	0.5 (1.3)	0.4 (1.0)	0.4 (1.2)	0.3 (0.9)	0.3 (0.7)
DM-PN Group
Both Feet Combined
Mean Volume	64.4	12.4	9.3	3.8	5.2	15.1	7.7	6.9	6.9	7.5	10.6	34.0
RMS-SD (LSC)	0.23 (0.64)	0.06 (0.16)	0.04 (0.12)	0.03 (0.08)	0.03 (0.08)	0.05 (0.15)	0.04 (0.12)	0.03 (0.09)	0.05(0.14)	0.03 (0.09)	0.05 (0.13)	0.10(0.27)
RMS-%CV (%LSC)	0.3 (0.9)	0.4 (1.2)	0.4 (1.2)	0.7 (2.0)	0.5 (1.5)	0.3(0.8)	0.5 (1.5)	0.5 (1.3)	0.6 (1.7)	0.4 (1.1)	0.4 (1.2)	0.3 (0.7)

^*Cal = calcaneus, Cub = cuboid, Cun1 = cuneiform 1, Cun2 = cuneiform 2, Cun3 = cuneiform 3, Met1 = metatarsal 1, Met2 = metatarsal 2, Met3 = metatarsal 3, Met4 = metatarsal 4, Met5 = metatarsal 5, Nav = navicular, Tal = talus;

^†root-mean-square standard deviation;

^§root-mean-square percent coefficient of variation;

^**Least significant change; ** Values calculated from Equation 1;

^#Values calculated from Equation 2.

Table 3.

Measurement precision for bone mineral densities (mg/cm³) in healthy controls and subjects with DM-PN with pooled rater results.

	Bone*
	Cal	Cub	Cun1	Cun2	Cun3	Met1	Met2	Met3	Met4	Met5	Nav	Tal
Healthy Controls
Both Feet Combined
Mean BMD	314	322	399	467	384	491	605	567	553	569	423	435
RMS-SD† (LSC)**	2.6 (7)	3.2 (9)	2.4 (7)	3.3 (9)	3.7 (10)	4.4 (12)	5.5 (15)	6.1 (17)	7.2 (20)	10.1 (28)	2.3 (6)	2.6 (7)
RMS-%CV§ (%LSC)#	0.9 (2.4)	1.0 (2.9)	0.6 (1.7)	0.7 (2.0)	1.0 (2.8)	0.9 (2.5)	1.0 (2.6)	1.2 (3.2)	1.4 (3.8)	1.8 (5.0)	0.6 (1.5)	0.6 (1.7)
DM-PN Group
Both Feet Combined
Mean BMD	304	285	384	436	369	444	568	527	514	535	416	400
RMS-SD (LSC)	3.0 (8)	3.6 (10)	3.7 (10)	5.2 (14)	5.0 (14)	5.1 (14)	7.0 (19)	7.9 (22)	8.6 (24)	10.3 (29)	3.3 (9)	3.5 (10)
RMS-%CV (%LSC)	1.0 (2.9)	1.3 (3.7)	1.0 (2.7)	1.2 (3.4)	1.5 (4.0)	1.3 (3.7)	1.4 (3.9)	1.7 (4.6)	1.8 (5.1)	1.9 (5.4)	0.9 (2.4)	1.0 (2.7)

^*Cal = calcaneus, Cub = cuboid, Cun1 = cuneiform 1, Cun2 = cuneiform 2, Cun3 = cuneiform 3, Met1 = metatarsal 1, Met2 = metatarsal 2, Met3 = metatarsal 3, Met4 = metatarsal 4, Met5 = metatarsal 5, Nav = navicular, Tal = talus;

^†root-mean-square standard deviation;

^§root-mean-square percent coefficient of variation;

^**Least significant change; ** Values calculated from Equation 1;

^#Values calculated from Equation 2

The RMS-SD and LSC for both groups ranged from 0.02 to 0.23 and 0.6 to 0.64, respectively. For both groups, the corresponding RMS-%CVs and %LSCs ranged from 0.1% to 0.9% and 0.4% to 2.5%, respectively.

BMD values ranged from 285 to 605 mg/cm³, with the young healthy subjects having slightly higher BMDs than the subjects with DM-PN (Tables 3). The RMS-SD and LSC for both groups ranged from 2.3 to 10.3 and 6 to 29, respectively. For both groups, the corresponding RMS-%CVs and %LSCs ranged from 0.6% to 1.9% and 1.5% to 5.4%, respectively.

Variance components analysis

For all 12 bones, the mean variation in volumes attributable to subjects was 90.9%, with foot (right or left), rater (1 or 2), and measurement (original or repeat) accounting for 8.9%, 0.1%, and 0.1% of the variation (Table 4). When data were analyzed with foot nested within subjects, subjects accounted for 91.0% of the variation and foot 9.0% of the variation. The mean variation in BMDs attributable to subjects was 93.3%, with foot, rater, and measurement accounting for 1.9%, 4.4%, and 0.4% of the variation (Table 5). When data were analyzed with foot nested within subjects, subjects accounted for 95.7% of the variation and foot 4.3% of the variation.

Table 4.

Variance components (percent of variation attributable to variables) for volume of foot bone with Group and Gender as fixed effects.

	Cal	Cub	Cun1	Cun2	Cun3	Met1	Met2	Met3	Met4	Met5	Nav	Tal
Random Effects
Subjects	97.26	96.08	94.13	84.97	92.86	95.00	73.44	88.13	86.22	93.60	93.25	95.68
Foot[Subjects]	2.66	3.82	5.79	14.43	7.02	4.95	26.31	11.71	13.55	6.35	6.41	4.17
Rater[Foot, Subjects]	<0.01	0.01	<0.01	0.16	<0.01	<0.01	0.05	0.04	<0.01	<0.01	0.25	0.08
Meas†[Rater, Foot, Subjects]	0.07	0.08	0.08	0.43	0.12	0.05	0.21	0.12	0.22	0.05	0.10	0.07
Total	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00
	Cal	Cub	Cun1	Cun2	Cun3	Met1	Met2	Met3	Met4	Met5	Nav	Tal
Random Effects
Subjects	97.32	96.15	94.19	85.32	92.95	95.04	73.57	88.23	86.37	93.63	93.43	95.77
Foot[Subjects]	2.69	3.85	5.82	14.68	7.05	4.96	26.43	11.78	13.63	6.37	6.57	4.23
Total	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00

^*Cal = calcaneus, Cub = cuboid, Cun1 = cuneiform 1, Cun2 = cuneiform 2, Cun3 = cuneiform 3, Met1 = metatarsal 1, Met2 = metatarsal 2, Met3 = metatarsal 3, Met4 = metatarsal 4, Met5 = metatarsal 5, Nav = navicular, Tal = talus;

^†measurement (original or repeat scan)

Table 5.

Variance components (percents of variation attributable to variables) for bone mineral densities of foot bones with Group and Gender as fixed effect.

	Cal	Cub	Cun1	Cun2	Cun3	Met1	Met2	Met3	Met4	Met5	Nav	Tal
Random Effects
Subjects	95.44	94.50	93.34	94.28	88.62	92.67	92.46	94.30	93.10	91.41	95.45	93.82
Foot[Subjects]	0.16	1.39	1.54	0.70	6.43	2.23	2.54	1.43	2.34	3.93	0.06	0.33
Rater[Foot, Subjects]	4.17	3.75	4.91	4.71	4.56	4.70	4.58	3.71	3.87	3.61	4.35	5.64
Meas†[Rater, Foot, Subjects]	0.24	0.36	0.20	0.30	0.39	0.41	0.42	0.57	0.70	1.05	0.15	0.20
Total	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00
	Cal	Cub	Cun1	Cun2	Cun3	Met1	Met2	Met3	Met4	Met5	Nav	Tal
Random Effects
Subjects	97.65	96.57	95.85	96.78	90.96	95.19	94.93	96.50	95.44	93.84	97.68	96.70
Foot[Subjects]	2.35	3.43	4.15	3.22	9.04	4.81	5.07	3.51	4.56	6.16	2.32	3.30
Total	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00

^*Cal = calcaneus, Cub = cuboid, Cun1 = cuneiform 1, Cun2 = cuneiform 2, Cun3 = cuneiform 3, Met1 = metatarsal 1, Met2 = metatarsal 2, Met3 = metatarsal 3, Met4 = metatarsal 4, Met5 = metatarsal 5, Nav = navicular, Tal = talus;

^†measurement (original or repeat scan)

DISCUSSION

Precise vQCT volume and BMD measurements can be used to monitor foot-bone osteolysis in subjects who have DM and PN. Such measurements would be particularly useful in monitoring treatments and could possibly be used to develop a biomarker to assess the risk of neuropathic Charcot arthropathy [24].

Our precision and LSC values for younger healthy subjects were slightly better than those for subjects with DM and PN. This difference is probably attributable to healthy subjects’ having better defined joint spaces, which enabled the edge detection methods to more easily identify the joint boundaries and the graph-cut methods to more easily separate the bones with minimal human intervention. Our BMD precisions for single bone measurements are similar to those found in previous studies. The short-term precision (RMS-%CV) of trabecular BMD in the spine as measured with single slice QCT was reported to range from 1.4% to 2.4% and from 1.3 to 1.7% for vQCT of L1 and L2 [9]. Depending on the skeletal site measured and the DXA system used, these precision values are somewhat higher than those (0.6% to 1.9%) for DXA [21]. The short-term precision measurements for total BMD of the distal forearm and tibia using peripheral QCT (pQCT) ranged from 0.3 to 2.2% [25]. The BMD precision of the forearm using a general purpose spiral whole-body CT scanner was 3% [25]. In our study, the talus and navicular had the best BMD precisions while metatarsals 4 and 5 had the lowest precisions.

We measured volumes and BMDs at a resolution of one part out of a 1000 [volume resolution was one cubic millimeter and BMD resolution was one HU, which is slightly less than 1 mg/cm3], so we do not think that differences in resolution contributed to differences in measurement precisions. Values for volumes were, however, approximately a factor of 10 larger than values for BMDs [volumes ranged from approximately 4000mm3 (cuneiform 2) to 70,000mm3 (calcaneus) and BMDs ranged from approximately 300 mg/cm3 (calcaneus) to 600mg/cm3 (metatarsal 2)]; therefore, even if the RMS-SDs were identical for a volume and BMD measurement, the factor-of-10-larger value for the volume measurement would result in a smaller RMS-%CV because RMS-%CV is computed by dividing the RMS-SD by the mean. The RMS-SD values were larger for the BMD measures compared with the volume measures, and this also added to the larger BMD RMS-%CV. Another reason why volume precision was better than BMD precision is that our edge detection software finds the surface of the bone, so volume measurement differences are small between scans whereas BMD measurements are not only susceptible to these surface differences but also to differences (between repeat scan volumes) in how cortical bone and trabecular bone are averaged with marrow fat. Because %LSC is computed directly from precision measurements, the %LSCs for BMDs were higher than those for volumes.

Compared with DXA, vQCT can be used to assess bone volumes and BMDs even when bones are closely aligned or overlapping. When compared with single-slice QCT, vQCT has several advantages. First, with vQCT, the BMD and volume for an entire bone is determined. This is important because bones are asymmetrical, and BMDs vary within bones (for instance, in metatarsals, the shafts are denser than are the bases and head regions). With single-slice QCT, it is important to carefully align the subject’s foot in the CT scanner from one scan to the next so that the same anatomical location is sampled in each of the single-slices. Such careful attention to foot alignment is not necessary with vQCT. Our vQCT methods appear to be well-suited for determining the impact of osteolysis or osteopenia in the tarsal and metatarsal bones. This could not be easily done with DXA or single-slice QCT.

There are limitations with this study. First, our sample size is small. For short-term precision studies, 30 degrees of freedom are recommended [18]. This can be achieved by scanning 30 subjects twice. Such a sample size assures that the upper limit for the 95% confidence interval of precision is not 34% greater than the calculated value. With methods described elsewhere, we did calculate the 95% confidence intervals for our precision measurements [19, 20]. These calculations indicated that additional subjects would probably not have had a clinically meaningful effect on our precision measurements—this is because our measurements had high precision. A second limitation of our study is that the accuracies of our measurements are not known. The determination of measurement accuracy is our focus in an ongoing phantom study. Third, our new semi-automated method is not yet rapid enough for clinical diagnostic purposes; however it is well suited for use in research studies comparing changes in foot bone volumes and BMDs between and within subjects, and subjects can be followed over time. The time required to segment each of the 12 bones for a subject varied between approximately 12 minutes and 2 hours and was largely dependent on the continuities and the densities of the cortical bones. Both raters found that if a bone had several thin cortical shell regions, small gaps in the cortical shell, or poorly delineated joint spaces, the time required to segment the bones increased. In general, bones in subjects with DM and PN required more time to segment than those in healthy subjects. A fourth limitation is that vQCT involves ionizing radiation, but because sensitive organs are not directly exposed, the effective radiation dose involved in peripheral vQCT is generally low and is comparable to less than a few months of exposure to natural radiation.

Although we did not detect statistically significant differences between raters or between left and right feet, a concern that we have is that with our variance components examination, we determined that ≥ 4% of the variance in our measurements were attributable to differences between right and left feet. If measurement pooling were used, these differences could exceed the differences through time that one would want to detect in a clinical study. Because we are aware of no biologic reason why BMD and volume should vary in a systematic fashion between right and left feet, the precision calculations could be based on variance of the sum of the right and left foot measurements [23]. At this point how to account for these differences is not clear to us, and in our ongoing clinical study, we plan to use the LSC calculated for a specific bone to determine if a change has occurred in that bone. In our ongoing study, we are developing a biomarker for discriminating between healthy patients, patients with diabetes mellitus and peripheral neuropathy, and patients with neuropathic (Charcot’s) arthropathy. Variables used to develop the biomarker include vQCT and clinical measurements.

CONCLUSION

VQCT BMD and volume of foot bones can be measured with high precision. These measurements can be used to detect relatively small changes over time, and are well suited for use in clinical studies to access the impact of localized osteolysis and osteopenia in diabetic foot disease.