Abstract
The expression, replication and repair of eukaryotic genomes require the fundamental organizing unit of chromatin, the nucleosome, to be unwrapped and disassembled. We have developed a quantitative model of nucleosome dynamics which provides a fundamental understanding of these DNA processes. We calibrated this model using results from high precision single molecule nucleosome unzipping experiments, and then tested its predictions for experiments in which nucleosomes are disassembled by the DNA mismatch recognition complex hMSH2-hMSH6. We found that this calibrated model quantitatively describes hMSH2-hMSH6 induced disassembly rates of nucleosomes with two separate DNA sequences and four distinct histone modification states. In addition, this model provides mechanistic insight into nucleosome disassembly by hMSH2-hMSH6 and the influence of histone modifications on this disassembly reaction. This model's precise agreement with current experiments suggests that it can be applied more generally to provide important mechanistic understanding of the numerous nucleosome alterations that occur during DNA processing.
INTRODUCTION
Eukaryotic DNA is packaged into chromatin by wrapping around histone protein octamers to form nucleosomes (1,2). These nucleosomes sterically occlude replication, transcription and repair complexes from their DNA target sites. DNA processing complexes appear to access their target sites via nucleosome unwrapping (3–5) and disassembly (6). However, the mechanism(s) associated with these nucleosome structural alterations are not well understood. An essential component in appreciating these nucleosome alterations is a quantitative and predictive model describing DNA unwrapping and disassembly from the histone octamer. Such a model will provide a critical tool in understanding in vivo DNA processing within chromatin.
The key concept in a model of nucleosomal DNA unwrapping is the unwrapping free energy landscape. This landscape quantitatively captures the free energy cost of unwrapping each individual base pair from the histone octamer. Previous studies determined qualitative features of the structure of this free energy landscape (4,5). Here, we develop a free energy landscape that not only accounts for these qualitative observations, but is calibrated from precise mechanical unzipping measurements of nucleosomal DNA (7). These experiments apply a force to pull apart the DNA base pairing, which concurrently unwraps the DNA from the histone octamer. We extract detailed information about the energy landscape from these experiments. By carefully adjusting our energy landscape, we obtain an excellent agreement with the highly complex measured unzipping profiles.
We then use this calibrated free energy landscape to model a completely separate experiment that investigates nucleosome disassembly by the human DNA mismatch recognition complex, hMSH2-hMSH6. This complex appears to function as a molecular switch that specifically binds DNA mismatches in the ADP bound form (8,9). Upon the exchange of ADP for ATP, hMSH2-hMSH6 forms a sliding clamp that diffuses along duplex DNA. This allows for iterative loading of multiple hMSH2-hMSH6 complexes onto the duplex DNA surrounding a mismatch, which directs the excision reaction during DNA mismatch repair.
This mismatch recognition process must occur within chromatin. Recently, it was demonstrated that hMSH2–hMSH6 disassembles nucleosomes near a DNA mismatch and that histone modifications in the DNA–histone interface of the nucleosome dramatically enhance the rate of disassembly (10,11). These results indicate that hMSH2-hMSH6 not only recognizes DNA mismatches but facilitates the DNA excision reaction by ensuring the DNA surrounding a mismatch is nucleosome and perhaps protein free. It was proposed that hMSH2-hMSH6 disassembles nucleosomes by trapping DNA unwrapping fluctuations through iterative loading of hMSH2-hMSH6 at the DNA mismatch (10).
We modeled this nucleosome disassembly process with our free energy landscape and found that disassembly of unmodified nucleosomes can be quantitatively understood using the same free energy landscape applied to unzipping experiments. We explain the influence of histone post translational modifications (PTMs) and DNA sequence on the disassembly rates with modest changes to the free energy landscape based on the location of the modifications and the known influence of DNA sequence and histone modifications on DNA–histone binding free energies (4,11,12). Furthermore, our model provides detailed mechanistic insight into the process of nucleosome disassembly by hMSH2-hMSH6.
MATERIALS AND METHODS
Calculation of the dynamics of nucleosome unwrapping
We treat the time evolution of the probability that 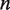 base pairs of nucleosomal DNA are unwrapped as a continuous-time Markov process. This allows us to write the rates of wrapping
base pairs of nucleosomal DNA are unwrapped as a continuous-time Markov process. This allows us to write the rates of wrapping  and unwrapping
and unwrapping 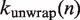 in a rate matrix
in a rate matrix 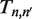 , which is defined by
, which is defined by
| (1) |
| (2) |
with all other entries in 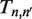 equal to zero. This rate matrix satisfies the master equation
equal to zero. This rate matrix satisfies the master equation
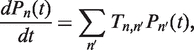 |
(3) |
where 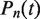 is the time–dependent probability of observing the unwrapped state
is the time–dependent probability of observing the unwrapped state 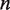 . The rate matrix
. The rate matrix 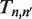 contains all of the information about the influence of external constraints, such as an applied force or a protein complex, on the probability and time evolution of each partially unwrapped nucleosome state
contains all of the information about the influence of external constraints, such as an applied force or a protein complex, on the probability and time evolution of each partially unwrapped nucleosome state 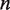 . Below, we describe how we determine the rate matrix that describes the influence of a mechanical unzipping force and a pressure from bound hMSH2-hMSH6 complexes on the nucleosome unwrapping probability and its time evolution. However, once this rate matrix is set up, the following solution to the master equation may be applied to any system where nucleosomes are unwrapped.
. Below, we describe how we determine the rate matrix that describes the influence of a mechanical unzipping force and a pressure from bound hMSH2-hMSH6 complexes on the nucleosome unwrapping probability and its time evolution. However, once this rate matrix is set up, the following solution to the master equation may be applied to any system where nucleosomes are unwrapped.
We solve the eigenvalue problem for this master equation to obtain 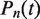 . We compute the eigenvalues
. We compute the eigenvalues 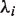 and eigenvectors
and eigenvectors 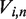 of
of 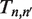 numerically (13). We then use the inverse of the matrix of eigenvectors
numerically (13). We then use the inverse of the matrix of eigenvectors 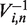 to express the initial state in the basis of the eigenvectors
to express the initial state in the basis of the eigenvectors
| (4) |
where 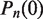 is the initial state in the basis of the unwrapping states. If the nucleosome is fully wrapped at time zero, then
is the initial state in the basis of the unwrapping states. If the nucleosome is fully wrapped at time zero, then 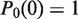 and
and 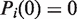 for
for 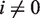 . This then allows us to write the solution to Equation 3 as
. This then allows us to write the solution to Equation 3 as
| (5) |
The term 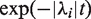 propagates each eigenvector with a decay rate given by its eigenvalue, and we multiply by
propagates each eigenvector with a decay rate given by its eigenvalue, and we multiply by 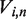 to transform back into the basis of unwrapping states. This solution allows us to calculate the complete dynamics of nucleosome unwrapping rapidly.
to transform back into the basis of unwrapping states. This solution allows us to calculate the complete dynamics of nucleosome unwrapping rapidly.
Rates of nucleosome unzipping
In unzipping experiments, an applied force 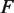 breaks apart the base pairing of DNA containing a nucleosome, which simultaneously unwraps the nucleosome. We compute
breaks apart the base pairing of DNA containing a nucleosome, which simultaneously unwraps the nucleosome. We compute 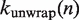 and
and 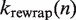 , the rates of nucleosome unwrapping and rewrapping at
, the rates of nucleosome unwrapping and rewrapping at 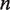 unwrapped base pairs, using the Gibbs free energy difference between the change in our energy landscape
unwrapped base pairs, using the Gibbs free energy difference between the change in our energy landscape 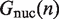 due to unwrapping and the work done on the nucleosome by the applied force. We multiply the base rate for wrapping fluctuations
due to unwrapping and the work done on the nucleosome by the applied force. We multiply the base rate for wrapping fluctuations 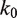 by a Gibbs factor, resulting in
by a Gibbs factor, resulting in
| (6) |
| (7) |
where 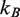 is Boltzmann's constant and
is Boltzmann's constant and  is the temperature. The applied force
is the temperature. The applied force 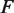 acts over a distance
acts over a distance 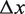 per opened base pair, and
per opened base pair, and 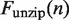 is the force required to break the DNA base pairing and stretch the DNA. Of the remaining force, a fraction
is the force required to break the DNA base pairing and stretch the DNA. Of the remaining force, a fraction 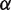 increases the unwrapping rate and
increases the unwrapping rate and 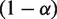 decreases the rewrapping rate. The parameter
decreases the rewrapping rate. The parameter 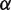 represents the relative position of the transition state between
represents the relative position of the transition state between 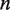 and
and 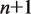 unwrapped base pairs. We may then insert these rates of unwrapping and rewrapping into Equations 1 and 2, and follow the procedure outlined in the previous section to calculate the dynamics of nucleosome unwrapping in unzipping experiments.
unwrapped base pairs. We may then insert these rates of unwrapping and rewrapping into Equations 1 and 2, and follow the procedure outlined in the previous section to calculate the dynamics of nucleosome unwrapping in unzipping experiments.
Calculation of dynamics in the presence of hMSH2-hMSH6
When hMSH2-hMSH6 is present we must model its binding to the DNA, the interactions between hMSH2-hMSH6 molecules, and the interactions between hMSH2-hMSH6 and the nucleosome. Given that the rate of hMSH2-hMSH6 diffusion along the DNA is faster than all other rates in the system, we treat hMSH2-hMSH6 diffusion as being in equilibrium with respect to all other processes in the system. We may then model the hMSH2-hMSH6 molecules as a 1D gas of hard spheres. This is known as a Tonks gas, and has a partition function given by (14)
| (8) |
where 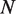 is the number of hMSH2-hMSH6 molecules bound to the DNA,
is the number of hMSH2-hMSH6 molecules bound to the DNA,  is the footprint of hMSH2-hMSH6 in base pairs and
is the footprint of hMSH2-hMSH6 in base pairs and  is the length of the DNA segment available to hMSH2-hMSH6 in base pairs (Figure 2A). To confirm that use of the Tonks gas solution is valid, for select cases we also performed simulations of the dynamics including each hMSH2-hMSH6 particle individually. We find that approximating the hMSH2-hMSH6 behavior as a Tonks gas gives results nearly identical to these simulations, and is much more computationally efficient (Supplementary Figure S1).
is the length of the DNA segment available to hMSH2-hMSH6 in base pairs (Figure 2A). To confirm that use of the Tonks gas solution is valid, for select cases we also performed simulations of the dynamics including each hMSH2-hMSH6 particle individually. We find that approximating the hMSH2-hMSH6 behavior as a Tonks gas gives results nearly identical to these simulations, and is much more computationally efficient (Supplementary Figure S1).
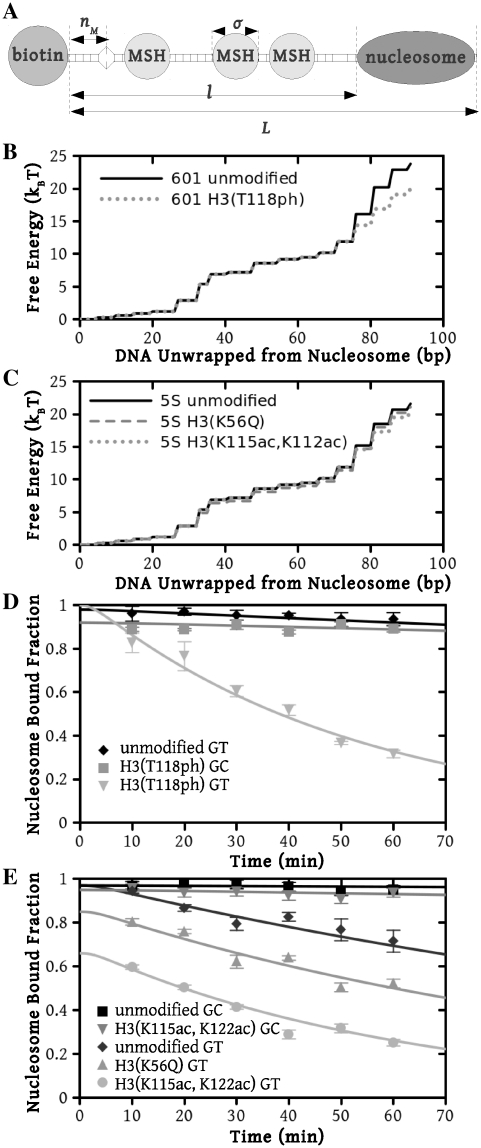
Figure 2.
Model predictions compared with experimental measurements for nucleosome displacement by hMSH2-hMSH6. (A) Graphical depiction of the experimental system [10]. Streptavidin bound to the biotinylated left end of the DNA prevents hMSH2-hMSH6 (MSH) from sliding off this end, while a nucleosome inhibits hMSH2-hMSH6 from sliding off the right end of the DNA. There is a mismatch located 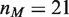 bp from the biotin bead, at which hMSH2-hMSH6 may bind. The total length of the DNA segment is
bp from the biotin bead, at which hMSH2-hMSH6 may bind. The total length of the DNA segment is 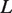 . The hMSH2-hMSH6 is confined to length
. The hMSH2-hMSH6 is confined to length  , the DNA between the biotin bead and the nucleosome. The footprint of one hMSH2-hMSH6 molecule is
, the DNA between the biotin bead and the nucleosome. The footprint of one hMSH2-hMSH6 molecule is  bp. Free energy landscapes for unwrapping nucleosomes on (B) the 601 positioning sequence and (C) the 5S positioning sequence. Numerical values for these energy landscapes are provided as a supplemental spreadsheet. A comparison of the results of our modeling (lines) using these energy landscapes to experimental measurements (points) of nucleosome displacement by hMSH2-hMSH6 shows excellent agreement for both (D) the 601 positioning sequence and (E) the Xenopus 5S positioning sequence.
bp. Free energy landscapes for unwrapping nucleosomes on (B) the 601 positioning sequence and (C) the 5S positioning sequence. Numerical values for these energy landscapes are provided as a supplemental spreadsheet. A comparison of the results of our modeling (lines) using these energy landscapes to experimental measurements (points) of nucleosome displacement by hMSH2-hMSH6 shows excellent agreement for both (D) the 601 positioning sequence and (E) the Xenopus 5S positioning sequence.
We can then use the Tonks gas partition function to calculate the probability that the bound hMSH2-hMSH6 molecules will block nucleosome rewrapping or the binding of more hMSH2-hMSH6. The probability that there are no hMSH2-hMSH6 particles within 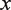 base pairs of one end of the available DNA segment for
base pairs of one end of the available DNA segment for 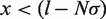 is
is
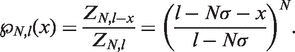 |
(9) |
To calculate the rates of unwrapping, 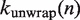 , and rewrapping,
, and rewrapping,  , we multiply the base rate for wrapping fluctuations
, we multiply the base rate for wrapping fluctuations 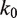 by a Gibbs factor determined from our free energy landscape, as in Equations 6 and 7
by a Gibbs factor determined from our free energy landscape, as in Equations 6 and 7
| (10) |
| (11) |
where 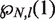 is the probability that an hMSH2-MSH6 particle does not block rewrapping of one base pair. Similarly, the rate of hMSH2-hMSH6 binding at the mismatch is
is the probability that an hMSH2-MSH6 particle does not block rewrapping of one base pair. Similarly, the rate of hMSH2-hMSH6 binding at the mismatch is
| (12) |
where 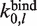 is the rate of binding to bare DNA of length
is the rate of binding to bare DNA of length  ,
, 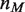 is the mismatch position, and
is the mismatch position, and 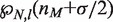 is the probability that binding is not blocked by the presence of another hMSH2-hMSH6 molecule. This assumes that the mismatch is within
is the probability that binding is not blocked by the presence of another hMSH2-hMSH6 molecule. This assumes that the mismatch is within 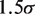 base pairs of the end of the DNA segment, such that there cannot be any hMSH2-hMSH6 molecules between the end of the DNA and the mismatch when an hMSH2-hMSH6 molecule is bound at the mismatch. If this is not true, one must sum over all combinations for the number of hMSH2-hMSH6 complexes bound on either side of the mismatch.
base pairs of the end of the DNA segment, such that there cannot be any hMSH2-hMSH6 molecules between the end of the DNA and the mismatch when an hMSH2-hMSH6 molecule is bound at the mismatch. If this is not true, one must sum over all combinations for the number of hMSH2-hMSH6 complexes bound on either side of the mismatch.
We then calculate the dynamics of nucleosome unwrapping following the method described in the ‘Calculation of the dynamics of nucleosome unwrapping’ section. Instead of indexing the probability in Equation 3 based only on 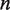 , we use
, we use 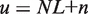 , where
, where 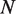 is the number hMSH2-hMSH6 molecules already bound to the DNA, and
is the number hMSH2-hMSH6 molecules already bound to the DNA, and 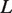 is the maximum number of bases which can unwrap from the histone before it dissociates from the DNA. This allows us to write a rate matrix
is the maximum number of bases which can unwrap from the histone before it dissociates from the DNA. This allows us to write a rate matrix 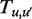 which includes not only rates of nucleosome wrapping and unwrapping, but also hMSH2-hMSH6 binding and dissociation.
which includes not only rates of nucleosome wrapping and unwrapping, but also hMSH2-hMSH6 binding and dissociation.
RESULTS
Mechanical unzipping of nucleosomes
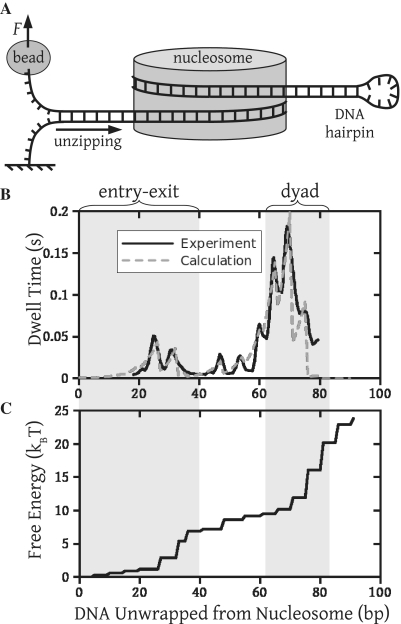
The most detailed method yet devised to probe nucleosome dynamics is mechanically unzipping the base pairing of DNA containing a nucleosome (7). In experiments performed by the Wang group (7), the nucleosome is positioned on the 601 high-affinity sequence (15). One strand of the DNA molecule is attached to a surface, and the other strand to a bead confined in an optical trap (Figure 1A). By carefully controlling the movement of the optical trap, a constant force may be exerted on the DNA. This force sequentially breaks the DNA base pairing, increasing the contour length of the single-stranded DNA between the bead and the surface. Measuring the position of the bead as a function of time establishes the number of DNA bases that are unpaired. When DNA wrapped around the nucleosome becomes critically unpaired, it must dissociate from the nucleosome. Thus, the number of broken base pairs equals the number of base pairs unwrapped from the nucleosome (solid line, Figure 1B). This method probes the interaction between the nucleosome and the DNA as a function of the number of base pairs unwrapped from the nucleosome.
Figure 1.
A free energy landscape consistent with measurements of mechanical unzipping of nucleosomes. (A) Experimental setup for unzipping experiments. One strand of the DNA is attached to a surface, and a constant force 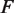 of 28 pN is applied to the other end via a bead in an optical trap, slowly pulling apart the DNA base pairing. As this unzipping of the base pairing moves through the nucleosome, the DNA must also be unwrapped from the nucleosome. (B) Dwell time as a function of the number of DNA base pairs (bp) unwrapped from the nucleosome. The solid line is determined from mechanical unzipping experiments, while the dashed line is calculated from (C) the free energy landscape for DNA unwrapping from a nucleosome on the 601 positioning sequence. Significant pauses when 20–30 bp are unwrapped (within the entry–exit region) and when 60–80 bp are unwrapped (within the dyad region) correspond to areas where the free energy landscape changes rapidly.
of 28 pN is applied to the other end via a bead in an optical trap, slowly pulling apart the DNA base pairing. As this unzipping of the base pairing moves through the nucleosome, the DNA must also be unwrapped from the nucleosome. (B) Dwell time as a function of the number of DNA base pairs (bp) unwrapped from the nucleosome. The solid line is determined from mechanical unzipping experiments, while the dashed line is calculated from (C) the free energy landscape for DNA unwrapping from a nucleosome on the 601 positioning sequence. Significant pauses when 20–30 bp are unwrapped (within the entry–exit region) and when 60–80 bp are unwrapped (within the dyad region) correspond to areas where the free energy landscape changes rapidly.
We calculate an energy landscape for unwrapping 601 positioning sequence DNA from a nucleosome, which is consistent with this unzipping data (Figure 1C). To obtain this landscape, we first create a trial landscape that we use to compute rates of nucleosome unwrapping. We then use these rates to calculate unzipping dynamics, and compare the result with experiments. Finally, we iterate the trial landscape until we obtain good agreement with experiments (Figure 1C) while respecting several qualitative features of the landscape known before our study.
In order to calculate experimental observables given an energy landscape, we compute 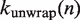 and
and  , the rates of nucleosome unwrapping and rewrapping at
, the rates of nucleosome unwrapping and rewrapping at 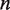 unwrapped base pairs, using Equations 6 and 7. In these experiments, the total applied force
unwrapped base pairs, using Equations 6 and 7. In these experiments, the total applied force 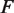 is held constant at 28 pN (7). The force
is held constant at 28 pN (7). The force 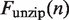 needed to unzip the base pairing and stretch the DNA can be calculated as a function of the DNA sequence (Supplementary Figure S2) (16). This results in an effective force responsible for nucleosome unwrapping averaging 10.9 pN, and ranging from 8.6 pN to 12.8 pN. Similarly, the increase in contour length from opening one base pair
needed to unzip the base pairing and stretch the DNA can be calculated as a function of the DNA sequence (Supplementary Figure S2) (16). This results in an effective force responsible for nucleosome unwrapping averaging 10.9 pN, and ranging from 8.6 pN to 12.8 pN. Similarly, the increase in contour length from opening one base pair 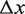 can be calculated to be
can be calculated to be 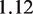 nm at this force (16). Since the relative position
nm at this force (16). Since the relative position 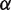 of the transition state between
of the transition state between 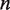 and
and 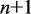 unwrapped base pairs is not known under the geometry of the experiments, we treat it as a fit parameter.
unwrapped base pairs is not known under the geometry of the experiments, we treat it as a fit parameter.
We find that our results are not very sensitive to the value of 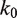 , the rate of nucleosome rewrapping in the absence of an applied force. We can fit the unzipping data with values of
, the rate of nucleosome rewrapping in the absence of an applied force. We can fit the unzipping data with values of 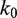 between
between 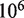 to
to 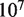 base pairs per minute by simultaneously making small adjustments to the nucleosome energy landscape and
base pairs per minute by simultaneously making small adjustments to the nucleosome energy landscape and 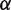 . We used the value of
. We used the value of 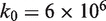 base pairs per minute that is in the middle of this range for all subsequent calculations.
base pairs per minute that is in the middle of this range for all subsequent calculations.
The trial landscape must conform to a number of experimental observations. First, the free energy landscape should be steepest in the dyad region (between about 63–84 bp), since the nucleosome contains the strongest contacts in this region (2,4). Second, the total height of the free energy landscape must be no more than 42 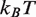 , of the free energy cost to disassemble a nucleosome from a compacted chromatin fiber in Xenopus egg extracts (17). The buffer conditions and presence of histone H1 in Xenopus egg extracts allow for strong interactions between nucleosomes, and promote chromatin compaction. We expect the free energy cost to disassemble the recombinant histones examined here to be significantly smaller, as the measurements are performed under conditions where chromatin compaction does not occur.
, of the free energy cost to disassemble a nucleosome from a compacted chromatin fiber in Xenopus egg extracts (17). The buffer conditions and presence of histone H1 in Xenopus egg extracts allow for strong interactions between nucleosomes, and promote chromatin compaction. We expect the free energy cost to disassemble the recombinant histones examined here to be significantly smaller, as the measurements are performed under conditions where chromatin compaction does not occur.
Third, the steps in the landscape occur approximately every 5.25 bp, which is the average spacing between DNA contacts in the nucleosome (2) and between peaks in the unzipping measurements (7). The positions of the peaks in the unzipping data (7) are extremely sensitive to the spacing between the steps in the unzipping landscape. For example, if we force all steps to be separated by exactly 5.25 bp, we are not able to accurately fit the unzipping data (Supplementary Figure S3). We can thus directly read off the spacing of the steps from the positions of the peaks in the unzipping data (7). This results in slight variations of the step spacing around the average of 5.25 bp consistent with the nucleosome crystal structure, which shows that DNA contacts in the nucleosome are not evenly spaced (2) either. We use discrete steps for simplicity, as we find no significant difference from using more gradual steps. Lastly, the landscape cuts off shortly after the dyad region, such that the histone octamer irreversibly dissociates from the DNA and cannot bind again once the system reaches this cut off. This corresponds with the observation that nucleosomes disassemble after the dyad is disrupted (7,18).
The free energy landscape is varied until the calculated DNA unzipping dynamics (dashed line, Figure 1B) agree with the experimental data. The free energy landscape shown (Figure 1C) conforms to all the constraints outlined above and also accurately reproduces the measured unzipping dynamics. Thus, we are able to extract detailed information about the structure of the nucleosome free energy landscape from these studies.
Because we do not know the value of 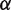 , the landscape is not completely constrained by the unzipping experiments. By making relatively small adjustments to the value of
, the landscape is not completely constrained by the unzipping experiments. By making relatively small adjustments to the value of 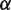 , we can obtain free energy landscapes that fit the unzipping data about as well as the one shown (Figure 1C), but that have total height as small as
, we can obtain free energy landscapes that fit the unzipping data about as well as the one shown (Figure 1C), but that have total height as small as 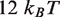 or as large as
or as large as 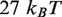 . We select a landscape with total height of
. We select a landscape with total height of 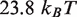 as this allows us to simultaneously fit measurements of nucleosome dissasembly by hMSH2-hMSH6 described in the next section.
as this allows us to simultaneously fit measurements of nucleosome dissasembly by hMSH2-hMSH6 described in the next section.
Nucleosome disassembly by hMSH2-hMSH6
To demonstrate the utility of our nucleosome free energy landscape, we apply it to measurements of the rate of nucleosome disassembly induced by the DNA mismatch recognition complex, hMSH2-hMSH6 (10,11). In these experiments, one end of a duplex DNA molecule is labeled with biotin, while the other end contains a nucleosome positioning sequence wrapped into a nucleosome (Figure 2A). The DNA molecule contains 99 or 75 base pairs between the biotin and the 5S or 601 positioning sequence, respectively, and a mismatch 21 base pairs from the biotin labeled end. hMSH2-hMSH6 binds the DNA mismatch and following ATP binding forms a clamp that slides freely along the DNA (9,19). Streptavidin bound to the biotin labeled end of the DNA prevents hMSH2-hMSH6 from sliding off that DNA end. At the opposite end, hMSH2-hMSH6 disassembles the nucleosome, allowing for hMSH2-hMSH6 to slide off the DNA.
Nucleosome disassembly by hMSH2-hMSH6 was demonstrated to depend on ATP binding but not ATP hydrolysis (10). We therefore consider a model where no ATP is hydrolyzed and hMSH2-hMSH6 cannot directly exert a force on the nucleosome. Rather, hMSH2-hMSH6 takes advantage of fluctuations in nucleosomal DNA unwrapping (3,5,20), which we calculate from our calibrated free energy landscape. hMSH2-hMSH6 binds at the DNA mismatch, forms a sliding clamp and then freely diffuses along the DNA. An additional hMSH2-hMSH6 complex can bind at the mismatch and form a sliding clamp once hMSH2-hMSH6 diffuses off the mismatch. As multiple hMSH2-hMSH6 clamps load onto the DNA, they can occupy unwrapped nucleosomal DNA, which prevents rewrapping thereby increasing the fraction of unwrapped nucleosomal DNA.
To accurately model hMSH2-hMSH6, we use known rates of hMSH2-hMSH6 sliding and binding. A rate of 5 per minute was used for hMSH2-hMSH6 binding and sliding clamp formation at a G/T mismatch, while 0.1 per minute was used for the rate of dissociation of the sliding clamp form of hMSH2-hMSH6 from DNA (8,19,21,22). A rate of 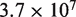 base pairs per minute was used for the step rate of hMSH2-hMSH6 clamps. This corresponds to the reported lower limit for the hMSH2-hMSH6 clamp diffusion constant on duplex DNA of
base pairs per minute was used for the step rate of hMSH2-hMSH6 clamps. This corresponds to the reported lower limit for the hMSH2-hMSH6 clamp diffusion constant on duplex DNA of 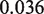
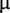 m2/s (21).
m2/s (21).
We calculated rates of hMSH2-hMSH6 induced nucleosome disassembly for comparison to rates measured by electrophoretic mobility shift assays (10,11). For computational efficiency, we used the fact that hMSH2-hMSH6 stepping along the DNA is the fastest process in our model, which allows us to model hMSH2-hMSH6 clamps as an equilibrated gas (14). This gas consists of particles of size  nm (8), which diffuse freely in one dimension along the DNA, but cannot pass through one another (Figure 2A) (see ‘Materials and Methods’ section). We find the calculated nucleosome disassembly rates using this approximation to be nearly identical to those from a full simulation including every hMSH2-hMSH6 complex explicitly (Supplementary Figure S1).
nm (8), which diffuse freely in one dimension along the DNA, but cannot pass through one another (Figure 2A) (see ‘Materials and Methods’ section). We find the calculated nucleosome disassembly rates using this approximation to be nearly identical to those from a full simulation including every hMSH2-hMSH6 complex explicitly (Supplementary Figure S1).
DNA sequence dependence of nucleosome disassembly by hMSH2-hMSH6
We begin by examining nucleosome disassembly measurements with the 601 positioning sequence. This allows us to employ the same free energy landscape used to model unzipping experiments (solid line, Figure 2B). We calculate the characteristic time for nucleosome disassembly to be 970 min, which agrees with the experimental observation that hMSH2-hMSH6 does not measurably disassemble nucleosomes in 60 min (diamonds, Figure 2D) (11,23).
Next, we consider the influence of the 5S nucleosome positioning sequence on nucleosome disassembly by hMSH2-hMSH6. We assume that the change in DNA sequence only influences the free energy landscape of nucleosome unwrapping. Therefore, we kept all model parameters fixed except for the nucleosome unwrapping free energy landscape. While detailed DNA unzipping measurements have not been reported for a 5S sequence, we expect this landscape to have the same general form as the 601 landscape, but a smaller total height. The sea urchin 5S sequence lowers the free energy of nucleosome formation by 4.7 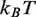 relative to 601 (15) and thus we expect a reduction of several
relative to 601 (15) and thus we expect a reduction of several 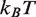 for the Xenopus 5S sequence as well (10). Furthermore, the DNA sequence near the dyad region appears to be responsible for the enhanced DNA–histone binding of the 601 sequence (4,15).
for the Xenopus 5S sequence as well (10). Furthermore, the DNA sequence near the dyad region appears to be responsible for the enhanced DNA–histone binding of the 601 sequence (4,15).
We modified the 601 landscape by decreasing it by a total of 2.2 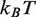 in the dyad region (solid line, Figure 2C). Nucleosome disassembly by hMSH2-hMSH6 is not sensitve to the detailed structure of the free energy landscape, so our choice to modify the landscape at the dyad region is based on empirical evidence that the increased binding affinity of the 601 sequence relative to 5S is due mainly to contacts in the dyad region (4,15). This landscape gives a good fit to the experimental data for unmodified nucleosomes containing the Xenopus 5S sequence (10) (diamonds, Figure 2E). This landscape allowed us to explain the behavior of nucleosome disassembly in the absence of a mismatch (squares, Figure 2E) where hMSH2-hMSH6 is permitted to bind at any position within the DNA at a rate of
in the dyad region (solid line, Figure 2C). Nucleosome disassembly by hMSH2-hMSH6 is not sensitve to the detailed structure of the free energy landscape, so our choice to modify the landscape at the dyad region is based on empirical evidence that the increased binding affinity of the 601 sequence relative to 5S is due mainly to contacts in the dyad region (4,15). This landscape gives a good fit to the experimental data for unmodified nucleosomes containing the Xenopus 5S sequence (10) (diamonds, Figure 2E). This landscape allowed us to explain the behavior of nucleosome disassembly in the absence of a mismatch (squares, Figure 2E) where hMSH2-hMSH6 is permitted to bind at any position within the DNA at a rate of 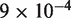 per minute, the experimental rate of hMSH2-hMSH6 binding to duplex DNA without a mismatch (8,19,22). These results suggest that modest changes in the free energy landscape due to alterations in the nucleosomal DNA sequence can lead to significant changes in the hMSH2-hMSH6 induced nucleosome disassembly rate.
per minute, the experimental rate of hMSH2-hMSH6 binding to duplex DNA without a mismatch (8,19,22). These results suggest that modest changes in the free energy landscape due to alterations in the nucleosomal DNA sequence can lead to significant changes in the hMSH2-hMSH6 induced nucleosome disassembly rate.
The influence of histone post-translational modifications of nucleosome disassembly by hMSH2-hMSH6
Histone PTMs within the DNA–histone interface reduce the free energy of nucleosome formation (11,12,24,25) and facilitate nucleosome disassembly by hMSH2-hMSH6 (10,11). We incorporated the influence of histone PTMs into our model by assuming that they specifically influence the DNA unwrapping free energy landscape close to the location of the PTM.
We first investigated the influence of histone PTMs near the nucleosome dyad: the phosphorylation of histone H3 at T118 [H3(T118ph)] and the double acetylation of H3 at K115 and K122 [H3(K115ac,K122ac)]. These modifications occur in vivo (26) and influence DNA repair (27). Recently, it was reported that H3(T118ph) reduces the DNA–histone binding free energy by 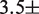 0.3
0.3 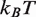 and that it increases the rate of hMSH2-hMSH6 induced nucleosome disassembly by 25 times (11). We found that a 3.8
and that it increases the rate of hMSH2-hMSH6 induced nucleosome disassembly by 25 times (11). We found that a 3.8 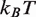 reduction of our 601 free energy landscape in the dyad region results in excellent agreement between the model predictions and the measured data (squares, Figure 2D).
reduction of our 601 free energy landscape in the dyad region results in excellent agreement between the model predictions and the measured data (squares, Figure 2D).
The dyad acetylations, H3(K115ac,K122ac), reduce the DNA–histone binding free energy by 
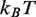 (12) and increase the rate of nucleosome disassembly by hMSH2-hMSH6 (10). We found that decreasing the free energy landscape for unmodified 5S by 1.2
(12) and increase the rate of nucleosome disassembly by hMSH2-hMSH6 (10). We found that decreasing the free energy landscape for unmodified 5S by 1.2 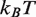 in the dyad region fits the experimental measurements for these modifications (circles, Figure 2E).
in the dyad region fits the experimental measurements for these modifications (circles, Figure 2E).
Histone acetylation in the DNA entry–exit region of the nucleosome, H3(K56ac), reduces the free energy of the nucleosome binding to DNA (24) and increases DNA unwrapping (25). From this increase in unwrapping, we estimate that H3(K56ac) reduces the binding free energy by 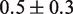
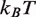 (25). This modification occurs within newly replicated DNA and appears important for DNA repair (6). Furthermore, the acetyllysine mimic at this location, H3(K56Q), enhances the rate of nucleosome disassembly by hMSH2-hMSH6 (10). We incorporated H3(K56Q) into our model by reducing the energy landscape by 0.5
(25). This modification occurs within newly replicated DNA and appears important for DNA repair (6). Furthermore, the acetyllysine mimic at this location, H3(K56Q), enhances the rate of nucleosome disassembly by hMSH2-hMSH6 (10). We incorporated H3(K56Q) into our model by reducing the energy landscape by 0.5 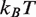 in the entry–exit region compared to the unmodified 5S landscape (dashed line, Figure 2C). This results in an excellent fit to the hMSH2-hMSH6 displacement data for H3(K56Q) (triangles, Figure 2E).
in the entry–exit region compared to the unmodified 5S landscape (dashed line, Figure 2C). This results in an excellent fit to the hMSH2-hMSH6 displacement data for H3(K56Q) (triangles, Figure 2E).
Finally, using the energy landscapes described above, we reproduce the disassembly rates without a mismatch for H3(T118ph) (inverted triangles, Figure 2D) and H3(K115ac,K122ac) 5S nucleosomes (inverted triangles, Figure 2E). We use the same hMSH2-hMSH6 binding conditions used to describe unmodified nucleosomes with no mismatch on 601, i.e. without fitting any other parameters. As before, measurements without mismatches were modeled by allowing hMSH2-hMSH6 to bind at any position within the DNA.
DISCUSSION
To our knowledge, we propose the first detailed quantitative free energy landscape for unwrapping DNA from a histone octamer. We develop this landscape from high resolution nucleosomal DNA unzipping experiments (7). We then demonstrate that this landscape accounts for the different hMSH2-hMSH6 induced nucleosome disassembly rates for two separate DNA sequences and four separate histone modification states. All parameters are held constant except for the free energy landscape. To model modifications and DNA sequence differences we only introduce modest landscape alterations located in the regions of the landscape associated with the modification or sequence difference. The magnitudes of these alterations are consistent (Table 1) with changes in DNA–histone binding free energies known from experiments (11,12,15,25). These results demonstrate that the nucleosome unwrapping free energy landscape provides an important tool for understanding enzyme provoked nucleosome disassembly.
Table 1.
Binding energy for modified nucleosomes relative to wild-type nucleosomes
| Sequence | Modification |
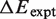 a a
|
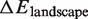 b b
|
|---|---|---|---|
 |
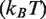 |
||
| 601 | H3(T118ph) | 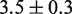 |
3.8 |
| 5S | H3(K56Q) | 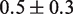 |
0.5 |
| 5S | H3(K115ac,K122ac) |  |
1.2 |
aExperimentally measured binding energies [11,12,25].
bBinding energies determined from our free energy landscapes.
The model's success in explaining numerous experimental results indicates that it captures the essential components of nucleosome disassembly by hMSH2-hMSH6 and that we can use the model to provide mechanistic insight into this disassembly process. The observation that multiple hMSH2-hMSH6 clamps loaded onto DNA behave as a 1D gas, also known as a Tonks gas (14), provides a mechanistic picture of hMSH2-hMSH6 induced nucleosome disassembly. The hMSH2-hMSH6 Tonks gas exerts a 1D pressure on the nucleosome (Supplementary Figure S4). The pressure builds as additional hMSH2-hMSH6 complexes load onto the DNA, which shifts the equilibrium amount of DNA wrapped into the nucleosome toward more unwrapped states. This enables the nucleosome to eventually reach an unwrapped state that allows for histone octamer disassociation.
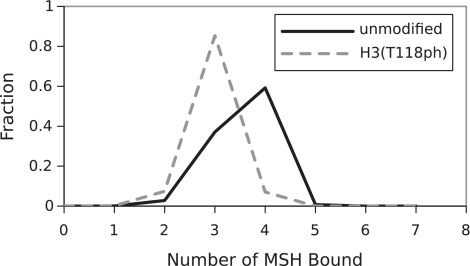
The number of hMSH2-hMSH6 clamps required to disassemble the nucleosome is three to four (Figure 3 and Supplementary Figure S5). However, this number of clamps is not sufficient to trap DNA unwrapping states out to the dyad. Instead, the plateau in the free energy landscape around 50 bp allows clamps to trap states with about 50 bp of unwrapped DNA often enough that an unwrapping fluctuation to the dyad occurs before the outermost clamp slides away from the nucleosome (Supplementary Figure S6).
Figure 3.
Distribution of the number of bound hMSH2-hMSH6 complexes needed to displace nucleosomes from the 601 positioning sequence. The solid line shows the result for unmodified nucleosomes, and the dashed line for the dyad modification H3(T118ph).
The model indicates that the mechanism by which dyad modifications, H3(T118ph) and H3(K115ac,K122ac) influence nucleosome disassembly is distinct from the DNA entry–exit modification mimic, H3(K56Q). None of the modifications influence the distance the outermost hMSH2-hMSH6 clamp invades into the nucleosome. The dyad modifications increase the probability for an unwrapping fluctuation that allows for histone octamer release when the outermost hMSH2-hMSh6 clamp has trapped about 50 bp of DNA (Supplementary Figure S6). In contrast, H3(K56Q) increases the probability that hMSH2-hMSH6 has trapped an unwrapping fluctuation of about 50 bp. This increases the time period the nucleosome exists in a partially unwrapped state and in turn the probability that the nucleosome will unwrap to the dyad and release the histone octamer. These mechanistic insights elucidate how fractional changes in the nucleosome unwrapping free energy landscape result in order of magnitude changes in the rate of disassembly.
The time for nucleosome disassembly varies from about 40 min to 16 h. Yet, all the processes involved with disassembly, including nucleosome unwrapping, hMSH2-hMSH6 sliding, and hMSH2-hMSH6 binding, are significantly faster. Our model explains this apparent discrepancy. The first and second hMSH2-hMSH6 clamps load on the scale of minutes. However, to load a third clamp, both loaded hMSH2-hMSH6 clamps must simultaneously move toward the nucleosome to provide enough space for the third hMSH2-hMSH6 clamp. This is strongly disfavored by entropy. Loading even larger numbers of hMSH2-hMSH6 clamps requires the coordination of nucleosome unwrapping with simultaneous sliding of multiple clamps, which is further disfavored by entropy. As a consequence, the number of hMSH2-hMSH6 clamps required for disassembly is three to four and the rates for loading the fourth clamp are similar to the rates for nucleosome displacement (Supplementary Figure S7). We conclude that the binding of multiple hMSH2-hMSH6 clamps is the rate-limiting step in nucleosome displacement.
Our model not only quantitatively explains recent experiments by Javaid et al. (10) and North et al. (11), but also explains the apparently contradictory studies that report nucleosomes are a barrier to hMSH2-hMSH6 sliding (23,28). The studies by Li et al. (23) observed no nucleosome disassembly by hMSH2-hMSH6. While their construct was similar to studies by Javaid et al. and North et al., Li et al. only used the 601 positioning sequence and unmodified histone octamers. As discussed above, we find that the 601 sequence largely prevents disassembly by hMSH2-hMSH6 with unmodified histone octamer, which was confirmed by North et al. (11). Gorman et al. (28) reported that nucleosomes create a boundary to yeast MSH2-MSH6 diffusion. Their experiments involve single molecule tracking of quantum dot labeled MSH2-MSH6 clamps on lambda DNA that contains nucleosomes but no mismatch. They track MSH2-MSH6 along the DNA after washing out free MSH2-MSH6. Because there is no mismatch and no additional MSH2-MSH6 to load onto the DNA, multiple MSH2-MSH6 clamps cannot be loaded onto the DNA between two nucleosomes. Thus, under the experimental conditions used by Gorman et al., the pressure of the 1D gas cannot reach the values required to disassemble a nucleosome and the nucleosome becomes a barrier to the sliding of a single MSH2-MSH6 clamp as they report.
The successful application of our nucleosome unwrapping free energy landscape indicates that it will prove useful for modeling a wide variety of experiments involving nucleosome unwrapping, and many different interactions between DNA binding proteins and nucleosomes in vivo. In particular, when a protein does not interact specifically with either the DNA or the nucleosome, as is the case with hMSH2-hMSH6, our free energy landscape completely describes the dynamics of the system. Even when this is not the case, the landscape should prove an invaluable tool. The model will facilitate the separation of the DNA–histone binding from additional interactions. This in turn will allow for determination of interactions between the nucleosome and other protein complexes, such as chromatin remodelers that disassemble, reposition and unwrap nucleosomes.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
National Science Foundation (under grant No. DMR-0706002 to R.B.); Burroughs Wellcome Career Award in the Basic Biomedical Sciences (to M.G.P.); the NIH GM083055 (to M.G.P.); the NIH CA067007 and GM080176 (to R.F.), and an American Heart Association Predoctoral Fellowship 0815460D (to J.A.N.). Funding for open access charge: National Science Foundation (grant No. DMR-0706002 to R.B.).
Conflict of interest statement. None declared.
Supplementary Material
REFERENCES
- 1.Van Holde K. Chromatin. Amsterdam, The Netherlands: Elsevier; 1989. [Google Scholar]
- 2.Luger K, Maeder AW, Richmond RK, Sargent DF, Richmond TJ. Crystal structure of the nucleosome core particle at 2.8 Å resolution. Nature. 1997;389:251. doi: 10.1038/38444. [DOI] [PubMed] [Google Scholar]
- 3.Polach KJ, Widom J. Mechanism of protein access to specific DNA sequences in chromatin: a dynamic equilibrium model for gene regulation. J. Mol. Biol. 1995;254:130–149. doi: 10.1006/jmbi.1995.0606. [DOI] [PubMed] [Google Scholar]
- 4.Thåström A, Bingham LM, Widom J. Nucleosomal locations of dominant DNA sequence motifs for histone–DNA interactions and nucleosome positioning. J. Mol. Biol. 2004;338:695–709. doi: 10.1016/j.jmb.2004.03.032. [DOI] [PubMed] [Google Scholar]
- 5.Anderson JD, Widom J. Sequence and position-dependence of the equilibrium accessibility of nucleosomal DNA target sites. J. Mol. Biol. 2000;296:979–987. doi: 10.1006/jmbi.2000.3531. [DOI] [PubMed] [Google Scholar]
- 6.Ransom M, Dennehey B, Tyler J. Chaperoning histones during DNA replication and repair. Cell. 2010;140:183–195. doi: 10.1016/j.cell.2010.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hall MA, Shundrovsky A, Bai L, Fulbright RM, Lis JT, Wang MD. High-resolution dynamic mapping of histone-DNA interactions in a nucleosome. Nat. Struct. Mol. Biol. 2009;16:124–129. doi: 10.1038/nsmb.1526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gradia S, Acharya S, Fishel R. The human mismatch recognition complex hMSH2-hMSH6 functions as a novel molecular switch. Cell. 1997;91:995–1005. doi: 10.1016/s0092-8674(00)80490-0. [DOI] [PubMed] [Google Scholar]
- 9.Gradia S, Subramanian D, Wilson T, Acharya S, Makhov A, Griffith J, Fishel R. hMSH2–hMSH6 forms a hydrolysis-independent sliding clamp on mismatched DNA. Mol. Cell. 1999;3:255–261. doi: 10.1016/s1097-2765(00)80316-0. [DOI] [PubMed] [Google Scholar]
- 10.Javaid S, Manohar M, Punja N, Mooney A, Ottesen JJ, Poirier MG, Fishel R. Nucleosome remodeling by hMSH2-hMSH6. Mol. Cell. 2009;36:1086–1094. doi: 10.1016/j.molcel.2009.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.North JA, Javaid S, Ferdinand M, Chatterjee N, Picking JW, Shoffner M, Nakkula RJ, Bartholomew B, Ottesen JJ, Fishel R, et al. Phophorylation of histone H3(T118) alters nucleosome dynamics and remodeling. Nucleic Acids Res. 2011 doi: 10.1093/nar/gkr304. doi:10.1093/nar/gkr304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Manohar M, Mooney AM, North JA, Nakkula RJ, Picking JW, Edon A, Fishel R, Poirier MG, Ottesen JJ. Acetylation of histone H3 at the nucleosome dyad alters DNA-histone binding. J. Biol. Chem. 2009;284:23312–23321. doi: 10.1074/jbc.M109.003202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Eaton JW. GNU Octave Manual, Network Theory Limited, UK. 2002. [Google Scholar]
- 14.Tonks L. The complete equation of state of one, two and three-dimensional gases of hard elastic spheres. Phys. Rev. 1936;50:955–963. [Google Scholar]
- 15.Lowary PT, Widom J. New DNA sequence rules for high affinity binding to histone octamer and sequence-directed nucleosome positioning. J. Mol. Biol. 1998;276:19–42. doi: 10.1006/jmbi.1997.1494. [DOI] [PubMed] [Google Scholar]
- 16.Habib F, Bundschuh R. Modeling DNA unzipping in the presence of bound proteins. Phys. Rev. E. 2005;72:031906. doi: 10.1103/PhysRevE.72.031906. [DOI] [PubMed] [Google Scholar]
- 17.Ranjith P, Yan J, Marko JF. Nucleosome hopping and sliding kinetics determined from dynamics of single chromatin fibers in Xenopus egg extracts. Proc. Natl. Acad. Sci. USA. 2007;104:13649–13654. doi: 10.1073/pnas.0701459104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shundrovsky A, Smith CL, Lis JT, Peterson CL, Wang MD. Probing SWI/SNF remodeling of the nucleosome by unzipping single DNA molecules. Nat Struct Mol Biol. 2006;13:549–54. doi: 10.1038/nsmb1102. [DOI] [PubMed] [Google Scholar]
- 19.Fishel R. Mismatch repair, molecular switches, and signal transduction. Gene. Dev. 1998;12:2096–2101. doi: 10.1101/gad.12.14.2096. [DOI] [PubMed] [Google Scholar]
- 20.Li G, Widom J. Nucleosomes facilitate their own invasion. Nat. Struct. Mol. Biol. 2004;11:763–9. doi: 10.1038/nsmb801. [DOI] [PubMed] [Google Scholar]
- 21.Jeong C, Cho W-K, Song K-M, Cook C, Yoon T-Y, Ban C, Fishel R, Lee J-B. MutS switches between two fundamentally distinct clamps during mismatch repair. Nat. Struct. Mol. Biol. 2011;18:379–385. doi: 10.1038/nsmb.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gradia S, Acharya S, Fishel R. The role of mismatched nucleotides in activating the hMSH2-hMSH6 molecular switch. J. Biol. Chem. 2000;275:3922–3930. doi: 10.1074/jbc.275.6.3922. [DOI] [PubMed] [Google Scholar]
- 23.Li F, Tian L, Gu L, Li G-M. Evidence that nucleosomes inhibit mismatch repair in eukaryotic cells. J. Biol. Chem. 2009;284:33056–33061. doi: 10.1074/jbc.M109.049874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Andrews AJ, Chen X, Zevin A, Stargell LA, Luger K. The histone chaperone Nap1 promotes nucleosome assembly by eliminating nonnucleosomal histone DNA interactions. Mol. Cell. 2010;37:834–842. doi: 10.1016/j.molcel.2010.01.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Neumann H, Hancock SM, Buning R, Routh A, Chapman L, Somers J, Owen-Hughes T, van Noort J, Rhodes D, Chin JW. A method for genetically installing site-specific acetylation in recombinant histones defines the effects of H3 K56 acetylation. Mol. Cell. 2009;36:153–163. doi: 10.1016/j.molcel.2009.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhang L, Eugeni E, Parthun M, Freitas M. Identification of novel histone post-translational modifications by peptide mass fingerprinting. Chromosoma. 2003;112:77–86. doi: 10.1007/s00412-003-0244-6. [DOI] [PubMed] [Google Scholar]
- 27.Hyland E, Cosgrove M, Molina H, Wang D, Pandey A, Cottee R, Boeke J. Insights into the role of histone H3 and histone H4 core modifiable residues in Saccharomyces cerevisiae. Mol. Cell. Biol. 2005;25:10060. doi: 10.1128/MCB.25.22.10060-10070.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gorman J, Plys AJ, Visnapuu M-L, Alani E, Greene EC. Visualizing one-dimensional diffusion of eukaryotic DNA repair factors along a chromatin lattice. Nat. Struct. Mol. Biol. 2010;17:932–8. doi: 10.1038/nsmb.1858. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.