Towards computional specificity screening of DNA-binding proteins

Abstract

DNA-binding proteins are key players in the regulation of gene expression and, hence, are essential for cell function. Chimeric proteins composed of DNA-binding domains and DNA modifying domains allow for precise genome manipulation. A key prerequisite is the specific recognition of a particular nucleotide sequence. Here, we quantitatively assess the binding affinity of DNA-binding proteins by molecular dynamics-based alchemical free energy simulations. A computational framework was developed to automatically set up in silico screening assays and estimate free energy differences using two independent procedures, based on equilibrium and non-equlibrium transformation pathways. The influence of simulation times on the accuracy of both procedures is presented. The binding specificity of a zinc-finger transcription factor to several sequences is calculated, and agreement with experimental data is shown. Finally we propose an in silico screening strategy aiming at the derivation of full specificity profiles for DNA-binding proteins.

INTRODUCTION

Specific binding of engineered protein domains to DNA offers exciting novel opportunities for precise genome manipulation (1). The field of applications spans a wide range from correcting inherited gene defects (2) over genetic engineering of plants (3) to synthetic biology. Chimeric proteins consisting of DNA-binding domains and DNA-modifying domains represent a novel class of high precision tools to target specific locations in a genome (4). Among these proteins, artificial zinc-finger nucleases (ZFNs) (5–8) are particularly promising. ZFNs consist of several DNA-binding domains (‘zinc-fingers’), ~30-residue domains with a ββα-fold that is stabilized by a zinc ion, often coordinated by two cysteine and two histidine residues, and an unspecific nuclease domain that induces a double-strand break in the DNA. Such double-strand breaks at specific spots in the DNA allow for precise genome editing via homologous recombination.

However, a key prerequisite for the successful application is the specific recognition of a particular DNA sequence. A zinc-finger domain recognizes a 3–4 bp site in a DNA double strand. ZFNs usually contain three or four zinc-finger domains, and, since the nuclease domain is only active as a dimer, their six to eight ZF domains target a recognition site of 18–24 bp length which, in the case of perfect specificity, is sufficient to target a single location in the entire human genome (9). If the DNA recognition domains also bind to other sites on the DNA, double-strand breaks would be induced at undesired locations, leading to severe cell toxicity. Thus, optimizing the specificity of zinc fingers is essential and a field of active research. Structures of zinc-finger DNA complexes (10) suggest that each zinc-finger domain specifically recognizes a base pair triplet and that arbitrary DNA sequences may be targeted by modular assembly of the appropriate zinc-finger module (11–13). However, this appealing concept has been recently challenged by a large scale assessment of artificial ZFNs (14). It was shown that only a small fraction (~6%) of ZFNs specifically cleave at the target site they are designed for, suggesting that either the assumption of modularity lacks generality or that individual zinc-finger domains do not show sufficient affinity and specificity to their target site.

Since experimental protein design, e.g. by directed evolution, is a very laborious task, computational methods that can reliably predict the specificity of a zinc finger for a particular DNA sequence are highly desired. Substantial progress has been made in the field of structure-based prediction of protein/DNA binding specifity (15–20); but since the relevant free energy differences are often only a few kilojoules per mole, the sufficiently accurate calculation of binding affinities as a function of the DNA sequence is still a considerable challenge.

Previously we showed that molecular dynamics-based free energy calculations can yield quantitative agreement with experimental data for thermodynamic stability changes resulting from point mutations in proteins (21). Here, employing the state-of-the-art alchemical free energy calculation techniques, we extend the method to compute thermodynamic properties for protein–DNA complexes. While considerable progress has been made in structure-based screening for DNA–protein interaction sites on the basis of simplified molecular mechanical approaches (22–24), we here apply rigorous methods to target the best quantitative accuracy attainable.

Since the in silico mutation of a DNA base pair represents a substantially larger perturbation as compared to a point mutation in a protein chain, we first evaluated different simulation protocols on a test system. In particular, we assessed the performance of methods based both on equilibrium and non-equilibrium sampling of alchemical transformation pathways. The use of fundamentally different approaches to sampling allows us to assess the relative strengths and weaknesses of each, while providing an internal consistency check with respect to sampling errors.

We applied both methods to calculate binding affinity differences between the zinc-finger transcription factor Zif268 and its recognition sequence GCGTGGGCG, and single base pair variants of this sequence. Free energy differences for all single mutations at eight positions have been calculated, and for those where precise measurements are available we obtained agreement with experiment. Based on the screening of the single mutants we propose a screening strategy that focuses on the essential mutations and show that from the vast number of possible sequences for a given recognition site only a small fraction needs to be explicitly calculated to obtain a complete specificity profile of a transcription factor.

METHODS

Equilibrium and non-equilibrium methods

In perturbation-based molecular dynamics free energy calculations, the Hamiltonians of two different states (e.g. the wild-type and the mutant) are coupled via a parameter λ. A transformation pathway between end states (λ = 0 and λ = 1) can be constructed to link the states of interest, and the free energy difference along this pathway can be calculated by any of a number of different methods (25).

In this work, we applied two fundamentally different approaches to sampling and free energy estimation along the transformation pathway. In the first, the transformation between end states was conducted by means of a continuously varying coupling parameter, using the Crooks–Gaussian intersection (CGI) method (26) to calculate free energy differences with rigorous treatment of the non-equilibrium effects that result from driving the system between the two states. In the second approach, a discrete number of intermediate points were chosen along each transformation pathway and held fixed over the course of the sampling period, assuming that sampling of each intermediate occurs sufficiently close to equilibrium; free energy differences between intermediate states were then calculated using Bennett's Acceptance Ratio method (BAR) (27).

CGI free energy calculations

The free energy difference between states at λ = 0 and λ = 1 can be accessed as follows (28):

This relationship formally allows the calculation of free energy differences from a transformation with continuously varying λ, but is based on the assumption that sampling occurs at equilibrium. In practice, changing the coupling parameter performs irreversible work and drives the system away from equilibrium, so that a formally correct result is only approached in the limit of an infinitely slow transformation. Based on the work of Jarzynski (29,30) and Crooks (31), alternative ‘fast-growth’ methods have been developed to calculate equilibrium free energy differences from non-equilibrium simulations (26,32). Here, we used the CGI method (26), in which multiple configurations from equilibrated ensembles at λ = 0 and λ = 1 are used as starting structures for subsequent independent simulations in which λ is switched from 0 to 1, and from 1 to 0, respectively. The distribution of work values calculated for each trajectory is then used to calculate ΔG as described in Goette and Grubmüller (26).

Replica Exchange/BAR free energy calculations

Free energy differences between two end states may also be calculated as a sum over a number of discrete intermediate stages, chosen to form a chain of overlapping ensembles that yield a tractable transformation pathway between end states. The value of λ is held fixed at each intermediate stage, such that the underlying assumption that each sample is representative of the respective ensemble at equilibrium is less problematic.

Here, we applied the multistate BAR (MBAR) (33) method for the estimation of free energy differences. We make use of Hamiltonian replica exchange (34,35) between intermediate states with the goal of enhancing sampling across barriers along the transformation pathway. We apply the Linear Soft Core potential we recently described, and the placement of intermediate states of the transformation made use of a systematic ensemble overlap-based technique described in the same report (36). The combined protocol will be referred to as Replica Exchange/MBAR (RE/MBAR).

Automated simulation setup

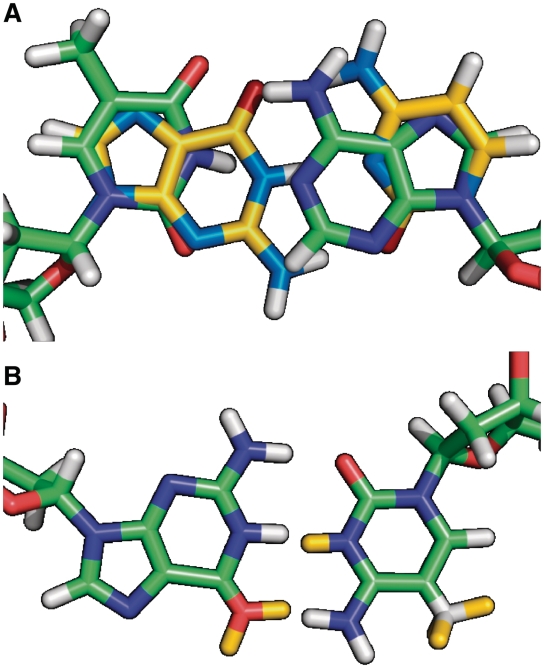
All simulations were carried out with the Gromacs molecular dynamics package (38–39) (version 4.0.7). Similar to our approach described for amino acid mutations (21) hybrid residues were construted for all possible DNA base pair mutations. Here, each hybrid residue consists of all necessary atoms to represent two different nucleotides as a function of λ. For mutations of nucleotides sharing the same heterocycle, hybrid residues were constructed so as to minimize the number of required dummy atoms (atoms that do not have non-bonded interactions at λ = 0). For mutations involving a change from a purine to a pyrimidine base, the hybrid residues were defined to contain a complete copy of both rings while sharing only the sugar and phosphate entities (Figure 1). Because the latter case may lead to unwanted rotation of the two ring copies with respect to each other, this motion was suppressed by imposing an improper dihedral that keeps the non-interacting dummy ring in the plane of the interacting ring.

Figure 1.

Nucleotide hybrid residues. (A) Definition of the hybrid residues for the mutation of thymine into guanine and adenine into cytosine. A complete copy of each heterocycle is used for the purine→pyrimidine transition. (B) Hybrid residues for the mutation of guanine into adenine and cytosine into thymine. In this case, the heterocycles are shared and only dummy atoms for the second state are added (yellow).

Simulation System I—DNA test system

To separate possible force field inaccuracies from convergence issues, we first studied a test system where, according to the thermodynamic cycle, ΔG must be 0. This test system also served to assess the accuracy of each approach as a function of simulation time.

All simulations were started from a modelled DNA double strand with idealized geometry. The DNA double strand was solvated in a dodecahedron water box with 9513 tip3p water molecules (39) and NaCl was added at a 150 mM concentration. The resulting simulation system was equilibrated at 298 K for 5 ns. Sampling was conducted at 298 K using a leap-frog stochastic dynamics integrator, with pressure kept at 1 atm using the Parrinello–Rahman barostat (40). Electrostatic interactions were calculated at every step with the particle-mesh Ewald method (41), short-range repulsive and attractive dispersion interactions were described by a Lennard-Jones potential with a cut-off of 1.1 nm, and a switching function was used between 1.0 and 1.1 nm. Dispersion correction for energy and pressure was applied. The SETTLE (42) algorithm was used to constrain bonds and angles of water molecules, and LINCS (43) was used for all other bonds, allowing a time step of 2 fs.

For the CGI protocol, the system was initially equilibrated at 298 K for 5 ns, after which simulation systems for all 12 possible base pair mutations were constructed. Both the A and the B states were sampled at 298 K for 80 ns using a leap frog stochastic dynamics integrator.

For the RE/MBAR protocol, the system was branched into 16 replicates, each destined to represent an intermediate state in the alchemical transformation. Ion positions were randomized for each replicate and 10 ns of equilibration was performed for each of the replicates. The resulting set of 16 equilibrated configurations was used to construct starting configurations for each of the 12 mutations. Based on an initial 100 ps sample, ensemble reweighting (36) was used to determine for each mutation a spacing of λ values yielding an approximately equal degree of phase space overlap between neighbouring ensembles; using 16 intermediates, average replica exchange acceptance probabilities were no less than 0.2 for any pair of neighbouring ensembles.

Simulation System II—Zif268 transcription factor

The thermodynamic cycle depicted in Figure 3 was used for the calculation of DNA-protein binding specificity. Simulations were started from the X-ray structure of Zif268 bound to DNA [PDB entry 1AAY (44)]. The protein–DNA complex was solvated in a dodecahedron water box with 14 366 tip3p water molecules and KCl was added at a 100 mM concentration to mimic the conditions described in Hamilton et al. (45). For the simulation system of DNA in solution a smaller simulation box with 6145 water molecules was used. Simulation details were the same as for the model DNA system.

Figure 3.

Thermodynamic cycle for binding affinity calculations. The difference in the binding affinity between the transcription factor and two different DNA sequences is given by ΔΔG_bind = ΔG3−ΔG4. According to the thermodynamic cycle ΔΔG_bind can also be calculated via the alchemical pathway ΔG1−ΔG2.

CGI calculations

For the calculation of free energy differences between two states we used a non-equilibrium fast-growth thermodynamic integration (FGTI) protocol and the CGI method. For the CGI method, non-equilibrium fast-growth simulations were conducted. Equilibrated A- and B-state ensembles were generated with 80 ns simulations of each. Snapshots taken from the A- and B-state ensembles were used to start short simulations in which λ was changed from 0 to 1 and from 1 to 0, respectively. A double-precision version of Gromacs 4.0 with a leap frog integrator and a velocity-rescaling thermostat (46) was used. Time step and pressure coupling were as described above for the equilibration runs. To account for atomic overlaps occurring close to λ = 0 and λ = 1, soft-core potentials were used for both electrostatics and Lennard-Jones interactions as implemented in Gromacs 4.0 (38) with α = 0.3, σ = 0.25 and a soft-core power of 1. For the model DNA system switching times of 50, 100 and 200 ps were used and compared. For the zinc-finger system, 100 ps switching times were used. For three DNA/protein simulations (C8A, C8G, and C8T) the switching time was increased to 200 ps since the work histograms of the 100 ps switches produced particularly poor overlap. For these cases only half of the fast-growth simulations were carried out as compared to the other cases such that the overall computational effort was the same.

The derivative of the Hamiltonian with respect to λ was recorded at every step, and free energy differences were calculated as described in Goette and Grubmüller (26).

RE/MBAR calculations

Data for each mutation was collected over 16 intermediate states, each describing a point in the transformation from initial to final states. Time step, pressure and temperature coupling were as described above for for the CGI protocol. Replica exchanges were attempted every 200 steps, alternately between even- and odd-indexed pairs of neighbouring states. Parameters for the Linear Soft Core potential and the application of ensemble reweighting for the positioning of intermediate simulations along the transformation pathway was as stated for Simulation System I. Free energy differences were estimated using the MBAR method (33).

RESULTS

CGI switching times

We first investigate how the accuracy of the free-energy calculations depends on different simulation parameters. When comparing results from simulations with experimental data deviations may arise from different sources such as shortcomings of the force field and water model as well as inaccuracies in the experiment itself. To exclude these influences and systematically evaluate the accuracy with respect to different sampling and switching times, we use a model DNA system of the sequence CGCGACGTCGCG and its complementary strand. Such a model system allows for testing of all possible base pair mutations and the construction of thermodynamic cycles which by definition yield 0 (Figure 2). Hence, the accuracy of the calculations with respect to the computational effort can be precisely determined.

Figure 2.

Thermodynamic cycle. Two different base pair mutations are calculated, which result in the same state B. Therefore, ΔG3 and ΔG4 are by definition 0 and ΔG1−ΔG2 must be 0 as well.

The application of the Crooks Theorem requires the two ensembles of which the starting configurations for the fast-growth simulations are derived to represent converged Boltzmann ensembles. The error arising from insufficient sampling in a trajectory of a given length therefore depends on the conformational dynamics of the particular system of interest. Since the work calculated from a single trajectory depends on the starting configuration an estimate of the convergence behaviour can be obtained by analysing the evolution of work values as a function of simulation time (Figure 4). A distinct drift here indicates that the system does not sample from an equilibrated ensemble and longer simulation times are required.

Figure 4.

Distribution of work over time for an alchemical C→T:G→A base pair mutations. In the left plot, the work values obtained from integration of δH_λ/δλ are shown as a function of the sampling time of the equilibrium states. Since the work values depend on the initial configurations, these curves indicate conformational dynamics on the nanosecond timescale, which requires long sampling times to obtain a reasonable approximation of a converged ensemble. The right plot shows the histograms of work values from which the free energy is calculated.

The CGI method computes free energy differences from the histograms of work values obtained from fast-growth thermodynamic integration simulations and the statistical uncertainty of this estimation depends on the number of work values and the overlap of the two histograms. This overlap depends on the dissipative work performed on the system and, hence, on the magnitude of the perturbation and the switching time (in the limit of infinitely slow switching two identical histograms should be obtained). For the case of point mutations in proteins, we found that 100 work values obtained from 50-ps long switching trajectories yield statistical errors in the order of ≤1 kJ/mol which represents a reasonable range. For base pair exchanges in a DNA double strand, however, the perturbation is larger since two residues are mutated at once. From initial simulations of the model system we found that 50 ps switches produce hardly any overlap between the histograms (Supplementary Figure S3), whereas for 100 ps switching time we found statistical errors in the range of 1 kJ/mol. For switching times of 200 ps the histogram overlap increases further, but as we found that the systematic errors arising from insufficient sampling are far more severe, the additional computational cost is better spent in sampling of the equilibrium states.

Replica exchange and sampling efficiency

For CGI and other non-equilibrium methods, there is a straightforward trade-off between the amount of time spent simulating just two equilibrium ensembles (initial and final) and the time spent on fast growth simulations. The CGI protocol therefore lends itself readily to the incorporation of relatively long (80 ns) equilibration stages. In contrast, equilibrium-based measurements are based on a larger number of shorter (7.5 ns) simulations of intermediate states along the transformation pathway. Although the total MD time simulated (in parallel) is the same, the conformational ensemble explored by each individual intermediate simulation is drawn from a shorter ‘linear’ time.

To counter the possibility of poorer sampling of slowly equilibrating degrees of freedom, we employ Hamiltonian replica exchange (34,35) to enhance sampling across the full set of equilibrium ensembles. If the intermediate simulations are initiated with a set of configurations representative of a Boltzmann-weighted ensemble, across which relevant slow degrees of freedom are satisfactorily sampled, replica exchange should act to enhance sampling ergodicity without requiring impractically long simulations for each intermediate.

DNA model system

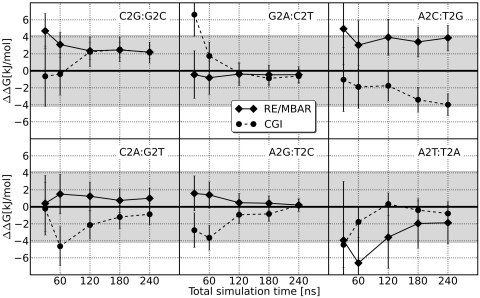
According to the thermodynamic cycle in Figure 2 the difference of the free energies of 2 bp mutations in the DNA model system is by definition 0. Figure 5 shows the difference in ΔG for the pair-wise mutations as a function of the total simulation time. For both the CGI and RE/MBAR methods, a total of 240 ns were simulated for each mutation. For CGI, this was composed of 80 ns each for the initial and final states, and 80 ns in total for the FGTI runs. For RE/MBAR, the 240 ns were divided evenly over the 16 intermediate states, corresponding to 15 ns simulations for each.

Figure 5.

Accuracy of free energy calculations depending on simulation time. Each double mutant should result in a free energy difference of 0. The grey shaded area marks a deviation of 1 kcal/mol. In most cases, longer simulation time leads to increased accuracy.

As can be seen from Figures 5 and 6 the accuracy depends on the total simulation time. As the total simulation time is extended from 30 ns to 240 ns, the root mean squared deviation from zero for the six mutant pairs decreases from 3.5 to 1.9 kJ/mol with the CGI method, and from 3.3 to 2.0 kJ/mol with RE/MBAR. The calculation for the result with the largest deviation from zero, A2C:T2G, was repeated, and after 240 ns resulted in values of 1.6 ± 1.5 and 0.5 ± 1.7 kJ/mol for CGI and RE/MBAR, respectively.

Figure 6.

Root mean squared deviation from zero. The root mean squared deviation from the ‘true’ value decreases with increasing computational effort.

Transcription factor Zif268 DNA-binding affinities

The results for the calculated DNA-binding affinities of the transcription factor Zif268 are shown in Figure 7.

Figure 7.

Experimental and calculated binding affinity differences for Zif268-DNA. Bars representing experimental values with lighter and darker shades indicate that the binding affinity decreases by at least 13.2 kJ/mol but exact binding affinities could not be determined.

The data set contains 14 DNA sequences (single mutants of the recognition sequence GCGTGGGCG) for which experimental binding affinity differences have been determined. For half of the mutations, the binding affinity could not be determined quantitatively but decreases by at least 13.2 kJ/mol.

Qualitatively, computational estimates from both methods studied agreed well with the experimental data. The measurements in question concern mutations disrupting an optimal DNA consensus sequence (45), and as such all 14 were shown experimentally to result in weaker binding. Both computational methods clearly reproduced this core finding, with 12 of 14 estimates unequivocally indicating weaker binding. For the remaining two cases, the computational estimates were consistent both with marginally strengthened and marginally weakened binding; these mutations, C2T and T4G, were also the least disruptive of the experimentally measured mutations.

Similarly, the seven mutations found to be strongly disruptive to binding ( 13.2 kJ/mol) were for the most part correctly identified, with five identified by the CGI protocol and six by the RE/MBAR protocol. Only one of the seven (T4C) was identified by neither protocol.

For the remaining mutations, the CGI estimates show excellent quantitative agreement, with an average absolute/root mean squared deviation of 1.29 and 1.38 kJ/mol, respectively. The RE/MBAR estimates show an average absolute and root mean squared deviations from experimental values of 5.40 and 6.24 kJ/mol.

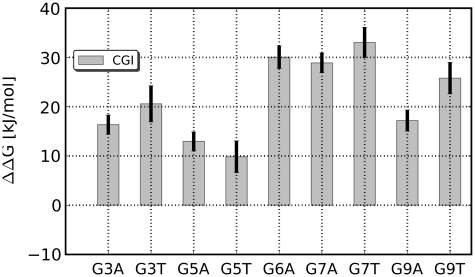
In addition to the mutations for which experimental data are available we calculated binding affinity differences for the remaining mutations at positions 3, 5, 6, 7 and 9 (Figure 8), using the CGI protocol. For all of these mutations, a strong decline of the binding affinity of >10 kJ/mol is predicted.

Figure 8.

Calculated binding affinity differences for the remaining single mutants. For all 10 mutants the computational approach predicts a decline of the binding affinity of >10 kJ/mol.

DISCUSSION

Free energy calculations of DNA mutants

In the present work, we systematically investigate the applicability of two free energy calculation methods, which represent significantly different approaches with respect to sampling of phase space, to quantitatively assess the thermodynamic consequences of base pair exchanges in DNA. We developed an automated protocol to set up simulation systems for all possible DNA mutations where a DNA base is transformed into another as a function of the coupling parameter λ. Using a test system of a 12-bp DNA double strand we assessed the accuracy of the method with respect to the sampling time and different switching times.

Our results from the CGI protocol indicate that a major source of error is insufficient sampling of the equilibrium states from which individual snapshots for the FGTI runs are taken, with long correlation times arising from slowly relaxing degrees of freedom apparent from the distribution of work values as a function of equilibration time (Supplementary Figure S3). (It should be noted that the slowly relaxing degrees of freedom that influence the convergence of free energy calculations are not necessarily related to functionally relevant collective protein motions on long time scales.) Although the number of FGTI runs, and hence the number of work values from which the free energy difference between two states are calculated, affect the statistical error, this aspect is less critical than the ‘quality’ of the equilibrium ensembles. For a given total computation time we, therefore, recommend spending at least two-thirds for the sampling of the equilibriums states. Furthermore, we found that in contrast to amino acid point mutations, DNA base pair mutations represent a larger perturbation which results in broad work distributions and poor histogram overlaps when using the same switching time of 50 ps. From our findings, we suggest a switching time of 100 ps as a lower bound for base pair mutations.

Analysis of the RE/MBAR method similarly emphasizes the importance of slowly relaxing degrees of freedom. Short of simply extending equilibration simulations in the protocol, we suggest that seeding the set of intermediate states with a set of structures representative of a Boltzmann-weighted ensemble, as opposed to simply branching a single input structure, can be advantageously combined with Hamiltonian replica exchange to facilitate the sampling of slow degrees of freedom. With this in mind, starting structures (of the DNA–protein complex and DNA in solution) were equilibrated for 10 ns each following branching from the initial input structure, with ion positions randomized to minimize one possible source of long correlation times (47).

Calculation of relative binding affinities

The results obtained for the relative binding affinities of Zif268 to different DNA sequences are in favourable agreement with experimental data. The correlation coefficient calculated from the seven data points where quantitative experimental data are available is 0.96 for the CGI protocol and 0.85 for RE/MBAR. Moreover, both the CGI and RE/MBAR protocols produced qualitatively correct results, correctly assessing that none of the mutations considered leads to stronger binding, and successfully identifying the majority of the mutations that strongly inhibit binding. From the computational aspect, these strongly disruptive mutations represent the more challenging cases. Since we start all simulations from one X-ray structure of a tight binding complex, the simulations at λ = 1 (the Hamiltonian of the mutant) never start from an equilibrium configuration. For mutants that cause a moderate change of the binding affinity one may assume that the structural differences are minor and ensembles sufficiently close to the respective equilibrium ensembles can be accessed by simulation on a multi-nanosecond time scale. However, for sequences with significantly lower binding affinity to the transcription factor this is not necessarily the case. In fact, we do not know whether these DNA sequences bind the transcription factor at all. In light of these obstacles the predictive power of the method is quite encouraging.

From a quantitative perspective, the CGI protocol achieved estimates deviating by <2.0 kJ/mol from the experimental value for all of the seven sequences for which data is available. These results indicate that alchemical free energy calculations represent the most accurate computational method for calculating relative zinc-finger–DNA-binding affinities thus far.

Comparison of equilibrium and non-equilibrium results

We here present free energy differences for a complex system of biological interest, calculated using two complementary and independent techniques. While the CGI protocol in this study yielded results in markedly better agreement with the experimental data available, systematic assessment of the relative performance of equilibrium and non-equilibrium methods was not the intention of this work. Rather, we consider the application of these two orthogonal approaches a rigorous accuracy check and uncertainty estimate with respect to the sampling errors that inevitably accompany any free energy calculation involving macromolecules. Simulations of complex macromolecular systems yield chains of correlated samples that show fluctuations on the nanosecond timescale and beyond (Figure 4). Established methods of estimating sampling errors in free energy calculations (48) are based on the assumption that each data set is composed of statistically independent samples from the underlying ensemble; for macromolecular systems, the presence of degrees of freedom that fluctuate slowly relative to the simulation timescale means that this condition is unlikely to be fully met, and sampling errors are likely to be underestimated. Likewise, no simulation protocol or estimator of free energy differences based on finite sampling can be entirely free of systematic bias. In this context, the comparison of results from two fundamentally different approaches to conformational sampling serves as a more informative internal check than conventional error estimates in isolation.

Towards exhaustive specificity screening of transcription factors

Many transcription factors bind not only to one distinct DNA sequence motif but have several high- and low-affinity target sequences (49), all of them important for their biological function. At first sight a complete quantiative specificity screening for a given transcription factor to all possible DNA sequences of a recognition site of length looks computationally intractable. The total number of sequences for a recognition site of length can be readily calculated according to

In the most simple view, is four for each position and the total number of sequences evaluates to N = 4⁸ = 65536 for an 8-bp site. This is indeed beyond today’s computational capability. However, as we can see from the experimental and calculated data, more than half of the mutations result in a strong reduction of the binding affinity (>10 kJ/mol). If we assume that such a mutation at position i cannot be compensated by a second base pair exchange, it can be regarded as a dead end. Hence, all sequences containing this base pair can be removed from the pool of possible sequences. Screening for such dead-end mutations represents a tractable problem of 8 × 3 mutations for an 8-bp recognition site as demonstrated and, depending on the number of dead-end mutations detected, a complete screening of all remaining relevant sequences may come in reach.

Since the individual free energy calculation approaches used for the present article exhibit different shortcomings in terms of limited sampling, we propose a conservative strategy to assess DNA-binding specificity: if we regard only those mutations as a dead end for which both computational methods predict strongly reduced binding affinity (>10 kJ/mol, which at 298 K represents a 57-fold reduction of the equilibrium binding constant K_D) we can construct a binary matrix of tolerated and dead end mutations for a given transcription factor (Figure 9). As can be seen, dead-end mutations were identified at five out of eight positions reducing the total number of sequences from 65 536 to 64, of which the 24 single mutants have already been calculated. Hence, 40 sequences remain to be screened which already represents a tractable problem. If we now continue evaluating the double mutants we would certainly end up with an additional set of double mutants with strongly decreased binding affinities that again reduces the number of possible sequences. Hence, we propose that from the vast number of possible sequences for an 8 bp recognition site only a small fraction of 40–100 actually need to be screened to obtain an essentially complete specificity profile for a given transcription factor.

Figure 9.

Binary matrix for single mutants of the Zif268 binding DNA sequence. Sequence variants marked by a green check have a minor effect on the binding affinity and are regarded as tolerable. Sequence variants marked by a red cross result in a strong loss of binding affinity and can be removed from the pool of possible sequences. The total number of remaining sequences is given by the product over the number of allowed nucleotides per position.

CONCLUSION

We presented the development of a mutant library for DNA bases based on the amber99sb force field which can be used to carry out alchemical free energy calculations. Two independent free energy calculation protocols, based on equilibrium and non-equilibrium sampling, were implemented and optimised for the calculation of DNA sequence-dependent binding free energy differences in a protein-DNA complex, resulting in estimates of binding free energy in favourable agreement with experimental data. We furthermore proposed a systematic approach for a computational specificity screening for DNA-binding proteins and showed that among the huge number of possible sequences for typical recognition site only a small fraction needs to be calculated explicitly in order to come up with a thorough characterization of the specificity and to predict those sequences with relevant affinity to a given protein.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Deutsche Forschungsgemeinschaft (DFG) (grant No. GR 2079/4-1). Funding for open access charge: Max Planck Society.

Conflict of interest statement. None declared.