IMPROVED PLANNING TIME AND PLAN QUALITY THROUGH MULTICRITERIA OPTIMIZATION FOR INTENSITY-MODULATED RADIOTHERAPY

Abstract

Purpose

To test whether multicriteria optimization (MCO) can reduce treatment planning time and improve plan quality in intensity-modulated radiotherapy (IMRT).

Methods and Materials

Ten IMRT patients (5 with glioblastoma and 5 with locally advanced pancreatic cancers) were logged during the standard treatment planning procedure currently in use at Massachusetts General Hospital (MGH). Planning durations and other relevant planning information were recorded. In parallel, the patients were planned using an MCO planning system, and similar planning time data were collected. The patients were treated with the standard plan, but each MCO plan was also approved by the physicians. Plans were then blindly reviewed 3 weeks after planning by the treating physician.

Results

In all cases, the treatment planning time was vastly shorter for the MCO planning (average MCO treatment planning time was 12 min; average standard planning time was 135 min). The physician involvement time in the planning process increased from an average of 4.8 min for the standard process to 8.6 min for the MCO process. In all cases, the MCO plan was blindly identified as the superior plan.

Conclusions

This provides the first concrete evidence that MCO-based planning is superior in terms of both planning efficiency and dose distribution quality compared with the current trial and error–based IMRT planning approach.

INTRODUCTION

Translating a clinician’s desires regarding the ideal treatment plan into an optimization formulation has been a struggle since the inception of intensity-modulated radiotherapy (IMRT) in the 1980s. The main reason for this is that there are usually several structures to consider when planning a case, and the relative importance of the dose delivered to these structures is difficult to articulate. Additionally, the idea of “dose to a structure” is a simplification: in reality, it is the dose distribution to a structure that matters, and there are still no definitive methods to evaluate a dose distribution (e.g., should one use mean dose, a set of dose–volume points, or generalized equivalent uniform dose). Even if agreed-upon functions did exist, the optimal balance of dose distribution to several structures, both targets and organs at risk, is not known, and additionally is highly patient-geometry dependent (1).

In previous publications (2–7), Pareto surface-based techniques for multicriteria optimization (MCO) as a method to efficiently explore tradeoffs between different treatment planning goals have been described. Briefly, rather than creating one plan, the treatment planning system creates a database of plans that satisfy different treatment planning goals. These plans compromise a “Pareto surface,” meaning that any change in dose to one organ results in a tradeoff in another organ, making all changes “Pareto efficient.” This format allows the physician to rapidly explore tradeoffs between different planning goals and select a plan to his or her liking.

Until this time, the advantages of MCO planning have been primarily speculative because almost no software implementing the Pareto surface-based MCO procedure had achieved clinical implementation (see, however, Thieke et al. [8]). In this report, we present the results of the first testing of the MCO software produced by RaySearch Laboratories (development version, October 2009; Stockholm, Sweden) compared with standard treatment planning as done using the XiO system (version 4.4; Elekta, Stockholm, Sweden). The RaySearch MCO module approximates the Pareto surface by using N + 1 treatment plans, where N is the number of objectives. N of the plans are from each of the objectives being minimized individually. The additional plan is a balanced plan formed by optimizing the equiweighted sum of all objectives. Each of these optimizations happens in fluence (beam-let) space. Navigation allows the user to smoothly interpolate between these base plans. When the user is finished navigating, the system creates a deliverable version of that plan by a direct aperture optimization algorithm that finds a segmented plan (a total of 50 segments is used in all cases) to match the navigated-to dose–volume histogram (DVH). System default dose grids are used (0.2-cm voxels in XiO and 0.3-cm voxels in RayStation).

Using these tools, we explored the impact of Pareto surface-based MCO on treatment planning in regards to physician plan preference and treatment planning time in glioblastoma and locally advanced pancreatic cancer.

METHODS AND MATERIALS

Glioblastoma and pancreatic cancer were identified as two reasonably frequent patient populations seen at Massachusetts General Hospital and treated standardly with IMRT. Tumor types were selected with the additional criteria of presenting adequate complexity to merit some challenges in treatment planning. In the normal workflow of patient IMRT treatment planning at Massachusetts General Hospital, such clinical cases were flagged by physicians at the time of structure contouring as appropriate for this study. This triggered study sheets to be sent to the treatment planners to record the planning details of the designated cases. In parallel, the patients were prepared for physician navigation in the MCO system. Physicians then used the MCO navigation module to select the most preferred MCO plan for each patient. The MCO planning time details were logged. The study workflows are depicted as a block diagram in Fig. 1. Treatment planning time and physician involvement time are compared for the two planning approaches using paired t-tests. The MCO planning time is the sum of problem setup time and database generation (i.e., the automated optimizations of the database plans) time.

Fig. 1.

Block diagram for the two treatment planning workflows compared in this study. MCO = multicriteria optimization; DVH = dose–volume histogram; LAPC = locally advanced pancreatic cancer.

Disease site–specific templates for the optimization formulation and beam angles were used for the MCO system (Table 1). The templates were designed according to the following general principals.

Table 1.

Planning templates used for generating the MCO databases

GBM multicriteria planning template: prescription = 60 Gy	LAPC multicriteria planning template: prescription = 50.4 Gy
Objectives	Objectives
Minimum target dose of 60 Gy	Minimum target dose of 50.4 Gy
Maximum target 60 Gy	Right kidney mean
Brainstem mean	Left kidney mean
Chiasm mean	Liver mean
Left optic nerve mean	Stomach mean
Right opt nerve mean	Spinal cord mean
Ramp slider @ 30 Gy (this slider targets all doses in the patient above 30 Gy and is useful for controlling hot spots anywhere in the patient)	Ramp slider at 25 Gy
Note: Not all used always. Selected from this set based on particular geometry]
Constraints	Constraints
Target: V60Gy ≥95%	Target: V50.4Gy ≥95%
Target: V57Gy ≥100%	Target: V47.9Gy ≥100%
Eyes ≤50 Gy	Spinal cord ≤45 Gy
Lenses ≤10 Gy	Overall max: 56.5 Gy
Overall maximum: 69 Gy
GTV ≥60 Gy
7 beams equispaced, starting AP	7 beams equispaced, starting AP

Abbreviations: MCO = multicriteria optimization; GBM = glioblastoma; LAPC = locally advanced pancreatic cancer; GTV = gross target volume; AP = anterior–posterior.

1. If an organ at risk is deemed important, it is added to the objective formulation as a mean dose structure. Controlling the mean dose is the most straightforward method to control the entire dose to a risk structure (minimizing the maximum dose can be ineffectual if the structure overlaps the planning target volume, in which case the maximum dose is fixed by the prescription dose) (5, 6).

2. Dose limits that the physicians are not willing to compromise on are included as hard constraints (spinal cord in pancreatic cancer; eyes, lenses, and gross tumor volume coverage in glioblastoma).

3. To control hot spots in the patient, a quadratic dose function starting at half the prescription dose value is used as an objective. This function penalizes all doses above the starting value.

4. For the targets, a minimum dose objective is used (this is implemented as a quadratic underdose term in RayStation). So that all database plans have adequate target coverage, two dose–volume constraints are also used for the planning target volumes: 95% of the volume covered at the prescription dose, and 100% of the volume covered at 95% of the prescription dose. This dose–volume “shoulder” was agreed upon by both physicians.

5. Maximum doses to all voxels are set with a hard constraint. One hundred fifteen percent of the prescription dose is used for the glioblastomas and 112% for the pancreatic cancers (physician-chosen values).

6. Seven equispaced beams starting with an anterior to posterior beam.

For the standard planning, no template was used, nor were beam angles specified, to capture the planning procedure currently used in-house. Using the XiO system, planners began by establishing beam angles according to their judgment of the best geometric arrangement. Between five and seven beams were used in all cases. Then, the planner entered the IMRT optimization formulation, which consists of a set of dose–volume points and weights, into XiO, and began the process of modifying the weights and parameters until a plan that they were satisfied with was achieved. At that point, the physician was notified that the plan was ready for review. According the opinion of the physician, multiple iterations of replanning may occur until the physician is satisfied with the final plan.

Although DVHs are not sufficient to judge a treatment plan, the authors agreed that if two plans for a patient were both approved by a physician, they could be compared later by examining only the DVHs. At a minimum of 3 weeks after the plans were generated and approved, for each patient the MCO plan and the standard plan were presented to the physicians as DVHs in a common format without distinction of origin of planning modality, and the physicians were asked to select the better plan or say whether neither plan was obviously better than the other. Because the physicians were always able to select one of the two plans as preferable, plan quality of the standard plans and the MCO plans were statistically compared using an exact binomial test.

Along with timing data, the planners were asked to rate the relative difficulty of each plan compared with other plans of the same type, by selecting the difficulty quintile, with 1 being the easiest 20% and 5 the hardest 20%. This was done to verify that a good range of plans regarding planning difficulty was chosen.

Although distinct dose engines are used in each software system, they both use industry standard superposition–convolution algorithms with the dose kernels fit to a Varian (Palo Alto, CA) 6-MV machine equipped with a Millenium 120-leaf multileaf collimator.

RESULTS

Planning times are shown in Table 2. The active planning time for the standard plans was much longer than the time required for MCO planning (p < 0.01). For treatment planner time, glioblastomas took an average of 156 min for the XiO system and 12.4 min with the MCO system. Pancreatic cancer cases took slightly less time for both planning modalities: 114 min for XiO planning vs. 11.6 min for MCO planning. Glioblastomas took on average slightly longer than pancreatic cancers for the standard planning process (not statistically significant). Individual planning times are displayed in Fig. 2. For all cases the MCO planning time was equally shared between problem setup and database generation: database generation optimization time was consistently between 5 and 7 min, with an overall average of 5.7 min.

Table 2.

Average and standard deviations for the treatment planner planning times and physician planning/plan review times

Parameter	Planner time (min)	Physician time (min)
GBM: Standard	156 ± 95.8	5.0 ± 2.5
GBM: MCO	12.4 ± 1.8	8.2 ± 2.8
LAPC: Standard	114 ± 32.9	4.5 ± 2.7
LAPC: MCO	11.6 ± 0.6	9.0 ± 2.2

Abbreviations as in Table 1.

Values are mean ± SD.

Fig. 2.

Treatment planner time recorded for individual cases, for both standard planning procedure and the multicriteria optimization (MCO)-based procedure. GBM = glioblastoma; LAPC = locally advanced pancreatic cancer.

Because of active physician involvement in the plan selection process for MCO planning, the physician time spent was slightly larger for MCO by a few minutes (for glioblastomas, p < 0.05; not statistically significant for the combined data set nor for pancreatic cancer data alone). Average physician involvement time for XiO planning was 4.8 min vs. 8.6 min for MCO planning.

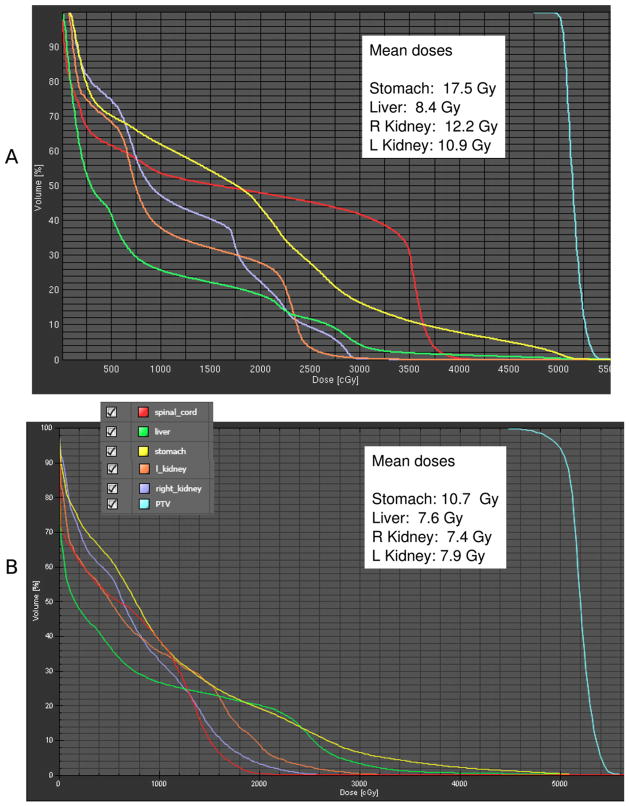
Example DVH comparisons as given to the physicians are shown in Figs. 3 (glioblastoma) and 4 (pancreatic cancer). In all cases, the MCO plan was selected as the better plan (p < 0.01).

Fig. 3.

Glioblastoma example of a pair of dose–volume histograms as given to the physician for choosing which is the superior plan. In this case, A is the multicriteria optimization plan and B is the standard (XiO) plan. Plan A is chosen as the superior plan. The physician chose to accept increased eye dose to achieve lower doses to the brainstem, chiasm, and the right optic nerve. ptv = planning target volume.

For the glioblastomas, the average difficulty as reported by the planners was 2.8 and for the pancreatic cancers, the average was 1.8. Thus, the pancreas plans were judged as generally among the easier plans, but both types averaged below average (average would be 3 on a scale of 1 to 5) in planning difficulty. This is likely a reflection that typical cases were chosen for inclusion into this study.

The planning time for the standard planning is dominated by performing optimization iterations with the system (i.e., setting parameters, having the system perform the optimization, evaluating the results, and repeating until the planner is satisfied). For the glioblastoma cases, the average and standard deviation for the number of optimization iterations was 7.4 ± 3.7, and for the pancreas cases, 5.4 ± 1.5.

DISCUSSION

Intensity-modulated radiotherapy has gained increasing popularity in both routine clinical practice and clinical trials owing to its ability to create highly conformal high-dose distributions. Thus, IMRT has been widely studied as a method to decrease side effects of treatment or as a tool for dose escalation to improve local control and possibly cure rates.

Intensity-modulated radiotherapy generally utilizes multiple beam angles, each of which is subdivided into multiple beamlets of varying intensity, allowing for an infinite number of treatment plans. However, despite the theoretical greater flexibility of treatment planning, in actuality the standard IMRT treatment planning process can decrease the flexibility for the physicians to alter radiation plans, owing to process inefficiency. Currently, if a physician does not like an IMRT plan, she will request that a plan be re-run. However, this requires the treatment planner to input a new treatment planning goal (or goals) to try to drive the inverse planning optimization plan. Even after all this, the physician may not think the new plan is actually better. To continue this iterative process increases the risk that the patient’s treatment start will be delayed and subsequently impact patient care. Hence, the current IMRT planning process places significant barriers to modification of plans or exploring tradeoffs for the plans. To phrase it concisely, the current IMRT treatment planning process (1) takes too long, and (2) does not encourage physician participation.

Pareto surface-based MCO seeks to directly address both of these issues. Unlike other MCO approaches that present the planner with a single result, such as various forms of prioritized optimization (9–11), Pareto surface-based MCO places the tradeoff exploration firmly into the hands of the physician. In a previous study (6), we evaluated 10 patients with locally advanced pancreatic cancer treated with IMRT and had noted that the physician chose plans with lower stomach dose when using Pareto surface-based MCO. Additionally, the plans were selected within 10 min. In this study, we sought to actually compare in real time whether we could shorten the treatment planning time and select plans that the physician preferred in two disease sites.

All traditional plans were generated with beam angles selected by the treatment planners. To make the MCO database generation fully automated, seven equispaced beams were used. This was done instead of using the planner-selected beam configuration in part to demonstrate that, for the two disease sites studies herein, beam angle selection is probably not a crucial part of treatment planning, and indeed with the right optimization framework, deviating from the simple seven equispaced beams is likely unnecessary. Research is currently being done on how to incorporate beam angle optimization into the MCO framework (12), but this is a very computationally demanding task and is not expected to find its way into clinical systems for some years to come.

It has long been speculated that the MCO approach will be both faster and yield better plans. This report supports this hypothesis, with active planning time dropping from approximately 2 h to 10 min, and in all 10 cases investigated, the physicians blindly selected the MCO-generated plans over the traditionally derived plans. The planners enrolled in this study were experienced treatment planners, so as to not bias the results toward MCO. The approximately 2-h planning time for traditional planning is made up of selecting beam angles and then performing a series of optimization iterations. The average number of optimization iterations performed per case is 6.4. This indicates one of the drawbacks of traditional treatment planning—the difficulty of choosing the set of optimization parameters that leads to an acceptable plan. Speeding up the standard optimization could certainly reduce this 2-h planning time, but the multiple iterations would still be necessary. Thus, optimization speeds being equal, the MCO approach, with its continuous control over the dose distributions and objective functions, seems quite rational.

These planning data lend support to the hypothesis that Pareto surface-based MCO is efficient and that, when armed with such a system, the physician will select different plans than those approved for treatment with the standard system. We believe this reflects the compromise that physicians accept with traditional planning, whereby the minimal achievement or approximation of target dose delivery with respect to normal tissue constraints is often accepted without further optimization even if a better plan can be attained. This may be a result of lack of physician awareness of further superior planning that can be achieved and also a result of failure to entirely articulate an ideal achievable plan, as compared with a minimally acceptable plan, to the planner.

According to our physicians’ experience in this study, the overwhelming feedback was positive for MCO. The standard iterative process with a planner was a system that physicians had adapted to because there was no alternative method. Sitting and watching active planning was not time efficient. Physicians agreed that they were generally satisfied with the standard methods because they had experience with many IMRT cases and learned what to expect for IMRT plans for their standard clinical cases. Through the iterative process of having done multiple prior similar cases with the same dosimetry group, there was learned behavior of both parties to understand the clinician’s desires and the likely planner’s results. That said, the experience with MCO provided physicians the freedom to review multiple plans within seconds and yielded much better understanding of the tradeoffs between both target and normal structures. The optimization of tradeoffs was a particularly desirable feature of MCO that is not readily achieved by standard planning methods. Both physicians admitted that the ultimate decision of target coverage to normal tissue sparing tradeoff was a clinical judgment that was not exactly reflected in the ideal target dose and constraints provided to the standard planners. This clinical decision arose after having reviewed the tradeoffs first. The physicians expressed satisfaction of MCO on three primary points: (1) ability to assess best possible dose tradeoffs among a set of optimized plans, knowing no lesser dose compromise between structures was feasible; (2) ease of navigation without an intermediate planner, allowing for physicians to explore a range of possible solutions freely; and (3) speed of planning with the MCO system, considerably more efficient that standard planning. Although physician time increased by a few minutes for MCO, in a clinical setting it is likely that the planners will navigate to a plan that they believe the physician might choose, thereby potentially reducing the time the physicians spend navigating the surface for those instances where the physicians choose to not examine the details of the tradeoffs.

One difficulty with the MCO approach remains validating that the plan the physician selects is actually the better plan. Decision-making scientists use the model shown in Fig. 5 to visualize how decisions are generally made for a two-dimensional problem (see, e.g., Johannesson [13]). Curve A represents the Pareto surface, also referred to as the possibility frontier. This curve represents the optimal plans that can be created—meaning for any plan on the frontier, a plan cannot be created that is better for both criteria. The rate at which the tradeoffs occur on the possibility curve is known as the marginal rate of transformation (MRT).

Fig. 5.

Curves illustrating the idea from decision theory that the optimal choice in a two-dimensional tradeoff is the point on the Pareto surface that maximizes utility. This is also the point where MRT (marginal rate of transformation, or the slope of the Pareto curve) is equal to MRS (marginal rate of substitution).

It is important to note that it does not mean that the plans on the possibility frontier are equally “good.” How “good” a plan is is defined by Curves 1–4, also known as utility curves. Any theoretical plan on a given utility curve would be deemed by the physician to be equivalent, meaning the physician views the given tradeoffs for any plan on a given curve to be equivalent. However, any plan on a higher-number curve would be “better” than any plan on a lower curve. The rate at which the tradeoffs occur on a utility curve, referred to as the marginal rate of substitution (MRS), indicates the this-for-that tradeoff (e.g., “I would accept an additional 5% chance of rectal toxicity for a 25% decrease in bladder toxicity”).

The ideal plan would be on whereby the MRS = MRT (i.e., the two curves are tangent to each other). This represents the point on the possibility frontier associated with the highest utility curve. The problem is that in radiation oncology, the MRS curves are not established. If the x- and y-axes represent two normal organs, the utility curves would involve normal tissue complication probabilities, but it is still not clear what tradeoff (what reduction in one complication probability is required to justify a unit gain in another) we would use.

In some sense, the navigation of the physician along the possibility curve is a measure of the physician’s internal sense of where the MRT is equal to the MRS. In other words, the rate of change that “feels” like a tradeoff, or substitution, that is deemed optimal to the physician is chosen. However, in the absence of utility curves, this remains highly subjective and an example of the “art” of medicine.

In conclusion, Pareto surface-based MCO is a new clinical tool that provides an efficient way for physicians to be their own decision makers in treatment planning. We plan to implement this technique for treatment planning in the coming year.

Fig. 4.

Pancreatic cancer example of a pair of dose–volume histograms (DVHs) as given to the physician for choosing which is the preferred plan. For the pancreatic cancer cases, the physician requested to see the displayed mean dose statistics in addition to the DVHs. In this case, A is the standard (XiO) plan and B is the multicriteria optimization plan. As was typical for the pancreas cases, the additional rounding of the target DVH allows for considerable improvement in organ-at-risk sparing. PTV = planning target volume; R = right; L = left.