Abstract
Background
The evolutionary success of Wolbachia bacteria, infections of which are widespread in invertebrates, is largely attributed to an ability to manipulate host reproduction without imposing substantial fitness costs. Here, we describe a stage-structured model with deterministic immature lifestages and a stochastic adult female lifestage. Simulations were conducted to better understand Wolbachia invasions into uninfected host populations. The model includes conventional Wolbachia parameters (the level of cytoplasmic incompatibility, maternal inheritance, the relative fecundity of infected females, and the initial Wolbachia infection frequency) and a new parameter termed relative larval viability (RLV), which is the survival of infected larvae relative to uninfected larvae.
Results
The results predict the RLV parameter to be the most important determinant for Wolbachia invasion and establishment. Specifically, the fitness of infected immature hosts must be close to equal to that of uninfected hosts before population replacement can occur. Furthermore, minute decreases in RLV inhibit the invasion of Wolbachia despite high levels of cytoplasmic incompatibility, maternal inheritance, and low adult fitness costs.
Conclusions
The model described here takes a novel approach to understanding the spread of Wolbachia through a population with explicit dynamics. By combining a stochastic female adult lifestage and deterministic immature/adult male lifestages, the model predicts that even those Wolbachia infections that cause minor decreases in immature survival are unlikely to invade and spread within the host population. The results are discussed in relation to recent theoretical and empirical studies of natural population replacement events and proposed applied research, which would use Wolbachia as a tool to manipulate insect populations.
Background
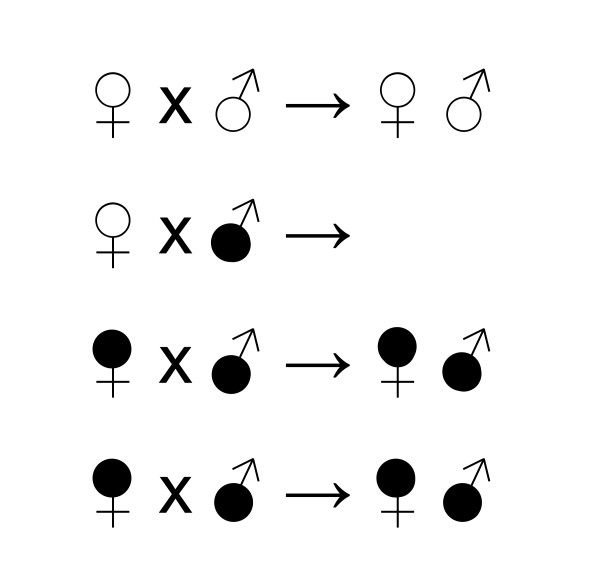
The success of obligate endosymbiotic organisms depends on their ability to invade, establish and persist in their host. Wolbachia pipientis, a well-studied endosymbiont, is a species of maternally inherited bacteria in the order Rickettsiales, and infections are estimated to occur in more than half of all insect species [1]. Prior studies have demonstrated the ability of Wolbachia to manipulate the reproduction of its host [2,3]; several phenotypes have been described, including male-killing [4,5], feminization [6,7], parthenogenesis [8-10], and cytoplasmic incompatibility (CI) [11-13]. CI affects a broad range of insect taxa and causes a reduction in egg hatch when Wolbachia-uninfected females and Wolbachia-infected males mate (Figure 1).
Figure 1.
Unidirectional cytoplasmic incompatibility crossing pattern. White circles represent uninfected individuals and black circles represent Wolbachia infected individuals. Crosses between the same infection type produces viable offspring. Cytoplasmic incompatibility occurs when uninfected females mate with Wolbachia infected males, resulting in reduced numbers of viable offspring. As a result, infected females have an effective mating advantage over uninfected females.
Prior models highlight three Wolbachia-specific parameters that affect the probability of Wolbachia invasion and establishment: the maternal inheritance rate, which is the proportion of infected offspring produced by an infected female; the level of CI, which is the proportion of embryos that fail to develop as a result of incompatible crosses [14]; and the fitness cost to females for carrying a Wolbachia infection, defined as a decrease in overall fecundity [15-20].
Previous studies predict that the successful invasion of Wolbachia into an uninfected host population requires low fecundity costs, high maternal inheritance rates, and high levels of CI [21,22]. Wolbachia infections that impose a 10% relative fecundity cost to adult females experience reductions in their invasion success [21]. Similarly, low maternal inheritance reduces the probability of Wolbachia invasion [22]. Higher initial Wolbachia infection frequencies are predicted to increase the probability of population replacement, which can offset the above costs [14]. Models have also addressed population structure at the adult stage, impacts on adult survival, stochastic effects, and overlapping generations [14,21-25].
The relative importance of Wolbachia effects on immature life stages has not been assessed theoretically. This is despite multiple examples demonstrating an effect of Wolbachia on immature hosts. In the stored product pest Liposcelis tricolor (Psocoptera: Liposcelidae), Wolbachia infections can decrease development periods and increase survivorship in some immature life stages [26]. Other studies demonstrate negative impacts of Wolbachia infections on larval survival and development time [27,28]. Recent studies have determined that when intraspecific competition is intense, Wolbachia-infected mosquito larvae experience reduced survival [29,30].
To better understand population replacement by CI-inducing Wolbachia, we have evaluated both Wolbachia infection dynamics and host population dynamics using a model that includes deterministic immature and adult male lifestages and a stochastic adult female lifestage. Since Wolbachia are transmitted maternally, the sex and infection status of hosts are explicit, and adult females are tracked individually. The focus of this modeling approach was to investigate changes in the probability of population replacement resulting from varying the relative larval viability (RLV), expressed as relative survival of infected to uninfected larvae. The results are presented in context with traditional parameters: the rate of CI, maternal inheritance (MI), the relative fecundity of infected females (RF), and the initial Wolbachia infection frequency (IF), on the probability of population replacement.
Methods
The model simulates a panmictic population that is closed to immigrants and emigrants. Consistent with previous studies, the model assumes mating is random and that Wolbachia infection has no effect on mating success. Females in the model mate once immediately upon reaching maturity. Adult survival is density-independent, but larval survival is density-dependent. The model presented here combines a stochastic adult female stage with deterministic adult male and immature stages. By implementing a deterministic immature stage, additional information regarding population dynamics is incorporated without developing a completely stochastic model, which would be considerably more computationally-intensive. The model incorporates overlapping generations [24] while tracking major life stages and considers females and males separately. Development time and survival during immature stages are addressed explicitly by the model. The model was designed assuming the host is a holometabolous insect, and the model was parameterized based upon estimates of mosquitoes in the genus Aedes as a case study.
Brief Description of Equations
The following is a brief overview of all equations and parameters implemented in the model presented here. Additional development details, initial parameter values, and sensitivity analysis are provided in Additional File 1.
| (1) |
Larval development rate R (developmental stage units): j is the maximum development rate (developmental stage units), h is the asymptotic minimum development rate (developmental stage units), Δt is the time step (units of time), q is the density-dependent development coefficient (units of (mass)-1), B is the total larval biomass (units of mass) and s is the total number of developmental stages. Derived from Gavotte et al. [30] and comparable to previously published data [31,32].
| (2) |
Larval survival, SL: μ is the baseline mortality rate of mosquito larvae in the absence of competition (units of (time)-1). α is the coefficient controlling density dependent mortality (units of (time)-1). B is the total larval biomass (dimensionless), β is the exponent controlling density dependent mortality (dimensionless), γ is the coefficient that decreases mortality as development stage increases (units of (time)-1), d is the developmental stage index, ε is the exponent that decreases mortality as development stage increases (dimensionless), and Δt which is the time step (units of time). Based on Dye [33] and similar to previously published studies [34-36].
| (3) |
Mosquito body mass, M (units of mass): mx (units of mass) is the theoretical maximum mass of a given mosquito at time T. mx is linked to c (dimensionless), which is the percent of mx that is attainable. k (dimensionless) is the growth coefficient; T0 (dimensionless) is the development time at which mass at pupation is mx/2 days, and T (dimensionless) is development time. d (dimensionless) represents the total number of development stages completed by the larval cohort. Derived from previously published data [30].
| (4) |
Female survivorship, Fs: g is the per capita mortality rate of adult females (units of (time)-1) and A is the current age of the female (units of time). Taken from Trpis and Hausermann [37].
| (5) |
Egg production, E: u is the egg production rate; Δt is the time step (units of time); v is the female mass coefficient (units of (mass)-1); Mf is the body mass of the ovipositing female (units of mass); w is the female mass intercept (units of mass), and z is the female mass exponent (dimensionless). Derived by combining two previously published functions [38,39].
Immature Life Stages
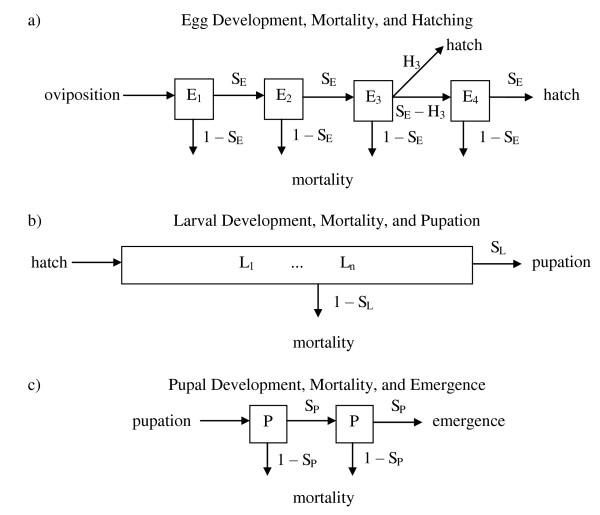
To simulate variation in egg hatch, the model assumes that some eggs (proportion equal to H3, Table S1 in Additional file 1) hatch on day three while the remaining eggs (1-H3) hatch on day four (Figure 2a) [40,41]. Eggs are separated into two cohorts based on infection status. Larvae are distributed into four categories for each of the possible combinations of sex and infection status.
Figure 2.
Immature population structure. a) Eggs develop through four discrete stages and each stage is one day. There are two cohorts of eggs, Wolbachia uninfected and infected. During development, eggs move through each stage consecutively, and the number of eggs advancing to the next stage reflects the product of the number of eggs present and SE, daily egg survivorship (Table S1). All eggs hatch after four days except a proportion of eggs hatch at day three (H3, Table S1). b) Larvae develop through s discrete stages, where s is an arbitrary number of developmental stages (s = 30). Larvae are divided into four categories: Wolbachia infected/uninfected and male/female. Larvae move R developmental stages in each time step, where R is the number of developmental stages a larval cohort will progress (Equation 1). The number of larvae progressing from their current development stage, e.g. L2, to their next developmental stage, L2+R, is equal to the product of the number of larvae in a developmental stage and larval survival (Equation 2). Larval survival and development are density dependent. If larvae are Wolbachia infected, they are subject also to the parameter RLV (Table 1), which can reduce the number of surviving larvae. Larvae that reach the last developmental stage become pupae. c) Pupae progress through two discrete development stages and are tracked similar to eggs. Each pupal developmental stage is one day and pupae are subject to SP, daily pupal survivorship (Table S1).
Larvae develop through discrete developmental stages, where the development rate is affected by density dependence, and larval survival is subject to both stage-dependent mortality and density-dependence (Figure 2b). The term "stage" is defined here as a measure of progress through larval development. The number of these discrete developmental stages is chosen to allow for variation in development time and is otherwise arbitrary (i.e., not linked to age or developmental instar explicitly). The number of larval developmental stages, s, can be varied, but was set to s = 30 for this study. Larval development rate, R, is the number of developmental stages through which a cohort of larvae will pass within 24 hours (Equation 1). The number of larvae surviving to the next day is the product of the number of larvae in the preceding time period and the larval survival rate (Equation 2). When the number of developmental stages within a day is not an integer, the larval cohort is distributed into two adjacent developmental stages in proportions that preserve the average development rate. The latter also introduces variation into the development rates of larval cohorts (Figure 2b). Density-dependence is based on the total mass of larvae (Equation 3). Male and female cohorts are considered separately to observe sex-specific patterns during development. For example, female mosquitoes require longer development time to become adults relative to males, and studies demonstrate that males and females respond to competition intensities differently [30].
Uninfected larval cohorts progress through development subject to stage-dependent mortality and density dependent effects only. Infected larval cohorts are subject also to a reduction in viability associated with Wolbachia infection. The relative larval viability (RLV, Table 1) for infected larvae is a proportion that indicates the relative survival of infected to uninfected larvae.
Table 1.
Glossary of notation, including the initial values for each key parameter
| symbol | definition | initial value |
|---|---|---|
| CI | proportion of embryos not hatching in incompatible CI crosses | 0.999 |
| MI | proportion of offspring receiving infection (maternal inheritance) | 0.999 |
| RF | relative fecundity of infected females to uninfected females | 0.999 |
| RLV | relative larval viability of infected larvae to uninfected larvae | 0.999 |
| IF | initial frequency of gravid infected females to the total adult population | 0.500 |
In all subsequent model runs, each value remains constant while one key parameter is varied. (For a list of all population dynamic parameters, see Table S1 in Additional file 1.)
Following the completion of larval development stages, individuals become non-feeding pupae, which have a daily survival that is independent of population density (Sp, Table S1; Figure 2c). After completing pupal development, emerging male adults are tracked separately as either infected or uninfected cohorts. Emerging female adults are tracked as individuals.
Adult Life Stages
Six variables are tracked over time and determine the state of individual females: the blood meal state (time since last feeding), age (days since emerging), Wolbachia infection status (infected or uninfected), the Wolbachia infection status of her mate (determined randomly based on the proportion of infected males in the population at the time she mates), size (body mass), and reproductive state (the number of gonotrophic cycles completed).
The probability that a female obtains a blood meal is determined by the frequency of potential blood meals per unit area, and each blood meal is associated with an additional mortality risk, regardless of mosquito age (Table S1). In the panmictic population simulated here, the availability of potential blood meals is assumed to be constant, but the model will allow downstream population structuring and geographic variation of bloodmeal availability.
Adult female daily survivorship Fs is age-dependent and probabilistic (Equation 4) [37]. A female that is Wolbachia uninfected and mated with an infected male will lay eggs, but a proportion of the eggs will not hatch, depending on the level of CI (Table 1). Infected females produce viable offspring regardless of their mate's infection status but are subject to a decrease in relative fecundity (RF, Table 1). The number of eggs laid by an individual female is determined by her mass (Equation 5), and larval development influences female body mass. Specifically, intense competition delays development and reduces the mass of adult females.
Adult males, which are dead end hosts for Wolbachia, are not tracked individually but are tracked as infected and uninfected cohorts. The male mortality rate is assumed to be age-independent and constant (SM, Table S1). The proportion of Wolbachia infected males in the population determines the probability of an incompatible mating for uninfected females.
Simulations
The model was written in MATLAB 7 (The MathWorks Inc., Natick, MA). A single simulation of the model produced population dynamics that are tracked over time (Figure 3). A series of simulations (n = 1000) were used to assess the impact of incremental parameter changes on the probability of population replacement. The parameters emphasized were cytoplasmic incompatibility (CI); maternal inheritance (MI); the relative fecundity of adult females (RF); the initial Wolbachia infection frequency, expressed as a proportion of the total number of adults (IF), and the relative larval viability (RLV). A population replacement event is defined as having occurred when the proportion of infected adults stabilizes above or equal to the MI value. During each series of simulations, individual parameters were varied singly, while the remaining parameter values were held constant as defined in Table 1. Each parameter was uniformly varied at one one-hundredth intervals from zero to one. At each interval, 1000 simulations were conducted, and the number of successful invasions was recorded to determine the probability of population replacement at that specific parameter value. The uniform sensitivity analysis was implemented for direct comparisons between all parameters across all intervals. Furthermore, previous analyses have not established minimum values for the spread of Wolbachia. Additional simulations tested two-way interactions between each of the emphasized parameters by varying two parameters simultaneously and evaluating the probability of population replacement. In the aforementioned simulations, parameters were varied uniformly. One parameter would be held constant while the other parameter varied as described above. The first parameter would then be incremented and the process above would be repeated. The probabilities resulting from two-way interactions were approximately the product of the two parameters and are not discussed further.
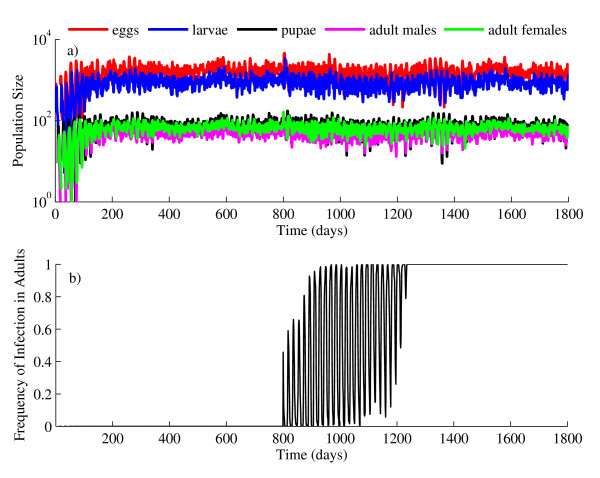
Figure 3.
Example of typical population dynamics produced by a simulation of the model. a) Populations begin with an uninfected cohort of eggs. The population is allowed to persist and self-regulate for 800 days, at which time Wolbachia is introduced to the population as gravid, bloodfed females at the rate defined in Table 1. The population is then allowed to self-regulate and persist until 1800 days have elapsed. b) The proportion of the female population that is infected with Wolbachia over time (i.e., infection frequency), demonstrating a population replacement event.
Results
Figure 3 provides an example of the typical population dynamics resulting from model simulations of a Wolbachia population replacement event. In the illustrated example, the population begins as cohort of uninfected eggs and stabilizes after approximately 150 days, with variation around a consistent population size and lifestage distribution (Figure 3a). In the example simulation, the introduction of Wolbachia occurs at day 800 by introducing blood-fed, gravid adult females at an initial Wolbachia infection frequency (IF) of 0.5 (Table 1). IF is the frequency of Wolbachia-infected females relative to the total number of adults such that an IF = 1 is synonymous with a 1:1 (infected to uninfected) ratio. Figure 3b illustrates the resulting variation in Wolbachia infection frequency in the host population versus time.
Due to the stochastic nature of the model, the number of individuals within each lifestage fluctuates considerably over time (Figure 3a). To examine for temporal patterns in the fluctuations that might correspond to periodic signals such as stage durations or generation time, we performed a spectral analysis on the time series data for both total adult and larval populations via Fast Fourier Transformation [42,43]. The analysis can identify temporal patterns that exist in what appear to be chaotic time series. No pattern was detected by the spectral analysis. Since no period was found, stochasticity appears to be the sole driver of population fluctuations.
Five parameters associated with Wolbachia infection were evaluated for their affect on the probability of population replacement. The value of each parameter was varied at one one-hundredth increments, from zero to one, while additional parameters were held constant as defined in Table 1. For each parameter value, the probability of population replacement was determined by the number of successful replacement events occurring in 1000 simulations, for a total of 101,000 simulations per parameter.
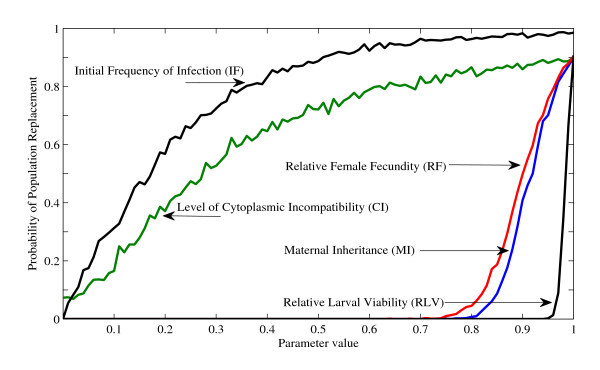
Maternal inheritance (MI), the relative fecundity of adult females (RF), and relative larval viability (RLV), exhibit strong threshold behavior with population replacement occurring only at parameter values exceeding 0.7 (Figure 4). Specifically, realistic probabilities of population replacement (i.e., > 50% probability of population replacement) require the magnitude of MI to be greater than 0.9. Similarly, RF must exceed 0.9 before realistic probabilities of population replacement are attained. The probability of population replacement is most sensitive to RLV, which requires a value of greater than 0.95 before population replacement can occur. Furthermore, realistic probabilities of population replacement only occur at high RLV (≥0.99), despite high maternal inheritance and CI (i.e., all other parameters held at values defined in Table 1).
Figure 4.
The probability of population replacement for five Wolbachia specific parameters. CI is the level of cytoplasmic incompatibility, MI is the level of maternal inheritance, IF is the initial frequency of Wolbachia infection, RF is the relative fecundity of Wolbachia-infected adult females, and RLV is the relative larval viability. Each line was generated by calculating the probability of a population replacement event at one one-hundredth increments for parameter values between zero and one (n = 1000 simulations/increment). IF and CI show similar responses to parameter value increases. The probability of population replacement increases, but then asymptotically approaches one. The response curves for RF, MI, and RLV behave similarly, each parameter requiring values to be greater than approximately 0.7. The curves then quickly increase toward one. RLV is the most sensitive parameter requiring values approaching 0.95 before a population replacement event can occur. Realistic probabilities of population replacement (i.e., population replacement occurs in greater than 50% of simulations) does not occur until RLV is greater than or equal to 0.99.
A different functional relationship is observed with the level of incompatibility (CI) and initial Wolbachia infection frequency (IF), each of which results in response curves that increase asymptotically (Figure 4). Assuming the parameters within Table 1, the model predicts that CI is not necessary for Wolbachia to spread (i.e., approximately 7% of simulations resulted in population replacement when CI = 0). Realistic probabilities of population replacement occur when CI approaches 0.3. Despite perfect CI (i.e., no egg hatch in incompatible crosses), population replacement did not occur in 10% of simulations (Figure 4). Additional simulations confirmed that a 90% probability of population replacement is an absolute maximum given the conditions defined here (Table 1). However, as the magnitude of IF increases, the probability of population replacement rapidly approaches one, with realistic probabilities of population replacement occurring when the frequency of infected females approaches 20% (Figure 4).
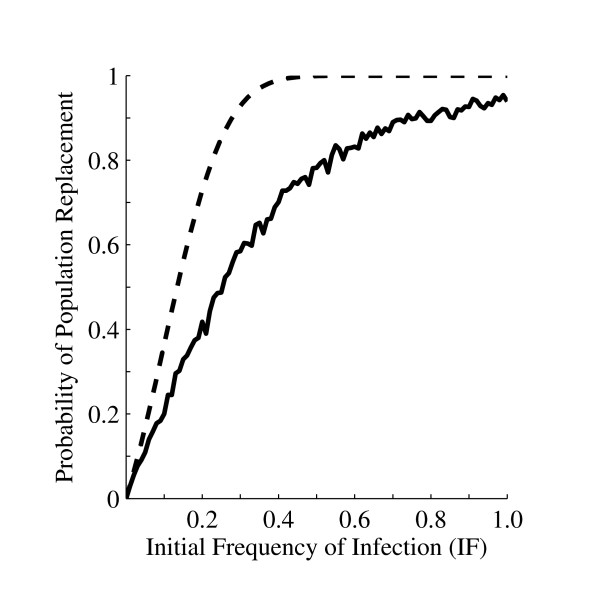
The results obtained from the model here were compared to a previously published stochastic model [22]. Table 2 compares the fixation probabilities calculated by the model presented here and those from Jansen et al. [22] using the conditions defined in the prior report, which includes the introduction of a single infected female into a population size of 100 and perfect CI. To allow direct comparison, the relative larval viability in our model was set to one. 50,000 simulations were performed for each combination of parameter values used in the prior publication. Both models predict the probability of population replacement decreases when MI and RF values are less than one (Table 2). Generally, our model predicted lower probabilities of population replacement than the previously published model. However, when either MI or RF was 80%, the model presented here reported higher probabilities (Table 2). Jansen et al. [22] predicted that Wolbachia infections with imperfect maternal inheritance and low adult fitness costs (MI = RF = 0.9) will still invade and establish in a population, but our model predicted no population replacement events (Table 2). The predictions of our model were also compared to those of Jansen et al. [22] assuming larger initial frequencies of Wolbachia infected individuals (Figure 5). Both models predict an asymptotic increase in the probability of population replacement with increasing magnitude of IF, but our model predicts lower probabilities of population replacement (Figure 5).
Table 2.
The probability of population replacement for given parameter values
| MI | RF | ||
|---|---|---|---|
| 1.0 | 0.9 | 0.8 | |
| 1.0 | 0.1023/0.0359 | 0.0224/0.0089 | 0.0004/0.0007 |
| 0.9 | 0.0158/0.0060 | 0.0004/0.0000 | / |
| 0.8 | 0.0001/0.0004 | / | / |
| Jansen et al. [22]/model presented here | |||
The probability of population replacement for given parameter values, assuming perfect CI and the release of a single infected adult female into an uninfected population with a size of 100. The fixation probabilities from our model are generally lower than the values predicted by Jansen et al.[22], except when maternal inheritance and the relative fecundity of infected adults is 0.8. The model presented here predicted population replacement would not occur when both maternal inheritance and the relative fecundity of infected adult females were 0.9. All probabilities generated from the model presented here reflect the proportion of population replacement events that occurred per 50,000 simulations of the model. Comparable values were estimated from Figure 2 in Jansen et al. [22].
Figure 5.
The probability of population replacement by Wolbachia given different initial infection frequencies. This figure assumes that the relative fecundity of infected females is 0.95, with perfect CI and maternal inheritance. The dashed line indicates the probability of population replacement as calculated by Jansen et al [22], and the solid line represents the predictions of this model. Our model predicts lower probabilities at all initial Wolbachia infection frequencies, but generates a similar functional response.
Discussion
The model presented here examines the probabilities of Wolbachia invasion into an isolated uninfected population. The model is unique in its individual-based representation of variation in key traits among adult females and in the resolution of larval dynamics within the host population. The model presented here predicts, as in previous modeling studies, that maternal inheritance (MI) and the relative fecundity of adult females (RF) are key parameters that determine the potential for population replacement. Specifically, population replacement occurs only at high MI or RF. In contrast, population replacement can occur at low CI or low IF. The simulation of adult females as individuals demonstrates that MI requires higher parameter values than RF for successful population replacement. The new parameter, relative larval viability (RLV), like MI and RF, requires high parameter values before population replacement can occur.
The relative larval viability between Wolbachia infected and uninfected individuals (RLV) is the most important determinant of population replacement, requiring the highest parameter values for invasion. The model predicts that reductions in infected larval survival can substantially reduce the probability of population replacement (Figure 4). While a majority of prior studies have examined for an effect in adults, recent studies have determined that, at high levels of intraspecific competition, Wolbachia infected larvae experience reduced survival [29]. However, few theoretical studies have examined the impact of immature lifestages on the invasion of Wolbachia. Here, we demonstrate that reductions in RLV will inhibit Wolbachia invasion into an uninfected host population.
Recent work has highlighted the prevalence of Wolbachia, and its ability to invade populations [1,20]. Studies have suggested that Wolbachia infection affects larval survival and development only when intraspecific competition is high [29,44]. Given the predictions from our model, Wolbachia can only invade a population when RLV is very high. Therefore, the density of conspecifics in larval habitats is predicted to have significant impacts on the probability of population replacement. Similarly, the abundance and variety of larval habitats may have significant impact on the invasion of Wolbachia. The distribution, utilization and variety of larval habitats is well known for some insects, particularly mosquitoes [45-48]. Theoretical studies considering the effect of metapopulation structure and larval rearing conditions may elucidate the mechanism by which Wolbachia can invade natural populations given low initial infection frequencies.
The level of CI in insects varies widely [44,49-51]. Our model shows that the intensity of CI has relatively little effect on the probability of population replacement when the rate of CI exceeds 60%. Furthermore, when CI = 0, the model presented here predicts population replacement can occur at low probabilities (Figure 4). Some Wolbachia infections do not cause CI, but are found at high frequencies in natural populations [44,50,52]. Previous theoretical studies indicate that CI or a sex-ratio distorter is not required for population replacement when endosymbionts can alter female traits [44,53]. However, results presented here suggest that non-CI inducing Wolbachia infections can establish and persist in a population without increasing or altering host fitness, given high MI, RF, and RLV. Since the population considered by the model presented here is relatively small (N ≈ 110 adults), genetic drift could perhaps influence the probability of population replacement [54]. To investigate the importance of genetic drift, the population size in the model was increased. In model simulations where the total adult population size is greater than approximately 200, population replacement does not occur when there is no effect of CI (i.e. CI = 0). However, when population size is increased, the general response patterns in Figure 4 are not altered.
High maternal inheritance rates have been observed consistently in natural populations [55-57]. Furthermore, theoretical studies predict the probability of population replacement declines as maternal inheritance decreases [12,21,22]. Similar to previous studies, results presented here suggest that maternal inheritance (MI) must be high for a Wolbachia infection to invade an uninfected population and persist. Specifically, MI must be higher than 90% to attain a realistic probability of population replacement.
The effect of Wolbachia infections on adult female fitness has been well documented empirically and theoretically [11,15,16,22,24,58,59]. Here, as in previous theoretical studies, the model predicts that the relative fecundity of adult females (RF) must be high to facilitate population replacement.
For all parameters, the probability of population replacement approached an absolute maximum of 90% given the conditions defined in Table 1. Here, the initially examined IF value is relatively high (0.5), analogous to artificial introductions examined in prior theoretical work [25]. Subsequently, lower IF values have been simulated (Figure 4), including the introduction of a single, infected female (Table 2). The model predicts that Wolbachia invasion can occur at the lowest IF values and demonstrates an increasing probability of invasion with the higher introduction levels, with the probability of population replacement approaching 100%. Additional simulations determined that when IF is held constant and the total adult population size is increased, the probability of population replacement approaches one given the conditions defined in Table 1. This result suggests genetic drift can affect the probability of population replacement in small populations and may facilitate or hinder the spread of Wolbachia from low initial frequencies [54].
The model presented here predicted lower population replacement probabilities than those predicted by previous stochastic models (Table 2 and Figure 5) [22]. Rasgon and Scott [25] noted a similar behavior where implementing population age-structure and overlapping generations increased deterministic thresholds. The inclusion of additional life stages and stage-structure in this stochastic model may explain the reduced probabilities of population replacement. However, the model presented here predicted marginally higher probabilities of population replacement when either maternal inheritance or the relative fecundity of infected females had a magnitude of 0.8. The increased probability of population replacement predicted by the model presented here is likely a result of the individual-based representation of the adult female life stage that includes stochastic survival.
The model here addresses a single, panmictic, isolated population but could be expanded to include metapopulation structure. If introduction events can be assumed to occur randomly, then the surrounding subpopulations should generally tend to inhibit population replacement, because migration between subpopulations would dilute the proportion of infected individuals. However, as demonstrated here, genetic drift may influence the invasion of Wolbachia in smaller subpopulations. The spatial spread of Wolbachia has been assessed analytically by others and defines the conditions needed for Wolbachia to spread through space [20,24].
The majority of models that address the invasion of Wolbachia into uninfected populations have examined populations without lifestage subdivisions, suggesting that additional empirical studies focused on understanding larval dynamics are needed [34]. Many of the parameters defined here may be difficult to determine in natural populations [25], but our results demonstrate the importance of understanding the role of life history parameters and their interactions, despite the difficulties. Furthermore, the sensitivity analysis of the model presented here demonstrates that the magnitudes of particular parameters strongly influence the potential for spread and establishment of Wolbachia; these (e.g., Wolbachia effects on immature fitness) should be the focus of future empirical and theoretical studies. Future theoretical studies could further address parameter sensitivity by hyper-cube sampling, but this would require information about the distribution of parameters to investigated [60].
Conclusions
Wolbachia is currently being utilized as the basis for a gene drive strategy in open field releases of Aedes aegypti [61,62]; however, the predictions of the model presented here suggest that minute reductions in RLV can inhibit population replacement. Research needs to focus on understanding the effects of novel Wolbachia infections on immature lifestages. Xi et al. [63] demonstrated that novel Wolbachia infections can establish in a new host species and replace an uninfected population, but the initial frequency of Wolbachia infected individuals needed to replace the population was higher than predicted. The authors suggested that differences in survival of immature lifestages could explain their results. Results presented here indicate that even reductions in RLV that are difficult to detect empirically will substantially reduce the probability of population replacement.
The rapid decline in the probability of population replacement associated with reduced larval viability indicates that empirical studies directed toward quantifying the effects of endosymbionts on immature insects are important for understanding and predicting Wolbachia invasion events. Recent empirical studies also suggest that a more complete understanding of the effects of Wolbachia on the immature life stages is generally needed through additional empirical and theoretical studies [28-30].
Authors' contributions
The original model was conceptualized by PRC, JWM and ES in a class taught by PHC. The model was revised by YH, PHC, and SLD. JWM and ES parameterized equations, which were derived by PHC. PRC coded the model and simulations in MATLAB, which was later optimized by PRC, PHC, and YH. The manuscript was written by PRC, PHC, and SLD. All authors have read and approved the final manuscript.
Supplementary Material
Model parameters, detailed equation appendix and sensitivity analysis. Portable Document File (pdf) containing all parameters, initial parameter values, and equations utilized by the model. Model development is discussed, and includes references from which each equation was developed/parameterized. Also includes the sensitivity analysis of all population dynamic parameters and discussion about the robustness of model predictions
Contributor Information
Philip R Crain, Email: philip.crain@uky.edu.
James W Mains, Email: jimmymains@uky.edu.
Eunho Suh, Email: esuh2@email.uky.edu.
Yunxin Huang, Email: yunxin.huang@gmail.com.
Philip H Crowley, Email: pcrowley@email.uky.edu.
Stephen L Dobson, Email: sdobson@uky.edu.
Acknowledgements
The authors would like to thank Michael Turelli and Peter Hammerstein for comments and suggestions on this project. This research was supported by grants from the National Institutes of Health [AI-067434] and the Bill and Melinda Gates Foundation [#44190]. This is publication 11-08-042 of the University of Kentucky Agricultural Experiment Station.
References
- Hilgenboecker K, Hammerstein P, Schlattmann P, Telschow A, Werren JH. How many species are infected with Wolbachia? - A statistical analysis of current data. Fems Microbiology Letters. 2008;281(2):215–220. doi: 10.1111/j.1574-6968.2008.01110.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werren JH. Biology of Wolbachia. Annu Rev Entomol. 1997;42:587–609. doi: 10.1146/annurev.ento.42.1.587. [DOI] [PubMed] [Google Scholar]
- Werren JH, Baldo L, Clark ME. Wolbachia: Master manipulators of invertebrate biology. Nature Reviews Microbiology. 2008;6(10):741–751. doi: 10.1038/nrmicro1969. [DOI] [PubMed] [Google Scholar]
- Hurst GDD, Jiggins FM, von der Schulenburg JHG, Bertrand D, West SA, Goriacheva II, Zakharov IA, Werren JH, Stouthamer R, Majerus MEN. Male-killing Wolbachia in two species of insect. P Roy Soc Lond B Bio. 1999;266(1420):735–740. doi: 10.1098/rspb.1999.0698. [DOI] [Google Scholar]
- Hornett EA, Charlat S, Wedell N, Jiggins CD, Hurst GDD. Rapidly shifting sex ratio across a species range. Curr Biol. 2009;19(19):1628–1631. doi: 10.1016/j.cub.2009.07.071. [DOI] [PubMed] [Google Scholar]
- Bouchon D, Rigaud T, Juchault P. Evidence for widespread Wolbachia infection in isopod crustaceans: Molecular identification and host feminization. P Roy Soc Lond B Bio. 1998;265(1401):1081–1090. doi: 10.1098/rspb.1998.0402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobayashi Y, Telschow A. Cytoplasmic feminizing elements in a two-population model: Infection dynamics, gene flow modification, and the spread of autosomal suppressors. J Evol Biol. 2010;23(12):2558–2568. doi: 10.1111/j.1420-9101.2010.02116.x. [DOI] [PubMed] [Google Scholar]
- Huigens ME, Luck RF, Klaassen RHG, Maas MFPM, Timmermans MJTN, Stouthamer R. Infectious parthenogenesis. Nature. 2000;405(6783):178–179. doi: 10.1038/35012066. [DOI] [PubMed] [Google Scholar]
- Kremer N, Charif D, Henri H, Bataille M, Prevost G, Kraaijeveld K, Vavre F. A new case of Wolbachia dependence in the genus Asobara: Evidence for parthenogenesis induction in Asobara japonica. Heredity. 2009;103(3):248–256. doi: 10.1038/hdy.2009.63. [DOI] [PubMed] [Google Scholar]
- Stouthamer R, Russell JE, Vavre F, Nunney L. Intragenomic conflict in populations infected by parthenogenesis inducing Wolbachia ends with irreversible loss of sexual reproduction. BMC Evol Biol. 2010;10 doi: 10.1186/1471-2148-10-229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turelli M, Hoffmann AA. Cytoplasmic incompatibility in Drosophila simulans dynamics and parameter estimates from natural populations. Genetics. 1995;140(4):1319–1338. doi: 10.1093/genetics/140.4.1319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farkas JZ, Hinow P. Structured and unstructured continuous models for Wolbachia infections. Bull Math Biol. 2010;72(8):2067–2088. doi: 10.1007/s11538-010-9528-1. [DOI] [PubMed] [Google Scholar]
- Dobson SL, Fox CW, Jiggins FM. The effect of Wolbachia-induced cytoplasmic incompatibility on host population size in natural and manipulated systems. P Roy Soc Lond B Bio. 2002;269(1490):437–445. doi: 10.1098/rspb.2001.1876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engelstadter J, Telschow A. Cytoplasmic incompatibility and host population structure. Heredity. 2009;103(3):196–207. doi: 10.1038/hdy.2009.53. [DOI] [PubMed] [Google Scholar]
- Caspari E, Watson GS. On the evolutionary importance of cytoplasmic sterility in mosquitos. Evolution. 1959;13(4):568–570. doi: 10.2307/2406138. [DOI] [Google Scholar]
- Fine PEM. Dynamics of symbiote-dependent cytoplasmic incompatibility in Culicine mosquitos. J Invertebr Pathol. 1978;31(1):10–18. doi: 10.1016/0022-2011(78)90102-7. [DOI] [PubMed] [Google Scholar]
- Hoffmann AA, Turelli M, Harshman LG. Factors affecting the distribution of cytoplasmic incompatibility in Drosophila simulans. Genetics. 1990;126(4):933–948. doi: 10.1093/genetics/126.4.933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurst LD. The evolution of cytoplasmic incompatibility or when spite can be successful. J Theor Biol. 1991;148(2):269–277. doi: 10.1016/S0022-5193(05)80344-3. [DOI] [PubMed] [Google Scholar]
- Turelli M. Evolution of incompatibility-inducing microbes and their hosts. Evolution. 1994;48(5):1500–1513. doi: 10.2307/2410244. [DOI] [PubMed] [Google Scholar]
- Turelli M, Hoffmann AA. Rapid spread of an inherited incompatibility factor in California Drosophila. Nature. 1991;353(6343):440–442. doi: 10.1038/353440a0. [DOI] [PubMed] [Google Scholar]
- Egas M, Vala F, Breeuwer JAJ. On the evolution of cytoplasmic incompatibility in haplodiploid species. Evolution. 2002;56(6):1101–1109. doi: 10.1111/j.0014-3820.2002.tb01424.x. [DOI] [PubMed] [Google Scholar]
- Jansen VAA, Turelli M, Godfray HCJ. Stochastic spread of Wolbachia. Proceedings of the Royal Society B-Biological Sciences. 2008;275(1652):2769–2776. doi: 10.1098/rspb.2008.0914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haygood R, Turelli M. Evolution of incompatibility inducing microbes in subdivided host populations. Evolution. 2009;63(2):432–447. doi: 10.1111/j.1558-5646.2008.00550.x. [DOI] [PubMed] [Google Scholar]
- Turelli M. Cytoplasmic incompatibility in populations with overlapping generations. Evolution. 2010;64(1):232–241. doi: 10.1111/j.1558-5646.2009.00822.x. [DOI] [PubMed] [Google Scholar]
- Rasgon JL, Scott TW. Impact of population age structure on Wolbachia transgene driver efficacy: Ecologically complex factors and release of genetically modified mosquitoes. Insect Biochem Molec. 2004;34(7):707–713. doi: 10.1016/j.ibmb.2004.03.023. [DOI] [PubMed] [Google Scholar]
- Dong P, Wang JJ, Hu F, Jia FX. Influence of Wolbachia infection on the fitness of the stored-product pest Liposcelis tricolor (Psocoptera: Liposeelididae) J Econ Entomol. 2007;100(4):1476–1481. doi: 10.1603/0022-0493(2007)100[1476:IOWIOT]2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- Islam MS, Dobson SL. Wolbachia effects on Aedes albopictus (Diptera: Culicidae) immature survivorship and development. J Med Entomol. 2006;43(4):689–695. doi: 10.1603/0022-2585(2006)43[689:WEOAAD]2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- McMeniman CJ, O'Neill SL. A virulent Wolbachia infection decreases the viability of the Dengue vector Aedes aegypti during periods of embryonic quiescence. Plos Neglect Trop D. 2010;4(7) doi: 10.1371/journal.pntd.0000748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gavotte L, Mercer DR, Stoeckle JJ, Dobson SL. Costs and benefits of Wolbachia infection in immature Aedes albopictus depend upon sex and competition level. J Invertebr Pathol. 2010;105(3):341–346. doi: 10.1016/j.jip.2010.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gavotte L, Mercer DR, Vandyke R, Mains JW, Dobson SL. Wolbachia infection and resource competition effects on immature Aedes albopictus (Diptera: Culicidae) J Med Entomol. 2009;46(3):451–459. doi: 10.1603/033.046.0306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbosa PP, Greenough MT, N C. Overcrowding of mosquito populations: Responses of larva Aedes aegypti to stress. Environmental Entomology. 1972;1(1):89–93. [Google Scholar]
- Peters TM, Barbosa P. Influence of population-density on size, fecundity, and developmental rate of insects in culture. Annu Rev Entomol. 1977;22:431–450. doi: 10.1146/annurev.en.22.010177.002243. [DOI] [Google Scholar]
- Dye C. Model for the population-dynamics of the Yellow Fever mosquito, Aedes aegypti. J Anim Ecol. 1984;53(1):247–268. doi: 10.2307/4355. [DOI] [Google Scholar]
- Magori K, Legros M, Puente ME, Focks DA, Scott TW, Lloyd AL, Gould F. Skeeter Buster: A stochastic, spatially explicit modeling tool for studying Aedes aegypti population replacement and population suppression strategies. Plos Neglect Trop D. 2009;3(9) doi: 10.1371/journal.pntd.0000508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Focks DA, Haile DG, Daniels E, Mount GA. Dynamic life table model for Aedes aegypti (Diptera: Culicidae) - Simulation and validation. J Med Entomol. 1993;30(6):1018–1028. doi: 10.1093/jmedent/30.6.1018. [DOI] [PubMed] [Google Scholar]
- Southwood T, Murdie G, Yasuno M, Tonn R, Reader P. Studies on the life budget of Aedes aegypti in Wat Samphaya, Bangkok, Thailand. Bulletin of the World Health Organization. 1972;46:211–226. [PMC free article] [PubMed] [Google Scholar]
- Trpis M, Hausermann W. Dispersal and other population parameters of Aedes aegypti in an African village and their possible significance in epidemiology of vector-borne diseases. Am J Trop Med Hyg. 1986;35(6):1263–1279. doi: 10.4269/ajtmh.1986.35.1263. [DOI] [PubMed] [Google Scholar]
- Blackmore MS, Lord CC. The relationship between size and fecundity in Aedes albopictus. Journal of Vector Ecology. 2000;25(2):212–217. [PubMed] [Google Scholar]
- Lounibos LP, Rey JR, Frank JH. Ecology of mosquitoes: Proceedings of a workshop. Vero Beach, Fla.: Florida Medical Entomology Laboratory; 1985. [Google Scholar]
- Gillett JD, Roman EA, Phillips V. Erratic hatching in Aedes eggs - New interpretation. P Roy Soc Lond B Bio. 1977;196(1123):223–232. doi: 10.1098/rspb.1977.0038. [DOI] [PubMed] [Google Scholar]
- Christophers SR. Aëdes aegypti (L.), the Yellow fever mosquito; its life history, bionomics, and structure. Cambridge Eng.: University Press; 1960. [Google Scholar]
- Wijnen H, Naef F, Young MW. Molecular and statistical tools for circadian transcript profiling. Methods Enzymol. 2005;393:341–365. doi: 10.1016/S0076-6879(05)93015-2. [DOI] [PubMed] [Google Scholar]
- Keegan KP, Pradhan S, Wang JP, Allada R. Meta-analysis of Drosophila circadian microarray studies identifies a novel set of rhythmically expressed genes. PLoS Comput Biol. 2007;3(11):2087–2110. doi: 10.1371/journal.pcbi.0030208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann AA, Clancy D, Duncan J. Naturally-occurring Wolbachia infection in Drosophila simulans that does not cause cytoplasmic incompatibility. Heredity. 1996;76:1–8. doi: 10.1038/hdy.1996.1. [DOI] [PubMed] [Google Scholar]
- Aldstadt J, Koenraadt CJM, Fansiri T, Kijchalao U, Richardson J, Jones JW, Scott TW. Ecological modeling of Aedes aegypti (L.) pupal production in rural Kamphaeng Phet, Thailand. Plos Neglect Trop D. 2011;5(1) doi: 10.1371/journal.pntd.0000940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrington LC, Ponlawat A, Edman JD, Scott TW, Vermeylen F. Influence of container size, location, and time of day on oviposition patterns of the Dengue vector, Aedes aegypti, in Thailand. Vector-Borne Zoonotic Dis. 2008;8(3):415–423. doi: 10.1089/vbz.2007.0203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrington LC, Ponlawat A, Scott TW, Edman JD. Does container size influence oviposition choices of the dengue vector Aedes aegypti? Am J Trop Med Hyg. 2005;73(6):914. [Google Scholar]
- Koenraadt CJM, Aldstadt J, Kijchalao U, Sithiprasasna R, Getis A, Jones JW, Scott TW. Spatial and temporal patterns in pupal and adult production of the Dengue vector Aedes aegypti in Kamphaeng Phet, Thailand. Am J Trop Med Hyg. 2008;79(2):230–238. [PubMed] [Google Scholar]
- Mercot H, Charlat S. Wolbachia infections in Drosophila melanogaster and D. simulans: Polymorphism and levels of cytoplasmic incompatibility. Genetica. 2004;120(1-3):51–59. doi: 10.1023/b:gene.0000017629.31383.8f. [DOI] [PubMed] [Google Scholar]
- Charlat S, Le Chat L, Mercot H. Characterization of non-cytoplasmic incompatibility inducing Wolbachia in two continental African populations of Drosophila simulans. Heredity. 2003;90(1):49–55. doi: 10.1038/sj.hdy.6800177. [DOI] [PubMed] [Google Scholar]
- Zabalou S, Apostolaki A, Pattas S, Veneti Z, Paraskevopoulos C, Livadaras I, Markakis G, Brissac T, Mercot H, Bourtzis K. Multiple rescue factors within a Wolbachia strain. Genetics. 2008;178(4):2145–2160. doi: 10.1534/genetics.107.086488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann AA, Hercus M, Dagher H. Population dynamics of the Wolbachia infection causing cytoplasmic incompatibility in Drosophila melanogaster. Genetics. 1998;148(1):221–231. doi: 10.1093/genetics/148.1.221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayashi TI, Marshall JL, Gavrilets S. The dynamics of sexual conflict over mating rate with endosymbiont infection that affects reproductive phenotypes. J Evol Biol. 2007;20(6):2154–2164. doi: 10.1111/j.1420-9101.2007.01429.x. [DOI] [PubMed] [Google Scholar]
- Hedrick PW. Genetics of populations. 4. Sudbury, Mass.: Jones and Bartlett Publishers; 2011. [Google Scholar]
- Narita S, Nomura M, Kageyama D. Naturally occurring single and double infection with Wolbachia strains in the butterfly Eurema hecabe: transmission efficiencies and population density dynamics of each Wolbachia strain. Fems Microbiology Ecology. 2007;61(2):235–245. doi: 10.1111/j.1574-6941.2007.00333.x. [DOI] [PubMed] [Google Scholar]
- Poinsot D, Montchamp-Moreau C, Mercot H. Wolbachia segregation rate in Drosophila simulans naturally bi-infected cytoplasmic lineages. Heredity. 2000;85(2):191–198. doi: 10.1046/j.1365-2540.2000.00736.x. [DOI] [PubMed] [Google Scholar]
- Rasgon JL, Scott TW. Wolbachia and cytoplasmic incompatibility in the California Culex pipiens mosquito species complex: Parameter estimates and infection dynamics in natural populations. Genetics. 2003;165(4):2029–2038. doi: 10.1093/genetics/165.4.2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weeks AR, Reynolds KT, Hoffmann AA, Mann H. Wolbachia dynamics and host effects: What has (and has not) been demonstrated? Trends Ecol Evol. 2002;17(6):257–262. doi: 10.1016/S0169-5347(02)02480-1. [DOI] [Google Scholar]
- Weeks AR, Turelli M, Harcombe WR, Reynolds KT, Hoffmann AA. From parasite to mutualist: Rapid evolution of Wolbachia in natural populations of Drosophila. PLoS Biol. 2007;5(5):997–1005. doi: 10.1371/journal.pbio.0050114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiparissides A, Kucherenko SS, Mantalaris A, Pistikopoulos EN. Global sensitivity analysis challenges in biological systems modeling. Ind Eng Chem Res. 2009;48(15):7168–7180. doi: 10.1021/ie900139x. [DOI] [Google Scholar]
- Marshall JM. The effect of gene drive on containment of transgenic mosquitoes. J Theor Biol. 2009;258(2):250–265. doi: 10.1016/j.jtbi.2009.01.031. [DOI] [PubMed] [Google Scholar]
- Enserink M. Australia to test 'mosquito vaccine' against human disease. Science. 2010;330(6010):1460–1461. doi: 10.1126/science.330.6010.1460. [DOI] [PubMed] [Google Scholar]
- Xi ZY, Khoo CCH, Dobson SL. Wolbachia establishment and invasion in an Aedes aegypti laboratory population. Science. 2005;310(5746):326–328. doi: 10.1126/science.1117607. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Model parameters, detailed equation appendix and sensitivity analysis. Portable Document File (pdf) containing all parameters, initial parameter values, and equations utilized by the model. Model development is discussed, and includes references from which each equation was developed/parameterized. Also includes the sensitivity analysis of all population dynamic parameters and discussion about the robustness of model predictions