Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2011 Oct;21(10):1728–1737. doi: 10.1101/gr.119784.110

A powerful and flexible statistical framework for testing hypotheses of allele-specific gene expression from RNA-seq data

Daniel A Skelly 1,3, Marnie Johansson 1, Jennifer Madeoy 1, Jon Wakefield 2, Joshua M Akey 1,3
PMCID: PMC3202289  PMID: 21873452

Abstract

Variation in gene expression is thought to make a significant contribution to phenotypic diversity among individuals within populations. Although high-throughput cDNA sequencing offers a unique opportunity to delineate the genome-wide architecture of regulatory variation, new statistical methods need to be developed to capitalize on the wealth of information contained in RNA-seq data sets. To this end, we developed a powerful and flexible hierarchical Bayesian model that combines information across loci to allow both global and locus-specific inferences about allele-specific expression (ASE). We applied our methodology to a large RNA-seq data set obtained in a diploid hybrid of two diverse Saccharomyces cerevisiae strains, as well as to RNA-seq data from an individual human genome. Our statistical framework accurately quantifies levels of ASE with specified false-discovery rates, achieving high reproducibility between independent sequencing platforms. We pinpoint loci that show unusual and biologically interesting patterns of ASE, including allele-specific alternative splicing and transcription termination sites. Our methodology provides a rigorous, quantitative, and high-resolution tool for profiling ASE across whole genomes.

Gene expression is the fundamental initial step in the process by which static genomic information gives rise to dynamic organismal phenotypes. Variation in gene expression has the potential to contribute significantly to phenotypic diversity within species and divergence between species (Britten and Davidson 1971; King and Wilson 1975). There is a diverse array of well-characterized examples of phenotypes influenced by regulatory polymorphisms, ranging from pelvic morphology in sticklebacks (Chan et al. 2010) to malaria susceptibility in humans (Tournamille et al. 1995). Although heritable variation in gene expression levels appears to be ubiquitous among individuals within species, an understanding of the distribution of regulatory variation and the mechanisms by which regulatory polymorphisms act remains limited (Rockman and Kruglyak 2006; Skelly et al. 2009).

Heritable differences in gene expression between individuals are ultimately caused by polymorphisms that affect the expression level of either one or both alleles (cis-acting or trans-acting polymorphisms, respectively) in a diploid. A powerful approach for identifying cis-acting regulatory variation is measuring allele-specific expression (ASE). An observation of differential allelic expression in a heterozygote indicates the presence of one or more variants that act in cis to affect the expression level of the gene. ASE has been studied by an assortment of methods, including variations of PCR (Cowles et al. 2002; Ronald et al. 2005a), pyrosequencing (Wittkopp et al. 2004), array-based platforms (Lo et al. 2003; Ronald et al. 2005b; Pant et al. 2006; Serre et al. 2008), and chromatin immunoprecipitation (Knight et al. 2003). A unifying theme of these studies has been that ASE is widespread both within and between a wide variety of species.

More recently, high-throughput sequencing has been used to assess ASE (Degner et al. 2009; Main et al. 2009; Zhang et al. 2009; Emerson et al. 2010; Heap et al. 2010; McManus et al. 2010; Montgomery et al. 2010; Pickrell et al. 2010), which affords a number of advantages compared to previous approaches. An RNA-seq approach gives measurements of ASE genome-wide for both protein-coding genes and noncoding RNA, provided transcribed polymorphisms are present to distinguish between alleles. Sequencing also offers an improved dynamic range over microarrays and results in digital allele counts with precision limited only by depth of coverage. Despite these advantages, inferences about ASE from high-throughput sequencing data have been made with simple statistical methods, which do not efficiently use all of the information contained in these large and complex data sets.

To address the lack of statistical methods for detecting ASE tailored to high-throughput sequencing data, we developed a Bayesian hierarchical model to analyze allelic read counts. We demonstrate that compared to existing approaches, our model is more powerful, accurately quantifies false-discovery rates (FDR), and facilitates more meaningful biological inferences. We use our method to characterize the landscape of ASE in a diploid hybrid of two diverse strains of Saccharomyces cerevisiae and find that our data are consistent with an overall proportion of nearly 80% of measured genes exhibiting ASE, 1991 of which are significant at FDR = 5%. Our statistical model also identified numerous genes with biologically interesting examples of ASE, including allele-specific alternative splicing and transcription termination sites. In addition, to highlight the advantages of our approach for more complex genomes, we applied our method to an RNA-seq data set in humans. Our analysis highlights the utility of using a carefully designed statistical framework to leverage the massive amount of information present in RNA-seq data sets to reveal biological insights.

Results

ASE in the yeast genome

We measured ASE by RNA-seq in a diploid hybrid of two diverse strains of S. cerevisiae, the laboratory strain BY4716 (BY, isogenic to S288C) and the wild vineyard strain RM11-1a (RM). We obtained sequence data from two independent high-throughput sequencing platforms, the ABI (Life Technologies) SOLiD System and the Illumina Genome Analyzer II (GAII) (Table 1). To eliminate any read-mapping bias (Degner et al. 2009), which could lead to erroneous inferences of allelic differences in transcript abundance, we developed strict criteria to call reads as matching the BY or RM allele (Methods). Furthermore, an insidious possible source of bias is differential allelic amplification that would manifest as differential allelic expression. To correct for this, we removed any reads that were potential PCR duplicates. Although this is a conservative approach for single-end reads, we found that naively including duplicate reads induced both global and gene-specific artifacts (Supplemental Note). Overall, we obtained allele-specific read counts for approximately 4500 protein-coding genes and noncoding RNAs in the yeast genome, each of which is expressed in rich media and contains at least one transcribed polymorphism.

Table 1.

Information on RNA-seq data sets

graphic file with name 1728tbl1.jpg

Open in a new tab

As a first attempt at quantifying ASE in the diploid hybrid, we summed counts of reads from the BY and RM alleles across all SNPs in each gene and conducted a simple binomial exact test of the null hypothesis that each allele is equally expressed. This is the primary test that has been employed in previous studies of ASE using RNA-seq (Supplemental Note). This test assumes that read counts within each gene are binomially distributed, with a significant test result indicating evidence for ASE. We restricted our analysis to genes with a coverage of at least 20 allele-distinguishing reads: 1208 and 1094 genes showed nominally significant ASE (binomial test P < 0.05) in our Illumina GAII and ABI SOLiD data sets, respectively. Although the simplicity of this test is appealing, it has several limitations. First, it is not clear how to allow for the possibility of extra-binomial variation in read counts caused by technical variability, as the binomial test cannot be tuned to the context of the experiment. Second, it is not straightforward to combine information from different experiments or replicates to obtain a composite measure of confidence in ASE. Third, it is difficult to calculate an accurate estimate of the FDR, the fraction of genes called as showing ASE that do not truly show ASE. Methods that make use of the complete distribution of P-values (Storey and Tibshirani 2003) to estimate this quantity are difficult to apply with the binomial exact test because the distribution of P-values under the null hypothesis is not uniformly distributed (Supplemental Methods). Finally, summing the counts of reads across SNPs to estimate ASE across a gene is undesirable as it masks heterogeneity in ASE at individual SNPs. When properly modeled, such information can provide valuable insights regarding the mechanistic basis of ASE, as we demonstrate below.

A hierarchical Bayesian model for measuring genome-wide ASE

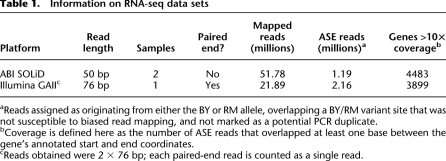
To address the limitations of standard binomial tests for ASE, we developed a powerful and flexible Bayesian hierarchical model for allelic read count data (Fig. 1; for further details, see Methods and Supplemental Methods). First, we calibrate our model for genes without ASE (Fig. 1A) using sequence data from genomic DNA, for which allele counts should vary only according to statistical sampling and technical variability. This enables us to allow for some “noise” in allele counts that does not have true biological relevance. Second, the model is motivated by our desire to classify genes according to whether they show ASE and whether patterns observed across SNPs are consistent with a constant level of ASE across the gene. We designed our model to partition genes into two broad categories: genes not showing ASE (Fig. 1A) and those showing ASE (Fig. 1B). Thus, we can directly estimate the global fraction of genes that show ASE in our experiment; we use the notation π0 to denote the fraction of genes that does not show ASE, with 1 − π0 representing the fraction that does show ASE. For genes showing ASE, we allow levels of ASE to vary across SNPs, as might be expected for genes with complicated patterns of ASE due to biological mechanisms such as allele-specific splicing, alternative polyadenylation site usage, or alternative transcription start sites (Fig. 1C). We label genes with varying levels of ASE across SNPs as showing “variable ASE.” We note that this model can accommodate multiple replicate data sets from different sequencing platforms in a statistically rigorous manner, while allowing for the possibility of platform-specific estimates of technical variability.

Figure 1.

Figure 1.

Open in a new tab

Schematic outline of our model. (A) The true fraction of reads from allele one should be exactly 0.5 in genomic DNA from a diploid. We use genomic DNA sequencing to calibrate our model in order to account for noise in read counts (arrow depicting width of distribution) at all SNPs as a result of technical variability inherent in the sequencing process. (B) Genes are partitioned into two categories: genes with ASE and those without ASE. For genes without ASE, the distribution of the fraction of reads from allele one is estimated as in A. We borrow information from across all genes to estimate the mean and variability of the corresponding distributions for genes with ASE, the second category. Some genes in this category have a mean different from 0.5 but low dispersion in read counts, like genes without ASE (blue distributions). Other genes in this category have greater dispersion in read counts (tan distributions). (C) Distributions for the fraction of reads from allele one are estimated for each gene. Differences in mean and variability of these gene-specific distributions allow for genes that do not show ASE (top), genes that show ASE that is constant across the transcript (middle), and genes that potentially show complex patterns of ASE (variable ASE), such as allele-specific alternative splicing (bottom). (Left panels) Gene-specific distributions of the fraction of reads from allele one. (Right panels) Simulated allele-specific read counts for a three-exon gene (gray boxes) containing four SNPs (red lines). Dots below the gene model indicate, at each SNP, the fraction of reads matching allele one.

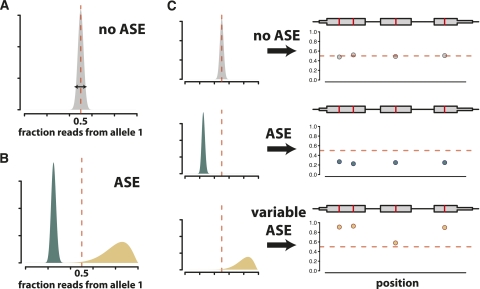
We perform inference using Markov chain Monte Carlo (MCMC). We conducted simulations to explore the power and robustness of our approach compared with the binomial exact test. We simulated read counts with levels of overdispersion (which could be introduced due to technical variability) estimated from our data (Supplementary Methods), and calculated the posterior probability of ASE for each simulated gene. We calculated the true-positive and false-positive rate across thresholds based on P-values for the binomial exact test and posterior probabilities of ASE for our model. Figure 2A shows that our model outperforms the binomial exact test across all thresholds. We also calculated a Bayesian analog to the FDR, which accurately represented the true FDR (Fig. 2B).

Figure 2.

Figure 2.

Open in a new tab

Performance of the Bayesian model for ASE. (A) Receiver operating characteristic (ROC) curve showing the performance of our model compared to the binomial exact test. Read counts were tabulated on simulated data with overdispersion, as described in the Supplemental Methods. The ROC curve plots the number of true positives called correctly and the number of false positives called incorrectly using P-value thresholds from 0–1 for the binomial test and posterior probabilities of no ASE from 0–1 for our Bayesian model. (B) Observed FDR closely tracks the true FDR. Observed and true FDRs were calculated for simulated data with overdispersion, as described in the Supplemental Methods. The dotted light gray line shows y = x.

Consistent estimates of ASE across different sequencing platforms

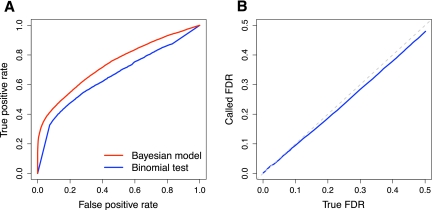
As noted above, an important feature of our model is that it can combine replicate data from different sequencing platforms in a statistically rigorous framework. However, before combining all of our sequencing data, we first compared estimates of ASE derived independently from separate analyses of the Illumina GAII and ABI SOLiD data sets. Overall, we found high concordance between the results from the two platforms. We obtained more usable allele-specific reads from our Illumina GAII data (Table 1), allowing us to call more genes as showing significant ASE than in our ABI SOLiD data. We examined lists of genes called as showing ASE at a FDR = 5%,and found 453 genes called significant in both experiments (Fig. 3A). Given the incomplete power of each experiment, we would not expect perfect overlap between lists of significant genes. We used estimates of the power and false-positive rate for each experiment along with simulations to demonstrate that the observed overlap between experiments is reasonably close to the expected level (Supplemental Methods).

Figure 3.

Figure 3.

Open in a new tab

Concordance of measurements of ASE obtained using different sequencing platforms. (A) Overlap between genes showing significant ASE at FDR = 5% for two sequencing platforms. (Orange square) Genes called significant in data from both platforms. (Blue squares) Genes called significant on only one platform, indicated on the far side of the square. Numbers in white indicate the number of genes falling into each category; the area of each square is proportional to this number. (B) Magnitude of log2-fold difference in gene expression for genes called significant at FDR = 5%. Log2-fold differences are computed with respect to the allele with lower expression, causing all values to be positive. Lines shown are continuous approximations to discrete densities. (Blue line) Density for genes called significant using only one sequencing platform. (Orange line) Density for genes called significant in data from both sequencing platforms.

Genes exhibiting significant ASE in both experiments might be expected to show, on average, more deviation from equal allelic expression than do genes with significant ASE in only one experiment. Indeed, the median magnitude of log2-fold change in expression for genes showing ASE in both experiments was significantly higher than for genes showing ASE in only one experiment (0.393 vs. 0.337, permutation test P = 0.0055) (Fig. 3B). Lastly, we examined the probability that each gene showed ASE in our Illumina GAII data set, and compared this to the same probability calculated using our ABI SOLiD data set. We observed a modest but highly significant correlation between these two measures of ASE (Spearman's ρ = 0.09; P = 1.0 × 10−8). Given the concordance between our measurements from the two technologies, we focus below on results inferred by simultaneously analyzing the data from both sequencing platforms.

Bayesian hierarchical model reveals features of ASE

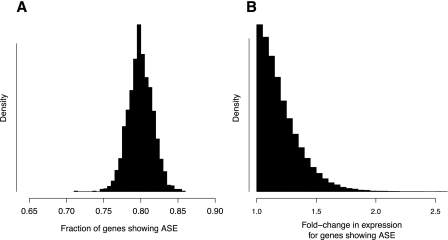
An important advantage of our statistical model is that we are able to leverage the wealth of information contained in an RNA-seq data set to make precise inferences about global parameters, averaging over the conclusions drawn from any single gene. For example, one basic quantity of interest is the total fraction of genes that exhibits ASE. This can be computed easily from our model using our estimate of π0, the fraction of genes that does not exhibit ASE. Combining all of our data, we estimate that ∼79% of genes interrogated show ASE between BY and RM (95% credible interval 76%–83%) (Fig. 4A). We also inferred the distribution of the magnitude of ASE for genes showing ASE and used this to plot the distribution of fold-change in expression for genes with ASE (Fig. 4B). In biological terms, this distribution supports the notion that most expression changes are relatively small (more than 90% of genes with ASE show expression changes less than 1.5-fold).

Figure 4.

Figure 4.

Open in a new tab

Global features of ASE in the yeast genome. (A) Posterior distribution of the fraction of genes showing ASE, 1 − π0. (B) Posterior distribution for the size of the fold-change in expression of genes showing ASE. Fold-change values are shown relative to the allele expressed at a lower level, meaning that all values are greater than one. Distribution depicts the estimated probability density from which the magnitude of the ASE would be drawn for a new gene known to show ASE. Distribution shown was simulated by randomly drawing values from beta distributions specified by posterior samples of f and g, which determine the shape of the probability density of the binomial parameter p for genes showing ASE.

Next, we sought to identify which genes showed the strongest evidence for ASE overall, as well as which genes were good candidates for variable ASE. We identified 1991 genes with significant evidence for ASE (5% FDR, corresponding to a posterior probability of ASE > 0.82). Among these genes, 22 are known noncoding RNAs, and the remainder encode proteins. A previous study employed expression levels measured using microarrays and identified 1428 genes with significant evidence for local gene expression QTL (eQTL) (Ronald et al. 2005a). We obtained ASE measurements for 1198 of these genes and detected significant evidence (5% FDR) for ASE in 637, supporting the assertion that these genes show cis-regulatory variation. Additionally, among 43 genes previously verified by quantitative PCR to show ASE (Ronald et al. 2005a), we called 30 as showing significant ASE.

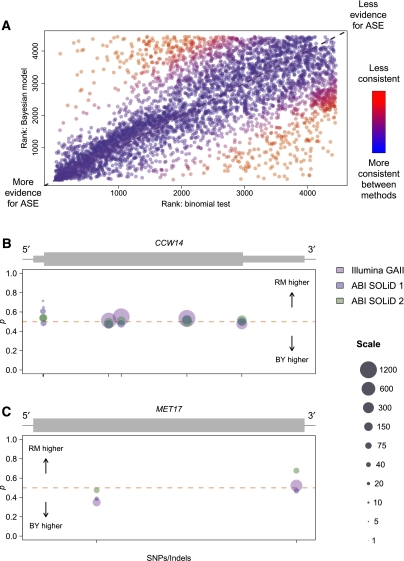
We also compared inferences of ASE made using our Bayesian model to those made using a binomial test of equal allelic expression for read counts summed across all data sets for all SNPs in each gene. As expected, measures of ASE were, on the whole, strongly correlated between methods (Spearman's ρ = 0.67; P < 2.2 × 10−16). However, there were many exceptions to this pattern. Figure 5A shows a plot of genes ranked by evidence for ASE in the two models and demonstrates that while most genes have similar rankings (blue points), a nontrivial proportion of genes show highly discrepant results (red points; 1078 genes differ in rank by at least 25% of the total number of genes).

Figure 5.

Figure 5.

Open in a new tab

Comparison of results from the binomial test and Bayesian model of ASE. (A) Plot comparing ranks of genes in terms of evidence for ASE for the binomial test versus the Bayesian model. Ranks were determined using P-values for the binomial test and using posterior probabilities of ASE for the Bayesian model. Ties were broken by random assignment of ranks to genes with equal P-values/posterior probabilities of ASE. Points are colored according to consistency of ranks between methods. As shown in the color bar to the right, redder points represent genes with ranks that are less consistent between methods, while bluer points show genes ranked more consistently between methods. Dotted gray line in background follows y = x. (B) Allele-specific read counts for the gene CCW14, which is called as showing ASE using the binomial test, but not with the Bayesian model. Plot depicts the gene model (gray rectangles), with thick rectangles representing exons, thinner rectangles representing 5′ and 3′ UTRs, and the thin black line representing intergenic sequence. Circles plotted below the gene model show allele-specific read count data organized by SNPs/indels within the gene. Circles are centered on the point p = (BY count)/(BY count + RM count), and sized according to the total number of reads contributing to the observation. Scaling of circle size follows the scale given on the far right, with all observations with more than 1200 reads set to the largest size shown (1200). Circle colors indicate which experiment the observation is derived from, as shown in the legend on the far right. Ticks on the x-axis indicate the location of SNPs or indels used to distinguish between alleles. Sequence coverage is high, and the slight departures from 50:50 allelic expression are likely due to technical variability rather than some underlying biological mechanism. (C) Allele-specific read counts for the gene MET17, which is called as showing ASE using the Bayesian model, but not with the binomial test. Plot is organized and colored identically to B. The data show a modest but reproducible change in ASE from read counts higher for the BY allele to read counts higher for the RM allele moving 5′ to 3′.

We further examined genes with highly discrepant measures of ASE between methods. There were 192 genes ranked among the top third most likely to show ASE by one method, but the bottom third least likely to show ASE by the other method. Figure 5, B and C, shows examples of two such genes and illustrates some of the advantages of our method over the binomial test. Figure 5B shows the gene CCW14 (YLR390W-A), a cell wall glycoprotein called as exhibiting significant ASE using the binomial exact test (P = 1.2 × 10−5). The sequence coverage at SNPs within this gene is high and allelic read counts occur at ratios close to 50:50, but there is enough departure from equal allelic expression for rejection of the binomial test. It seems likely that the slight variations from perfectly equal allelic expression are due to technical variability rather than some underlying biological mechanism, and reassuringly, this gene shows no evidence for ASE using our Bayesian model (posterior probability of ASE < 0.4). Figure 5C shows the gene MET17 (YLR303W), a methionine and cysteine synthase called as significant using our Bayesian model (FDR = 5%) but not the binomial test (P = 0.86). The data show a modest but reproducible change in ASE from read counts higher for the BY allele to read counts higher for the RM allele moving 5′ to 3′. This example emphasizes the fact that our model can detect variable ASE, while such genes are difficult to identify by the binomial test.

Variable ASE leads to mechanistic insights into ASE

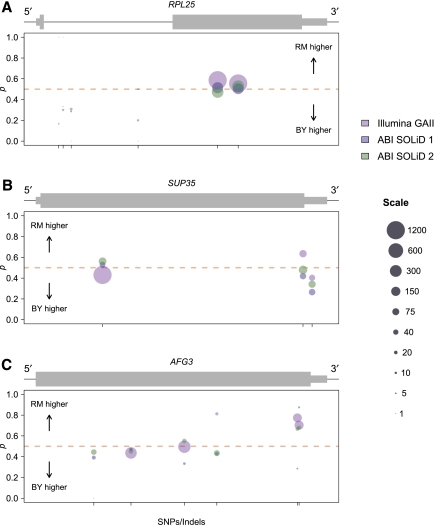
There are a variety of possible mechanisms that might cause a gene to exhibit variable ASE, such as allele-specific alternative splicing, allele-specific polyadenylation site usage, allele-specific transcription start sites, or allele-specific antisense transcription encroaching over a portion of a gene. We found candidate genes showing variable ASE by ranking genes by the parameter ei, which measures dispersion around the mean level of ASE for all SNPs in a gene (Supplemental Methods). We found examples of genes with variable ASE likely caused by some of the above mechanisms by visually examining read counts at loci that ranked among the 10% most variable (Fig. 6). Figure 6A shows the gene RPL25 (YOL127W), a protein component of the large ribosomal subunit with read counts consistent with allele-specific alternative splicing. In particular, we observed high read counts and reproducibly equal allelic expression in the second exon of the gene, but lower read counts and expression biased in favor of the BY allele at four SNPs in the intron. Our observations are consistent with the sampling of a modest number of immature mRNA transcripts, with the BY allele present at a higher level, and a larger number of mature mRNA transcripts, with equal allelic expression. One possible mechanistic explanation for this observation is that splicing of the BY allele is inefficient, causing either a longer persistence time of immature mRNAs or a higher percentage of intron retention in mature mRNA than for the RM allele.

Figure 6.

Figure 6.

Open in a new tab

Examples of genes showing variable ASE. Plots are organized and colored identically to Figure 5, B and C. (A) Allele-specific read counts for the gene RPL25. Thin black line represents both intronic and intergenic sequence. Read counts indicate reproducibly equal expression in exon two of the gene, but expression biased in favor of the BY allele at four SNPs within the intron, consistent with allele-specific differences in splicing. (B) Allele-specific read counts for the gene SUP35. Higher expression of the BY allele at a SNP in the 3′ UTR suggests allele-specific variation in UTR length. (C) Allele-specific read counts for the gene AFG3. Higher expression of the RM allele near the 3′ end of the gene is consistent with allele-specific variation in transcript structure that could occur some distance away from the SNP tagging the ASE.

In addition to allele-specific alternative splicing, we found genes that appeared to demonstrate allele-specific variation in transcriptional start or stop sites. For example, Figure 6B shows the gene SUP35 (YDR172W), which codes for a protein involved in translation termination. We observed nearly equal expression of both alleles within the coding sequence of the gene, but higher expression of the BY allele at a SNP in the 3′ untranslated region (UTR) of the gene (Fig. 6B). This observation suggests that the length of the 3′ UTR may vary between alleles, with a shorter 3′ UTR associated with the RM allele. Another example of variation in transcript structure is the gene AFG3 (YER017C), a component of a mitochondrial inner membrane protease. For AFG3 we observed equal allelic expression at the 5′ end of the gene and strong but reproducibly biased expression in favor of the RM allele near the 3′ end of the gene (Fig. 6C). This pattern is consistent with premature termination of transcription in the BY background or a shorter 3′ UTR associated with the BY allele. We note that because our data derive from 50- to 76-bp reads (paired-end reads for Illumina GAII data), observations of ASE at particular SNPs could reflect variation in transcript structure located some distance from the SNP in question. The ability to identify these biologically complicated examples of ASE is an important strength that is unique to the statistical approach we develop.

Application to measuring ASE in the human genome

To explore the utility of our method for characterizing ASE in a more complex mammalian genome, we obtained RNA-seq reads from four lanes on the Illumina GAII generated by Pickrell et al. (2010) from an individual of African descent, a member of the Yoruba in Ibadan, Nigeria, with high-quality phased genotypes available from the International HapMap Project (The International HapMap 3 Consortium 2010). This individual is heterozygous at about 164,000 annotated transcribed sites, and we detected reads with distinguishable alleles mapping to 5780 genes. Pickrell et al. (2010) conducted a targeted test of 244 genes with significant evidence for local eQTL to explore whether ASE contributed to expression variation among 69 individuals. In contrast, we carried out a genome-wide survey of ASE in this single individual (NA18498). By performing our analysis on a single individual, we avoid the possible complication of differences in genetic background confounding the relative expression levels of two alleles. This data set has significantly lower sequencing depth than the yeast data described above, with only 2082 genes containing 10 or more reads that overlap a transcribed polymorphism.

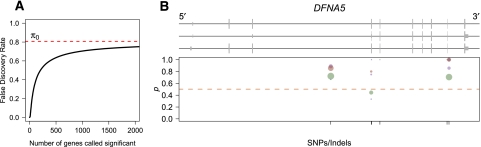
We identified 17 genes with evidence for significant ASE (5% FDR) in individual NA18498. These genes corresponded well to those identified by summing reads across SNPs and performing a binomial test. As it is difficult to calibrate the FDR for the binomial test, we chose a P-value threshold of 0.001 (corresponding to an expectation of about five expected false positives), which resulted in a significant test result for 18 genes. Of these 18 genes, our Bayesian model identified 15 (FDR = 5%). The genes called as showing significant ASE by the binomial test but not using our model all had a high skew in allelic expression but few reads mapping (less than 30), while the two genes called as significant by our model were marginally significant by the binomial test (P < 0.05). Although we pinpoint 17 genes as showing significant ASE, we estimate the fraction of the complete set of genes tested showing ASE to be ∼19% (95% credible interval 11%–30%) (Fig. 7A). Although it is difficult to obtain a precise figure for the fraction of genes showing ASE in an individual human due to differences in study design, power, and statistical methodology, this range is generally consistent with previous studies of ASE in humans (Bray et al. 2003; Pastinen et al. 2004; Serre et al. 2008; Ge et al. 2009).

Figure 7.

Figure 7.

Open in a new tab

ASE in the human genome. (A) Plot of the false-discovery rate as a function of the number of genes called significant. Since the human RNA-seq data set is low coverage for most genes, it is not possible to identify many genes showing significant ASE without risking a relatively large proportion of false discoveries. (B) Human gene DFNA5, which shows significant ASE in individual NA18498. Plot is organized identically to Figure 5, B and C, with different colored dots representing measurements obtained from separate Illumina sequencing lanes. Although the number of reads is low for any given dot, the proportion of reads from allele one is consistently higher than that for allele two.

We also searched for genes showing complicated patterns of ASE that might inform our understanding of mechanisms of ASE at these loci. Given the low overall coverage of this data set, we did not find any convincing examples of variable ASE. However, an examination of read counts at multiple SNPs within a gene can still be informative about potential mechanisms of ASE. For example, Figure 7B shows the gene DFNA5 (ENSG00000105928), which has three transcript isoforms and is implicated in nonsyndromic hearing impairment in humans (van Camp et al. 1995). Although read counts at SNPs within this gene are quite low, this gene was called as showing significant ASE (FDR = 5%). As is apparent from Figure 7B, the proportion of reads from allele one is consistently high across all SNPs in the gene, with the exception of two points with relatively few reads (green point just below 0.5 represents a total of only nine reads). Such read counts would be most consistent with a variant in the promoter affecting transcription initiation or a variant in the 3′ UTR affecting decay rates that acts uniformly across the transcript, rather than allele-specific variation in transcript structure. In the future, advances in sequencing technology and RNA-seq read-mapping software are likely to lead to data sets with deeper coverage and more accurate reconstruction of transcript structure, which will allow a more complete picture of the landscape of ASE in humans.

Discussion

We describe a novel method for gaining insight on the genome-wide characteristics of cis-regulatory variation and discovering loci with complex patterns of ASE. We demonstrate that inferences of ASE made using different sequencing platforms are highly concordant, and identify about 2000 genes showing ASE (FDR = 5%) between two diverse yeast strains. Our model provides a framework for analyzing allele-specific read count data obtained at multiple SNPs within genes over multiple experimental replicates in a statistically rigorous manner. Combining information from SNPs across the length of a transcript and allowing for technical variation in read counts are key advantages that allow our model to outperform the binomial test. In addition, we demonstrate that explicitly allowing levels of ASE to vary across SNPs within genes can lead to the identification of genes showing biologically interesting patterns of ASE that may have remained invisible by other analysis methodologies (Fig. 6). Modeling complicated mechanisms of ASE is likely to be even more critical as we move toward studying ASE in deeply sequenced mammalian transcriptomes, where phenomena such as alternative splicing are pervasive.

A unique strength of our approach is its ability to simultaneously make use of all of the sequence data to infer global parameters of interest. Of the genes that have transcribed polymorphisms, we estimate that nearly 80% exhibit ASE. This estimate is higher than a previous estimate for the same two yeast strains (∼20%) based on verification of cis-acting regulatory variation by allele-specific quantitative PCR for genes with local eQTL (Ronald et al. 2005a). However, several details of differences in study design and methodology can account for this discrepancy. First, only genes with a transcribed polymorphism can be assessed for ASE with RNA-seq, while the estimate of Ronald et al. (2005a) relied on eQTL that were detected without this requirement. Ronald et al. (2005a) showed that there is a higher rate of local regulatory variation (most of which acts in cis to produce ASE) in more polymorphic regions of the yeast genome. Thus, our estimate is likely higher in part due to measurements made on genes found in regions of the yeast genome ascertained to have a high occurrence of cis-acting regulatory variants. Second, microarray measurements of gene expression levels may miss some of the transcript variants that we detect and classify as variable ASE if probes are designed to regions of the gene with equal allelic expression. Finally, we note that RNA-seq affords the opportunity to measure transcript levels with very high precision (Wang et al. 2009). Given the large number of polymorphic noncoding sites found between BY and RM (more than 30,000), it may be that nearly every gene in the genome shows some level of ASE when measured with sufficient precision, which raises a fundamental question: What level of ASE is biologically significant? In the future, it will be critical to move beyond describing and cataloging variation in transcript levels toward a more complete understanding of the functional relevance of expression variation.

Finally, although we applied our statistical methodology to study ASE, our framework is general and can be used to characterize allelic differences of any functional genomics phenotypes derived from sequence data, such as methylation (Shoemaker et al. 2010) or protein–DNA interactions (Hesselberth et al. 2009). As new applications of high-throughput sequencing are conceived (Morozova et al. 2009), it will become increasingly important to develop statistical methods tailored to these large and formidably complex data sets in order to maximize the biological insights derived from such experiments.

Methods

Experimental design

We mated strains BY4716 and RM11-1a and used auxotrophic deletions to select for the diploid hybrid during mating. These strains have been described in detail elsewhere (Brem et al. 2002). We grew the strains to mid-log phase (OD600, 0.8–1.0) in rich media (YPD). We extracted RNA by the acid phenol method (Schmitt et al. 1990) and confirmed RNA integrity using an Agilent 2100 Bioanalyzer (Agilent Technologies). We extracted genomic DNA using a modified version of the yeast smash and grab protocol (Hoffman and Winston 1987).

We provide a brief overview of sequencing library preparation here and give full details with kit numbers in the Supplemental Materials. We prepared genomic DNA libraries according to the manufacturer-recommended protocols. For all RNA samples, we performed poly(A) enrichment and one round of ribosomal RNA depletion. For RNA samples submitted to the Illumina GA, we fragmented RNA to 60–200 bp, made cDNA by random priming, and followed the manufacturer-recommended protocols for the remainder of sequencing library preparation. For RNA samples submitted to the SOLiD System, we prepared libraries according to the manufacturer-recommended protocols. All SOLiD samples were tagged with four barcodes per library.

Yeast allele-specific read mapping

We obtained complete genome sequences for BY from the Saccharomyces Genome Database (June 2008 sequence; http://www.yeastgenome.org/) and for RM from the Broad Institute (http://www.broadinstitute.org/). After repeat masking (Smit et al. 2010) the sequences, we used LASTZ (http://www.bx.psu.edu/miller_lab) to infer alignment scoring parameters appropriate for aligning the BY and RM genomes and to generate pairwise alignments between all chromosomes of the two strains. We then used TBA (Blanchette et al. 2004) to compute a whole-genome alignment that is not biased in favor of any particular reference genome. We masked any nucleotides that were ambiguous in either genome, projected this alignment to both BY and RM genomic coordinates to construct reference genomes for the strains, and mapped all reads to both genomes. To align reads in colorspace or nucleotide space, we used the program BFAST (Homer et al. 2009; Supplemental Methods).

Next, we examined the alignment of each read to the BY genome and to the RM genome in order to search for reads with a distinguishable allelic origin. We analyzed only the highest-scoring alignment of each read to each genome. We required reads to map to approximately the same genomic location in BY and RM; specifically, we required each read to map within the same alignment block in each strain. We used a simple probabilistically motivated, base quality–aware scoring scheme implemented in the program cross_match (http://phrap.org/phredphrapconsed.html) to score the alignment of the read to the genome of each strain (Supplemental Methods), and considered a read to be a candidate BY read if the score was higher for the alignment to the BY genome and vice versa. Any read with an alignment to one genome that scores higher must overlap a SNP, indel, or chromosomal breakpoint between the strains. At a small proportion of SNPs, read mapping is strongly biased toward one of the two alleles, as has been noted previously in humans (Degner et al. 2009). To overcome this potential source of bias, we simulated 50-bp reads with sequencing errors overlapping every SNP and indel ascertained from our whole-genome multiple alignment of BY and RM, and mapped the simulated reads using the same pipeline described above (Supplemental Methods). For our experimentally acquired data, we then filtered out all allelically mapped reads that overlapped a SNP showing a deviation >5% from equal mapping of alleles in our simulated reads. To assign reads to genes, we used gene annotations from the Saccaromyces Genome Database, along with 5′ and 3′ UTRs predicted by RNA-seq (Nagalakshmi et al. 2008). We ignored SNPs or indels that occurred within more than one overlapping genomic feature. For reads that overlapped multiple SNPs, we randomly assigned the read count to one of the SNPs. It has been noted by other investigators that base composition has a significant effect on the propensity of a molecule to be sequenced using high-throughput sequencing technologies (Dohm et al. 2008; Bullard et al. 2010; Pickrell et al. 2010). This phenomenon could affect our results only when the BY and RM alleles at a particular locus differ greatly in base composition (which is rare), since our analysis only compares relative allelic expression. Nevertheless, we performed a correction for GC content by (1) calculating expected sequencing depth for windows of a given GC content using our genomic DNA data and (2) adjusting relative RNA read counts based on the difference in predicted read depth between fragments of BY or RM allelic GC content (Supplemental Methods).

Finally, we removed any reads marked as potential PCR duplicates to ensure that differential allelic expression was not due to differential allelic amplification. For our Illumina single-end and paired-end data, we used Picard's MarkDuplicates command-line tool (http://picard.sourceforge.net/). For our ABI SOLiD data, we took advantage of the four molecular barcodes tagging each sequencing library. Since the barcodes are embedded in bridge primers used for PCR amplification, reads possessing different barcodes must originate from distinct molecules. As such, for each genomic position, we kept a maximum of one read per barcode and marked the remaining reads as PCR duplicates.

Human allele-specific read mapping

We obtained four lanes of RNA-seq data (two 35-bp and two 46-bp single-end data sets) generated by Pickrell et al. (2010) for individual NA18498. This individual had the most RNA-seq reads of any sample sequenced by Pickrell et al. (2010). We obtained phased genotype information from the International HapMap Project (The International HapMap 3 Consortium 2010). We mapped reads to the reference human genome (hg18/build 36) using the program GSNAP version 2011-03-11 (Wu and Nacu 2010), which features SNP-tolerant alignment. We also took advantage of GSNAP's ability to detect splicing events using a database of known splice junctions compiled using Ensembl gene annotations (Hubbard et al. 2002). We ran GSNAP with the options --use-snps, --splicesites, --max-mismatches=0.05, --npaths=1, --trim-mismatch-score=0, and --quiet-if-excessive to obtain unique alignments of each read. To ensure that GSNAP's SNP-tolerant alignment feature eliminated the mapping bias in favor of the reference allele (Degner et al. 2009), we simulated reads (35 and 46 bp in length, the lengths of the actual reads) of both alleles at every position overlapping the SNP. We mapped these reads to the human genome using the same commands used to map the real data. We found that mapping bias was completely eliminated for all but a small number of SNPs (about 2600 SNPs, or about 1.5% of all SNPs), which we removed from further consideration.

In order to obtain allele-specific read counts, we group SNPs by Ensembl-annotated gene and examined any genic SNPs overlapping a mapped read. We assigned reads as originating from haplotypes A or B (as defined by the phased HapMap data; labels are arbitrary for our purposes). For reads overlapping multiple SNPs, we randomly chose a single SNP and incremented the read count for that SNP. This procedure results in allele-specific read counts for SNPs within each gene that are stratified as originating from either haplotype A or B, which served as input to our Bayesian model. As the RNA-seq data from Pickrell et al. (2010) were not accompanied by genomic DNA sequence data, we used the same estimates of the dispersion in read counts as our full analysis of the yeast data (i.e., the analysis of Illumina and ABI data using estimates derived from yeast genomic DNA sequencing data).

Statistical analysis

We used the R statistical environment for all statistical analyses (R Development Core Team 2010). For our initial analysis of allelic count data using the binomial exact test, we used the binom.test function. We provide a brief summary of our Bayesian hierarchical model here and provide a detailed description in the Supplemental Methods. We construct a three-stage hierarchical model for allelic read counts. We denote the count of reads mapping to RM at SNP j in gene i and replicate r as Yijr, and in the first-stage model, these counts are binomially distributed with parameters Nijr (coverage at the SNP) and pij. At the second stage, the pij arises from a gene-specific beta distribution with parameters αi and βi. The second stage allows for the possibility that pi may not be constant across all SNPs within gene i. These steps can be collapsed to give a beta-binomial model. We reparameterize the beta distribution as pi = αi/(αi + βi) and ei = 1/(1 + αi + βi), which have straightforward interpretations as the mean amount of ASE (pi) and the dispersion around the mean (ei) for gene i. As the dispersion ei approaches zero, the counts converge to binomially distributed. Finally, we place a two-component mixture prior on pi, ei

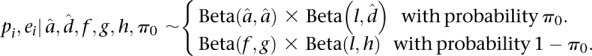graphic file with name 1728equ1.jpg

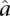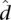The parameters Inline graphic and Inline graphic are estimated from genomic DNA data and provide a measure of the “noise” in read counts due to technical variability. 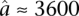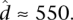We estimated these parameters separately using genomic DNA data from each technology platform and found that the estimates were similar (95% credible intervals overlapped), so in our analysis of data from both platforms, we used the median of all posterior samples as our estimate for these parameters: Inline graphic and Inline graphic We implement this model using MCMC, running multiple Markov chain simulations for at least 500,000 iterations and examining time series plots of model parameters to verify convergence. 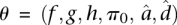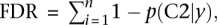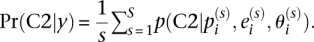For any list of i = 1, …, n genes (out of m total genes) and s = 1, …, s draws from the posterior distribution of each parameter obtained via MCMC, if we let Inline graphic, we can calculate the FDR achieved when calling those genes significant using the formula Inline graphic with Inline graphic In this formula, C2 signifies component 2 of the two-component mixture prior described above and is calculated using Bayes' formula as detailed in the Supplemental Methods. R code to implement the statistical model we describe is available in the Supplemental Material and from the website http://akeylab.gs.washington.edu/downloads.shtml.

Data access

Raw data are accessible at the NCBI Sequence Read Archive (http://trace.ncbi.nlm.nih.gov/Traces/sra/sra.cgi) under accession number SRP007477.

Acknowledgments

We thank Choli Lee for assistance with Illumina Genome Analyzer sequencing and the University of Washington High-Throughput Genomics Unit for assistance with ABI SOLiD System sequencing. This work was supported by an NIH grant (1R01GM078105) to J.M.A.

Authors' contributions: M.J. and J.M. performed experiments. J.W., D.A.S., and J.M.A. designed the statistical model. D.A.S. analyzed the data. D.A.S., J.M.A., and J.W. wrote the paper.

Footnotes

[Supplemental material is available for this article.]

Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.119784.110.

References

  1. Blanchette M, Kent WJ, Riemer C, Elnitski L, Smit AF, Roskin KM, Baertsch R, Rosenbloom K, Clawson H, Green ED, et al. 2004. Aligning multiple genomic sequences with the threaded blockset aligner. Genome Res 14: 708–715 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bray NJ, Buckland PR, Owen MJ, O'Donovan MC 2003. Cis-acting variation in the expression of a high proportion of genes in human brain. Hum Genet 113: 149–153 [DOI] [PubMed] [Google Scholar]
  3. Brem RB, Yvert G, Clinton R, Kruglyak L 2002. Genetic dissection of transcriptional regulation in budding yeast. Science 436: 701–703 [DOI] [PubMed] [Google Scholar]
  4. Britten RJ, Davidson EH 1971. Repetitive and non-repetitive DNA sequences and a speculation on the origins of evolutionary novelty. Q Rev Biol 46: 111–138 [DOI] [PubMed] [Google Scholar]
  5. Bullard JH, Purdom EA, Hansen KD, Dudoit S 2010. Evaluation of statistical methods for normalization and differential expression in mRNA-Seq experiments. BMC Bioinformatics 11: 94 doi: 10.1186/1471-2105-11-94 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chan YF, Marks ME, Jones FC, Villarreal G, Shapiro MD, Brady SD, Southwick AM, Absher DM, Grimwood J, Schmutz J, et al. 2010. Adaptive evolution of pelvic reduction in sticklebacks by recurrent deletion of a Pitx1 enhancer. Science 327: 302–305 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cowles CR, Hirschhorn JN, Altshuler D, Lander ES 2002. Detection of regulatory variation in mouse genes. Nat Genet 32: 432–437 [DOI] [PubMed] [Google Scholar]
  8. Degner JF, Marioni JC, Pai AA, Pickrell JK, Nkadori E, Gilad Y, Pritchard JK 2009. Effect of read-mapping biases on detecting allele-specific expression from RNA-sequencing data. Bioinformatics 25: 3207–3212 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dohm JC, Lottaz C, Borodina T, Himmelbauer H 2008. Substantial biases in ultra-short read data sets from high-throughput DNA sequencing. Nucleic Acids Res 36: e105 doi: 10.1093/nar/gkn425 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Emerson JJ, Hsieh LC, Sung HM, Wang TY, Huang CJ, Lu HH, Lu MY, Wu SH, Li WH 2010. Natural selection on cis and trans regulation in yeasts. Genome Res 20: 826–836 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Ge B, Pokholok DK, Kwan T, Grundberg E, Morcos L, Verlaan DJ, Le J, Koka V, Lam KC, Gegné V, et al. 2009. Global patterns of cis variation in human cells revealed by high-density allelic expression analysis. Nat Genet 41: 1216–1222 [DOI] [PubMed] [Google Scholar]
  12. Heap GA, Yang JH, Downes K, Healy BC, Hunt KA, Bockett N, Franke L, Dubois PC, Mein CA, Dobson RJ, et al. 2010. Genome-wide analysis of allelic expression imbalance in human primary cells by high-throughput transcriptome resequencing. Hum Mol Genet 19: 122–134 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hesselberth J, Chen X, Zhang Z, Sabo PJ, Sandstrom R, Reynolds AP, Thurman RE, Neph S, Kuehn MS, Noble WS, et al. 2009. Global mapping of protein-DNA interactions in vivo by digital genomic footprinting. Nat Methods 6: 283–289 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hoffman CS, Winston F 1987. A ten-minute DNA preparation from yeast efficiently releases autonomous plasmids for transformation of Escherichia coli. Gene 57: 267–272 [DOI] [PubMed] [Google Scholar]
  15. Homer N, Merriman B, Nelson SF 2009. BFAST: An alignment tool for large scale genome resequencing. PLoS ONE 4: e7767 doi: 10.1371/journal.pone.0007767 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hubbard T, Barker D, Birney E, Cameron G, Chen Y, Clark L, Cox T, Cuff J, Curwen V, Down T, et al. 2002. The Ensembl genome database project. Nucleic Acids Res 30: 38–41 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. The International HapMap 3 Consortium 2010. Integrating common and rare genetic variation in diverse human populations. Nature 467: 52–58 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. King MC, Wilson AC 1975. Evolution at two levels in humans and chimpanzees. Science 188: 107–116 [DOI] [PubMed] [Google Scholar]
  19. Knight JC, Keating BJ, Rockett KA, Kwiatkowski DP 2003. In vivo characterization of regulatory polymorphisms by allele-specific quantification of RNA polymerase loading. Nat Genet 33: 469–475 [DOI] [PubMed] [Google Scholar]
  20. Lo HS, Wang Z, Hu Y, Yang HH, Gere S, Buetow KH, Lee MP 2003. Allelic variation in gene expression is common in the human genome. Genome Res 13: 1855–1862 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Main BJ, Bickel RD, McIntyre LM, Graze RM, Calabrese PP, Nuzhdin SV 2009. Allele-specific expression assays using Solexa. BMC Genomics 10: 422 doi: 10.1186/1471-2164-10-422 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. McManus CJ, Coolon JD, Duff MO, Eipper-Mains J, Graveley BR, Wittkopp PJ 2010. Regulatory divergence in Drosophila revealed by mRNA-seq. Genome Res 20: 816–825 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Montgomery SB, Sammeth M, Gutierrez-Arcelus M, Lach RP, Ingle C, Nisbett J, Guigo R, Dermitzakis ET 2010. Transcriptome genetics using second generation sequencing in a Caucasian population. Nature 464: 773–777 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Morozova O, Hirst M, Mirra MA 2009. Applications of new sequencing technologies for transcriptome analysis. Annu Rev Genomics Hum Genet 10: 133–151 [DOI] [PubMed] [Google Scholar]
  25. Nagalakshmi U, Wang Z, Waern K, Shou C, Raha D, Gerstein M, Snyder M 2008. The transcriptional landscape of the yeast genome defined by RNA sequencing. Science 320: 1344–1349 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Pant PV, Tao H, Beilharz EJ, Ballinger DG, Cox DR, Frazer KA 2006. Analysis of allelic differential expression in human white blood cells. Genome Res 16: 331–339 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Pastinen T, Sladek R, Gurd S, Sammak A, Ge B, Lepage P, Lavergne K, Villeneuve A, Gaudin T, Brandstrom H, et al. 2004. A survey of genetic and epigenetic variation affecting human gene expression. Physiol Genomics 16: 184–193 [DOI] [PubMed] [Google Scholar]
  28. Pickrell JK, Marioni JC, Pai AA, Degner JF, Engelhardt BE, Nkadori E, Veyrieras JB, Stephens M, Gilad Y, Pritchard JK 2010. Understanding mechanisms underlying human gene expression variation with RNA sequencing. Nature 464: 768–772 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. R Development Core Team 2010. R: A language and environment for statistical computing. http://www.R-project.org
  30. Rockman MV, Kruglyak L 2006. Genetics of global gene expression. Nat Rev Genet 7: 862–872 [DOI] [PubMed] [Google Scholar]
  31. Ronald J, Brem RB, Whittle J, Kruglyak L 2005a. Local regulatory variation in Saccharomyces cerevisiae. PLoS Genet 1: e25 doi: 10.1371/journal.pgen.0010025 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Ronald J, Akey JM, Whittle J, Smith EN, Yvert G, Krugylak L 2005b. Simultaneous genotyping, gene-expression measurement, and detection of allele-specific expression with oligonucleotide arrays. Genome Res 15: 284–291 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Schmitt ME, Brown TA, Trumpower BL 1990. A rapid and simple method for preparation of RNA from Saccharomyces cerevisiae. Nucleic Acids Res 25: 3091–3092 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Serre D, Gurd S, Ge B, Sladek R, Sinnett D, Harmsen E, Bibikova M, Chudin E, Barker DL, Dickinson T, et al. 2008. Differential allelic expression in the human genome: a robust approach to identify genetic and epigenetic cis-acting mechanisms regulating gene expression. PLoS Genet 4: e1000006 doi: 10.1371/journal.pgen.1000006 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Shoemaker R, Deng J, Wang W, Zhang K 2010. Allele-specific methylation is prevalent and is contributed by CpG-SNPs in the human genome. Genome Res 20: 883–889 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Skelly DA, Ronald J, Akey JM 2009. Inherited variation in gene expression. Annu Rev Genomics Hum Genet 10: 313–332 [DOI] [PubMed] [Google Scholar]
  37. Smit AFA, Hubley R, Green P 2010. RepeatMasker Open-3.0. http://www.repeatmasker.org
  38. Storey JD, Tibshirani R 2003. Statistical significance for genomewide studies. Proc Natl Acad Sci 100: 9440–9445 [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Tournamille C, Colin Y, Cartron JP, Le Van Kim C 1995. Disruption of a GATA motif in the Duffy gene promoter abolishes erythroid gene expression in Duffy-negative individuals. Nat Genet 10: 224–228 [DOI] [PubMed] [Google Scholar]
  40. van Camp G, Coucke P, Balemans W, van Velzen D, van de Bilt C, van Laer L, Smith RJ, Fukushima K, Padberg GW, Frants RR, et al. 1995. Localization of a gene for non-syndromic hearing loss (DFNA5) to chromosome 7p15. Hum Mol Genet 4: 2159–2163 [DOI] [PubMed] [Google Scholar]
  41. Wang Z, Gerstein M, Snyder M 2009. RNA-Seq: a revolutionary tool for transcriptomics. Nat Rev Genet 10: 57–63 [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Wittkopp PJ, Haerum BK, Clark AG 2004. Evolutionary changes in cis and trans gene regulation. Nature 430: 85–88 [DOI] [PubMed] [Google Scholar]
  43. Wu TD, Nacu S 2010. Fast and SNP-tolerant detection of complex variants and splicing in short reads. Bioinformatics 26: 873–881 [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Zhang K, Li JB, Gao Y, Egli D, Xie B, Deng J, Li Z, Lee JH, Aach J, LeProust EM, et al. 2009. Digital RNA allelotyping reveals tissue-specific and allele-specific gene expression in human. Nat Methods 6: 613–618 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES