Slow Dissociation of a Charged Ligand: Analysis of the Primary Quinone Q_A Site of Photosynthetic Bacterial Reaction Centers

Abstract

Reaction centers (RCs) are integral membrane proteins that undergo a series of electron transfer reactions during the process of photosynthesis. In the Q_A site of RCs from Rhodobacter sphaeroides, ubiquinone-10 is reduced, by a single electron transfer, to its semiquinone. The neutral quinone and anionic semiquinone have similar affinities, which is required for correct in situ reaction thermodynamics. A previous study showed that despite similar affinities, anionic quinones associate and dissociate from the Q_A site at rates ≈10⁴ times slower than neutral quinones indicating that anionic quinones encounter larger binding barriers (Madeo, J.; Gunner, M. R. Modeling binding kinetics at the Q_A site in bacterial reaction centers. Biochemistry2005, 44, 10994–11004). The present study investigates these barriers computationally, using steered molecular dynamics (SMD) to model the unbinding of neutral ground state ubiquinone (UQ) and its reduced anionic semiquinone (SQ^–) from the Q_A site. In agreement with experiment, the SMD unbinding barrier for SQ^– is larger than for UQ. Multi Conformational Continuum Electrostatics (MCCE), used here to calculate the binding energy, shows that SQ^– and UQ have comparable affinities. In the Q_A site, there are stronger binding interactions for SQ^– compared to UQ, especially electrostatic attraction to a bound non-heme Fe²⁺. These interactions compensate for the higher SQ^– desolvation penalty, allowing both redox states to have similar affinities. These additional interactions also increase the dissociation barrier for SQ^– relative to UQ. Thus, the slower SQ^– dissociation rate is a direct physical consequence of the additional binding interactions required to achieve a Q_A site affinity similar to that of UQ. By a similar mechanism, the slower association rate is caused by stronger interactions between SQ^– and the polar solvent. Thus, stronger interactions for both the unbound and bound states of charged and highly polar ligands can slow their binding kinetics without a conformational gate. Implications of this for other systems are discussed.

Introduction

Because of their diverse electrochemistry and lipid solubility, quinones are primary players in energy coupling electron transfer reactions that occur during oxidative metabolism and photosynthesis.^1,2 Transmembrane proteins that use quinones include NADH:quinone reductase (Complex I), cytochrome bc1 oxidoreductase (Complex II), succinate quinone reductase (Complex III), photosystems I and II, and bacterial reaction centers.³⁻⁵ While bound to these proteins, quinones undergo highly regulated electron transfer reactions which can lead to formation of the singly reduced semiquinone radical. Since the semiquinone is unstable,(6) it can initiate production of toxic reactive oxygen species if it is released.^2,7−10

Reaction centers (RCs) from Rhodobacter sphaeroides were one of the first transmembrane proteins to be crystallized.(11) This photosynthetic protein uses the energy of a photon to initiate a series of electron transfer reactions between bound cofactors. These reactions have been the subject of extensive experimental and computational studies.¹²⁻¹⁸ RCs contain three protein subunits (L, M, and H) and 10 bound cofactors (Figure 1). The cofactors include 2 ubiquinones (2,3-dimethoxy-5-polyprenyl-1,4-benzoquinone), bound both at the primary (Q_A) and secondary (Q_B) quinone sites and a non-heme Fe²⁺ bound between them. When a photon excites the bacteriochlorophyll dimer cofactor, the anionic semiquinone (SQ^–) is formed in the Q_A site. SQ^– reduces the secondary ubiquinone at the Q_B site, reforming the ground state neutral quinone in the Q_A site (UQ). Thus, the ubiquinone bound at the Q_A site cycles between the neutral ground and anionic semiquinone states.^19,20 Under physiological conditions, the only cofactor that dissociates from RCs is the neutral doubly reduced quinol product formed at the Q_B site after a second excitation of the protein.^1,21,22

Figure 1.

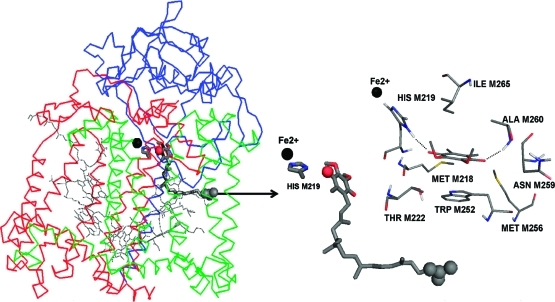
Crystal structure of the photosynthetic reaction center from R. sphaeroides (PDB entry 1AIJ). The three polypeptide chains are shown as green (M chain), blue (H chain), and red (L chain) ribbons. The ubiquinone bound to the Q_A site is shown as dark gray sticks with the tail atoms C27–C31 and headgroup carbonyl O4 atom depicted by spheres. The rest of the bound cofactors are shown as lines. The non-heme iron (Fe²⁺) is shown as a black sphere and HIS M219 as sticks. The arrow depicts the direction and point of application of the pulling force during steered molecular dynamics (SMD) simulations. The middle panel magnifies the Fe²⁺, HIS M219 and the quinone in their initial positions. For calculations of the headgroup interaction with the protein, the 50-carbon isoprene tail is replaced with a methyl group. The right panel shows the quinone, 2,3-dimethoxy, 5,6-methyl benzoquione headgroup in the Q_A site. Residues with the strongest binding interactions are included. Dashed lines depict the hydrogen bonds of the quinone carbonyls with HIS M219 and the ALA M260 backbone.

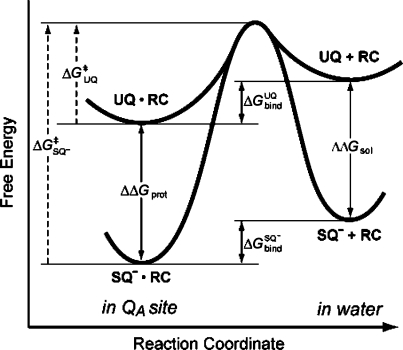
To minimize energy losses and suppress the formation of toxic oxygen species, reactive semiquinone intermediates must remain sequestered. In general, ligands can be trapped into specific binding pockets either thermodynamically, by stabilizing the bound state relative to the unbound state, or kinetically by a barrier that causes slow association and dissociation rates (Scheme 1). Since the anionic semiquinone is bound only ≈1.5 kcal/mol tighter than the neutral quinone, the Q_A site does not impose a significant thermodynamic trap.^1,23,24 This is important for RC function because a highly stabilized semiquinone at the Q_A site would deter forward electron transfer to the secondary quinone at the Q_B site. Rather, the semiquinone dissociates more slowly than the neutral ground state quinone from the Q_A site, indicating a kinetic trap.^25,26

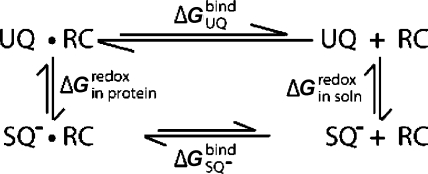
Scheme 1. Thermodynamic Cycle for the Q_A Site of Bacterial RCs Showing the Relationship between the Binding Free Energy for UQ (ΔG_UQ^bind) and SQ^– (ΔG_SQ–) and Free Energy of Reduction in the Protein (ΔG_{in protein}^redox) and Solution (ΔG_{in soln}).

The reduction free energy is shifted from its value in solution by an amount equivalent to the difference in affinity between UQ and the anionic SQ^–. If SQ^– binds tighter than UQ, ΔG_red becomes more favorable creating a thermodynamic trap for the SQ^–. If SQ^– and UQ affinities are the same but SQ^– has slower association and dissociation rates, a SQ^– kinetic trap is created. This is shown by the shorter arrows for the SQ^– binding on the bottom leg of the cycle.

To quantify this difference in UQ and SQ^– dissociation rates, a previous study used stable anionic hydroxyl quinones as semiquinone models.(27) The Q_A site affinity and binding kinetics for several anionic quinones and neutral quinones were compared. The binding free energies differed by less than 10-fold, similar to the difference between quinone and semiquinone.^1,23 Despite their similar affinity, anionic quinones dissociate ≈10⁴ times more slowly than the neutral quinones. It is therefore the negative charge of the semiquinone, rather than its free radical properties, which result in larger dissociation barriers. In addition, the association of anionic quinones is a slow process with a unimolecular rate-limiting step, while neutral quinones associate with a faster, bimolecular rate-limiting step.

The work presented here provides a detailed analysis of dissociation from the Q_A site of bacterial RCs, comparing the neutral ubiquinone (UQ) and its reduced anionic semiquinone (SQ^–). Steered Molecular Dynamics (SMD) is used to determine the exit pathway for both redox states. A larger dissociation barrier for SQ^– is identified. This barrier is dominated by the loss of a long-range electrostatic attraction to the nearby bound non-heme Fe²⁺ cofactor. SQ^– exhibits stronger interactions with the protein in the binding site but also stronger interactions with water in the dissociated state. This leaves affinity unaffected, but increases the barriers to both association and dissociation. Comparing the SMD trajectories, the SQ^– headgroup interacts with more water molecules in the latter stages of dissociation and has fewer accessible dissociation pathways than does UQ.

Methods

The coordinates 1AIJ for the photosynthetic reaction center were obtained from the Protein Data Bank(11) and used to model unbinding of ubiquinone or semiquinone from the Q_A site. The lauryl dimethylamine-N-oxide detergent molecules, which are all on the surface and should not interfere with quinone dissociation, were removed. The semiquinone (SQ^–) and ubiquinone (UQ) have the same atomic positions, but UQ has a net charge of 0 and SQ^– a net charge of −1. For SMD simulations, all ionizable residues are in their standard ionization state at pH 7, except GLU L104 and GLU L212, which are neutral.(28) GLU L212 is known to be coupled with ASP L213 near the Q_B site and the net charge of this cluster is −1.^1,28 GLU L104 donates a hydrogen bond to the keto group of the bacteriopheophytin. For both SMD and Multi Conformational Continuum Electrostatics (MCCE) calculations, the four histidines bound to iron (HIS L190, L230, M219, and M266) are neutral, with a hydrogen on ND1. All bacteriochlorophylls and bacteriopheophytins are fixed in their neutral ground state.

RCs are transmembrane proteins. The results presented, done with either implicit or explicit solvent, do not consider the membrane or detergent. This should not significantly influence the comparison with previous experiments, which were carried out in 0.005% LDAO detergent.(27) This concentration is below the CMC and thus not expected to significantly affect RC structure or quinone binding rate.^24,29

SMD Simulations

SMD is a nonequilibrium simulation method that has been used to study dynamic processes such as protein folding and ligand dissociation.³⁰⁻³² All molecular dynamics simulations were performed using the GROMACS software version 4.0.7,(33) with the OPLS-AA force field.(34) The parameters for RC cofactors were generously provided by Marchi and Ceccarelli.^28,35 Initially, the RC was solvated with SPC water molecules in a dodecahedron box, with the box edge approximately 1.2 nm from the RC surface. Ions were added to neutralize the system. For RC with ubiquinone bound in the Q_A site (UQ), there were 2 Na⁺ ions and 32 743 water molecules. For RC with semiquinone in the Q_A site (SQ^–), there were 3 Na⁺ ions and 32 742 water molecules. The Lincs algorithm(36) was used to constrain bonds to their equilibrium lengths, allowing a time step of 2 fs. A steepest descent algorithm was used for energy minimization, with the tolerance of 100 kJ/(mol/nm). After energy minimization, a 30 ps position restrained molecular dynamics simulation was performed to equilibrate the water molecules, with all RC atoms fixed. The temperature (300 K) and pressure (1 bar) of the system were controlled with the Berendsen algorithm.(37) Afterward, a molecular dynamics simulation of the system was carried out for 5.5 ns, at constant molecular number, pressure, and temperature (NPT).

The coordinates of the initial structures for the constant velocity SMD simulations were taken from the 5.5 ns NPT MD simulation. Starting at 1.1 ns, coordinates were retrieved every 100 ps. Thus, 45 SMD simulations were generated for each redox state. The quinone (UQ or SQ^–) was pulled out of the Q_A binding site of the RC by applying an external force with a force constant of 3000 kJ/(mol/nm²) and velocity of 0.0005 nm/ps. The pulling force was applied on the center of mass of the C27, C28, C29, C30, and C31 atoms of the quinone tail, in the −z direction, as shown in Figure 1. This encourages movement of the headgroup through regions initially occupied by the tail. In different X-ray structures, the analogous Q_B quinone is found in multiple positions along the tail binding channel.^11,38,39 In addition, docking experiments identified weak binding sites for the quinone headgroup along these regions on the Q_A site (data not yet published). Thus, we believe it is reasonable to pull the quinone in this direction to study the process of quinone head dissociation from the Q_A binding site.

The SMD simulations were carried out until the quinone was completely unbound, requiring at least ≈9 ns. For all simulations, Particle Mesh Ewald was used for the calculation of electrostatics. Coulomb and nonbonded van der Waals interactions were cut off at 0.9 nm, and periodic boundary conditions were applied in all three dimensions. Nonpolar hydrogens were not considered. The pulling distance is linearly dependent on time. A pulling distance at step i is calculated as z_i = z_i–1 + v∗dt, where v is the pulling velocity (v = 0.005 Å/ps) and dt is the time step (in ps).

MCCE Calculations

MCCE was used to calculate binding free energy at five selected time points along the SMD unbinding trajectories. MCCE uses an equilibrium Monte Carlo Poisson–Boltzmann Surface Area (MC-PBSA) method to investigate linked conformational and ionization states. MCCE generates side-chain heavy atom conformers to add flexibility to the continuum electrostatics model.^18,40 It was originally developed to calculate midpoint potentials (E_m’s) and residue and cofactor pK_a’s but has recently been extended to calculate ligand and ion binding energies.^28,40−42 The binding energy calculated by MCCE is the net free energy associated with transferring the quinone from an implicit solvent with a dielectric constant of 80 to positions in the protein found in the SMD trajectories.

MCCE(40) determined the binding affinity of UQ and SQ^– at 2000, 4800, 5800, 6400, and 8000 ps. Forty-five structures were analyzed for each time point corresponding to each SMD trajectory. Each initial structure was energy minimized, by the steepest descent algorithm as described above, before the MCCE calculation. All water molecules, sodium ions, detergent, and quinone bound at the Q_B site were also removed. The affinity of the quinone headgroup, 2,3-dimethoxy, 5-6-dimethyl benzoquinones, was determined with a methyl group in place of the native isoprenoid tail. This highlights the part of the molecule that is different between SQ^– and UQ. The quinone ring was fixed in the position found in the particular trajectory. The partial charge distribution for the quinone and semiquinone was determined using DFT in the Gaussian 98 program at the UB3LYP/6-31G level of theory (see Supporting Information).(43)

During the MCCE calculations, the protein backbone remains fixed. All nonpolar hydrogen atoms were removed and their charges merged onto heavy atoms. The MCCE QUICK calculation was used.(40) For this method, isosteric positions are generated for hydroxyls, His tautomers, and the interchange of oxygen and nitrogen for residues Asn and Gln.^28,40 Next, Delphi is used to solve the Poisson–Boltzmann equation and get the electrostatic pairwise interaction and desolvation energies.^44,45 The desolvation energy is the energy needed to move the quinone from the high dielectric implicit solvent (dielectric of 80) into the low dielectric binding site (in a protein with a dielectric constant of 4 surrounded by water). This energy is always positive accounting for the loss of interactions with the polar solvent water. The electrostatic pairwise interactions can be positive or negative as they depend on the atomic charges of the protein and quinone. The calculation is carried out in 150 mM salt using PARSE charges and Born radii and Amber van der Waals and torsion parameters as described previously.(28)

The final MCCE step involves full Grand Canonical Monte Carlo (GCMC) sampling as a function of the unbound UQ or SQ^– concentration, which is modeled as the imposed quinone chemical potentials at pH 7.(28) Since UQ and SQ^– have the same atomic structures, it is assumed they have the same rotational/translational degrees of freedom in the unbound state of both redox species. GCMC sampling determines the Boltzmann distribution of microstates as a function of the chemical potential. A microstate consists of a single conformation and charge distribution for each residue and cofactor. During GCMC, the quinone has both a bound and unbound conformer available for sampling at all specified chemical potentials. The probability of quinone being bound is determined by the Boltzmann distribution of microstates. The output is a titration curve which plots the occupancy of each quinone state at a given potential. The chemical potential at which there is 50% occupancy of the bound and unbound state is the binding affinity.^41,46

The positions of the five residues (HIS M219, M266, L190 and L230, and GLU M234) that are ligands to the iron atom are held fixed in their appropriate tautomeric and ionization states for the entire MCCE calculation. The ionization states of all other protonable residues are determined during the GCMC sampling and thus remain in equilibrium with the UQ or SQ^– position in the protein.

Abbreviations

RCs, reaction centers; MCCE, multiconformation continuum electrostatics; SMD, steered molecular dynamics; SQ^–, anionic semiquinone; UQ, neutral ubiquinone; GCMC, grand canonical Monte Carlo.

Results

Qualitative Comparison of UQ and SQ^– Unbinding Pathways

The reaction center (PDB 1AIJ) with neutral ubiquinone (UQ) or anionic semiquinone (SQ^–) bound to the Q_A site was equilibrated in a 5.5 ns MD simulation. Starting at 1.1 ns, the coordinates were retrieved every 100 ps and used as the initial structure for SMD. This yielded 45 SMD dissociation trajectories for each redox state. The average root-mean-square deviation (rmsd) of the Cα atoms in the 45 initial structures is 1.57 ± 0.16 Å for UQ and 1.55 ± 0.16 Å for SQ^–, relative to the crystal structure. During all the SMD simulations, the Cα rmsd increases to a maximum of ≈2.0 Å. The superimposed RC backbones, at selected frames, show that the overall structure is well preserved (see Supporting Information, Figure S2).

A pulling force was applied to the terminal isoprene unit of the ubiquinone-10 cofactor bound to the Q_A site (Figure 1). This force induced the dissociation of the quinone. The 2,3-dimethoxy, 5,6-dimethyl benzoquinone headgroup is the focus of this study. In the native crystal structure, the HIS M219 side chain and ALA M260 backbone are hydrogen bonded to the 2 quinone carbonyls (Figure 1).(11) Other residues important for binding to the Q_A site include Fe²⁺, MET M218, THR M222, TRP M252, MET M256, ASN M259, and ILE M265.

The average pulling energy, calculated from the 45 SMD trajectories for UQ and SQ^–, is plotted against simulation time (Figure 2A). Pulling energy is proportional to the squared deviation of the constrained atom from its desired position. It is dependent on the pulling velocity and not a direct measurement of the physical activation energy. Instead, the greater magnitude of pulling energy observed in the SQ^– profile (Figure 2A) is qualitative evidence of a larger energy barrier for dissociation relative to UQ. This is in agreement with the experimental observation of slower dissociation rates for anionic quinones.(27) Five time points, 2000, 4800, 5800, 6400, and 8000 ps from each of the 45 SMD trajectories, representing 225 structures for each redox state, are chosen for in depth structural and energetic analysis. The time points at 4800, 5800, and 6400 ps represent the highest energy structures (Figure 2A). Since unbinding is guided by a pulling force applied to the end of a long tail, the headgroup is free to sample different positions during its escape (Figure 2C,D).

Figure 2.

(A) Average pulling energy for neutral UQ (gray squares) and anionic SQ^– (black squares) plotted against SMD simulation time. Each point represents the average pulling energy (±0.121 kcal/mol) over 50 ps and includes data from 45 SMD trajectories. The dashed guide lines depict the 5 selected time points (2000, 4800, 5800, 6400, and 8000 ps), analyzed throughout this paper. (B) The average distance between the quinone head atom O4 (squares) or tail atom C29 (triangles) and the Fe²⁺ atom for UQ (gray points) and SQ^– (black points). (C and D) The distance between quinone headgroup (O4 atom) and Fe²⁺ at the 5 selected time points, in all 45 SMD trajectories, for UQ (C) and SQ^– (D). The large gray diamonds represent the average distance at the specified time.

Structural Comparison of Unbinding Pathways

The average distance between the quinone head O4 atom and Fe²⁺, which moves very little during SMD simulations, was determined at the chosen time points (Figure 2B). Before pulling, the distance between O4 and Fe²⁺ is 6.8 Å and this oxygen is hydrogen bonded to HIS M219. Comparing UQ and SQ^–, the largest difference in the distance between the headgroup and the iron occurs between 4800 ps, where the SQ^– is 9.0 Å and UQ 12.5 Å from the iron, and 5800 ps, where the distances are 11.2 Å for SQ^– and 16.4 Å for UQ. With increasing pulling force, the anionic SQ^– headgroup stays closer to the iron for more time than the neutral UQ (Figure 2A). On the other hand, the difference between the average C29 positions for UQ and SQ^– is never more than 2.5 Å (Figure 2B). At ≈5800 ps, the required pulling force begins decreasing as dissociation of the SQ^– headgroup accelerates. By 6400 ps, the SQ^– headgroup has caught up to UQ and the required forces are similar for both ligands.

The fractional solvent accessible surface area (SASA) of the quinone head was calculated at the 5 selected time points (Figure 3). At 0, 2000, and 4800 ps, UQ and SQ^– are well buried and their SASAs are comparable. At 5800 ps, the SQ^– head is less exposed than UQ indicating that SQ^– remains buried for a longer time. Between 5800 and 6400 ps, the SASA for SQ^– shows a sharp increase as the headgroup accelerates into the solvent. By 8000 ps, in most trajectories, the UQ and SQ^– head groups are close to the protein surface but not yet fully unbound.

Figure 3.

Average SASA of the 45 SMD trajectory for the UQ (A) and anionic SQ^– (B) headgroup. SASA is expressed as a percentage of the SASA of the quinone head fully exposed to solvent. These calculations were done with the explicit water removed.

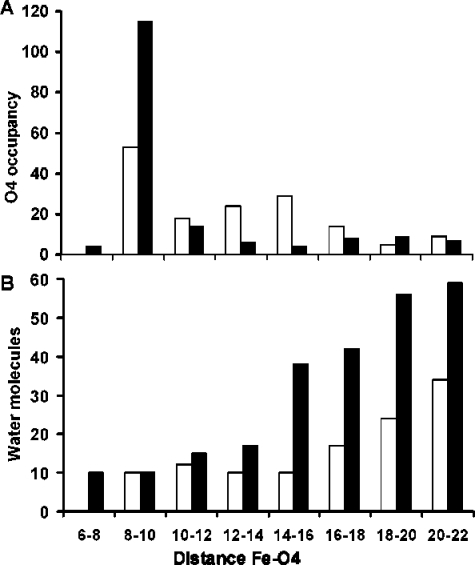
To visualize the unbinding trajectories, the positions of the quinone O4 atom (Figure 1), at the selected time points, for all 45 SMD simulations are superimposed on the RC backbone (Figure 4). During unbinding, the neutral UQ headgroup positions are more evenly distributed compared to SQ^– (Figure 4A). Before 6400 ps, the SQ^– headgroup is confined near the Q_A site (Figure 4B). This is followed by a region where the fewest SQ^– head groups are found indicating the shortest transit time and the maximum pulling force. Counting the number of times that O4 is found at specific distances from Fe²⁺ reveals that the SQ^– head occupies the region 8–10 Å away from the Fe²⁺ atom twice as frequently as UQ (Figure 5A). The region with the lowest SQ^– headgroup occupancy is between 12 and 16 Å away from Fe²⁺, where UQ is found ≈5 times more frequently than SQ^–. This region contains the SQ^– dissociation transition state in these simulations. Both ligands have a similar distribution of positions when O4 is more than 18 Å away from the iron (Figure 5A) showing that the SQ^– headgroup gains more structural freedom after passing the transition state. This suggests that the unbinding landscape for SQ^– has a narrower low energy path compared to UQ.

Figure 4.

Position of the quinone head O4 atom of UQ (top) and SQ^– (bottom) at five selected time points in the 45 SMD simulations. The positions are depicted by colored balls where each color represents a specific time point: orange (2000 ps), green (4800 ps), magenta (5800 ps), blue (6400 ps), and red (8000 ps). On the right, the quinone containing regions are magnified to compare the UQ and SQ^– unbinding pathways.

Figure 5.

Quinone headgroup location and number of surrounding waters at the 5 selected time points of the 45 simulations for UQ (white bars) and SQ^– (black bars). The x-axis depicts the distance between the quinone carbonyl O4 and Fe²⁺ in angstroms. (A) The number of times the O4 atom is found at different distances from the iron. (B) Average number of water molecules within 9 Å of the quinone head groups within the given range of O4–iron distances.

Interaction Energies

The total interaction energy between the RC and quinone headgroup was compared for SQ^– and UQ along their trajectories. These energies were calculated with both explicit solvent GROMACS and implicit solvent MCCE analyses (Figure 6). All energies are averaged over the 45 SMD trajectories for each redox state. In the explicit solvent analysis, the protein dielectric constant is 1 and all interaction energies are calculated with respect to the UQ or SQ^– in vacuum. In contrast, for the implicit solvent analysis, the protein dielectric constant is 4 and the solvent is 80. Thus, explicit solvent electrostatic interactions will be at least 4-fold stronger than with implicit solvent. Qualitatively, these two analyses yield an identical view of the nature and positions of the barriers that distinguish the UQ and SQ^– unbinding pathways (Figure 6). The total interaction with the binding site is stronger for SQ^– than UQ (Figure 6A). Before ≈4800 ps, there are minimal changes in RC-SQ^– interaction energy. The most rapid weakening of these interactions occurs between 5800 and 6400 ps. The slope is less steep at later times after the strongest interactions are broken. The electrostatic attraction between SQ^– and Fe²⁺ is a significant component of the total interaction energy and weakens in the same time window (Figure 6B). On the other hand, at any given time, the UQ headgroup has nearly zero interaction energy with Fe²⁺ (Figure 6B) and very little barrier for dissociation.

Figure 6.

Interaction energies for UQ (blue) and anionic SQ^– (red) headgroups using the GROMACS explicit solvent analysis (top) and MCCE Poisson–Boltzmann implicit solvent analysis (bottom). All energies are averaged over the 45 SMD trajectories for each redox state. The black dashed lines show the 5 selected time points: 2000, 4800, 5800, 6400, and 8000 ps. (A) Sum of the pairwise electrostatic and van der Waals interaction energies between quinone and the reaction center. This does not include interactions with the explicit water in the GROMACS analysis. For the MCCE analysis, the solvation energy is not included, but the pairwise interactions with the protein are screened by the protein dielectric constant of 4 and the implicit solvent with a dielectric constant of 80. (B) Specific interaction energies with Fe⁺² (solid lines), which become less negative during the unbinding trajectories and with the solvent (dots for explicit and dashed line for implicit), which becomes more negative. The isolated points on the right axis (*) show the implicit reference GCMC solvation energy for UQ (blue) and SQ^– (red) in the unbound state.

The pairwise residue interaction energy for SQ^– and UQ is decomposed based on amino acid type. These interaction energies, calculated using MCCE analysis at the 5 selected time points, are plotted against distance between O4 and Fe²⁺ atoms (Figure 7). Only residues with more than 1 kcal/mol interaction energy are considered. For both UQ and SQ^–, short-range van der Waals interactions with hydrophobic and aromatic residues remain fairly uniform throughout the unbinding process. These interactions make the largest contribution for UQ while SQ^– shows additional longer range interactions with acidic and basic residues. The net contribution of charged amino acids is insignificant, as the unfavorable repulsions with acids remain nearly equal to the favorable attractions with bases (Figure 7B). On the other hand, the long-range interaction between SQ^– and Fe²⁺ is a dominant contribution to the binding energy, weakening to near 0 when the quinone–Fe²⁺ distance has increased to ≈16 Å.

Figure 7.

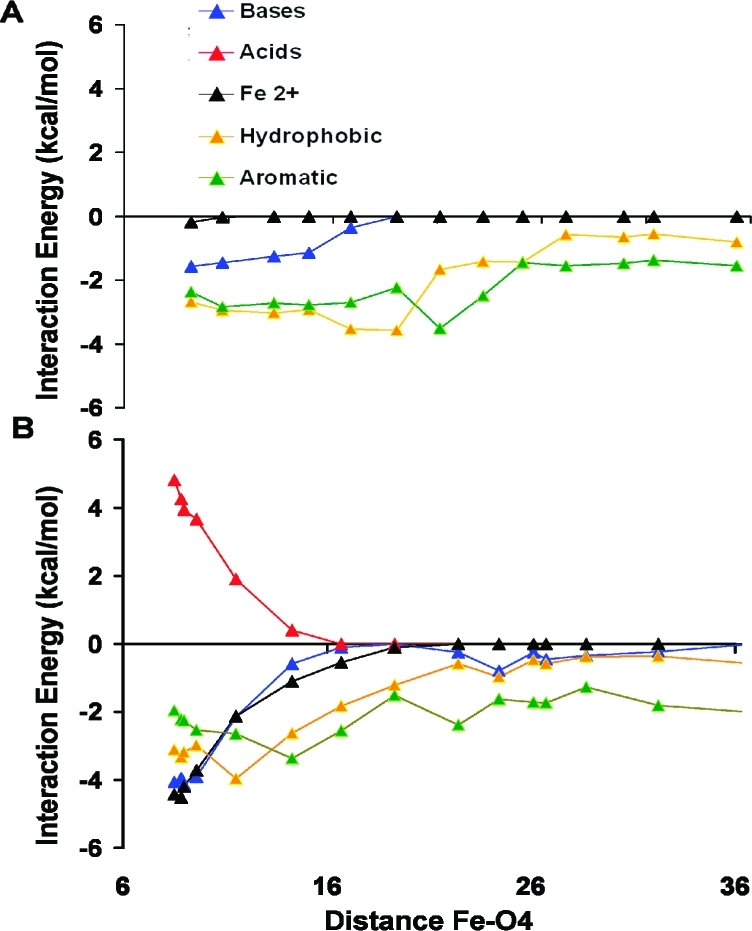
Pairwise interaction energies between the quinone headgroup and different classes of residue side chains. Implicit solvent MCCE interaction energies are plotted for UQ (A) and SQ^– (B) against the distance between O4 and Fe²⁺ atoms. Residues are categorized as bases (LYS, ARG, HIS); acids (ASP, GLU); hydrophobic (ILE, LEU, VAL, ALA); aromatic (PHE, TRP, TYR); and Fe²⁺. Energies are averaged for all quinone positions at the specified distance between the headgroup and the iron (see Figure 5A).

Solvation Energy

Unbound SQ^– interacts more strongly with water than UQ, but in the Q_A site, interactions with water are nearly zero for both redox states (Figure 6B). The interaction between SQ^– and the solvent increases most rapidly between 4800 and 6400 ps, when its attraction to Fe²⁺ is most rapidly declining (Figure 6B). Counting the number of water molecules within 9 Å of the quinone head shows that SQ^– unbinding is associated with a larger penetration of water into the RC during SMD trajectories (Figure 5B). For UQ, the average number of water molecules surrounding the headgroup remains relatively constant as does its water interaction energy (Figure 6B). On the other hand, when the SQ^– headgroup is between 12 and 16 Å from the Fe²⁺, the number of water molecules surrounding it increases from an average of 17 (±7) to 38 (±4). Since this is the transition-state region where the maximum pulling force is required, this observation is consistent with solvation contributing to the rate-determining step. Similar observations have been made with other systems where electrostatic interactions with the solvent and solvent reorganization play an important role in tuning dissociation rates.⁴⁷⁻⁵⁰

Binding Energies

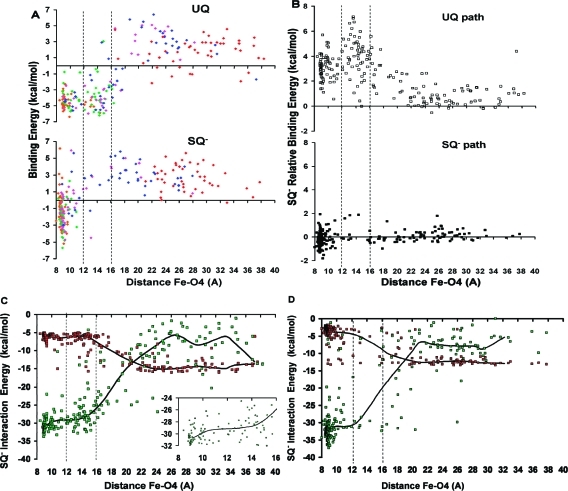
MCCE has previously been used to calculate the binding free energy for a variety of benzoquinones in the Q_A binding site.(28) It is used here to determine the binding free energy for the UQ and SQ^– headgroups at the 5 specified time points. In agreement with experiments, which estimate only a 1.5 kcal/mol difference between the binding energies for UQ and SQ^–,^23,51 the calculated binding energies for the UQ and SQ^– headgroups, in the crystal structure position, are similar, namely, −8.2 and −8.3 kcal/mol, respectively. Figure 8A shows the UQ and SQ^– headgroup binding energy against the distance between the O4 and Fe²⁺ atoms. UQ maintains its binding energy in the region less than 18 Å from Fe²⁺, while SQ^– loses its binding energy after it moves ≈12 Å away. The transition-state region, between 12 and 16 Å, clearly has very little SQ^– headgroup occupancy. For the few trajectories where this region is occupied, the binding free energy is positive indicating that the unbound state is more favorable than the bound state at that particular location in the protein.

Figure 8.

Energies calculated with the MCCE implicit solvent method plotted against the distance between Fe²⁺ and the quinone carbonyl O4 atom along the SMD unbinding trajectories. Vertical dashed lines depict the suggested transition-state region where few SQ^– headgroups are found (Figure 5A). (A) Binding free energy for UQ and SQ^–. The color of each point indicates the SMD time point of the structure used for the calculation: orange (2000 ps), green (4800 ps), magenta (5800 ps), blue (6400 ps), and red (8000 ps) (Figure 4). (B) Relative binding energy of SQ^– with respect to UQ (ΔG_bind,SQ– – ΔG_bind,UQ) in structures obtained from both the UQ and SQ^– unbinding paths. Positive values indicate that SQ^– is less stable than UQ in the regions of the protein away from the Q_A site. (C and D) SQ^– total protein interaction (green) and implicit solvation energy (red). These energies are calculated along the UQ (C) and SQ^– (D) exit pathways. The thick black lines plot the median energy at ≈2 Å intervals as a guide to the eye. The inset in (C) magnifies the transition-state region where SQ^– loses stabilizing interactions with the protein.

The lack of SQ^– headgroup occupancy between 12 and 16 Å away from Fe²⁺ indicates it is less stable in this region. This was quantified using the UQ unbinding trajectories as a probe. The difference between the binding energy of SQ^– and UQ was compared at positions along both the UQ and SQ^– exit pathways. Positive energies indicate regions where SQ^– is less stable than UQ. SQ^– and UQ are equally stable along the narrower SQ^– exit pathway (Figure 8B). However, along the broader UQ unbinding trajectories, between 12 and 16 Å away from Fe²⁺, SQ^– is ≈3 kcal/mol less stable than UQ (Figure 8B).

A higher SQ^– desolvation penalty and/or weaker RC–SQ^– interactions can account for the loss of binding energy in the transition-state region. To determine these contributions, SQ^– implicit solvation and total protein interaction energies were calculated along the UQ and SQ^– pathways (Figure 8, panels C and D, respectively). When the SQ^– headgroup is less than 10 Å from the iron, it has similar protein interaction and solvation energies along both pathways. Along the UQ pathway, between ≈10 and 16 Å away from the iron, SQ^– loses protein interaction energy without an increase in solvation (Figure 8C). Thus, weaker protein interactions, rather than a higher desolvation, account for the loss of SQ^– binding energy along the broader UQ pathway. Because there are so few quinone headgroups captured in SQ^– transition-state region, it is harder to establish the relative importance of a loss of SQ^––protein interactions without a compensatory gain in solvation when SQ^– dissociates along its own pathway (Figure 8D).

Discussion

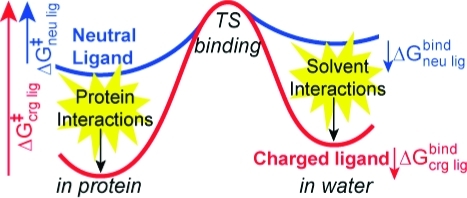
The relative affinity of reactants and products determines reaction thermodynamics in the protein (Scheme 1). On the other hand, differences in the absolute interaction with the binding site will influence dissociation kinetics. The results presented here investigate the relationship between binding thermodyanimics and kinetics for the neutral quinone (UQ) and anionic semiquinone (SQ^–) in the Q_A site of photosynthetic reaction centers. Studies measuring the SQ^– lifetime in the Q_A site show that it dissociates much more slowly than the neutral UQ.(26) Anionic, hydroxyl semiquinone analogues dissociate 10⁴ times more slowly than neutral quinones with the same affinity. If the difference in dissociation rate caused an equivalent increase in binding affinity, the semiquinone would be stabilized in the Q_A site by ≈5.6 kcal/mol (≈240 meV); thus, the physiological forward electron transfer to the secondary quinone in the Q_B site would be uphill (Scheme 1). Instead, the anionic semiquinone binds only ≈1.5 kcal/mol more tightly than the neutral ground state quinone.^1,17,23,51 This shifts the quinone E_m by ≈90 mV in the Q_A site, compared to solution. Thus, anionic and neutral quinones with similar structures can have the same binding thermodymanics while having much different association and dissociation kinetics (Figure 9).

Figure 9.

Dissociation energy profile comparing neutral UQ and anionic SQ^–. The free energy of binding to the Q_A site (ΔG_bind) is similar for both redox states. Since SQ^– has a larger interaction energy with the solvent in the unbound state (ΔΔG_sol), stronger protein interactions are required (ΔΔG_prot). Assuming the same transition-state energy, the physical consequence of this is a larger activation energy for SQ^– dissociation (ΔG^⧧_SQ– > ΔG^⧧_UQ).

To gain more quantitative insight, previous experiments measured the affinity and binding rates of neutral and anionic quinones at the Q_A site.(27) Since semiquinones are not stable in aqueous solution,(2) deprotonated hydroxyl containing quinones were used as semiquinones analogues. The affinity of the anionic quinones was found to be comparable to that of neutral quinones of similar size and shape.(27) However, the anionic quinones displayed association and dissociation rates 10⁴-times slower than neutral quinones implying an activation barrier ≈5.5-kcal/mol higher. In addition, neutral quinones associate via a bimolecular mechanism, at rates close to the diffusion-controlled limit, while anionic quinones use a unimolecular mechanism with a first-order rate-limiting step.(27)

Classical molecular mechanics is used here to investigate the unbinding pathways of neutral ubiquinone (UQ) and its anionic semiquinone (SQ^–). Constant velocity SMD with explicit solvent is used to construct 45 unbinding trajectories for each redox state. UQ and SQ^– interaction energies are calculated using GROMACS explicit solvent and MCCE implicit solvent methods. MCCE calculations show that the equilibrium binding energies for UQ and SQ^– are comparable in the Q_A site, while SMD results indicate that the dissociation energy barrier is larger for SQ^– than for UQ (Figure 2A). Thus, the observations from our computational model are in agreement with the experimental observations.

A rough estimate of the difference between the SQ^– and UQ activation energy can be determined from energies calculated with the implicit solvent MCCE method.(46) The largest difference in these two unbinding barriers occurs between 4800 and 6400 ps (Figure 2A). During this time, UQ loses ≈10 kcal/mol of the total protein interaction it had in the Q_A site and gains ≈1 kcal/mol of solvation energy yielding a ≈9 kcal/mol barrier (Figure 6). On the other hand, SQ^– loses ≈19.5 kcal/mol of total protein interaction energy and gains ≈5.5 kcal/mol solvation energy yielding a ≈14 kcal/mol barrier. The difference is ≈5 kcal/mol, in good agreement with the experimental estimate. Methods to extract free energy profiles from SMD trajectories^31,52−54 when applied to our data did not give credible results, presumably due to convergence problems. Instead, we use this data qualitatively to show that the dissociation energy barrier is larger for SQ^– compared to UQ.

In light of the computational results presented here, we can understand how large kinetic barriers are encountered during SQ^– dissociation without altering binding affinity or requiring a conformational gate. For SQ^– to have the same affinity as UQ, stronger binding interactions are required. These interactions compensate for the additional loss of solvation energy incurred when the anion is transferred from the polar environment of the solvent to the hydrophobic Q_A site (Figure 9). In the unbound state, SQ^– has a ≈13 kcal/mol more favorable solvent interaction energy than UQ (Figure 6B). Thus, in the bound state, SQ^– needs to have an additional ≈13 kcal/mol protein interaction energy. The process of unbinding for both redox species involves progressive weakening of their equilibrium binding interactions with simultaneously increasing solvation. During unbinding, neither ligand becomes involved in new interactions that significantly favor binding nor did we observe significant differences in protein conformations. It is therefore reasonable to assume relatively similar transition-state energies for UQ and SQ^–. Given this assumption, the physical consequence of these stronger binding site interactions is that the SQ^– dissociation barrier is increased relative to UQ (Figure 9).

Our computational results also offer an explanation for the experimentally observed difference in anionic and neutral quinone association mechanisms.(27) The neutral quinones associate with the expected concentration dependent, second-order (bimolecular) rate-limiting step. In contrast, anionic quinones have a slower concentration independent, first-order (unimolecular) rate-limiting step for binding. Just as stronger SQ^––protein interactions increase the dissociation barrier, stronger SQ^––solvent interactions will do the same for the association barrier (Figure 9). We hypothesize that the rate-limiting step for association is the desolvation of the quinone which occurs after the protein–quinone complex has been formed in a fast bimolecular association step. With unbinding, significant SQ^– solvation by water occurs while it is still buried in the protein (Figures 5B and 7B). By microscopic reversibility, desolvation on binding should take place within the protein before the transition state. Desolvation has also been suggested as a main contribution to the rate-limiting step for other process including protein–protein association.^49,55

Slow association and dissociation of charged ligands is likely more general than just the Q_A site in RCs. Many proteins bind ligands that subsequently undergo a change in charge state. These include redox active, protonatable and phosphorylated substrates, intermediates, and products. To maintain similar affinity for reactant and product, the binding site must provide stronger interactions for the more polar or charged ligand. Thus, it is likely that the species with the highest charge density has the slowest dissociation rate. Slow semiquinone dissociation rates with only modest thermodynamic stabilization are observed in the Q_B site of the RC(25) as well as the Q_A site studied here. For RCs, the intrinsic slowness of anionic quinone dissociation naturally protects the cell from the deleterious effects of an unbound semiquinone radical.

While these simulations and the experiments that they are modeling were carried out in water, the RC is a transmembrane protein with the Q_A site located near the lipid headgroup region. The long tail of the unbound quinone is localized in the membrane, with the more hydrophilic headgroup mostly found near the water. When the headgroup dissociates from the binding site, it must pass through a hydrophobic region of the membrane, which will only add to the high energy barrier to SQ^– dissociation. In addition, the solvation of the dissociating SQ^– will occur later in the dissociation reaction. This would be expected to slow the binding rate, and thus, addition of the membrane would not change the qualitative conclusions of this study.

Acetylcholinesterase is an enzyme that produces charged enzymatic products.(56) Here, built-in electrostatic steering potentials regulate dissociation barriers causing neutral and charged ligands to follow different binding pathways for efficient product release.(57) Thus, for this system, the protein has evolved to counteract the intrinsic kinetic trap for the charged species. Slow dissociation of highly charged catalytic products is also thought to play a role in thermostable enzymes. For example, in a thermally stable carbamoyl phosphate sythetase, the slow catalytic rate was attributed to slow dissociation of the charged product as it interacts with an extended ion-pair network along its unbinding pathway.(58) Calcium binding can also display slow association rates.^47,59 Another example where this mechanism may be seen is in the Na⁺Fo ATPase. Extremely slow association rates have been observed for sodium binding to the transmembrane c ring.(48) In this system, the associated a subunit provides an alternative, hydrophilic pathway catalyzing Na⁺ transfer.

Conclusions

This study presents a detailed comparison of unbinding for a slow charged (SQ^–) and fast neutral (UQ) ligand from the Q_A site of bacterial RCs. The two long-range interactions that dominate the larger SQ^– dissociation barrier are electrostatic attraction to Fe²⁺ and solvation (Figure 6). Strong attraction to the Fe²⁺ atom initially confines SQ^– to positions near the binding site, while UQ has little interaction with Fe²⁺ and more structural freedom. As dissociation progresses, the attraction to Fe²⁺ weakens and the solvent interactions become stronger. The magnitudes of both these interaction energies are much smaller for UQ, which has very little barrier for dissociation. An apparent transition state for SQ^– unbinding occurs when interactions with Fe²⁺ are weakening while aqueous solvation is increasing (Figure 6B). This happens between 4800 and 5800 ps of SMD simulation time, when the SQ^– headgroup passes through the region 12–16 Å away from the Fe²⁺.

Despite their differences in dissociation rates, SQ^– and UQ have similar binding affinities in the Q_A site. The favorable electrostatic attraction to Fe²⁺ compensates for the higher SQ^– desolvation penalty, allowing both ligands to have similar net binding energies. This additional interaction energy also increases the dissociation barrier for SQ^– relative to UQ (Figure 9). We conclude that the slower anionic semiquinone dissociation rate is a direct physical consequence of its charge, rather than a unique adaption of the protein. It is because of its charge that it interacts more strongly with the solvent and therefore requires stronger binding interactions to obtain affinity similar to the neutral quinone. If these stronger interactions were not present, SQ^– would bind more weakly than UQ, and thus, reduction in the Q_A site would be unfavorable (Scheme 1). The Q_A site has evolved to provide these stronger interactions mostly through electrostatic attraction to a bound non-heme Fe²⁺ cofactor.

Protein conformational changes are frequently cited as the major contribution to the rate-limiting step during slow ligand association and dissociation reactions.⁶⁰⁻⁶³ The tendency of highly polar and charged ligands to be involved with stronger protein interactions that compensate for their stronger solvent interactions will slow their association and dissociation rates without a conformational change. This simple model should be considered for any binding reaction where slow rates are observed for polar ligands.

Supporting Information Available

Partial charges for the quinone and semiquinone head groups, superimposed RC backbones at selected times from the 45 SMD trajectories, structure of important pairwise residues, list of authors for GAUSSIAN software. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

^‡ These authors contributed equally.

Funding Statement

National Institutes of Health, United States