Dependence of Effective Peak Capacity in Comprehensive Two-Dimensional Separations on the Distribution of Peak Capacity between the Two Dimensions

Abstract

One of the basic tenets of comprehensive two-dimensional chromatography is that the total peak capacity is simply the product of the first and second dimension peak capacities. As formulated the total peak capacity does not depend on the relative values of the individual dimensions but only on the product of the two. This concept is tested here for the experimentally realistic situation wherein the first dimension separation is undersampled. We first propose that a relationship exists between the number of observed peaks in a two-dimensional separation and the effective peak capacity. We then show here for a range of reasonable total peak capacities (500 to 4000) and various contributions of peak capacity in each dimension (10 to 150) that the number of observed peaks is only slightly dependent on the relative contributions over a reasonable and realistic range in sampling times (equal to the first dimension peak standard deviation, multiplied by 0.2 to 16). Most of this work was carried out under the assumption of totally uncorrelated retention times. For uncorrelated separations the small deviations from the product rule are due to the “edge effect” of statistical overlap theory and a recently introduced factor that corrects for the broadening of first dimension peaks by undersampling them. They predict that relatively more peaks will be observed when the ratio of the first to the second dimension peak capacity is much less than unity. Additional complications are observed when first and second dimension retention times show some correlation but again the effects are small. In both cases deviations from the product rule are measured by the relative standard deviations of the number of observed peaks, which are typically 10 or less. Thus although the basic tenet of two-dimensional chromatography is not exact when the first dimension is undersampled, the deviations from the product rule are sufficiently small as to be unimportant in practical work. Our results show that practitioners have a high degree of flexibility in designing and optimizing experimental comprehensive two-dimensional separations.

Introduction

One of the basic tenets of comprehensive two-dimensional chromatography (hereafter c-2DC) is that the total peak capacity (n_c,2D) is the product of the peak capacities of the first (¹n_c) and second (²n_c) dimensions [1]

$$n_{c,2D}={}^{1}n_c{}^{2}n_c$$ (1)

We refer to Eq. 1 as the product rule. As posed the equation suggests that one should get the same total peak capacity and thus observe the same number of peaks (see below), regardless of how the total peak capacity is distributed between the two dimensions. The question is: is this ideal equation applicable under real chromatographic conditions? This work addresses the issue of whether the number of peaks observed in c-2DC depends on how the total peak capacity is partitioned between the first and second dimensions.

Almost a decade after its first report, Guiochon and coworkers provided detailed physicochemical descriptions of total peak capacity largely consistent with the product rule [2,3]. Giddings then suggested that a two-dimensional (2D) chromatogram be thought of as a rectangular bed that is occupied by a grid where each ‘bin’ in the grid represents a unit of total peak capacity [4]. This is an intuitive and convenient concept, completely consistent with Eq. 1. Subsequent theoretical work by Davis and coworkers showed that 1) the rectangular grid model underestimates the true total peak capacity, because peaks can fall anywhere in the bed and not just at ‘bin’ centers [5,6], and 2) the edge effect, which is influenced by the ratio of the first and second dimension peak capacities, significantly increases the probability of observing peaks near the edges and corners of the bed [7,8]. The reason why edges and corners show more observed peaks and less peak overlap is that unlike the central regions of the grid there is no possibility of overlap from peaks whose retentions lie outside the periphery as such peaks simply don't exist. These studies also apply to all comprehensive 2D separations (hereafter c-2D separations, of which c-2DC is just one type) and suggest that the way in which such separations are carried out might well affect the separation performance, as measured by any of a number of common metrics perhaps most importantly the number of observed peaks.

To be clear, suppose our goal is to generate a total peak capacity of 1600. We are concerned that seriously different results (e.g. numbers of observed peaks) might be obtained if conditions are chosen that produce a square bed (¹n_c = 40, ²n_c = 40) compared to those that produce a very asymmetric bed (¹n_c = 160, ²n_c = 10). Experimentalists familiar with the difficulties and constraints associated with c-2DC recognize that some combinations of ¹n_c and ²n_c are much easier to achieve than others, in terms of total time, and that some combinations are currently inaccessible due to limitations of existing instrumentation.

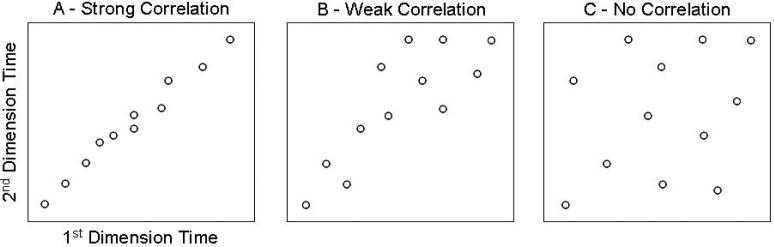
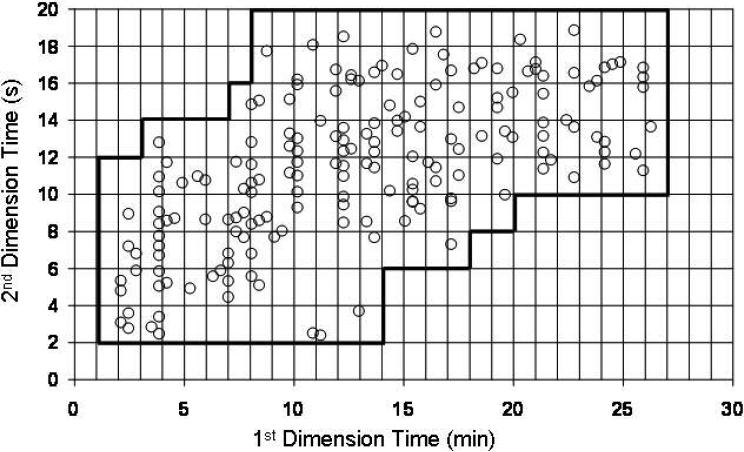
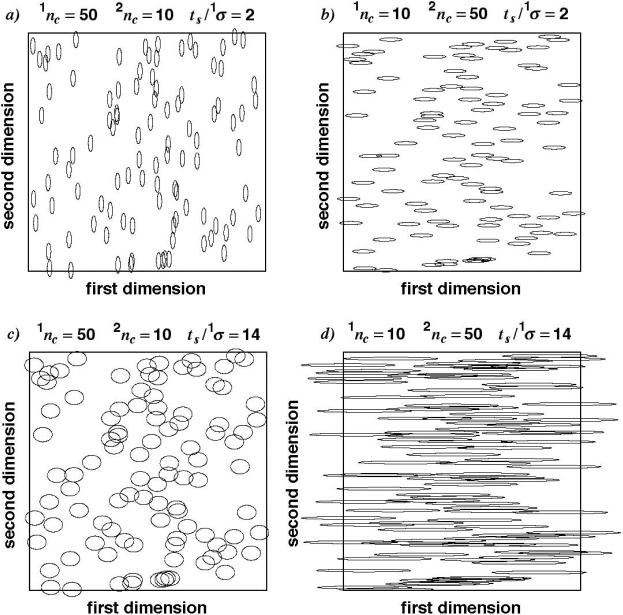
Another reason exists to compare metrics for symmetric and asymmetric beds in c-2DC. Generally the mechanics of peak processing in the first and second dimensions are very different. The resultant data matrix typically is composed of tens to hundreds of first dimension times at which samples are taken, each sample being associated with hundreds to thousands of second dimension concentrations (or signals) and times. For each first dimension sampling time, the integration (sum) of its associated second dimension separation represents a mass balance on the first dimension sampling. This data matrix is very asymmetric in the first and second dimensions. It is not clear that the product rule, which does not distinguish between the first and second dimensions, connects the asymmetric data matrix to usual metrics of interest. Thus far only for the case of completely randomly distributed peaks has the very highly developed statistical overlap theory (SOT) [5-8] allowed the derivation of an exact mathematical relationship between the average number of observed peaks and the total peak capacity. We propose here that for each type of distribution of peak coordinates (strong correlation, weak correlation, or no correlation; see Figure 1), a relationship exists between the average number of observed peaks and the total peak capacity. Some researchers have taken this proposal to its logical extreme, suggesting that a practical peak capacity should be defined relative to the fraction of total peak-capacity ‘bins’ that are occupied, with no regard for the surrounding empty space [9]. Figure 2 illustrates a slightly relaxed version of this concept (using experimental retention times from LC × LC data in ref 10) where the fraction of the 2D separation bed that is utilized is defined by the fraction of bins contained by the solid line relative to the total number of bins. For non-random peak distributions, the relationship between the number of observed peaks and the total peak capacity depends on the type of distribution of peaks, with different types of distributions having different relationships. Unlike the case of random distributions which can be treated by the equations of SOT these relationships generally are unknown. However, we believe that such relationships must exist and this is the basis on which we infer that the number of observed peaks, for a particular peak distribution, tells us something about the total peak capacity, although only in an indirect way.

1.

Classification of different types of distributions of peak coordinates observed in c-2D separations.

2.

Illustration of the fraction of ‘bins’ in a 2D separation bed that are occupied by peaks. The fraction corrects the total peak capacity for incomplete usage of the separation space. Circles represent coordinates of observed peaks in an experimental LC × LC separation [10]. The solid line defines the perimeter around the bins which are considered to be occupied.

A brief summary of the prior work that has led us to this study is useful. One of the chief complications and limitations of c-2DC is that the undersampling of its first dimension and subsequent reconstruction of the 2D chromatogram from the sampled data causes serious broadening of the reconstructed peaks and concomitantly a loss of total peak capacity. The sampling-induced broadening was investigated first by Murphy et al. [11] and Seeley [12]. The standard deviation of the resulting reconstructed first dimension peak can be expressed as the product of the standard deviation of the peak before sampling (¹σ) and a dimensionless peak broadening factor which depends mainly on the sampling rate but also other factors defined below (here and throughout, we use the notation of Schoenmakers et al. [13] to describe the attributes of 2D separations, with superscripts identifying the relevant dimension (e.g., ¹σ, ¹n_c, and ²n_c)). Since the peak capacity of a one-dimensional gradient chromatogram (i.e., solvent in LC or temperature in GC) is inversely proportional to the average peak standard deviation, Horie et al. [14] defined the effective peak capacity of a c-2D separation as the total peak capacity expressed by Eq. 1, divided by the average value of this broadening factor at a given sampling rate.

In a recent study of the problem of sampling-induced broadening, we proposed a more accurate metric based on results derived from a random distribution of peak coordinates. We took the effective peak capacity of a c-2D separation which involved an undersampled first dimension separation to be the total peak capacity of the same ideally sampled 2D separation, which had been degraded by broadening the first dimension peaks by that factor which produces the same number of observed peaks in both separations [15]. This metric is the logical result of the proposition that the average number of observed peaks and the total peak capacity are related. It also bases the effective peak capacity on the most practically important metric of a c-2D separation namely the number of observed peaks. We believe it to be the more realistic “correction” to the total peak capacity as it includes the effect of multiple peak overlaps in both dimensions and is based not just on the behavior of a single first dimension peak as was the basis for all earlier correction factors [11,12,14]. We used 2D SOT to determine the average standard deviation of sampled first dimension Gaussian peaks, < β > ¹σ, that satisfied this metric. We found that > β >, our correction factor, is well approximated by the empirical equation

$$<\beta >\approx \sqrt{1+0.21{\left(\frac{t_s}{1_{\sigma }}\right)}^2}$$ (2)

over the range, 0.2 ≤ t_s / ¹σ ≤ 16, where t_s is the time between sampling points in the first dimension. This peak broadening factor is numerically close to that predicted by Murphy et al. [11] and Seeley [12] at fast sampling rates but is larger at slow sampling rates. Henceforth we will use the terminology of Seeley and refer to the term t_s/¹σ as the dimensionless sampling period [12]. A small value of t_s/¹σ corresponds to a fast sampling rate. Eq. 2 also was shown to be similar to the average peak broadening factor obtained by randomly sampling a first dimension Gaussian peak and representing the sampled profiles by continuous wireframe-like distributions, in which the sampled average concentrations are connected by lines. A large number of computer simulations confirmed that Eq. 2 satisfies the proposed metric. A few of these simulations were made in which the peak capacities of the two dimensions were reversed, with the number of observed peaks remaining virtually the same. Recently, Blumberg et al. proposed an independent theory, leading to a result identical in form to Eq. 2 but with the empirical coefficient, 0.21, replaced by 1/4 [16].

On combining Eqs. 1 and 2, we obtain the effective peak capacity n_c,2D of a c-2D separation [15]

$$n_{c,2D}^{\prime }=n_{c,2D}∕<\beta >={}^{1}n_c{}^{2}n_c∕<\beta >\approx {}^{1}n_c{}^{2}n_c∕\sqrt{1+0.21{\left(\frac{t_s}{1_{\sigma }}\right)}^2}$$ (3)

The replacement of < β > in Eq. 3 by the average peak broadening factor of Murphy et al. [11] and Seeley [12] produces the effective peak capacity of Horie et al. [14].

In light of Eq. 3, the idea that the average number of observed peaks and the total peak capacity are related must be modified by replacing the total peak capacity with the effective peak capacity (n_c,2D). Because the effective peak capacity depends on both the product rule and the dimensionless sampling period we think it is essential to ask: do different values of ¹n_c and ²n_c having the same product and associated with the same dimensionless sampling period generate the same number of observed peaks in a c-2D separation having a specific type of peak distribution (as illustrated in Figure 1)? Perhaps more important than a general answer to this question is the question: does the product rule work under conditions of practical 2D chromatography so that as practitioners we can use it to guide the optimization of a 2D separation? We answer these questions by counting the observed peaks in simulated c-2D separations, in which various but realistic combinations of peak capacities were chosen to satisfy Eq. 1. The simulation algorithm is essentially identical to that of our previous study [15]. The simulations studied here were based on both random peak coordinates and on data taken from separations of real mixtures. The advantage of using simulations in this study is that many c-2D separations can be investigated, some of which may be difficult (or currently even impossible) to realize experimentally.

The results of this study should not be misinterpreted, since the total peak capacity of a 2D chromatogram actually changes as the dimensionless sampling period is varied. The practical, not theoretical, details of how chromatographic total peak capacities should be optimized is very dependent on the interaction of the dimensionless sampling period with the first dimension peak capacity and is the subject of work which will be presented elsewhere. However, we point out here that at a fixed first dimension gradient time, the effective 2D peak capacity initially increases as t_s is increased from zero, passes through a maximum and then decreases as t_s becomes larger. This results from two facts: first, as t_s is increased from very small values the peak capacity of the second dimension increases and then approaches an asymptote; second, as t_s increases above a certain time the undersampling of the first dimension becomes more and more serious, leading to a decrease in the effective peak capacity of the first dimension. Since these variations complicate an evaluation of the product rule, they are not included in this study.

Theory

Terminology and assumptions

We use the same terminology as in our previous paper [15]. Sampling is defined as the acquisition of aliquots of first dimension effluent. The sampling time (t_s) is the interval over which the first dimension effluent is collected. The sampling device is the reservoir that collects and transfers effluent between dimensions. The duty cycle is the fraction of the sampling time during which sample is collected [12]. The word “peak” describes the concentration profile of a single mixture constituent in either one or two dimensions; thus the numbers of peaks in the separation and mixture constituents are the same. The words “observed peak” describe the concentration profile that is detected in the reconstructed 2D separation and has a single maximum. Observed peaks can be due to the presence of one or more mixture constituents. Finally, an “ideally sampled” 2D separation is a hypothetical c-2D separation in which sampling is so rapid (e.g., 40 or more samples per first dimension peak) that sampling-induced broadening can be neglected.

We also made five assumptions [15], which apply here. First, peaks are Gaussian in both dimensions. Second, all peaks in a given dimension have the same width (standard deviation) but peaks in the two dimensions usually have (very) different widths. Third, the sampling device behaves ideally and instantaneously transfers focused sample to the second dimension. Fourth, sampling has no effect on the second dimension standard deviation. Finally, the sampling device has a 100% duty cycle.

2D statistical overlap theory (SOT)

The average number of observed peaks (p) in a c-2D separation containing randomly distributed peaks can be predicted from 2D SOT [15]. The basis of 2D SOT is discussed in detail elsewhere [5-8]. Geometrically, peak overlap is modeled in two dimensions by the overlap of ellipses representing the peak contours. The ellipses are randomly distributed in a plane but their major axes are oriented in the same direction. The major and minor axes are proportional to the standard deviations ¹σ (or < β > ¹σ) and ²σ of peaks in the corresponding c-2D separation, and to the average minimum resolution between the two nearest-neighbor peaks in two observed peaks. This resolution varies with the amount of overlap. The total number of isolated ellipses and groups of overlapping ellipses is the cluster number. The cluster number varies among members of a large ensemble of planes and ellipses, which differ only in the coordinates of the ellipse centers. The average cluster number equals the average number of observed peak maximums, p, in the corresponding ensemble of 2D separations.

Definition of peak capacity

In a 2D separation with the time spans ¹D and ²D in the first and second dimensions, the peak capacities ¹n_c and ²n_c are [17]

$${}^{1}n_c={}^{1}D∕\left(4{}^1\sigma {}^{1}R_s\right)$$ (4a)

$${}^{2}n_c={}^{2}D∕\left(4{}^2\sigma {}^{2}R_s\right)$$ (4b)

where ¹R_s and ²R_s are the resolutions of adjacent peak pairs in the first and second dimensions that are sufficient for separation. The values of ¹R_s and ²R_s depend on the goals of the separation but are usually taken as unity.

Eq. 4 is not appropriate, when the standard deviations of peaks vary in the separation. In such cases, the method of Lan and Jorgenson based on the additivity of reciprocal peak widths can be used to more accurately calculate the peak capacity [18].

Procedures

Simulation of comprehensive and ideally sampled 2D separations

The computational details of the algorithm used to simulate c-2D separations were given in our previous paper [15]. For this study, peak coordinates were assigned to the central 64% of a reduced 2D space of unit length and width (i.e., ¹D = ²D = 0.8) to avoid loss of peak maximums near boundaries. The number of randomly distributed constituents, m, was 100, 250, 400, or 550. Correlated separations were modeled using 95 to 598 retention times of observed peaks taken from experimental c-2D chromatograms [10,19], which were scaled to fit in the reduced 2D space. First dimension Gaussian peaks were computed with exponentially random heights, for which the probability of any peak height lying between h and h + dh equaled exp(–h/H) dh/H, with the average peak height H equal to one (this produced more small peak heights than large ones). The first dimension standard deviations were calculated from the peak capacity using Eq. 4a, with unit resolution. The average peak concentrations at different dimensionless sampling periods were determined. To speed up the computations, these average concentrations were evaluated by interpolating values of the error function evaluated for arguments spaced by 0.001 and not by numerical integration as before [15]. Exponentially random peak heights were used because they have some empirical basis [20-23]. The sampled concentrations were “injected” into the second dimension as Gaussians having standard deviations calculated from the relevant peak capacity using Eq. 4b, with unit resolution. The numbers of observed peak maximums were then counted. Maximums were determined as values of the three-dimensional concentration matrix, which were larger than their eight surrounding nearest-neighbor concentrations [15]. Each simulation was repeated fifty times with different exponentially random peak heights (and uniformly random peak coordinates, when dealing with this case), and the average number of observed peaks was calculated. Six or seven combinations of ¹n_c, ²n_c values spanning 10 to 150 were examined for simulations based on random peak coordinates and a set of five total peak capacities ranging from 500 to 4000. Values of ¹n_c greater than 150 were not considered due to extensive computational time. For the weakly correlated peak coordinates, taken from actual experimental studies, the arbitrarily chosen (i.e., not experimental) total peak capacities of 500 and 2000 were used. The peak capacity combinations are reported in Table 1. They were chosen to span the upper peak-capacity range in nearly linear increments, with the lower range determined by the product rule. Some arbitration was involved, with the ratio of ¹n_c to ²n_c varying for different n_c,2D to keep the peak capacities within reasonable bounds. Computations were made for t_s/¹σ varying from 0.2 to 16 to cover the range of almost infinitely fast sampling to values large enough to encompass sampling rates typical of practice.

Table 1.

One dimensional (¹n_c, ²n_c) and total (n_c,2D) peak capacities in this study.^a Symbols identify average numbers of observed peaks in Figures 3, 4, and 6.

Symbol	nc,2D
	500		1000		2000		3000		4000
	1nc	2nc	1nc	2nc	1nc	2nc	1nc	2nc	1nc	2nc
circle	50	10	100	10	150	13.3	150	20	150	26.7
square	42	11.9	80	12.5	120	16.7	120	25	120	33.3
diamond	34	14.7	60	16.7	90	22.2	90	33.3	90	44.4
cross	26	19.2	40	25	60	33.3	60	50	60	66.7
plus sign	18	27.8	20	50	40	50	30	100	40	100
triangle, apex up	10	50	13.3	75	26.7	75	23.1	130	32	125
triangle, apex down	--	--	10	100	13.3b	150b	20	150	26.7	150

^a1R_S = ²R_S = 1

^bcombination not used with correlated peak coordinates due to retention-time discretization

Simulations of ideally sampled 2D separations of peaks with weakly correlated first and second dimension retention times were made in the reduced 2D space as discussed previously [15]. In brief, ¹σ and ²σ were calculated from Eqs. 4a and 4b with unit resolution for different peak capacities given in Table 1 for n_c,2D equaling 500 and 2000. To mimic sampling-induced broadening at t_s/¹σ values from 0.2 to16, ¹σ was multiplied by < β > as per Eq. 2. The profiles of bi-Gaussian peaks having the scaled correlated coordinates, standard deviations < β > and ²σ, and exponentially random heights were summed, and the numbers of observed peaks were counted. The simulation was repeated fifty times with different exponentially random heights, and the average number of observed peaks was calculated. Each average was compared to the average number of observed peaks in the corresponding simulated comprehensive 2D separation having the same scaled correlated coordinates.

Calculation of average number of observed peaks by 2D SOT

The average number of observed peaks was calculated by 2D SOT as described previously [15]. The parameters of the calculation were the number of constituents, the ratio of first and second dimension peak capacities, and the effective peak capacity. The last depends on the first dimension peak broadening factor and on the peak standard deviations and dimensional spans as shown by Eqs. 1 - 4. Calculations were made for constituent numbers (or peak numbers) equaling 100, 250, 400, and 550, dimensionless sampling periods spanning from 0.2 to 16, and all peak capacity combinations given in Table 1.

Results and Discussion

Accuracy of the product rule with uncorrelated peak coordinates

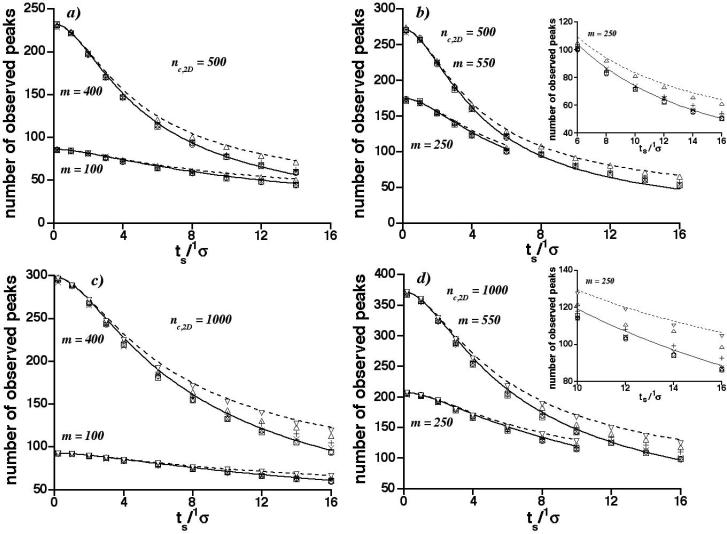
Figures 3 and 4 give graphs of the average number of observed peaks vs. the dimensionless sampling period for various numbers of constituents and total peak capacities. The different symbols identify results for the different combinations of ¹n_c and ²n_c in Table 1. These results are relevant not only to c-2D separations but in the limit of very fast sampling to traditional 2D separations in beds or gels as well (this conclusion follows because the profiles of very rapidly sampled peaks and unsampled peaks are virtually indistinguishable). In most cases, regardless of the number of constituents and total peak capacity, there is almost no change in the number of observed peaks as the ratio of n_c,2D to ²n_c is varied regardless of the dimensionless sampling period. In other words, the number of observed peaks is largely independent of the peak capacity distribution, when the total peak capacity is constant and the dimensionless sampling period t_s / ¹σ (or the peak broadening factor < β >) is held constant. This means that for random c-2D separations even when the first dimension is severely broadened by undersampling the product rule (Eq. 1) works well. Thus we conclude that the assumptions of all previous workers, although not absolutely correct, are close enough that the error is minor and not practically important. This “negative result” is very important. Clearly, if this were not the case the experimental optimization of c-2D separations would be enormously more complicated.

3.

Graphs of average number of observed peaks vs. the dimensionless sampling period (t_s/¹σ) for m = 100, 250, 400, and 550 randomly distributed constituents, and for total peak capacities (n_c,2D) of 500 and 1000. Symbols are identified in Table 1 for different ¹n_c, ²n_c combinations and represent the average of 50 simulations. Curves are predictions by 2D SOT (- - -, smallest ¹n_c and largest ²n_c; —, largest ¹n_c and smallest ²n_c).

4.

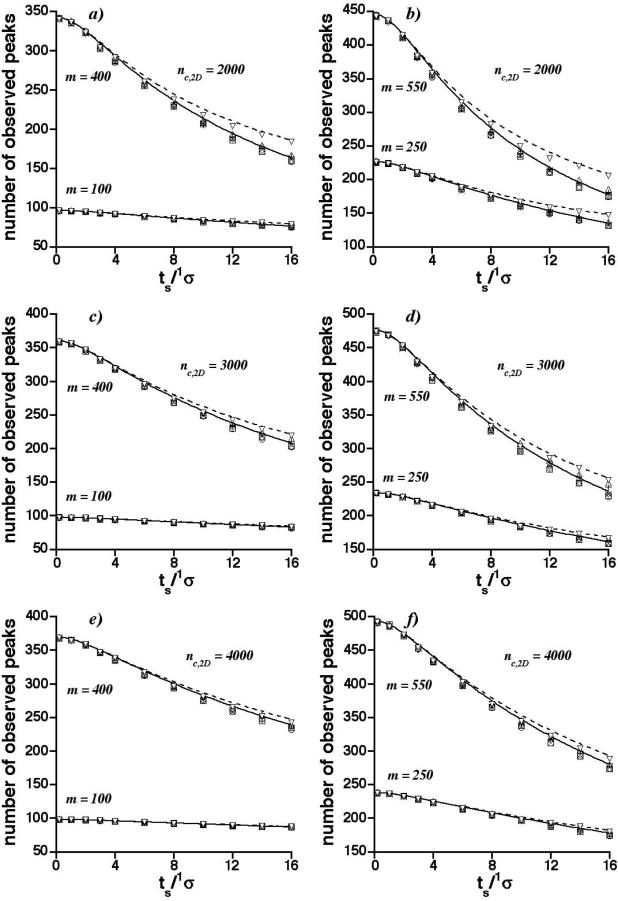
As in Figure 3, but for total peak capacities (n_c,2D) of 2000, 3000, and 4000.

The dashed curves in each graph are the average numbers of observed peaks predicted by 2D SOT for the smallest ¹n_c and largest ²n_c used here, whereas the solid curves represent the 2D SOT predictions for the largest ¹n_c and smallest ²n_c used here. The predictions for other ¹n_c, ²n_c combinations almost lie (see below) between these extremes and are not shown. The results and predictions are given in different graphs for clarity. For example, the superposition of Figures 3a and 3b for n_c,2D = 500 would be confusing, because some results are numerically similar.

Several trends are clear. For any number of constituents and total peak capacity the number of observed peaks decreases with increasing dimensionless sampling period [15]. At any dimensionless sampling period, the fraction of constituents appearing as observed peaks decreases as the number of constituents increases and as the total peak capacity decreases. Furthermore, the number of observed peaks does not change very much with the number of constituents at low sampling rates when the total peak capacity is small (e.g., 500) thus demonstrating the severe consequences of undersampling inefficient separations.

However, as pointed out above, by far the most important finding is that for any number of constituents, total peak capacity, and dimensionless sampling period, the average number of observed peaks depends only weakly on the specific values of ¹n_c and ²n_c, provided that the product of the two peak capacities is fixed. The average numbers of observed peaks increase only slightly as ¹n_c decreases. To evaluate their variation, the percentage difference between the smallest and largest average in all ¹n_c, ²n_c combinations was calculated for different constituent numbers m, dimensionless sampling periods t_s / ¹σ, and total peak capacities n_c,2D. The relative standard deviation (RSD) of the averages was also calculated for all ¹n_c, ²n_c combinations and different m, t_s/¹σ, and n_c,2D. Table 2 reports the maximum of these metrics for each n_c,2D. The maximum percentage difference is about 25-30% for small n_c,2D and decreases to about 5% for large n_c,2D, and is associated with large m (400 and 550) and large t_s / ¹σ (16). The maximum RSDs are associated with the same m and t_s / ¹σ, and typically are 10 or less (only one RSD out of 280 exceeds 10). The reason for these trends is discussed below. These relatively small numbers suggest that the choice of specific ¹n_c, ²n_c combinations in c-2D separations is largely irrelevant, provided that sampling time t_s can be adjusted to maintain the appropriate dimensionless sampling period. Since the mechanics of processing first and second dimension peaks are very different, this is, to us, a somewhat surprising and fortuitous finding.

Table 2.

Maximum percentage difference between, and RSD of, average numbers of observed peaks in c-2D separations with random peak coordinates for all ¹n_c, ²n_c combinations, m, t_s/¹σ, and n_c,2D. Maximums are reported as a function of n_c,2D. Values of m associated with maximums are reported. t_s/¹σ, = 16 in all cases.

nc,2D	Maximum percentage differencea	Maximum RSD	m
500	26.3	8.6	400
1000	28.1	10.1	400
2000	17.9	6.2	550
3000	11.0	4.2	550
4000	5.5	2.0	550

^acalculated relative to smaller number

Predictions of 2D SOT for uncorrelated peak coordinates

The predictions by 2D SOT shown in Figures 3 and 4 agree well with the simulation results. Many of the reported trends can be explained by the systematic decrease in the number of observed peaks with increasing saturation factor (α) [7,8,15] defined below:

$$\alpha =4\pi \stackrel{‒}{m}<\beta >{}^1\sigma {}^2\sigma {\left(R_s^{\ast }\right)}^2∕\left({}^{1}D{}^{2}D\right)=\frac{\pi }{4}\frac{{\left(R_s^{\ast }\right)}^2}{{}^{1}R_s{}^{2}R_s}\frac{\stackrel{‒}{m}}{n_{c,2D}^{\prime }}$$ (5)

where m̄ is a statistical approximation to the number of constituents and $R_s^{\ast }$ is the average minimum resolution required for two observed peaks to be formed [8,24]. $R_s^{\ast }$ itself depends on the saturation factor [8]. The final expression in Eq. 5 is obtained by combining the central expression with Eqs. 3 and 4, showing that the saturation factor is inversely proportional to the effective peak capacity. The number of observed peaks decreases with increasing dimensionless sampling period because the correction < β > for undersampling gets bigger (see Eq. 2), the effective peak capacity gets smaller, and consequently the saturation factor increases. Similarly, the fraction of constituents appearing as observed peaks decreases at any dimensionless sampling period with a large number of constituents m and small total peak capacity, because the saturation factor increases. Finally, the number of observed peaks is weakly dependent on the number of constituents at low sampling rates and small total peak capacities because the saturation factor is high, and the number of observed peaks is less sensitive to the saturation factor when it is large as compared to when it is small (i.e., dp / dα decreases with α).

For any given number of constituents, total peak capacity, and dimensionless sampling period, the numbers of observed peaks in Figures 3 and 4 must all have the same saturation factor (see Eq. 5); consequently, the small deviations among them as the relative contribution of the two dimensions to the total peak capacity is varied must be due to some issue other than the saturation factor. 2D SOT also predicts that the number of observed peaks can increase because of the “edge effect” [7]. This is the reduced likelihood that peaks overlap near the edges of 2D separations. As stated previously, the likelihood of overlap is lower in the edge regions because no peaks lie beyond the edges; thus, they cannot cause overlap. A detailed discussion of the edge effect in c-2D separations is given in the Appendix to this paper. There, it is shown that for a given number of constituents, total peak capacity, and dimensionless sampling period, the number of observed peaks increases with decreasing values of the first dimension peak capacity and decreasing fraction of the total peak capacity that is distributed in the first dimension.

Accuracy of the product rule with correlated peak coordinates

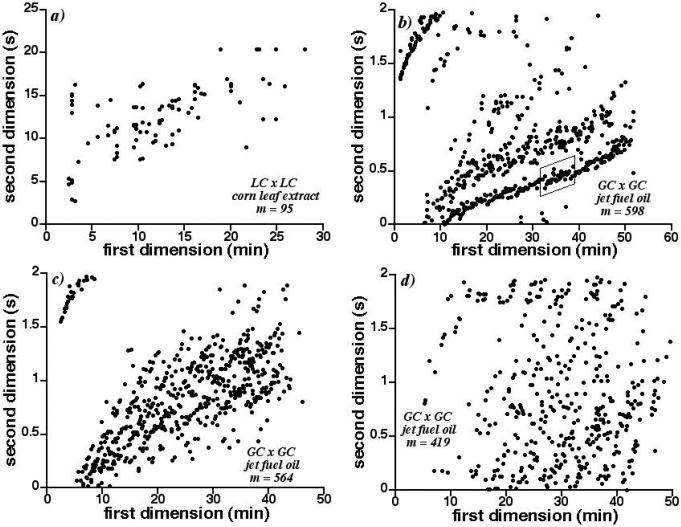
The purpose of this section is to evaluate whether the chief findings discussed above also apply to correlated distributions of peaks. This is important because typically peaks in real c-2D separations are not entirely randomly distributed. Usually their coordinates are positively correlated to some extent because the separation mechanisms in the two dimensions are not fully independent [25,26]. Figure 5a is a graph of the retention times of experimental observed peaks for a LC × LC of corn-leaf extract [10]. Figures 5b - 5d are the retention times of experimental observed peaks for a GC × GC of jet fuel oil [19], as detected by mass spectrometry at three different mass-to-charge ratios using peak-finding software described elsewhere [27] (the parallelogram in Figure 5b is discussed below). The three detection channels produced different retention time distributions and numbers of observed peaks due to different ion fragmentations, with numbers m equaling 598, 564, and 419 for mass-to-charge ratios of 57 (Figure 5b), 95 (Figure 5c), and 105 (Figure 5d), respectively. Similar work has been reported on highlighting different perspectives of sample composition by detecting GC × GCs at multiple mass-to-charge ratios [28]. Various degrees of correlation are apparent, with the largest in Figure 5a and the smallest in Figure 5d, as measured by the linear correlation coefficient. This metric is perhaps not the best, since it is based on a presumed fit of a line to all retention times. For example, a part of Figure 5b is extremely correlated. However, the retention times clearly are not random.

5.

Weakly correlated retention times of observed peaks in experimental separations by a) LC × LC [10] and b - d) GC × GC [19]. GC × GC retention times were determined at mass-to-charge ratios of b) 57, c) 95, and d) 105.

It has been argued that results on peak overlap obtained from simulations of random peak coordinates, such as discussed above, are not important to separations acquired with highly selective detection, such as mass spectrometry. However, these GC × GC retention time distributions show that very complex mixtures can yield literally hundreds of observed peaks even at a single mass-to-charge ratio [19], with peak overlap being a realistic concern. Unlike the simulations described below, these GC × GCs were collected at modest sampling rates (i.e., three or more samples per first dimension peak) [19] and represent the true sample complexity with little sampling-induced peak broadening.

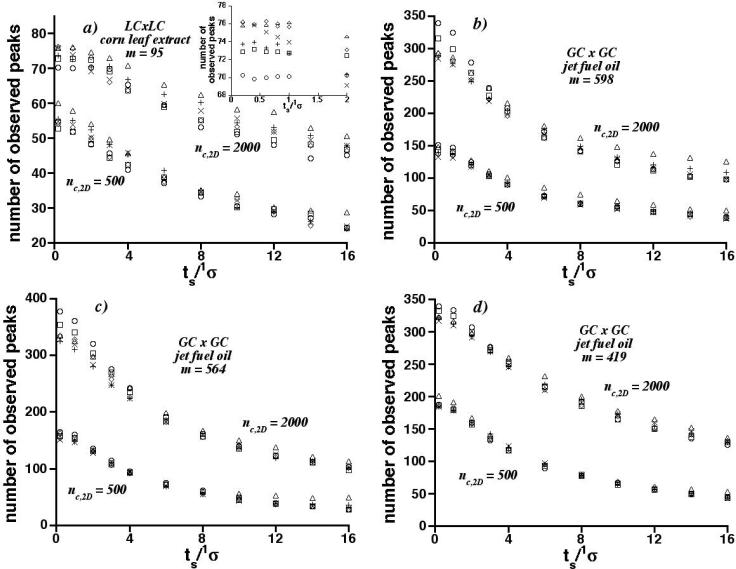
The retention times were scaled and used as the coordinates in simulations of c-2D separations. Figure 6 shows graphs of the average numbers of observed peaks vs. the dimensionless sampling period for total peak capacities of 500 and 2000. The symbols and peak capacity combinations are given in Table 1. Larger total peak capacities were not considered because the experimental retention times were determined to only three significant digits, and peak widths at larger total peak capacities were less than or equal to the digitized intervals between retention times, causing some anomalies. Predictions by 2D SOT are not useful in this case and thus not shown because the retention times are not random.

6.

Graphs of average number of observed peaks vs. the dimensionless sampling period (t_s/¹σ) for constituents having retention times in Figure 5 and the arbitrarily chosen total peak capacities (n_c,2D), 500 and 2000. Inset in a) shows convergence of average number of observed peaks at small t_s/¹σ for n_c,2D = 2000. Symbols are identified in Table 1.

Overall, the findings are similar to those obtained for random peak coordinates. As before, the average number of observed peaks decreases with increasing dimensionless sampling period and at any dimensionless sampling period it increases with increasing total peak capacity. Most importantly, as in the case of random peak distributions it is largely independent of the specific combination of ¹n_c and ²n_c used to produce the total peak capacity. As above, the edge effect produces slightly greater numbers of observed peaks at low sampling rates for small ¹n_c and large ²n_c (see Appendix).

However, unlike the case of totally random peak coordinates, the number of observed peaks depends on the specific ¹n_c, ²n_c combination as the sampling rate becomes fast (i.e., as t_s / ¹σ decreases). This is a consequence of the asymmetric distribution of vacant space around the correlated peak coordinates, which favors better separations for certain ¹n_c, ²n_c combinations than for others (see below). As expected on mathematical grounds, however, the number of observed peaks for any particular ¹n_c, ²n_c combination asymptotically approaches a constant value as the sampling rate becomes very fast. This behavior is shown in the inset to Figure 6a. The rate of convergence depends on ¹n_c, ²n_c; here, it is slow for ¹n_c = 60 and ²n_c = 33.3 (i.e., the results represented by crosses).

As before, the variation among average numbers of observed peaks was evaluated by calculating percentage differences between the smallest and largest averages, and by calculating RSDs of averages, for all ¹n_c, ²n_c combinations, t_s / ¹σ and n_c,2D. Table 3 reports the maximum of these metrics for both n_c,2D. They are similar to ones reported in Table 2 for random peak coordinates, with the maximum percentage differences ranging from about 10 to 35% and the maximum RSDs typically equaling 10 or less (82 out of 88 RSDs are less than 10). Both metrics usually are associated with large dimensionless sampling periods (t_s / ¹σ ≥ 12). This may be surprising, because variations of the observed peak numbers are very noticeable in Figure 6 at small t_s / ¹σ and large n_c,2D. Two exceptions to the trends are found for the GC × GC results in Figure 6c. First, the variation is much larger than usual for n_c,2D = 500 due to the large observed peak number for ¹n_c = 10, ²n_c = 50. Second, the variation is greatest at small t_s / ¹σ when n_c,2D = 2000.

Table 3.

Maximum percentage difference between, and RSD of, average numbers of observed peaks in Figure 6 for all ¹n_c, ²n_c combinations, t_s / ¹σ, and n_c,2D. Maximums are reported as a function of n_c,2D. Values of t_s / ¹σ, associated with maximums are reported in parentheses.

peak coordinates	nc,2D	Maximum percentage differencea	Maximum RSD
LC × LC, Figure 5a	500	20.1 (16)	7.4 (16)
	2000	19.7 (14)	6.3 (12)
GC × GC, Figure 5b	500	34.5 (16)	11.6 (16)
	2000	29.3 (14)	10.7 (16)
GC × GC, Figure 5c	500	79.9b (16)	25.9c (16)
	2000	16.5 (1)	5.8 (0.2)
GC × GC, Figure 5d	500	22.5 (16)	8.0 (16)
	2000	12.3 (14)	4.3 (14)

^acalculated relative to smaller number

^bbecomes 30.0 on excluding datum for ¹n_c = 10, ²n_c = 50

^cbecomes 11.7 on excluding datum for ¹n_c = 10, ²n_c = 50

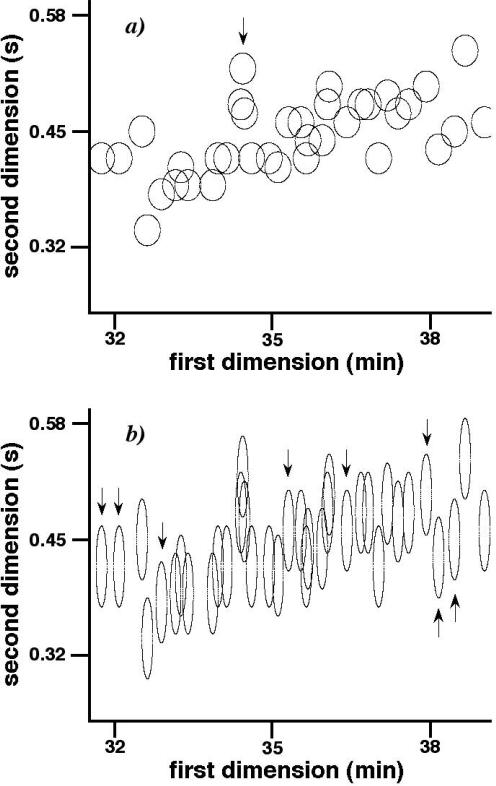
With correlated peak coordinates, small variations of the average number of observed peaks for the same, fast sampling rate but different ¹n_c, ²n_c are not surprising. We will illustrate this by discussing two examples. In Figure 5b, a parallelogram encloses 36 highly correlated GC × GC retention times. Figure 7a is a panel of elliptical contours centered about these times for t_s/¹σ = 0.2, ¹n_c = 60, and ²n_c = 33.3 (n_c,2D = 2000). Figure 7b is a similar panel with the same total peak capacity but now ¹n_c = 150 and ²n_c = 13.3. The cluster number in Figure 7b (21) is almost twice that in Figure 7a (12), with arrows identifying contours that are isolated in one panel but not the other. The cluster numbers also are similar to the average numbers of observed peaks (19.9 and 14.2, respectively) determined from 50 simulated c-2D separations. Here, the separation is better for large first dimension and small second dimension peak capacities, because the correlated retention times are more closely aligned with the first dimension than the second dimension. Consequently, better separation in the first dimension favors larger numbers of observed peaks. This trend is observed in all the GC × GCs.

7.

Elliptical peak contours centered on 36 retention times in parallelogram of Figure 5b. Arrows point to contours isolated in one panel but not the other. Ellipse areas are the same in both panels. t_s/¹σ = 0.2, n_c,2D = 2000. a) ¹n_c = 60, ²n_c = 33.3; b) ¹n_c = 150, ²n_c = 13.3.

In contrast, the LC × LC coordinates in Figure 5a produce more observed peaks with small first dimension and large second dimension peak capacities, when t_s/¹σ is small and n_c,2D = 2000 (see Figure 6a). By constructing graphs of ellipse clusters like Figure 7, we found this behavior is mostly caused by the 27 peaks eluting within the first 8 minutes. In this region, many peaks have identical first dimension retention times, with separation occurring exclusively in the second dimension. Consequently, broad second dimension peaks produce relatively poor separations, whereas narrow ones produce better separations. For example, in this region we found only 17 ellipse clusters for ¹n_c = 150, ²n_c = 13.3, but we found 25 clusters for ¹n_c = 26.7, ²n_c = 75 (t_s/¹σ = 0.2).

The different trends in the GC × GCs and LC × LC arise from the specifics of the asymmetric vacant space around the peak coordinates. Although these examples show that we can analyze the coordinate patterns and decide which ¹n_c, ²n_c combinations are favorable or unfavorable, we are unaware of a simple metric for this purpose. As shown in Figure 6, however, the trends largely disappear as the sampling rate decreases. At very low sampling rates many peaks merge into a single sample of first dimension effluent, with a partial loss of the asymmetric vacant space around them and the subtle interaction the space produces. A similar result is found on reducing the total peak capacity from 2000 to 500, that is, the asymmetric space is occupied by broader peaks, and the changes in the number of observed peaks are not as pronounced (see Figures 6b – 6d).

We observe that the GC × GCs of jet fuel oil represent an extreme case of retention-time correlation, since this mixture contains principally only four compound classes (acyclic alkanes, cyclic alkanes, alkylmonoaromatics, and alkyldiaromatics). Consequently, the departures in Figure 6 from trends for random retention times are likely to be larger than for most mixtures, and consequently set an upper bound on such departures.

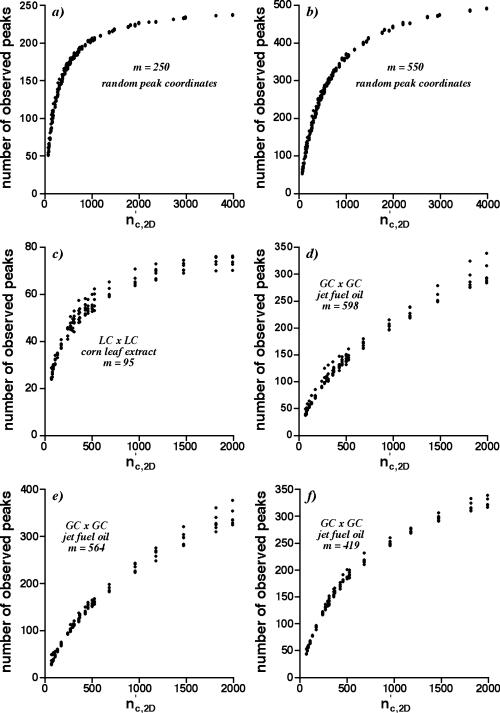
Relationship between average number of observed peaks and effective peak capacity

The results in Figures 3, 4, and 6 can be expressed relative to the effective peak capacity n_c,2D using the dimensionless sampling periods, the total peak capacity, and Eq. 3. Figure 8 gives graphs of the average number of observed peaks vs. the effective peak capacity for 250 and 550 random peak coordinates and for the correlated peak coordinates in Figure 5. All average numbers of observed peaks and total peak capacities were used. A relationship exists in all cases, with the average increasing rapidly with the effective peak capacity and asympotically approaching the number of constituents. A relationship is not surprising for random peak coordinates, since the saturation factor α of 2D SOT principally determines the average number of observed peaks and α depends on n_c,2D (see Eq. 5). As postulated in the Introduction, however, relationships also exist for correlated peak coordinates, although they are not as precise or currently predictable from equations. These relationships support the hypothesis that any combination of total peak capacity and dimensionless sampling period generating the same effective peak capacity produces nearly the same number of observed peaks for a given distribution of peak coordinates.

8.

Graphs of the average number of observed peaks vs. the effective peak capacity (n_c,2D) for a), b) random peak coordinates and c) - f) correlated peak coordinates in Figure 5. Data were taken from Figures 3, 4, and 6, with n_c,2D calculated from total peak capacities, dimensionless sampling periods, and Eq. 3.

Validation of the peak broadening factor < β > for correlated c-2D separations

In our previous work [15], ideally sampled 2D separations containing bi-Gaussians having first and second dimension standard deviations equaling < β > ¹σ and ²σ, respectively, were simulated to verify that they contain (on average) the same number of observed peaks as c-2D separations simulated at various dimensionless sampling periods. However, only 33 trials were made with correlated peaks. Further investigation of correlated peaks is warranted, even though this section of the paper is not directed at the main topic, since the expression for < β > (see Eq. 2) was based solely on random peaks.

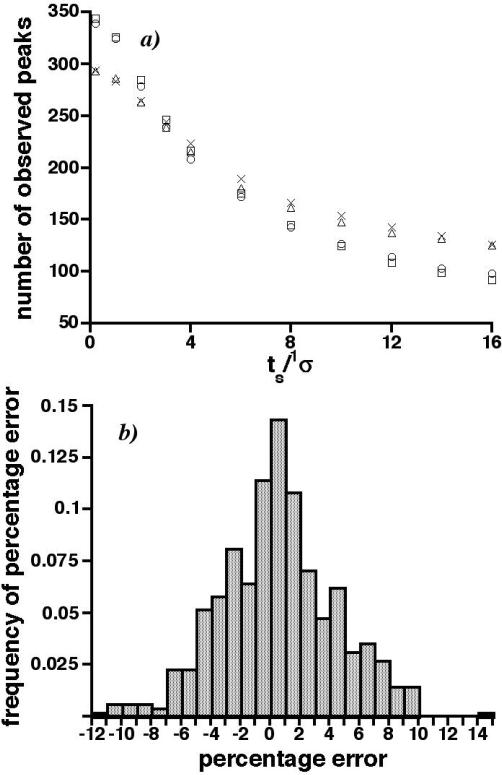
One might expect < β > to account poorly for the subtle issues affecting peak overlap such as the edge effect and the asymmetric distribution of vacant space that are possible with correlated retention times. For example, as shown in Figure 6b when n_c,2D = 2000, ¹n_c = 150, and ²n_c = 13.3 the observed peak numbers (represented by circles) are relatively large at fast sampling and relatively small at slow sampling; however, when again n_c,2D = 2000 but ¹n_c = 26.7 and ²n_c = 75 the observed peak numbers (represented by triangles) are smaller at fast sampling and larger at slow sampling. The SOT based < β > factor does predict these trends thereby validating its use with correlated retentions, at least in this instance. Figure 9a is a graph of these numbers vs. the dimensionless sampling period, with the superposition of the average numbers of observed peaks in 50 ideally sampled 2D separations. The agreement is nearly exact.

9.

a) Graph of average number of observed peaks vs. the dimensionless sampling period (t_s/¹σ) for comprehensive and ideally sampled 2D separations having retention times in Figure 5b and the total peak capacity, 2000. Numbers for comprehensive and ideally sampled simulations are represented by circles and squares, respectively, for ¹n_c = 150, ²n_c = 13.3; and by triangles and crosses, respectively, for ¹n_c = 26.7, ²n_c = 75. b) Frequency of 480 percentage errors between average numbers of observed peaks in comprehensive and ideally sampled 2D separations having the weakly correlated retention times in Figure 5. Percentage errors were calculated relative to the average numbers of observed peaks in c-2D separations. Distribution average, standard deviation: 0.45, 3.94.

In general, the average numbers of observed peaks in Figure 6 provide a large database to test how well < β > works with correlated separations. Figure 9b shows the frequency of the percentage error between these numbers and their counterparts in ideally sampled 2D separations for t_s/¹σ values greater than or equaling one. The number of different combinations of ¹n_c, ²n_c, and t_s/¹σ was 480, with the ²n_c/¹n_c ratio spanning the range, 0.089 ≤ ²n_c/¹n_c ≤ 5 (as calculated from Table 1 for n_c,2D equaling 500 and 2000). The average and standard deviation of the frequency are 0.45 and 3.94, respectively. The 25 outliers, as measured by two standard deviations from the mean, have no common pattern other than with t_s/¹σ ≥ 6 (with one exception). The frequency in Figure 9b only resembles a Gaussian but it is not (the Pearson statistic is 50.5 for 26 degrees of freedom and significant at the 95% confidence level). The frequency's near-zero average and small standard deviation show that < β >, as calculated from Eq. 2, is a good measure of the average first dimension peak broadening factor even in weakly correlated separations.

Conclusions

1. The most practically significant result is that there is only a weak dependence of the numbers of observed peaks on the distribution of the total peak capacity between the first and second dimensions. This offers a great deal of flexibility in method development for 2D separations, in that the instrumental configuration that yields the largest total peak capacity will also yield (for the same peak distribution) the largest number of observed peaks. Since the effective peak capacity depends on the dimensionless sampling period (see Introduction), it is indeed fortunate that there is no a priori reason to prefer to put more effort into the first or second dimension to obtain more observed peaks. There may, of course, be very practical reasons to prefer to put more effort into one dimension versus the other but these will vary with the methodologies used to do the 2D separation.

2. At slow sampling rates where there is a small dependence (RSDs of 10 or less) of the number of observed peaks on the distribution of peak capacity, the trend favors asymmetric peak capacity distributions with small ¹n_c relative to ²n_c. This too is a fortuitous outcome, as it is far easier to adequately sample a low peak capacity first dimension separation having relatively wide peaks and then generate the bulk of the total peak capacity in the second dimension, than is the converse. This is especially true in gradient elution LC × LC when the gradient cycle time of the second dimension of the system is considered. Nonetheless, it is not advisable to deliberately make ¹n_c smaller than ²n_c simply for the sake of capitalizing on the edge effect.

3. At slow sampling rates, this small increase in the number of observed peaks for asymmetric peak capacity distributions results from larger edge effects caused by first dimension undersampling. Interestingly, the effect of sampling-induced broadening acts to make the space more symmetric when ²n_c is smaller than ¹n_c, but the reverse occurs when ²n_c is larger than ¹n_c. This is the primary reason that asymmetric peak capacity distributions with relatively low first dimension peak capacities are generally favored.

4. At fast sampling rates, the number of observed peaks depends weakly (typical RSDs of 10 or less) on the peak capacity distribution when vacant space is asymmetrically distributed around correlated peak coordinates. In some cases more observed peaks are produced when ¹n_c > ²n_c but in other cases when ¹n_c < ²n_c. At this time, the most favorable ¹n_c, ²n_c combination cannot be predicted from a simple metric. The dependence weakens as the sampling rate decreases. This variation, which is not observed with random peak coordinates because the vacant space is symmetrically distributed, differs from the predictable outcome of the edge effect and supports the prevailing paradigm that the separation mechanism used in c-2D separations should be highly orthogonal.

5. Simulations of c-2D separations using weakly correlated retention times taken from real LC × LC and GC × GC experiments showed that the sampling-induced peak broadening factor < β >, which was described in a preceding paper and determined using random peak coordinates, also accurately describes first dimension broadening in real 2D separations, where peak coordinates are not entirely random.

Table A1b.

As in Table A1a, but t_s/1σ = 4, < β > = 2.10, α = 0.20.

1nc	%1nc	δ	observed peak number	p
150	7.5	0.19	352.6 ± 8.0	364.1
120	6.0	0.29	353.7 ± 8.2	363.5
90	4.5	0.52	354.6 ± 8.6	363.1
60	3.0	1.17	355.5 ± 8.7	362.9
40	2.0	2.63	354.1 ± 8.7	363.3
26.7	1.33	5.92	356.2 ± 7.6	364.3
13.3	0.67	23.7	358.4 ± 8.8	368.0

Table A1c.

As in Table A1a, but t_s/¹σ = 8, < β > = 3.83, α = 0.32.

1nc	%1nc	δ	observed peak number	p
150	7.5	0.34	265.8 ± 9.8	277.2
120	6.0	0.53	266.2 ± 9.2	276.6
90	4.5	0.95	268.5 ± 9.1	276.3
60	3.0	2.13	266.8 ± 8.7	276.8
40	2.0	4.79	270.3 ± 8.4	278.2
26.7	1.33	10.8	271.2 ± 8.8	281.0
13.3	0.67	43.1	281.7 ± 9.0	290.0

Appendix. Edge Effect in c-2D Separations

The edge effect is responsible for the reduced probability of peak overlap seen in the edges and corners of rectangular 2D separations. For random peak distributions, the number of observed peaks in these regions increases with smaller constituent number, larger saturation factor, and larger aspect ratio, which is the ratio of the first and second dimension peak capacities at equal resolution [7]. Since the first two variables are constant at any dimensionless sampling period in the panels of Figures 3 and 4, it is the aspect ratio that is related to the variation of the average number of observed peaks. A shortcoming of the aspect ratio (as defined in ref 7) in treating c-2D separations is the fact that it does not depend on which peak capacity is larger. Since undersampling in c-2D separations always reduces the effective ¹n_c but has no effect on ²n_c, a function related to the aspect ratio is needed, but one that distinguishes between the peak capacities of the two dimensions. We introduce

$$\delta =<\beta >{}^{2}n_c∕{}^{1}n_c$$ (A1)

where the factor < β >, as described above, accounts for the reduction of the first dimension peak capacity due to undersampling. The traditional aspect ratio equals either δ or 1/δ, depending on which is larger. Because ¹n_c/< β > is the effective peak capacity of the first dimension will call δ the specific aspect ratio, meaning it is defined with ²n_c in the numerator and the effective ¹n_c in the denominator. The meaning of δ is simple: in a reduced 2D space of unit length and width [7], δ is greater than one for peaks broadened mostly in the first dimension, and is less than one for peaks broadened mostly in the second dimension. For a given number of constituents and saturation factor, the edge effect is large for either very large or very small δ; it reaches a minimum at δ = 1.

It is useful to relate δ to the percentage of the total peak capacity, due to the first dimension

$$\%{}^{1}n_c=100{}^{1}n_c∕n_{c,2D}$$ (A2)

By combining Eq. 1 with Eqs. A1 and A2, we find

$$\delta =100<\beta >∕(\%{}^{1}n_c{}^{1}n_c)$$ (A3)

which tells us that a large edge effect from the first dimension (δ >> 1) will be obtained when < β > is large due to undersampling, and %¹n_c and ¹n_c are small. Since δ is inversely proportional to the product of %¹n_c and ¹n_c, for a given number of constituents and saturation factor the edge effect and number of observed peaks in c-2D separations will be enhanced at low sampling rates when both %¹n_c and ¹n_c are small.

The consequences of varying %¹n_c, ¹n_c, and < β > are shown in the four panels of Figure A1. Here the ellipses representing the contours of 100 peaks are randomly distributed over four different 2D separations (shown as reduced spaces of unit length and width) all having a total peak capacity of 500. In all cases, the peak coordinates are the same and lie within the space, but the peak contours near the space's edges can lie outside. Geometrically, the edge effect is large when large portions of peak areas lie near and outside the space [7]. In Figures A1a and A1c, ¹n_c is large and ²n_c is small, whereas in Figures A1b and A1d their values are reversed. The sampling rate is fast in Figures A1a and A1b but is slow in Figures A1c and A1d. Specific values are reported in the figure and caption.

A1.

Elliptical peak contours predicted from 2D SOT for 100 randomly distributed peaks and total peak capacity of 500. In a) and b), α = 0.103, t_s/¹σ = 2, and < β > = 1.36; in c) and d), α = 0.376, t_s/¹σ = 14, and < β > = 6.55. Ellipse areas are the same in panels a) and b), and in panels c) and d). a) ¹n_c = 50, %¹n_c = 10, ²n_c = 10, δ = 0.272, cluster number = 84; b) ¹n_c = 10, %¹n_c = 2, ²n_c = 50, δ = 6.81, cluster number = 88; c) ¹n_c = 50, %1 = 10,²n_c = 10, δ = 1.31, cluster number = 49; d) ¹n_c = 10, %¹n_c = 2, 2 = 50, δ = 32.7, cluster number = 57.

We first consider exchanging ¹n_c and ²n_c at fast sampling rates, where < β > is small (Figures A1a and A1b). In both cases, δ is close to one, the edge effect is small, and the number of observed peaks (ellipse clusters) is about the same, although the primary dimension of peak broadening changes. A different result is found, however, on exchanging ¹n_c and ²n_c at slow sampling rates, where < β > is large. As before, δ is close to one for large %¹n_c and ¹n_c (Figure A1c) and the edge effect is small, although relative to a fast sampling rate the primary dimension of peak broadening is reversed (cf. Figures A1a and A1c). However, for small %¹n_c and ¹n_c (Figure A1d), δ and the edge effect are large, significant portions of peak areas lie outside the space, and the number of observed peaks increases.

The 2D SOT predicted “lengths” and “widths” (i.e., axes) of ellipses in Figure A1 are $4^1\sigma <\beta >R_s^{\ast }{∕}^{1}D$ and $4^2\sigma R_s^{\ast }{∕}^{2}D$ [7,8]. Using Eqs. 4a and 4b, they can be expressed as $<\beta >R_s^{\ast }∕\left({}^{1}n_c\right)$ and $R_s^{\ast }∕\left({}^{2}n_c{}^{2}R_s\right)$. Unlike the resolutions ¹R_s and ²R_s, however the value of $R_s^{\ast }$ in 2D SOT is not arbitrary; it varies with the amount of peak overlap but is always less than one for peaks having exponentially random heights [8,24]. This explains why the “lengths” and “widths” in Figure A1 are smaller than the reciprocal peak capacities.

We do not mean to overstate the importance of δ. The edge effect also depends on the constituent number and saturation factor [7], and a large δ is not sufficient by itself to markedly increase the average number of observed peaks. For example, the largest δ associated with Figures 4e and 4f, 42.0, exceeds that in Figure A1d, but the edge effect is minor because the total peak capacity is large (4000) and the saturation factor is small. The importance of the saturation factor is also seen in Table 2, where the edge-effect induced variations of the average number of observed peaks are greatest for large m, large t_s / ¹σ, and small n_c,2D because all increase the saturation factor (see Eq. 5).

Some trends illustrating the subtleties of the edge effect are best described using tabular data. Tables A1a – A1d report values of ¹n_c, %¹n_c, δ, the 2D SOT predicted number of observed peaks p, and the average and standard deviation of numbers of observed peaks in 50 simulated c-2D separations for 550 randomly distributed constituents, several dimensionless sampling periods (t_s/¹σ = 2, 4, 8, and 16), and the ¹n_c, ²n_c combinations in Table 1 for a total peak capacity of 2000. In Tables A1a – A1d, δ evolves from a number less than one to a number exceeding one as ¹n_c and %¹n_c decrease, with the primary dimension of peak broadening in the reduced space shifting from the second to the first. For any specific ¹n_c and %¹n_c, δ increases with increasing dimensionless sampling period, because < β > increases (see Eq. A3). For each dimensionless sampling period, the minimum p predicted by 2D SOT is found at intermediate ¹n_c and %¹n_c values, for which δ nearly equals one. The minimum is associated with larger ¹n_c and %¹n_c as the dimensionless sampling period increases, because < β > increases. For the largest ¹n_c and %¹n_c considered here, δ is not small enought for a large edge effect in the second dimension, and p increases only slightly above its minimum value. Thus, the solid curves in Figures 3 and 4 for the largest ¹n_c and smallest ²n_c combinations are virtually indistinguishable from ones for the smallest p. In general, the p's in Tables A1a – A1d agree with the average numbers of observed peaks in simulations. The simulation RSDs range from 1.8 to 4.4, which mask the small edge effect for δ < 1. However, the large edge effect for δ >> 1 is apparent. For the dimensionless sampling period of 16 in Table A1d, statistical differences are found among the average numbers of observed peaks as δ increases (e.g., the error bar of the final entry does not overlap with the error bars of the other entries).

Table A1a.

Attributes for random distribution of m = 550 constituents with ¹n_c, ²n_c combinations reported in Table 1. n_c,2D = 2000, t_s/¹σ = 2, < β > = 1.36, α = 0.14.

1nc	%1nc	δ	observed peak number	p
150	7.5	0.12	412.5 ± 7.8	416.2
120	6.0	0.19	410.7 ± 8.2	415.7
90	4.5	0.34	411.3 ± 9.4	415.3
60	3.0	0.76	410.8 ± 8.4	415.0
40	2.0	1.70	410.5 ± 8.6	415.0
26.7	1.33	3.83	412.4 ± 8.1	415.4
13.3	0.67	15.3	414.5 ± 7.5	417.2

Table A1d.

As in Table A1a, but t_s/¹σ = 16, < β > = 7.47, α = 0.51.

1nc	%1nc	δ	observed peak number	p
150	7.5	0.66	174.0 ± 7.0	177.7
120	6.0	1.04	175.0 ± 6.1	177.5
90	4.5	1.84	175.1 ± 6.5	177.9
60	3.0	4.15	174.7 ± 7.7	179.9
40	2.0	9.34	180.1 ± 6.2	183.7
26.7	1.33	21.0	185.7 ± 5.9	189.9
13.3	0.67	84.0	205.2 ± 6.7	208.5

^a α and < β > are not proportional because resolution $R_s^{\ast }$ depends on α (see Eq. 5)