Improving the usefulness of the Multidimensional Pain Inventory

The biopsychosocial model of pain regards the maintenance of chronic pain as a dynamic interaction among biological, psychological, behavioural and social-cultural factors. This study demonstrates that the content of the Multidimensional Pain Inventory (MPI), which is based on biopsychosocial theory, can be largely captured by three well-distributed and relatively independent summary scales. A cluster analysis of these scales yields a taxonomy similar to the original MPI taxonomy. The authors argue that summary scales are less prone to skew, are more stable than individual MPI subscales, and may have greater usefulness when assessing individuals who suffer from chronic pain. A new method of predicting the likelihood of change among MPI psychosocial profiles is introduced. Based on this method, the authors demonstrate how summary scales enhance profile stability across time.

Abstract

BACKGROUND:

The Multidimensional Pain Inventory (MPI) is a reliable and valid self-report instrument that measures the impact of pain on an individual’s life, quality of social support and general activity. Criticism of the MPI has focused on this instrument’s internal structure and the stability of its classification taxonomy.

OBJECTIVES:

To determine whether empirical summary scales could be developed for the MPI based on a large sample of respondents diagnosed with fibromyalgia syndrome. It was hypothesized that summary scales would improve the psychometric quality of the MPI and increase the stability of respondents’ taxonomy profiles across time.

METHODS:

Respondents completed the MPI on two occasions before their admission to a multidisciplinary pain management program.

RESULTS AND CONCLUSIONS:

Based on principal components analysis, three summary scales were developed that reflected level of impairment, social support and activity. Summary scales possessed good psychometric qualities and, when cluster analyzed, replicated the MPI taxonomy. Exploratory analyses of the MPI taxonomy revealed that goodness-of-fit values generally became less reliable as respondent profiles approached the overall sample mean. When the relative distance between respondents fit to taxonomy profiles and the distance from the sample mean was considered, profile stability using summary scales was predicted with good precision. These results suggest that summary scales may enhance the usefulness of the MPI, and that the traditional method of determining profile fit within the MPI is not stable and needs to be reconsidered.

The biopsychosocial model of pain regards the maintenance of chronic pain as a dynamic interaction among biological, psychological, behavioural and social-cultural factors (1,2). Assessment and treatment that follows this theory focuses not only on the physical and psychological effect of persistent pain, but also on the quality of available social support. One questionnaire that is based on biopsychosocial theory and offers a comprehensive assessment of chronic pain is the Multidimensional Pain Inventory (MPI [3]).

The MPI is an easily accessible, reliable and valid self-report questionnaire that measures the impact of pain on an individual’s life, how others respond to that person’s expression of pain and the frequency at which the individual engages in specific activities of daily life. Evidence-based and consensus reviews of the MPI (4,5) have recommended this instrument for the assessment of individuals suffering from chronic pain and as a core outcome measure within clinical trials. In addition, the MPI has proven to be useful in identifying specific psychosocial profiles or patterns of response among individuals suffering from chronic pain (6). These profiles, labelled “dysfunctional”, “interpersonally distressed” and “adaptive coper”, have been generally well replicated and promoted as an efficient method of providing more tailored treatment to individuals experiencing chronic pain (7).

Despite the evident value of the MPI, some concerns have been raised regarding the internal structure of this instrument as well as the stability of its associated profiles. Analyses of the MPI at the item level have shown mixed results, with some studies demonstrating acceptable replication of the MPI internal structure, and others describing inadequate or poor replication (8–10). Moreover, in their investigation of the classification of subgroups of individuals based on MPI profiles, Broderick et al (11) and Junghaenel and Broderick (12) found that approximately one-third of respondents may spontaneously change their classification across a short interval of time. These authors cautioned that the MPI subgroup classification may lack sufficient stability and, therefore, be of questionable use in either treatment matching or measurement of treatment outcome. As a consequence, several authors have recommended that the MPI be revised. Suggestions have ranged from modification of instructions offered to respondents, to a complete restructuring of the entire inventory and taxonomy (9,13,14). Although revision of the MPI to enhance its usefulness and psychometric quality has considerable merit, modification may also lead to a potentially confusing array of competing versions of the MPI. An alternative method that may both protect the integrity of the MPI and enable improvement of its psychometric qualities is the development of composite or summary scales. Summary scales may serve to better reflect the internal structure of the MPI and, potentially, enhance the stability of its profile and classification taxonomy without the need for any major revision of the original instrument. One summary scale currently exists and consists of a composite of MPI activity subscales (6). Although it has been suggested that the MPI may profit from the inclusion of additional composite or summary scales (9), to date, little research has been conducted in this regard.

The current article focuses on the development of summary scales for the MPI based on a large sample of patients suffering from fibromyalgia syndrome (FMS). We demonstrate that summary scales are better distributed and more stable than individual MPI subscales, and suffer less restriction of range. We show that cluster analyses of summary scales tend to yield psychosocial profiles that are similar to those identified by Turk and Rudy (6). Finally, we suggest that profile stability can be enhanced through the use of summary scales.

METHODS

Participants and data collection

Participants in the present study consisted of 472 adults admitted to the Rheumatology Day Care Program at London Health Sciences Centre, which is a tertiary care hospital affiliated with the University of Western Ontario (London, Ontario). All participants met the American College of Rheumatology criteria for a diagnosis of FMS (15). There were 458 female and 14 male participants. The average age of participants was 47.25 years (range 20 to 78 years). All participants were aware that their involvement was completely voluntary and consented to the use of their assessment information for research purposes. Approval was granted by the University of Western Ontario Research Ethics Board.

The present study used the revised or second version of the MPI. The source of the second version of the MPI is unclear but is often referenced as either the original publication or as the version written by Rudy (16). The second version of the MPI contains 61 items, of which, only 56 items are used for scoring. The MPI is divided into three sections, with each section containing separate subscales. The first section addresses the impact of pain on an individual’s life and contains five subscales: Pain Severity, Interference, Life Control, Affective Distress and Support. The second section measures the types of responses made by significant others when there is an expression of pain and contains three subscales: Negative Responses, Solicitous Responses and Distracting Responses. The final section assesses the frequency that an individual engages in common activities of daily life and contains four subscales: Household Chores, Outdoor Work, Activities Away from Home and Social Activities. The MPI also provides a General Activity summary scale, which is the averaged sum of the four MPI activity subscales.

Participants completed the MPI on two occasions. All participants initially completed the MPI as part of a general assessment battery before admission to the treatment program. Participants then completed the MPI a second time, immediately following admission to the program. The average time between the first and second completion of the MPI was 55.87 days. Complete information was available for 376 (79.7%) of the 472 participants across both assessments.

Data analyses and procedure

Data analyses proceeded sequentially and were separated into three sections. In the first section, summary scales were developed through principal components analysis of respondents’ initial MPI subscale scores. In the second section, a series of k-means cluster analyses were performed on the summary scales to determine whether summary scale clusters would replicate the psychosocial profiles described by Turk and Rudy (6). In the third section, the stability or test-retest reliability of summary scale profiles was assessed.

RESULTS

Section 1: Development of summary scales

To determine whether reasonable linear composites could be created for the MPI, a principal components analysis of respondents’ initial MPI subscale scores was conducted. The means and SDs of respondents’ scores on the 12 MPI subscales are presented in Table 1. An exploratory approach was required due to the absence of any previous study that has performed a factor analysis of the 12 MPI subscales in isolation. Instead, previous studies have focused on either attempting to replicate the original scale structure of each MPI section separately (8,10), investigating the MPI at the individual item level (9) or conducting multi-inventory analyses that have included the MPI (17–20). Principal components analysis represented the most appropriate and preferred choice of factor extraction due to our focus on data reduction (21).

TABLE 1.

Respondents’ scores on the 12 Multidimensional Pain Inventory subscales

Scale	Score, mean ± SD
Pain Severity	4.35±0.88
Interference	4.56±0.86
Life Control	2.84±1.11
Affective Distress	3.65±1.11
Support	4.00±1.50
Negative Responses	1.98±1.53
Solicitous Responses	3.02±1.42
Distracting Responses	2.02±1.23
Household Chores	3.68±1.39
Outdoor Work	0.93±0.87
Activities Away From Home	2.40±0.98
Social Activities	2.17±1.03

Parallel analysis and scree test criteria converged well on a three-factor solution, accounting for 60% of the total variance. The first three factors had eigenvalues of 3.10, 2.53 and 1.52. Eigenvalues for the remaining factors were well below 1.00. Simple structure was achieved through oblique rotation (22). Oblique rotation was preferred due to its ability to solve for both uncorrelated and correlated factors (21). Bentler’s simplicity index (23) was high (S=0.99) and suggested a well-defined factor structure following rotation.

Table 2 provides the final factor solution of the MPI scales following rotation. All MPI subscales loaded above 0.60 on their respective factors. Two subscales (Negative Responses and Household Chores) demonstrated moderate cross-loadings. The remaining 10 subscales demonstrated minor or near zero cross-loadings. Rotated factors demonstrated low to moderate intercorrelations and indicated good separation of dimensions. The first factor was defined by high loadings among MPI subscales measuring pain severity and interference, life control and affective distress, and reflected a general distress or global impairment dimension. The second factor captured the subscales related to social support or caring response by significant others. The third factor reflected general activity and was comprised of the four activity subscales of the MPI. To assess replicability, bootstrap factor analyses (24) were conducted across 1000 re-samples. Bootstrap analyses demonstrated a high degree of replicability in our sample data with low SEs among eigenvalues and rotated component loadings.

TABLE 2.

Multidimensional Pain Inventory principal components analysis with oblique (Promin) rotation

Scale	Factor loadings
	1	2	3
Pain Severity	0.72	0.08	−0.12
Interference	0.66	0.11	−0.21
Life Control	–0.79	0.05	−0.09
Affective Distress	0.82	−0.13	0.06
Support	0.05	0.87	0.03
Negative Responses	0.37	–0.60	0.12
Solicitous Responses	0.12	0.87	0.06
Distracting Responses	0.07	0.78	0.04
Household Chores	−0.11	−0.31	0.61
Outdoor Work	0.13	−0.07	0.65
Activities Away from Home	−0.07	0.18	0.72
Social Activities	−0.07	0.20	0.73
Factor	Interfactor correlation
	1	2	3
1	1.00	–	–
2	−0.11	1.00	–
3	−0.23	−0.03	1.00

The highest loading for each subscale is shown in bold

Consistent with our principal components solution, three MPI summary scales were created and labelled Impairment, Social Support and Activity. Each scale represented the averaged sum of MPI subscales that loaded most highly on each factor. Two MPI subscales (Life Control and Negative Responses) demonstrated negative loadings and were reversed before summing. Whereas the Impairment and Social Support summary scales were unique constructs, the Activity summary scale was identical in form and derivation to the General Activity scale found in the revised version of the MPI. The correlation pattern of the summary scales closely replicated the correlations of the rotated principal components. Summary scales retained simple structure without loss of information.

Table 3 provides descriptive statistics of the summary scales. Overall, summary scales demonstrated good psychometric properties. Impairment and Activity summary scales were well shaped with minimal skew and kurtosis. Social Support displayed moderate negative skew but fell within acceptable limits (25). Impairment and Social Support summary scales were internally consistent and reliable with Cronbach’s alpha (α) greater than 0.75 across both scales. The internal consistency of the Activity summary scale was more modest (α=0.62).

TABLE 3.

Multidimensional Pain Inventory summary scale descriptive statistics

Scale	Score, mean ± SD	Skew	Kurtosis	Rel (α)
Impairment	3.93±0.76	−0.08	−0.17	0.76
Social Support	3.27±1.13	−0.48	−0.28	0.79
Activity	2.30±0.74	−0.10	−0.25	0.62

Impairment is calculated as (Pain Severity + Interference + [6 – Life Control] + Affective Distress)/4. Social Support is calculated as (Support + (6 – Negative Responses] + Solicitous Responses + Distracting Responses)/4. Activity is calculated as (Household Chores + Outdoor Work + Activities Away from Home + Social Activities)/4. Internal consistency reliability (Rel) is measured by Cronbach’s alpha (α)

In terms of distribution, all summary scales extended at least 2 SDs from the mean, with no significant ceiling or floor effects. In contrast, seven of the 12 subscales contained in the MPI suffered noticeable restriction of range and failed to provide a broad range of scores beyond 2 SDs from the mean (Table 4).

TABLE 4.

Multidimensional Pain Inventory subscale and summary scale range

Scale	Standardized score (T)
	Raw score of 0	Raw score of 6	Range of 0–6
Pain Severity	0.69	68.72	68.03
Interference	−3.23	66.86	70.09
Life Control	24.34	78.59	54.25
Affective Distress	16.96	71.21	54.25
Support	23.37	63.32	39.95
Negative Responses	37.03	76.35	39.32
Solicitous Responses	28.65	71.02	42.37
Distracting Responses	33.58	82.48	48.90
Household Chores	23.56	66.63	43.07
Outdoor Work	39.33	108.54	69.20
Activities Away from Home	25.54	86.58	61.04
Social Activities	28.97	87.00	58.03
Impairment	−1.64	77.20	78.84
Social Support	21.16	74.16	53.00
Activity	19.08	99.84	80.75

Test-retest reliability was assessed by comparing respondents’ MPI subscale and summary scale scores at preadmission and admission. Stability coefficients (r) for MPI subscales were consistent with previous analyses (11). The average stability of MPI summary scales (mean r=0.70 [range 0.58 to 0.81]) was greater than the average stability of individual MPI subscales (mean r=0.65 [range 0.38 to 0.78]).

Section 2: MPI classification taxonomy

A series of k-means cluster analyses was conducted to determine whether summary scales would define groups similar to those demonstrated by Turk and Rudy. A three-cluster solution was deemed to be optimal based on comparison of between-cluster and within-cluster variance (26). The means and SDs for each cluster are presented in Table 5. Cluster membership was evenly distributed with clusters containing 133, 131 and 112 respondents, respectively. The first cluster was defined by respondents who reported greater levels of impairment and lower levels of activity, and was similar in content to the Dysfunctional profile described by Turk and Rudy. The second cluster consisted of respondents who described reduced impairment and greater levels of activity, and suggested an Adaptive Coper profile. The final cluster was populated by respondents who reported poorer quality of social support and was consistent with an Interpersonally Distressed profile.

TABLE 5.

Multidimensional Pain Inventory summary scale clusters

Scale	Cluster
	1	2	3
Impairment	4.26±0.58	3.31±0.60	4.27±0.66
Social Support	4.09±0.63	3.60±0.65	1.89±0.70
Activity	1.86±0.64	2.80±0.54	2.22±0.71

Data presented as mean ± SD

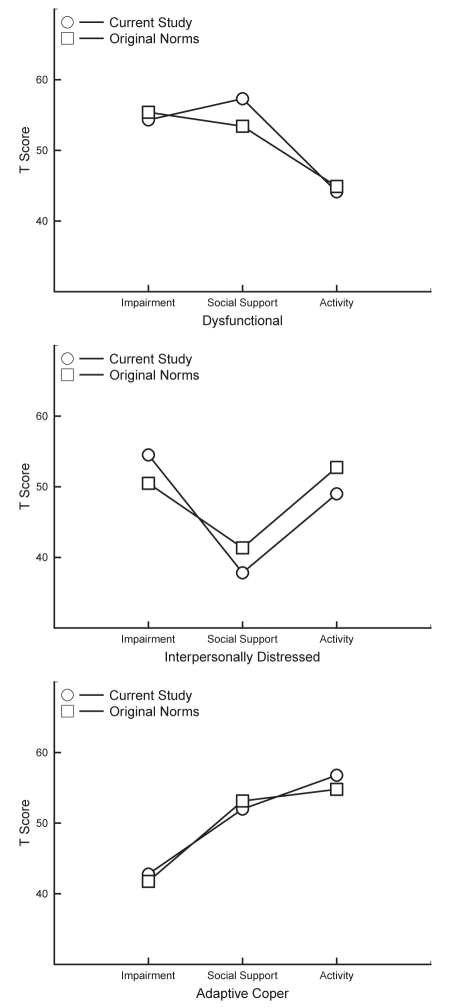
The current summary scale cluster profiles were converted to standardized T scores to enable a direct comparison of the cluster solution with the original taxonomy described by Turk and Rudy. Summary scales were estimated based on the original profile T scores provided in Table 2 (column 1) of the article by Turk and Rudy (6). These two sets of summary scales were plotted and are presented in Figure 1. Despite differences between samples across time, diagnoses, sample sex composition and method of deriving summary scales, the current and archival cluster solutions were virtually identical.

Figure 1).

Comparison of summary scale cluster profiles with the original taxonomy by Turk and Rudy (6)

Section 3: Profile goodness of fit and profile stability

Consistent with the procedure originally used by Turk and Rudy, the generalized squared distances (D²) were calculated for each respondent by comparing respondents’ summary scale scores with the three MPI profiles. This resulted in three D² values for each respondent, with the lowest value representing best profile fit. Best D² fit was then compared with the k-means cluster assignment. To automate this procedure, a computer program was written by the authors; the program scores the MPI for each respondent and then calculates that respondent’s best MPI profile fit. The program and a description of the exact method used to determine profile fit can be downloaded at www.scarthmckillop.ca/research.html.

Classification agreement was good, with only 11 of the 376 respondents misclassified (3%, Cohen’s kappa = 0.96), and suggested that generalized D² approximated the summary scale cluster solution. Stability of summary scale profiles was assessed by comparing respondents’ classification at preadmission with respondents’ classification at admission. Of the 376 respondents, 125 (33.2%) changed classification from preadmission to admission. For comparison, this procedure was repeated with the original Turk and Rudy subscale taxonomy. The results of that analysis demonstrated a moderately higher rate of instability, with 135 of the 376 respondents (35.9%) changing classification from preadmission to admission.

Classification stability of summary scale profiles was not predicted by magnitude of best D² fit. No significant difference was found between degree of best profile fit among respondents whose classification remained stable (median D²=1.37) and respondents who changed classification (median D²=1.42). However, the distance from respondents’ summary scale profiles to the overall sample mean was significant, with stable profiles clustering toward the perimeter (median D²=2.96) and unstable profiles resting closer to the centre (median D²=2.19; U=12702, P<0.01). To adjust for distance from the sample mean, a measure of relative distance was created by subtracting the best-fitting profile distance value from the overall mean distance value for each respondent. Respondents who changed classification had significantly lower relative distance values (mean = 0.49) than respondents whose classification remained stable (mean = 1.49; t[374]=7.35, P<0.001; d=0.76). A comparison of the relative distance values between stable and unstable subscale profiles was also significant but with a lower effect size (t[374]=4.65, P<0.001; d=0.48).

To further assess the relationship between relative distance and classification stability, a quartile split was performed on relative distance values and the frequency of classification stability in each quartile was compared. As shown in Table 6, a clear linear trend existed between relative distance and classification stability for MPI summary scale profiles. Classification stability ranged from 44.68% in the lowest quartile to 90.43% in the highest quartile. A similar trend was also found between relative distance and subscale profile stability, but with a reduced range. The lowest quartile classification stability for subscale profiles was 51.06% and the highest quartile stability was 78.72%.

TABLE 6.

Mean relative distance scores and stability percentages according to quartiles for Multidimensional Pain Inventory summary scale and subscale profiles

Quartile	Summary scale profiles		Subscale profiles
	Distance	Percentage	Distance	Percentage
Low	−0.29	44.68	−0.19	53.19
Moderate-low	0.53	60.64	0.59	64.89
Moderate-high	1.38	71.28	1.52	64.89
High	3.00	90.43	3.09	86.17

Each quartile contains 94 respondents

DISCUSSION

The current study focused on the development of summary scales for the MPI based on a large sample of respondents diagnosed with FMS. Respondents completed the MPI on two occasions before their admission to a multidisciplinary pain management program. Principal components analysis of respondents’ initial MPI subscale scores demonstrated that the content of the MPI can be largely captured by three well-formed and relatively independent dimensions. Based on these dimensions, summary scales were constructed that reflected respondents’ overall level of impairment, social support and activity. Descriptive analyses indicated that summary scales possessed good distribution, range and stability, and were generally superior to MPI subscales in terms of their psychometric qualities. Furthermore, despite its accepted use, descriptions of or rationales for how the General Activity summary scale of the MPI was created or derived are limited. To the best of our knowledge, our study provides the first empirical support for this summary scale.

Following principal component and descriptive analyses, we performed a cluster analysis of summary scales. The results of the cluster analysis suggested that the MPI classification taxonomy was robust across summary scales and yielded three psychosocial profiles consistent with those originally developed by Turk and Rudy. Despite the improved psychometric quality of summary scales and replication of the MPI taxonomy, summary scale profiles were not more stable than MPI subscale profiles. Exploratory analyses of the MPI taxonomy revealed that goodness-of-fit values generally became less reliable as respondent profiles approached the overall sample mean. When the relative distance between respondents fit to taxonomy profiles and the distance from the sample mean were considered, we were able to predict profile stability with good precision. Moreover, in this sample, summary scale profiles outperformed subscale profiles.

Due to their optimal shape and range, the summary scales described in the present study should enhance the usefulness of the MPI, and provide a more parsimonious and economical method of describing the experience of individuals who suffer from chronic pain. Summary scales offer a clear psychometric advantage over reliance on MPI sub-scales alone while preserving the integrity of the existing item and subscale structure of the MPI. These scales provide an efficient method of summarizing complex diagnostic information.

By definition, individuals who experience chronic pain tend to report heightened suffering, changes in the quality of intimate relationships and a reduction in activity levels. As a result, self-report instruments that measure the effect of pain may demonstrate a clustering of respondents’ scores at the low or high end of those scales. When clustering is extreme, the distribution of respondents’ scores may become poorly formed and demonstrate restriction of range due to skew, or ceiling or floor effects.

The multidimensional nature of the MPI invites comparison between subscales. However, restriction of range may lead to distortion in the interpretation of respondents’ scores and difficulty in making meaningful comparisons between subscales. For example, in the current study, the MPI Support subscale has a mean of 4.00 and an SD of 1.50. Because MPI subscales have a range of 0 to 6, the majority of respondents are clustering toward the top end of this scale and endorsing a high level of social support from significant others. When standardized, the maximum score of 6 on the Support subscale represents a T score of approximately 63. Within a normal distribution, a T score of 63 represents the 91st percentile. However, in our current sample, a T score of 63 on the Support subscale, by definition, represents the 100th percentile. Consequently, if we compare, for example, the Support subscale with a less restricted and better distributed sub-scale, such as Affective Distress, it would be improper to say that a T score of 70 on Affective Distress is greater than a T score of 63 on Support in the sample.

At the other extreme, the Outdoor Work subscale of the MPI has a mean of 0.93 and an SD of 0.87. In our sample, the majority of respondents indicated that they engage in very limited or no outdoor activities. A respondent who engages in no outdoor activity (a raw score of 0) has a T score of approximately 39. In contrast, the Household Chores subscale has a higher mean, so a respondent who engages in very few household chores but more than none (a raw score of 1) would translate to a T score of 31. It is counterintuitive to suggest that a respondent who participates in no outdoor activities engages in even fewer household chores. However, this description of a respondent’s scores on the MPI is not uncommon in research and clinical assessment. Again, restriction of range within MPI subscales constrains our ability to compare differences between subscales.

In the present study, we found that seven of the 12 MPI subscales suffered from restriction of range and failed to provide a full range of scores within 2 SDs of the mean. This is not a trivial problem. Several strategies exist that may correct poor or restricted distributions such as data transformation or percentile-based rescaling. These strategies, however, have not been typically applied to the MPI and, if applied, would demand a comprehensive re-norming of the MPI. In the current study, we elected to focus on the creation of summary scales as a more simple and transparent solution. As demonstrated in our results, summary scales are empirically reasonable and easily calculated, and possess good distribution and less restriction of range. Interpretive errors that may arise among comparisons of MPI subscales are significantly decreased through the use of summary scales.

Of equal importance is the implication that MPI profile instability may be a function of how profiles are fit. When individuals are asked to complete the MPI, they tend to respond in one of three common patterns or profiles: dysfunction, relationship discord or positive adaptation. MPI profiles have been promoted as a useful typology or taxonomy that enables customized treatment and provides a useful outcome measure. Similar to biological classification, it has been assumed that the MPI taxonomy is stable and should not normally change without intervention. However, recent research has demonstrated that MPI profiles may be less stable than originally assumed (11,12), with approximately one-third of individuals changing their profile assignment after a short period of time. Instability within the MPI taxonomy is problematic and reduces confidence in the use of MPI profiles for either treatment selection or as a measure of treatment outcome.

In the present study, we focused on improving the psychometric quality of the MPI through the creation of summary scales. We hypothesized that summary scales may lead to greater stability of MPI profiles. Our results, however, indicated that summary scale profiles were only marginally more stable than MPI subscale profiles. On review, we noted that the rate of instability found in the present study was consistent with the rates previously reported in earlier studies. This rate was consistent despite different sample compositions, different intervals between first and second administration of the MPI, and different methods of determining subgroup assignment. Given that previous research has demonstrated that profile instability is not likely due to differences among respondents and that the current study found no increase in stability despite improvement of the psychometric quality of clinical scales, we investigated whether profile instability is a function of the method by which profiles are fit.

In our exploration of MPI profile instability, we found that profiles closer to the overall sample mean, independent of subgroup assignment, were less reliable than profiles at the perimeter of multidimensional space. Based on this result, we created a measure of relative distance by subtracting the best-fitting profile distance value from the overall mean distance value for each respondent. A comparison of relative distance between stable and unstable summary scale profiles was significant and demonstrated a large effect size. When we performed a quartile split on relative distance values and compared frequency of classification stability, summary scale profiles at the top quartile demonstrated a high rate of stability. In contrast, the relative distance between stable and unstable MPI subscale profiles demonstrated a lower effect size and a lower rate of stability.

Cluster assignment within the MPI taxonomy has typically relied on a direct comparison of goodness-of-fit values between respondents’ clinical profiles and MPI profiles. Although it is reasonable to assume that identical distance values within any MPI subgroup should be equally stable, the results of our study suggest that this assumption may well be incorrect. Instead, distance values that reside farther away from the overall sample mean will be more stable than distance values that reside closer to the sample mean. Therefore, respondent profile goodness of fit, by itself, is not sufficient and offers us no information regarding the stability of profiles. Conversely, relative distance or corrected goodness of fit does provide an accurate index of profile fit and stability by incorporating both the distance from clinical profiles to the overall sample mean and the distance to taxonomy-derived profiles.

We strongly recommend that corrected goodness of fit be considered in future studies that investigate or rely on MPI taxonomy profiles. We are confident that if a researcher or clinician was offered the choice between two methods of scoring the MPI, with one method demonstrating greater stability, the choice would be obvious. Notwithstanding this recommendation, it should be noted that the generalizability of these findings are limited by sample characteristics. These include predominantly female respondents diagnosed with FMS awaiting admission to a multidisciplinary pain management program. Future replication will be required to determine whether the current results can be generalized to other samples of individuals with chronic pain.