Assessing the Peak Capacity of IMS-IMS Separations of Tryptic Peptide Ions in 300 K He

Abstract

Two-dimensional ion mobility spectrometry (IMS-IMS) coupled with mass spectrometry is examined as a means of separating mixtures of tryptic peptides (from myoglobin and hemoglobin). In this study we utilize two distinct drift regions that are identical in that each contains He buffer gas at 300 K. The two-dimensional advantage is realized by changing the structures of the ions. As ions arrive at the end of the first drift region, those of a specified mobility are selected, exposed to energizing collisions, and then introduced into a second drift region. Upon collisional activation some ions undergo structural transitions, leading to substantial changes in their mobilities; others undergo only slight (or no) mobility changes. Examination of peak positions and shapes for peptides that are separated in the first IMS dimension indicates experimental peak capacities ranging from ~60 to 80; the peak shapes and range of changes in mobility that are observed in the second drift region (after activation) indicates a capacity enhancement ranging from a factor of ~7 to 17. Thus, experimental (and theoretical) evaluation of the peak capacity of IMS-IMS operated in this fashion indicates that capacities of ~480 to 1360 are accessible for peptides. Molecular modeling techniques are used to simulate the range of structural changes that would be expected for tryptic peptide ions and are consistent with the experimental shifts that are observed.

Introduction

Mobility-based separations of ions in the gas phase arise from differences in ion structure, charge state, dynamics associated with ion-buffer gas collisions, as well as any structural fluctuations that ions experience during the time that they spend diffusing through the gas.^1,2 For biological species such as proteins and peptides, introduced into the gas phase by electrospray ionization (ESI),³ there is evidence that some structures that are formed as ions emerge from the charged droplet may be related to solution conformations, while others may correspond to favored gas-phase states.^4–11 Because of this, measurements of mobility (or other properties associated with conformation) of biological ions may differ depending upon experimental conditions associated with how the ions are produced (and when their structures are probed).

Although issues associated with ion formation explain some differences in measurements of structure, a number of the studies have shown that it is possible to perturb populations of conformations of the isolated gas-phase ions in a reproducible manner.^11–14 For example, when [M+7H]⁷⁺ ions of ubiquitin formed by ESI are gently injected into a drift tube for mobility measurements, distributions of compact structures are observed (for a range of solution conditions), with cross sections similar to those calculated for the folded (native) solution state.^{5– 7,13,14} However, at high injection energies, the folded state disappears and new extended states, having cross sections that are much larger than native solution state structures are favored. In injected-ion studies, ion kinetic energy is thermalized as ions enter the drift tube¹⁵ resulting in a transient heating/cooling cycle that leads to structural changes. Presumably this process anneals the gas-phase ion into an extended structure that is more stable because it maximizes favorable intramolecular interactions and minimizes Coulombic repulsion. Similar changes in structure are observed when these ions are stored in Paul geometry ion traps.¹³

Although the understanding of which conformations are produced by activating ions is limited, the reproducibility of changes in the distributions of states makes this a potentially remarkable tool for analyzing mixtures.^7,9,12–14 In this paper we explore the utility of changing structures as a means of increasing the number of peaks from complex mixtures that can be resolved by ion mobility spectrometry (IMS). The peak capacity of a separation is a measure of the range over which features can be observed divided by the peak width. Thus, one can improve the peak capacity of IMS either by increasing the region of accessible drift time (the range) or by improving the resolving power. We approach this problem using a newly developed ion mobility spectrometry (IMS) instrument that incorporates multiple drift regions and activation regions within a single drift tube and examine the ability to induce structural changes in mixtures of tryptic peptides that lead to changes in structure (and hence mobility).¹⁶ The approach is very simple in concept. A packet containing a mixture of ions is separated in the first drift region and ions having a specified mobility are selected, collisionally activated, and then allowed to separate again in a second drift region. The mobilities of the selected ions (measured in the first drift region) are determined by their initial structures; the mobilities in the second region are defined by the structures that are favored after collisional activation. In favorable cases, the differences in these structures are substantial. Ultimately, the ability to influence structure makes it possible to shift peaks into new regions of the distribution (increasing the range), and can be used to enhance IMS peak capacity.

In order to understand the shifts that are observed, we take advantage of significant advances in molecular modeling methods¹⁷ and recently developed theory for calculating cross sections for trial geometries.^2,18 The present work is also closely related to work that aims to increase the separation capacity of IMS, including: the use of different buffer gases;^{19, 20} changes in drift field, including field asymmetric (FA) IMS and hybrid FAIMS-IMS techniques;^19,20 variation in temperature;⁶ and incorporation of molecular adducts.²¹

Experimental

General

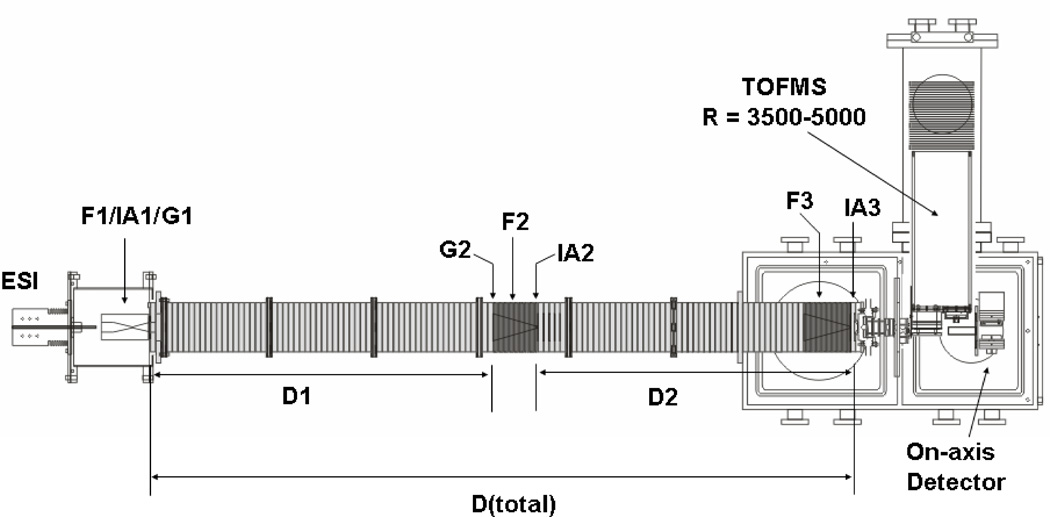
Figure 1 shows a schematic diagram of the IMS-IMS instrument used for these studies. Details of IMS theory and instrumentation (including the instruments used here) are described elsewhere^{1,2,16,18,22–29} only a short description of the instrumentation is given here. Briefly, a continuous beam of electrosprayed ions is introduced directly into a Smith geometry ion funnel region (F1).³⁰ This region of the instrument is used to focus, accumulate and release pulses of ions for mobility experiments. During operation the concentrated ion packet in F1 is released via an electrostatic gate (G1) into the first drift tube (D1). The drift tube contains ~3.00 Torr of He buffer gas at 300 K; ions migrate through the tube under the influence of a weak electric field and different species separate due to differences in their mobilities through the gas. As ions exit the first drift region, they pass through a second ion gate (G2) and enter another ion funnel (F2) that is used to radially focus the diffuse ion clouds and transmit species into the front of a second drift region (D2). Immediately following F2 is an activation region (IA2); this configuration allows ions of a specified mobility to be selected and energized prior to additional separation.

Figure 1.

Schematic of IMS-IMS-TOF instrument. Ions are gated through G1, where they undergo mobility separation in D1. Ions can be selected based on mobility at G2. Ion activation is carried out at the region labeled IA2. For more detail on ion selection and activation, refer to text.

Although the present work (and the discussion provided here) is primarily based on work that has been done using an IMS-IMS instrument, recently we have extended the drift tube by incorporation of another IMS region. This IMS-IMS-IMS instrument is analogous in design except that there is a third drift region (D3). This instrument provides slightly higher resolving powers and the opportunity to manipulate conformations more than once. Below, we show a single dataset that illustrates slightly higher resolution (and for a tryptic digest of a different protein). Except for providing fundamental information about its operation, we do not describe this instrument any more in this manuscript, as it is so similar in operation to the IMS-IMS design.

The total length of the IMS-IMS drift tube in Figure 1 is ~182 cm; taken separately, D1 is 87.0 cm, and D2 is 94.9 cm. The drift regions can be operated over a range of fields; in these studies we have explored conditions ranging from ~8 to 12 V·cm⁻¹, while the funnels are operated at 11 to 18 V·cm⁻¹. The similar IMS-IMS-IMS instrument used is ~290 cm long; D1 is 95.1 cm, and the remaining drift regions are 194.9 cm. Drift regions are held at 8 V·cm⁻¹, while the ion funnels are operated at 10 V·cm⁻¹. RF fields in the ion funnels range from 70 to 130 V_p-p, at frequencies of 450 to 480 kHz.

Ion activation inside of the drift tube

These drift tubes contain multiple activation regions as indicated in the schematic (Figure 1). Activation regions are simple to implement and control as they are made by varying voltages applied to the last two funnel lenses (which are typically spaced by 0.3 cm, and kept RF-free). The voltages associated with activation can be used to create conditions for the ions that range from very mild heating (5 to 80 V applied) to relatively severe (>150 V) conditions that lead to significant fragmentation.³¹

Electrospray source conditions

For the tryptic digests of horse myoglobin and human hemoglobin, 15 mg of protein (Sigma, 90% purity each) was dissolved in 3 mL of 2 M urea (in 0.2 M Tris(hydroxymethyl)aminomethane and 10 mM CaCl₂, pH 8). To that, 2% (w/w) TPCK-treated trypsin (Sigma) in 0.2 M Tris(hydroxymethyl)aminomethane, 10 mM CaCl₂ (pH 8) was added, and the reaction was allowed to proceed for 24 hours at 37 °C. The sample was then filtered using C-18 Sep-Pak cartridges (Waters), and lyophilized.

Electrospray solutions were prepared as follows. Dry samples (as powders) were used to prepare 0.25 mg·mL⁻¹ solutions in water:acetonitrile:acetic acid (49:49:2%). Ions were produced by sending the solution through a fused silica capillary (360 µm o.d. × 75 µm i.d., laser pulled to ~10 µm at the tip), at a flow rate of 0.25 µL·min⁻¹, controlled by a syringe pump (kd Scientific, Holliston, MA). The pulled capillary was held at a DC bias 2.0 to 2.2 kV above the drift voltage. A PEEK microtee was used to couple the capillary tip, the syringe, and a platinum electrode.

Cross section measurements

Cross sections can be determined in several ways using the drift tubes described above. Cross sections for initial (mobility-selected) structures are calculated using equation (1),¹

$$\mathrm{\Omega }=\frac{{(18\pi )}^{1/2}}{16}\frac{ze}{{(k_{b}T)}^{1/2}}{\left[\frac{1}{m_I}+\frac{1}{m_B}\right]}^{1/2}\frac{t_{d}E}{L}\frac{760}{P}\frac{T}{273.2}\frac{1}{N}$$ (1)

where z, e, k_b, m_I, and m_B are the charge state, fundamental charge, Boltzmann’s constant, and the masses of the ion and buffer gas, respectively, and N is the neutral number density. The field strength (E), drift tube length (L), pressure (P) and temperature (T) can be accurately and precisely determined such that any two cross section measurements typically agree to within ± 1% (relative uncertainty). The drift time is denoted as t_d and corresponds to parameters that define a specific region of the instrument. For initial structures (determined by the selected-ion methods described above), values of t_d are determined by the delay time (t_D1) associated with selecting ions of a specified mobility. An interesting aspect of this approach is that there is no correction time associated with time that ions spend in other portions of the instrument. Therefore, selected ion cross sections are anticipated to be more accurate than measurements that involve corrections for time that ions spend outside of the drift region.

Using the IMS-IMS-IMS configuration (an extension of the IMS-IMS instrument shown in Figure 1) it is possible to carry out a second selected ion measurement of cross sections for ions that were produced upon activation (for the purpose of accurately measuring the cross sections for these ions). We have not done this in the present study. Instead, we have used a simple calibration to ions with known cross sections in order to determine the final ion cross sections. We anticipate that calibrated cross sections are accurate to within ±2 percent.

Generation of trial structures and cross section calculations

Molecular modeling techniques and cross section calculations were performed on several peptides to provide information about the range of structures that should be accessible for the types of ions studied here. All structures were generated in the Insight II suite of programs using the AMBER force field.¹⁷ An issue that emerges in molecular modeling studies is how best to sample the vast number of conformations that are accessible. To do this, we begin by generating different types of starting structures. These may vary in the positions chosen for protonation as well as geometry (e.g., various helices, globules, or linear conformations). Each initial structure is then taken through simulated annealing processes. The details of this process may be varied in order to change what types of structures are accessed. One typical approach would be to increase the ion temperature from 300 to 800 K (over a time period of 2 ps), allow the structure that is formed to equilibrate at 800 K (for 2 ps), and then cool the structure to 300 K (over 1 ps). This process can be repeated many times to generate a range of conformations with different energies for each starting sequence, structure and charge assignment.

Below, we are interested in the cross sections associated with the range of conformations that is produced and do not attempt to assign conformations. Thus, we show plots of 150 structures having relatively low energies. It is understood that higher-energy structures (trapped during the ESI process) may also exist; however, it is thought that these will have cross sections that fall over the range of structures that are shown. Visual examination of the output of the molecular modeling results show that conformations range from very compact globules to relatively extended structures that are quite open in appearance. Cross sections are calculated using the EHSS method that has been calibrated to values obtained from the trajectory method (as described previously).^32,33 This approach is expected to be accurate to within a few percent.

Results and discussion

Illustration of a two-dimensional separation using a hypothetical dataset

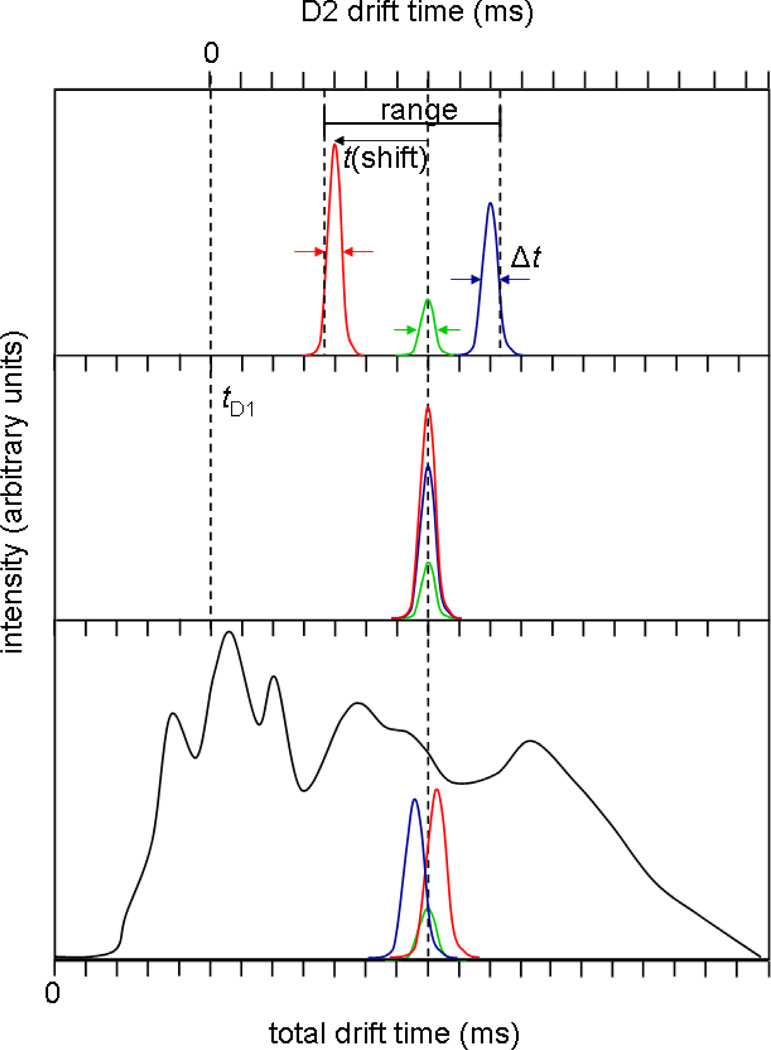
It is useful to illustrate the basic ideas and definitions of the present approach using a hypothetical dataset. Consider an ion mobility distribution for a very complex ion mixture (Figure 2, bottom). As the number of components in the mixture exceeds the capacity of the separation, broad features corresponding to many unresolved species, as well as species that interconvert over the course of the drift separation, will be observed. As illustrated for three components which make up a part of the more complex mixture, the instrumental resolution as determined from peaks associated with individual components is substantially greater than is suggested from the appearance of the spectrum for the entire mixture (i.e., while the individual peaks are sharp, they all overlap in mobility).

Figure 2.

Hypothetical drift distribution for a tryptic digest, highlighting three overlapping peptide ions (bottom). A mobility selection at G2 centered about the dotted line t_D1 (center) will include all three ions, which, with no activation, will all arrive at the same drift time. Collisional activation in IA2 may lead to shifts in mobility and therefore resolution of the three ions in the second drift dimension (top). Although the second drift dimension spans from the time ions are selected at G2 to the time they are detected, the true separation space is between the highest and lowest mobility species detected, and therefore the peak capacity is calculated using this range.

Figure 2 also shows the result of the initial selection that leads us to transmit only a narrow range of ions (in this case a selection that would contain populations of each of the three ions that are shown as narrow peaks). By definition these ions have identical mobilities at the time and position of selection (Figure 2, center). However, upon activation in IA2, some ions may change structure (Figure 2, top). In the present case, one species favors a population of more compact states (having higher mobilities) and another favors more extended conformations (having lower mobilities); the remaining ions may have changed structure but did not show any apparent change in mobility.

It is important to point out that for tryptic peptides from a single protein we believe that the primary advantage of the two-dimensional IMS-IMS method arises from the structural changes that occur upon activation. Although we do not describe this in more detail, another possibility is that in some cases the two-dimensional approach leads to the selection of leading or trailing edges of large peaks. In such a case, the tail of the distribution may continue to separate as the average mobility in the second IMS dimension. Although this has an advantage in moving signals apart, it does not necessarily involve a structural change. It is likely that this mechanism becomes increasingly apparent for digests of protein mixtures (in which different proteins vary substantially in concentration).

Returning to the illustration in Figure 2, we define the peak capacity of the first dimension as the range over which peaks are separated divided by the full-width-at-half maximum (FWHM) of peaks associated with the selected ions. The peak capacity of the second drift dimension is highly dependent upon which ions are selected at G2. In the hypothetical example, the range is defined by the positions of the highest- and lowest-mobility ions formed after activation. In this case, we use the half-height of the peak associated with the high-mobility ions to define the leftmost boundary, while the location of the half height of the peak associated with the lowest-mobility species defines the rightmost boundary. This range, divided by the average FWHM of the peaks is used to estimate the peak capacity for the second dimension. The two-dimensional peak capacity is the product of this peak capacity and that of the first drift dimension. If there are no changes in structure observed upon activation of the mobility selected ions, then the second IMS separation is analogous to the first, and the two-dimensional peak capacity is simply that of the first separation multiplied by unity. For cases in which the mobilities of the selected ions change, the gain in peak capacity is dependent on the range of structures observed in the second drift separation, which is different for each selection.

Theoretical and practical considerations associated with assessing peak capacity of the first dimension

Detailed discussions of peak capacity of multidimensional measurements have been described by Giddings and others.^34–36 The discussion given above effectively defines peak capacity in terms of the maximum number of peaks that could be resolved (using a 50% valley definition) within the associated spectrum. Therefore, values of peak capacity will be influenced by changing the spectral range or instrumental resolving power. The range used to establish the peak capacity of the second IMS separation is rigorously defined as the time between the leading and falling sides (at half height) of the highest- and lowest-mobility peaks. Here, we provide considerations about the range of the separation in the first IMS dimension (associated with D1).

In order to understand the peak capacity that arises from the separation in D1, it is useful to consider IMS resolving power in more detail. In theory, the resolving power [R = t/Δt, where Δt corresponds to the full-width-at-half-maximum (FWHM) of a peak] of a drift tube can be calculated from equation (2)¹

$$\frac{t}{\mathrm{\Delta }t}={\left(\frac{LEze}{16k_{B}T\ln 2}\right)}^{1/2}$$ (2)

In practice resolving powers for biological ions are typically much less than theory (because many unresolved configurations or structures that interconvert over the course of the drift experiment may exist).⁷

The present studies use back-to-back drift tubes with the detector located at the exit of the second drift tube (Figure 1). Therefore, we do not measure the peak shapes associated with the D1 separation region directly (as these ions must pass through the D2 region prior to detection). Instead, we characterize the resolution in separate experiments in which the D2 portion of the instrument has been removed (i.e., a single drift tube instrument of the same length as the D1 region of the IMS-IMS instrument). Under the range of conditions that are typically employed for the D1 instrument it is common to measure values of R = 70 to 90 for peptide ions. Measured values of R, through the entire length of the drift tube (where L for both drift regions is a factor of 2 or 3 times that of D1) are consistent with the separate measurements for D1. Therefore, we use R(D1) = 70 to 90 in these studies and for peptides.

The actual peak capacity is slightly less than the resolving power because of a correction associated with the time required for the highest-mobility ions to travel through the drift tube. That is, there is a time after injection in which no ions have traversed the entire length of the drift tube, and this “dead time” should not be included in the range. For peptide ions ranging in m/z from ~100 to 2000 we estimate that more than 90% of the total drift time can be effectively used for separation. Combining this factor with the measured values of R, we estimate a typical peak capacity for D1 to be ~60 to 80. It should be understood that for some types of ions, specifically those with transition half lives in the 1– 100 ms regime, the broad nature of peaks may reduce the peak capacity. However, based on our experience the 60 to 80 estimates for D1 are believed to be typical of most tryptic peptide ions.

IMS-IMS of a mixture of tryptic peptides from horse myoglobin

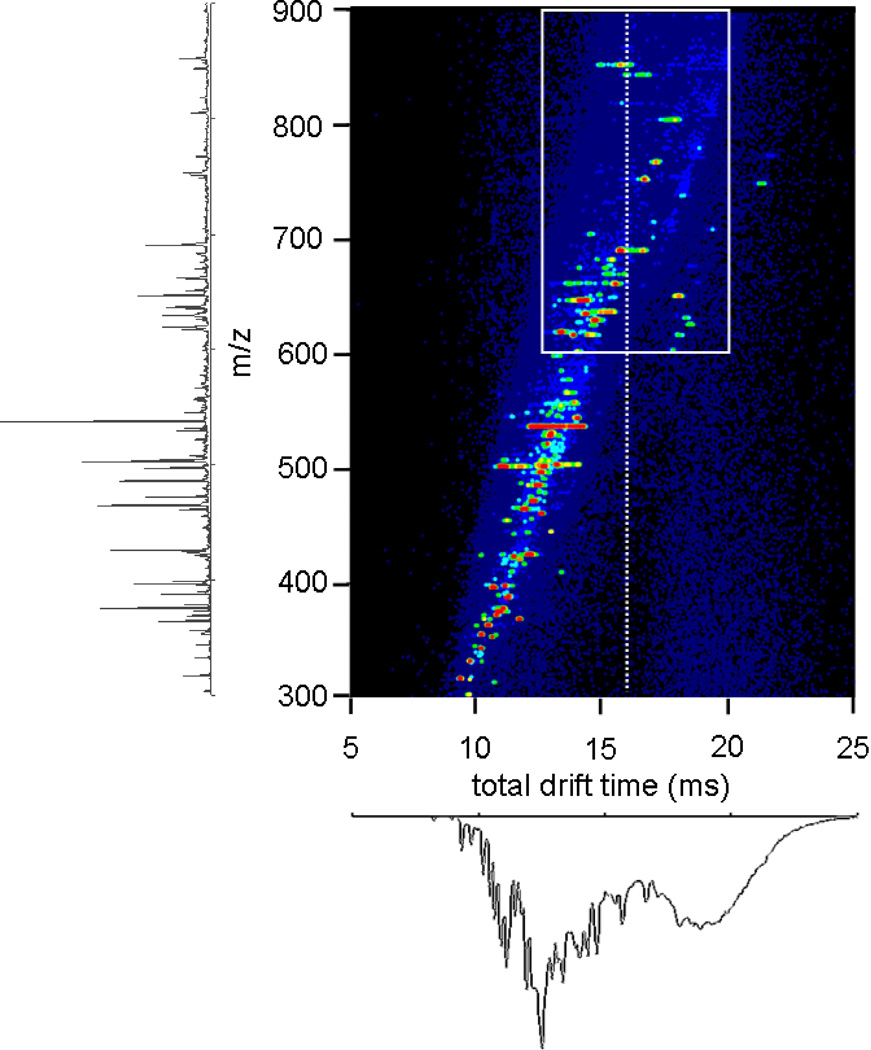
Figure 3 shows a nested t_d(m/z) dataset for a mixture of peptides obtained from digestion of myoglobin with trypsin. These data correspond to a standard IMS-MS measurement through the drift tube in Figure 1. Analysis of the peaks observed shows evidence for 38 m/z values corresponding to 41 different possible peptides (including two sets of isobaric peptides) across the +1 to +4 charge states. As noted previously,^37–41 the combined IMS-MS analysis allows many features that are not observed by MS alone to be resolved. In this dataset there are seven peptides that would not be detected with the MS analysis alone. Having noted this, this system is of sufficient complexity that there is still substantial spectral congestion. This is especially apparent upon examining the integrated IMS distribution (Figure 3, bottom). Especially in the case of tryptic peptides, it is often the case that [M+2H]²⁺ and [M+3H]³⁺ ions for different sequences have identical drift times. Here, we illustrate an approach for resolving some of these.

Figure 3.

Nested drift(flight) distribution for electrosprayed horse myoglobin tryptic peptides, obtained by allowing all ions to traverse the whole drift tube, along with the integrated mass spectrum and drift distribution. The white box highlights the range examined in Figure 4.

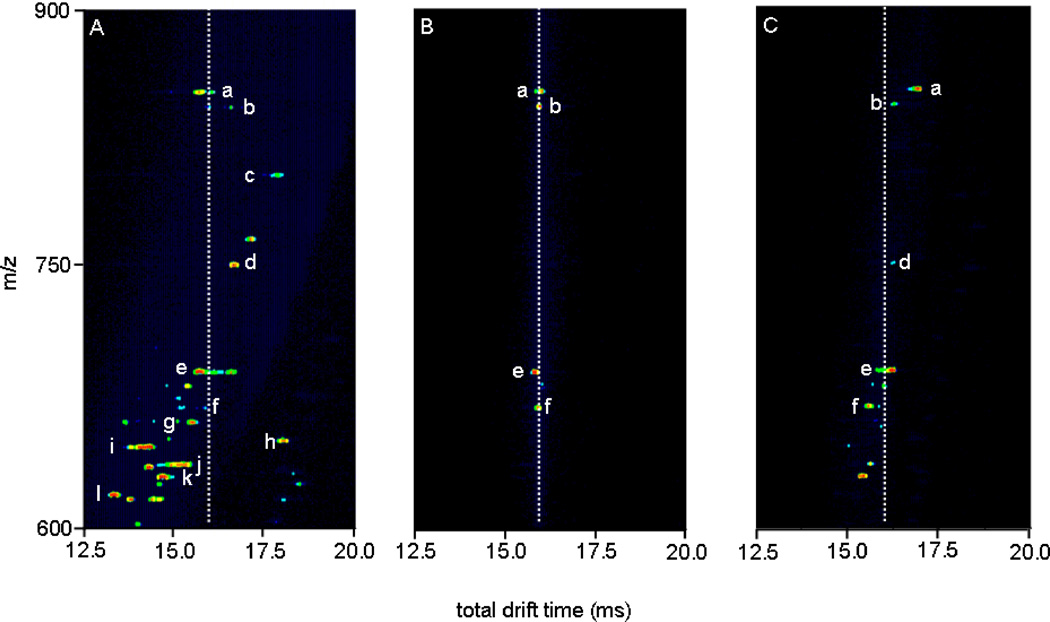
It is useful to examine a narrow region of this spectrum in more detail. Figure 4 considers activation of the ions that are defined by the region of outline that is shown in Figure 3: spanning drift times from 12.5 to 20.0 ms, and m/z values of 600 to 900. Selection of a narrow region of ions by fixing G2 to pass ions from 7.55–7.65 ms allows us to isolate four primary peaks (a, b, e, and f; note all peaks are assigned in the figure caption). Prior to being selected, these four ions exhibit a range of structures, including those with mobilities corresponding to the time of selection (Figure 4A, white dashed line). Only these structures are transmitted into the second drift tube upon selection; with no activation, each of these ions shows stability over the course of the D2 separation and has a total drift time of ~16 ms (Figure 4B). Application of 120V at IA2 causes the positions of peaks to shift (Figure 4C). We also note that two new peaks (presumably fragment ions formed during activation) are observed at t_d(m/z) = 15.3(629.7) and 15.6(636.7).

Figure 4.

Nested drift(flight) time distributions for horse myoglobin tryptic digest, total distribution (A, left), ions mobility selected at G2 (t_D1 = 7.55–7.65 ms) with IA2 = 0 V (B, center), and same selection with IA2 = 120 V(C, right). The dotted lines denote the arrival times for inactivated mobility-selected ions, to show the degree of separation. a, [G₁-R₃₁+4H]⁴⁺; b, [Y₁₀₃-K₁₃₃+4H]⁴⁺; c, [K₆₃-K₇₈+2H]²⁺ or [H₆₄-K₇₉+2H]²⁺; d, [H₁₁₉-K₁₃₃+2H]²⁺; e, [H₆₄-K₆₇+2H]²⁺; f, [V₆₈-K₇₇+2H]²⁺; g, [K₇₉-K₉₆+3H]³⁺; h, [L₃₂-K₄₇+3H]³⁺; i, [L₃₂-K₄₂+2H]²⁺; j, [Y₁₀₃-K₁₁₈+3H]³⁺; k, [G₈₀-K₉₆+3H]³⁺; l, [E₁₄₈-G₁₅₃+H]⁺. Note that the nomenclature used refers to the position of the peptide by providing the location (with respect to the intact protein sequence) and single letter abbreviation of the N- and C-terminal residues, respectively.

In assessing the peak capacity we begin by noting that the range of drift time shifts for the selected and activated species a through f is 1.56 ms. The measured values for FWHM of peaks a, b, d, e, and f are 0.207, 0.295, 0.118, 0.148, and 0.207 ms, respectively, giving an average value of 0.195 ms. Thus, although the total shift range (1.56 ms) seems relatively small, this leads to a peak capacity of 8 for the second IMS dimension. Combining this value with the capacity of the first IMS dimension (~60 to 80) we determine a two-dimensional peak capacity range of ~480 to 640. Analysis of other selected regions with a range of activation conditions yields similar results for the two dimensional peak capacities.

Analysis of human hemoglobin tryptic digest at higher resolution

Similar experiments were carried out with the tryptic digest of human hemoglobin on an IMS-IMS instrument with a D2 region that is twice the length of the D2 region that was used to collect the previous data. The D1 regions in these experiments were of similar length and field such that they possessed identical peak capacities. This longer second drift region extends the range associated with shifts observed upon activation and also leads to larger resolving power in the D2 region. Figure 5 shows a narrow range of data for transmission of a 150 µs wide pulse of ions at G2 (initiated at 9.366 ms). These ions were subsequently activated by applying a 65 V bias across the IA2 region. The white dashed line in the figure shows the initial position of peaks prior to activation. Visual inspection of the data indicates that many features undergo substantial changes in mobility. Although it is possible to find regions where fewer (or more) peptide ions shift, these data are typical of selections and activations across the dataset.

Figure 5.

Expanded view of an activated selection of human hemoglobin tryptic peptides with t_D1 = 9.366 ms. The white dashed line denotes the time at which mobility-selected ions with no activation are observed, while the dotted yellow lines show the new effective separation space of the second IMS experiment (~ 4.8 ms). Drift slices for several peptides are shown, along with shifts from original (inactivated) drift times for all ions. Peptide nomenclature is carried out the same as in Table I and Figure 4.

Of the peaks that are shown in Figure 5, seven are assigned to expected tryptic peptide ions for human hemoglobin (as labeled in the figure). The degree to which each peak I s shifted from the initial selection time after activation varies depending upon the ion. Peaks associated with [T₄₁-K₅₆+3H]³⁺, [V₆₇-K₈₂+3H]³⁺, and [M₃₂-K₄₀+2H]²⁺ are shifted to longer times by 4.8, 2.0, and 1.5%, respectively. These shifts indicate that upon activation these ions adopt more open conformations with larger cross sections. On the other hand, the [V₁₇-R₃₁+3H]³⁺, [E₁₂₁-K₁₃₂+3H]³⁺, and [V₉₃-K₉₉+2H]²⁺ shift to higher mobilities by 6.2, 5.5, and 11.3%. These shifts indicate that upon activation these ions have adopted more compact geometries.

The range of shifts of the drift times associated with separation in the second drift region is 4.8 ms, and typically values of FWHM for peaks vary from 0.2 to 0.3. Table I provides a summary of drift times (in the second IMS region) and peak FWHM values for three different selections (each activated at 65 V). Using the average FWHM (0.277 ± 0.09 ms) and 4.8 ms range, we determine the peak capacity for the second IMS separation to be 17 for the data shown in Figure 5. On average, the peak capacity for all three selections tabulated in Table I is ~14. This, combined with the capacity estimate of 60 to 80 for the first IMS separation, leads to a two-dimensional peak capacity of ~840–1120; if the capacity for D2 of 17 described in Figure 5 is used the upper limit is 1360.

Table I.

Peak positions and FWHMs for selected and activated hemoglobin peptides^a

selection time (ms)b	peptidesc	tD2 (FWHM)
8.236	β-chain [L96-R104+3H]3+	13.24 (0.20)
		15.18 (0.20)
	β-chain [V133-K144+3H]3+	14.17 (0.20)
	α-chain [V93-K99+2H]2+	14.36 (0.42)
	α-chain [V17-R31+3H]3+	15.04 (0.45)
	β-chain [L105-K120+4H]4+	15.18 (0.30)
	α-chain [T41-K56+4H]4+	15.25 (0.21)
	β-chain [S9-K17+2H]2+	15.37 (0.26)
9.366	α-chain [V93-K99+2H]2+	13.96 (0.21)
		17.09 (0.26)
	β-chain [E121-K132+3H]3+	15.24 (0.15)
	α-chain [V17-R31+3H]3+	15.04 (0.21)
		16.43 (0.21)
		17.04 (0.31)
	α-chain [M32-K40+2H]2+	17.13 (0.39)
		17.59 (unresolved)
	β-chain [V67-K82+3H]3+	17.44 (0.46)
	β-chain [L96-R104+2H]2+	17.13 (0.31)
	α-chain [T41-K56+3H]3+	17.11 (unresolved)
		18.45 (0.26)
10.908	α-chain [T41-K56+3H]3+	16.99 (0.15)
		19.00 (0.23)
		20.69 (0.15)
	β-chain [G83-K95+2H]2+	19.73 (0.26)
	β-chain [V18-R30+2H]2+	20.02 (0.36)
	α-chain [F128-K139+2H]2+	19.67 (0.13)
		20.18 (0.31)

^aAll activations were carried out with IA2 = 65 V.

^bSelection time is when a 150 µs wide pulse was applied to G2 to transmit ions.

^cPeptide sequence listed as N-terminal residue to C-terminal residue, including information about their position in the sequence of the intact protein.

^dNote: if no shift occurs, t_D2 ≈ 1.8 × t_D1. Because the time the precursor spent in the ion funnel is subtracted to obtain t_D2, the relation is not exact.

Further examination of Figure 5 and Table I raises some interesting issues. Most of the activated peptide ions observed have sharp (150 to 300 µs wide) peaks, an indication that after activation the narrow range of selected states forms a new distribution that also favors a narrow range of structures. Presumably, this activation process follows a heating and cooling cycle that is similar to the process that has been described previously for injected ion drift tube studies.¹⁵ That is, as the thermalized ions enter the activation region, they are accelerated through the buffer gas in a manner that heats them up; and upon leaving this region they are rethermalized to the temperature of the gas. This process should be similar to annealing and thus, these narrow peaks presumably correspond to final states that have lower energies than initial states.

However, in some cases, peak widths are substantially broader, or appear to show evidence for multiple resolved structures. For example, the [M₃₂-K₄₀+2H]²⁺ ion shows evidence for two partially resolved populations of ions, having different structures. This suggests the possibility of multiple low-energy product structures that may compete during the cooling process; or, the heating process may drive some transitions that lead to kinetically trapped intermediates. The ability to trap components in unstable configurations is interesting as these species may be expected to change conformation again in an IMS-IMS-IMS experiment. Finally, we note that although the selection and activation led to substantial enhancement in the ability to resolve peaks and most peaks show some shift, five of the seven peptides in Figure 5 (selected at 9.366 ms) remain only partially resolved based on the IMS-IMS separation.

Understanding the magnitude of observed shifts using molecular modeling techniques

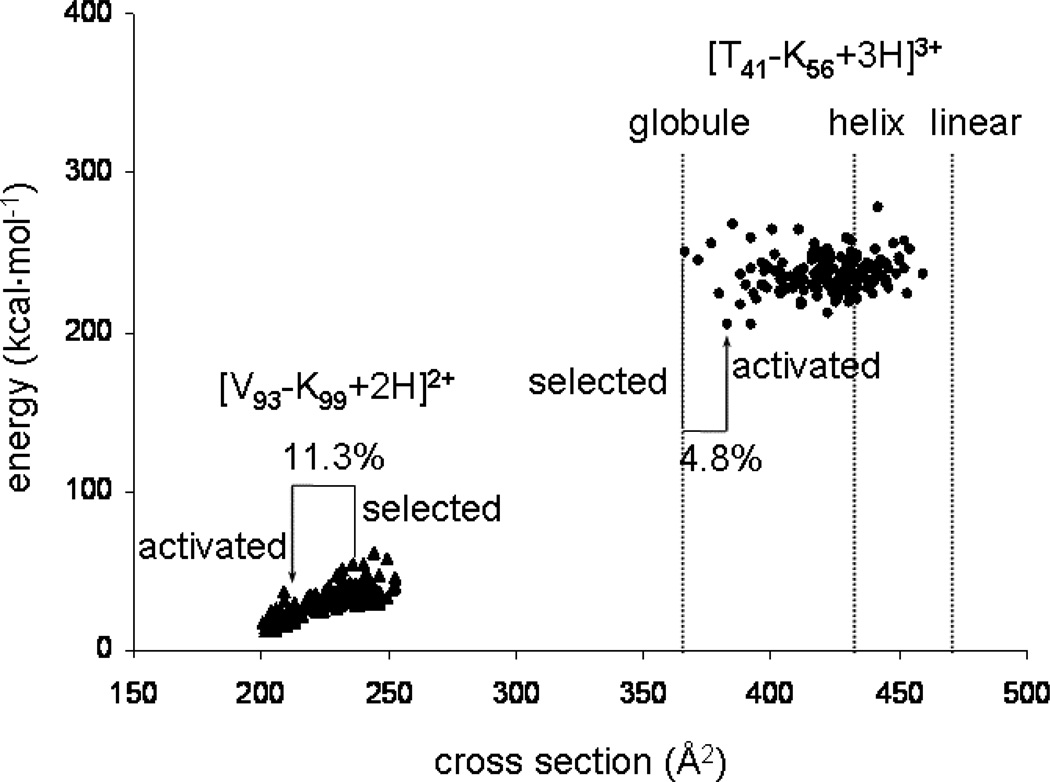
In order to understand the range of shifts that is observed experimentally we have examined two tryptic peptides of hemoglobin that were observed in Figure 5 ([V₉₃-K₉₉+2H]²⁺ and [T₄₁-K₅₆+3H]³⁺) in more detail using molecular modeling¹⁷ and cross section calculation methods.^2,18 As noted above, modeling and cross section calculations can be carried out on a range of charge site configurations, initial starting structures, and simulated annealing cycles were employed for these studies. These considerations are similar to those discussed previously.^2,18,42 For the purposes of this study, the aim is to gain a feeling for the range of mobilities (or cross sections) that may be accessed upon activation (as this ultimately defines the shifts that will be observed experimentally).

A series of 150 relatively low-energy conformations for each sequence is shown in Figure 6. Overall, the range of cross sections that is calculated agrees with the experimental data. That is, the experimental measurement of cross sections for the initial and final structures of each of the sequences is within the range of cross sections for the distributions of calculated structures. Figure 6 attempts to capture the shifts that are observed by including the positions of the initial and final cross sections that are observed experimentally. The [V₉₃-K₉₉+2H]²⁺ species has an initial conformation that is relatively extended and upon activation collapses to a more compact structure. Molecular modeling and cross section calculations indicate that this is a reasonable transition because the initial extended conformation is relatively unstable. Rough estimates (from the data in Figure 6) suggest that the more compact states are about 10 kcal·mol⁻¹ more stable than the initial structures.

Figure 6.

Plots of energy versus conformer cross section of the 150 lowest energy structures post simulated-annealing for two peptides from Figure 5: [V₉₃-K₉₉+2H]²⁺ and [T₄₁-K₅₆+3H]³⁺, as well as cross sections of the energy minimized structures of the [T₄₁-K₅₆+3H]³⁺ ion modeled as a helix and linear structure, denoting the range of structures available to each sequence. Cross sections of the selected and activated structures for each sequence are highlighted, along with percent shifts from the mobility-selected structure. Peptide nomenclature same as in Figure 5.

In contrast [T₄₁-K₅₆+3H]₃₊ is initially very compact and upon activation appears to open up to a somewhat larger structure. The energy calculations suggest that many conformations have similar energies; thus, while theory does not pick up an obvious change in energy that would help drive this transition, we also see no large increase in the energies of these structures that would prohibit the transition.

Finally, we note that theory suggests a range of structures available upon activation greater than those observed experimentally. For example, the range of calculated cross sections for [T₄₁-K₅₆+3H]³⁺ is ~40%, while the experimental shift is less than 5%. We are currently investigating other selections and activation approaches in order to try to access larger shifts between initial and final conformations.

Summary and conclusions

The peak capacity of a two dimensional IMS-IMS separation approach has been examined. In this approach, both separations are carried out under identical separation conditions. That is, the drift fields, buffer gas and temperature are constant. Instead, the approach utilizes changes in the ion structure as a means of gaining additional capacity. Considerations of resolution and range associated with both dimensions of separation lead us to conclude that capacities in excess of 1000, prior to MS analysis are accessible. The method has been demonstrated for mixtures of tryptic peptides. Theoretical results, produced from an annealing cycle that induces conformational changes, are consistent with the experimental shifts that are observed and suggest that in some cases these shifts may lead to even greater advantages in peak capacity. Currently, the efficiency of the method suffers from the need to select a narrow range of ions for activation.

One additional factor that will influence the resolving power of the second IMS separation is the duration of the G2 pulse. In the present studies we limit this width to 100 µs. This value may limit the ultimate resolution of the second IMS separation. In order to maximize experimental efficiency, the pulse width should be scaled according to the time of selection. That is, narrower pulses should be used at short times and longer pulses should be used for ions with lower mobilities. We are currently carrying out more experiments in order to refine the two-dimensional IMS efficiency.