Multi-Level Ewald: A hybrid multigrid / Fast Fourier Transform approach to the electrostatic particle—mesh problem

Abstract

We present a new method for decomposing the one convolution required by standard Particle-Particle Particle-Mesh (P³M) electrostatic methods into a series of convolutions over slab-shaped subregions of the original simulation cell. Most of the convolutions derive data from separate regions of the cell and can thus be computed independently via FFTs, in some cases with a small amount of zero padding so that the results of these sub-problems may be reunited with minimal error. A single convolution over the entire cell is also performed, but using a much coarser mesh than the original problem would have required. This “Multi-Level Ewald” (MLE) method therefore requires moderately more FFT work plus the tasks of interpolating between different sizes of mesh and accumulating the results from neighboring sub-problems, but we show that the added expense can be less than 10% of the total simulation cost. We implement MLE as an approximation to the Smooth Particle Mesh Ewald (SPME) style of P³M, and identify a number of tunable parameters in MLE. With reasonable settings pertaining to the degree of overlap between the various sub-problems and the accuracy of interpolation between meshes, the errors obtained by MLE can be smaller than those obtained in molecular simulations with typical SPME settings. We compare simulations of a box of water molecules performed with MLE and SPME, and show that the energy conservation, structural, and dynamical properties of the system are more affected by the accuracy of the SPME calculation itself than by the additional MLE approximation. We anticipate that the MLE method’s ability to break a single convolution into many independent sub-problems will be useful for extending the parallel scaling of molecular simulations.

1 Introduction

Observing biochemical processes through computer simulations requires thorough equilibrium sampling of a protein or nucleic acid system with thousands of degrees of freedom. The quality of the molecular model is of utmost importance, but validation requires extensive simulations to yield precise results for properties such as equilibrium conformations, ¹ crystallographic temperature factors, ² binding energies, ³ and molecular folding rates. ⁴ The capabilities of molecular simulations and the models themselves therefore evolve in step with computer performance and parallel algorithm design.

The central challenge with parallel molecular dynamics algorithms is the treatment of electrostatic interactions. Because the electrostatic potential decays as the inverse distance, charged particles influence one another at long range, implying a great deal of information sharing and potentially a great deal of algorithmic complexity–as much as O(N²) in the number of particles N. Particle ⇋ mesh implementations of the Ewald sum,^5,6 and more generally Particle-Particle Particle-Mesh (P³M) methods,⁷ are popular choices for treating long-ranged electrostatic forces in molecular simulations because of the favorable complexity of the algorithms—O(MlogM) or O(M) for a number of mesh grid points M depending on the choice of Poisson solver. For commodity hardware, Poisson solvers based on the Fast-Fourier Transforms (FFTs) are commonly used because of their computational efficiency,^5,8 which is so great that the parallel scaling of these approaches is still limited, on most clusters, to a few hundred processors. Most molecular dynamics codes meet high scaling targets by dedicating a subset of the processors to the FFT, but the number of messages and the amount of data that must be shared can still limit the total number of processors that can be devoted to the calculation and thus the maximum speed of molecular simulations.

Some recent variations of P³M^9,10 make use of real-space Poisson solvers based on finite difference or multigrid methods. These approaches offer better algorithmic complexity (O(M) for the real-space methods, versus O(MlogM) for the FFT-based methods) and asymptotically better inter-processor communication in parallel calculations. However, because the real-space solvers require significantly more work to map the particles’ charge density to the mesh and extract forces from the mesh, their only successful application has been on specialized hardware. ⁹

Other strategies for solving particle ⇋ mesh problems can be found in the broad class of Multilevel Summation methods pioneered by Brandt¹¹ and developed for molecular simulations by Skeel¹² and others, the Fast-Multipole Method,¹³ and Adaptive P³M techniques used in astrophysical gravity calculations.^14,15,16 Thesemesh refinement techniques, along with the basic P³M method, may all be viewed as variations on the theme of smoothly and (in essence) isotropically splitting a long-ranged potential into short- and long-ranged components that can be accurately represented on meshes of different resolutions. Like multigrid Poisson solvers, when applied to condensed-phase systems, the mesh refinement methods also exchange computational effort for scaling benefits, but the simplicity of the algorithms and communication patterns makes these methods highly adaptable for applications on commodity hardware and general-purpose graphics processor units.

In this article, we present an alternative method for replacing the one convolution required by traditional electrostatic P³M solvers with a series of convolutions, each pertaining to a slab subdomain of the simulation cell, building up to a single convolution involving a coarsened mesh which describes the entire simulation cell. In contrast to the smooth splitting employed by other mesh refinement methods, our approach is to split the mesh-based potential sharply and anisotropically such that the individual components all contain discontinuities but can nonetheless recover a smooth potential when summed. This “Multi-Level Ewald” (MLE) approach produces the electrostatic potential in a single pass over all levels of the mesh; the extra computational effort is small.

We explore numerous strategies for manipulating the parameters of MLE scheme itself and the details of the associated particle ⇋ mesh operations in order to tune the accuracy of the resulting forces and energies with small amounts of overlap between adjacent slabs. Approximating the reciprocal space convolution using MLE can incur scarcely more error in the resulting particle forces than would be obtained with an equivalent P³M calculation. We expect that MLE can reduce the data communication requirements of molecular dynamics simulations for modern networked computing architectures, and will prove adaptable for balancing communication loads when the network connectivity is heterogeneous.

2 Theory

2.1 The problem of computing long-ranged electrostatics, the Ewald solution, and its evolution into P³M

The Ewald method can be summarized as splitting the calculation of the electrostatic energy of a periodic system of point (or otherwise highly localized) charges E^(coul) into a “reciprocal space” sum describing the energy of a system of spherical Gaussian charges, which has identical coordinates to the system of interest, and a “direct space” sum which modifies the energy of the reciprocal space sum to recover the energy of the system of point charges:

$$\begin{array}{c}\hfill E^{\left(\mathrm{coul}\right)}=\frac{1}{2}\sum _{\mathbf{n}}\sum _i\sum _{j\ne i}\frac{q_i{q}_j}{4\pi {\epsilon }_0\mid \mathbf{n}\cdot \mathbf{L}+{\mathbf{r}}_{ij}\mid }\hfill \\ \hfill E^{\left(\mathrm{dir}\right)}\simeq \frac{1}{2}\sum _i\sum _{j\ne i}\frac{q_i{q}_j(1-\mathrm{erf}(\beta \mid \mathbf{r}\mid \left)\right)}{4\pi {\epsilon }_0\mid {\mathbf{r}}_{ij}\mid }=\sum _i\sum _{j\ne i}{q}_i{q}_j{\theta }^{\left(\mathrm{dir}\right)}\hfill \\ \hfill E^{\left(\mathrm{rec}\right)}=\frac{1}{2}\sum _{\mathbf{n}}\sum _i\sum _{j\ne i}\frac{q_i{q}_j\mathrm{erf}(\beta \mid \mathbf{r}\mid )}{4\pi {\epsilon }_0\mid \mathbf{n}\cdot \mathbf{L}+{\mathbf{r}}_{ij}\mid }=\sum _i\sum _{j\ne i}{q}_i{q}_j{\theta }^{\left(\mathrm{rec}\right)}\hfill \\ \hfill E^{\left(\mathrm{coul}\right)}=E^{\left(\mathrm{dir}\right)}+E^{\left(\mathrm{rec}\right)}\hfill \end{array}$$ (1)

In these equations, n · L represents images of the unit cell throughout all space, i and j run over all charged particles in the system, r_{i j} is the distance between particles i and j, ε₀ is the permittivity of free space, and β is the “Ewald coefficient.” The reciprocal and direct space sums, E^(rec) and E^(dir), obtain their names because each converges absolutely in Fourier (reciprocal) or real (direct) space, respectively. The splitting is necessary because a straightforward summation over many periodic images of all charges in the system will not converge absolutely.

In its original formulation, the Ewald method relies only on the positions of particles. The direct space calculation involves a loop over all particles with a nested loop over each particle’s neighbors within a cutoff distance L_cut sufficient to give a convergent direct space sum. The reciprocal space calculation involves a loop over all particles with a nested loop that again involves all particles.

Splitting a potential into short- and long-ranged components is also the basis of Particle-Particle Particle-Mesh (P³M) methods.⁷ These similarities led Darden and colleagues to propose “Particle Mesh Ewald”⁶ as a special case of P³M which incorporated a Gaussian function for splitting the potential function. Many variants of this particular case have since been developed, ^5,9,10 along with distinct approaches for optimizing the influence function that modulates the interaction of charges on the mesh.¹⁷ In all of these methods, the basic procedure may be summarized: 1.) assign charges to the density mesh Q using the positions and charges of particles plus a suitable particle → mesh interpolation kernel, 2.) solve the field on the mesh by convolution with the mesh-based representation of the inter-particle potential function, and 3.) interpolate forces on all particles given the particle positions, charges, field values, and particle → mesh interpolation kernel.

The most common motivation for using particle-mesh strategies is to exploit the convolution theorem, which states that for two sequences of numbers f₁ and f₂,

$$f_1\star f_2={ℱ}^{-1}[ℱ(f_1)\cdot ℱ(f_2\left)\right]$$ (2)

Above, ⋆ represents a convolution, ℱ(f) is the (Fast) Discrete Fourier Transform (FFT) of f, ℱ⁻¹(f) is the inverse FFT of f such that ℱ⁻¹(ℱ(f)) = f, and ℱ(f₁)·ℱ(f)₂ is the element-wise product of ℱ(f)₁ and ℱ(f)₂.

The most popular variant of P³M for electrostatics, Smooth Particle Mesh Ewald (SPME),⁵ makes use of cardinal B-splines¹⁸ to map the system’s charges to the mesh Q. An elegant derivation of the Fourier transform of the reciprocal space pair potential, ℱ(θ^(rec)), is obtained by folding together Euler exponential splines in the mesh B (the Fourier-space representation of B-splines are Euler splines) and the Fourier-space representation of the Gaussian charge smoothing function W (the Fourier transform of a Gaussian is another Gaussian):

$$\begin{array}{c}\hfill B(x,y,z)=\mid b\left(x\right)\mid \cdot \mid b\left(y\right)\mid \cdot \mid b\left(z\right)\mid \hfill \\ \hfill b\left({\eta }_{\alpha }\right)=\frac{\exp \left(2\pi i\right(n-1){\eta }_{\alpha }∕g_{\alpha })}{\left[\sum _{p=0}^{n-2}{M}_n(p+1)\exp (2\pi ip{\eta }_{\alpha }∕g_{\alpha })\right]}\hfill \end{array}$$ (3)

$$W(x,y,z)=\frac{\exp (-4{\pi }^2{\mid \mathbf{k}\mid }^2{\sigma }^2)}{\pi V{\mid \mathbf{k}\mid }^2}$$ (4)

$$ℱ\left({\theta }^{\left(\mathrm{rec}\right)}\right)=B\cdot W$$ (5)

In the equations defining B and W, M_n represents a cardinal B-spline of order n, i is the square root of −1, α is one of the mesh dimensions x, y, or z, η_α is a displacement in the mesh dimension α, and g_α is the size of the mesh in α. Also, in the equation defining W, V is the volume of the simulation cell, σ is the RMS of the Gaussian charge smoothing function (note that σ = 1/(2β)), and k is the displacement from the origin in Fourier space. (Readers should consult the original SPME reference⁵ for a detailed presentation of the derivation of this approximation to θ ^(rec) and particle ⇋ mesh interpolation using B-splines. We have provided the most important definitions here because they will be important later as we develop our new method.) After ℱ(θ^(rec)) has been prepared, the electrostatic potential U^(rec) is computed with only two FFT operations:

$$U^{\left(\mathrm{rec}\right)}={ℱ}^{-1}\left[ℱ\left(Q\right)\cdot ℱ\left({\theta }^{\left(\mathrm{rec}\right)}\right)\right]$$ (6)

The electrostatic potential energy of the system E^(rec) may then be obtained by element-wise multiplication of the charge density Q with the electrostatic potential:

$$E^{\left(\mathrm{rec}\right)}=Q\cdot U^{\left(\mathrm{rec}\right)}$$ (7)

This operation would be performed in real space, and would require that a copy of the original charge density be saved before computing U^(rec). To avoid this extra memory requirement, FFT-based Poisson solvers use an identity to obtain E^(rec) during the element-wise multiplication in Fourier space, when the system virial is available as well. However, we emphasize the real-space expression for the energy as this will be necessary as we develop a replacement to the convolution step of P³M methods in electrostatics.

2.2 Accurate Decomposition of the Mesh-Based Sum: The MLE Method

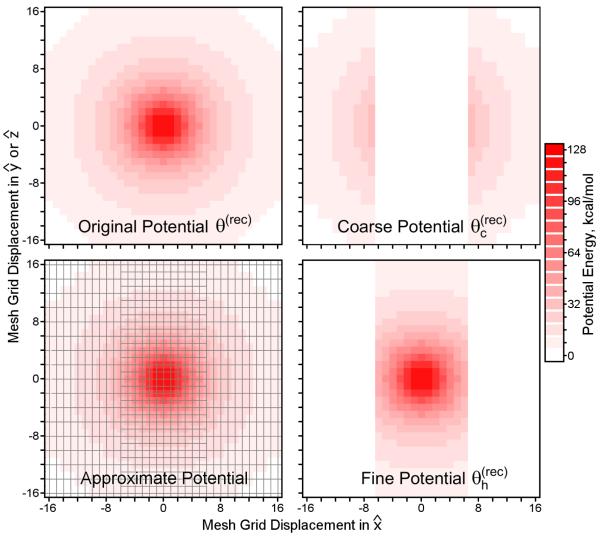
In the interest of improving the parallel scaling of P³M methods for molecular electrostatics, we focused on improving the method in which Q ⋆ θ ^(rec) is computed while preserving other aspects of the algorithm. Our approach was to split θ ^(rec) into fine and coarse resolution components as shown in Figure 1. Rather than splitting the potential isotropically in terms of the absolute distance between points, however, the splitting is done anisotropically along planes perpendicular to one dimension, which we will call $\widehat{x}$. The fine resolution potential ${\theta }_h^{\left(\mathrm{rec}\right)}$ exactly describes the interactions between any two mesh points separated by up to (and including) T_cut in $\widehat{x}$, regardless of the distance between the points in the other unit cell dimensions $\widehat{y}$ and $\widehat{z}$. Conversely, the low resolution pair potential ${\theta }_h^{\left(\mathrm{rec}\right)}$ approximately describes the interactions of points separated by more than T_cut in $\widehat{x}$, no matter their locations in $\widehat{y}$ and $\widehat{z}$. For convenience, we will refer to the set of mesh points which share the same coordinate in the $\widehat{x}$ direction as a “page” of the mesh. The meshes of different resolutions used in our approximation will be refered to as different “levels” of mesh. Our convention is to call the finest resolution mesh the lowest level; the extent of the reciprocal space pair potential grows as the mesh level becomes higher.

Figure 1. A multi-level mesh-based approximation to the Ewald reciprocal space pair potential.

In Ewald mesh calculations, the reciprocal space pair potential θ ^(rec) can be visualized in real space. At short range, θ ^(rec) ~ erf(β∣r∣)/(4πε₀∣r∣), where ε₀ is the permittivity of free space and erf is the error function. θ ^(rec) was computed for a 96Å cubic box on a mesh of 96³ points; slices of the potential through the xy (or xz) planes are shown with varying intensities of red to indicate the magnitude. The color scale is deliberately coarse to make the potential isocontours apparent. θ ^(rec) varies most rapidly along paths passing directly through the source at (0,0,0); paths that move tangentially to the source encounter much slower variations in θ ^(rec). It is more feasible to approximate θ ^(rec) with high- and low-resolution potentials ${\theta }_h^{\left(\mathrm{rec}\right)}$ and ${\theta }_c^{\left(\mathrm{rec}\right)}$ as shown, avoiding mesh ⇋ mesh interpolation along vectors pointed at the source as much as possible. ${\theta }_c^{\left(\mathrm{rec}\right)}$ uses double the mesh spacing along the $\widehat{y}$ and $\widehat{z}$ axes, as indicated by the mesh overlay in the lower left panel, but the same spacing as ${\theta }_h^{\left(\mathrm{rec}\right)}$ in the $\widehat{x}$ direction. ${\theta }_c^{\left(\mathrm{rec}\right)}$ therefore presents a fine mesh spacing for interpolating gradients of the true potential θ ^(rec) when the true potential varies rapidly, but presents a coarse spacing when the true potential varies slowly.

With θ ^(rec) split into two components, the convolution can be restated:

$$Q\star {\theta }^{\left(\mathrm{rec}\right)}\simeq Q\star {\theta }_h^{\left(\mathrm{rec}\right)}+Q_c\star {\theta }_c^{\left(\mathrm{rec}\right)}=U_h^{\left(\mathrm{rec}\right)}+U_c^{\left(\mathrm{rec}\right)}\simeq U^{\left(\mathrm{rec}\right)}$$ (8)

where Q _c is a coarsened charge mesh interpolated from Q. (Note that, while ${\theta }_h^{\left(\mathrm{rec}\right)}$ is sparse and ${\theta }_c^{\left(\mathrm{rec}\right)}$ contains a void where ${\theta }_h^{\left(\mathrm{rec}\right)}$ is nonzero, Q and Q_c are full: every point in Q_c is interpolated from the appropriate points in Q.) This approximation does not immediately reduce the communication requirements of computing Q ⋆ θ ^(rec), but because ${\theta }_h^{\left(\mathrm{rec}\right)}$ is zero in all but a narrow region 2(T_cut) + 1 pages thick, the convolution $Q\star {\theta }_h^{\left(\mathrm{rec}\right)}$ can be accomplished as a series of convolutions:

$$Q\star {\theta }_h^{\left(\mathrm{rec}\right)}=\sum _{i=1}^P\left[Q_i\star {\theta }_h^{\left(\mathrm{rec}\right)}\right]$$ (9)

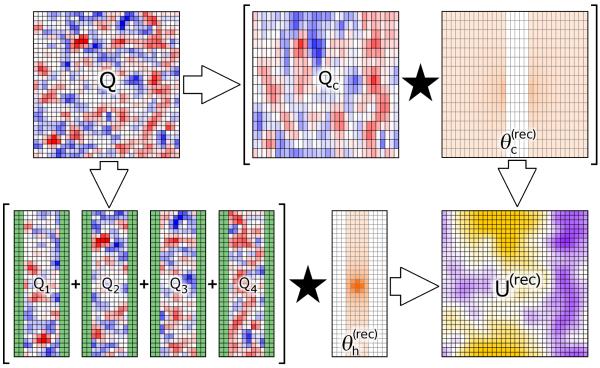
where each sub-mesh Q_i spans the simulation box in $\widehat{y}$ and $\widehat{z}$ and is zero-padded 2T_cut pages in $\widehat{x}$. We will refer to these sub-meshes as “slabs.” Each of the P slabs of the lowest level mesh is therefore padded by 2T_cut pages of zeroes, and each of the series of convolutions described in equation 9 can be computed independently. The padding is done so that FFTs may be used for the convolution without having charges near the yz faces of any slab “wrap around” and erroneously influence other parts of the same slab, and so that the influence of charges near the yz faces of each slab will be recorded as the results of all these convolutions over slabs are then spliced back together to accumulate the approximation to U^(rec). The electrostatic influence of charge density in slab Q_i on the neighboring slabs is recorded in its zero-padded pages. (Generally, the neighbors of Q_i are Q_i−1 and Q_i+1, although Q_P and Q₁ are neighbors due to the periodicity of the unit cell.) The basic procedure is illustrated in Figure 2. In principle, convolutions with many radially symmetric potential functions could be split in this manner, though we focus on the case of the inverse distance kernel for application to biomolecular simulations. Numerous styles of P³M are also compatible with this convolution splitting procedure; we have chosen to implement it within the Smooth Particle Mesh Ewald style described above and call the new method “Multi-Level Ewald” (MLE).

Figure 2. Illustration of the Multi-Level Ewald convolution procedure.

In typical Smooth Particle Mesh Ewald (SPME) calculations, the charge mesh Q is convoluted with θ ^(rec) to arrive at the reciprocal space electrostatic potential U^(rec). In Multi-Level Ewald (MLE), this single convolution is replaced with many smaller ones. In a basic two-level variation of MLE, the mesh Q is split, with no interpolation, into multiple subregions (slabs) Q₁ …Q_L as shown. The slabs are then zero-padded, as highlighted in green in the diagram, so that they may be convoluted with the high-resolution reciprocal space pair potential ${\theta }_h^{\left(\mathrm{rec}\right)}$, which is itself extracted from θ ^(rec) without interpolation. The coarsened charge mesh Q_c is interpolated from Q and convoluted with the coarsened reciprocal space pair potential ${\theta }_c^{\left(\mathrm{rec}\right)}$ (see Figure 1). An electrostatic potential at the resolution of the fine mesh is then interpolated from the result of $Q_c\star {\theta }_c^{\left(\mathrm{rec}\right)}$ to complete the approximation of Q ⋆ θ ^(rec). This figure was made using an actual MLE calculation on a 32ų box of 4000 randomly distributed ions. The color scales are not given as the diagram is qualitative, but in the meshes Q, Q_c, and Q₁ … Q₄ red and blue signify negative and positive charge, the intesity of orange signifies the intensity of the pair potential, and purple and gold signify negative and positive electrostatic potential in the resulting $U_c^{\left(\mathrm{rec}\right)}$. Each colored pixel corresponds to a point in a plane cutting through the mesh in the actual MLE calculation.

In our MLE implementation, the coarsened reciprocal space pair potential ${\theta }_c^{\left(\mathrm{rec}\right)}$ is obtained simply by extracting points from θ ^(rec) at regular intervals of the coarsening factor, C_yz, in the $\widehat{y}$ and $\widehat{z}$ directions:

$${\theta }_c^{\left(\mathrm{rec}\right)}(i,j,k)=\{\begin{array}{ccc}{\theta }^{\left(\mathrm{rec}\right)}(i,C_{yz}j,C_{yz}k)\hfill & \hfill ,\hfill & i>T_{\text{cut}}\text{or}i<=g_x-T_{\text{cut}}\hfill \\ 0\hfill & \hfill ,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (10)

where i, j, and k represent coordinates in the $\widehat{x}$, $\widehat{y}$, and $\widehat{z}$ directions, respectively, and g_x is the mesh size in the $\widehat{x}$ direction. (Here, k should not be confused with k used earlier to describe a vector in Fourier space.) While this approach may appear to discard much of the information present in θ ^(rec), we will show that it can produce very high accuracy depending on the other MLE parameters. We wrote an optimization procedure to try and improve the coarsened reciprocal space pair potential mesh by using steepest descent optimization to adjust the values of ${\theta }_c^{\left(\mathrm{rec}\right)}$ at individual mesh points and minimize the root mean squared (RMS) error in the approximate U^(rec). This approach could only reduce the error rate of MLE calculations by about 2% (data not shown) and was not given further consideration in these studies.

Similar to the construction of ${\theta }_c^{\left(\mathrm{rec}\right)}$, Q_c is interpolated from Q using cardinal B-splines¹⁸ similar to those used for particle ⇋ mesh interpolation in standard SPME. However, mesh ⇋ mesh interpolation is a two-dimensional process as the mesh resolution is only reduced in $\widehat{y}$ and $\widehat{z}$ and maintained in $\widehat{x}$. Each page of the mesh Q_c is interpolated from the corresponding page of Q. As we will show in the results, it can be advantageous to use relatively high values of the order of mesh ⇋ mesh interpolation I^(mm) as opposed to the order of particle ⇋ mesh interpolation I^(pm). In the same way that higher values of I^(pm) improve the accuracy of SPME calculations, higher values of I^(mm) improve the accuracy of the MLE approximation; however, whereas the cost of an SPME calculation scales as the cube of I^(pm) because each particle has a different alignment to the mesh, the regularity of the mesh ⇋ mesh interpolation makes it separable in each dimension and thus the operation scales merely as I^(mm).

While ${\theta }_h^{\left(\mathrm{rec}\right)}$ will typically span a small region of the simulation box, if ${\theta }_c^{\left(\mathrm{rec}\right)}$ were to span the rest it might be impractical to compute $Q_c\star {\theta }_c^{\left(\mathrm{rec}\right)}$ as a series of convolutions. However, it is still possible to add more mesh levels by splitting ${\theta }_c^{\left(\mathrm{rec}\right)}$ into its own “fine” and “coarse” resolution components ${\theta }_{c,1}^{\left(\mathrm{rec}\right)},{\theta }_{c,2}^{\left(\mathrm{rec}\right)},\dots ,{\theta }_{c,n}^{\left(\mathrm{rec}\right)}$, in the same manner that the original θ ^(rec) was split (see Figure 3). The most general expression of the MLE method is then:

$$Q\star {\theta }^{\left(\mathrm{rec}\right)}=\sum _{i=1}^{P_1}\left[Q_i\star {\theta }_h^{\left(\mathrm{rec}\right)}\right]+\sum _{j=2}^{L-1}\sum _{k=1}^{P_j}\left[Q_{c,j,k}\star {\theta }_{c,j}^{\left(\mathrm{rec}\right)}\right]+Q_{c,L}\star {\theta }_{c,L}^{\left(\mathrm{rec}\right)}$$ (11)

The scheme above involves L–1 coarsened meshes with as many distinct coarsening factors. In general, a single convolution of the highest level charge mesh with the coarsest component of the reciprocal space pair potential must be performed, involving data collected over the entire simulation cell. However, because the mesh spacing in the highest level charge mesh can be 2 to 6 times larger than the mesh spacing in Q, calculating $Q_{c,L}\star {\theta }_{c,L}^{\left(\mathrm{rec}\right)}$ is not so demanding as calculating Q ⋆ θ ^(rec), and the communication burden is likewise reduced.

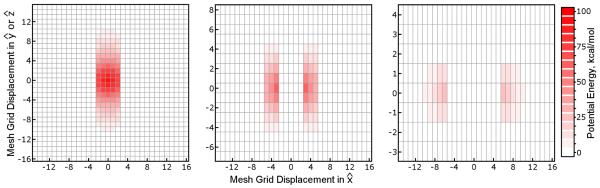
Figure 3. A three-level MLE scheme.

As illustrated above, the reciprocal space pair potential mesh can be split into three (or more) separate meshes, each with successively larger coarsening factors. Here, there are two coarsened meshes, with coarsening factors C_yz of 2 and 4, respectively. In this scheme, the pair potential in the lowest level mesh extends 2 pages; slabs of the lowest level charge mesh would require 4 pages of zero-padding. The pair potential in the intermediate level mesh has T_cut = 5, although only 6 of its pages have nonzero potential values in them (the thickness of the nonzero region of the mesh is 2 × 5 + 1 = 11 pages). While slabs of the intermediate-level charge mesh would require 10 pages of zero-padding, the intermediate level mesh is much smaller than the lowest level mesh, making such a degree of padding more economical. The color scale is not the same as that for Figure 1 because the SPME calculation this MLE scheme approximates was not the same; the diagram is intended for qualitative understanding only.

2.3 Considerations for constant pressure simulations

It is important to note that, in order to make MLE run efficiently, θ ^(rec) must be computed by taking the inverse Fourier transform of ℱ(θ^(rec)) as is typically computed in particle-mesh methods, then extracting ${\theta }_h^{\left(\mathrm{rec}\right)}$ and ${\theta }_c^{\left(\mathrm{rec}\right)}$, and finally computing the Fourier transforms $ℱ\left({\theta }_h^{\left(\mathrm{rec}\right)}\right)$ and $ℱ\left({\theta }_c^{\left(\mathrm{rec}\right)}\right)$. This preparatory work must be done at the beginning of the simulation so that during each step of dynamics the necessary convolutions described in Equation 8 or 9 can be accomplished with only two Fourier transforms each. This necessity may appear to limit the applicability of the MLE approximation to constant volume systems, where θ ^(rec) is constant throughout the simulation. However, if the unit cell volume rescaling in constant pressure simulations is isotropic, and the Gaussian charge smoothing parameter σ and the mesh spacing μ vary in proportion to the unit cell dimensions, the updated pair potentials ${\theta }_h^{\left(\mathrm{rec}\right)\ast }$ and ${\theta }_c^{\left(\mathrm{rec}\right)\ast }$ for any new unit cell volume can be obtained be simply rescaling the ${\theta }_h^{\left(\mathrm{rec}\right)}$ and ${\theta }_c^{\left(\mathrm{rec}\right)}$ obtained at the beginning of the simulation.

3 Methods

3.1 The MDGX Program

In order to test the Multi-Level Ewald (MLE) method, we wrote an in-house molecular dynamics program, MDGX (Molecular Dynamics with Gaussian Charges and Explicit Polarization—not all parts of the acronym are yet fulfilled, as the purpose of the program is to be a proving ground for new algorithms). Routines in MDGX are able to read AMBER topology files and produce outputs in a format like that of the SANDER module in the AMBER software package.¹⁹ The MDGX program is able to run unconstrained molecular dynamics trajectories of systems such as a box of SPC-Fw water molecules²⁰ in the microcanonical (NVE) ensemble, or simply compute energies and forces acting on all atoms of a system for a single set of coordinates. The MDGX program implements both Smooth Particle Mesh Ewald (SPME) as well as our new MLE method, and also offers the option of using different particle ⇋ mesh interpolation orders in different dimensions, a feature which we will show is very helpful for tuning MLE. When run with identical parameters, the SPME reciprocal space electrostatic forces computed by MDGX agree with those of sander to 1.0×10⁻⁹ relative precision. MDGX links with the FFTW²¹ library to perform its FFTs.

3.2 A Matlab Ewald Calculator

While the MDGX program is an excellent tool for testing MLE and other new variants of P³M, it currently only works with orthorhombic unit cells (the reciprocal space code is actually set up to perform calculations with non-orthorhombic cells, but the direct space domain decomposition is not yet ready in this respect). The MDGX program was therefore only used for calculations involving rectangular unit cells.

Before MDGX was created, Multi-Level Ewald was discovered and verified through a set of script functions written for the Matlab software package (The MathWorks, Inc., Natick, MA, U.S.A.). These scripts, which can easily produce forces and energies for a particular set of coordinates and charges but are not efficient enough to propagate a lengthy molecular dynamics trajectory, were used for any calculations involving non-orthorhombic unit cells. The calculator facilitates analysis of every stage of the Multi-Level Ewald process through Matlab’s high-level programming language, and is available from the authors on request.

3.3 Test Systems

As presented in Table 1, we chose a number of systems representative of those found in typical, condensed phase, biomolecular simulations. The first, a system of 1024 SPC-Fw water molecules, was used for testing energy conservation and ensemble properties of the system collected over long molecular dynamics runs. The other systems were much larger protein-in-water and protein crystal systems used in our previous study developing a different P³M method.²² Most importantly, these systems span a variety of unit cell types: as will be shown, MLE can be performed with any type of unit cell, but the geometry of the unit cell itself affects the accuracy of the MLE approximation.

Table 1. Test cases for the Multi-Level Ewald method.

The cases presented here span a variety of simulation cell geometries. All systems are in the condensed phase and were pre-equilibrated by molecular dynamics simulations at constant pressure.

Case	Cell Dimensions (a, b, c), Å	Cell Dimensions (α, β, γ)	Atom Count
Water	31.4 × 31.4 × 31.4	90°, 90°, 90°	3072
Streptavidin	89.7 × 89.7 × 89.7	90°, 90°, 90°	73305
Protein Crystal	71.4 × 71.4 × 75.6	90°, 90°, 120°	36414
Glycerol Solution	69.7 × 69.7 × 89.0	60°, 90°, 90°	39808
Cyclooxygenase-2	114.8 × 114.8 × 114.8	109.5°, 109.5°, 109.5°	118833

3.4 Smooth Particle Mesh Ewald Accuracy Standards and Reference Calculations

Standards for the accuracy of electrostatic forces in molecular simulations must be established before assessing the accuracy of MLE approximations with respect to SPME targets. Generally, we chose the accuracy obtained by the default settings of the SANDER molecular dynamics engine in the AMBER software package¹⁹ as a reasonable level of accuracy for molecular simulations. These settings are mesh spacing μ as close to 1.0Å as possible given a mesh size g with prime factors 2, 3, 5, and possibly 7, particle ⇋ mesh interpolation order I^(pm) = 4, and direct sum tolerance D_tol = 1.0×10⁻⁵ with direct space cutoff L_cut = 8.0Å leading to a Gaussian charge smoothing half width σ = 1.434Å. They can be expected to produce electrostatic forces with a root mean squared (RMS) error of about 1.0×10⁻² kcal/mol-Å, but the exact number varies depending on the system composition and geometry. Most SPME calculations for this work were performed with these parameters, and most modifications to the parameters were made in such a way as to conserve the overall accuracy of the calculation. For reference, very high quality SPME calculations were performed with μ ~ 0.4Å, I^(pm) = 8, and an identical value of σ to ensure that the direct space and reciprocal space components of the SPME calculation could both be compared to the reference. The reference calculations produced forces convergent to within 1.0×10⁻⁶ kcal/mol-Å.

4 Results

4.1 Accuracy of Forces and Energies Computed with Multi-Level Ewald

The most important products of our new Ewald reciprocal space approximation are correct reproduction of the electrostatic energy of a system of particles and correct reproduction of the gradients of that energy. As our implementation of Multi-Level Ewald (MLE) is an approximation to the Smooth Particle Mesh Ewald (SPME) method, we performed SPME calculations with high-accuracy “reference” parameters as well as typical molec-ular dynamics parameters and compared MLE results to both. In typical SPME calculations, there are two sources of error to consider, arising from the direct and reciprocal space parts of the calculation, respectively. MLE uses the same direct space sum but approximates the reciprocal space sum, introducing “coarsening” errors into the electrostatics calculation. We define the coarsening errors as deviations in the MLE approximation away from the equivalent SPME calculation, where the “equivalent” SPME calculation uses the same σ, I^(pm), and μ parameters as the MLE calculation and has its own degree of inaccuracy relative to the SPME reference calculation. Fundamentally, the coarsening errors are errors in the scalar values of the electrostatic potential at points in U^(rec) (see Equation 6), which in turn imply errors in the forces on charged particles interpolated from U^(rec). We will first focus on the errors in forces, as these are of greatest importance in molecular simulations; energies will be discussed in another section.

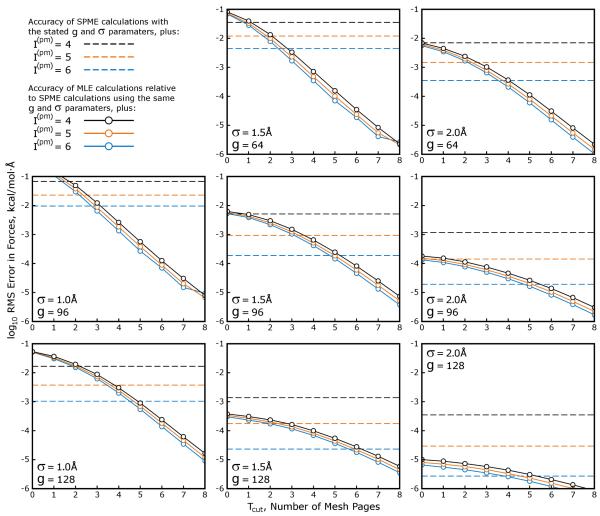
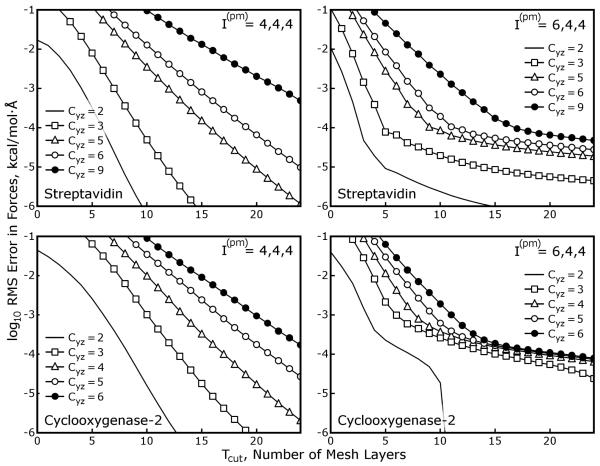
In order to quantify the coarsening errors as a function of the SPME parameters, we ran calculations on the Streptavidin test case described in Table 1 using a range of values for the SPME mesh spacing μ, Gaussian charge smoothing function half width σ, and interpolation order I^(pm). We then approximated the SPME results with MLE calculations using C_yz = 2, mesh ⇋ mesh interpolation order I^(mm) = 8, and a range of values for T_cut (C_yz and I^(mm) can be varied to benefit the accuracy of MLE calculations, as we will show later, but their values were fixed for simplicity in this test). The results in Figure 4 show that the accuracy of the MLE approximation improves exponentially with T_cut, and is also very sensitive to the parameters of the equivalent SPME calculation, particularly σ and μ and to a lesser extent I^(pm). Though the values of μ and σ are widely varied and not thoroughly sampled, Figure 4 establishes another important result, that MLE can be used to approximate a wide range of different SPME calculations and, without large values of T_cut, incur less error than the SPME calculation itself.

Figure 4. Accuracy of MLE calculations shows dependence on the parameters of the SPME calculation that is being approximated.

SPME calculations were performed on the streptavidin test case with a range of Gaussian charge smoothing half widths σ and mesh sizes g × g × g. In practice, SPME calculations run with particle ⇋ mesh interpolation order I^(pm) = 4 require that σ be at least 1.5× the mesh spacing μ to produce reasonable accuracy in the forces arising from the reciprocal space part; however, if I^(pm) is set to 6, σ :μ ratios as small as 1.0 can be used. The σ :μ ratio in the center panel is roughly 1.6, and it increases moving across the panels from left to right or top to bottom. The σ = 1.0Å, g = 64 case is omitted because it would be far too inaccurate for molecular simulations, no matter the value of I^(pm). In each panel, horizontal dashed lines show the accuracy of SPME calculations with the stated parameters (the “equivalent” SPME calculations) relative to a high-accuracy reference calculation performed as described in Methods. Solid lines with open circles depict the accuracy of MLE calculations relative to the equivalent SPME calculations.

Although at first it appears that the accuracy of MLE is least sensitive to I^(pm), this parameter can be manipulated to great advantage in MLE calculations. Of all the commercially or academically available molecular dynamics codes, the Desmond software package²³ is, to our knowledge, the only one to permit different settings of I^(pm) in different directions. However, we found that this is a powerful way to improve the accuracy of an MLE approximation. As we showed in previous work, ²² setting I^(pm) = 6 permits μ to be set as much as 1.5× larger than I^(pm) = 4 would allow; the result in fact applies in one, two, or all three dimensions. Strictly in terms of the number of operations, increasing I^(pm) to 6 in only one dimension offers the most reduction in the mesh size per increase in the amount of particle ⇋ mesh work. For example, a mesh of 90³ points could be replaced by a mesh of 60 × 90 × 90 points, at the expense of mapping particles to 6 × 4 × 4 = 96 points rather than 4 × 4 × 4 = 64. In contrast, setting I^(pm) = 6 in all dimensions could produce comparable accuracy in the aforementioned problem with a mesh of 60³ points, but at the expense of mapping all particles to 216 mesh points.

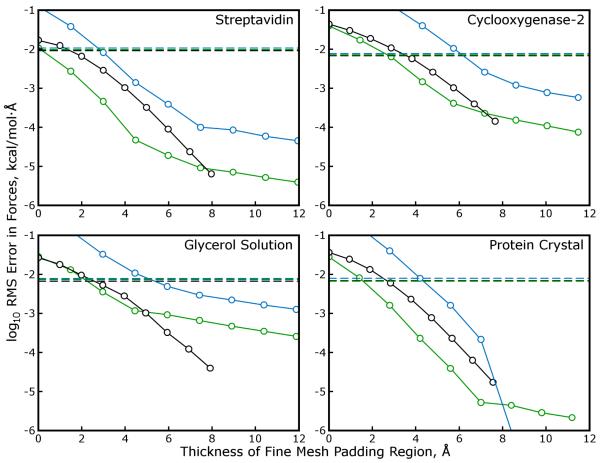
We performed additional SPME and MLE calculations on the streptavidin system, this time using the AM-BER default parameters (as described in Methods) and a variation on those parameters using I^(pm) = 6 and μ approaching 1.5Å in the $\widehat{x}$ direction or in all directions. We also performed tests on other systems described in Table 1 to confirm the accuracy of MLE when applied to non-orthorhombic unit cells. All of these results are presented in Figure 5. While all of the different combinations of I^(pm) and μ produce comparable accuracy in the SPME calculation, and while raising I^(pm) will improve the accuracy of MLE calculations if all μ (and σ) are held fixed, increasing μ in this manner appears to be detrimental to the accuracy of the subsequent MLE approximation. However, if only $I_x^{\left(\mathrm{pm}\right)}$ is raised and μ_x is increased accordingly, the accuracy of the subsequent MLE approximation is improved significantly in three out of the four cases. Anisotropic interpolation orders and a longer mesh spacing in the $\widehat{x}$ direction therefore permit significant reductions in the number of pages T_cut that must be computed in zero-padded FFTs and transmitted between neighboring slabs, making MLE cheaper to apply.

Figure 5. Anisotropic mesh spacings and interpolation orders enhance the accuracy of MLE calculations.

SPME calculations were performed on four of the test cases from Table 1, this time using the AMBER default parameters σ ~ 1.4Å, $I_x^{\left(\mathrm{pm}\right)}=I_y^{\left(\mathrm{pm}\right)}=I_z^{\left(\mathrm{pm}\right)}=4$, and the smallest mesh dimensions g_x, g_y, and g_z such that the g_x, g_y, and g_z were multiples of 2, 3, and 5 and the mesh spacings μ_x, μ_y, and μ_z were less than 1.0Å. Accurate MLE approximations of such SPME calculations are possible for all these systems, which include monoclinic and triclinic unit cells in addition to the cubic streptavidin system. Modifying the SPME parameters by increasing μ_x to 1.5Å and increasing I^(pm) to compensate maintains the accuracy of the SPME calculation with a smaller amount of mesh data and can also increase the accuracy of MLE approximations. As in Figure 4, dashed lines represent the accuracy of SPME calculations relative to a high accuracy reference, and lines with open circles represent the accuracy of MLE calculations relative to SPME. Black, green, and blue lines correspond to I^(pm) = (4,4,4), (6,4,4), and (6,6,6), respectively. Because the SPME/MLE calculations in each panel use different values of μ_x the results are plotted in terms of the physical thickness of the padding needed for each MLE approximation, T_cut × μ.

As can be seen in Figure 4, raising I^(pm) is not the only way to compensate for an increase in μ. Raising σ itself is another way to maintain the critical ratio of σ to μ. Larger values of σ are obtained by using a longer direct space cutoff L_cut; many codes^23,24 and specialized hardware for running molecular simulations²⁵ make use of longer values of L_cut in order to reduce the size of the reciprocal space mesh. We therefore tested the accuracy of MLE calculations if larger values of σ, rather than higher I^(pm), were used in conjunction with a larger μ. The results in Figure 6 stand in contrast to the results of Figure 5: the MLE approximation becomes more accurate when longer μ are used, insofar as σ is increased accordingly. When using higher σ and larger μ, anisotropic particle ⇋ mesh interpolation is still effective at conserving the accuracy of the SPME calculation and continues to benefit the accuracy of the MLE approximation.

Figure 6. Wider Gaussian smoothing functions enhance the accuracy of MLE.

Although using a larger mesh spacing μ in conjunction with isotropic 6^th order particle ⇋ mesh interpolation is detrimental to the accuracy of MLE approximations, it is possible to improve the accuracy of MLE by using a larger μ and increasing σ, the RMS of the Gaussian charge smoothing function, to maintain the accuracy of the equivalent SPME calculation. The accuracy of MLE approximations for the streptavidin and cyclooxygenase-2 systems is plotted as a function of μ. For each of the equivalent SPME calculations, σ was adjusted in proportion to μ to maintain the σ to μ ratio that would be obtained in each system by the AMBER default parameters, roughly 1.42. As shown by the solid lines with open circles, this approach is also effective at conserving the accuracy of the equivalent SPME calculation, even improving it slightly as μ gets larger. The accuracies of MLE approximations improve steadily as a function of μ. The inset legend in the lower left panel applies to all panels.

Noting that non-orthorhombic unit cells are detrimental to the accuracy of MLE (though only to the extent that T_cut must be raised by 1 or 2), we tried MLE calculations with several other monoclinic unit cells, each with only one of the α, β, or γ angles different from 90°. While we had hoped that MLE might be able to give the same accuracy in monoclinic unit cells as in orthorhombic ones if the coarsening occured in certain dimensions with respect to the non-orthogonal unit cell vectors, the accuracy of MLE showed similar degradation no matter which angle differed from 90° (data not shown).

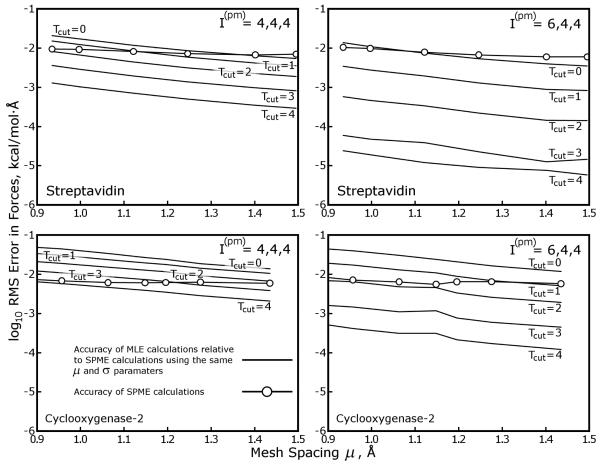
As mentioned in the Theory section, the MLE approximation is tunable in the I^(mm) parameter as well as in T_cut. Knowing that high values of I^(mm) are economical in terms of the number of arithmetic operations, we tested the accuracy of MLE for orders of mesh ⇋ mesh interpolation ranging from 4 to 16. The AMBER default parameters and variants with I^(pm) = 6 were again used for this test. As shown in Figure 7, if a low order of mesh ⇋ mesh interpolation can produce accuracy on the order of the SPME reciprocal space calculation, raising I^(mm) can improve the accuracy of an MLE approximation by an order of magnitude.

Figure 7. Higher mesh ⇋ mesh interpolation orders can benefit MLE calculations.

Interpolation between the finest mesh and higher level meshes in MLE is, like the particle ⇋ mesh interpolation in standard SPME calculations, based on cardinal B-Splines; the grid points of the finest mesh can be thought of as particles to map onto coarser meshes. However, mesh ⇋ mesh interpolation of order I^(mm) only occurs in only two dimensions and, because of the regularity of the fine grid, the operations are separable in each dimension leading to O(I^(mm)) complexity and the possibly much higher orders of I^(mm) than I^(pm). The accuracy of MLE approximations to the SPME calculations described in Figure 5 was therefore re-evaluated as a function of I^(mm) for the streptavidin test case. The results suggest that raising I^(mm) is effective if the equivalent SPME calculation makes use of a high σ :μ ratio in the dimensions along which the mesh is coarsened (i.e. $\widehat{y}$ and $\widehat{z}$). The inset legend in the leftmost panel applies to all panels.

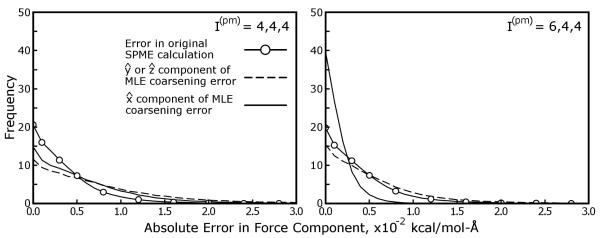
Figures 5 and 7 show that, with proper choices of T_cut and I^(mm) to accomodate the parameters of the equivalent SPME calculation, the coarsening errors in MLE calculations can be well below the level of reciprocal space error in the equivalent SPME calculation. However, the form of the coarsening errors themselves must be examined. As will be discussed in the following section, the reciprocal space electrostatic forces accumulate errors as a consequence of inaccuracies in the mesh U^(rec), but because the interpolation of U^(rec) itself is done only along certain dimensions in MLE calculations the resulting errors in the reciprocal space electrostatic forces could be expected to be somewhat anisotropic. Figure 8 shows the magnitudes of the coarsening errors acting on individual atoms of the streptavidin system in the $\widehat{x}$, $\widehat{y}$, and $\widehat{z}$ directions under an aggressive MLE approximation (details are given in the figure itself). As might be expected, the coarsening errors tend to be greater in the $\widehat{y}$ and $\widehat{z}$ directions, but only slightly: coarsening errors in the electrostatic forces also have significant components in the $\widehat{x}$ direction, despite the fact that no mesh coarsening was done in $\widehat{x}$. As was shown in Figure 5, use of anisotropic SPME parameters reduces the overall error in the MLE approximation, but the individual errors in forces become even more shifted towards the $\widehat{y}$ and $\widehat{z}$ directions. Conceptually, anisotropic errors are less desirable than isotropic ones, as they might impart the wrong energetics to interactions based on, for example, the orientation of a protein in the simulation cell. However, we stress that this test used an aggressive MLE approximation for demonstrative purposes, and that other MLE parameters can yield errors well below those of the equivalent SPME calculation. We attempted the same test with more conservative parameters (data not shown), and found the shapes of the force error histograms to be very similar to those in Figure 5, but on an exponentially smaller scale.

Figure 8. Errors arising from the MLE approximation are anisotropic.

Because the MLE approximation is applied in only two of the three unit cell dimensions, errors arising from the approximation may be larger in some dimensions than others. Electrostatic forces on atoms of the streptavidin system in Table 1 were computed using SPME and the AMBER default parameters with the particle ⇋ mesh interpolation schemes given in each panel. As shown by these histograms, the coarsening errors (differences between the equivalent SPME calculation and an aggressive MLE approximation with T_cut = 0, C_yz = 2, and I^(mm) = 8), are indeed more pronounced in the directions along which the reciprocal space mesh was coarsened, $\widehat{y}$ and $\widehat{z}$, even if the equivalent SPME calculation uses isotropic μ and σ parameters. Increasing μ_x to ~ 1.5Å and setting $I_x^{\left(\mathrm{pm}\right)}=6$ reduces errors in all directions, but the accuracy of MLE-approximated forces in the $\widehat{x}$ direction shows the most improvement by far, even exceeding the accuracy of the equivalent SPME calculation. The frequencies of errors in the $\widehat{y}$ and $\widehat{z}$ directions were averaged and presented together as they were indistinguishable in this cubic unit cell. For comparison, we also show a histogram of the magnitudes of errors inherent in the equivalent SPME reciprocal space calculation, as judged by a high accuracy standard. The inset legend in the leftmost panel applies to both panels.

4.2 Larger coarsening factors and Incorporation of Multiple Higher-Level Meshes

While there may be some advantage in being able to split the convolution Q ⋆ θ ^(rec) into multiple pieces (and, if T_cut can be set as low as 0, obtain $Q_h\star {\theta }_h^{\left(\mathrm{rec}\right)}$ by performing only two-dimensional FFTs, saving some FFT work and a major data transpose operation), C_yz can be larger than 2 to reduce the size and processing requirements of the $Q_c\star {\theta }_c^{\left(\mathrm{rec}\right)}$ convolution even further. The MLE scheme is also not limited to just one higher level mesh: the charge mesh Q can be split into a series of meshes Q_c,1, Q_c,2, …, Q_c,L, staged with increasing values of C_yz,1, C_yz,2, …, C_yz,L depending on the size of the problem.

Figure 9 shows the accuracy of Multi-Level Ewald on two of the systems in Table 1 using larger values of C_yz, demonstrating that MLE can be applied with C_yz as high as 4 to 6 for 16-36 fold reductions in the amount of data present in the coarsest mesh. However, setting T_cut to 4 or 6 could be very expensive in terms of the extra FFT work and communication cost. If eight MLE slabs were used with a mesh of 64 × 96 × 96 points with C_yz set to 4 and T_cut set to 5, each MLE slab would measure (64/8) + 2 × 5 = 18 points thick; the FFT work needed to compute $Q_c\star {\theta }_c^{\left(\mathrm{rec}\right)}$ would be more than 16 times less than that needed to compute Q ⋆ θ ^(rec) in the equivalent SPME calculation, but the FFT work needed to compute the series ${\sum }_i{Q}_i\star {\theta }_h^{\left(\mathrm{rec}\right)}$ would be roughly twice the original FFT burden. There would also be a considerable burden for communicating the zero-padded regions of each MLE slab.

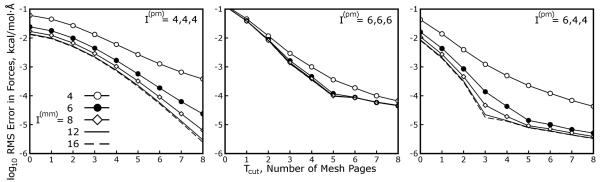
Figure 9. Larger coarsening factors are available in MLE.

Thus far, the results have focused on the performance of the MLE approximation for a variety of SPME calculations, emphasizing what values of I^(mm) and T_cut are necessary to achieve accurate results with a coarsening factor C_yz of 2, but C_yz is itself a tunable parameter of MLE. These plots show the accuracy of the MLE approximation for the streptavidin and cyclooxygenase-2 test cases (in cubic and triclinic unit cells, respectively) for numerous coarsening factors as shown in each diagram. The coarsening factors are limited to common factors of the mesh sizes in the $\widehat{y}$ and $\widehat{z}$ directions, but we do not expect this to be a serious limitation in practice. In these tests, I^(mm) was fixed at 8. The AMBER default SPME paramaters, or the variant with anisotropic interpolation discussed in previous figures and the maint text, were used for the SPME calculations as indicated in each diagram. While larger values of C_yz require larger values of T_cut to produce accurate results, MLE with C_yz as high as 6 can imply modest additional error with T_cut as low as 7 if anisotropic particle ⇋ mesh interpolation is used. As shown in Table 2, a third, intermediate mesh level, typically with C_yz = 2, is helpful for reducing the computation and communication burden of larger values of T_cut, making it possible to efficiently coarsen the reciprocal space mesh in stages.

In order to bridge the gap between Q and Q_c, we introduced another mesh with an intermediate coarsening factor (i.e. C_yz,2 = 2). Following the nomenclature in the Theory section, we will refer to this intermediate mesh as Q_c,2 and refer to the highest level mesh, coarsened by a high value of C_yz,3, as Q_c,3. Previously we have used T_cut to describe the extent of the reciprocal space pair potential applied to the finest mesh Q or the number of zero-padded pages in each of its slabs. When multiple coarse meshes are involved, we refer to the extent of the potential for the n^th mesh as T_cut,n and the coarsening factor for the n^th mesh as C_yz,n. (In principle, for the lowest level mesh, C_yz,1 = 1 and for the highest level mesh T_cut,L is not defined.) In a three-mesh scheme, convoluting the lowest and intermediate level meshes Q and Q_c,2 with an intermediate-ranged pair potential ${\theta }_{c,2}^{\left(\mathrm{rec}\right)}$ can be accomplished as a series of convolutions over slabs as was done for Q in previous MLE calculations. The slabs of the intermediate coarsened mesh, much less dense than Q, could be padded by a high value of T_cut,2 without adding greatly to the overall FFT computation or communication burden.

The MDGX program, but not the Matlab MLE calculator, was written to accommodate more than one level of mesh coarsening. We therefore tested the accuracy of MLE with several three-level mesh schemes on the cubic streptavidin system, as shown in Table 2. The performance of MLE in these three-level schemes is almost exactly what would be expected if the errors associated with separate two-level MLE calculations using the same parameters were combined.

Table 2. Multi-Level Ewald calculations performed with three mesh levels.

All calculations in this table pertain to the Streptavidin test case. Parameters for the equivalent SPME calculations included $I_y^{\left(\mathrm{pm}\right)}=I_z^{\left(\mathrm{pm}\right)}=4$, σ/μ = 1.439, L_cut = 5.578σ, and any parameters listed in the table pertaining to particular cases. I^(mm) was set to 8 for all MLE calculations. The values of σ, μ and L_cut in the first case are those obtained with the AMBER default settings for this system. All RMS errors listed in this table are uncorrelated: when examined in detail the Pearson correlation coefficients for the errors arising from distinct parts of the calculation are all smaller than 0.02.

Calc. Typea	σ	$I_x^{\left(\mathrm{pm}\right)}$	Cyz	Tcut	⟨ΔF(dir)⟩ b	⟨ΔF(rec)⟩ c	⟨ΔF(cor)⟩ d	⟨ΔF(ref)⟩ e
SPME	1.434	4			7.850	9.288		12.152
MLE	1.434	4	2	2	7.850	9.288	6.670	13.879
MLE	1.434	4	5	9	7.850	9.288	7.066	14.065
MLE	1.434	4	2,5	2,9	7.850	9.288	9.714	15.579
SPME	1.434	6			7.850	9.826		12.598
MLE	1.434	6	2	1	7.850	9.826	2.756	12.890
MLE	1.434	6	5	5	7.850	9.826	2.859	12.924
MLE	1.434	6	2,5	1,5	7.850	9.826	3.972	13.209
SPME	2.151	4			5.492	7.005		8.903
MLE	2.151	4	2	2	5.492	7.005	1.890	9.108
MLE	2.151	4	5	9	5.492	7.005	2.425	9.228
MLE	2.151	4	2,5	2,9	5.492	7.005	3.072	9.425

^aType of calculation

^bRMS error in the direct space forces on all particles, relative to a high-accuracy SPME calculation (× 1.0×10⁻³kcal/mol-Å)

^cRMS error in the SPME reciprocal space force (× 1.0×10⁻³kcal/mol-Å)

^dRMS MLE coarsening error (× 1.0×10⁻³kcal/mol-Å)

^eTotal RMS error of the SPME or MLE calculation (× 1.0×10⁻³kcal/mol-Å)

4.3 Energy Conservation and Equilibrium Properties in Simulations with Multi-Level Ewald

The accuracy of forces obtained by the MLE approximation are encouraging, but we must still test whether the type of errors introduced by MLE, which are of a different nature than the errors in direct or reciprocal space forces arising from a standard SPME calculation, are possibly detrimental in the context of simulations. We therefore used the MDGX program to simulate a system of 1024 SPC-Fw water molecules in the microcanonical ensemble. Two different MLE schemes were used, as described in Table 3, both of them with three mesh levels. Trajectories were propagated at a 0.5fs time step for 50ns each, and the MLE or SPME reciprocal sums were computed at every time step to provide a stringent test of energy conservation. Coordinates were collected every 0.5ps and energies arising from electrostatic, Lennard-Jones, and harmonic bond and angle terms were collected every 0.05ps.

Table 3. Parameters used in long-timescale simulations of SPC-Fw water, and the accuracy of forces resulting from each approximation.

The four simulations utilize either SPME or MLE calculations for long-ranged electrostatic interactions. While all simulations make use of the same direct space cutoffs, the “conservative” simulations use roughly 60% more data in Q for their SPME or MLE calculations. The “conservative” MLE scheme approximates the SPME results much more accurately than the equivalent SPME calculation obtains the true electrostatic force on each particle, as judged by a high-quality SPME calculation using g = (96×96×96) and I^(pm) = 8. In contrast, the “aggressive” SPME scheme is somewhat less accurate and the “aggressive” MLE scheme introduces roughly the same amount of error as the equivalent SPME scheme. Results from the simulations are presented in Figures 10 and 11 and Table 6.

Parameter	Conservative		Aggressive
	SPME	MLE	SPME	MLE
Lcut (LJ, Å)a	10.0	10.0	10.0	10.0
Lcut (Elec, Å)b	9.0	9.0	8.0	8.0
σ, Å	1.58	1.58	1.43	1.43
g	(24×36×36)	(24×36×36)	(21×32×32)	(21×32×32)
I (pm)	(6×4×4)	(6×4×4)	(6×4×4)	(6×4×4)
I (mm)		8		8
Cyz,2, Cyz,3		(2,4)		(2,4)
Tcut,1, Tcut,2		(1,5)		(0,4)
⟨ΔF(dir)⟩ c	4.9×10−3	4.9×10−3	7.7×10−3	7.7×10−3
⟨ΔF(rec)⟩ d	2.3×10−3	2.5×10−3	8.9×10−3	1.3×10−2

^aLennard-Jones potential truncation length

^bElectrostatic direct space trucation length

^cRMS error in direct space electrostatic forces with this approximation

^dRMS error in reciprocal space electrostatic forces with this approximation (including MLE approximation, if applicable)

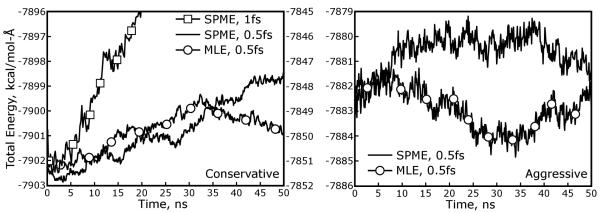
The evolution of the total energy of the 1024 water system, simulated using each of the four methods described in Table 3, is shown in Figure 10. For comparison, the energy of the same system run using the “conservative” SPME parameters but a 1fs time step is juxtaposed with the results at a 0.5fs time step. While all of the 0.5fs runs shown some upward drift in the energy over 50ns, it is very slow and the time step itself clearly has a much greater impact on the energy conservation than the choice of SPME or MLE for a long-ranged electrostatics approximation. Neither MLE approximation, whether “aggressive” or “conservative,” shows a visible difference when compared to the corresponding SPME calculation on the basis of energy conservation. Moreover, the differences between the two SPME methods are greater than the differences between the MLE approximations and the equivalent SPME calculations: while the axes in each panel of Figure 10 have similar scales, the energy of the system run with aggressive SPME and MLE parameters is somewhat higher and the fluctuation of the energy is noticeably larger. The reason for this increase in the recorded energy can be traced to the inaccuracies inherent in the SPME reciprocal space calculation when the σ to μ ratio becomes smaller, as explained in the Supporting Information for our previous work on Ewald sums.²² When run with the same aggressive SPME parameters, the MLE approximation returns similar increases in the absolute energy and fluctuations in that energy; adding more aggressive MLE parameters on top of the lower-quality SPME method does not seem to affect the results much further.

Figure 10. The Multi-Level Ewald approximation yields equivalent energy conservation to traditional Smooth Particle Mesh Ewald.

Simulations of a system of 1024 SPC-Fw water molecules show that MLE is able to conserve the system’s energy over 50 ns trajectories. Parameters for each simulation are given in Table 3, and the length of the time step or style of Ewald summation is given in the legend of each figure. In each simulation, the total energy of the system fluctuates because both Ewald methods entail some degree of error as the particles move relative to the mesh and the Lennard-Jones potential is sharply truncated at 10.5Å. The total energy is therefore plotted as a series of mean values averaged over 200 frames each. Many investigators consider the energy conservation yielded by a 1fs time step in systems with flexible bonds to hydrogen atoms acceptable. Comparison of the results obtained with a 1.0fs time step (results should be read from the y-axis on the right side of the left-hand panel) to those obtained with a 0.5fs time step shows that the time step itself can be a more significant contributor to the upward drift of the total system energy than many of the other parameters. (With the 0.5fs time step, the temperature drift in each simulation is only about 0.5K over 50ns.) As the quality of the SPME calculations decreases, the fluctuation of the total system energy increases, as evident by comparing the results for SPME simulations in each panel. The MLE approximation also reproduces these changes in the sizes of fluctuations in the total energy.

As shown in Table 4, the bulk properties of the SPC-Fw water are not significantly perturbed by any of the SPME or MLE approximations. When taken in the context of a macroscopic observable such as the heat of vaporization, the differences between the total energy of the system measured by aggressive or conservative electrostatic parameters are negligible.

Table 4. Bulk properties of 1024 water molecules simulated in the microcanonical ensemble.

All values are given as averages over 12.5ns blocks of each simulation, with standard deviations.

Property		Conservative		Aggressive
	PMEMD d	SPME	MLE	SPME	MLE
ΔHvap, kcal/mol a	10.89 ± 0.00	10.88 ± 0.00	10.88 ± 0.00	10.88 ± 0.00	10.89 ± 0.00
T, K b	289.07 ± 0.08	289.59 ± 0.14	289.65 ± 0.03	291.72 ± 0.13	291.79 ± 0.17
D, × 10−5 cm2/s c	1.81 ± 0.02	1.83 ± 0.04	1.86 ± 0.05	1.85 ± 0.08	1.83 ± 0.07

^aHeat of vaporization, calculated by ΔH^vap = −⟨E⟩+RT, where E is the mean potential energy, R is the gas constant, and T is the mean temperature

^bMean temperature of the simulation

^cDiffusion coefficient

^dResults obtained using the PMEMD implementation of the SANDER program from the AMBER software package, running SPME with the “Aggressive” parameters, but I^(pm) set uniformly to 4 and g set uniformly to 32

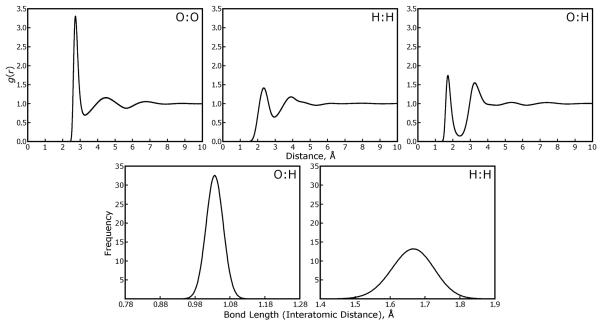
We also investigated the microscopic structure of the water when simulated with each approximation. One reason for choosing the flexible SPC-Fw water model was to test whether the MLE method, which produces its lowest accuracy when computing interactions between very nearby particles, could perturb the behavior of bonded atoms. (Although electrostatic interactions are excluded between bonded atoms in most molecular force fields, this exclusion is done by computing the interaction of two Gaussian-smoothed charges at the specified distance and subtracting this from the reciprocal space sum, which necessarily computes all interactions during the mesh convolution.) As shown in Figure 11, neither the MLE approximation nor the quality of the SPME method has any significant effect on either the oxygen:hydrogen bond length, the hydrogen:hydrogen distance within each water molecule, or the radial distributions of oxygen and hydrogen atoms on different water molecules.

Figure 11. The average structure of SPC-Fw water molecules is maintained under different Ewald approximations.

Analysis of the microscopic structure of the water molecules was performed to complement the energy conservation studies presented in Figure 10. Radial distribution functions for oxygen to oxygen, hydrogen to hydrogen, and oxygen to hydrogen atoms of SPC-Fw water molecules are displayed in the top three panels. Histrograms of the oxygen-hydrogen bond length and hydrogen-hydrogen intramolecular distance are shown in the lower two panels. Results from simulations with all four of the Ewald approximations listed in Table 3 are shown with solid black lines in each plot; the distributions overlap so precisely that they are indistinguishable.

The timings for these single-processor MLE runs also provide an indication of how much more computational effort MLE would require over the standard SPME method. The fact that simulating the 1024 water molecules requires only 6-10% longer with MLE than with SPME indicates that most codes with well-optimized FFT routines could implement MLE without much more computational effort than SPME. Notably, while the MLE schemes are more costly in terms of FFT work, the majority of the extra cost actually comes from the mesh ⇋ mesh interpolation. The FFTW libraries used by MDGX are among the fastest available, but as shown in Table 5, many other aspects of the MDGX code are not as efficient as their counterparts in PMEMD. (We are looking into compiler optimizations that may make the difference, as we believe we have coded routines such as the particle ⇋ mesh interpolation as efficiently as possible and there appears to be little difference between the structure of our routines and those of PMEMD.) The estimates presented in Table 5 do not include the cost of computing FFTs over zero-padded regions of each MLE slab or the possible benefits of performing numerous FFTs over small regions rather than one large FFT; instead, a single convolution over a single mesh is done at all levels of the calculation in these single-processor runs. The estimates in Table 5 also neglect some possible benefits in the case of the “aggressive” MLE parameters. Setting T_cut,1 = 0 permits convolutions of the lowest level mesh to be completed with two-dimensional FFTs, saving roughly 1/3 of the FFT work for that mesh level. We are continuing to develop the MDGX program to take advantage of these optimizations.

Table 5. Timings for MDGX or PMEMD on a single processor.

20000 steps of dynamics were run using PMEMD or MDGX in SPME or MLE mode on an Intel Q9550 processor (Core2 architecture, 6MB L2 cache, 2.83GHz clock speed). Simulations made use of the parameters in Table 6; the PMEMD simulation for the “aggressive” parameters used I^(pm) = 4 and g = 32. Timings for different categories of calculations in the MDGX code were measured using the UNIX gettimeofday() function; those in the PMEMD code were measured with PMEMD’s internal profiling functions. Because the two programs are structured differently, the exact content of each category of calculation may not match exactly—for instance, MDGX and PMEMD use different styles of pair list, and the convolution kernel is computed more rapidly in MDGX than PMEMD because PMEMD always computes virial contributions while MDGX skips them if they are not needed. Total run times for both programs are greater than the sums of all categories in each column because timings for miscellaneous routines are not listed. Standard deviations were collected over ten trials to estimate errors in the timings; they were less than 1% across all categories, but are omitted to condense the table.

Routine	Conservative		Aggressive
	SPME	MLE	PMEMD	SPME	MLE
Bonded Interactions	5.8	5.9	4.6	5.8	5.8
ΔE(dir), Pair List	7.7	7.9	31.3	7.7	7.8
ΔE(dir), Interactions	383.9	383.6	216.7	323.8	323.9
ΔE(dir), Total	391.6	391.6	248.0	331.5	331.7
ΔE(rec), B-Splines	14.3	14.4	2.6	14.2	14.3
ΔE(rec), Particle → Mesh	16.2	16.4	6.0	15.9	16.1
ΔE(rec), Convolution a	2.4	1.2	11.6	1.7	0.8
ΔE(rec), FFT	17.3	22.6	28.4	9.1	11.8
ΔE(rec), Mesh → Particle	22.5	22.6	11.1	22.2	22.3
Mesh ⇋ Mesh b		42.1			29.0
ΔE(rec), Total	72.8	119.3	59.8	63.1	94.2
Total Wall Time	473.1	522.5	316.1	405.9	435.6

^aMultiplication of the charge mesh and reciprocal space pair potential in Fourier space

^bInterpolation between different levels of MLE mesh

5 Discussion

5.1 Development of Multi-Level Ewald for parallel applications

We do not yet have a parallel version of MDGX to run Multi-Level Ewald on many processors. However, we believe that MLE can benefit massively parallel simulations, particularly when extremely powerful, multicore nodes must be connected by comparatively weak networks, when other forms of network heterogeneity are involved, or when the problem size is very large. With MLE, there are extra communication steps as the coarse meshes must be assembled and the electrostatic potential data deposited in the zero-padded “tails” of each slab must be passed to neighboring slabs. However, because these are all local effects the number of messages that must be passed to create the coarse meshes and contribute $U_c^{\left(\mathrm{rec}\right)}$ to U^(rec) is bounded, whereas the number of messages that must be passed in a convolution involving the whole P³M reciprocal space mesh grows, at best, as the square root of the number of processors. ²⁶ For example, distributing the convolution for a 60 × 90 × 90 mesh in the streptavidin test case over six multicore nodes would require each node to transmit at least 0.65MB (megabytes) of data (if data is transmitted in 32-bit precision). With a three-level MLE scheme placing one fine mesh slab and one intermediate mesh slab on each node and setting C₂ = 2, T_cut,1 = 0, C₃ = 5, T_cut,2 = 5, the total volume of data transmission between nodes could be reduced nearly four-fold, to 0.19MB, in the convolution step.

Several challenges remain to implementing MLE in an efficient parallel code. The most obvious is load-balancing: MLE introduces another layer of complexity for scheduling the completion of coarse mesh convolutions, plus the associated mesh ⇋ mesh interpolation. Another challenge is that, while MLE can be tuned to reduce data transmission between weakly connected processors, if many networked nodes must collaborate on each MLE slab, the original data communication problems resurface. Whereas each of K nodes must pass 4 × sqrt(K) messages in the original P³M convolution, with MLE and P slabs with K ⪢ P the number of messages is 4 × sqrt(K/P) + M (for nodes devoted to fine mesh calculations) or 4 × sqrt(K)/C + M (for K/C² nodes devoted to coarse mesh calculations), where M is a small constant for mesh ⇋ mesh interpolation. One possible extension of the MLE method may be helpful for the case of many (multicore) nodes collaborating on each MLE slab: subdividing the convolutions over fine mesh pages into pencils using an analogous sharp, anisotropic splitting technique, and then applying a one-dimensional coarsening to meshes spanning each MLE slab.

5.2 Application to Multiple Time Step Algorithms

The different mesh levels in MLE calculations may be excellent candidates for updates at different time steps, particularly because the anisotropic splitting completely captures local changes to a molecular system’s electrostatics in the lower charge mesh levels. In contrast, the highest level charge mesh requires the most communication between processors devoted to disparate regions of the simulation cell, in order to complete the global convolution. The novel splitting approach of MLE may create its own unique types of artifacts in such simulations, however. We have shown that the sum of contributions from all mesh levels can recover a smooth potential, but this may be perturbed if the electrostatic potential of each mesh level is updated at different times. With any multiple timestep method there can be subtle resonances that affect the statistical properties of the system;²⁷ we intend to investigate the stability and efficiency of MLE with multiple time steps in the future.

5.3 Application to Systems With Two-Dimensional Periodicity

While periodic boundary conditions in three dimensions have been shown to be equivalent or superior to alternative boundary conditions for many condensed-phase biomolecular simulations,^28,29 there are classes of problems, notably membrane protein simulations, ³⁰ that produce different results if periodicity is suppressed in one dimension. Regular Ewald methods are available for imposing two-dimensional periodicity,^31,32 but they are prohibitively expensive for systems of many thousands of atoms. For larger systems, a pseudo-two-dimensional periodicity may be imposed by lengthening the simulation cell in one dimension, say $\widehat{x}$, confining the system to the middle of the simulation cell along $\widehat{x}$ by some stochastic boundary condition or, more directly, by a physical set of walls such as sheets of platinum atoms, and then running P³M calculations as usual, with three dimensional periodicity, on the extended system.³³ This approach has been further refined by adding an electrostatic field to counteract the net dipole of the system in $\widehat{x}$,³⁴ mirroring the way in which modified potential functions and zero-padding have been used in plasma physics and astrophysical gravity calculations.³⁵

The MLE method may be suitable for systems with two-dimensional periodicity, although membrane protein simulations run in the isothermal-isobaric (NPT) ensemble tend to require anisotropic system rescaling which MLE cannot accomodate exactly. It is likely possible to extend the MLE method to work in such cases by storing a small array of pre-computed solutions of each mesh potential with different unit cell ratios and thereafter interpolating the solution for any particular time step. Other, more general, solutions to the problem of isolated boundary conditions are again found in Adaptive P³M methods,^14,15,16,36 and the Multilevel Summation method.^37,38 In all of these approaches, the advantage for isolated boundary conditions in one or more dimensions is that only the coarse mesh must be evaluated in the zero-padded, empty regions of the simulation cell.

5.4 Diversity of problem decompositions for future machines

In conclusion, we have shown that, for pairwise potentials that decay as the inverse distance between particles it is feasible to subdivide the convolution in particle ⇋ mesh calculations sharply and anisotropically into many separate slabs without significantly adding to the overall cost of the calculation. This technique and the many smooth splitting approaches that already exist should be applicable to simulations on current and nextgeneration parallel computers, where hundreds to thousands of processors must collaborate in order to deliver longer simulation trajectories. It is worthwhile to develop a variety of these multi-level decompositions, as future supercomputers may come in come in novel architectures that offer huge advantages depending on the details of the parallel algorithm.