Plithotaxis and emergent dynamics in collective cellular migration

Abstract

For a monolayer sheet to migrate cohesively, it has long been suspected that each constituent cell must exert physical forces not only upon its extracellular matrix but also upon neighboring cells. The first comprehensive maps of these distinct force components reveal an unexpected physical picture. Rather than showing smooth and systematic variation within the monolayer, the distribution of physical forces is dominated by heterogeneity, both in space and in time, which emerges spontaneously, propagates over great distances, and cooperates over the span of many cell bodies. To explain the severe ruggedness of this force landscape and its role in collective cell guidance, the well know mechanisms of chemotaxis, durotaxis, haptotaxis are clearly insufficient. In a broad range of epithelial and endothelial cell sheets, collective cell migration is governed instead by a newly discovered emergent mechanism of innately collective cell guidance – plithotaxis.

Cellular motility within complex multicellular systems

In essential physiological functions including morphogenesis, wound healing, and tissue regeneration, the prevalent mode of cellular migration is collective. Collective cellular migration is also recognized as being an ubiquitous mechanism of invasion in cancers of epithelial origin. Indeed, virtually all living tissue is constructed and remodeled by collective cellular migration [1]. During morphogenesis, for example, the complex architecture of branched organs such as lung, kidney, pancreas, and vasculature is shaped by collective migration of sprouting vessels and ducts [2, 3]. In other developmental processes, clusters of cells are first specified at one location but then travel long distances to the location where they carry out their ultimate biological function. In the case of oogenesis in Drosophila, for example, the border cell cluster squeezes though nurse cells to migrate cohesively from follicle to oocyte [4]. Similarly, the lateral line sensory machinery of the zebrafish is deposited by a primordium comprising roughly 100 cells that travels the entire anterior-posterior axis of the embryo [5].

Some of these morphogenetic mechanisms are recapitulated in postnatal life to repair injured tissue [6]. Reepithelialization during wound healing, for example, involves the collective migration of epithelial cells and fibroblasts onto and through a denuded basement membrane. To provide oxygen and nutrients to newly assembled tissue, a tip cell guides collective migration of sprouting capillaries into the wounded region.

Collective cellular migration plays a role not only in development, physiology, and repair, but also in devastating diseases including cancer. In the vasculature and lymphatics of cancer patients, increasing evidence now points to the existence of clusters of metastatic cells that invade collectively [7, 8]. Collective invasion processes are also evidenced in histopathological sections of a broad diversity of differentiated carcinomas in which the primary tumor is surrounded by secondary cancer cells that take the form of clusters, chains, and sheets [9].

If complexity is an essential feature, how much is enough?

Because of its importance to so many branches of biology, the question of collective cellular migration has been studied for a long time, at multiple levels, and in many different experimental model systems. For the particular questions at issue in this review, the intercellular forces that arise when only two or three cells interact in vitro [10–12] are of substantial interest even though such systems are not sufficiently complex to demonstrate the emergent phenomena described below. Of greater interest, in principle, would be the distribution of intercellular forces in migrating cell sheets or clusters in vivo, but these distributions are not yet measurable. Accordingly, we focus here on the intermediate situation of the extended epithelial or endothelial cell sheet in vitro. Such systems are sufficiently simple that one can measure the distribution of physical forces that guides collective cellular migration, as described below, but are sufficiently complex to reveal new phenomena and physiological mechanisms.

In connection with such model systems in vitro, the traditional scratch wound-healing assay initiates collective cellular migration by the sudden creation of free space together with the creation of injured cells near the denuded boundary and, in most cases, the simultaneous creation of a spatial gradient in composition of extracellular matrix, ECM [13, 14]. It is perhaps not surprising that injury to boundary cells and gradients in ECM composition have profound effects upon the monolayer migration, but newer methods have shown that free space – without creation of cellular injury or gradients in ECM composition – is sufficient to initiate collective cellular migration [15–19]. Although cell injury and/or gradients of ECM composition lead to different initial conditions, boundary conditions, and, potentially, different mechanisms of cellular migration, the simpler situation in which collective migration is not complicated by these factors comprise the focus of this review.

The hidden hand

Collective cellular migration in a wide range of circumstances tends to be regulated by the same extrinsic cues that guide single cells in isolation, but these cues ordinarily act on but a small subset of cells that in turn guide naïve followers [1, 20]. But how does this subset within the motile group guide its global motion? The notion of a relay of guidance molecules is well studied, and it has it been suggested that the direct transmission of physical forces from cell-to-cell can be transduced locally and then used as a signaling cue to guide local motion [21]. In addition, these same physical forces might act to steer local cellular motions mechanically [21]. While it seems certain that group migration is regulated in some fashion by the combined influences of extrinsic cues, cell-cell signaling, and local mechanical cell-cell interactions [20], for more than a century this question has been the subject of confusion and controversy [22, 23] and the underlying physical picture has remained rather unclear.

In the literature, the prevalent physical picture is that cells at the leading edge of the sheet – the so-called leader cells – are specialized to generate active physical forces that drag along the cells that follow passively behind, much as a train locomotive is specialized to drag along the many passive carriages that follow. Indeed, a broad body of observations support the idea that, compared with the follower cell, the leader exhibits systematic functional and structural differences in adhesiveness, protrusion, polarization, and cytoskeletal organization that are consistent with a role specialized for pulling [24]. With a physical picture based upon leader cells pulling from the front, it follows logically that passive followers could only be in a state of mechanical tension.

Nonetheless, improved microscopy techniques now demonstrate that cells located many rows behind the leader extend cryptic lamellipodia beneath cells in front of them [25]. Based upon those structural observations, many have inferred that sub-marginal cells may play an active role in driving cell sheet motion. Moreover, mathematical models in which each cell is regarded as being self-propelled are able to capture with reasonable accuracy some of the dynamics of the advancing cell sheet [26, 27], suggesting that global motion of the group may be a simple consequence of the self-propelled motion of each of its individual constituent cells, much as each automobile advances in traffic, as each fish swims in a school, or as each bird flies in a flock. In such mathematical models, each actor undergoes independent random motion, or independent random motion with directed drift in a manner analogous to directed diffusion. As in automobile traffic, fish schools and bird flocks, a physical picture of collective cellular migration based upon independent actors that are each self-propelled implies that the average mechanical stress transmitted from cell-to-cell within the sheet must be zero.

Still a different physical picture is that the leading edge is not at all dragging follower cells along, but rather is being pushed forward by the pressure created by cell proliferation in the ranks far behind. This mechanism has long been assumed to be the mode of expansion for proliferative tissues such as epidermal sheets or tumors [28]. Such a pressure is a compressive stress – similar in kind but opposite in sign from mechanical tension [29].

Each of these three alternative physical pictures is widely invoked in the literature and corresponds to one of three competing schools of thought. But no matter how plausible each may seem, or how strong the structural or biochemical evidence might be, these alternatives are mutually exclusive. At any given position at any given time, the mechanical stress at the cell-cell junction can be positive (tensile) or negative (compressive) or zero, but logically cannot be all three at once. And yet another distinct possibility is that the cell-cell junction might also support mechanical shear stress (Box 1); compression and tension are stresses exerted normal to the surface (although with opposite signs) whereas shear stress is exerted tangent to the surface. Because it had been impossible to measure these forces in a direct manner, the question stood unresolved and each different school grew to favor its own interpretation. The reason that discrimination has been difficult is that molecular manipulations together with imaging can be used modulate monolayer behavior in specific ways, and thereby provide pivotal clues, but by themselves do not measure stresses transmitted across the cell-cell junction. In this connection, tissue recoil after focal laser ablation has been an important finding because it establishes evidence that virtually every tissue exists in a state of tension [30–32], but is also somewhat limited because it does not provide model-independent maps of the distinct stress components within the monolayer and because its invasiveness precludes time-lapse studies. The transduction of shear stresses applied to the luminal surface of endothelial monolayers, as by flowing blood, is well studied [33], but the role of shear forces applied by one cell on its neighbor remained virtually unstudied.

Box 1: Mechanical stress comes in two flavors: shear stress and normal stress.

At each point of the cell-cell junction (panel A below) there exist two independent components of mechanical stress: a normal stress (green arrow perpendicular to the surface, which can be tensile or compressive) and a shear stress (panel B below; orange arrow tangent to the surface). The shear stress is the force per unit area that one cell exerts on its neighbor in the direction parallel to the local tangent of the junction. Continuum mechanics shows that for each point in the medium there always exist two directions for which the shear stress vanishes. These directions are mutually orthogonal, moreover, and describe the two directions along which normal stress is maximal and minimal, respectively.

When cell-cell junctions are intact, but not when they are disrupted, cells within the monolayer tend to migrate in the direction in which the normal stress is greatest and the shear stress least [24]. This phenomenon is called plithotaxis and implies that the cell-cell junction and associated cytoskeletal structures are incapable of bearing appreciable shear stress or, alternatively, that they actively remodel so as to minimize the shear stress. In either case, it remains equally unclear to what extent plithotactic cellular motion is a response mediated through the agency of mechanosensation or instead is a direct mechanical response of the cell to physical forces applied.

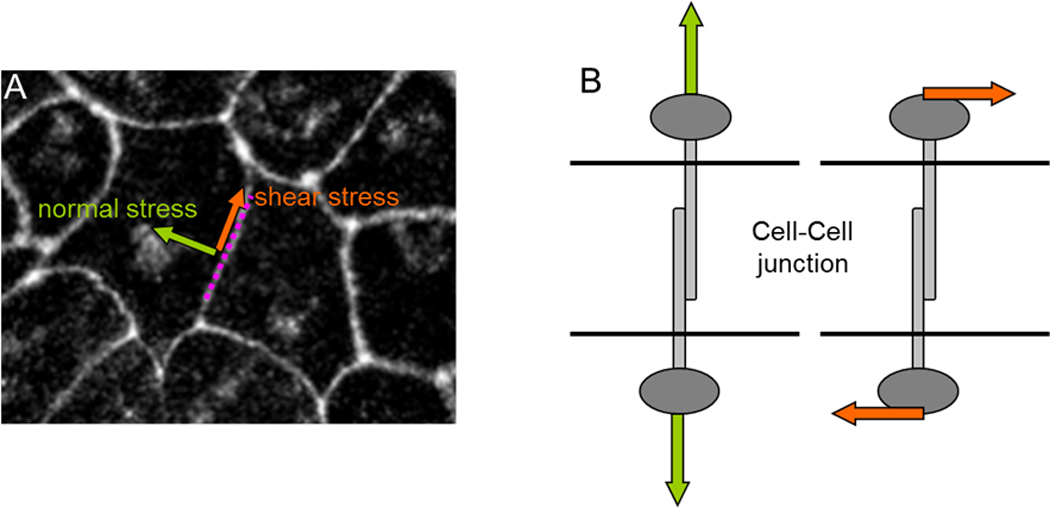
Newton was the first to recognize the simple but inescapable fact that the motion of any object cannot be fully understood except in the context of forces. Investigation of the governing relationship between motions and forces is called the field of mechanics. If mechanistic understanding of cellular motions is our ultimate goal – but the governing forces themselves remain invisible – Newton tells us that within that blind spot there is ample opportunity for conflicting interpretations to arise, and he tells us further that these conflicts cannot be resolved rationally. Distinguishing between plausible alternative interpretations can be resolved only with the measurement of the local forces themselves.

Making traction forces visible

The first direct measurements of traction forces exerted beneath an advancing cell sheet were obtained using micropillar assays [34] and, more recently, using traction microscopy [17]. With either approach, experiments clearly demonstrate that cells at the leading edge do indeed pull on their substrate in a direction consistent with pulling forward cells in the ranks behind, thus ruling out the notion that the leading monolayer edge is pushed forward by a compressive stress. Nonetheless, these experiments also show that traction forces are not at all restricted to the leading edge or even to a few rows immediately behind. Instead, cells located far behind the leading edge generate traction forces with magnitudes only somewhat smaller than those generated by specialized leader cells [17]. Indeed, these results show that, on balance, leader cells may be a bit more forceful but their overall contribution to cellular tension in the ranks behind is altogether trivial, the simple reason being that in the global tug-of war that causes the monolayer to advance the leader cells are vastly outnumbered (Figs. 1 and 2). While these leader cells do play important roles in local guidance and signaling [35], data show unequivocally that their contribution to this mechanical tug-of-war has been over-stated [17].

Fig 1.

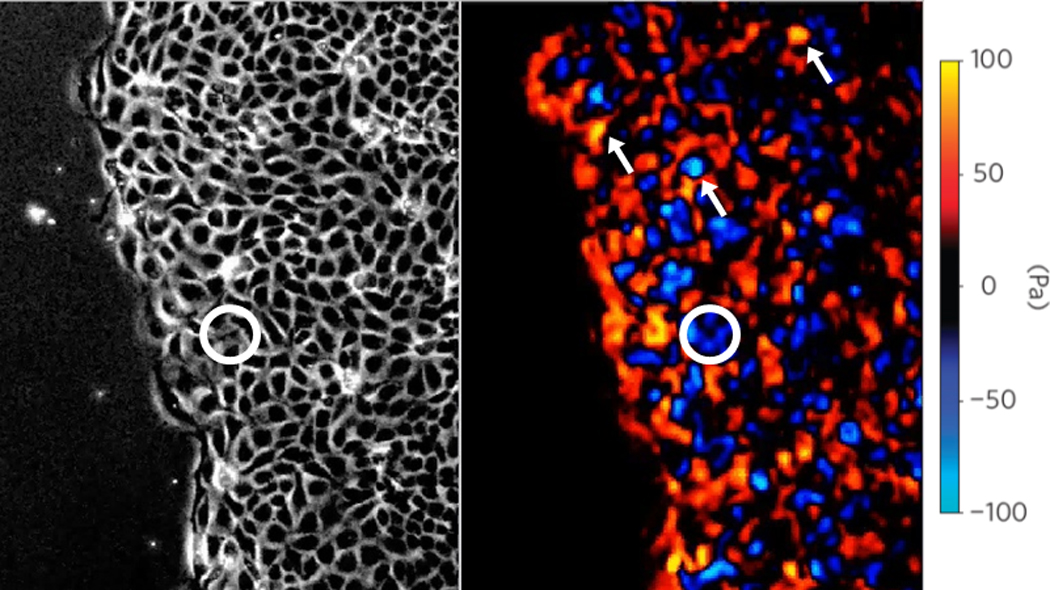
Traction forces exerted by an MDCK monolayer upon its substrate in the direction perpendicular to the leading edge. Spatial distributions of tractions are heterogeneous, and extreme mechanical events (cells generating very large tractions such as those pointed by arrows) are frequent both at the leading edge and many rows behind it. The circle encloses one of the many cells that appear to be pulling the “wrong” way. Adapted from [17] with permission from Nature Physics.

Fig 2.

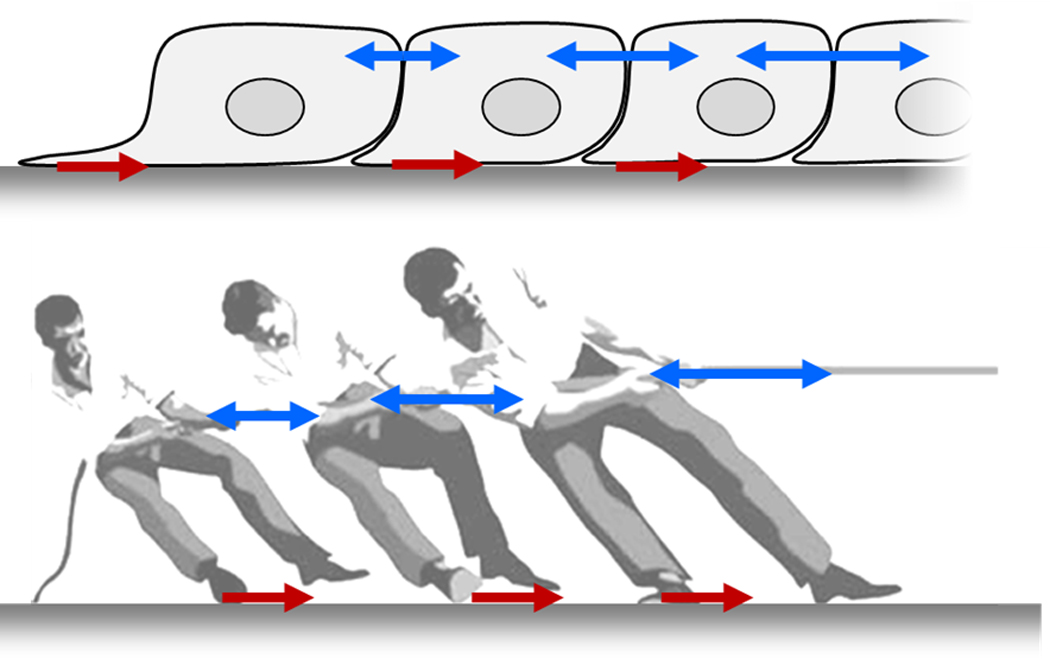
Cells use a tug-of-war mechanism to integrate local tractions (red) into long-ranged gradients of intra- and inter-cellular tension (blue). Tension in the monolayer reflects the spatial accumulation, or pile-up, of traction forces. Equivalently, the local traction force is the spatial derivative of the intercellular stress.

We consider now in greater depth the nature of the intercellular physical forces that are at work within the monolayer, and then return to the question of the mechanisms that might guide its motion and growth.

Dynamic heterogeneity: The median is not the message

With each cell of the continuous monolayer sheet being attached tightly to its substrate by adhesion molecules, being attached tightly to each neighboring cell by junctional proteins [36], and advancing systematically forward toward the leading edge, we had anticipated that the underlying pattern of traction forces that drives these motions would be comparably smooth, stable, and systematic, allowing of course for some modest degree of random biological noise. Observations show precisely the opposite. On a cell-to-cell scale, the biological ‘noise’ far exceeds what one might have thought to be any smooth and systematic ‘signal’ (Fig. 1, right panel). Traction forces are strongly heterogeneous and fluctuate dramatically both in space and in time [17]. This heterogeneity is a dynamic heterogeneity, therefore, and cannot be tied to any one cell, to any one region, or to any one moment. Rather, traction forces flicker on and off, here and there, in this direction and that, in a wild and chaotic dance.

Indeed, if the forces that drive cell division are imagined to be orchestrated quite precisely as in an orderly minuet, then the forces that drive collective cellular migration are closer to those experienced in a mosh. Deep below that chaos are buried small systematic variations to be sure, but unless averaged over a great many cells these systematic variations are almost indiscernible. Only over a scale of hundreds of cells, for example, does it become clear that traction fluctuations are biased with a median value that is only slightly different from zero so as to pile up tensile stresses within the monolayer in a systematic fashion that acts to pull toward the leading edge [17].

At any finer scale of resolution, however, chaos reigns. And if it is not bad enough that traction forces are profoundly heterogeneous, and that those heterogeneities are dynamic, closer examination shows that the statistical distribution of these fluctuations are strange, by which we mean that traction fluctuations depart systematically and dramatically from any Gaussian distribution [17, 37], as do cellular velocities [38]. Instead, they are governed by an anomalous distribution (exponential) that, compared with a Gaussian distribution, shows extreme traction fluctuations occurring far more frequently – orders of magnitude more frequently – than would be expected based upon the skinny tail that is characteristic of any Gaussian distribution. The observed distribution has a fat tail, in other words, implying that extreme force hotspots occur with a frequency that is unexpectedly high (Fig 1b). At the level of the traction force that the cell exerts on its substrate, anomalous statistical behavior such as this tells us that underlying cellular mechanisms must differ in a fundamental manner from independent random variation. There is more at work than just biological noise, therefore, because the central limit theorem demands that large collectives of independent random processes, no matter how complex, must always give rise in the end to Gaussian statistics. The hidden hand – the traction forces that drive collective cellular migration – we now understand to be a shaky one indeed. Its statistics tells us, further, that such shaking cannot be thought of as arising from any collection of independent random processes. Instead, beneath this chaos there is at work strong intercellular cooperativity. But how does that cooperativity come about?

Making intercellular forces visible

For any given cell within a monolayer, defining comprehensively the forces at work requires knowledge not only of the traction force exerted by that cell upon its substrate, but also the forces exerted at its boundaries with adjacent neighbors at cell-cell junctions (Fig. 2a). Measurement of these forces at cell-cell boundaries, as well as stresses borne within the cell body, is now accessible. Monolayer Stress Microscopy (MSM) starts with the traction forces at the cell-substrate interface of a monolayer cell sheet [17] and then uses a straightforward balance of forces to measure the distribution of physical forces at every point within that monolayer [18]. The reasoning behind this technology is illustrated by a simple tug-of-war (Fig 2b); if all traction forces at the player-ground interface are known, then by Newton’s laws the state of stress everywhere in the rope is easily determined. Indeed, if the traction forces are known, then in order to define the local state of stress borne by the rope one does not need to know if the rope is soft or stiff, elastic or viscoelastic, uniform or non-uniform, or even linear or non-linear. In much the same way, MSM does not require assumptions about the mechanical properties of the monolayer itself. MSM does assume, however, that attention is restricted to regions interior to the optical field of view wherein the influences of distant regions (i.e. outside the optical field of view) are minimal, and that forces within the monolayer are everywhere in balance as demanded by Newton’s laws.

Taken together, tractions and intercellular stresses now rule out definitively the notion of a bimodal distribution of cell mechanical behaviors, with one mode corresponding to leader cells and the other to followers. These data rule out as well the notion of the leading edge advancing by means of a compressive stress pushing it forward. And while each cell does indeed have the capacity to be mechanically self-propelled, these data show that the forces that these cells generate, and the motions that they undergo, depart dramatically from the notion of independent random process, as in diffusive motions or even diffusion with drift. Instead, the forces at work, and the motions that they create, are strongly heterogeneous but at the same time are also strongly cooperative [18].

A rugged stress landscape emerges from cooperative stress pile-up

Like maps of traction forces beneath epithelial or endothelial cell sheets, maps of inter- and intra-cellular stresses also reveal a physical picture that is dominated by dynamic heterogeneity. But because the intercellular stress is essentially a spatial integral, or accumulation, of the traction forces (Fig. 2), the length scale of its fluctuations is longer and the time scale of its fluctuations is slower [18]. Even though structure is relatively homogeneous, mechanical stresses within the monolayer define a landscape that is rugged, with stresses fluctuating abruptly both in space and in time (Fig. 3).

Fig 3.

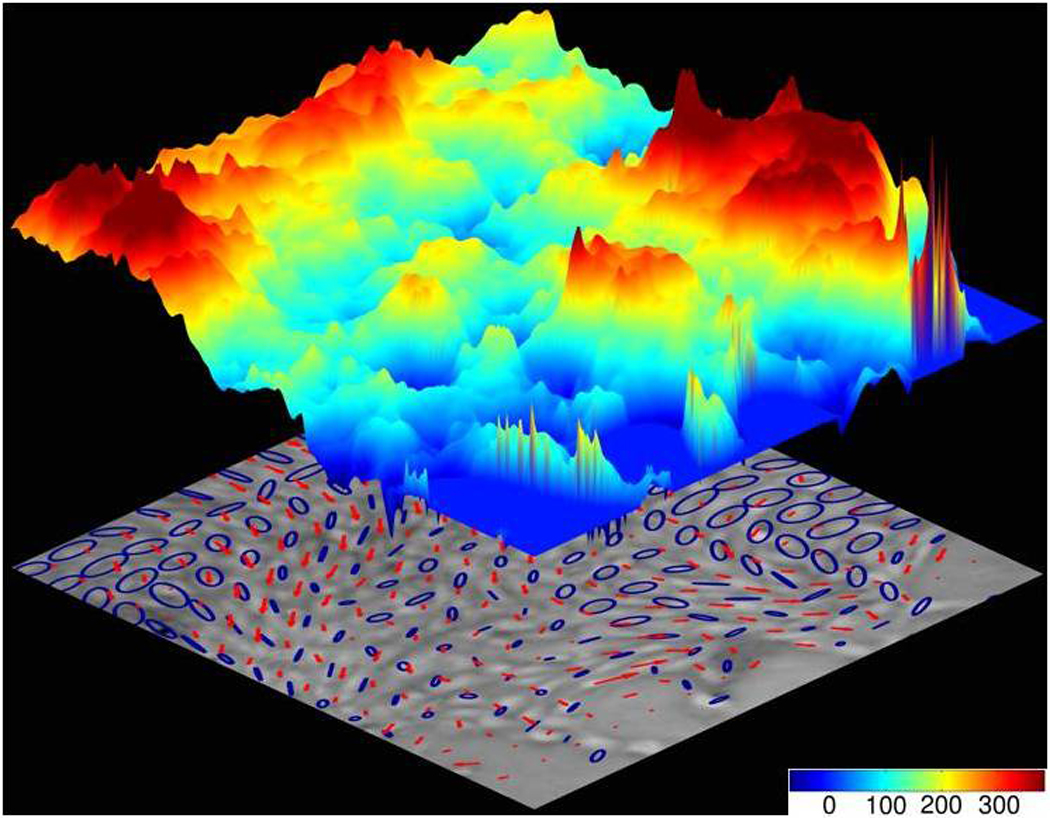
Fragile cells [47] trekking rugged stress landscape make for resilient monolayers. Cellular migrations (red arrows) follow stress orientations (blue ellipses) over a rugged stress landscape (colored topography denotes local tensile stress; scale bar units: Pa). Cell navigation on this scale – plithotaxis – is innately collective, strongly cooperative, and dynamically glassy. Adapted from [18].

Like a hiker trekking the Himalayas, the constituent cell trekking the monolayer must navigate a stress landscape that is severely rugged. But unlike the hiker, the constituent cell also contributes appreciably to that landscape and actively remodels it. Moreover, the stress fluctuations that the cell encounters, and the stresses that it generates actively, are comparable in magnitude to the shear modulus of the cell itself. As such, the scale of cellular deformations observed during the cell trek are expected to be comparable in magnitude to cell dimensions, and strains are therefore expected to be large. As such, the cell not only contributes to that stress landscape but also must sense it and respond actively to it. Resulting fluctuations of intercellular stress are coherent over multiple cell diameters, thus revealing the cooperative transmission of forces from cell to cell across numerous intercellular junctions. Analysis of stress correlation reveals characteristic relaxation times of roughly 5–30 minutes and characteristic distances of force transmission of roughly 10–20 cell diameters, although some stress fluctuations expand to span the entire cell monolayer [17, 18].

Collective cell guidance

For the single cell in isolation to undergo directed migration, it must follow chemical or physical gradients. As a central part of the immune response, for example, the crawling neutrophil will follow the gradient of signals released by target pathogens or damaged cells (chemotaxis) [39]. Similarly, a cell that encounters a gradient in adhesion will tend to crawl up the adhesion gradient (haptotaxis), and a cell that encounters a gradient in substrate stiffness will tend to crawl up the stiffness gradient (durotaxis) [40].

Cells migrating collectively are likely to use similar guidance mechanisms, but the ability of each cell within the moving group to interact physically with its immediate neighbors provides the cell within additional mechanisms of guidance, and those mechanisms appear to be quite potent. For example, the small cell cluster circled in Fig. 1 is generating large traction forces directed so as to pull those cells to the right, but somehow, nonetheless, they are being swept to the left. Another example is migration of the neural crest cell, which has been shown to follow a gradient of the chemokine sdf1a, but only when cell-cell junctions are intact [41]. In addition, cells at the leading edge of a group can synthesize, degrade, or deform the surrounding matrix to influence the dynamics of their followers. Similarly, mesoderm cells have been shown to require cell-cell adhesion to undergo collective and directed migration during gastrulation in zebrafish [42]. These findings point to the existence of an integrative mode of guidance that is inherently collective, but the mechanism has remained obscure.

Plithotaxis

How are we to explain the motion of the individual cell navigating within the stormy monolayer? A mechanism was recently described by which collective cell guidance is mediated by the direct transmission of physical forces across cell-cell junctions [18]. From a map of the complete stress field within and between cells comprising the monolayer, the direction in which normal stresses (i.e. perpendicular to a surface) are maximal and minimal, respectively, can be determined; in engineering mechanics these are called maximal and minimal principal stresses and the corresponding principal orientations. These special stresses and orientations show the stress field to be quite anisotropic (this anisotropy is depicted by the ellipses in Fig. 3). Within this anisotropic stress field there exists a strong and systematic tendency for a broad range of epithelial or endothelial cell types to migrate preferentially along the orientation of the local maximal principal stress [18]. Importantly, along principal orientations the shear stress is necessarily zero, implying that cell-cell junctions either remodel actively so as to minimize shear stress or are unable to support shear stress (Box 1; Glossary). Moreover, the correlation between the orientation of the maximal principal stress and that of cellular velocity is greatest in regions were stress anisotropy is strongest. But when cell-cell junctions are disrupted using calcium chelation or anti-cadherin antibodies, cells no longer move along the orientation of the maximal principal stress. Similarly, in epithelial cell lines expressing weak or non-existent levels of cell-cell junctional proteins, the relationship between migration orientation and stress orientation is abrogated. For cells to follow the direction of maximal principal stress, therefore, they need to be connected to one another mechanically. As such, this mechanism of collective cell guidance is an emergent property of the cell group, but unlike flocking of birds or schooling of fish, it requires direct mechanical cell-cell contacts and force transmission across those contacts. This collective tendency for each cell comprising the sheet to steer along the local orientation of maximal principal intercellular stress, or, equivalently, minimal intercellular shear stress, is called plithotaxis [18], from the Greek πλήΘος denoting crowd, swarm, or throng. But the extent to which plithotaxis might act in synergy with chemotaxis, haptotaxis, and durotaxis remains an open question.

Plithotaxis, crowding, and soft glasses

Anomalous behaviors of the kinds described above, taken together, are strongly reminiscent of what physicists call non-equilibrium matter [43], the paradigm of which is the special class of materials called soft glasses [43, 44]. Soft glassy matter is typified by its ability either to flow or to solidify depending upon conditions of particle repulsion, particle attraction, and mutual crowding. Such matter can solidify or jam, however, without undergoing the structural ordering that always accompanies solidification of equilibrium matter. Glassy matter is innately malleable but messy, therefore, and remains poorly understood. Glassy behavior is virtually ubiquitous in nature, subsuming molecular and polymeric liquids, granular media like sand and powders, colloidal suspensions, foams and pastes, plastics, metallic alloys, and even the cytoskeleton of the living cell [45–48]. In the context of the dynamics of the living monolayer, what can we learn from the dynamics of inert glasses?

To answer that question we start with perhaps the most intuitive example of a glass-forming system, which is a dispersion of uncharged, micron-sized, rigid spherical particles suspended in a simple liquid. If the fraction of the volume that is occupied by particles is small, then each particle is able to diffuse freely and independently of the others, and fluctuations follow statistical distributions that are Gaussian [49]. When the volume fraction of particles increases sufficiently, however, the motion of each particle can become progressively constrained, or caged, by the presence of its neighbors. And with more crowding still, a particle is unable to move outside its cage unless many of its neighbors cooperate so as to rearrange collectively; the system becomes cooperative, in other words, and clustered motions emerge (Box 2) [50]. And even though all particles are precisely identical, dynamic heterogeneity dominates the landscape [43] and is governed by statistical distributions with fat tails. As the volume fraction is increased further still, the number of particles that must rearrange for any single particle to move expands dramatically, the size of mobile clusters increases to span the system boundaries, and the system ultimately freezes. This behavior is called kinetic arrest [51].

Box 2: Dynamic heterogeneity in inert and living matter.

With increasing overall density of constituent inert particles, spontaneous local motions become progressively more heterogeneous. This heterogeneity is not structural in nature, therefore, but rather dynamic; while the structure of the system remains relatively homogeneous the velocity field becomes markedly heterogeneous. Moreover, for reasons that remain the subject of investigation, faster particles cluster together cooperatively, as do slower particles (panel A). These dynamic heterogeneities mark the onset of the glass transition.

With increasing density of constituent cells within the living monolayer, spontaneous motions exhibit dynamic heterogeneities of much the same kind [43,53]. With increasing cellular density, faster cells cluster together and the average cluster size increases. (panel B).

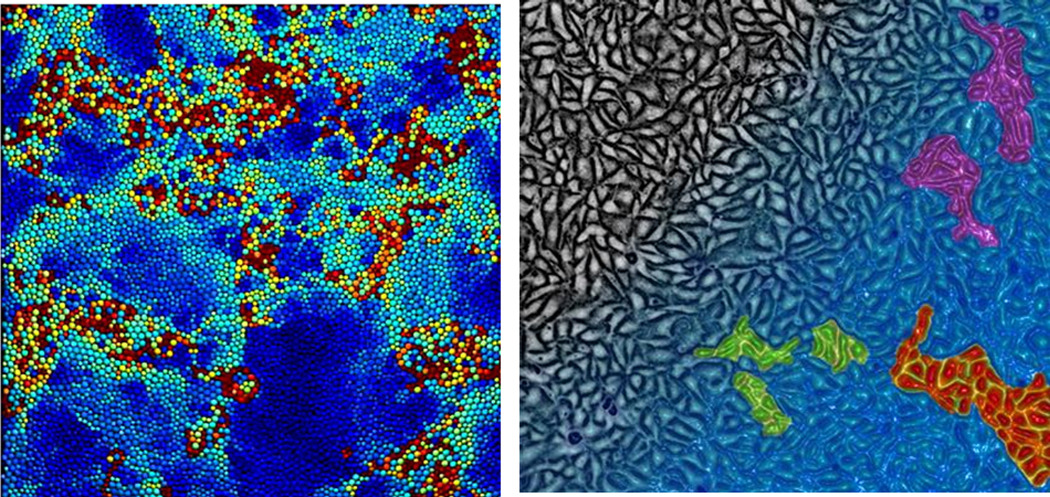
Panel A(left). Dynamic heterogeneity in an inert glass-forming system. In an inert system, each particle is color-coded according to its instantaneous mobility, where less mobile particles are blue while more mobile particles are dark red. Faster and slower particles are seen to self-organize into cooperative clusters (adapted from [43] with permission from the PNAS).

Panel B (right). Dynamic heterogeneity in MDCK monolayer. Gradient of cellular density is depicted from lower density (black) to higher density (blue), with the monolayer approaching the onset of the glass transition at the lower right. Cells with higher mobility are color-coded to illustrate the emergence of cooperative velocity clusters that increase in size with increasing cellular density (Artist rendition adapted from [70] with permission from the PNAS).

This physical picture describes a glass transition, but at the same time describes no less well the key features characterizing dynamics of the living monolayer [18, 43, 52, 53]. Much as in a glass transition, slower cellular units are now understood to organize into cooperative clusters, the size of which increases with increasing cellular density (Box 2). Less intuitive but nonetheless robust physical signatures of proximity to a glass transition occur in the monolayer sheet such as caging, superdiffusion, exponential distributions of stress and motion, diminishing self-diffusivity of short-wavelength motions, and growing peaks in the vibrational density of states [17, 18, 38, 53–55]. And as in the dynamics of an inert glass, those of a living monolayer depend powerfully upon volume exclusion, adhesive interactions, and deformability of the unitary particle. But unlike the unitary particles comprising the inert glass, of course, the unitary particles comprising the monolayer are active and motile.

Using monolayers of keratocytes, Szabo et al [56] reported what they called a kinetic phase transition with much the same features of the glass transition. Fine-scaled models containing many mechanical features [21], as well as minimal models with simple rules of local interaction [57] have been used in order to predict local cell steering and resulting collective cellular migration. Collective migration of epithelial cells show velocity correlations spanning many cells [55] and in a manner that is sensitive to the density of cells [53]. In trying to understand biological mechanism, it is sobering to recognize that a dispersion of inert rigid spheres, if taken at sufficiently high density, shows experimentally many of these same collective features [58], which may be reflecting generic properties of any soft glassy system.

Might the unexpected finding that the behavior of the cellular monolayer is similar to that of glass-forming systems shed light onto the unresolved phenomenon of contact inhibition of locomotion, wherein the motile cell protrudes and migrates progressively less as it becomes increasingly surrounded by other cells [59]? We do not resolve that question here, although we note that each cell within a monolayer tends to become immobilized by adhesion to its basement membrane, adhesion to its neighboring cells, and mutual volume exclusion. These factors, taken together, are consistent with cells migrating progressively less as they become increasingly frozen in a glassy phase [18, 53].

Positional sensing

We now return to a central question in development and regeneration, namely, how are patterns of growth and differentiation specified? More specifically, within a homogeneous tissue how does a cell know its location in order to differentiate into a specific cell type? Or within a growing tissue, how does a cell know when it must stop dividing? The prevalent answer to this question is that there must exist some form of positional sensing together with long range feedback, such as a chemical gradient, that the cell is able to sense, interpret, and respond to [60]. This idea was postulated at the beginning of the 20th century and championed by Lewis Wolpert in the 1960s using the so-called French Flag model [61]. Wolpert proposed that a stable gradient of a given morphogen from a source to a sink could be established along a tissue by simple diffusion. He postulated, further, that each cell interprets this concentration according to a set of thresholds that would determine the boundaries of gene expression patterns. Nearly 20 years later, Driever and Nüsslein-Volhard studied early development of the Drosophila embryo and established that an exponential distribution of bicoid protein along the anterior-posterior axis determines the position of body segments [62]. Since then, other morphogen gradients have been linked to positional sensing including gradients of Decapentaplegic (Dpp) in the Drosophila imaginal wing disk [63, 64], and gradients of activin in Xenopus [65].

Despite the evidence for morphogen gradients as cues for positional information, the extent to which these gradients can be established and tuned with sufficient precision, robustness, and feedback to ensure proper development remains problematic [66]. In the case of bicoid, the absence of cell membranes between the nuclei during early stages of Drosophila development facilitates the generation and stability of the diffusive gradient. In the general case in which morphogens diffuse within a heterogeneous cellularized medium, however, robust positional information based on chemical gradients seems unlikely without the presence of tight feedback mechanisms. Diverse models for such feedback mechanisms have been proposed based on the spatio-temporal dynamics of morphogens and their receptors [67].

Alternative feedback mechanisms for positional sensing were proposed in which the control cue is mechanical rather than chemical [68, 69]. It was postulated in these models that tissue growth causes a buildup of compressive stress that is transduced locally and fed back into the proliferation machinery to regulate global tissue growth. We now know that stresses within the monolayer are mainly tensile rather than compressive, with heterogeneous dynamics as well, but the notion of positional sensing by mechanical stresses is no less appealing because these stresses form long range gradients, and these gradients are paralleled by gradients of cell density [17]. This new experimental evidence substantially complicates but also enriches the question of positional sensing by means of mechanical stress. Given a stress landscape that is both rugged and dynamic (Fig. 3), we cannot rule out that positional sensing might occur through tension or shear stress, their gradients in space or their fluctuations in time. Such stresses are transmitted directly through the cytoskeleton and across cell-cell junctions, can extend enormous distances within a tissue or organism, and in doing so can provide robust cues that are absolute rather than relative.

Concluding remarks

The existence of a relationship between physical forces and cellular motions for the monolayer in vitro is of course only a starting point for a more comprehensive understanding of collective cell migration in more complex systems. Future investigations need to address the extent to which the main behaviors found to date might scale up to tissues in vivo, which comprise greater phenotypic diversity and architectural complexity; based upon existing data there is no reason to rule these behaviors in, but no reason to rule them out. More importantly, the availability of direct measurements of intercellular physical forces now opens the possibility to study how these forces are transduced and fed back into the integrative pathways that regulate multicellular dynamics.

The first measurements of the physical forces that drive collective cell migration establish dynamics that are unexpectedly rich (Box 3). Simple ideas based on mechanical leaders and followers have now given way to a physical picture dominated by dynamic heterogeneities and intercellular cooperativity. The transmission of cooperative forces at cell-cell junctions are at the origin of a newly discovered mode of cell guidance – plithotaxis – that is innately collective. Taken together, these findings highlight the fact that this mode of guidance is not a particular property of any constituent cell but rather an emergent phenomenon of the collective system.

Box 3: Mechanics of Monolayer Migration*.

• Cells generate a long range gradient of intercellular tension by engaging in a multi-cellular tug-of-war.

• As cellular density or mutual adhesion increases, monolayer fluctuations become increasingly rugged, sluggish, and cooperative in a manner strongly reminiscent of approach to kinetic arrest in a glass transition.

• Each cell tends to trek along local orientations of maximal principal stress** or, equivalently, minimal intercellular shear stress, across a rugged stress landscape.

* Mechanics: the relationship between motions and the forces that drive them

**Chemotaxis, durotaxis, and haptotaxis cause cellular motions. Underlying forces are not separate from these three laws but rather is subsumed by them.

Glossary

Stress

force per unit area.

Normal stress

local stress exerted normal to a defined surface.

Shear stress

local stress exerted tangent to a defined surface.

Traction force

the local stress exerted by a cell upon its substrate

Principal stresses

In any continuum, the local stress field can be decomposed into a maximal and minimal principal stress, each acting along a corresponding principal orientation.

Principal orientations

Orientations that are mutually perpendicular and define the directions along which the shear stress is zero.

Plithotaxis

The tendency for each individual cell within a monolayer to migrate along the local orientation of the maximal normal stress, or equivalently, minimal shear stress. Plithotaxis requires force transmission across many cell-cell junctions and therefore is an emergent property of the cell group.