Direct measurements of electric fields in weak OH · · π hydrogen bonds

Abstract

Hydrogen bonds and aromatic interactions are of widespread importance in chemistry, biology and materials science. Electrostatics play a fundamental role in these interactions, but the magnitude of the electric fields that support them has not been quantified experimentally. Phenol forms a weak hydrogen bond complex with the π-cloud of benzene and we used this as a model system to study the role of electric fields in weak OH · · π hydrogen bonds. The effects of complex formation on the vibrational frequency of the phenol OH or OD stretches were measured in a series of benzene-based aromatic solvents. Large shifts are observed and these can be converted into electric fields via the measured vibrational Stark effect. A comparison of the measured fields with quantum chemical calculations demonstrates that calculations performed in the gas-phase are surprisingly effective at capturing the electrostatics observed in solution. The results provide quantitative measurements of the magnitude of electric fields and electrostatic binding energies in these interactions and suggest that electrostatics dominate them. The combination of vibrational Stark effect (VSE) measurements of electric fields and high-level quantum chemistry calculations is a general strategy for quantifying and characterizing the origins of intermolecular interactions.

Introduction

Hydrogen bonding is of fundamental importance for structure, function and dynamics in a vast number of chemical and biological systems.^1–6 In conventional hydrogen bonds, X – H · · · A, a hydrogen atom bridges the proton donor X and proton acceptor A. The donor is usually very electronegative, e.g. O or N, whereas the acceptor is an electronegative atom with at least one lone pair of electrons. Hydrogen bonds vary enormously in bond energy from ~15–40 kcal/mol for the strongest interactions, to less than four kcal/mol for the weakest. It is proposed, largely based on calculations, that strong hydrogen bonds have more covalent character, whereas electrostatics are more important for weak hydrogen bonds, but the precise contribution of electrostatics to hydrogen bonding is widely debated.²

In this work we consider a class of hydrogen bonds that are important in non-covalent aromatic interactions^2,7 - where π-electrons play the role of the proton acceptor - which are a very common phenomenon in chemistry and biology.^8,9 They play an important role in the structures of proteins and DNA as well as in drug-receptor binding and catalysis.^10,11 For example, edge-to-face interactions between the partially positively charged hydrogen of one aromatic system with the partially negative π-cloud of another aromatic system contribute to the stereoselectivity of organic reactions and to self-assembly in crystals of benzene and are widespread in proteins.^9,12,13 Another important class of these interactions is the cation-π interaction, where cations, such as the charged side chains of arginines and lysines, interact with the π-cloud of an aromatic system such as tyrosine, phenylalanine and tryptophan. These interactions are ubiquitous in proteins and are believed to be important for their structures,¹⁰ but as yet no experimental measurements of electric fields have been made to determine the extent to which these interactions are dictated by classical electrostatics as opposed to other effects (e.g. van der Waals, charge-transfer, etc.).

Here we present the first experimental measurements of the magnitude of electric fields in aromatic edge-to-face interactions using a model system consisting of phenol and a series of substituted benzene derivatives. We used the OH (or OD) stretch modes of phenol as vibrational probes of the change in electric field upon complex formation, where shifts in the IR spectra are directly related to electric field changes through the vibrational Stark effect. We chose this system based on the elegant studies of Fayer and coworkers on hydrogen bond exchange dynamics for phenol and benzene which form an edge-to-face (or OH · · π hydrogen bonding) complex in solution.¹⁴ The structure of this complex has been studied by DFT calculations in the gas-phase and by MD simulations in solution.^14,15 The calculations suggest that the hydroxyl group of phenol is pointing towards the center of one C-C bond of the benzene ring and interacts with the favorable electrostatic potential of the benzene π-system in a weak OH · · π hydrogen bond (strength < 4 kcal/mol).

As shown in the following, the electrostatic potential can be systematically manipulated by using substituted benzene derivatives to tune the charge density of the π-cloud by adding either methyl substituents as electron-donating groups or by adding chlorine substituents as electron-withdrawing groups. The effect of this systematic variation of the electric field experienced by the OH (or OD) group was detected using the vibrational absorption of the OH (or OD). These small model complexes enable high-level DFT calculations of their electrostatic properties, and we present a comparison between the theoretical results and our experimental data obtained with vibrational spectroscopy. We found a linear relationship between the observed IR peak frequency and the calculated electric fields at the OH (or OD) probes whose slope agrees very well with their independently measured vibrational Stark tuning rates. These results suggest that the electrostatic component of the phenol/aromatic interaction (or of the weak OH · · π hydrogen bond) is large and that DFT calculations are capable of accurately quantifying them.

Results and discussion

Vibrational spectroscopy

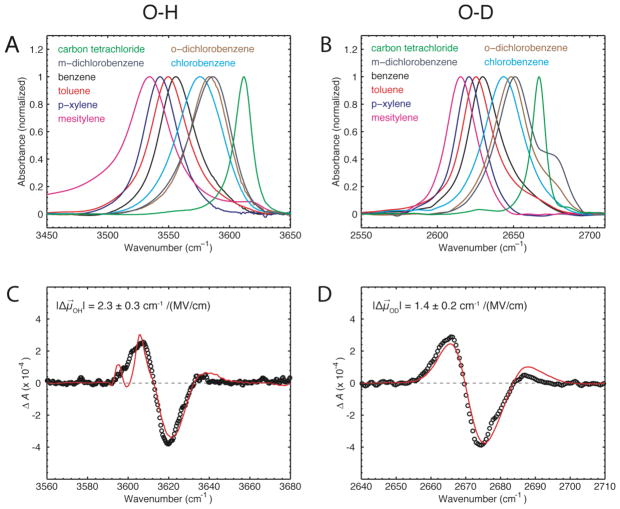
We employed FTIR spectroscopy to probe the stretching modes of OH or OD of phenol dissolved in different solvents. Figure 1A shows the FTIR spectra of free phenol in carbon tetrachloride (CCl₄) and of phenol dissolved in and complexed to different substituted benzene derivatives. The peak for free phenol in CCl₄ is located at 3611 cm⁻¹; all peaks for the complexed phenol are red-shifted with respect to the free phenol. The observed peak shifts follow a clear trend with the peaks appearing in the spectra in an order that corresponds to the degree of electron-withdrawing (or electron-donating) character of the substituents of the benzene derivatives. The most red-shifted complex is formed between mesitylene and phenol (3534 cm⁻¹). The phenol-OH peaks in the presence of benzene, toluene and para-xylene are separated by 6–7 cm⁻¹ from each other and are shifted progressively more to the red (see Table 1). Substitution of benzene with chlorines produces complexes that are less red-shifted from the free phenol in CCl₄.

Figure 1.

(A, B) Experimental FTIR spectra of 200 mM phenol dissolved in different organic solvents. The OH/OD stretch mode of free phenol in carbon tetrachloride is shown in green. The OH/OD stretch modes for phenol in aromatic solvents are all red-shifted. The shoulder of phenol-OD in m- and o-dichlorobenzene might arise either from a Fermi resonance or a second geometry of the complex in these solvents. (C, D) Vibrational Stark spectra of 2,6-di-t-butylphenol (approximately 1:1 OH and OD) in toluene measured at an applied field of 1 MV/cm at T = 77 K (black) with fit (red).

Table 1.

Observed wavenumbers for the OH and OD stretch modes of phenol dissolved in different aromatic solvents. The relative shift is relative to the peak of the phenol/benzene complex

solvent	OH frequency (cm−1)	Linewidth (cm−1)	rel. shift (cm−1)
mesitylene	3534.3	40.5	−21.6
p-xylene	3542.9	33.2	−13.0
toluene	3549.6	36.3	−6.3
benzene	3555.9	37.6	0.0
chlorobenzene	3575.8	34.6	19.9
o-dichlorobenzene	3583.4	36.0	27.5
m-dichlorobenzene	3586.1	39.6	30.2

solvent	OD frequency (cm−1)	Linewidth (cm−1)	rel. shift (cm−1)
mesitylene	2615.3	23.0	−14.4
p-xylene	2620.8	21.5	−8.9
toluene	2625.3	24.5	−4.4
benzene	2629.7	24.9	0.0
chlorobenzene	2643.5	29.9	13.8
o-dichlorobenzene	2648.5	27.3	18.8
m-dichlorobenzene	2651.0	28.6	21.3

The phenol-OH proton can be exchanged for deuterium, which shifts the vibrational mode from ~3600 cm⁻¹ into a different spectral region around ~2700 cm⁻¹. The same trend in the IR spectra is observed for deuterated phenol in the series of aromatic solvents (Fig. 1B), but the relative peak shifts are consistently smaller (~4–5 cm⁻¹), suggesting a smaller sensitivity of OD than OH to field (see below). The ratio of the peak shifts is $\mathrm{\Delta }{\stackrel{\sim }{\nu }}_{OD}^{\mathit{obs}}/\mathrm{\Delta }{\stackrel{\sim }{\nu }}_{OH}^{\mathit{obs}}=0.7$. The linewidths are affected by the isotope exchange by a similar factor of ~ 0.7.

To rule out the possibility that the peak shifts observed in the different aromatic solvents arise from differences in the solvent reaction field we performed several control experiments. The aromatic solvents containing the dissolved phenol were each diluted with CCl₄ to shift the equilibrium such that phenol was present in a mixture of free and complexed forms (Fig. S1). Under these conditions two peaks are observed in the IR spectra corresponding to the free and bound phenol, and while the peak for the bound phenol shifts as expected with the different aromatic solvents, the peak for free phenol remains virtually at the same position in all samples. In addition, we calculated the solvent reaction field for each aromatic solvent based on Onsager’s model.¹⁶ The result is presented in Fig. S2 and shows that the expected solvent reaction fields are small. These results strongly suggest that the observed peak shifts of the phenol OH (or OD) stretch in different aromatic solvents are reporting on complex formation between phenol and the aromatic molecules.

Vibrational Stark spectroscopy

One possible explanation for the peak shifts in the FTIR spectra is that complex formation between phenol and the different benzene derivatives produces electric fields which shift the OH (or OD) IR bands via the vibrational Stark effect. To test this hypothesis we determined the sensitivity of the OH and OD stretches to an external electric field. The linear sensitivity of a spectral probe to an electric field is the Stark tuning rate |Δμ⃗| (in cm⁻¹/(MV/cm)) and can be calibrated by vibrational Stark spectroscopy by recording the effect of a unidirectional defined electric field on the IR spectrum of an isotropic immobilized sample in a frozen glass solvent.^17,18 Due to solvent dielectric properties and field-induced perturbations of the solvent near the sample molecules, the actual electric field at the vibrational probe is greater than the externally applied electric field ( F⃗_local = f · F⃗_external). We therefore report the measured Stark tuning rates as the ratio |Δμ⃗|/f, where f is the local field correction factor.¹⁸ The value of f is estimated to be in the range of 1.1–1.3 for a frozen organic glass.¹⁹

It is not possible to measure the Stark tuning rate |Δμ⃗| of phenol itself because at low temperature the phenol molecules form hydrogen bonds with each other that result in very broad OH stretching bands unsuitable for Stark spectroscopy. Instead we used 2,6-di-t-butylphenol in the vibrational Stark experiments as the bulky tert-butyl groups prevent the formation of these phenol:phenol interactions. The tuning rates of phenol and 2,6-di-t-butylphenol are likely to be very similar, as extensive studies on other vibrational probes, particularly nitriles, have shown that the Stark tuning rate is a local property of the vibrational mode and does not vary significantly with small changes to the chemical structure.¹⁸ The bulky tert-butyl groups also prevent formation of complexes with the aromatic molecules so unfortunately these molecules and complexes can not all be studied under identical conditions.

We simultaneously measured |Δμ⃗|/f for OH and OD stretches on samples in which the H/D ratio of the hydroxyl group was approximately 1:1. Stark spectra were measured with an applied field of 1 MV/cm (Figs. 1C, 1D). The spectra were fit as/described elsewhere¹⁸ giving the Stark tuning rates: |Δμ⃗_OH|/f = 2.3 ± 0.3 cm⁻¹/(MV/cm) and |Δμ⃗_OD|/f = 1.4 ± 0.2 cm⁻¹/(MV/cm). The Stark tuning rate for OH is larger than for OD and the ratio is |Δμ⃗_OD|/|Δμ⃗_OH| = 0.7.²⁰ Very similar sensitivities of OH and OD to electric field were obtained by previous computational studies (see supporting information).²¹

If the observed peak shifts in the IR spectra of the phenol/aromatic complexes $\mathrm{\Delta }{\stackrel{\sim }{\nu }}_{OH}^{\mathit{obs}}$ (or $\mathrm{\Delta }{\stackrel{\sim }{\nu }}_{OD}^{\mathit{obs}}$) are a consequence of the changes of the electric field ΔF⃗_complex = F⃗_complex − F⃗_CCl4 sensed by the spectral probe whose sensitivity is calibrated by the vibrational Stark effect, then the spectral shifts of the probe in different complexes are given by $hc\mathrm{\Delta }{\stackrel{\sim }{\nu }}_{OH}^{\mathit{obs}}=-\mathrm{\Delta }{\overrightarrow{\mu }}_{OH}·\mathrm{\Delta }{\overrightarrow{F}}_{\mathit{complex}}$ (or $hc\mathrm{\Delta }{\stackrel{\sim }{\nu }}_{OD}^{\mathit{obs}}=-\mathrm{\Delta }{\overrightarrow{\mu }}_{OD}·\mathrm{\Delta }{\overrightarrow{F}}_{\mathit{complex}}$), where h is Planck’s constant, and c is the speed of light. The OH stretch is a well-defined local mode, meaning the direction of Δμ⃗_OH (or Δμ⃗_OD) must be along the OH (or OD) bond vector, so $\mathrm{\Delta }{\stackrel{\sim }{\nu }}_{OH}^{\mathit{obs}}$ depends on the projection of ΔF⃗_complex along this vector. It is evident that the IR shifts of the OH (or OD) probe measured in our phenol/aromatic complexes follow a trend that is consistent with the sensitivity of the probes to electric fields because the ratio of the OH and OD Stark tuning rates is roughly equal to the ratio of the observed peak shifts for the OH and OD stretches in the phenol/aromatic solvent studies ( $\mathrm{\Delta }{\overrightarrow{\mu }}_{OH}/\mathrm{\Delta }{\overrightarrow{\mu }}_{OD}\approx \mathrm{\Delta }{\stackrel{\sim }{\nu }}_{OH}^{\mathit{obs}}/\mathrm{\Delta }{\stackrel{\sim }{\nu }}_{OD}^{\mathit{obs}}$); in the following we demonstrate a quantitative relationship based on calculated fields using DFT.

Structure of the phenol/aromatic complexes

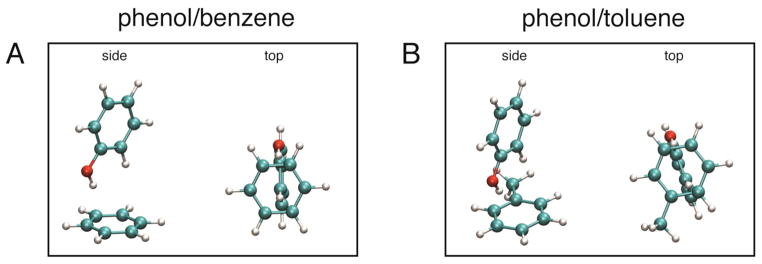
In order to further understand the physical origin of the observed IR peak shifts, we performed DFT calculations on each phenol/aromatic complex. The geometry of all phenol/aromatic complexes was optimized using DFT methods implemented in the Gaussian 09 package.²² The B3LYP functional^23,24 and 6-31+G(d,p) basis set were used for all calculations. Representative structures for the phenol/benzene and the phenol/toluene complexes are shown in Figure 2, and the geometries and coordinates for all other complexes can be found in the supporting material (Fig. S3). All complexes have the expected T-shaped structure where the OH group of phenol is pointing towards the middle of one C-C bond of benzene, as reported earlier,²⁵ and the geometry optimized structures overlay very well. The distance of the OH proton to the two closest carbon atoms of benzene is 2.6 Å (2.9 Å to the center of the ring) and the distance of the oxygen to the two closest carbon atoms is 3.5 Å (3.9 Å to center of ring).

Figure 2.

Geometry optimized structures of the (A) phenol/benzene and (B) phenol/toluene complexes are shown in side and top views.

Comparison with calculated electric fields

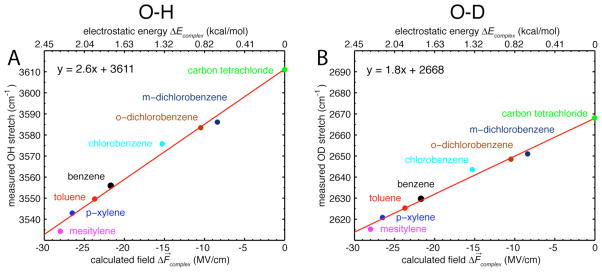
After geometry optimization the phenol was removed and the oxygen and proton of the hydroxyl group were replaced by ghost atoms. The projection of the electric field along the OH (or OD) bond arising from the different substituted benzene derivatives was then calculated for each complex using DFT. Figure 3 illustrates a linear relationship between the observed IR frequencies of the OH (or OD) probes and the calculated field projections. The electric fields experienced by the probe range from −8 MV/cm for m-dichlorobenzene to −28 MV/cm for mesitylene. Fitting of the data to a straight line results in a slope of 2.6 cm⁻¹/(MV/cm) for the OH stretch and 1.8 cm⁻¹/(MV/cm) for the OD stretch. These values are in excellent agreement with the experimentally measured Stark tuning rates of 2.3 cm⁻¹/(MV/cm) and 1.4 cm⁻¹/(MV/cm). Extrapolating this best fit line for the OH data to ΔF⃗_complex = 0 gives a prediction for the frequency of the OH in the absence of complex formation which is 3611 cm⁻¹, in remarkable agreement with the frequency of the OH stretch for free phenol in CCl₄ (3611 cm⁻¹, Fig. 3A). For the OD data, extrapolation leads to 2668 cm⁻¹, and the observed frequency for free phenol-OD in CCl₄ is 2668 cm⁻¹ (Fig. 3B).^26–28 The observation that both slopes and intercepts (four independent parameters) agree with measured values of the Stark tuning rates and frequencies of the uncomplexed phenol suggests that the shifts of the OH/OD stretch upon complex formation are due entirely to electrostatic effects, i.e. that the purely electrostatic relationship $hc\mathrm{\Delta }{\stackrel{\sim }{\nu }}_{OH}^{\mathit{obs}}=-\mathrm{\Delta }{\overrightarrow{\mu }}_{OH}·\mathrm{\Delta }{\overrightarrow{F}}_{\mathit{complex}}$ (or $hc\mathrm{\Delta }{\stackrel{\sim }{\nu }}_{OD}^{\mathit{obs}}=-\mathrm{\Delta }{\overrightarrow{\mu }}_{OD}·\mathrm{\Delta }{\overrightarrow{F}}_{\mathit{complex}}$) explains the spectral shifts. Furthermore, the observed linear behavior confirms that Stark tuning rates measured in laboratory-achievable applied fields of 0.2 – 1 MV/cm can be extrapolated to fields that are larger by two orders of magnitude. This is a non-trivial observation as the linear relationship between vibrational frequency and electric field described by the linear Stark effect is expected to break down in very large electric fields, where non-linear effects become significant.²⁹ To further understand this we calculated the effect of electric fields of different magnitude on the vibrational frequency of the OH group of phenol using DFT (see the supporting material for the methodology used). The results show that the effect of electric field on the vibrational frequency is linear within the range of fields experienced in the phenol/aromatic complexes (Fig. S4).

Figure 3.

(A, B) Plot of the measured frequencies of the phenol OH/OD stretch in different solvents versus the calculated projections of the electric field along the OH/OD bond. The straight line shows the best fit using only data for the aromatic solvents, and the slope of this line corresponds to the theoretical Stark tuning rate. Extrapolation of this line to ΔF⃗_complex = 0 leads to a prediction for the frequency of OH (or OD) in the absence of complex formation that agrees well with the OH/OD stretch in carbon tetrachloride.

The observation that the IR shifts are due almost exclusively to electrostatics makes it possible to convert the values of ΔF⃗_complex into electrostatic energies of complex formation according to ΔE_complex = −μ⃗ · ΔF⃗_complex, where μ⃗ is the overall ground-state dipole moment of the phenol OH group (1.66 D ^30–32) and ΔF⃗_complex the projection of the electric field along the OH (or OD) bond axes. Estimation of the total electrostatic binding energy ΔE_complex from the calculated electric fields ΔF⃗_complex produced values of 2.28 kcal/mol for phenol/mesitylene, 2.16 kcal/mol for phenol/p-xylene, 1.94 kcal/mol for phenol/toluene and 1.77 kcal/mol for phenol/benzene (Fig. 3, top axis). These values agree very well with experimental dissociation enthalpies ΔH⁰ obtained by Zheng et al.²⁵ suggesting that electrostatics are the dominant contribution to binding (−2.45 kcal/mol for phenol/mesitylene, −2.2 kcal/mol for phenol/p-xylene, −2.0 kcal/mol for phenol/toluene and −1.7 kcal/mol for phenol/benzene).

Conclusion

Implications of the agreement between experiment and theory

The data presented here show an excellent agreement between measured electric fields for phenol/aromatic complexes in solution and the electrostatics of the aromatic molecule calculated with DFT methods in the gas-phase. This is a significant result because it indicates that the interaction in solution is dominated by the electrostatic properties of the hydrogen bond acceptor, with effects such as polarization of the phenol by the benzene π-cloud, which is not modeled in our calculations, being of secondary importance. The phenol/aromatic interaction can be considered as a dipole-quadrupole interaction, which, according to our results, is dominated by electrostatics. From this it would be expected that the cation-π interaction, which can be considered a monopole-quadrupole interaction, should also be dominated by electrostatics.¹⁰

Due to the excellent agreement between experiment and theory we are also able to estimate the value of the local field correction factor f for the 2,6-di-t-butylphenol/toluene system. The measured Stark tuning rates were |Δμ⃗_OH|/f = 2.3 ± 0.3 cm⁻¹/(MV/cm) and |Δμ⃗_OD|f = 1.4 ± 0.2 cm⁻¹/(MV/cm). Comparison with the calculated Stark tuning rates |Δμ⃗_OH| = 2.6 cm⁻¹/(MV/cm) for the OH stretch and |Δμ⃗_OD| = 1.8 cm⁻¹/(MV/cm) for the OD stretch yields f ≈ 1.2, which is in the expected range between 1.1–1.3.¹⁹ However, the small discrepancy between the measured and calculated Stark tuning rates could also result from small non-electrostatic contributions to the observed IR shifts.

The isotope effect of the Stark tuning rate allows one to use either the OH or OD stretching modes to measure electric fields at the same position with two different spectral probes in one sample. Additionally the isotope effect shifts the OD mode into a different spectral window, which might be useful for studies in more complex systems like peptides. This combination suggests the possibility of direct measurements of these interactions in biological macromolecules, where the importance of such interactions has been widely discussed.

This work demonstrates that vibrational Stark effect measurements combined with gas-phase calculations provide a powerful tool to study intermolecular interactions in solution. This technique can generally be used to quantify the electrostatic contributions in inter- or intramolecular interactions ranging from hydrogen bonding or cation-π interactions to aromatic interactions. Further studies involving different kinds of hydrogen bonds are currently in progress.