Isotope-Induced Desymmetrization Can Mimic Isotopic Perturbation of Equilibria. On the Symmetry of Bromonium Ions and Hydrogen Bonds

Abstract

The desymmetrizing effect of isotopic substitution on the geometry of otherwise symmetrical structures can be surprisingly large when there is anharmonic coupling between a desymmetrizing mode and modes whose zero-point energies are strongly isotope-dependent. This phenomenon is found to account for experimental observations that had been previously interpreted as implying asymmetry in bromonium ions and in hydrogen phthalate ions in aprotic solvents. The unlabeled structures are concluded to have the higher symmetry found in computed structures. Great care must be taken in applying isotopic perturbation as a test of asymmetry.

It is well understood that isotopic substitution desymmetrizes the time-averaged geometry of otherwise symmetrical structures.¹ However, the effect of isotopic substitution on geometry is often assumed to be small, and this assumption is important in many experiments. We describe here a way in which the effect of isotopic substitution on the geometry of a symmetrical structure can be surprisingly large and how this can mislead the interpretation of experimental observations. The results affect the understanding of hydrogen bonds in solution.

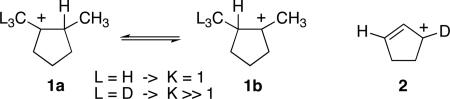
The experimental distinction between a symmetrical structure versus two degenerate equilibrating structures of lower symmetry has been a common problem in chemistry. This issue is most vexing when the conjectured equilibration would be rapid and the applicable spectroscopic techniques have a low time resolution, as in NMR studies of simple molecules. To address this problem, Saunders developed one of the most elegant experiments of classical physical organic chemistry in the observation of isotopic perturbation effects on the NMR spectra of molecules of interest.² The Saunders experiment proved its power by convincingly addressing the structure of the norbornyl cation,³ and over the last 30 years it has been employed broadly in organic and organometallic chemistry.^4,5,6

The idea behind the Saunders experiment is that desymmetrizing isotopic substitution affects the equilibrium between two equilibrating structures but cannot have a strictly analogous effect on a single symmetrical structure where no equilibration is present. For example, deuterium substitution in a methyl group of 1a/1b strongly affects the equilibrium between structures that would otherwise be degenerate. The ¹³C NMR spectrum of 1 with L = D reflects the breaking of the degeneracy, and widely separate signals are observed for carbons that were overlapping in the unlabeled 1 (L = H). With 2, in contrast, there is no equilibrium to affect. The NMR spectrum of 2 still reflects an asymmetry that results from intrinsic isotope effects on chemical shifts, but the separation of carbons that were equivalent in the unlabeled structure is much smaller than in the case of 1. As a result, the ¹³C NMR spectra of 1 (L = D) versus 2 readily distinguish the equilibrating from nonequilibrating structures.

We envisioned that under certain circumstances the intrinsic isotope effects on the chemical shifts for single “symmetrical” structures might be much larger than normally anticipated, making these structures appear to be unsymmetrical equilibrating structures. The observed shifts of lines in an NMR spectrum are time-averages of the isotope-independent instantaneous chemical shifts of atoms in each specific nuclear configuration accessed by molecules due to thermal and zero-point energy (ZPE) motion. Intrinsic isotope effects on chemical shifts⁷ may then be viewed as resulting from two effects - changes in the span of geometries accessed by a molecule upon isotopic substitution, and changes in the time-averaged geometry of a molecule. The latter requires anharmonicity. Changes in molecular geometry, such as differing C-H and C-D bond lengths, can arise from simple cubic terms in the potential V versus normal coordinate displacement Q without any coupling of normal modes, e.g., from α_iij terms in eq 1 with all α_iij = 0. However, the resulting isotope effects on the shift of atoms more than one bond distant are generally small. The more interesting effect of anharmonicity that we considered would arise when a mode i (or a series of modes), whose ZPE is affected strongly by isotopic substitution, is coupled (|α_iij| >> 0) with a mode j that desymmetrizes an otherwise symmetrical molecule. In such a case, isotopic substitution in atoms moved by i can affect the time-averaged displacement of the “distant” model j.

$$V=\sum _i{k}_{ii}{Q}_i^2+\sum _i{\alpha }_{iii}{Q}_i^3+\sum _{i,j(i\ne j)}{\alpha }_{iij}{Q}_i^2{Q}_j+\cdots$$ (1)

An example of this phenomenon arises in the tetramethylbromonium ion 3. Ohta and coworkers found that the ¹³C NMR signals for the quaternary carbons in 3 (L = D) are separated (“Δ”) by 3.61 ppm.⁵ This shift is more than an order of magnitude larger than normal two-bond intrinsic H/D isotope effect on a ¹³C chemical shift in the absence of equilibrating structures.^7b Accordingly, Ohta concluded that 3 is not a C_2v-symmetric⁸ 1,2-bridged structure (3a), but rather is a rapid equilibrium of β-bromocarbenium ions (3b). The data appeared to force this conclusion,⁹ but it is a bothersome one since a long history of experimental observations has supported the bridged structure, as reflected in every undergraduate textbook of organic chemistry. In addition, theoretically calculated potential-energy minima for 3 uniformly support the C_2v symmetry of the bridged ion 3a.

In the calculated C_2v structures for 3a, such as the MPW1PW91/6-31+G**¹⁰ structure 4 in Figure 1, a low-energy B2 mode⁸ “j” (167 cm^-1) rocks the axis of the central C-C bond versus the bromine atom. If motion of the bromine atom toward the CH3 groups in 3a (L = D) is defined as “positive” motion in j, then a series of modes associated with C-H stretching and bending vibrations exhibit positive cubic force constants α_iij (i being the stretching and bending modes), while an equivalent series of modes associated with C-D stretching and bending vibrations exhibit negative α_iij (calculated from finite differences of Cartesian Hessians¹¹). In other words, motion of the bromine atom toward the CH₃ groups strengthens the C-H stretching and bending vibrations, particularly those associated with the hydrogens anti to the bromine atom, while weakening the corresponding C-D vibrations. This fits with the intuitive structural ideas used to understand β-deuterium isotope effects in carbocations. Because of the lower ZPE in C-D vibrations, the molecular ZPE is decreased as the bromine is displaced toward the CD₃ groups. Based on the cubic force constants, the difference in ZPE between the two classical turning points of mode j would be over 20 cm^-1. This is a substantial correction relative to the gradual potential energy curve for mode j and should lead to a significant time-averaged displacement of mode j away from the C_2v structure.

Figure 1.

Structures and NMR predictions for the bromonium ion derived from d₆-tetramethylethylene. Structure 4 is the MPW1PW91/6-31+G** potential energy minimum while the remaining structures have allowed for anharmonicity in various ways (see text). The Δ is the shift for the quaternary carbon distal to the deuteriums minus the shift for the quaternary carbon proximal to the deuteriums. Uncertainties in the last digits of the distances are given in parentheses. All uncertainties are 95% confidence intervals.

We used three methods to estimate the desymmetrization of 3. The first and conceptually simplest approach treats the motion in the low-energy mode j as slow and separable from the motion in the other modes, so that the ZPE in the other modes can be applied directly as a correction to the energy curve governing mode j. Numerical solution of Schrodinger's equation for the resulting energy curve affords a wavefunction from which the average displacement of mode j can be calculated. The overall structure 5a from this “one-dimensional” approach then assumes that all other modes are at their potential energy minimum. The second method applied second-order perturbation theory based on the cubic and semi-diagonal quartic force constants,¹² resulting in structure 5b. The third method made use of quasiclassical direct-dynamics trajectory calculations.^13,14 A series of quasiclassical trajectories on the MPW1PW91/6-31+G** surface were started from 4. Each normal mode was given its ZPE plus a Boltzmann sampling of additional energy appropriate for the temperature of the simulation, along with a random phase and sign for its velocity. The trajectories were then propagated in 1 fs up to a 500 fs time limit (to minimize nonphysical redistribution of the ZPE). The trajectory geometries (>450,000 in each case) in curvilinear coordinates were then averaged, affording structures 5c, 5d, and 5e at 0, 193, and 298 K, respectively.

All three methods predict significant desymmetrization of the bromonium ion. For comparison, the change in the C-Br bond length in (CH₃)₂CHBr versus (CH₃)₂CHBr as predicted by the second-order perturbation theory method is only 0.0004 Å, so the geometry change in 5 is a factor of 20 greater than might have been expected from a structurally similar model. The trajectory method predicts somewhat greater desymmetrization than either the one-dimensional or perturbation theory approach. A notable observation is that the desymmetrization changes with temperature.¹⁵

It is overly simplistic but enlightening to calculate the NMR spectra based on these time-averaged structures. For each geometry 5a-e, the separation of the quaternary-carbon ¹³C NMR chemical shifts, Δ, was calculated by the GIAO method in MPW1PW91/6-31+G** calculations, and the results are summarized in Figure 1. The striking observation is that the predicted Δ for each structure is in the range of the experimentally observed Δ. In other words, the experimental observation appears to result from the large change in the time-averaged geometry of the molecule due to the anharmonicity effect described above. However, these single-structure calculations do not allow for the change in the span of accessed nuclear configurations due to isotopic substitution. We therefore employed the non-simplistic, if arduous, approach of calculating Δ based on NMR calculations at each point of the trajectories at 193 K.^14,16 By averaging the calculated shifts for over 200,000 points, a Δ of 4.8 ± 0.6 was obtained. This more rigorous result is again in the range of the experimentally observed Δ. Overall, as is consistent with both classical mechanistic studies and computational studies, the NMR observation may be explained without the need to postulate any asymmetry in the unlabeled bromonium ion.

A more difficult but more broadly consequential example to consider is the hydrogen phthalate anion 6. The nature of the hydrogen bond (H-bond) in anions of this type has been of considerable interest, both from a fundamental perspective and with regard to the disputed importance of “low-barrier” or “short, strong” H-bonds in catalysis. The structure of 6 has been considered in terms of two limiting possibilities, either having the proton centered between the oxygens as in the “symmetrical” (C_2v) 6a, or having the proton localized in one well of a double-well potential with a rapid equilibration of the two tautomeric forms as in the “asymmetric” 6b. X-ray and neutron diffraction studies have observed the symmetrical structure,¹⁷ and gas-phase computations favor this structure. The interesting question has been the structure of the anion in solution. Primary isotope effects on the chemical shift in 6, i.e. comparison of the chemical shifts of H versus D versus T have favored the symmetrical structure in solution.¹⁸ However, a series of papers by Perrin and coworkers have applied a Saunders-type isotopic perturbation experiment to 6 and a variety of related ions, and in all cases the experimental observations have been interpreted as supporting asymmetric structures.^6,19 Perhaps the most striking observation is that the isotopic perturbation experiment appears to support an asymmetric structure for 7, a molecule designed to avoid desymmetrizing counterion effects, even in relatively non-polar dichloro-methane solutions. The sweeping conclusion from these observations has been that “H-bonds are not symmetric in solution”.^6c Rather, the necessarily asymmetric instantaneous environment effected by any solvent is taken as sufficient to break the molecular symmetry. By extension, these studies have been interpreted as denying any extra stabilization associated with short-strong hydrogen bonds.¹⁹

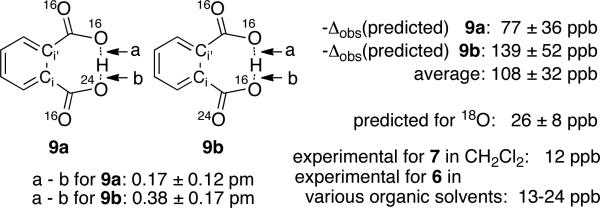
The key Perrin experiment involves the study of hydrogen phthalates containing a single ¹⁸O-label, as in 8. The presence of the ¹⁸O leads to a separation of the ¹³C NMR signals (Δ_obs) for carboxylate carbons C_c versus C_c' and ipso carbons C_i versus C_i'. Assuming that the peak separation in the corresponding diacid forms under identical conditions represents the intrinsic isotope effects on the chemical shift, Δ₀, the consistent observation that |Δ_obs| > |Δ₀| triggers the conclusion that that hydrogen phthalate ions consist of equilibrating tautomers rather than single symmetrical structures. However, outside of water and methanol, the carboxylate carbons were not diagnostic of equilibrating tautomers owing to very low differences between Δ_obs and Δ₀, ≤ 4 ppb. Instead, conclusions relied on observations of Δ_obs versus Δ₀ for the ipso carbons. For 7 (R = octyl, labeled with ¹⁸O) in CD₂Cl₂, -Δ_obs was 12 ppb while -Δ₀ was 2 ppb. For the tetrabutylammonium salt of 6 (labeled with ¹⁸O) in various aprotic organic solvents, -Δ_obs was 13 to 24 ppb, while -Δ₀ was 1 ppb. These observations were considered to be conclusive support for equilibrating tautomers.

MPW1PW91 gas phase structures for 6 have C_2v symmetry. Our hypothesis was that the presence of an ¹⁸O in 6 would engender significant asymmetry in the gas phase structure and that this asymmetry could account for the experimental Δ_obs for the ipso carbons in organic solvents, i.e., that the Δ_obs results from isotope-induced desymmetrization rather than equilibrating tautomers. To test this hypothesis, we applied the methods used to study 3. All of the methods encounter substantial difficulties owing to the roughly 200-fold smaller effect of ¹⁸O in phthalates versus six deuterium in 3. Treating the B2 modes as separable faced the problem that there are eight relevant B2 modes and that very slight motions along any of these desymmetrizing modes would affect the NMR spectrum significantly. The use of second-order perturbation theory faced a particular problem with regard to numerical convergence (see the Supporting Information (SI) for a discussion), and while the calculated vibrationally averaged structures consistently placed the phthalate proton nearer the oxygen of the labeled carboxylate, slightly differing calculations predicted a difference in O-H distances that varied from 0.01 pm up to 0.60 pm.

We ultimately focused on trajectory studies and particularly on the most rigorous procedure of calculating the NMR spectrum at each point of a very large number of quasiclassical trajectories at 25 °C. This method itself has the substantial problem that the ¹⁸O isotope effect on the chemical shifts in 8 converges exceedingly slowly relative to the small experimental Δ_obs. We estimate that it would take an impractical 120,000,000 force and NMR calculations or 1500 processor-years to obtain a satisfactory statistical significance for the predicted Δ_obs. To get around this problem, we employed the nonphysical ²⁴O in trajectories, making the assumption that this would increase the magnitude of the isotope effect by approximately a factor of four. This decreases the computations required by a factor of 16. A series of quasiclassical trajectories on the gas-phase MPW1PW91/6-31G* surface were started from 9a and 9b, giving each normal mode its ZPE plus a Boltzmann sampling of additional energy appropriate for the 25 °C, along with a random phase and sign for its initial velocity. The trajectories were then propagated both forward and backward in time for 500 fs. At each point in the trajectories, the isotropic shielding was calculated by the GIAO method. The time-averaged Δ₀ was then calculated from the average of NMR shifts from approximately 5,000,000 trajectory points for 9a and 2,500,000 trajectory points for 9b.

The results are summarized in Figure 2. For comparison, trajectories and perturbation-theory calculations were also carried out on ²⁴O-labeled formic acid. In either oxygen position by either method, the change in the average O-H distance was 0.01 to 0.02 pm. In contrast, the changes in O-H distances due to labeling in 9a and 9b from the trajectories (which are in the same direction as predicted by perturbation theory) are greater by approximately 20-fold. This shows that a carboxylic acid is not a good model for the effect of isotopic labeling in hydrogen phthalates. More significantly, the predicted NMR shifts directly compromise the previous interpretation of the experimental data. The predicted -Δ_obs of 26 ± 8 ppb for ¹⁸O labeling is slightly larger than the experimental observation for 7 and most of the observations for 6, but considering the limitations of the calculations the agreement is very good. Keeping in mind that the trajectories are gas-phase calculations on a C_2v potential energy surface, the results show that the NMR observation may be understood without the need to postulate any asymmetry in the unlabeled hydrogen phthalate ion.

Figure 2.

Trajectory-based predictions of the asymmetry and -Δ_obs for 9a and 9b. The predicted -Δ_obs for the ¹⁸O isotopologue was obtained by averaging the results for 9a and 9b and dividing by four.

Would symmetry in the hydrogen phthalate ion in aprotic organic solvents be surprising? The rationalization for the presence of asymmetric equilibrating tautomers, as in the Perrin interpretation of the NMR results, was that the solvent environment is asymmetric at any instant. This is of course correct, but its significance is lessened by further consideration. In particular, it should be recognized that the hydrogen phthalate molecule is by itself asymmetric at any instant. This asymmetry is not trivial; as is readily observed in the gas phase trajectories, vibrational twisting of either carboxylate relative to the benzene ring can give rise to structures in which the proton stays localized on one of the two carboxylates for an extended time (50% of the time, the proton stays closer to one of the carboxylate oxygens for a period of 33 fs or longer before switching to the other carboxylate, and periods of proton localization longer than 100 fs are common). From this microscopic and instantaneous viewpoint, the distinction between 6a and 6b would become meaningless, but it was recognized long ago that this is not the best way to understand structures. That is, for symmetry to mean anything, structures must be considered as an average of geometries over some time scale, and the time scale depends on the experimental observation at hand. The asymmetry of a solvent environment is then meaningful only when it is of a sufficient strength and duration to affect some experimental observation. Our results do not support that this is the case for NMR spectra of hydrogen phthalate ions in aprotic organic solvents.

The results here have merely shown that the experimental observations in 3 and 6 attributed to isotopic perturbation of equilibria are consistent with isotope-induced desymmetrization on symmetrical potential energy surfaces. It is plausible that isotopically perturbed equilibria could account for the same observations, but in the absence of independent affirmative support for asymmetry, the most economical conclusion is that the structures have the higher symmetry supported by calculations. Obviously, our results suggest that great care should be taken when isotopic perturbation experiments suggest asymmetry in a molecule, but nothing here should be taken as compromising studies that have reached the opposite conclusion, as in the norbornyl cation example.