Forward Masking Additivity and Auditory Compression at Low and High Frequencies

Abstract

The additivity of nonsimultaneous masking can be used as a measure of nonlinearity in the auditory system. For example, two equally effective forward maskers should produce 3 dB of additional masking when they are combined, assuming linearity with respect to intensity. A combined effect greater than this (excess masking) indicates compression. In the present experiments, the signal was a 10-ms pure tone presented 20 ms after a 200-ms narrowband noise masker and/or immediately after a 20-ms narrowband noise masker. The signal frequency was 250, 500, or 4000 Hz. The signal threshold produced by combining two equally effective maskers was measured. At all three frequencies, little excess masking was observed for a signal 10 dB above absolute threshold, indicating linear additivity (no compression). At signal levels 30 dB above absolute threshold, excess masking was observed at all three frequencies. The estimated compression exponents were 0.29 at 250 Hz, 0.34 at 500 Hz, and 0.17 at 4000 Hz. In contrast with physiological studies on other mammals, the present results provide evidence for substantial compression at low frequencies in humans.

INTRODUCTION

In recent years, several studies have used nonsimultaneous masking to investigate the nonlinear characteristics of the human cochlea (Oxenham and Plack 1997; Hicks and Bacon 1999; Moore et al. 1999; Nelson et al. 2001). The main advantage of using nonsimultaneous masking as opposed to simultaneous masking is that the gap between the masker and the signal is usually sufficient to ensure that there is little temporal overlap on the basilar membrane (BM). It can be assumed, therefore, that the masker and the signal are processed independently by the BM.

In the study reported here, the additivity of forward masking was used to investigate the characteristics of compression in the auditory system. An energy-summation model predicts that two equally effective maskers, when combined, will result in a 3-dB increase in signal threshold compared to either of the maskers presented individually. Typically, however, when two equally effective nonsimultaneous maskers are combined, additional (“excess”) masking of around 10–15 dB is observed. This occurs for combinations of nonoverlapping forward maskers (Penner 1980; Penner and Shiffrin 1980; Widin and Viemeister 1980; Hanna et al. 1982; Cokely and Humes 1993) and for combinations of forward and backward maskers (Patterson 1971; Wilson and Carhart 1971; Cokely and Humes 1993; Oxenham and Moore 1994, 1995). The deviation from the energy-summation prediction can be explained if it is assumed that the signal is subject to a compressive nonlinearity prior to temporal integration (Penner 1980; Penner and Shiffrin 1980; Humes and Jesteadt 1989; Oxenham and Moore 1994, 1995). Briefly, if the effective increase in internal masking is 3 dB, then the physical signal level will have to increase by more than this to compensate for the compression. For example, 5:1 compression (0.2 dB/dB) would require a 15-dB increase in physical signal level to produce a 3-dB increase in the level prior to integration. The derivation of the compression exponent from additivity data depends on certain assumptions about the independence of the maskers and the signal, and the nature of the decision mechanism, which will be considered in the Discussion section. Nevertheless, the excess masking observed in additivity studies using nonsimultaneous masking is consistent with direct measurements of BM compression (e.g., Ruggero et al. 1997). The implication that excess masking is a consequence of cochlear nonlinearities is supported by the finding that listeners with moderate sensorineural hearing loss show linear (3 dB) additivity of forward and backward masking (Oxenham and Moore 1995). Physiological models have indicated that sensorineural hearing loss is associated with a loss of BM compression (Ruggero and Rich 1991; Ruggero et al. 1997).

Measurements from nonhuman mammals suggest that the BM is highly compressive (5:1, 0.2 dB/dB) at high characteristic frequencies (CFs) (Rhode and Robles 1974; Robles et al. 1986; Murugasu and Russell 1995; Ruggero et al. 1997; Russell and Nilsen 1997; Rhode and Recio 2000), but much less compressive (<2:1, 0.5 dB/dB) at CFs below 1000 Hz or so (Cooper and Yates 1994; Cooper and Rhode 1995; Rhode and Cooper 1996; Zinn et al. 2000). Psychophysical studies from human listeners seem to confirm this pattern (Hicks and Bacon 1999; Plack and Oxenham 2000). However, the technique used by Plack and Oxenham, and at least two of the techniques used by Hicks and Bacon, relied on the assumption that the response of the BM to a tone well below CF is linear. In this way, the response to a masker below the signal frequency could provide a “linear yardstick” for estimating the compression at CF. At low CFs, however, it appears that this assumption may not be valid. What compression there is may affect a broad band of frequencies relative to CF (Rhode and Cooper 1996).

Two recent psychophysical studies that did not rely on the assumption of below-CF linearity reported very different results to those described above. Lopez-Poveda et al. (2003) measured the forward masker level required to mask a low-level signal as a function of the masker-signal interval. The growth in masker level with masker-signal interval (temporal masking curve, TMC) is assumed to be determined by both the decay of the internal excitation produced by the masker and the compression applied to the masker. Lopez-Poveda et al. found that TMCs were just as steep at a signal frequency of 500 Hz as at higher frequencies (e.g., 4000 Hz). Either temporal resolution is more acute at low CFs, which is unlikely based on studies of gap detection (Shailer and Moore 1987), or there is just as much compression at low CFs as at high. Plack and Drga (2003) also found this effect, and in addition found that the growth of on-frequency forward masking (signal level against masker level) was just as shallow at 250 and 500 Hz as at 4000 Hz. It has been argued that the shallow growth of forward masking at low signal levels is a result of the masker being in the midlevel compressive region of the BM response and the signal being in the low-level linear region of the BM response (Oxenham and Moore 1995; Plack and Oxenham 1998). The estimates of compression from the experiments of Plack and Drga were in the range 5:1–3.3:1 (compression exponents of 0.2–0.3) at all frequencies tested.

The aim of the present study was to use two nonoverlapping forward maskers to measure auditory compression at low and high frequencies. It was hoped to find evidence that could help evaluate the claims regarding low-CF compression. The main advantage of using the additivity technique is that any excess masking observed should depend only on the compression applied to the signal. In most other psychophysical studies, the estimates of compression depend on assumptions regarding the relative compression applied to the signal and masker or on the relative compression between on- and off-frequency maskers.

METHOD

Rationale

The measurements were conducted in two stages. In the first stage (Experiment 1), the levels of two nonoverlapping forward maskers were found that were roughly equally effective at masking the signal. In the second stage (Experiment 2), thresholds for the signal were measured in the presence of each equally effective masker presented individually and in the presence of the two maskers presented together. For each condition, the compression exponent was then calculated on the basis of these three signal thresholds.

Stimuli

The sinusoidal signal had a total duration of 10 ms, which consisted of 5-ms raised-cosine onset and offset ramps (no steady state). Masker 1 (M1) had a total duration of 200 ms, including 5-ms onset and offset ramps and 190-ms steady state. Masker 2 (M2) had a total duration of 20 ms, including 5-ms onset and offset ramps and 10-ms steady state. The silent interval between the end of M1 and the start of the signal (0 V points) was 20 ms. The offset of M2 coincided with the onset of the signal. Figure 1 shows a schematic of the temporal parameters of the stimuli.

Figure 1.

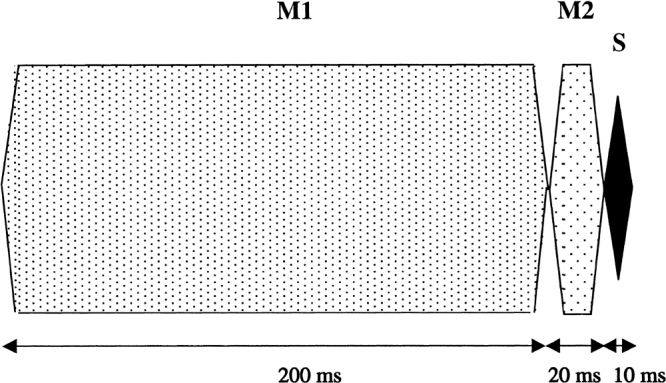
A schematic illustration of the temporal parameters of the stimuli used in the experiments, showing Masker 1 (M1), Masker 2 (M2), and the signal (S).

Three frequency conditions were run, two low-frequency conditions and one high-frequency condition. In the two low-frequency conditions, the sinusoidal signal was set at f_s = 250 or 500 Hz, and the noise maskers were lowpass filtered at 1000 Hz (3-dB cutoff, 90 dB/octave). In the high-frequency condition, the signal was set at f_s = 4000 Hz, and the noise maskers were bandpass filtered between 2800 and 5600 Hz (3-dB cutoff, 90 dB/octave).

The experiment was controlled by custom-made software from a PC workstation located outside a double-walled sound-attenuating booth. All stimuli were generated digitally with 32-bit resolution and were output by an RME Digi96/8 PAD 24-bit soundcard set at a clocking rate of 48 kHz. The headphone output of the soundcard was fed via a patch-panel in the sound booth wall to Sennheiser 580 headphones without filtering or amplification. Stimuli were presented to the right ear. Each listener sat in the booth and decisions were recorded via a computer keyboard. Listeners viewed a computer monitor through a window in the sound booth. Lights on the monitor display flashed on and off concurrently with each stimulus presentation and provided feedback at the end of each trial.

Procedure

A three-interval forced-choice forward masking experiment was run using an interstimulus interval of 300 ms. The individual or combined masker was presented in all three intervals. The signal was presented following the masker in only one of the three intervals, chosen at random with probability 1/3. Threshold was determined using a two-up one-down (masker thresholds) or a two-down one-up (signal thresholds) adaptive procedure that tracked the 70.7% correct point on the psychometric function (Levitt 1971). The level step size was 4 dB for the first 4 turnpoints, which reduced to 2 dB for 12 subsequent turnpoints. The mean of the last 12 turnpoints was taken as the threshold estimate for each block of trials. At least four estimates were made for each condition and the results averaged.

Listeners

Four normal-hearing listeners took part in the experiment. Listeners DM, AB, and NJ were college students paid an hourly wage for their participation. Author CO was also a listener. Each listener received at least two hours of practice before data collection began.

EXPERIMENT 1: DETERMINING LEVELS OF EQUALLY EFFECTIVE FORWARD MASKERS

Conditions

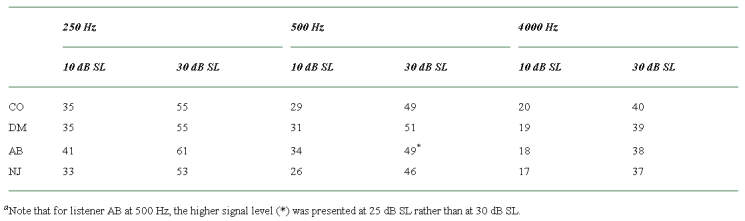
The aim of Experiment 1 was to determine the levels of M1 and M2 that were roughly equally effective at masking the signal. First, absolute thresholds for the signal in quiet were measured at the three signal frequencies. The signal was then presented at 10- or 30-dB sensation level (determined individually for each listener). The exception to this rule was for listener AB at 500 Hz. It was found that a signal presented at 30 dB produced levels of M1 during the adaptive procedure that just started to clip (the maximum output of the apparatus was 102 dB SPL rms). Accordingly, for this listener at 500 Hz the signal was presented at 25-dB sensation level. The signal levels used are shown in Table 1. For each signal level and frequency, the spectrum level of M1 or M2 (presented individually) was varied adaptively to determine the level needed to mask the signal. Conditions were presented in a random order.

Table 1.

The signal levels (in dB SPL) used in Experiment 1

Results

The results are shown in Table 2 and Figure 2. The average standard errors for these values were 1.56, 1.01, 1.18, and 1.44 dB for listeners CO, DM, AB, and NJ, respectively. In all cases, M1 was a less effective masker than M2, requiring a higher spectrum level to mask the signal. Notice also that as the signal level was increased by 20 dB, from 10- to 30-dB sensation level, the masker level required usually increased by more than 20 dB. The increase was greatest for M1. Following the arguments of Plack and Oxenham (1998), this nonlinear growth may be considered a consequence of cochlear nonlinearity, with the masker subject to higher levels of compression than the signal over the range of levels used. Since M1 was higher in level than M2, it is likely that M1 was compressed more than M2, which may explain why the nonlinear growth was more pronounced for M1. The fact that nonlinear growth was observed at 250 and 500 Hz, as well as at 4000 Hz, suggests that there is substantial compression at all three frequencies. This is essentially the same finding reported by Plack and Drga (2003).

Table 2.

The results of Experiment 1 showing the masker spectrum levels (in dB) required to mask the signal as a function of signal frequency and signal sensation level

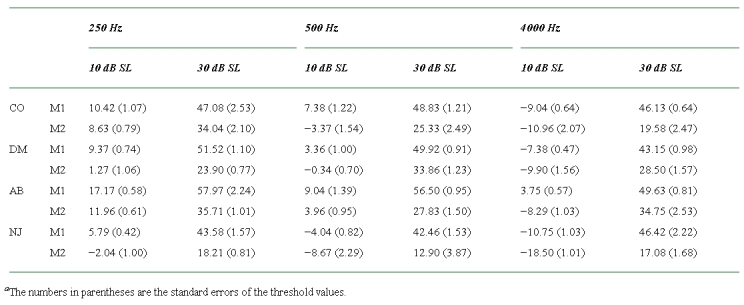
Figure 2.

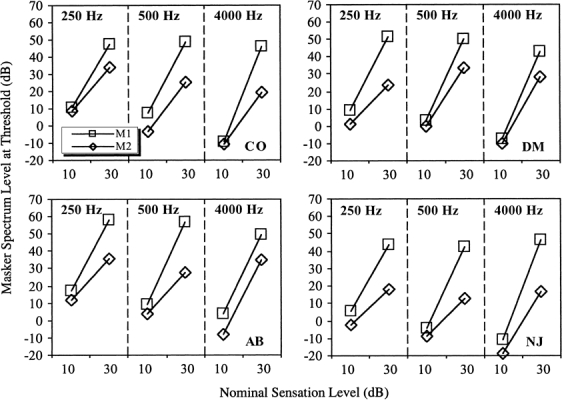
The results of Experiment 1, showing the masker spectrum levels required to mask the signal as a function of signal frequency and signal sensation level.

EXPERIMENT 2: SIGNAL THRESHOLDS IN PRESENCE OF EQUALLY EFFECTIVE FORWARD MASKERS

Conditions

In Experiment 2, the effect on signal threshold of combining two equally effective forward maskers was measured. The masker levels used were those measured in Experiment 1 (see Table 2). The signal thresholds for the individual maskers should be similar to the signal levels used in Experiment 1 (see Table 1). Rather than relying on this prediction, however, and to allow for a full randomization of conditions, it was decided to measure signal threshold in the presence of M1 and M2 combined and when presented as individual maskers. In other words, three signal thresholds were measured for each signal frequency and for each nominal sensation level. Conditions were presented in a random order. Using this procedure meant that it was not necessary that M1 and M2 were exactly equally effective maskers. So long as their masking effects were not too dissimilar, a reasonably accurate estimate of compression could be obtained from an analysis of the three thresholds.

Results

The results are shown in Table 3 as threshold values in dB SPL. The results are also plotted in Figure 3, expressed in terms of sensation level. The average standard errors for these values were 0.78, 0.82, 0.91, and 1.44 dB for listeners CO, DM, AB, and NJ, respectively. As expected, the thresholds for the single-masker conditions were generally similar to the nominal sensation levels (i.e., the signal levels used in Experiment 1 to determine the masker levels used in Experiment 2). For CO at 500 and 4000 Hz, DM at 4000 Hz, and AB at 500 Hz, the single-masker thresholds at the 30-dB sensation level were slightly lower than predicted. This may reflect an effect of practice between the two experiments. However, since the conditions were fully randomized in Experiment 2, and since the estimated compression exponents depended on the relative increase in threshold from one masker to two, this was not considered to have important consequences for the interpretation of the results.

Table 3.

The results of Experiment 2 showing the signal levels at threshold (in dB SPL) in the presence of Masker 1 alone (M1), Masker 2 alone (M2), and Masker 1 and Masker 2 combined (M1 + M2)

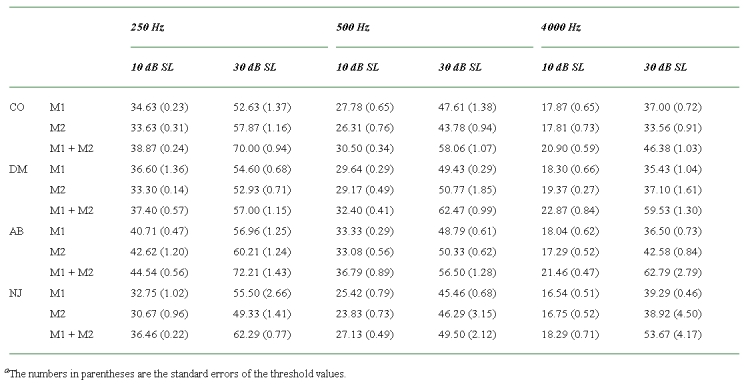
Figure 3.

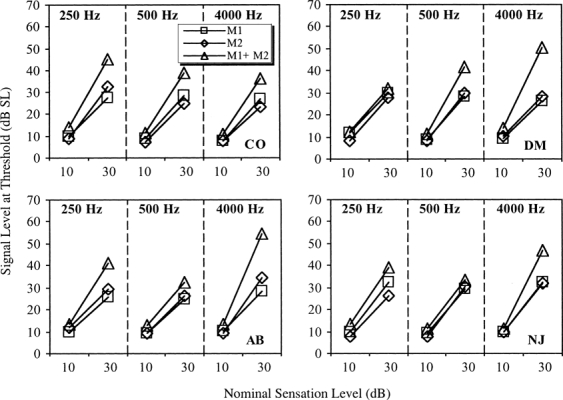
The results of Experiment 2 showing the signal levels at threshold (in dB sensation level) in the presence of Masker 1 alone (M1), Masker 2 alone (M2), and Masker 1 and Masker 2 combined (M1 + M2).

The pattern of results for the combined-masker conditions (M1 + M2) at a sensation level of 10 dB showed little variation across listeners. In all cases there was only a small increase in threshold compared with the single-masker conditions. In contrast, the results at a sensation level of 30 dB varied considerably between the four listeners. In most cases, considerable excess masking was observed, with the thresholds for the combined-masker conditions being much higher than the single-masker conditions, which is consistent with a compressive response to the signal. The exceptions to this were DM at 250 Hz and NJ at 500 Hz, where little excess masking was observed. It should be noted that the main source of the variability in the data was between listeners rather than within listeners. The standard errors show that there was generally little variability between replications for a given listener.

Calculation of compression exponents

The derivation of the compression exponent from the signal threshold data was based on the power-law formulations described by Lutfi (1983, 1985), Humes et al. (1988), Humes and Jesteadt (1989), and Oxenham and Moore (1994, 1995). The overall approach rests on a number of assumptions, the validity of which will be considered in the Discussion section. With specific regard to the derivation, it was assumed that the ratio of the internal (i.e., postcochlear) signal intensity to the internal (or effective) masker intensity is a constant at signal threshold. It was also assumed that the internal signal intensity is a power-law transformation of physical signal intensity. Hence,

where I_M represents the internal effect of the masker, S_M is the physical signal intensity at masked threshold, c is the compression exponent, and k is a constant. It was assumed further that the effect of combining two maskers is a linear summation of their individual effects. Hence,

Substituting Eq. (1) in Eq. (2) and factoring out the constant k leaves:

In other words, if S_M1+M2 (the signal intensity at threshold for the combined maskers), S_M1 (the signal threshold for M1 alone), and S_M2 (the signal threshold for M2 alone) are all known, it is possible to determine the compression exponent c. This was achieved using the “Solver” algorithm in Microsoft Excel^® 2001 (Microsoft Corp., Redmond, WA). The compression exponents derived from the data are shown in Table 4 and Figure 4, together with the reciprocal mean (the reciprocal of the mean of the reciprocals of these values) and the median. It was decided to use the reciprocal mean because the compression exponents have a linear relationship with the reciprocal of the difference in the signal levels at threshold between the single-masker and combined-masker conditions. To put it another way, a given change in signal threshold has a much larger effect on the estimated compression exponent when the excess masking is low than when it is high. It is reasonable, therefore, to weight large exponents less than small exponents when calculating the mean.

Table 4.

The compression exponents derived from the masking results of Experiment 2

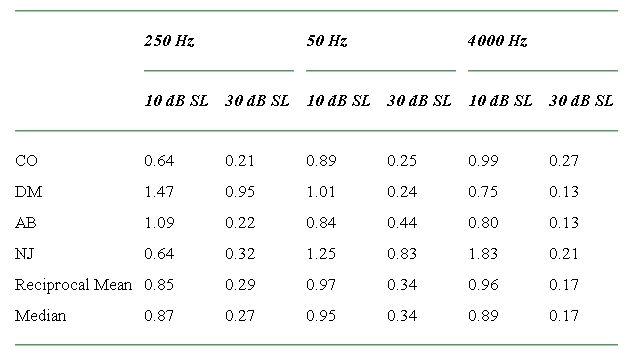
Figure 4.

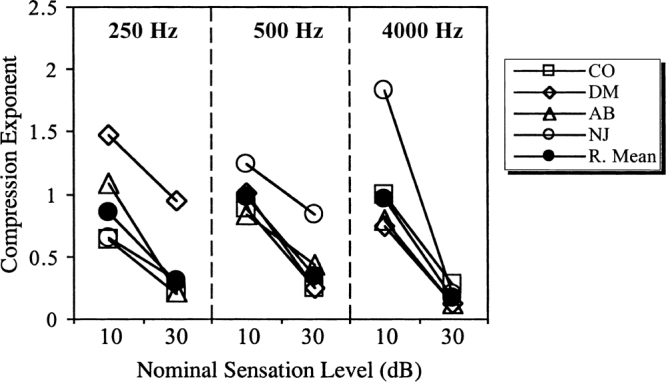
The compression exponents derived from the results of Experiment 2. The filled symbols show the reciprocal of the mean of the reciprocals of the individual exponents derived from the four listeners (see text for details).

The compression exponents for the low signal level (nominally, 10-dB sensation level) were fairly constant across listener and frequency. As indicated above, a certain amount of variability is expected when the combined-masker thresholds are only slightly greater than the single-masker thresholds, since in this region the compression exponent is extremely sensitive to changes in masker level. For example, if the combined-masker thresholds were equal to the single-masker thresholds, then the derived exponent would be infinite. Just a 3-dB increase in the combined-masker threshold brings the exponent down to 1. Taking this into account, the results overall suggest that the system is roughly linear at low sensation levels across all frequencies.

The compression exponents for the higher signal level (nominally, 30-dB sensation level) at 4 kHz were also reasonably similar for the four listeners. The results indicate substantial compression, with exponents ranging from only 0.13 for listeners AB and DM to 0.27 for listener CO. The results for the two lower frequencies at the higher signal level were more variable across listeners. Listener DM showed an almost linear exponent (0.95) at 250 Hz, and listener NJ showed a similar exponent (0.84) at 500 Hz. The remaining values all indicate substantial compression, with exponents ranging from 0.21 (CO at 250 Hz) to 0.44 (AB at 500 Hz). Despite the variability, it can be stated that every listener showed substantial compression for at least one of the two lower frequencies tested in the experiments. In addition, all the listeners showed a decrease in the compression exponent as the sensation level was increased. It should be emphasized again that the main variability seen here is between listeners, not within listeners. For a given listener, the compression exponents were generally well defined by the data.

A two-factor (sensation level × frequency) repeated-measures analysis of variance (ANOVA) was conducted on the reciprocals of the compression exponents. The ANOVA revealed a significant effect of sensation level [F(1,3) = 78.40, p = 0.003] but no significant effect of frequency [F(2,6) = 2.15, p = 0.197] and no significant interaction [F(2,6) = 3.72, p = 0.089]. Paired comparisons (Tukey) revealed that the compression exponents for the 10-dB sensation level were significantly greater than the exponents for the 30-dB sensation level at all three frequencies: 250 Hz (q = 5.31, p < 0.05), 500 Hz (q = 4.53, p < 0.05), and 4000 Hz (q = 11.85, p < 0.01).

DISCUSSION

Assumptions of the approach

Independent compression

The derivation of compression exponents from the additivity data depends on a number of assumptions. First, it is assumed that the two maskers and the signal are all compressed independently and that they do not influence the internal representations of each other. In many forward masking studies this is a reasonable assumption to make, since the gap between the masker and the signal is such that there is little chance of an interaction between the two on the BM. In the present experiments, on the other hand, the offset of M1 coincided with the onset of M2, and the offset of M2 coincided with the onset of the signal. The temporal proximity was necessary to ensure that the masker levels needed were less than the maximum output of the apparatus. However, spacing the stimuli so closely does raise the possibility that there was overlap between M1 and M2, and between M2 and the signal, on the BM. The risk was greatest for the lower signal frequencies, since the temporal response of the BM is longest at low CFs.

Predicting the exact effect of the overlap is problematic, partly because it is not clear how the nonlinearity interacts with the temporal response of the BM. (To take an extreme example, if the stimuli were compressed before filtering, the overlap produced by the filtering would have no effect on the compression estimate, since the compressed stimuli would be combined in a linear way, as assumed by the model.) However, a rough estimate of the degree of overlap can be made by passing the stimuli through a linear bandpass filter that simulates the response of the BM. According to Glasberg and Moore (1990), at a center frequency of 250 Hz the equivalent rectangular bandwidth (ERB) is 52 Hz. This bandwidth was used to derive the impulse response of a second-order gammatone filter (Patterson et al. 1988). The impulse response was convolved with representations of M1, M2, and the signal, as used in the experiments. To reduce the variability, M1 and M2 were replaced by 250-Hz sinusoids with the same temporal characteristics as the maskers used in the experiments. The peak levels of M1, M2, and the signal used in the simulation were the same.

Figure 5 shows the simulated BM excitation level produced by the three stimuli as a function of time. Excitation level was taken as the envelope of the gammatone output expressed in dB. While there is some overlap between the stimuli, the effect is not too severe. Around the time of the peak response to M2, the excitation level of M1 has decayed by about 35–40 dB. It is unlikely, therefore, that the overlap between M1 and M2 was a very significant factor, except perhaps when M1 was much higher in level than M2. At the two lower frequencies and a sensation level of 30 dB, the level difference between M1 and M2 was large for DM at 250 Hz (27.6 dB), AB at 500 Hz (28.7 dB), and NJ at 500 Hz (29.6 dB).

Figure 5.

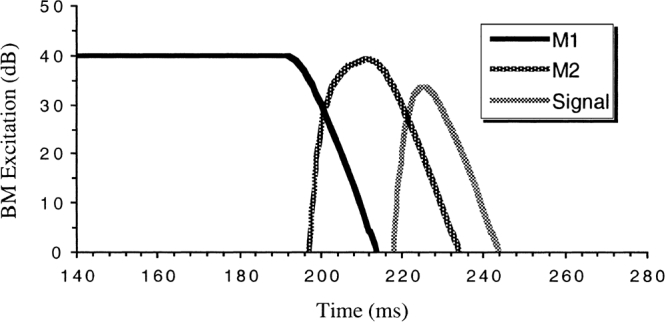
A simulation of the level of excitation on the BM (as a function of time) produced by M1, M2, and the signal. All three stimuli were presented at the same peak level and had the same temporal characteristics as the stimuli used in the experiments. The stimuli were passed through a second-order gammatone filter with a bandwidth of 52 Hz. Time is measured relative to the onset of M1.

The degree of overlap between M2 and the signal in the simulation suggests that the highest ratio of signal-to-masker excitation on the BM may have been about 20 dB, if it is assumed that M2 and the signal had the same peak level. Based on the ERB equation of Glasberg and Moore (1990), the noise power passed by the auditory filter would have been about 17 dB [10 log₁₀(52)] above the spectrum level at 250 Hz and about 19 dB [10 log₁₀(79)] above the spectrum level at 500 Hz. In all cases bar one (DM at 500 Hz and 30 dB), the signal level used in the experiments was greater than the level of M2 per ERB, so the difference in BM excitation levels would have been at least 20 dB. It is unlikely, therefore, that overlap between M2 and the signal on the BM had a significant effect on the results.

If temporal overlap did have any effect, it would most likely have led to an underestimate of the amount of compression. The combined effects of two maskers (and therefore the amount of excess masking) will be greatest when they are compressed before summation, as opposed to after summation. For example, consider the extreme case where the two maskers are gated together. In this case, adding two equally effective maskers will produce about a 3-dB increase in the physical level of the combined-masker over the single-masker condition. Now if the masker is subjected to 3:1 compression, this will be equivalent to a 1-dB increase in the BM response. If the signal is in the linear region of the BM response, then the physical signal level will have to increase by only 1 dB to maintain the signal-to-masker ratio. If the signal is also subject to 3:1 compression, then the physical signal level will have to increase by 3 dB. In both cases, the compression exponents derived from Eq.(3) (3 and 1) will be greater than the true exponents of the compression applied to the signal (1 and 0.33). The effects of an overlap between M2 and the signal are not so obvious. However, it has been shown that suppression produces a partial linearization of the BM response (Ruggero et al. 1992). If the signal was suppressed by M2, then the observed compression would have been less than that in the absence of suppression.

In summary, temporal overlap between the stimuli on the BM probably occurred at 250 and 500 Hz. If anything, the effect of the overlap would have been an underestimation of compression at these frequencies. It is very interesting to note, therefore, that the three cases where overlap between M1 and M2 was probably greatest (DM at 250 Hz, AB and NJ at 500 Hz) also produced the smallest compression estimates (largest exponents) for the 30-dB sensation level. It is tempting to suggest temporal overlap as a possible reason for these anomalous results.

Detection cues

Another assumption of the approach is that the same detection cue (the level change produced by the addition of the signal) was used in the combined-masker conditions as in the single-masker conditions. It is conceivable that this may not have been the case. For example, if the signal were detected by virtue of the increase in total stimulus duration produced when added to M2, then the further addition of M1 could have removed this cue by making the combined-masker duration too long for duration discrimination to occur: The duration just noticeable difference is about 10–20% (Abel 1972). Another (related) possibility is that a long-duration combined masker could have increased the possibility of confusion as to where the masker ends and the signal starts, so raising threshold (Neff 1986). Although both of these effects could, in principle, have led to excess masking in Experiment 2, this is considered unlikely for two reasons: First, little excess masking was observed at the lower signal level. It is hard to explain why a problem with duration discrimination or confusion should be manifest only at the higher level. Second, the noise had a wide bandwidth (1000 Hz at 250 and 500 Hz, 2800 Hz at 4 kHz). This bandwidth should be wide enough to clearly distinguish the masker offset from the signal onset, and so encourage listeners to detect the signal as a separate auditory event rather than as a continuation of the masker (Moore and Glasberg 1982).

Noise floor

A final assumption of the model is that the results were unaffected by an internal “noise floor.” Other models of masker additivity have included an additional additive masker to simulate absolute threshold (Humes and Jesteadt 1989; Oxenham and Moore 1995). The way the compression exponent was derived from the masking data in the present study meant that it was difficult to add an internal noise component. This was because the model assumes the compression exponent is independent of level. While this is a reasonable assumption over a small range of levels, it is probably not correct to assume that the compression is the same at absolute threshold as it is at the masked thresholds.

For the 30-dB sensation level, this omission should not be a major problem, as any noise floor should be too far below the signal level to make a significant contribution to masking. For the 10-dB sensation level, however, the proximity of absolute threshold may have influenced the results, so it is worth exploring this possibility. Adding a noise floor to the masker means that Eq. (1) becomes:

where N is the intensity of the noise floor. Substituting in Eq. (2) gives:

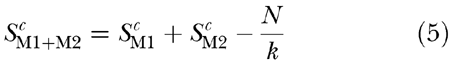If it is assumed that the values of k and c are the same at absolute threshold as they are at higher levels:

where S₀ is the intensity of the signal at absolute threshold. Substituting into Eq. (5) gives:

A rough estimate of the effect of a noise floor on the compression estimates can be obtained by assuming that the system is almost linear at low levels. If S_M1+M2 = 2S_M1 = 2S_M2 (3-dB increase, no excess masking), and if S₀ is zero (no noise floor), the value of c is 1. If the masked thresholds are kept the same but the intensity of S₀ is set to one tenth the intensity of S_M1 and S_M2, as would be the case at a sensation level of 10 dB, then solving Eq. (7) gives c = 0.91. So it is possible that the omission of a noise floor may have produced around a 10% overestimate of the compression exponent at the 10-dB sensation level.

Comparison with previous studies

The derived compression exponents for the signals presented at 10-dB sensation level are consistent with previous results suggesting that the BM is roughly linear at low levels (Cooper and Yates 1994; Cooper and Rhode 1995; Rhode and Cooper 1996; Zinn et al. 2000). The compression exponents for the 30-dB sensation level at 4 kHz are also consistent with previous physiological and psychophysical data that suggest that the cochlea is highly compressive at high CFs and moderate sound levels. The mean value of 0.17 is very similar to the value of 0.16 estimated by Oxenham and Plack (1997) at 6 kHz and is also consistent with estimates from direct BM measurements. In these two respects, the present data match the previous findings very well, which suggests that the technique may have some validity as a means of estimating cochlear compression.

In contrast, the compression exponents for the higher signal levels at the two lower frequencies are not consistent with many of the previous estimates. The present results suggest that there is substantial auditory compression at low CFs. There is some indication that the system is more linear at the lower frequencies than at 4 kHz. However, the mean compression exponents of around 0.3 at 250 and 500 Hz are less than the value of 0.5 estimated by Cooper and Rhode (1995) at 500 Hz, and much less than the nearly linear response reported in some other studies (Hicks and Bacon 1999; Plack and Oxenham 2000; Zinn et al. 2000). It should be remembered, however, that the psychophysical estimates relied on the assumption that the response to a below-CF tone is linear. This assumption has been questioned recently (Lopez-Poveda et al. 2003; Plack and Drga, 2003). The discrepancy becomes even more apparent when the individual results are examined. As described previously, it is possible that the compression estimates for the 30-dB sensation level for DM at 250 Hz and for AB and NJ at 500 Hz were affected by overlap between M1 and M2 on the BM. If these results are removed, the reciprocal means for the 30-dB sensation level are 0.24 at both 250 and 500 Hz. Four of the individual compression exponents for the low frequencies were between 0.21 and 0.25.

The low-frequency results are consistent with the recent forward masking data of Lopez-Poveda et al. (2003) and Plack and Drga (2003). Unlike previous psychophysical measurements, these studies did not rely on the assumption of below-CF linearity. Lopez-Poveda et al. estimated compression exponents in the range 0.2–0.3 across frequencies from 500 to 8000 Hz. Similarly, Plack and Drga estimated compression exponents in the range 0.2–0.3 at 250 and 500 Hz. The results are also consistent with other psychophysical findings. For instance, there is very little variation across frequency in the shallow growth of loudness with intensity, at least for frequencies above 100 Hz (Robinson and Dadson 1956). It has been suggested that loudness may be a linear function of BM intensity (Schlauch et al. 1998). Hence, the finding of shallow loudness growth with level at low frequencies is suggestive of high cochlear compression at low CFs. Furthermore, Oxenham and Dau (2001) reported large effects of the relative phase of harmonics on the amount of masking produced by a complex tone, even down to signal frequencies of 125 Hz. An effect on masking of harmonic phase, which alters the crest factor of the waveform, is taken as evidence for auditory compression.

Where is the source of the low-frequency compression?

Although the results have been presented in a way that implies that the additivity technique is measuring peripheral processes, this cannot be confirmed directly. Psychophysical measurements are influenced by the characteristics of the whole system from stimulus to response. The close correspondence between the psychophysical data and the BM measurements at high CFs suggests that the former reflect cochlear processing. However, such a correspondence was not found between the present results and the physiological results at low CFs. One possibility is that the discrepancy reflects a real interspecies difference. Another possibility is that the apical surgical procedure used in the BM measurements may compromise the highly sensitive physiological processes that are thought to underlie the nonlinearity. A third possibility, however, is that the compression measured by the forward masking techniques is postcochlear in origin, perhaps reflecting the saturation of nerve fibers elsewhere in the auditory system. As pointed out by Plack and Drga (2003), it seems unlikely that the low-CF saturation is at the level of the auditory nerve. Recordings from the guinea pig suggest that the rate-level functions of auditory nerve fibers seem to exhibit slightly less saturation as CF is decreased (Sachs and Abbas 1974; Cooper and Yates 1994).

The issue may be resolved by measuring compression at low CFs in listeners with sensorineural hearing loss at these frequencies. If the compression is cochlear in origin, then these listeners may show less compression at low CFs than normals. On the other hand, if the compression is postcochlear, then there should be little difference between the estimated compression exponents for impaired listeners and normals, once the overall reduction in sensitivity is taken into account.

CONCLUSIONS

At a low sensation level of 10 dB, two nonoverlapping forward maskers showed nearly linear additivity in their masking effects at all frequencies tested (250, 500, and 4000 Hz). When combined, the two equally effective maskers produced around 3 dB more masking than when presented individually.

At a higher sensation level of 30 dB, considerable excess masking was observed at all three frequencies. When combined, the two equally effective maskers generally produced much more than the 3-dB increase expected on the basis of linear additivity.

The results of this study are consistent with a high degree of auditory compression (exponents around 0.17) at high CFs. Although the estimated compression was less at the two lower frequencies, the derived values (exponents around 0.3) are still indicative of substantial nonlinear processing in these frequency regions.