Synthetic incoherent feedforward circuits show adaptation to the amount of their genetic template

Variable gene dosage is a major source of fluctuations in gene expression in both endogenous and synthetic circuits. Synthetic incoherent feedforward regulatory motifs using RNA interference are shown to robustly adapt to changes in DNA template amounts in mammalian cells.

Abstract

Natural and synthetic biological networks must function reliably in the face of fluctuating stoichiometry of their molecular components. These fluctuations are caused in part by changes in relative expression efficiency and the DNA template amount of the network-coding genes. Gene product levels could potentially be decoupled from these changes via built-in adaptation mechanisms, thereby boosting network reliability. Here, we show that a mechanism based on an incoherent feedforward motif enables adaptive gene expression in mammalian cells. We modeled, synthesized, and tested transcriptional and post-transcriptional incoherent loops and found that in all cases the gene product adapts to changes in DNA template abundance. We also observed that the post-transcriptional form results in superior adaptation behavior, higher absolute expression levels, and lower intrinsic fluctuations. Our results support a previously hypothesized endogenous role in gene dosage compensation for such motifs and suggest that their incorporation in synthetic networks will improve their robustness and reliability.

Introduction

Biological networks typically contain small-scale subnetworks of recurring topology called ‘motifs’ (Milo et al, 2002; Balazsi et al, 2005; Ma'ayan et al, 2005). The most common motifs are feedforward and feedback (autoregulatory) loops (Shen-Orr et al, 2002), with the former being largely dominated by an ‘incoherent’ connectivity (Mangan and Alon, 2003) in bacteria (Mangan et al, 2006) and yeast (Lee et al, 2002). Incoherent feedforward motifs were also observed in mammalian cells (Boyer et al, 2005), although to the best of our knowledge their prominence remains to be determined. The canonical three-node incoherent loop contains input, auxiliary regulator, and output nodes. The output is controlled directly by the input and the auxiliary regulator. The latter is also controlled by the input, introducing an additional indirect effect of the input on the output. In incoherent loops, the input controls the auxiliary regulator node in such a way that input's overall indirect action on the output via this node counteracts its direct effect. In a motif named ‘type I incoherent feedforward loop’ (I1-FFL), the input's direct effect is activating, as is its control of the auxiliary node, while the auxiliary node controls the output through repression. Because this motif comprises about 30% of all three-node interaction loops in transcriptional circuits (Mangan et al, 2006), a number of studies have attempted to uncover the reasons behind its prevalence by artificially creating plausible operating scenarios and testing whether the topology is superior to alternative arrangements.

One line of research studied transcription factor (TF)-based motifs by experimentally perturbing small molecule TF cofactors. Using this setup, a synthetic incoherent motif was shown to act as pulse generator in cell communication experiments (Basu et al, 2004), while in another study (Mangan et al, 2006) a naturally occurring motif embedded in a galactose utilization pathway produced a faster response to its cognate environmental signal compared with the baseline. Other studies showed that steady-state output levels peak at an intermediate input level, generating a non-monotonic transfer function in synthetic (Entus et al, 2007) and natural (Kaplan et al, 2008) systems. Recently, the topology has been shown to enable a ‘fold-change’ detection in the strength of the input signal when the intensity of the transient response was used as output (Goentoro et al, 2009) (provided that certain scaling transformations preserve the form of the system (Shoval et al, 2010)) and to possess a type of ‘memory’ effect of the intensity of previously seen step signals (Sontag, 2010).

Enzyme-based incoherent motifs were identified and classified in a study that sought adaptive properties in a computationally generated library of network topologies in signaling pathways (Ma et al, 2009). In such a motif, enzyme A (input) activates enzyme C (output) as well as enzyme B (auxiliary regulator) that in turn inactivates enzyme C. The enzymatic circuit functions as a pulse generator, similarly to its transcriptional counterpart. Similar architectures had been devised earlier from first principles (Tyson et al, 2003) and analyzed from a theoretical standpoint (Sontag, 2010). Finally, it was mathematically shown that two-component genetic circuits with elements of opposite regulatory activity constitute the minimal requirement for network-dosage invariance (Acar et al, 2010).

We propose a novel implementation of the I1-FFL, where the input (black circle in Figure 1A) is a DNA fragment coding for both the auxiliary regulator (brown circle) and the output (red circle), with the regulator negatively affecting the output. We might expect the transient and steady-state input–output relation of our circuits to be similar to those of the previously described systems. However, while enzymatic or TF inputs can be experimentally modulated in single cells in a temporal manner, it is not so with DNA inputs. Therefore, our main interest lies in the steady-state relation between the amount of DNA template and the amount of the output protein. Aforementioned studies showed pulse-like output response, or output adaptation, to abrupt temporal changes in the input, meaning that different input levels generate the same output in the steady state. This leads to a conjecture that in our circuits, the steady-state output levels will not depend on the number of DNA molecules that code for the circuit, a property we also call adaptation. An affirmative answer to this conjecture would add experimental support to the hypothesis (Veitia et al, 2008) that similar circuitry might be employed by cells to implement gene dosage compensation in the context of neuronal homeostasis (Tsang et al, 2007), sex determination (Lucchesi et al, 2005), and ploidy changes. It would also suggest that such circuits could become valuable tools (Holtz and Keasling, 2010) in the construction of increasingly complex synthetic networks (Russell and Aloy, 2008; Cantone et al, 2009; Lu et al, 2009) because they will contribute to overall robustness of the system by decreasing natural variability in the circuits' components.

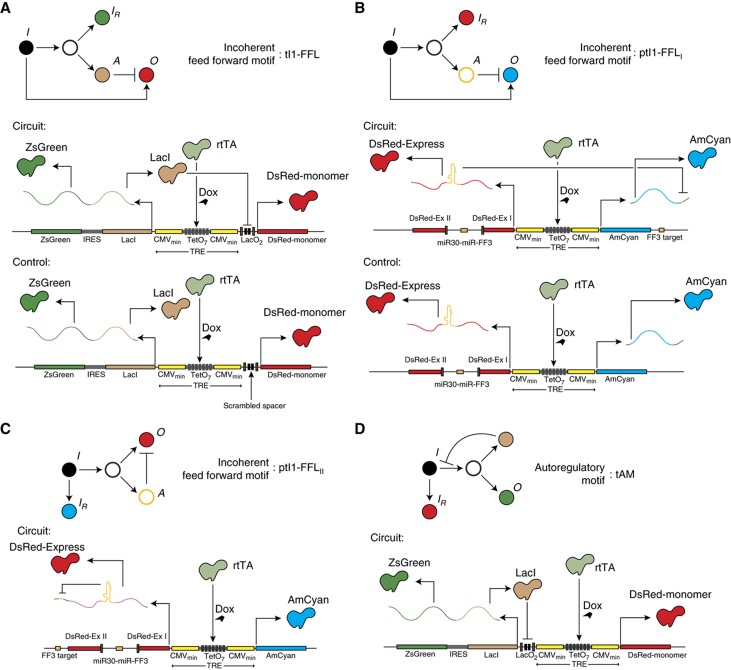
Figure 1.

Schematics of the synthetic networks. Pointed and blunt arrows denote activation and repression, respectively. In all constructs, the output protein and the repressor are transcribed from the same bidirectional promoter in the constant and non-limiting presence of the TF rtTA that does not constitute an input to the system. In the diagrams, I indicates input node, I_R is the input reporter, A is the auxiliary regulator, and O is the output. (A) Transcriptional type I incoherent feedforward motif (tI1-FFL): the output protein is DsRed and the auxiliary repressor is LacI. The plasmid copy number is reported by the ZsGreen1 fluorescent protein, cotranslated with the LacI protein using IRES. Corresponding control circuit is also shown. (B) Post-transcriptional type I incoherent feedforward motif version I (ptI1-FFL_I): the output protein is AmCyan and the auxiliary repressor is a microRNA. Plasmid copy number is reported by the DsRed protein coexpressed with the output. DsRed mRNA also contains an intron coding for the regulator microRNA. Corresponding control circuit is also shown. (C) Post-transcriptional type I incoherent feedforward motif version II (ptI1-FFL_II): the output protein is DsRed, repressed by a microRNA processed from the intron in its own mRNA. The input is reported by the divergently expressed AmCyan protein. The control circuit is identical to the one in (B). (D) Transcriptional negative autoregulation motif (tAM): auxiliary repressor LacI becomes the output and represses its own transcription as well as the level of the ZsGreen output reporter contranslated via IRES. The input is reported by a divergently expressed DsRed protein.

We tested our circuits in mammalian cells, motivated by their potential relevance to eukaryotic dosage compensation and to mammalian synthetic biology, and in order to explore RNA interference (RNAi) as a negative regulation mechanism. We compared them to a negative autoregulatory motif (Becskei and Serrano, 2000; Isaacs et al, 2003) that had been shown in bacteria to weaken the dependency of the expression level on DNA template amount as well as to reduce protein expression fluctuation.

Results

Study rationale and circuit details

In order to explore the input–output behavior of any given system, and specifically adaptation, one needs to generate a wide range of input values and measure the corresponding outputs. Here, to test our hypothesis regarding I1-FFL adaptation to copy number, we relied on transient transfection of DNA plasmids into mammalian cells that generates large variability in the number of plasmids internalized by individual cells. Single plasmids were used to encode all circuit components in order to minimize irrelevant fluctuations typical of plasmid cotransfection. The circuit's input, that is, the number of plasmid copies in a cell, is determined using a constitutively expressed fluorescent protein. Published literature generally supports the view that in transient transfections, fluorescence depends linearly on the copy number of transfected plasmids (Tseng et al, 1997; Pollard et al, 1998; Cohen et al, 2009; Schwake et al, 2010); in addition, we verified this assertion experimentally as shown below. While strictly speaking, this reporter level also depends on many other potentially fluctuating parameters such as global synthesis and degradation rates, it is the differences in the copy number that are the major source of cell-to-cell variability in transient transfections. Therefore, as a first approximation, the copy number is considered as the sole contributor to the differences in reporter levels. Another fluorescent protein, whose expression is controlled by the input and the auxiliary regulator, serves as the output.

We considered three motif variants to test the effect of both transcriptional and post-transcriptional repression by the auxiliary node (Figure 1A–C). In the first variant, a transcriptional repressor LacI coexpressed with the DsRed-monomer output downregulates this output via binding to LacO operator in its promoter, implementing a transcriptional tI1-FFL (Figure 1A). Four LacO mutants are used to quantify the effect of weakened LacI binding on circuit performance, while the plasmid copy number is judged by the level of ZsGreen1 fluorescent reporter that is cotranslated with LacI using an internal ribosome entry site (IRES). Control circuit for this motif contains fully scrambled spacer instead of LacO-binding site. In the second variant, a post-transcriptional type I incoherent feedforward motif version I (ptI1-FFL_I; Figure 1B), the auxiliary regulator is a synthetic microRNA (miR-FF3) that targets a complementary RNA sequence fused into the 3′-UTR of the output AmCyan mRNA (Rinaudo et al, 2007). miR-FF3 is processed post-splicing from an intron (Leisner et al, 2010) inserted between two exons coding for a fluorescent protein DsRed-Express. Corresponding control circuit does not contain a target site for miR-FF3, eliminating the RNAi against AmCyan. The third variant of an incoherent motif uses a negative miR regulator that is processed from an intron fused into a protein-coding mRNA; the miR then downregulates this mRNA post-splicing (Figure 1C). This post-transcriptional I1-FFL version II (ptI1-FFL_II) utilizes the same DsRed–miR-FF3 fusion construct as ptI1-FFL_I but this time the FF3 target is inserted into 3′-UTR of DsRed mRNA itself. In this particular topology, unspliced RNA that is the input for the motif generates the output mRNA as well as the miR regulator of this output. If the regulator acted on the unspliced RNA molecule then the topology would become that of negative autoregulation, but that is not the case here, as the splicing is completed before the miR enters the RNAi pathway. The AmCyan fluorescent protein, divergently expressed from a pTRE promoter, serves as a copy number reporter. Control construct for this last motif is identical to the one used for version I circuit, because RNAi against DsRed is non-functional due to the absence of miR-FF3 target in DsRed 3′-UTR.

We compare the behavior of our circuits with the well-studied negative feedback motif (Figure 1D). This transcriptional autoregulatory motif (tAM) was constructed by inverting the promoter region of the tI1-FFL, thus placing the LacO sequences in front of the LacI-coding frame. As a result, the LacI protein represses the transcription of its own mRNA, and the circuit's output is now reflected in the level of ZsGreen1 reporter, while the copy number is judged based on the divergently expressed DsRed protein.

Modeling of input–output relation

We preceded our experiments with mathematical modeling and computer simulations in order to gain insight into circuits' qualitative behavior (for details, see Supplementary Information). First, we ran numerical simulations using the Matlab SimBiology toolbox. Second, we derived a set of ordinary differential equations based on our current mechanistic understanding of individual interactions in the motifs, and studied the circuits analytically. Numerical simulations show that the output of all incoherent motifs adapts to copy number changes (Figure 2A and B) and the input–output response is well fitted by a ‘rational function’ (Supplementary Figure S1A and B; Supplementary Table S1), where the nominator and the denominator are first-degree polynomials. Weaker inhibition results in slower adaptation, eventually leading to a linear input–output mapping. This is manifested by the gradual increase in EC₅₀ values, that is, input values at which the output reaches half of its saturated value (Figure 2C and D).

Figure 2.

Simulations for the transcriptional and post-transcriptional (ptI1-FFL_I) type I incoherent feedforward motif. (A) Noise-free parametric simulations of the tI1-FFL with increasing binding strength of the LacI inhibition, from weak inhibition case (black curve) to strong inhibition (orange curve). Binding rate constants in 1/(mol^*sec) units used to generate the different curves are similarly color coded. (B) Noise-free parametric simulations of the ptI1-FFL_I with increasing efficiency of the miRNA inhibition, from weak inhibition (gray curve) to strong inhibition (green curve). Identically color-coded binding rate constant values are shown in 1/(mol^*sec) units. (C) Fitted EC₅₀ values of the simulated tI1-FFL response for the binding rate constants in panel (A). (D) Fitted EC₅₀ values of the simulated ptI1-FFL_I response for the binding rate constants in panel (B). (E) Two special cases in circuits' response. The orange curve shows a biphasic input–output behavior of the tI1-FFL, while the green curve shows the first derivative of the output in ptI1-FFL_I consistent with the transition from a saturated to a proportional response. (F) Noisy simulations of the tI1-FFL for increasing binding of the LacI. The colors correspond to the LacI-binding rate constants in panel (A). (G) The coefficients of variation obtained in the noisy simulations of tI1-FFL. The colors correspond to the LacI-binding rate constants of panel (A). (H) Noisy simulations of the ptI1-FFL_I for increasing strength of the miRNA binding. The colors correspond to the binding rate constants in panel (B). (I) Coefficients of variation of the noisy simulations of the ptI1-FFL_I. The colors correspond to the miRNA-binding rate constants of panel (B).

The qualitative ODE analysis (Supplementary Figure S6) reproduced numerical simulations and provided important additional information about the system. We found that when LacI di- and tetramerization are very fast and essentially irreversible resulting in no detectable degradation of LacI monomers and dimers, and LacI tetramer degradation rate is low, the output (y) depends on the input (x) according to the following Michaelis–Menten form

for positive constants V and K, where the constant K is directly proportional to the strength of LacI binding to the LacO operator. In the unrepressed case (K=0), y is simply proportional to x. As a way to model a non-zero mean value of the output when the copy number is zero (important when fitting flow cytometry data), we modify the above formula to the more general form

or, using different parameterization,

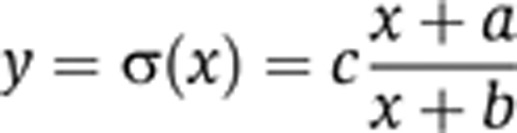We observe that all the above formulas belong to the category of rational functions that exhibit saturating behavior in agreement with our numerical simulations. When no assumptions are made regarding LacI multi-merization, while still assuming that the degradation of the LacI species is very slow, we obtain

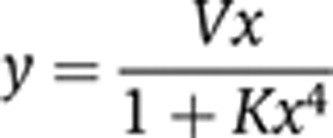Note that this is a ‘biphasic’ function that increases from zero to some maximal value and then decreases to zero (Figure 2E, orange curve).

We next analyzed the model of the ptI1-FFL_I circuit, and again concluded that the output saturates with increasing input. However, for high copy numbers and low concentrations of RNA-induced silencing complex (RISC), we observe that an increase in the copy number does not lead to an increase in the feedforward inhibition due to saturation of RISC, resulting in the loss of adaptive behavior. We plot a derivative dy/dx of this response (Figure 2E, green curve) with low derivative values at low input values characteristic of adaptation, and high values at high input values indicating linear dependency.

Modeling of noisy data

Next, we attempted to generate in silico flow cytometry data likely to be obtained in transient transfections by executing the code multiple times, each time corresponding to a single-cell readout. The consecutive runs differed in their initial conditions and the parameter values in order to reflect copy number variability between different cells in transient transfection as well as fluctuations in individual cells (i.e. intrinsic noise). Since the values for neither variability nor fluctuations can be obtained from first principles, we measured them in a number of control experiments. First, copy number distribution was measured using transiently transfected ZsGreen1-encoding plasmid. The amplitude of the measured fluorescence was assigned to correspond to 100 plasmid copies based on our experimental estimation (see below), and the distribution redrawn in copy number units assuming linear relationship between the fluorescence and the copy number (see below). Plasmid copy number was then picked randomly from that distribution and used as an initial condition for each code execution (Supplementary Figure S1C and D).

Second, we experimentally measured intrinsic noise in certain components of our system, that is, fluctuations in the relative protein amounts generated from the same DNA template. Two easily identifiable sources of fluctuations are coexpression from the bidirectional promoter and cotranslation from a bicistronic mRNA. In addition, one could expect fluctuations in the negative regulation step by an auxiliary node, meaning that for given steady-state levels of the regulator (e.g. LacI) and its target (e.g. pTRE-LacO-DsRed) the output (e.g. DsRed) levels in different cells will change stochastically due to uncertainty in the exact amount of active and inactive (e.g. bound to LacI) targets. These noisy steps combine to determine the distribution of the output values for a given input reporter value in our circuits. Fluctuations in the bidirectional promoter were measured by coexpressing AmCyan and DsRed from pTRE-Tight promoter (Supplementary Figure S1E); fluctuations in cotranslation were measured by coexpressing DsRed and ZsGreen from a bicistronic mRNA (Supplementary Figure S1F) driven by a constitutive CMV promoter.

The data were used to randomize parameter values and simulate a set of stochastic single-cell readouts. Those readouts are then processed as follows: (1) the range of input values is divided into a number of bins of equal width; (2) all ‘cells’ whose simulated input values fall into a particular bin are collected together and assumed to have the same input value, corresponding to the center of a bin; (3) the mean output values of these cells and the coefficient of variance (CV) of these values are used to determine, respectively, the mean circuit response and its intrinsic noise for this input. We apply the same procedure to the experimental data (Supplementary Figure S2A–D).

As shown in Supplementary Figure S1H, the CV is ∼0.25 for the bidirectional promoter and ∼0.3 for the IRES. When plugged into the simulation of tI1-FFL (Figure 2F and G), these values generate ∼0.35 variability in the negative control circuit variant without a functional LacO site, and the variability decreases slightly to ∼0.3 when we turn on LacI repression. However, experimental measurement of the negative control circuit showed variability of ∼0.55 (Supplementary Figure S1G and H), indicating that there are additional noise sources even in the absence of negative regulation. One possible reason for this increase is pTRE promoter symmetry breaking with a spacer. Similarly, we simulated ptI1-FFL_I taking into account bidirectional promoter noise. We predict CV of ∼0.25 variability regardless of miR efficiency (Figure 2H and I), which compares to the observed CV of ∼0.5 in the negative control circuit. Here, the extra noise could arise from the asymmetry introduced by splicing in one of the transcripts, but not the other.

Experimental characterization

We commenced our experiments with testing data reproducibility by comparing the mean output values and their fluctuations measured under various conditions. The averaged input–output function of the tI1-FFL and the noise levels exhibit the following characteristics: (1) they are insensitive to changes in plasmid amounts used in transfections as well as Dox levels (Supplementary Figure S2E–K); (2) that are slightly sensitive to changes in transfection reagent (Supplementary Figure S2L and M); and (3) they do not change between 48 and 72 h post-transfection (Supplementary Figure S2N and O). The latter result suggests that the system is in a quasi-steady state during this time window, even though transient transfections result in eventual loss of plasmids from the cells. Unlike the transcriptional circuit, ptI1-FFL_I reaches different saturated levels and exhibits different intrinsic noise (Supplementary Figure S3A and B) depending on the DNA amount and the reagent. However, these responses were reproducible for a given combination of both (Supplementary Figure S3C–F). We were not able to atribute this to any single experimental parameter and hypothesize that it is related to global changes in RNAi pathway activity in the cells that might be affected by transfection conditions. After initial calibration, we collected data from all circuit variants using 500 ng of the plasmids and LipoLTX transfection reagent. We note that in order to compare different circuits that used different fluorescent proteins to report on input and output values, we normalized the raw values obtained in FACS measurements to those from the tI1-FFL negative control circuit so that the data from the respective negative control constructs used for different circuit families would all overlap post-normalization (Supplementary Figure S3G and H). Additionally, in our processing of the flow cytometry data, we restricted our analysis to those bins whose mean output value is less than half the dynamic range of the instrument (125 000 units) in order to avoid biased calculations of mean and s.d. by including saturated data points (data not shown).

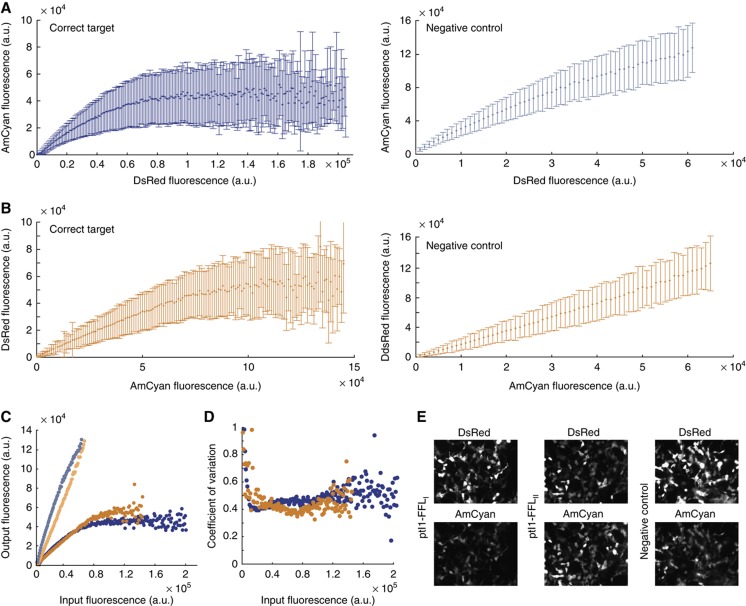
First, we transfected transcriptional incoherent motifs with varying LacO sites (Figure 3A, C, and D). Qualitatively, one observes that the response becomes less dependent on the copy number as the binding strength increases, but it never becomes strictly saturated. The intrinsic noise (Figure 3B) appears to decrease with increasing copy number and is directly proportional to the strength of the LacI inhibition, indicating that extra variability is introduced at the binding step. We then tested the post-transcriptional feedforward loops. Version I shows excellent adaptive response to the increasing copy number of the input plasmid (Figure 4A). Version II (Figure 4B) exhibits comparable behavior, but the input values span a shorter range, limiting the sampling at the high input end. We juxtapose the two data sets in Figure 4C and observe that their outputs virtually overlap for similar input values. We also find that the absolute ouput expression levels at saturation are higher for both post-transcriptiponal circuits as compared with the trancriptional incoherent motif. At the same time, the intrinsic noise (Figure 4D) is about three times lower compared with the transcriptional circuits. Figure 4E shows representative microscopy images of the signals DsRed and AmCyan for the post-transcriptional feedforward loops versions I, II, and the negative control.

Figure 3.

Experimental results with tI1-FFL motifs. Microscopy images are used for illustration, accompanied by the quantitative data obtained from flow cytometry analysis of at least 200 000 cells from each transfected well. (A) Experimentally measured input–output response of tI1-FFL. Red curve corresponds to wild-type LacO; orange, dark cyan, green, and light green curves represent four mutants with gradually decreasing LacI binding; brown curve is the negative control. (B) Coefficient of variation for each of the constructs illustrated in panel (A) using identical color coding. (C) Representative microscopy images of the circuits and controls. (D) Processed flow cytometry data measured for six tI1-FFL constructs, showing mean output values and their s.d. in each bin. Source data is available for this figure at www.nature.com/msb.

Source data for Figure 3 ^{(111.5KB, xls)}

Figure 4.

Experimental results obtained with ptI1-FFL_I and ptI1-FFL_II motifs. Microscopy images are used for illustration, accompanied by the quantitative data obtained from flow cytometry analysis of at least 200 000 cells from each transfected well. (A) ptI1-FFL_I; left: correct target, right: negative control, (B) ptI1-FFL_II; left: correct target, right: negative control, (C) Overlap of the input–output responses of the two versions (blue, ptI1-FFL_I and orange, ptI1-FFL_II). (D) Coefficients of variation of the two motifs (blue, ptI1-FFL_I and orange, ptI1-FFL_II). (E) Representative microscopy images. Source data is available for this figure at www.nature.com/msb.

Source data for Figure 4 ^{(88KB, xls)}

We further compared our circuits with the negative autoregulatory motif. We measured two circuit variants, the first with two repeats of the LacO site and the second with one LacO site. For a negative control, we abolished LacI binding by using IPTG (Figure 5A–C). The results qualitatively show that input dependency on the output weakens with increasing binding strength while the noise levels are above those of the post-transcriptional loops but are lower than the transcriptional ones. Quantitative analysis of all circuits' characteristics is given in the following section.

Figure 5.

Experimental results obtained with tAM motifs. Microscopy images are used for illustration, accompanied by the quantitative data obtained from flow cytometry analysis of at least 200 000 cells from each transfected well. (A) Input–output behavior of the tAM motifs. (Left) Negative control response measured in the presence of IPTG; (middle) single LacO repeat; (right) double LacO repeat. (B) Representative microscopy images. (C) Juxtaposed mean output values obtained for the different circuits (dark gray curve: IPTG control, orange curve: single LacO repeat, light brown curve: double LacO repeat). (D) Coefficients of variation in the output values measured in the experiments shown in panel (A). Color coding is the same as in panel (C). (E) Plots of log(output) versus log(input) constructed using the mean output values measured in three replicas for each circuit variant. Source data is available for this figure at www.nature.com/msb.

Source data for Figure 5 ^{(52KB, xls)}

Having measured input–output behavior, we performed additional experiments to characterize the relationship between the fluorescence and plasmid copy number, and to explain observed differences in the input range between certain circuits and their corresponding controls. To address the former, we sorted cells transfected with the transcriptional motif into four fractions based on input fluorescence intensity and quantitatively measured the copy number of nuclear-localized plasmids using qPCR. The results confirmed that the number of transcriptionally active plasmids depends linearly on the fluorescence intensity, with a certain threshold number of plasmids required to effect measurable gene expression (Supplementary Figure S7).

To answer the latter, we focused on the post-transcriptional ptI1-FFL_I, since this topology gives the largest difference between the input range in the circuit and its control. All the interactions between this circuit's components are post-transcriptional, thus it is highly unlikely that differences in the input range are due to decreased transcription rate of DsRed mRNA; instead, those differences are probably caused at the translational level. Accordingly, we conjectured that simple reduction in protein translation from AmCyan mRNA due to RNAi, rather than any topology-specific circuit feature, leads to an increase in protein translation from the DsRed mRNA and the observed increase in the input range. To test this assumption, we targeted the AmCyan mRNA in the control circuit by siRNA molecules complementary to AmCyan-coding region (Supplementary Figures S8 and S9). In Supplementary Figure S8, we show distributions of both DsRed and AmCyan markers in the circuit and the control (red and blue lines, respectively), as well as similar distributions for control circuit cotransfected with anti-AmCyan siRNA at varying concentrations. We observe that AmCyan is repressed to its levels in the functional circuit (green, orange, black, and purple data sets), while at the same time, DsRed distribution increases to circuit levels. This increase in DsRed span due to RNAi directed against the AmCyan output apparently occurs thanks to increased ribosome availability. We note that neither this increase in DsRed span nor addition of anti-AmCyan siRNA in transfection result in output adaptation to copy number (Supplementary Figure S9)

Analysis of input–output relationship

Our theoretical study showed that the exact functional form of input–output relationship should be a rational function, where the nominator and the denominator are first-degree polynomials. Therefore, we first fit the measured response to the function

whose range is the interval [ca/b, c] (we expect that ca/b will be approximately zero after fitting). The coefficient of determination (R²) was used to quantify the goodness of fit, while the input value at which the output reaches half of its value at saturation (EC₅₀, b in the σ function) was used to rank the motifs in terms of their adaptivity. Our theoretical study predicted that stronger repression would lead to better adaptivity (smaller parameter b) and lower saturated output level compared with circuits with weak repressor binding.

The experimentally observed response of incoherent circuits confirmed these expectations and produced good-to-excellent fits to the rational function (Table I; Supplementary Table S2), in particular with post-transcriptional motifs. As expected, the adaptivity is reduced (EC₅₀ increases) with increasing number of mutations in the LacO sites. (The absolute EC₅₀ value drops again for the fourth mutant and for the negative control, but we attribute this behavior to the truncation of the cytometry data that was necessary in order to avoid using saturated measurements.) Notably, the fitted EC₅₀ of the post-transcriptional motif is the lowest, confirming our qualitative observation.

Table 1. Goodness of fit of the data for a range of functions and EC₅₀ values for the rational fit.

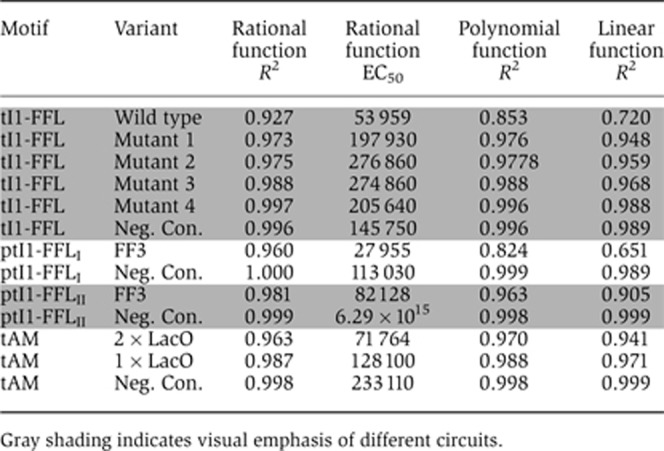
We further examined the anticipated (Becskei and Serrano, 2000) square-root input–output dependency in the autoregulatory circuit. First, we observe that the log–log plot of the output versus copy number should be fitted well by a straight line whose slope is 0.5. Indeed, transformed data obtained in three independent replicas (Supplementary Figure S4A) can be fitted by a straight line (Figure 5E). Strongly repressed motif (2 × LacO) has a slope of 0.57, close to the expected value, weak inhibition (1 × LacO) results in a slope of 0.67, and the negative control experiment in 0.87 (close to the expected value of one). The slope measured for strong negative regulation agrees with previous reports. To further explain the slope values, we assume that the dynamics of the negative feedback are governed by an expression of the form

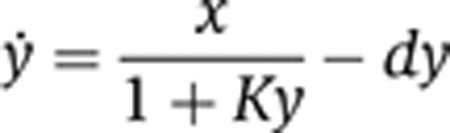where y is the output, x is the input, K is the strength of the negative feedback, and d is the degradation rate constant. At steady state we obtain the solution

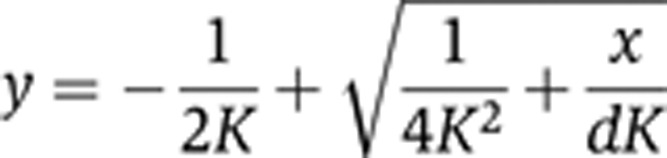or

For a very strong inhibition K, a is very small, which results in a slope of ∼0.5, and for a very weak inhibition, a is large, resulting in a slope of ∼1, which again agrees with Figure 5E. To further confirm this expectation, we fitted the motifs to π₁ and obtained excellent fit (R²>0.97) for the autoregulatory motif (Table I; Supplementary Table S3). Finally, we replaced the exponent of 0.5 with a free parameter and fitted the motifs to the function

The results (Supplementary Table S4) show goodness of fit that is comparable to π₁ as exemplified by R², and outputs exponent values c of 0.5664, 0.6502, and 0.8490 for the 2 × LacO, 1 × LacO, and negative control, respectively.

We further confirmed our analysis by cross-fitting the data: the incoherent motifs were fitted to polynomial functions, while autoregulatory motifs were fitted to the above-mentioned rational function. In addition, we verified our fitting methods by checking the goodness of fit to a ‘null hypothesis’ described by a complete lack of adaptation, that is, a linear function. We find that in general, the incoherent motifs that implement strong inhibition by an auxiliary regulator fit well neither the polynomial nor the linear functions, confirming that indeed they exhibit saturating behavior that is not expected in the autoregulated case. The goodness of fit to the linear function (Table I; Supplementary Table S5) increases gradually for the transcriptional motif from R²=0.72 for the wild-type LacO sequence to R²=0.99 for the negative control, indicating progressive loss of adaptation with weakened repression efficiency. Likewise, the incoherent circuits with strong repression did not fit well to the non-saturating polynomial function, but the fit improved as the repression weakened. On the other hand, the autoregulatory motif was fit well by a rational function and considerably well by a linear function, making it hard to conclusively decide if saturation might be obtained experimentally with appropriately chosen LacI-binding sites.

Analysis of fluctuations

We analyzed the noise characteristics (Elowitz et al, 2002; Ozbudak et al, 2002; Blake et al, 2003; Paulsson, 2004; Raser and O'Shea, 2005; Raj et al, 2006; McCullagh et al, 2009; Kittisopikul and Suel, 2010) of different motifs, as measured by the coefficient of variation of the input values in individual bins. The transcriptional I1-FFL is significantly more noisy than the post-transcriptional implementations, resulting in CV values that range from ∼1.2 for low-to-medium input fluorescence to ∼0.9 for high input fluorescence, while the post-transcriptional I1-FFL exhibits CV of ∼0.45 for both implementations (Figure 4D). Post-trancriptional FFL motifs are also less noisy than the autoregulated circuits, whose noise level stands at ∼0.6 (exhibiting higher noise for low expression levels). The CV values compiled for all motifs are shown in Supplementary Figure S5.

Our simulations helped rationalize these observations. The control circuits allowed us to estimate individual noise contributions of certain circuit components. Using these experiments we calculated the CV of ∼0.25 for the bidirectional promoter, and ∼0.3 for IRES. These values alone would result in the total expected noise of ∼0.35 in the negative control circuit (lacking LacI inhibition), with increasing the strength of the negative feedforward loop leading to reduced CV of ∼0.30. However, the values observed in experiments were much higher, rising from about 0.55 in the negative control to more than 1 in fully active motifs. This shows that variability introduced by the IRES or the pTRE cannot explain the observation and leads to a hypothesis that the overall noise is dominated by the fluctuations in LacI–LacO interaction. In the case of the post-trancriptional motif, the bidirectional promoter is expected to contribute CV of ∼0.25 regardless of miRNA inhibition strengths, while experimentally measured value was ∼0.45 for both implementations. This suggests that there is no apparent reduction in fluctuations when the microRNA targets an mRNA spliced out of its own precursor (as in version II), compared to version I. Moreover, both the negative controls and the active circuits exhibited similar levels of fluctuation, suggesting that the discrepancy between the expected and the observed noise levels are not due to the negative regulation step but rather due to other steps in the process, such as splicing. This also suggests that RNAi inhibition is much less noisy than repression by LacI. In another interesting observation we show that the fluctuations in the autoregulated motif are not reduced as a result of the LacI binding; however, they do not increase either, as opposed to the incoherent motif. This indicates that the autoregulatory motif counteracts the increasing fluctuations of the LacI inhibition.

Discussion

We show that synthetic incoherent feedforward motifs can function as adaptive expression units in mammalian cells. Both transcriptional and post-transcriptional implementations exhibit adaptation to the amount of their genetic template, pointing to a universal property of this particular topology. The post-transcriptional RNAi-based circuits are significantly less noisy and show superior adaptability, leading to a hypothesis that nature might use such mechanisms to maintain homeostasis, filter external perturbations, and increase network robustness. Remarkably, recent studies have identified somewhat similar mechanisms of gene regulation in mammalian cells. One example, consistent with our hypothesis, is of an activator that upregulates a gene and a microRNA that then downregulates that same gene (Nakamoto et al, 2005; Tsang et al, 2007).

Our results also shed new light on the long-standing question of molecular mechanisms of gene dosage compensation. While many dosage compensation processes involve genome-wide changes, it has been hypothesized that feedback and negative feedforward effects could have a role in some cases (Tsang et al, 2007; Veitia et al, 2008; Stenberg et al, 2009), and mathematical analysis revealed that a two-component genetic circuit with elements of opposite regulatory activity (activator and inhibitor) constitutes a minimal requirement for network-dosage invariance (Acar et al, 2010). Our study shows that in fact incoherent feedforward, but not feedback, connectivity generates asymptotic response, in principle allowing dosage compensation. While qualitatively our circuits exhibit dose compensation and adaptation for increased DNA amount, the actual input values that exhibit efficient compensation are relatively high. In endogenous systems, compensation may be required when the copy number increases from two to three or two to four, or even one to two, and such compensation is unlikely to be caused by the exact replicas of our circuits. Having said that, there are examples in cancer where the amplification is eight-fold, that is, 16 copies of the gene are present in cells (Keyomarsi and Pardee, 1993), well within adaptation range in our circuits. If such dramatic amplifications are biologically feasible, the cell might pre-empt their negative effects by evolving a repressor or microRNA-binding site targeted by closely located and potentially coamplified negative regulators. In addition, future research will address the fine-tuning of the input–output response in our circuits and attempt to uncover the ‘knobs’ that control the half-saturation point, or EC₅₀, of the input. It is not infeasible that proper adjustments to circuit architecture could lower this value significantly in a rational manner and cause adaptive behavior even at very low copy numbers of one to four.

Finally, our study is a step toward sophisticated synthetic expression units whose gene product will depend only weakly on the number of unit copies in a cell and on global transcription and translation efficiency. Such stand-alone units, combined into larger networks, could be expected to function reliably in the face of large internal fluctuations. We note that our theoretical approach enabled us to quantitatively characterize these networks using transient transfections and noisy data; this approach eliminates the need to construct stable cell lines and dramatically reduces the time required to develop functional synthetic networks in mammalian cells.

Materials and methods

Recombinant DNA constructs

The circuits were derived from a plasmid (pTRE-Tight-Bi, Clontech), with a bidirectional pTRE-Tight promoter consisting of seven rtTA binding sites (TET_O) flanked by diverging minimal CMV promoters (CMV_MIN) and multiple cloning sites (MCS_I and MCS_II). For the cloning details see Supplemental Information, DNA Plasmids section. Using rtTA-expressing HEK293, Tet-On cells with saturating Dox concentration effectively turned pTRE-Tight into a constitutive promoter. We chose pTRE over divergently oriented pair of constitutive promoters such as CMV or UbC due to superior correlation between divergently expressed genes (data not shown).

Transfections

Approximately 120–140 thousand cells in 1 ml of complete medium were plated into each well of 12-well uncoated glass-bottom (MatTek) or plastic (Falcon) plates and grown for ∼24 h. For Lipofectamine Plus transfection, mixtures were prepared by mixing all plasmids into 40 μl of Dulbecco's modified Eagle's medium (DMEM). A total of 2.4 μl of the Plus reagent (Invitrogen) was added to the final mix and incubated for 20 min at room temperature. In parallel, 1.6 μl Lipofectamine (Invitrogen) were mixed with 40 μl DMEM. Plus- and Lipofectamine-containing solutions were mixed and incubated for 20 more minutes at room temperature before application to the cells. Shortly before transfection, the medium was replaced with 1 ml DMEM without supplements with a single medium wash step. The transfection mixture (typically 90 μl) was applied to the wells and mixed with the medium by gentle shaking. Three hours after transfection, 120 μl fetal bovine serum (FBS) was added to the wells and the cells were incubated for up to 48 h before the analysis. For Lipofectamine 2000 transfections, mixtures were prepared by mixing all plasmids into 100 μl of DMEM. In parallel, 4 μl Lipofectamine 2000 (Invitrogen) were mixed with 100 μl DMEM and incubated for 5 min. Plus- and Lipofectamine 2000-containing solutions were mixed and incubated for 20 more minutes at room temperature before application to the cells. Shortly before transfection, the medium was replaced with 1 ml DMEM without supplements with a single medium wash step. The transfection mixture was applied to the wells and mixed with the medium by gentle shaking. Three hours after transfection, 120 μl FBS was added to the wells and the cells were incubated for up to 48 h before the analysis. For Lipofectamine LTX transfection, mixtures were prepared by adding each plasmids into 200 μl of DMEM. A total of 0.5 μl of the Plus reagent (Invitrogen) was added to the final mix and incubated for 5 min at room temperature. Finally, 2.5 μl Lipofectamine LTX (Invitrogen) were added. Plus- and Lipofectamine LTX-containing solutions were mixed and incubated for 30 more minutes at room temperature before application to the cells. The transfection mixture was applied to the wells and mixed with the medium by gentle shaking. The cells were incubated for up to 48 h before the analysis.

Determination of transfected plasmid copy number

For these experiments, we employed an electroporation-based method called Nucleofection using a Nucleofector 4D device (Lonza). Three million Tet-On HEK293 cells were trypsinized, spun down at 90 g for 5 min and resuspended in 200 μl of SF nucleofection medium. A total of 5 μg of PureLink (Invitrogen)-purified plasmid encoding incoherent transcriptional motif was added and the mixture split into two nucleocuvettes, about 100 μl per cuvette. The cells were nucleofected using the program CM-130 and seeded into a single T75 flask with pre-warmed growth medium pre-mixed with Dox. Cells were grown for 48 h, trypsizined, resuspended in PBS with 2 mM EDTA and sorted into four populations of varying ZsGreen intensity on a MoFlo Legacy instrument using 488 nm laser. The sorted cells as well as the unsorted population were reanalyzed on BD LRS Fortessa to confirm differential ZsGreen levels in the sorted fractions. Nuclear fraction of the sorted cells was isolated using Nuclear/Cytosol Fractionation Kit (BioVision) using provided instructions with an additional wash step of the nuclear fraction. The nuclear fraction precipitate was resuspended in PBS and DNA was extracted using DNAEasy kit (Qiagen) using the manufacturer's protocol. qPCR was performed using GoTaq qPCR master mix (Promega) using the manufacturer's instructions, with a pair of primers specific to LacI-coding region (TGCAAATGCTGAATGAGGGCATCG and ACGGCGGGATATAACATGAGCTGT) and a pair of primers specific to ACTB internal reference gene (AATGTGGCCGAGGACTTTGATTGC and AGGATGGCAAGGGACTTCCTGTAA). Calibration curves were built using known concentrations of either the transfected plasmid or subcloned ACTB cDNA (Origene). qPCR reactions were run on Lightcycler 480.

Data gathering

We transiently transfected HEK293 Tet-On cells (Clontech) using LipoLTX and assayed the output 48 h post-transfection using microscopy and flow cytometry (FACS). The small-molecule cofactor Doxycycline (Dox) was always added at saturating concentration. We used FACS data to characterize the constructs. For each cell, we measured the fluorescent intensity of the output and of the copy number reporter. The readouts ranged from 0 to about 250 000 instrument units. We sorted the cells according to their input value into equal bins of 1000 units ranging from 0 to 1000, from 1000 to 2000, etc. We then calculated the mean and the s.d. of the output levels of the cells in each bin.

Microscopy

All microscopy images were taken from live cells grown in glass-bottom wells (MatTek) in the transfection medium supplemented with 10% FBS. We used the Zeiss Axiovert 200 microscope equipped with Sutter filter wheels, prior mechanized stage and an environmental chamber (Solent) held at 37°C during measurements. The images were collected by Orca ERII camera cooled to −60°C, in the high precision (14 bit) mode using a × 20 PlanApochromat NA 0.8, PH2 objective. The filter sets are as follows: 430/25 × (excitation) and 470/30 m (emission) for AmCyan, 565/55 × (excitation) and 650/70 (emission) filters for DsRed-monomer, 430/25 × (excitation) and 525/40 m (emission) for ZsGreen1. Data collection and processing were performed by the Metamorph 7.0 software.

FACS

The cells were prepared for the FACS analysis by trypsinizing each well with 0.5 ml 0.25% trypsin-EDTA, collecting the cell suspension and centrifuging at 4000 r.p.m. for 2 min. Trypsin was removed and the pellet was resuspended by short vortexing in 0.5 ml PBS buffer (Invitrogen). The cells were analyzed on a BD LSRII flow analyzer. AmCyan was measured with a 405-nm laser and a 450/50 emission filter, DsRed-monomer with a 488-nm laser and a 575/26 emission filter, and ZsGreen1 with a 488-nm laser and a 530/30 emission filter.

Cell culture

HEK293 Tet-On Advanced cell lines (Clontech, Cat # 630931) were used in all the experiments. The cells were grown at 37°C, 100% humidity, and 5% CO₂. The cells were initially transferred into CD-293 medium and a week later moved to the DMEM (Invitrogen, Cat # 11965-11810) supplemented with 0.1 mM of MEM non-essential amino acids (Invitrogen, Cat # 11140-050), 0.045 units/ml of Penicillin and 0.045 μg/ml Streptomycin (Penicillin–Streptomycin liquid; Invitrogen) and 10% FBS (Invitrogen). The adherent culture was maintained in this medium by trypsinizing with Trypsin-EDTA (0.25% Trypsin with EDTAx4Na; Invitrogen) and diluting in a fresh medium upon reaching 50–90% confluence.

Supplementary Material

Supplementary Information

Supplementary Figures S1–9, Supplementary Tables S1–5