Abstract
The mechanical properties of a healing bone fracture depend not only on the geometry of the fracture callus but also on the material properties of the callus tissues. Despite the biomechanical importance of callus tissues in restoring mechanical integrity to the injured bone, little is known about the material properties of these tissues and whether these properties can be estimated non-invasively. This study used nanoindentation to quantify the spatial variations in indentation modulus throughout the fracture callus and correlated the measurements of modulus with measurements of tissue mineral density (TMD) obtained from images from micro-computed tomography (µCT). Fracture calluses were harvested from rats 24 days following creation of a full-thickness, transverse osteotomy in the femoral mid-diaphysis. Calluses were imaged using µCT, and the average TMD and the median grayvalue (X-ray attenuation) of five, pre-defined volumes of interest (VOIs) in each callus were computed. Nanoindentation was then performed at multiple, regularly spaced locations across 150 µm-thick, sagittal sections of the calluses. The indentation modulus ranged from 0.51 to 1680 MPa throughout the callus, with the highest moduli in the center of the fracture gap and the lowest in the periphery of the gap (P < 0.05). TMD was also highest in the center of the gap (P < 0.05). An increasing trend in both modulus and TMD was observed in the regions of the callus adjacent to the periosteal surfaces of the cortex. While no correlation was found between the average indentation modulus in a given VOI and the median grayvalue of that VOI, the average indentation modulus and the average TMD were positively correlated (R = 0.70, P < 0.05). Together, these findings establish the spatial heterogeneity in the mechanical behavior of tissues in fracture calluses and indicate that the indentation modulus of these tissues can be estimated by non-invasive measurements of tissue mineralization.
Introduction
Healing of a fracture is a regenerative process in which, after an initial inflammatory phase, the callus that forms around the fracture undergoes a transition from cartilage to bone that recapitulates many aspects of endochondral bone development. From a biomechanical perspective, the mechanical behavior of a fracture callus depends not only on the geometry of the callus but also on the material properties of the callus tissues. Measurement of the material properties of callus tissue, and how these properties vary throughout the callus, can thus provide important insights into the biomechanics of the healing process and the spatial patterns of chondrogenesis and osteogenesis throughout the callus. For instance, such measurements can be used to determine the respective contributions of the geometry and material properties of calluses to the stiffness and strength of the callus at various stages of healing and to understand the biomechanical basis for enhanced or impaired healing. In addition, measurement of the mechanical properties of callus tissue could be of enormous value to computer models of the effects of mechanical loading on healing and regeneration of bone (Prendergast et al. 1997; Claes and Heigele 1999; Gardner et al. 2000; Smith-Adaline et al. 2004).
Due to the heterogeneous composition of the fracture callus, mechanical tests performed on the whole callus (bending, torsion and compression) are not sufficient to quantify the mechanical properties of the individual tissues such as bone, cartilage, and granulation tissue that are found in the callus. The two studies to date that have measured the mechanical properties of callus tissues have used indentation tests, and both found that the indentation stiffness or indentation modulus is correlated with measures or estimates of calcium content (Markel et al. 1990; Leong and Morgan 2008). In parallel, many prior studies have estimated the mechanical properties of callus tissue from image data. In a series of studies by Gardner et al. that used finite element (FE) analysis to estimate the distributions of strains and stresses throughout the fracture callus, regions of the callus with similar values of image intensity in digitized radiographs were assumed to have similar material properties (Gardner et al. 2000; Gardner and Mishra 2003; Gardner et al. 2004). The specific values of the tissue elastic moduli were determined through an iterative process that sought to match the FE-computed reaction forces and moments with those obtained experimentally. Similarly, in creating high-resolution FE models of rodent fracture calluses from micro-computed tomography (µCT), Shelfelbine et al. (Shefelbine et al. 2005) grouped image voxels by similar intensities and assigned each group a single elastic modulus. These two approaches have relied on the reasonable assumption that attenuation of X-rays is proportional to tissue density and that, consistent with the published data on indentation of fracture callus tissues (Markel et al. 1990; Leong and Morgan 2008), the elastic modulus is proportional to tissue density. However, to our knowledge, no direct correlation between attenuation of X-rays and tissue modulus has been established for the range of tissues and range of mineralization present in fracture calluses. Investigation of this relationship has clear and numerous applications in non-invasive assessment of callus' mechanical properties, skeletal healing, and skeletal regeneration.
The overall goals of this study were to quantify the distribution of tissue modulus throughout the fracture callus and to investigate µCT-based approaches for non-invasive assessment of callus tissue moduli. Following µCT, rat calluses were prepared for nanoindentation by machining multiple, thin, longitudinal sections from the callus, and an array of indents was performed on each section. Our specific objectives were: (1) to quantify the repeatability of the nanoindentation technique for the different types of tissue present in the callus (cortical bone, newly formed woven bone, cartilage, and granulation tissue); (2) to quantify the spatial heterogeneity in tissue modulus throughout the fracture callus; and (3) to investigate relationships between tissue modulus and measurements of X-ray attenuation and tissue mineral density (TMD) obtained via µCT.
Methods
Operative procedure
Two male, retired breeder Sprague Dawley rats (500 and 530 g; age ∼5 months) were used. All animal-care and experimental procedures were in compliance with NIH guidelines and the Institutional Animal Care and Use Committee at Boston University. The operative procedure involved creation of a full-thickness, 2-mm transverse osteotomy in the left femoral mid-diaphysis followed by stabilization of the defect with four bi-cortical pins and a unilateral external fixator (Salisbury-Palomares et al. 2009). At the start of the surgical procedure, each animal was anesthetized with isofluorane (4% induction and 2% maintenance) and the animal's left femur then shaved and prepped with betadine. The animal was given a subcutaneous injection of Baytril (0.44 ml/kg) as antibiotic and intramuscular injection of Buprenex (0.1 mg/kg) as analgesic. An incision was then made on the posterior lateral thigh, and the lateral intramuscular septum was dissected to expose the diaphysis of the femur. With a stainless steel template as a guide, four bi-cortical pin holes were created on the mid-shaft using a sterile 0.8-mm drill bit, and the pins were inserted using a swivel pin vise. The template was removed once the pins were properly secured. The skin on the posterior thigh was pulled over the ends of the pins and pierced with four 16-gauge needles so that the pins could be passed through the skin. The fixator was inserted onto the pins and held in place with set screws. Once the fixator was securely attached, an osteotomy was created between the two inner pins using a sterile, 1.8-mm dental burr attached to an electric dental hand grinder. The site was then irrigated with sterile saline solution and the incision site was closed using surgical staples. Diagnostic X-rays were taken on a weekly basis to ensure proper positioning of the pins and to monitor the surgical site for signs of infection. The animals were euthanized via CO2 asphyxiation on postoperative Day 24 and the intact, harvested calluses were wrapped in gauze soaked in phosphate-buffered saline (PBS) and were frozen at –20°C until preparation for subsequent imaging and indentation testing. All indentation testing and µCT scanning were performed within 12 months following harvesting. The 24-day timepoint was chosen based on the results of a previous study using this model (Salisbury-Palomares et al. 2009). In that prior study, histological analyses indicated that healing is well underway at 24 days but that the callus exhibits a highly heterogeneous mixture of tissues ranging from granulation tissue to well-mineralized woven bone.
Micro-computed tomography
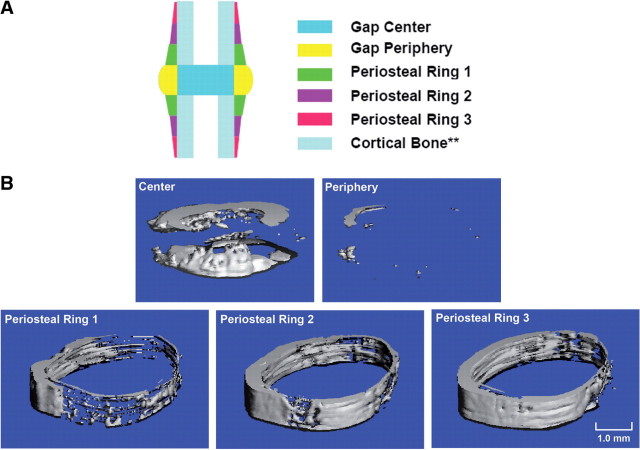
The intact calluses were imaged via micro-computed tomography (55 kVp, 145 µA, 200 ms integration time; Scanco µCT40, Scanco Medical, Brüttisellen, Switzerland) at a resolution of 36 µm/voxel before proceeding to nanoindentation. Calluses were submerged in 1X PBS (pH 7.4) during scanning. A Gaussian filter (sigma = 0.8, support = 1) was applied to the images for reduction of noise. Five volumes of interests (VOI)s within the callus were identified, based on the locations of the fracture gap and the proximal and distal boundaries of the callus (Fig. 1): the center and periphery of the gap, and three periosteal rings. The median grayvalue and mean TMD of each VOI were computed. The median, rather than the mean, grayvalue was used because of the nonGaussian distribution of grayvalues that was observed in each VOI. To compute the TMD, a fixed, global threshold of 25% of the maximum grayvalue (32 767) was used to exclude unmineralized and poorly mineralized tissue from consideration. This threshold corresponded to a mineral density of 641.9 mg HA/cm3 and was chosen on the basis of an earlier study that examined the effect of the choice of threshold on μCT assessment of the structure and mineralization of calluses (Morgan et al. 2009). In that earlier study, it was determined that a threshold at 25% corresponds to ∼45% of the mineral density of mature cortical bone. However, in the present study, the effect of the specific threshold was also investigated by varying the threshold from 10% to 50% of the maximum grayvalue. Grayvalues that exceeded the threshold were then converted to mineral density using a linear calibration curve obtained from scanning a hydroxyapatite (HA) phantom that was provided by the system manufacturer and that consisted of cylinders of five known mineral densities (0, 100, 200, 400, and 800 mgHA/ccm). Also, in calculating TMD, two voxels were removed from all surfaces in order to reduce partial-volume effects in accordance with the manufacturer's standard procedures.
Fig. 1.
(A) Schematic of a longitudinal callus section depicting the five VOIs: center of the gap, periphery of the gap, periosteal rings 1, 2, and 3. **Cortical bone is not one of the VOIs but is shown for reference. The proximal and distal boundaries of the center of the gap and the periphery of the gap were defined by the osteotomy cut. The boundary between the center and the periphery of the gap was determined by the location of the periosteal surface of the original cortex. Each of the periosteal rings was 1 mm in length. (B) Three-dimensional renderings of the µCT image data for each VOI from one fracture callus. Only voxels with intensities exceeding the threshold (25%) are shown.
Nanoindentation
To prepare multiple sections from each callus for nanoindentation, the fresh-frozen calluses were embedded in freezing medium (Histo Prep, Fisher Scientific, Pittsburgh, PA) on the freeze stage of a sledge microtome (HM 450 Richard Allan, Kalamazoo, MI). Serial, 150-μm thick, sagittal sections were cut, and each section was mounted on a microscope slide with cyanoacrylate glue. During sectioning, a thin polyester membrane coated with freezing medium was placed on the exposed surface of the callus in order to help preserve the overall morphology of the callus during sectioning (Leong and Morgan 2008). Ten to 15 sections were obtained, and subsequently indented, from each callus, depending on the size of the callus.
Nanomechanical testing (Hysitron TriboIndenter, Hysitron Inc., Minneapolis, MN) was performed at room temperature using a 50 µm conospherical tip. This tip geometry was chosen over a pyramidal-shaped Berkovich tip in order to reduce peak stresses, and hence the possibility of damage to the tissues being indented (Bei et al. 2005). The spacing between indents was 500 µm. With this indent spacing, the size of the osteotomy gap permitted three rows of indents to be performed in both in the centers and in the peripheries of the gaps: one row in the proximal third of each gap, one row in the center and one row in the distal third. In the periosteal regions, a single column of indents was performed adjacent and parallel to the periosteal surface of the cortex. All indents were performed in load control. For each indent, a preload of 0.1 µN was applied for 6 s for measurement of system's drift, followed by a 2-s loading ramp to a peak force of either 20 or 300 µN (depending on the local stiffness of the tissue), a 15-s hold at the peak load, and a 2-s unloading ramp. The hold period of 15-s was introduced in order to minimize viscoelastic effects (Klapperich, 2001), and the peak force was chosen such that the depth of indentation would be at least 10 times the surface roughness (Zhang and Xu 2002; Donnelly et al. 2006) of the sections (33 ± 12 nm as determined by atomic force microscopy). Depth of indentation ranged from 300 to 4800 nm, with smaller depths corresponding to indents on cortical bone and larger depths to those on granulation tissue. The machine compliance was 4.0 nm/mN which was considered negligible given the relatively small peak loads applied. Tissue sections were kept hydrated at all times with distilled water containing protease inhibitors and penicillin-streptomycin to avoid degradation of tissue and infection by bacteria. The solution was applied intermittently during testing and was kept confined to the glass slide by a boundary created on the slide with a hydrophobic pen. Indents performed on each longitudinal section were binned into the five VOIs, using the locations of the cortical bone and osteotomy gap as references. A total of 277 indents (104 and 173 from the two calluses, respectively) were performed: 176 in the center of the gap; 39 in the periphery of the gap; 21 in periosteal ring 1; 20 in periosteal ring 2; and 21 in periosteal ring 3.
For each indent, the reduced modulus, reported as indentation modulus, was calculated using the Oliver-Pharr (1992) method, as
| (1) |
where S is the unloading stiffness and Ac is the contact area. S was calculated as the initial slope (slope at 95%) of a polynomial function fit over 95–20% of the unloading curve. The tip area function, Ac(h), where h is the displacement in depth, was obtained using polycarbonate (E = 2.95 GPa) as the calibration material. The elastic modulus of the tissue, Es, is related to the reduced modulus by
| (2) |
where νs and νt are the Poisson's ratios of the tissue and indenter tip (diamond-coated stainless titanium; Et = 1140 GPa, νt = 0.07), respectively. However, because of difficulties in measuring the Poisson's ratio of the individual callus tissues, the reduced modulus values were not converted into elastic moduli. The reduced modulus values are reported as indentation moduli in the present article. The mean and standard deviation in indentation modulus were computed for each VOI. The indentation modulus at some of the indent locations was reported as nonmeasurable (N.M.) because the tissue in those regions was so compliant that the displacement of the tip exceeded the system's limit of 5 µm, even for a peak load of 20 µN.
Repeatability
In order to quantify the repeatability of measurements made by nanoindentation of callus tissues, sets of indents were performed on specimens of the four main types of tissues found in fracture calluses: mature cortical bone, newly formed woven bone, cartilage, and granulation tissue. Specimens of mature cortical bone and normal hyaline cartilage were harvested from contralateral femora of a rat. Using cortical bone and articular cartilage from contralateral bones enabled comparison of the resulting indentation moduli to values from the literature. A 1-mm-thick longitudinal section of the femoral mid-diaphysis was prepared using an oscillating dental saw and mounted on a magnetic stainless steel disc (Ted Pella Inc., Redding, CA) by a small amount of cyanoacrylate glue, such that indents were performed in the transverse direction (i.e., perpendicular to the plane of section). The distal epiphysis was also harvested and mounted such that the articular cartilage of the distal femoral condyles was exposed for indentation. Regions of woven bone and granulation tissue were located within a 200-µm-thick longitudinal section of a fracture callus obtained from an earlier study (Leong and Morgan 2008); these regions were identified based on color, texture, and opacity as previously described. At least four repeated indents were performed on each type of tissue using the indentation protocol described above. A recovery time of 15 min was allowed between indents. Tissues were kept hydrated at all times.
Statistical analysis
Kruskal–Wallis nonparametric analyses of variance (ANOVAs) followed by the Dunn-Sídak method of multiple comparisons were used to test for differences in indentation moduli among the five VOIs and to test for differences in moduli among the proximal, middle and distal thirds of the osteotomy gap. Standard parametric ANOVAs with Tukey post hoc tests were carried out with TMD as the dependent variable. Pearson correlation analyses were conducted to test for an association between indentation modulus and median grayvalue and between indentation modulus and TMD. Data from both specimens were pooled, because preliminary analyses performed separately on the data from each specimen showed very similar trends between specimens. All statistical analyses were carried out with JMP 6.0 (SAS Institute Inc., NC, USA) and used a significance level of 0.05.
Results
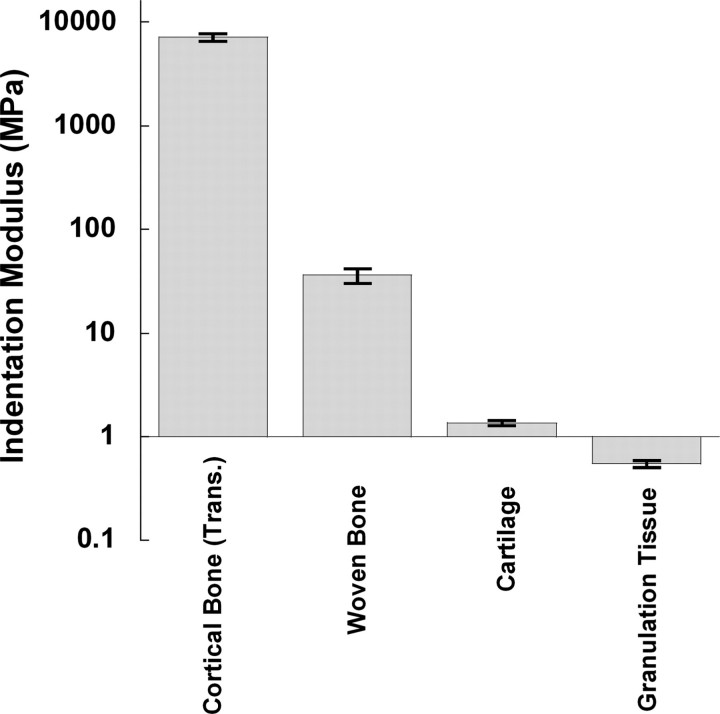
Nanoindentation provided repeatable measurements of indentation modulus for the callus tissues. Although the indentation moduli spanned four orders of magnitude when considering all four types of tissue together, the coefficients of variation (ratio of the standard deviation to the mean) ranged only from 5.7% to 16.5% (Fig. 2). Mean (± standard deviation) moduli for cortical bone, newly formed woven bone, articular cartilage, and granulation tissue were 7.2 (±0.61) GPa, 36.2 (±5.84) MPa, 1.36 (±0.078) MPa, and 0.55 (±0.04) MPa, respectively.
Fig. 2.
Measurements of the repeatability of indentation modulus. The height of each bar represents the mean; the error bar represents one SD of the four repeated indents on each type of tissue.
Indentation moduli throughout the callus were spatially heterogeneous (Fig. 3). Overall, the indentation modulus of the callus tissues ranged from 0.51 to 1680 MPa (median = 2.84 MPa, inter-quartile range = 26.7 MPa) and was highest in the center of the gap (P < 0.05). In comparison, tissue found in the periphery of the gap was approximately 50 times less stiff (1.91 MPa versus 86.1 MPa). Contingency analysis revealed a higher proportion of nonmeasurable indents in the periphery than in the center (P < 0.05), further indicating the presence of highly compliant tissues in the periphery. Within the gap itself, indentation moduli were lower in the middle third of the gap as compared to the proximal third (P = 0.04). For the three periosteal regions, a gradient with increasing modulus was observed with increasing distance from the osteotomy gap.
Fig. 3.
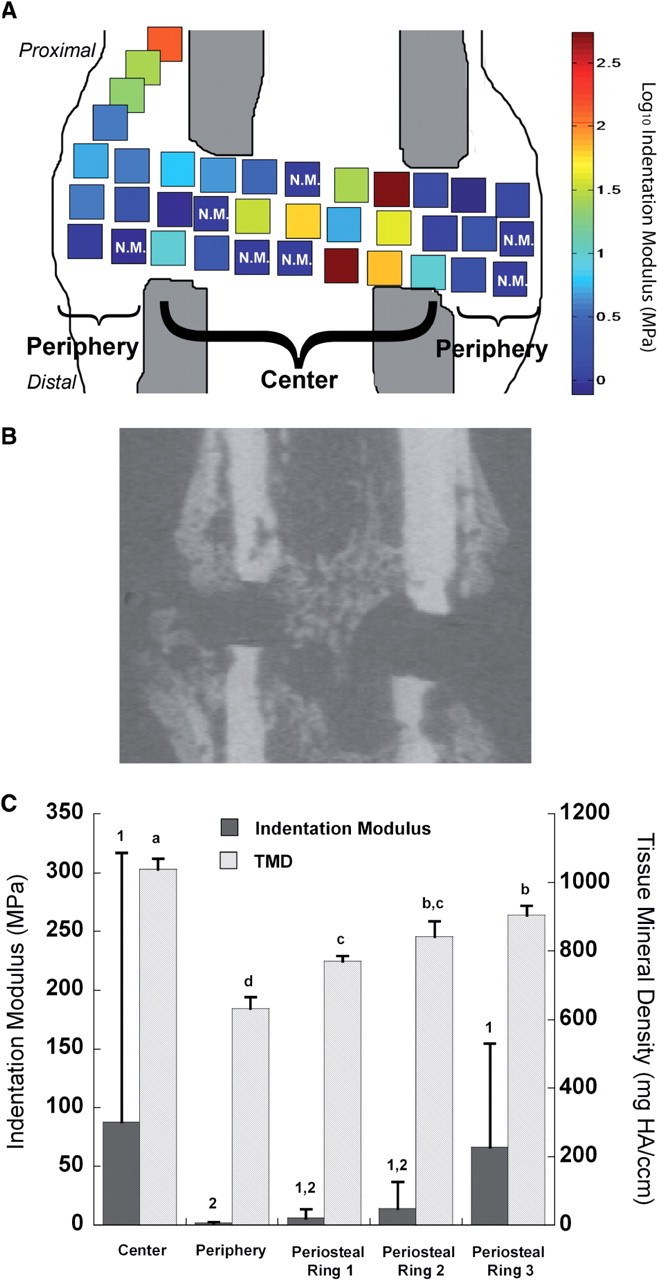
(A) Schematic of a representative section of a callus showing the spatial heterogeneity in indentation modulus across the callus. Higher modulus values were found within the center of the gap compared to lower moduli found in the periphery (P < 0.05). N.M. denotes nonmeasurable indents due to extremely high compliance of the tissue at those indent locations. (B) Approximately matched µCT cross-section to (A). (C) Indentation modulus and TMD for each of the five VOIs defined in Fig. 1. For indentation modulus, the height of each bar and of each error bar represents the mean and standard deviation, respectively, of all indents in the VOI for both calluses (e.g. n = 176 for the center of the gap). In contrast, each callus yields only one value of TMD for each VOI. Hence, for TMD, the height of each bar and of each error bar represent the mean and standard deviation, respectively, of the average TMD values of the two calluses (n = 2 for each VOI). Bars that are not labeled with the same number (indentation modulus) or letter (TMD) are significantly different from one another (P < 0.05).
Measurements of TMD were consistent with those of indentation modulus. TMD was highest in the center of the gap and lowest in its periphery; a gradient in mineral density along the periosteal regions was also noted (Fig. 3C). However, no differences in TMD were found among the proximal, middle, and distal thirds of the gap. The rank order of TMD among the five VOIs (i.e., center of gap > periosteal ring 3 > periosteal ring 2 > periosteal ring 1 > periphery of gap) was preserved for thresholds as low as 20% and as high as 40% of the maximum grayvalue.
Measurements of the average indentation modulus in a given VOI and the average TMD in that same VOI were positively correlated (P = 0.024, r = 0.70) (Fig. 4A). This correlation held for threshold values as low as 15% and as high as 45% of the maximum grayvalue (P < 0.047, r > 0.64). In contrast, no correlation was found between indentation modulus and the median grayvalue (Fig. 4B).
Fig. 4.
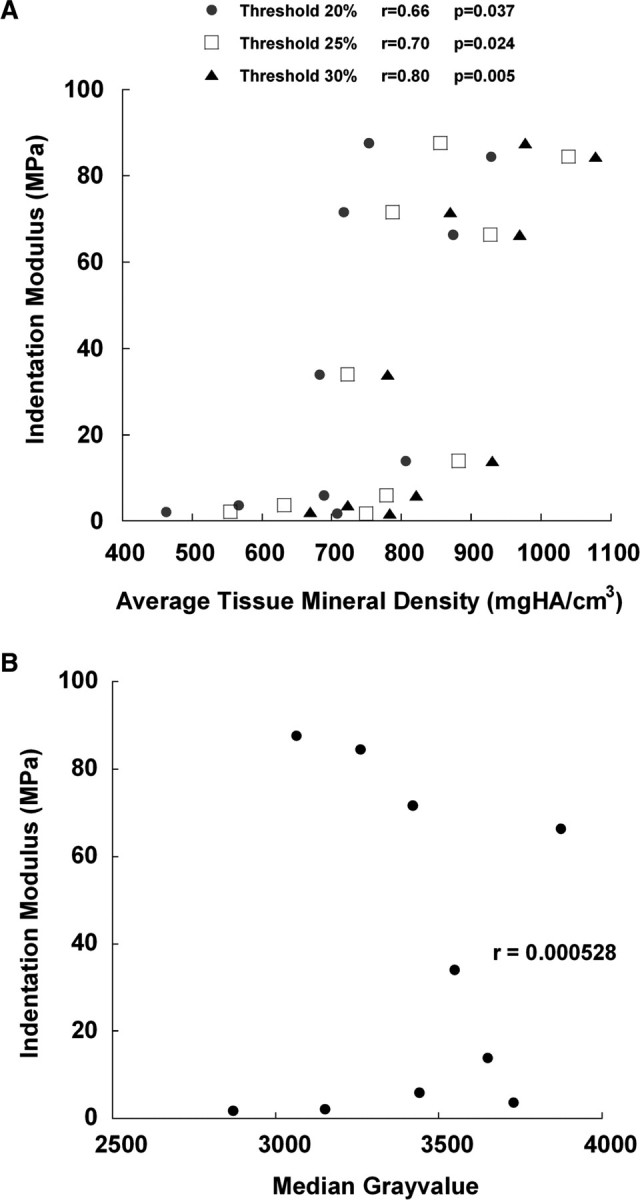
(A) Plot of the average indentation modulus of each VOI against the TMD for that VOI at thresholds of 20, 25, and 30%. There were 10 data points at each threshold as a result of 5 VOIs from each of the 2 animals. A significant correlation was found between indentation modulus and TMD. (Some values of TMD are slightly lower than the mineral density that corresponds to the threshold because of small changes in voxel grayvalues produced by the Gaussian filter that is applied for reduction of image noise). (B) Plot of the average indentation modulus of each VOI against the median grayvalue for that VOI. No correlation between indentation modulus and median grayvalue was found (P > 0.95).
Discussion
In the interest of elucidating the mechanical behavior of callus tissues and their functional role in restoration of stiffness and strength to the healing bone, the overall goals of this study were to quantify the distribution of tissue modulus throughout the fracture callus and to investigate µCT-based approaches for non-invasive assessment of callus tissue moduli. The measurements of repeatability revealed low coefficients of variation for all four types of tissue, indicating that our subsequent measurements of indentation modulus throughout the callus reflected true regional variations in elastic properties as opposed to experimental artifact. Results from the indents performed throughout the fracture calluses indicate the presence of substantial spatial heterogeneity in indentation modulus, varying over 3000-fold within a single callus. Indentation modulus was highest in the center of the osteotomy gap and lowest in the periphery of the gap, and the intermediate values for the periosteal regions exhibited an increasing trend with distance from the gap. Similar patterns of spatial heterogeneity in TMD were found, and the indentation modulus and TMD were positively correlated with each other. Taken together, these findings establish the spatial heterogeneity in the mechanical behavior of tissues in fracture calluses and indicate that the large variations in modulus are associated with regional differences in TMD.
The strengths of this study include several aspects of the experimental protocols and the choice of fracture model. We used protocols for preparation and indentation of sections that were designed specifically to allow testing of viscoelastic tissues spanning a wide range of stiffness and to enable testing of these tissues in a hydrated environment. The repeatability of our measurements of indentation modulus, together with the close agreement between the indentation moduli of articular cartilage (1.36 MPa) and cortical bone (7.2 GPa in transverse direction) and the modulus values reported in the literature for these tissues (Liu et al. 1999; Athanasiou et al. 2000; Dong and Guo 2004; Li et al. 2006; Franke et al. 2007), lends confidence to our subsequent nanoindentation measurements of the spatial heterogeneity present in the callus. The indentation modulus of woven bone (36.2 MPa) is also within the range of values reported previously (Leong and Morgan 2008). Our experimental design specified performing indents at regularly spaced intervals across the callus sections, in contrast to an earlier study (Leong and Morgan 2008) that identified locations of indentations prospectively by the type of tissue present at those locations. The choice of regular spacing was made to provide unbiased measurements of the spatial heterogeneity in modulus.
Regarding our fracture model, the use of an osteotomy, as opposed to a closed fracture, resulted in a well-defined region of injury and enabled precise determination of the five volumes of interest. This, in turn, facilitated paired comparisons of indentation modulus to X-ray attenuation and to TMD. While a transverse osteotomy does not replicate all aspects of clinical fractures, it is a well-established model of bony healing. We also note that both the results of the measurements of indentation modulus and of TMD and X-ray attenuation were very consistent between the two calluses. The indentation moduli in each of the calluses ranged 0.5–1250 MPa and 0.78–1680 MPa, respectively. Also, for each VOI the differences in TMD between calluses differed by no >45 mg HA/ccm, which is less than the differences between VOIs when the data from both specimens were pooled. These relatively small variations between specimens in terms of indentation modulus and TMD across the five VOIs may be due to the use of an osteotomy with a high degree of stabilization as opposed to a closed fracture, where less control could be imposed over the geometry of the fracture.
There are also several limitations in this study. First, only two fracture calluses were analyzed due to the time-consuming nature of the nanoindentation. Although the Triboindenter system allows for a high degree of automation when performing an array of indents, this feature could not be used for the callus sections because of the wide range of tissue compliance and the uneven topography of the surfaces. The range in compliance necessitated varying the peak force according to the tissue compliance at the indent site in order to ensure adequate depth of indent and yet to avoid exceeding the system-displacement limit of 5000 nm. The roughness of the surface required performing an initial step in order to detect the surface; this step involved slowly lowering the tip until a minimal resistance force was detected. Omitting this step would have risked overloading the transducer during series of indents on an uneven surface. Each of these factors also limited the number of indents that could be performed on each section because of constraints on the amount of time that a given section could remain in the Triboindenter chamber. The callus sections were fresh, as opposed to formalin-fixed, and hence were kept in the chamber for no >8 h each because of concerns about degradation of the tissues.
A second limitation of the present work is that the Oliver-Pharr method, which was used in calculation of the indentation moduli, assumes linear elastic and isotropic material properties. Bone and cartilage are known to be viscoelastic and anisotropic; however, the extent of viscoelasticity in bone is relatively mild (Fan and Rho, 2003) and it is standard in the literature to use the Oliver-Pharr method for this tissue (Rho et al. 1999; Zysset et al. 1999; Hengsberger et al. 2002; Silva et al. 2004). While cartilage is often modeled as a poroelastic material, no analytical solution for indentation of a poroelastic material with a spherical tip has been reported. Similarly, no methods for anisotropic analysis of data from indentation tests have been established to our knowledge. Third, measuring TMD and attenuation with µCT are subject to artifacts such as partial-volume effects and beam hardening, and these measurements have not been standardized across systems to the extent that they have been for mineral density measured by quantitative computed tomography. In the present study, the partial-volume effects were reduced through two-voxel ‘peeling’ and by averaging TMD over all voxels within each VOI. The influence of beam hardening is difficult to assess; however, the cupping artifact created by this phenomenon typically results in lower attenuation in the central region of a specimen and yet in the present study, the center of the gap was found to have the highest TMD. Thus, beam hardening would not produce the ranking of the VOIs in TMD we observed. In addition, our results on the correlation between indentation modulus and TMD, as well as a suggestion of a nonlinear relationship between the two (Fig. 4A), are consistent with previous studies that used well-established methods of measuring calcium concentration and that investigated tissues spanning a similarly wide range of mineralization (Ferguson et al. 2003; Currey 2004; Gupta et al. 2005). One final limitation is that the values of TMD reported in the present study are specific to our choice of threshold. However, we did investigate thresholds ranging from 10% to 50% of the maximum grayvalue and found that the relative differences among VOIs in TMD and the correlation between modulus and TMD were unchanged for thresholds as low as 20% and as high as 40%.
The results presented here for indentation modulus and TMD are consistent with previously published histological analyses of the healing of fractures. The highest moduli and mineral density were found in the center of the gap and in the periosteal ring furthest from the gap (ring 3). These regions are those in which bone formation occurs first, provided that fractured fragments are relatively well stabilized (McKibbin 1978; Sarmiento 1995; Salisbury-Palomares et al. 2009). The higher indentation modulus and TMD in the center compared to periosteal ring 3 may be a result of close proximity of the gap center to the marrow space and, hence, the marrow stroma and vascular supply. In the periosteal regions, bone formation occurs via intramembranous ossification and proceeds from locations more remote to the gap, along the cortex, towards the fracture line (McKibbin 1978; Einhorn 1998). This spatiotemporal progression in ossification is most likely the cause of the gradient in modulus and TMD from periosteal rings 3 to 1. In previous studies using this animal model, bone formation in the osteotomy gap has been shown to occur via both intramembranous and endochondral ossification, and at the 24-day timepoint, some isolated regions of cartilage were observed in the periphery of the gap (Salisbury-Palomares et al. 2009). These regions of cartilage may be the reason why the lowest values of indentation modulus and TMD were found in the periphery of the gap.
The difference in the strength of the correlation between indentation modulus and TMD versus that between indentation modulus and median grayvalue has important implications for studies that seek to estimate material properties based on µCT measurements of mineralization and attenuation. Comparison of the results of the two correlation analyses indicates that when a threshold is applied to exclude the tissue with little, or no, mineral content from consideration, higher values of indentation modulus are associated with higher values of mineral density. However, without the threshold applied, no association between modulus and attenuation was found. Collectively, these results suggest that no single relationship exists between indentation modulus and attenuation for the diverse set of tissues comprising the fracture callus. Although additional studies are needed to confirm this result across the different existing types of fracture models and also in the clinical setting, our results do indicate that TMD shows promise as a non-invasive surrogate measure of the material properties of callus tissues. As such, these findings offer important insights into the tissue-level biomechanics of fracture healing that could be applied in clinical assessments of bony healing, in studies of bone-tissue engineering and skeletal development, and in creation of finite element models for prediction of the mechanical behavior of fracture calluses.
Acknowledgments
This work was supported by National Institutes of Health (AR053353). Use of the Hysitron Triboindenter was graciously provided by Dr Catherine Klapperich. Pui Leng Leong was supported by CIMIT (Center for Integration of Medicine and Innovative Technology) Fellowship. The authors would also like to thank Zachary Mason for technical support on obtaining µCT images of the specimens.
References
- Athanasiou KA, Zhu CF, Wang X, Agrawal CM. Effects of aging and dietary restriction on the structural integrity of rat articular cartilage. Ann Biomed Eng. 2000;28:143–9. doi: 10.1114/1.238. [DOI] [PubMed] [Google Scholar]
- Bei H, George EP, Hay JL, Pharr GM. Influence of indenter tip geometry on elastic deformation during nanoindentation. Phys Rev Lett. 2005;95:045501. doi: 10.1103/PhysRevLett.95.045501. [DOI] [PubMed] [Google Scholar]
- Claes LE, Heigele CA. Magnitudes of local stress and strain along bony surfaces predict the course and type of fracture healing. J Biomech. 1999;32:255–66. doi: 10.1016/s0021-9290(98)00153-5. [DOI] [PubMed] [Google Scholar]
- Currey JD. Tensile yield in compact bone is determined by strain, post-yield behaviour by mineral content. J Biomech. 2004;37:549–56. doi: 10.1016/j.jbiomech.2003.08.008. [DOI] [PubMed] [Google Scholar]
- Dong XN, Guo XE. The dependence of transversely isotropic elasticity of human femoral cortical bone on porosity. J Biomech. 2004;37:1281–7. doi: 10.1016/j.jbiomech.2003.12.011. [DOI] [PubMed] [Google Scholar]
- Donnelly E, Baker SP, Boskey AL, van der Meulen MC. Effects of surface roughness and maximum load on the mechanical properties of cancellous bone measured by nanoindentation. J Biomed Mater Res A. 2006;77:426–35. doi: 10.1002/jbm.a.30633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Einhorn TA. The cell and molecular biology of fracture healing. Clin Orthop. 1998:S7–21. doi: 10.1097/00003086-199810001-00003. [DOI] [PubMed] [Google Scholar]
- Fan Z, Rho JY. Effects of viscoelasticity and time-dependent plasticity on nanoindentation measurements of human cortical bone. J Biomed Mater Res A. 2003;67:208–14. doi: 10.1002/jbm.a.10027. [DOI] [PubMed] [Google Scholar]
- Ferguson VL, Bushby AJ, Boyde A. Nanomechanical properties and mineral concentration in articular calcified cartilage and subchondral bone. J Anat. 2003;203:191–202. doi: 10.1046/j.1469-7580.2003.00193.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franke O, Durst K, Maier V, Goken M, Birkholz T, Schneider H, Hennig F, Gelse K. Mechanical properties of hyaline and repair cartilage studied by nanoindentation. Acta Biomater. 2007;3:873–81. doi: 10.1016/j.actbio.2007.04.005. [DOI] [PubMed] [Google Scholar]
- Gardner TN, Mishra S. The biomechanical environment of a bone fracture and its influence upon the morphology of healing. Med Eng Phys. 2003;25:455–64. doi: 10.1016/s1350-4533(03)00036-5. [DOI] [PubMed] [Google Scholar]
- Gardner TN, Mishra S, Marks L. The role of osteogenic index, octahedral shear stress and dilatational stress in the ossification of a fracture callus. Med Eng Phys. 2004;26:493–501. doi: 10.1016/j.medengphy.2004.03.009. [DOI] [PubMed] [Google Scholar]
- Gardner TN, Stoll T, Marks L, Mishra S, Knothe TM. The influence of mechanical stimulus on the pattern of tissue differentiation in a long bone fracture–an FEM study. J Biomech. 2000;33:415–25. doi: 10.1016/s0021-9290(99)00189-x. [DOI] [PubMed] [Google Scholar]
- Gupta HS, Schratter S, Tesch W, Roschger P, Berzlanovich A, Schoeberl T, Klaushofer K, Fratzl P. Two different correlations between nanoindentation modulus and mineral content in the bone-cartilage interface. J Struct Biol. 2005;149:138–48. doi: 10.1016/j.jsb.2004.10.010. [DOI] [PubMed] [Google Scholar]
- Hengsberger S, Kulik A, Zysset P. Nanoindentation discriminates the elastic properties of individual human bone lamellae under dry and physiological conditions. Bone. 2002;30:178–84. doi: 10.1016/s8756-3282(01)00624-x. [DOI] [PubMed] [Google Scholar]
- Klapperich CM, Komvopoulos K, Pruitt L. Nanomechanical properties of polymers determined from nanoindentation experiments. J Tribol. 2001;123:624–31. [Google Scholar]
- Leong PL, Morgan EF. Measurement of fracture callus material properties via nanoindentation. Acta Biomater. 2008;4:1569–75. doi: 10.1016/j.actbio.2008.02.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C, Pruitt LA, King KB. Nanoindentation differentiates tissue-scale functional properties of native articular cartilage. J Biomed Mater Res A. 2006;78:729–38. doi: 10.1002/jbm.a.30751. [DOI] [PubMed] [Google Scholar]
- Liu D, Weiner S, Wagner HD. Anisotropic mechanical properties of lamellar bone using miniature cantilever bending specimens. J Biomech. 1999;32:647–54. doi: 10.1016/s0021-9290(99)00051-2. [DOI] [PubMed] [Google Scholar]
- Markel MD, Wikenheiser MA, Chao EY. A study of fracture callus material properties: relationship to the torsional strength of bone. J Orthop Res. 1990;8:843–50. doi: 10.1002/jor.1100080609. [DOI] [PubMed] [Google Scholar]
- McKibbin B. The biology of fracture healing in long bones. J Bone Joint Surg Br. 1978;60-B:150–62. doi: 10.1302/0301-620X.60B2.350882. [DOI] [PubMed] [Google Scholar]
- Morgan EF, Mason ZD, Chien KB, Pfeiffer AJ, Barnes GL, Einhorn TA, Gerstenfeld LC. Micro-computed tomography assessment of fracture healing: relationships among callus structure, composition, and mechanical function. Bone. 2009;44:335–44. doi: 10.1016/j.bone.2008.10.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oliver WC, Pharr GM. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J Mater Res. 1992;7:1564–83. [Google Scholar]
- Prendergast PJ, Huiskes R, Soballe K. ESB Research Award 1996. Biophysical stimuli on cells during tissue differentiation at implant interfaces. J Biomech. 1997;30:539–48. doi: 10.1016/s0021-9290(96)00140-6. [DOI] [PubMed] [Google Scholar]
- Rho JY, Zioupos P, Currey JD, Pharr GM. Variations in the individual thick lamellar properties within osteons by nanoindentation. Bone. 1999;25:295–300. doi: 10.1016/s8756-3282(99)00163-5. [DOI] [PubMed] [Google Scholar]
- Salisbury-Palomares KT, Gleason R, Mason ZD, Cullinane DM, Einhorn TA, Gerstenfeld LC, Morgan EF. Mechanical stimulation alters tissue differentiation and molecular expression. J Orthop Res. 2009 doi: 10.1002/jor.20863. 2009 Feb 25 [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarmiento A, Latta LL. Functional fracture bracing: tibia humerus ulna. Berlin: Springer Verlag; 1995. pp. 239–40. [Google Scholar]
- Shefelbine SJ, Simon U, Claes L, Gold A, Gabet Y, Bab I, Muller R, Augat P. Prediction of fracture callus mechanical properties using micro-CT images and voxel-based finite element analysis. Bone. 2005;36:480–8. doi: 10.1016/j.bone.2004.11.007. [DOI] [PubMed] [Google Scholar]
- Silva MJ, Brodt MD, Fan Z, Rho JY. Nanoindentation and whole-bone bending estimates of material properties in bones from the senescence accelerated mouse SAMP6. J Biomech. 2004;37:1639–46. doi: 10.1016/j.jbiomech.2004.02.018. [DOI] [PubMed] [Google Scholar]
- Smith-Adaline EA, Volkman SK, Ignelzi MA, Jr, Slade J, Platte S, Goldstein SA. Mechanical environment alters tissue formation patterns during fracture repair. J Orthop Res. 2004;22:1079–85. doi: 10.1016/j.orthres.2004.02.007. [DOI] [PubMed] [Google Scholar]
- Zhang T-Y, Xu W-H. Surface effects on nanoindentation. J Mater Res. 2002;17:1715–20. [Google Scholar]
- Zysset PK, Guo XE, Hoffler CE, Moore KE, Goldstein SA. Elastic modulus and hardness of cortical and trabecular bone lamellae measured by nanoindentation in the human femur. J Biomech. 1999;32:1005–12. doi: 10.1016/s0021-9290(99)00111-6. [DOI] [PubMed] [Google Scholar]