Calibration of DFT Functionals for the Prediction of ⁵⁷Fe Mössbauer Spectral Parameters in Iron-Nitrosyl and Iron-Sulfur Complexes: Accurate Geometries Prove Essential

Abstract

Six popular density functionals in conjunction with the conductor-like screening (COSMO) solvation model have been used to obtain linear Mössbauer isomer shift (IS) and quadrupole splitting (QS) parameters for a test set of 20 complexes (with 24 sites) comprised of nonheme nitrosyls (Fe–NO) and non-nitrosyl (Fe–S) complexes. For the first time in an IS analysis, the Fe electron density was calculated both directly at the nucleus, ρ(0)_N, which is the typical procedure, and on a small sphere surrounding the nucleus, ρ(0)_S, which is the new standard algorithm implemented in the ADF software package. We find that both methods yield (near) identical slopes from each linear regression analysis but are shifted with respect to ρ(0) along the x-axis. Therefore, the calculation of the Fe electron density with either method gives calibration fits with equal predictive value. Calibration parameters obtained from the complete test set for OLYP, OPBE, PW91, and BP86 yield correlation coefficients (r²) of approximately 0.90, indicating that the calibration fit is of good quality. However, fits obtained from B3LYP and B3LYP* with both Slater-type and Gaussian-type orbitals are generally found to be of poorer quality. For several of the complexes examined in this study, we find that B3LYP and B3LYP* give geometries that possess significantly larger deviations from the experimental structures than OLYP, OPBE, PW91 or BP86. This phenomenon is particularly true for the di- and tetranuclear Fe complexes examined in this study. Previous Mössbauer calibration fit studies using these functionals have usually included mononuclear Fe complexes alone, where these discrepancies are less pronounced. An examination of spin expectation values reveals B3LYP and B3LYP* approach the weak-coupling limit more closely than the GGA exchange-correlation functionals. The high degree of variability in our calculated S² values for the Fe–NO complexes highlights their challenging electronic structure. Significant improvements to the isomer shift calibrations are obtained for B3LYP and B3LYP* when geometries obtained with the OLYP functional are used. In addition, greatly improved performance of these functionals is found if the complete test set is grouped separately into Fe–NO and Fe–S complexes. Calibration fits including only Fe–NO complexes are found to be excellent, while those containing the non-nitrosyl Fe–S complexes alone are found to demonstrate less accurate correlations. Similar trends are also found with OLYP, OPBE, PW91, and BP86. Correlations between experimental and calculated QSs were also investigated. Generally, universal and separate Fe–NO and Fe–S fit parameters obtained to determine QSs are found to be of good to excellent quality for every density functional examined, especially if [Fe₄(NO)₄(μ₃-S)₄]⁻ is removed from the test set.

Introduction

Mössbauer (MB) spectroscopy is an extremely valuable experimental tool in bioinorganic chemistry because it can provide information on the spin and oxidation state of the MB atom and fine structure parameters like zero-field splitting and the hyperfine coupling tensor.¹ By far, ⁵⁷Fe represents the most commonly probed nuclei, though it is worth noting that ⁶¹Ni and ⁶⁷Zn are two other biologically relevant MB-active isotopes. MB spectroscopy relies on the recoilless resonant absorption of γ-radiation by the MB active nuclei from a source emitter. For ⁵⁷Fe, it is the resonant absorption of 14.4 keV γ-rays emitted from a radioactive ⁵⁷Co source that is measured. A major advantage of MB spectroscopy is that all MB active nuclei are probed simultaneously in the sample. Challenges in using this technique include the requirement of ⁵⁷Fe (or other) enrichment and deconvoluting complicated spectra when several active nuclei are present. In conjunction with rapid freeze-quench techniques, MB spectroscopy is a particularly valuable tool in bioinorganic chemistry because the Fe environment can be monitored during the course of a biochemical reaction to give insight into the nature of short-lived intermediates and the reaction mechanisms they participate in.²

Two key parameters extracted from Mössbauer spectra are the isomer shift (IS) and quadrupole splitting (QS). ISs provide information on metal-ligand covalency and the spin and oxidation states of the Fe center. Contributions to the magnitude of ISs are effects from shielding of the 3s electrons by the Fe 3d electrons, covalency effects, and changes in bond lengths.³ The IS can be calculated by linear regression of the following equation:

$$\delta =\alpha [\rho (0)-A]+C$$ (1)

where δ is the experimental IS (mm s⁻¹), ρ(0) is the calculated s-electron density at the nucleus (e a₀⁻³), α is the slope (e⁻¹ a₀³ mm s⁻¹), and C is the intercept (mm s⁻¹). A is a large constant chosen to be near ρ(0) in magnitude. This aids in the numerical stability of the fitting in the linear regression equation. The factors α, A, and C are determined in calibration procedures, often with calculations involving a specific level of theory.

QSs are the other key parameter obtained from MB spectroscopy arising from the interaction of the quadrupole moment of the first nuclear excited state of ⁵⁷Fe (I = 3/2) with the electric field gradient surrounding the Fe nucleus. QS parameters are very sensitive to the local chemical environment of the Fe nucleus and give information on the population of its 3d orbitals and their ligand environment. The quadrupole interaction splits the ⁵⁷Fe (I = 3/2) nucleus into two doubly degenerate states (m_I ± 1/2 and m_I ± 3/2) whose energy difference is calculated as:

$$\mathrm{\Delta }{E}_Q=\frac{1}{2}{\mathit{eQV}}_{zz}{(1+{\eta }^2/3)}^{1/2}$$ (2)

where e is the positive electric charge, Q is the nuclear quadrupole moment (in barns), and V_zz is the electric field gradient. η is an asymmetry parameter defined as (V_xx – V_yy)/V_zz with |V_zz| ≥ |V_yy| ≥ |V_xx|.

Density functional theory (DFT) has become an increasingly popular tool to calculate structures and Mössbauer properties.⁴ Its application to Fe-containing and other metalloenzymes to delineate their mechanisms-of-action offers atomic-level understanding of these intricate processes.^5–7 Clearly, the success of this approach results from accurate and insightful comparisons with experiment that allow a rationalization of existing data and the suggestion of new experiments. To further support this synergy between theory and experiment our aim in the present study is to calibrate Mössbauer parameters for a variety of commonly used DFT functionals including OLYP, OPBE, PW91, BP86, B3LYP, and B3LYP* using a test set comprised of nonheme nitrosyls including low- (S = 1/2) and high-spin (S = 3/2) {FeNO}⁷, {Fe(NO)₂}⁹ species, and other non-nitrosyl iron-sulfur complexes. We follow the nomenclature of Enemark–Feltham to count the electrons in the {FeNO}ⁿ and {Fe(NO)₂}ⁿ species, where n is the number of d electrons on the metal plus the number of electrons in the π* orbitals of NO.⁸ Nonheme nitrosyls represent an attractive target to probe the relationship between theory and experiment because of their unusual and complex electronic structure.^9–12 Indeed, the spin densities of iron nitrosyls exhibit broken-symmetry character and consequently there is a strong tendency for the majority and minority spin densities to be spatially separated.^13–16 The complexes within our test set possess mono- and polynuclear Fe centers and thus represent a challenge to theory to describe accurately their electronic structure and properties.

It is worth noting that a number of DFT calibration studies of Mössbauer isomer shifts and quadrupole splittings have been reported in the literature.^3,17–26 For example, Neese and coworkers have found that fit parameters are relatively insensitive to whether nonrelativistic or quasi-relativistic (via the zero-order regular approximation, ZORA) DFT methods are employed.^22,25 The ZORA Fe electron densities are shifted towards the four-component Dirac–Fock limit, but no improvement in the correlation is observed. Further, no improvement in the calculated quadrupole splittings were observed when the ZORA approach was used instead of a nonrelativistic treatment.²² Very recently, Lippard and co-workers have reported the performance of eight density functionals for the prediction of ISs and QSs. They found the B3LYP and O3LYP density functionals to have the lowest errors while M06-2X and SVWN5 possess the highest for their large test set of 31 iron-containing complexes (35 signals), including both mononuclear and dinuclear systems.²⁶

While these previous efforts have proven to be valuable in their own right, it should be noted that most of the complexes examined have been mononuclear Fe complexes, with the exception of a few. The present effort, which includes mononuclear, dinuclear, and tetranuclear complexes in the training set, is our latest contribution to this growing field and represents an important step forward by providing accurate calibrations fits for spectroscopic isomer shifts and quadrupole splitting parameters. One aspect of this work that this is particularly valuable is our finding that the commonly used functional B3LYP (and B3LYP*) performs poorly in predicting accurate geometries, especially for the dinuclear and tetranuclear Fe complexes. We find that these poor geometries lead to very poor isomer shift calibration fits.

For the first time in an isomer shift calibration study we compare two methods used to calculate the Fe electron density. The typical procedure determines this quantity directly at the Fe nucleus. More recently, the ADF software package has by default begun to determine this quantity on a small sphere surrounding the Fe nucleus, which better reflects the underlying physics of the Mössbauer-active nucleus, since the nuclear radius changes from the ground to the excited ⁵⁷Fe state. Moreover, this approach prohibits the four-component Dirac-Fock electron density from becoming infinite in the limit of a large enough basis set at a point charge nucleus during relativistic calculation. Because it is not know a priori how the choice in method used to calculate to Fe electron density will affect isomer shift calibration fits, we sought to examine this issue by calibrating six exchange-correlation potentials for each approach. We believe this work will provide wide utility for those wishing to calculate accurate Mössbauer parameters for comparison with experiment.

Computational Methods

Geometry optimizations using the PW91,^27,28 BP86,^29,30 OLYP,^31,32 OPBE^31,33,34, B3LYP,^32,35,36 and B3LYP*³⁷ exchange-correlation functionals were carried out with the Amsterdam Density Functional (ADF) 2009.01^38,39 software package. These particular functionals have been chosen because they have previously been shown to be give accurate geometries, energy and/or spin-state splittings for transition metal complexes with weak field ligands. All-electron Slater-type triple-ζ plus polarization (STO-TZP) basis sets were used for both the geometry optimizations and subsequent Mössbauer calculations, with the numerical integration accuracy set to 5.5. This approach is identical to that taken in our previous work in this area.¹¹ The ‘AddDiffuseFit’ feature of ADF was also employed for the B3LYP and B3LYP* calculations to minimize numerical problems found with hybrid functionals and the fit procedure used by ADF. The ORCA 2.8.0⁴⁰ software package was also used to calculate Mössbauer parameters for the complexes of this study with B3LYP and B3LYP*. For the latter calculations, the Gaussian-type basis set TZVP of Ahlrichs^41,42 was used for the geometry optimizations with ‘Grid4’. Single-point energy calculations were then performed using the TZVP basis set for all elements but Fe, where for this element we used the CP(PPP) basis set,³ which utilizes the Ahlrichs (2d2fg, 3p2df) polarization functions from the Turbomole basis set library under ftp.chemie.uni-karlsruhe.de/pub/basen and 2p functions⁴³ plus additional one f-function from the Turbomole library. In addition, the ‘SpecialGrid’ option was used to enhance the integration accuracy of Fe to 7.0. In both ADF and ORCA, solvent effects were modeled with the COnductor-like Screening MOdel (COSMO),⁴⁴ using methanol as the solvent (dielectric constant = 32.6).

All of the S_t = 0, 1/2, or 1 polynuclear complexes in this study have high-spin metal sites and exhibit antiferromagnetic coupling. Therefore, spin-unrestricted broken symmetry DFT was used to describe the electronic structure of these systems.⁴⁵ This approach constructs a wave function such that the spin-up (α) electron density occupies a different spatial region than the spin-down (β) electron density. In practice, this is achieved by first constructing a high-spin ferromagnetically coupled state and then exchanging the α and β electron densities of the appropriate iron atoms. Re-converging the wave function then produces the desired antiferromagnetically coupled state.

In some cases we were not able to converge the geometry of a given species to sufficient accuracy with the B3LYP and B3LYP* exchange-correlation functionals. Consequently, in such cases we used OLYP geometries for the B3LYP and B3LYP* STO-TZP COSMO single-point energy calculations for the following complexes: [Fe₂S₂(S₂-o-xyl)₂]²⁻, [Fe₄S₄(SCH₂CO₂Et)₄]²⁻, [Fe₄S₄(SPh)₄]²⁻, and [Fe₂(NO)₂(Et-HPTB)(O₂CPh)]²⁺. In addition, we use an OLYP/STO-TZP COSMO geometry for the B3LYP/STO-TZP COSMO single-point energy calculation for [Fe₄S₄(SPh)₂Cl₂]²⁻. Finally, a B3LYP*/TZVP COSMO geometry is used for the B3LYP/CP(PPP)-TZVP COSMO single-point energy calculation for [Fe₂(NO)₂(Et-HPTB)(O₂CPh)]²⁺.

As previously noted, Mössbauer ISs are proportional to the s-electron density at the nucleus, ρ(0). This quantity is often calculated directly at the nucleus. However, the latest ADF codes (2009 and 2010) calculate the Fe electron density at points on a small spherical surface around the center of the nucleus, where the average electron density over these points is reported.³⁹

This spherical surface method better represents the underlying physics of the isomer shift phenomena. Upon γ-ray absorption, the ⁵⁷Fe radius changes between the ground and excited states and the isomer shift is due to the contact interaction of the electron density with the thin spherical shell between these radii. An additional appeal of this approach is to prohibit the four-component Dirac-Fock electron density from becoming infinite in the limit of a large enough basis set at a point charge nucleus during relativistic calculations. The use of a small sphere surrounding the nucleus circumvents this issue because the relativistic electron density remains finite there. Further, if a proper finite-sized nucleus is used, then the relativistic density will remain finite even at the center of the nucleus. In any event, these differences in approach led us to assess how the Mössbauer calibration parameters were affected, since it is valuable to have available in the literature calibration parameters that can be applied to standard output from software packages. To evaluate the Fe ρ(0) directly at the nucleus in ADF, we use our in-house hyper2003⁴⁶ program in conjunction with ADF’s TAPE21 as in our previous work. We note that by default ORCA also evaluates ρ(0) at the nucleus.

Finally, the nuclear quadrupole moment of ⁵⁷Fe is of interest since ADF and ORCA use slightly different values (0.15 vs 0.16 electron-barns, respectively). Previously, our group had used eQ = 0.15 electron-barn.⁴⁷ For the current study, however, we use eQ = 0.158 electron-barn, which is taken from recent non-relativistic quantum chemical calculations.²²

Results and Discussion

a. Details of the Test Set

Table 1 provides a detailed summary of the complexes used in this study, which follows on from our earlier work where the performance of the OLYP exchange-correlation functional to calculate Mössbauer parameters was assessed.¹¹ The twelve non-nitrosyl (Fe–S) complexes of this study include synthetic analogues of the [Fe(SR)₄] center bacterial rubredoxins, plant-like 2Fe–2S ferredoxins and Rieske proteins, and the 4Fe–4S cubane centers in ferredoxins and high-potential iron proteins (HiPIPs). The three mononuclear Fe–S complexes are high-spin Fe centers, with S_tot of either 5/2 or 2. Table S1 in the Supporting Information shows the Mulliken Fe spin populations of these species calculated at various levels of theory. As is expected for these high-spin Fe³⁺ and Fe²⁺ centers, the magnitudes of these populations range from ca. 3.4 to 3.9, with the Fe³⁺ centers possessing the larger spin populations. All of the three 2Fe–2S complexes possess high-spin S = 5/2 Fe³⁺ centers and are antiferromagnetically coupled to give S_tot = 0. An examination of the Mulliken Fe spin populations (Table S1) confirms this, with their (absolute) values ranging from ca. 3.3 to 3.9 for the broken-symmetry states. Similarly, the 4Fe–4S complexes are antiferromagnetically coupled to give S_tot = 0, but here each Fe center is considered to possess an oxidation state of +2.5, which may be regarded as resulting from the pair-wise interaction of Fe²⁺ ferromagnetically coupled to Fe³⁺ and associated electron delocalization. In these cases, the absolute values of the Fe spin populations range from 2.9 to 3.7. For all of the complexes studied, the hybrid density functionals B3LYP and B3LYP* give higher Mulliken spin populations than do the OLYP, OPBE, PW91, and BP86 density functionals. For the pure functionals, we note that PW91 gives the lowest degree of localized spin on the Fe centers, while OPBE gives the highest.

Table 1.

Details of the Iron Complexes Examined in this Study

complex	structurea	Pt Gr.	St	Fe oxidation	Temp. (K)	δexp (mm s−1)	|ΔEQ|exp (mm s−1)	refb
[Fe(SEt)4]−	CANDAW10	C1	5/2	Fe3+	4.2	0.25	0.62	52,53
[FeS4C8O4]2−	PTSQFE10	C1	2	Fe2+	4.2	0.668	3.97	54
[Fe(SPh)4]2−	PTHPFE10	C1	2	Fe2+	4.2	0.66	3.24	54
[Fe(H2O)5(NO)]2+		C1	3/2	{FeNO}7	80	0.76	2.10	55
[Fe(NO)(dtci-Pr2)2]c	PRCBFE	C1	1/2	{FeNO}7	4.2	0.35	0.89	56,57
[Fe(SPh)2(NO)2]−	SI	C1	1/2	{Fe(NO)2}9	4.2	0.182	0.692	58
[Fe(SC2H3N3)(SC2H2N3)(NO)2]	EYABOV	C1	1/2	{Fe(NO)2}9	296	0.188	1.118	59,60
[Fe2S2(S2-o-xyl)2]2−	XLDTSF	Cs	0	2*Fe3+	4.2	0.28	0.36	61–63
[Fe2S2(OPh-p-CH3)4]2−	GIBCUP	Cs	0	2*Fe3+	4.2	0.37	0.32	63
[Fe2S2(C4H4N)4]2−	CONSED10	C2v	0	2*Fe3+	77	0.26	0.49	63
[Fe2(NO)2(Et-HPTB)(O2CPh)]2+ d	RABHAD	C1	0	2*{FeNO}7	4.2	0.67	1.44	64
[Fe(NO)2{Fe(NO)(N(CH2CH2S)3)}-S,S′]	SI	C1	1	{FeNO}7 {Fe(NO)2}9	77	0.37 0.18	1.15 1.04	65
[Fe4S4(SPh)4]2−	FEMJAI02	C1	0	4*Fe2.5+	4.2	0.46	1.07	66,67
[Fe4S4(OPh)4]2−	CAPGAB	C1	0	4*Fe2.5+	4.2	0.50	1.21	68
[Fe4S4(SPh)2Cl2]2− g	CIYKUQ	C1	0	2*Fe2.5+–SPh 2*Fe2.5+–Cl	4.2	0.48 0.51	0.90 1.22	66
[Fe4S4(OPh)2Cl2]2− g	CIYLAX	C1	0	2*Fe2.5+–OPh 2*Fe2.5+–Cl	4.2	0.51 0.52	1.01 1.28	66
[Fe4S4Cl4]2−	NUSROI	C2v	0	4*Fe2.5+	4.2	0.52	1.09	66,69
[Fe4S4(SCH2CO2Et)4]2−	CEQYAY	C2	0	4*Fe2.5+	78	0.43	0.81	70
[Fe4(NO)4(μ3-S)4]e	KOCBUZ	C2v	0	4*{FeNO}7	78	0.15	1.473	71,72
[Fe4(NO)4(μ3-S)4]−	BIBMOO	C2v	1/2	2*{FeNO}7.5 2*{FeNO}7	RTf	0.156 0.156	0.935 0.935	73

^aCambridge ID or reference to cif file, SI = Supporting Information.

^bReferences for crystal structures and Mössbauer parameters.

^cdtc = dithiocarbamate.

^dEt-HPTB = N,N,N′,N′-tetrakis-(N-ethyl-2-benzimidazolylmethyl)-2-hydroxy-1,3-diaminopropane.

^eOxidation state assignment dependent upon the electronic state.

^fRT = room temperature, assumed to be 298 K.

^gExperimental values were assigned such that the smaller isomer shift is assigned to the higher electron density.

All eight iron-nitrosyl complexes within this study include {FeNO}⁷ and/or {Fe(NO)₂}⁹ moieties. Table S2 shows the Fe center and NO ligands of each FeNO unit. It can be seen that each unit exhibits oppositely aligned Fe and NO spin populations. Four mononuclear {FeNO}⁷ and {Fe(NO)₂}⁹ iron-nitrosyl complexes were examined with S = 3/2 or 1/2. The Fe spin population in the S = 3/2 [Fe(H₂O)₅(NO)]²⁺ complex ranges from 3.4 – 3.8. Here, the {FeNO}⁷ unit may be described as a high-spin (S = 5/2) Fe³⁺ antiferromagnetically coupled to NO⁻ (S = 1).⁴⁸ In contrast, the FeNO units in [Fe(NO)(dtci-Pr₂)₂], [Fe(SPh)₂(NO)₂]⁻, and [Fe(SC₂H₃N₃)(SC₂H₂N₃)(NO)₂] exhibit substantially lower Fe spin populations. For these cases, the {FeNO}⁷ unit in [Fe(NO)(dtci-Pr₂)₂] can be described as an intermediate-spin Fe³⁺ center (S = 3/2) coupled to an S = 1 NO⁻, while the S = 1/2 {Fe(NO)₂}⁹ units in [Fe(SPh)₂(NO)₂]⁻, and [Fe(SC₂H₃N₃)(SC₂H₂N₃)(NO)₂] may be described as high-spin Fe³⁺ antiferromagnetically coupled to two NO⁻ diradicals or as high-spin Fe¹⁺ (S = 3/2) coupled to two NO^• radicals. The interested reader is referred elsewhere for the details of previous DFT calculations and associated molecular orbital arguments to explain the factors that affect the FeNO angle.^9,49–51

Two dinuclear nitrosyl complexes included in our study are the diamagnetic bis-{FeNO}⁷ [Fe₂(NO)₂(Et-HPTB)(O₂CPh)]²⁺ and the paramagnetic S = 1 thiolate-bridged {FeNO}⁷-{Fe(NO)₂}⁹ complex [Fe(NO)₂{Fe(NO)(N(CH₂CH₂S)₃)}-S,S′]. The dinuclear S = 0 [Fe₂(NO)₂ (Et-HPTB)(O₂CPh)]²⁺ complex contains oppositely aligned S = 3/2 {FeNO}⁷ units with (absolute) spin populations of 3.2 – 3.8. The [Fe(NO)₂{Fe(NO)(N(CH₂CH₂S)₃)}-S,S′] complex may be viewed as an S = 3/2 {FeNO}⁷ unit antiferromagnetically coupled with an S = 1/2 {Fe(NO)₂}⁹ unit to give an S = 1 complex.

The neutral and reduced [Fe₄(NO)₄(μ₃-S)₄]^0/− complexes possess 4Fe–4S cubane cores as discussed above. Each iron–NO in the neutral complex is a {FeNO}⁷ unit, while the reduced form can be described as having two of the iron centers as {FeNO}⁷ units and two as {FeNO}^7.5 units. Further details about all the complexes studied in this work can be found in our previous work.¹¹

b. Isomer Shift

The experimental Fe isomer shifts (IS) used in this study were obtained at temperatures ranging from 4.2 to 298 K. Increases in temperature will result in a lower isomer shift, principally due to the second-order Doppler effect. Thus, to enable a meaningful comparison with our calculated values, we correct the experimental ISs to a common temperature of 4.2 K. This correction is expected to be linear with temperature,⁷⁴ and in the present work is taken to be 0.12 mm s⁻¹ over the range 4.2 to 300 K.

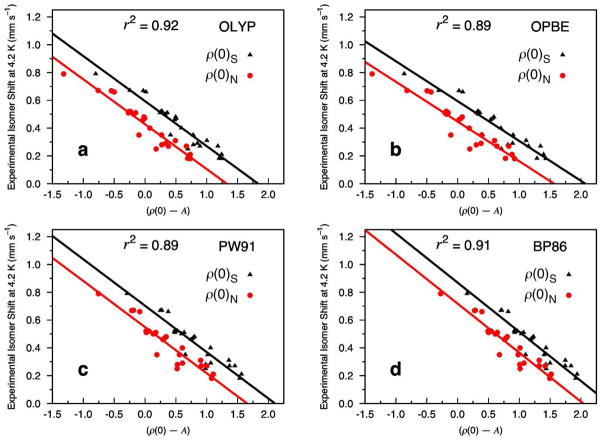
Figure 1 displays four of our universal IS fits based on calculations of 8 iron–nitrosyl (Fe–NO) and 12 non-nitrosyl (Fe–S) complexes, comprising a total of 24 distinct iron sites. For each level of theory the Fe electron density is calculated both at the nucleus, ρ(0)_N, and on a small sphere surrounding the nucleus, ρ(0)_S. Generally, the linear regression analysis yields near identical values for α, but different values for C and A for the two methods (cf. Eq. (1)).

Figure 1.

Isomer shift fit based on 8 Fe–NO and 12 Fe–S complexes (24 sites) calculated at the OLYP, OPBE, PW91, and BP86 level of theory using COSMO and the STO-TZP basis set. The Fe electron density is calculated directly at the nucleus (ρ(0)_N, circles) and on a small sphere around the center of the Fe nucleus (ρ(0)_S, triangles).

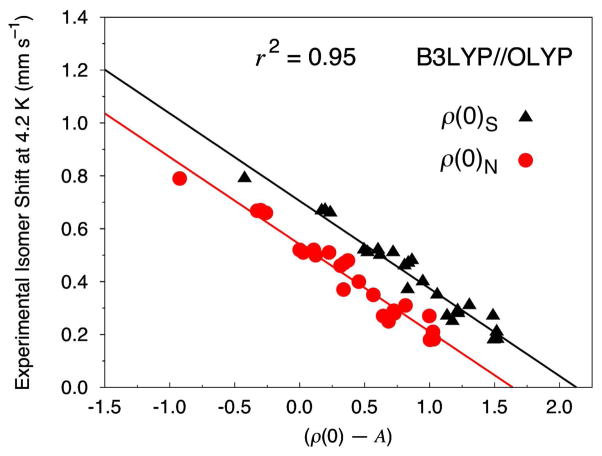
Figure 1a shows the results for calculations with the OLYP/STO-TZP COSMO level of theory. For ρ(0)_N, the analysis yields values of α = −0.323, C = 0.428, and A = 11877, while for ρ(0)_S these values are α = −0.324, C = 0.594, and A = 11820. The r² value for both methods is 0.92 with a mean absolute error (MAE) of 0.037 mm s⁻¹. The complexes that exhibit the largest MAEs are [Fe((SEt))₄]⁻ (0.12 mm s⁻¹) and [Fe₂S₂(OPh-p-CH₃)₄]²⁻ (0.09 mm s⁻¹). When these two complexes are removed from the analysis the total MAE is reduced to 0.029 mm s⁻¹ and the r² becomes 0.95. The corresponding linear regression values are α = −0.322 and C = 0.603 for ρ(0)_S and α = −0.321 and C = 0.437 for ρ(0)_N (of course, the A values remain constant). As will be shown below, [Fe(SEt)₄]⁻ and [Fe₂S₂(OPh-p-CH₃)₄]²⁻ emerge consistently as structures that exhibit the poorest comparisons with experiment for the OLYP, OPBE, PW91, and BP86 functionals. Interestingly, inspection of their calculated geometries does not reveal significant deviations from the experimental structures.

Figure 1b shows our isomer shift fit based on OPBE/STO-TZP COSMO calculations of all the complexes in our test set. In this case, the linear regression analysis for ρ(0)_N yields values of α = −0.286, C = 0.447, and A = 11877, while for ρ(0)_S these values are α = −0.287, C = 0.594, and A = 11820. The r² for both methods is 0.89 with a MAE of 0.041 mm s⁻¹, which is slightly worse than is observed for OLYP. As found with OLYP, the calculated isomer shifts of [Fe(SEt)₄]⁻ and [Fe₂S₂(OPh-p-CH₃)₄]²⁻ show the largest variations relative to experiment (0.14 and 0.11 mm s⁻¹, respectively), and their removal from the analysis improves the MAE and r² appreciably; specifically, the MAE is reduced to 0.030 mm s⁻¹ with an r² of 0.94. The linear regression parameters then become α= −0.287 and C = 0.458 for ρ(0)_N, and α = −0.288 and C = 0.606 for ρ(0)_S.

Figure 1c displays the results we obtain with our PW91/STO-TZP COSMO calculations. Overall, PW91 yields a slightly worse MAE (of 0.042 mm s⁻¹) relative to experiment for our complete test set than is observed for either OLYP or OPBE. The linear regression analysis for ρ(0)_N yields values of α = −0.332, C = 0.549, and A = 11874. These values are α = −0.334, C = 0.703, and A = 11827 for ρ(0)_S, with an r² value of 0.89. [Fe(SEt)₄]⁻ and [Fe₂S₂(OPh-p-CH₃)₄]²⁻ again show the largest variations relative to experiment (0.13 and 0.12 mm s⁻¹, respectively). Removing them from the analysis yields a MAE of 0.034 mms s⁻¹ and an r² of 0.94. We also observe slightly changed linear regression values for ρ(0)_N and ρ(0)_S of α = −0.333 and C = 0.561 and α = −0.335 and C = 0.715, respectively.

Interestingly, BP86 performs quite well in our universal calibration analysis (Figure 1d), yielding a total MAE of 0.040 mm s⁻¹ and an r² of 0.91 for the test set, which places it second to the best performing functional thus far (OLYP, MAE of 0.037 s⁻¹ and r² of 0.92). Calculation of the Fe electron density at the nucleus, ρ(0)_N, yields linear regression values of α = −0.353, C = 0.718, and A = 11889, while calculation of the density at points on a small sphere around the center of the Fe nucleus, ρ(0)_S, gives values of α = −0.354, C = 0.869, and A = 11832. Consistent with our previous findings, [Fe(SEt)₄]⁻ and [Fe₂S₂(OPh-p-CH₃)₄]²⁻ give the largest variations in calculated δ relative to experiment (0.11 mm s⁻¹ for each). The MAE improves to 0.033 mms s⁻¹ when these two structures are removed from the analysis, with an r² of 0.95. The corresponding linear regression values become α = −0.353 and C = 0.728 for ρ(0)_N and α = −0.354 and C = 0.879 for ρ(0)_S.

In Figure S1 in the Supporting Information we show the universal calibration fitting results obtained with the B3LYP/STO-TZP COSMO level of theory. Overall, we find a poor linear correlation of the calculated Fe electron density versus the experimental IS for our test set as the linear regression analysis gives an r² value of 0.64 with a MAE of 0.086 mm s⁻¹. This poor performance is rather surprising since several other studies show B3LYP to demonstrate excellent performance.^22,25,26 This discrepancy appears to be both a consequence of the makeup of our test set and the relatively poor geometries we obtain with this functional for polynuclear Fe complexes (see below).

Previously, it was shown that grouping different oxidation states of Fe will produce different IS calibration lines.²⁴ Hopmann et al. recently observed slightly improved linear regression parameters when the Fe–NO complexes of their test set were determined separately.¹¹ Specifically, the fit r² value is reported to change from 0.915 to 0.979, while the MAE decreased from 0.039 to 0.029 mm s⁻¹ for a test set that included only Fe–NO complexes.

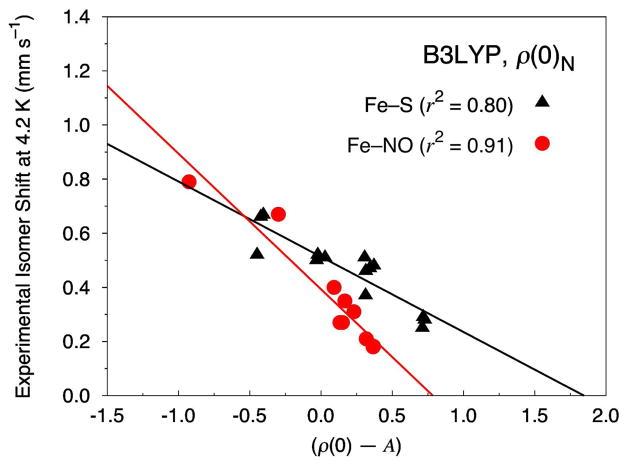
In this spirit, when our current test set is split into non-nitrosyl (i.e., Fe–S) or iron-nitrosyl (i.e., Fe–NO) complexes we observe a very good correlation between the calculated ρ(0)_N and the experimental isomer shift for the Fe–NO complexes with the B3LYP functional (Figure 2), but not for the Fe–S complexes. Similar results for when the Fe electron density is calculated on a small sphere around the center of the Fe nucleus can be found in Figure S2 in the Supporting Information. For completeness, we note also that Figures S3 to S10 of the SI correspond to linear correlation plots for the OLYP, OPBE, PW91 and BP86 levels of theory when the test set is split into Fe–S and Fe–NO complexes.

Figure 2.

Isomer shift fit based on 12 Fe–S (14 sites, triangles) and 8 Fe–NO (10 sites, circles) complexes calculated at the B3LYP/STO-TZP COSMO level of theory with the Fe electron density calculated directly at the nucleus (ρ(0)_N).

When only the 12 Fe–S complexes are considered, which include 14 distinct Fe sites, we obtain linear correlation parameters for ρ(0)_N of α = −0.278, C = 0.513, and A = 11880, with an r² value of 0.80 and a MAE of 0.045 mm s⁻¹. The largest IS outliers in this set correspond to the Fe–Cl and Fe–OPh sites in [Fe₄S₄(OPh)₂Cl₂]²⁻, with MAEs of 0.12 and 0.08 mm s⁻¹, respectively. It is interesting to note that when this complex is removed from our analysis the r² value improves greatly to 0.92.

Turning our attention to the 8 Fe–NO complexes, we find an r² of 0.91, a MAE of 0.050 mm s⁻¹, and linear correlation parameters for ρ(0)_N of α = −0.501, C = 0.393, and A = 11880. With a MAE of 0.13 mm s⁻¹, the {FeNO}⁷ site in [Fe₂(NO)₂(Et-HPTB)(O₂CPh)]²⁺ is the largest outlier. We note that an OLYP geometry was used for this structure because we were unable to converge the B3LYP geometry to sufficient accuracy. However, it is unlikely that this approximation is the primary source of this error, since in many cases excellent agreement is observed between our calculated OLYP structures and those obtained from experiment (see, e.g., Table 2 and 3).

Table 2.

Comparison of Deviations from Experiment and Mean Absolute Deviations (MAD) of Selected Calculated Average Bond Distances (Å) of the Fe₄S₄ Structures of this Study^a

		Expt.	OLYP	OPBE	PW91	BP86	B3LYP	B3LYP*	B3LYPb	B3LYP*b
[Fe4S4(SPh)4]2−	Fe–Fe	2.736	−0.012	−0.075	−0.066	−0.052	n/ac	n/ac	+0.144	+0.147
	Fe–S	2.286	+0.022	−0.017	−0.014	−0.007			+0.071	+0.075
[Fe4S4(OPh)4]2−	Fe–Fe	2.753	+0.017	−0.031	−0.051	−0.037	+0.205	+0.157	+0.150	+0.153
	Fe–S	2.294	+0.028	−0.010	−0.008	−0.002	+0.076	+0.062	+0.071	+0.076
[Fe4S4(SPh)2Cl2]2−	Fe–Fe	2.745	+0.010	−0.071	−0.060	−0.043	n/ac	+0.127	+0.155	+0.110
	Fe–S	2.278	+0.029	−0.011	−0.007	−0.001		+0.066	+0.080	+0.033
[Fe4S4(OPh)2Cl2]2−	Fe–Fe	2.766	+0.005	−0.061	−0.060	−0.001	+0.206	+0.133	+0.159	+0.155
	Fe–S	2.285	+0.028	−0.007	−0.005	+0.001	+0.084	+0.063	+0.079	+0.080
[Fe4S4Cl4]2−	Fe–Fe	2.700	+0.005	−0.072	−0.063	−0.049	+0.159	+0.114	+0.130	+0.126
	Fe–S	2.289	+0.017	+0.017	−0.014	−0.009	+0.064	+0.051	+0.063	+0.066
[Fe4S4(SCH2CO2Et)4]2−	Fe–Fe	2.754	−0.008	−0.093	−0.084	−0.066	n/ac	n/ac	+0.116	+0.117
	Fe–S	2.303	+0.018	−0.015	−0.015	−0.013			+0.098	+0.077
[Fe4(NO)4(μ3-S)4]	Fe–Fe	2.651	−0.016	−0.097	−0.049	−0.045	+0.208	+0.131	+0.307	+0.298
	Fe–S	2.217	−0.010	−0.064	−0.038	−0.034	+0.094	+0.069	+0.143	+0.145
[Fe4(NO)4(μ3-S)4] −	Fe–Fe	2.688	+0.015	−0.080	−0.039	−0.031	+0.208	+0.151	+0.232	+0.229
	Fe–S	2.231	+0.008	−0.051	−0.032	−0.027	+0.107	+0.083	+0.127	+0.129
MAD (Fe–Fe)			0.011	0.073	0.059	0.041	0.197	0.136	0.174	0.167
MAD (Fe–S)			0.020	0.023	0.017	0.012	0.085	0.066	0.092	0.085

^aCalculated values reported as deviations from experiment. Unless otherwise noted, all values are calculated at the OLYP/STO-TZP COSMO level of theory in ADF.

^bCalculated with ORCA using COSMO in combination with a CP(PPP) basis set on Fe and a TZVP basis set on the remaining atoms.

^cGeometry is not available at this level of theory. The OLYP/STO-TZP COSMO geometry is used instead. See Computational Methods section for details.

Table 3.

Comparison of Deviations from Experiment of Selected Calculated Average Bond Distances (Å) and Angles (°) of Selected Mononuclear Fe Structures of this Study^a

		Expt.	OLYP	OPBE	PW91	BP86	B3LYP	B3LYP*	B3LYPb	B3LYP*b
[Fe(SEt)4]−	Fe–S	2.269	+0.061	+0.028	+0.029	+0.032	+0.052	+0.048	+0.055	+0.068
	S–C	1.880	−0.033	−0.051	−0.029	−0.023	−0.026	−0.025	−0.017	−0.010
[Fe(SPh)4]2−	Fe–S	2.353	−0.012	−0.053	−0.053	−0.047	+0.046	+0.026	+0.046	+0.059
	S–C	1.767	+0.006	−0.008	+0.011	+0.015	+0.021	+0.014	+0.021	+0.025
[FeS4C8O4]2−	Fe–S	2.389	+0.011	−0.030	−0.014	−0.007	+0.060	+0.045	+0.051	+0.063
	S–C	1.688	+0.011	0.000	+0.014	+0.017	+0.016	+0.016	+0.027	+0.030
[Fe(NO)(dtci-Pr2)2]	Fe–S	2.288	+0.016	−0.031	+0.006	+0.015	+0.056	+0.045	+0.060	+0.068
	Fe–N	1.676	−0.008	−0.034	−0.017	−0.015	+0.083	+0.040	+0.083	+0.060
	N–O	1.161	+0.032	+0.021	+0.033	+0.034	+0.027	+0.024	+0.018	+0.017
[Fe(SC2H3N3)(SC2H2N3)(NO)2]	Fe–S	2.308	+0.039	−0.011	−0.010	−0.005	+0.084	+0.065	+0.081	+0.092
	Fe–N	1.673	−0.002	−0.023	−0.012	−0.010	+0.083	+0.054	+0.085	+0.071
	N–O	1.154	+0.028	+0.021	+0.029	+0.031	+0.023	+0.022	+0.016	+0.017
MAD (Fe–S)			0.028	0.030	0.022	0.021	0.060	0.048	0.058	0.070
MAD (S–C)			0.016	0.020	0.017	0.019	0.022	0.020	0.023	0.022
MAD (Fe–N)			0.006	0.027	0.016	0.015	0.082	0.047	0.083	0.066
MAD (N–O)			0.029	0.021	0.030	0.031	0.027	0.021	0.018	0.019

^aCalculated values reported as deviations from experiment. Unless otherwise noted, all values are calculated at the OLYP/STO-TZP COSMO level of theory in ADF.

^bCalculated with ORCA using COSMO in combination with a CP(PPP) basis set on Fe and a TZVP basis set on the remaining atoms.

^cGeometry is not available at this level of theory. The OLYP/STO-TZP COSMO geometry is used instead. See Computational Methods section for details.

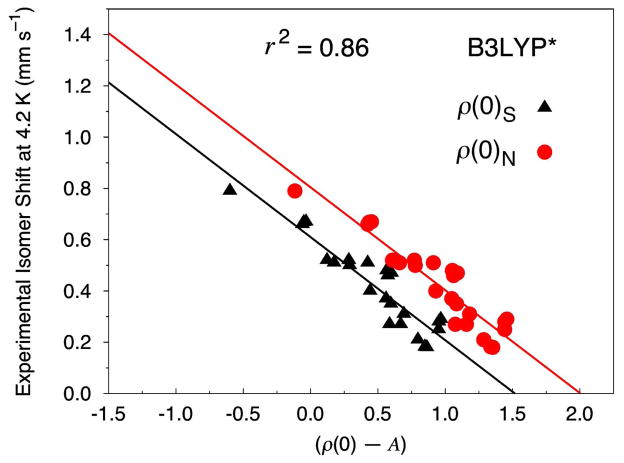
As found with our B3LYP calculations, B3LYP* performs worse in predicting accurate ISs than OLYP, OPBE, PW91 or BP86. Unlike B3LYP (Figure S1), however, B3LYP* is found to show reasonable performance over the entire test set (Figure 3). The total MAE over the entire test set is 0.053 mm s⁻¹ with an r² of 0.86. The linear regression values for the calculation of ISs at this level of theory for ρ(0)_N are α = −0.401, C = 0.804 and A = 11876. When the Fe electron density is calculated as ρ(0)_S, the values are α = −0.402, C = 0.610, and A = 11820. The Fe sites that yield the highest MAEs (of 0.10 mm s⁻¹ each) relative to experiment for B3LYP* include [Fe₄S₄(SCH₂CO₂Et)₄]²⁻, the {FeNO}^7.5 fragment of [Fe₄(NO)₄(μ₃-S)₄]⁻, and the Fe–SPh sites in [Fe₄S₄(SPh)₂Cl₂]²⁻. Interestingly, the poor performance of OLYP, OPBE, PW91, and BP86 to predict accurate isomer shifts for [Fe(SEt)₄]⁻ and [Fe₂S₂(OPh-p-CH₃)₄]²⁻ is not reproduced with B3LYP* (or B3LYP for that matter). In fact, two of the lowest MAEs determined from these B3LYP* calculations are [Fe(SEt)₄]⁻ (0.02 mm s⁻¹) and [Fe₂S₂(OPh-p-CH₃)₄]²⁻ (0.01 mm s⁻¹).

Figure 3.

Isomer shift fit based on 8 Fe–NO and 12 Fe–S complexes (24 sites) calculated at the B3LYP*/STO-TZP COSMO level of theory. The Fe electron density is calculated directly at the nucleus (ρ(0)_N, circles) and on a small sphere around the center of the Fe nucleus (ρ(0)_S, triangles).

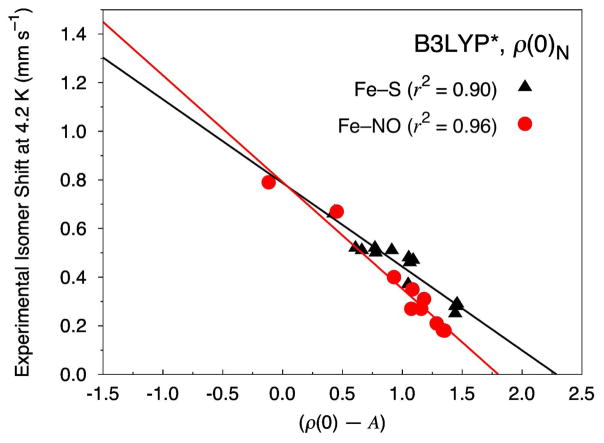
Improved performance of B3LYP* is observed if our test set is split into separate groupings of non-nitrosyl (Fe–S) and iron-nitrosyl (Fe–NO) complexes. Figure 4 shows the results when the Fe electron density is calculated at the nucleus, ρ(0)_N; see Figure S11 in the Supporting Information for the analogous data for ρ(0)_S. If only the 12 non-nitrosyl complexes are considered, an r² value of 0.90 and a MAE of just 0.034 mm s⁻¹ is determined for B3LYP*. In this case, all the complexes exhibit very good MAEs of not more than 0.06 mm s⁻¹. For the 8 iron-nitrosyl complexes, a MAE of 0.033 mm s⁻¹ with an r² of 0.96 is found. Similar to our observations of B3LYP, the largest outlier within the iron-nitrosyl test set is the {FeNO}⁷ site in [Fe₂(NO)₂(Et-HPTB)(O₂CPh)]²⁺, which here possesses a MAE of 0.08 mm s⁻¹.

Figure 4.

Isomer shift fit based on 12 Fe–S complexes (14 sites, triangles) and 8 Fe–NO complexes (10 sites, circles) calculated at the B3LYP*/STO-TZP COSMO level of theory with the Fe electron density calculated directly at the nucleus (ρ(0)_N).

We extended the scope of the B3LYP and B3LYP* calculations through the use of basis sets derived from Gaussian-type orbitals (GTOs, refer to the Computational Methods section for further details). In this case, we find that B3LYP/CP(PPP)-TZVP and B3LYP*/CP(PPP)-TZVP yield similar trends to our results obtained with Slater-type orbitals. That is, B3LYP* performs slightly better than B3LYP, but both methods show limitations in providing good quality universal fit parameters. Indeed, a universal fit for B3LYP using GTOs gives an r² of 0.69 and a MAE of 0.079 mm s⁻¹. For B3LYP*, these quantities are 0.77 and 0.064 mm s⁻¹, respectively. Clearly, the rather poor performance of these two functionals over the entire test set appears to be independent of the type of basis set used.

Figures S12 and S13 in the Supporting Information show the calibration lines when we separate the non-nitrosyl (Fe–S) and iron-nitrosyl (Fe–NO) complexes for our B3LYP and B3LYP* calculations that use the CP(PPP)-TZVP basis set. The B3LYP linear regression parameters for the Fe–S complexes are α = −0.285, C = 0.641, and A = 11816. Relative to universal fitting parameters, the r² value improves from 0.69 to 0.82 and the MAE reduces from 0.079 to 0.044 mm s⁻¹ when the Fe–S complexes are considered separately. The largest outliers in this case are [Fe₄S₄(SPh)₂Cl₂]²⁻ and [Fe₄S₄(OPh)₂Cl₂]²⁻, with MAEs of 0.08 or 0.09 mm s⁻¹ for the Fe sites. The Fe–NO complexes give calibration parameters of α = −0.476, C = 0.614, and A = 11816. The MAE is 0.048 mm s⁻¹ and the r² value improves significantly to 0.93. The largest outlier within the Fe–NO complex test set (with a MAE of 0.09 mm s⁻¹) is the {FeNO}⁷ site in [Fe₄(NO)₄(μ₃-S)₄]⁻.

Figure S13 shows results for our B3LYP*/CP(PPP)-TZVP COSMO calculations. Here, the B3LYP* calibration line for the iron-sulfur complexes yields an r² value of 0.84 and an overall MAE of 0.037 mm s⁻¹. The linear regression parameters are α = −0.326, C = 0.529, and A = 11815. The largest outlier in this fit is for the Fe–SPh site in [Fe₄S₄(SPh)₂Cl₂]²⁻, which gives a MAE relative to experiment of 0.12 mm s⁻¹. The Fe–NO complexes exhibit linear regression parameters of α = −0.435, C = 0.428, and A = 11815, with an r² of 0.93 and an overall MAE of 0.045 mm s⁻¹. The largest outliers within the Fe–NO complexes are for the {FeNO}⁷ sites in [Fe₄(NO)₄(μ₃-S)₄] as well as [Fe₂(NO)₂(Et-HPTB)(O₂CPh)]²⁺, which each possess MAEs of 0.08 mm s⁻¹.

Overall, we note that regardless of the type of basis set used, B3LYP and B3LYP* give structures that deviate more from experiment than is observed with structures calculated with the OLYP, OPBE, PW91, and BP86 functionals (Tables 2, 3, and 4). This is especially true for the Fe–Fe distances in the 4Fe–4S polynuclear complexes of our test set, where we observe mean absolute deviations of 0.136 to 0.197 Å for B3LYP and B3LYP* relative to the experimental structures (Table 2). In contrast, the Fe–Fe distances calculated with OLYP, OPBE, PW91, and BP86 deviate from experiment no more than 0.1 Å and possess MADs from 0.011 to 0.073 Å. Likewise, B3LYP and B3LYP* also overestimate the Fe–S bond distances, with MADs ranging from 0.066 to 0.092 Å, which are significantly larger than the MADs observed for the other functionals (0.012 to 0.023 Å, Table 2).

Table 4.

Comparison of Deviations from Experiment of Selected Calculated Average Bond Distances (Å) and Angles (°) of Selected Dinuclear Fe Structures of this Study^a

		Expt.	OLYP	OPBE	PW91	BP86	B3LYP	B3LYP*	B3LYPb	B3LYP*b
[Fe2S2(S2-o-xyl)2]2−	Fe–Fe	2.698	+0.018	−0.032	−0.021	−0.006			+0.143	+0.142
	Fe–S	2.257	+0.026	−0.008	−0.002	+0.004	n/ac	n/ac	+0.049	+0.058
	Fe-S-Fe	75.3	−0.4	−0.8	−0.6	−0.4			+2.1	+1.9
[Fe2S2(OPh-p-CH3)4]2−	Fe–Fe	2.749	+0.049	+0.011	−0.032	−0.027	+0.172	+0.122	+0.126	+0.125
	Fe–S	2.223	+0.031	+0.004	+0.001	+0.004	+0.068	+0.058	+0.061	+0.064
	Fe-S-Fe	76.4	+0.4	+0.2	−1.1	−1.0	+2.8	+1.7	+1.6	+1.5
[Fe2S2(C4H4N)4]2−	Fe–Fe	2.677	+0.086	+0.030	−0.003	+0.016	+0.177	+0.142	+0.163	+0.167
	Fe–S	2.191	+0.037	+0.007	+0.006	+0.012	+0.068	+0.057	+0.071	+0.074
	Fe-S-Fe	75.1	+1.5	+0.9	−0.1	+0.3	+3.3	+2.6	+2.7	+2.7
[Fe(NO)2{Fe(NO)(N(CH2CH2S)3)}-S,S′]	Fe–Fe	2.766	+0.051	−0.055	−0.049	−0.037	+0.282	+0.224	+0.254	+0.257
	Fe–S	2.297	+0.029	−0.025	−0.022	−0.013	+0.103	+0.084	+0.099	+0.105
	Fe-S-Fe	73.4	+0.6	−0.6	−0.6	−0.5	+4.7	+3.7	+3.9	+3.8
MAD (Fe–Fe)			0.051	0.032	0.026	0.022	0.158	0.122	0.172	0.173
MAD (Fe–S)			0.031	0.011	0.008	0.008	0.080	0.066	0.070	0.075
MAD (Fe-S-Fe)			0.7	0.6	0.6	0.6	3.6	2.7	2.6	2.5

^aCalculated values reported as deviations from experiment. Unless otherwise noted, all values are calculated at the OLYP/STO-TZP COSMO level of theory in ADF.

^bCalculated with ORCA using COSMO in combination with a CP(PPP) basis set on Fe and a TZVP basis set on the remaining atoms.

^cGeometry is not available at this level of theory. The OLYP/STO-TZP COSMO geometry is used instead. See Computational Methods section for details.

The relatively poor performance of B3LYP and B3LYP* in predicting accurate geometries is also evident in the mono- and dinuclear Fe complexes. For example, Table 3 shows the Fe–S bond distances in the mononuclear Fe complexes to deviate from experiment slightly more for these hybrid density functionals (MADs ranging from 0.048 to 0.070 Å) than for OLYP (MAD of 0.028 Å), OPBE (MAD of 0.030 Å), PW91 (MAD of 0.022 Å) and BP86 (MAD of 0.021 Å). Similar behavior is observed for the Fe–N bond distances. However, for both the S–C and the N–O distances in the mononuclear complexes, all the functional tend to perform with comparable accuracy.

For the four dinuclear Fe complexes in Table 4, we note the very large MADs for the Fe–Fe distance for B3LYP and B3LYP* (ranging from 0.122 to 0.173 Å) compared with the other functionals (MADs ranging from 0.022 to 0.051 Å). Further, we also observe large MADs from experiment for the Fe–S distances (ranging from 0.060 to 0.080 Å), as well as the Fe-S-Fe bridge angle (ranging from 2.5° to 3.6°) for the B3LYP and B3LYP* functionals. These relatively large MADs are not observed with the results obtained with OLYP, OPBE, PW91, or BP86 (Table 4). The observation that pure functionals give geometries in better agreement with experiment than hybrid functionals like UB3LYP has also been found for a series of iron-nitrosyl complexes, including Roussin’s red and black salts.¹⁶ Further, significant variations in Fe–NO spin densities calculated with different exchange-correlation functionals were observed.^12,16,75,76

The possible role of dispersion to correct the geometries obtained with B3LYP (and B3LYP*) has been examined by calculating a representative set of structures from our test set with the B3LYP-D functional, which includes a dispersion correction.⁷⁷ Table 5 reports the deviations from the experimental structures for four mononuclear Fe complexes, two dinuclear Fe complexes, and three tetranuclear Fe complexes. In general, B3LYP-D reduces the deviations from experiment for the mono- and dinuclear complexes relative to structures obtained with B3LYP. However, the geometries obtained with B3LYP-D for the tetranuclear complexes show even larger deviations than we observe for geometries calculated with B3LYP. Also, reproduced in Table 5 are the deviations from experiment for the geometries calculated with the OLYP functional, which show OLYP’s rather good performance across all types of Fe complexes.

Table 5.

Comparison of Deviations from Experiment of Selected Calculated Average Bond Distances (Å) and Angles (°) of Selected Mono- and Polynuclear Fe Structures of this Study^a

		OLYP	B3LYP	B3LYP-D	Experiment
[Fe(SEt)4]−	Fe–S	+0.061	+0.052	+0.042	2.269
	S–C	−0.033	−0.026	−0.028	1.880
[FeS4C8O4]2−	Fe–S	+0.011	+0.060	+0.055	2.389
	S–C	+0.011	+0.016	+0.018	1.688
[Fe(NO)(dtci-Pr2)2]	Fe–S	+0.016	+0.056	+0.054	2.288
	Fe–N	−0.008	+0.083	+0.081	1.676
	N–O	+0.032	+0.027	+0.026	1.161
[Fe(SC2H3N3)(SC2H2N3)(NO)2]	Fe–S	+0.039	+0.084	+0.068	2.308
	Fe–N	−0.002	+0.083	+0.079	1.673
	N–O	+0.028	+0.023	+0.023	1.154
[Fe2S2(C4H4N)4]2−	Fe–Fe	+0.086	+0.177	+0.157	2.677
	Fe–S	+0.037	+0.068	+0.063	2.191
	Fe-S-Fe	+1.5	+3.3	+2.8	75.1
[Fe(NO)2{Fe(NO)(N(CH2CH2S)3)}-S,S′]	Fe–Fe	+0.051	+0.282	+0.269	2.766
	Fe–S	+0.029	+0.103	+0.095	2.297
	Fe-S-Fe	+0.6	+4.73	+4.7	73.43
[Fe4S4Cl4]2−	Fe–Fe	+0.005	+0.159	+0.216	2.700
	Fe–S3	+0.017	+0.0643	+0.070	2.2893
[Fe4(NO)4(μ3-S)4]	Fe–Fe	−0.016	+0.208	+0.245	2.651
	Fe–S3	−0.010	+0.0943	+0.1013	2.2173
[Fe4(NO)4(μ3-S)4]−	Fe–Fe	+0.015	+0.208	+0.255	2.688
	Fe–S	+0.008	+0.1073	+0.1123	2.2313

^aOLYP, B3LYP and B3LYP-D values use the STO-TZP basis set with a COSMO representation of the solvent. See Computational Methods for further details.

It is also instructive to consider spin expectation values of our complexes and the possible role of spin contamination and its effect on the calculated geometries. Spin contamination arises from the mixing of higher spin states into a given wave function. Previously, it has been shown that broken symmetry (BS) state geometries exhibit longer Mn–Mn and Fe–Fe distances in [Mn(III)₂(μ-O)₃(NH₃)₆]²⁻ and [Fe₂S₂(SCH₃)₄]²⁻ than their spin-projected S = 0 ground state geometries.⁷⁸ Similar results have also been found for the Cr dimer.⁷⁹ It is therefore reasonable to conceive that spin contamination may adversely affect the geometries of the Fe complexes of this study.

Table 6 reports the pure spin-state expectation values, the broken-symmetry (BS) spin-state expectation values in the weak-coupling (WC) limit, and the BS spin-state expectation values of our complexes calculated at various levels of theory. For the iron-nitrosyl complexes, we assume that the coupling within the Fe–NO unit is strong, such that it can be described as being essentially covalent. The pure spin-state values are obtained in the usual way via the relation S(S + 1), where S is the total spin. The calculated BS values are obtained using equations (3)⁸⁰ or (4)⁸¹

Table 6.

Pure and Broken Symmetry Spin-State Expectation Values for the Iron Complexes Examined in this Study^a

complex	Fe oxidation	〈S2〉pure	${\langle S^2\rangle }_{BS}^{WC}$ b	OLYP	OPBE	PW91	BP86	B3LYP		B3LYP*
								//B3LYP	//OLYP	//B3LYP*	//OLYP
[Fe(SEt)4]−	Fe3+	8.75	n/a	8.76	8.76	8.76	8.76	8.77	8.77	8.77	8.77
[FeS4C8O4]2−	Fe2+	6.00	n/a	6.06	6.07	6.02	6.02	6.01	6.01	6.01	6.01
[Fe(SPh)4]2−	Fe2+	6.00	n/a	6.03	6.03	6.02	6.02	6.02	6.00	6.02	6.02
[Fe(H2O)5(NO)]2+	{FeNO}7	3.75	5.75	4.28	4.29	4.12	4.14	4.53	4.49	4.45	4.41
[Fe(NO)(dtci-Pr2)2]	{FeNO}7	0.75	2.75	0.86	0.83	0.79	0.79	1.74	1.37	1.36	1.13
[Fe(SPh)2(NO)2]−	{Fe(NO)2}9	0.75	4.75	1.02	0.95	0.82	0.83	2.65	2.07	2.12	1.67
[Fe(SC2H3N3)(SC2H2N3)(NO)2]	{Fe(NO)2}9	0.75	4.75	1.08	0.99	0.84	0.86	2.54	2.08	2.08	1.71
MAD (〈S2〉pure)				0.19	0.17	0.09	0.10	0.79	0.58	0.58	0.43
[Fe2S2(S2-o-xyl)2]2−	2*Fe3+	0.0	5.00	4.31	4.27	4.04	4.08	n/ac	4.65	n/ac	4.55
[Fe2S2(OPh-p-CH3)4]2−	2*Fe3+	0.0	5.00	4.47	4.45	4.21	4.22	4.80	4.74	4.72	4.67
[Fe2S2(C4H4N)4]2−	2*Fe3+	0.0	5.00	4.31	4.27	3.99	4.03	4.69	4.64	4.59	4.55
[Fe2(NO)2(Et-HPTB)(O2CPh)]2+	2*{FeNO}7	0.0	3.00	4.24	4.20	3.62	3.67	n/ac	4.90	n/ac	4.69
[Fe(NO)2{Fe(NO)(N(CH2CH2S)3)}-S,S′]	{FeNO}7 {Fe(NO)2}9	2.00	3.00	3.06	2.76	2.32	2.38	5.54	4.72	4.83	4.11
MAD ( ${\langle S^2\rangle }_{BS}^{WC}$)				0.64	0.69	0.81	0.79	1.02	0.92	0.84	1.01
[Fe4S4(SPh)4]2−	4*Fe2.5+	0.0	9.00	7.26	7.02	6.23	6.36	n/ac	8.24	n/ac	7.99
[Fe4S4(OPh)4]2−	4*Fe2.5+	0.0	9.00	7.59	7.42	6.71	6.81	8.67	8.43	8.45	8.24
[Fe4S4(SPh)2Cl2]2−	4*Fe2.5+	0.0	9.00	7.35	7.11	6.37	6.47	8.47	8.28	8.29	8.05
[Fe4S4(OPh)2Cl2]2−	4*Fe2.5+	0.0	9.00	7.49	7.34	6.64	6.75	8.61	8.37	8.40	8.16
[Fe4S4Cl4]2−	4*Fe2.5+	0.0	9.00	7.43	7.26	6.58	6.67	8.56	8.31	8.32	8.09
[Fe4S4(SCH2CO2Et)4]2−	4*Fe2.5+	0.0	9.00	7.20	7.08	6.13	6.18	n/ac	8.21	n/ac	7.97
[Fe4(NO)4(μ3-S)4]	4*{FeNO}7	0.0	6.00	1.70	0.60	0.23	0.32	7.12	5.15	5.58	4.07
[Fe4(NO)4(μ3-S)4]−	2*{FeNO}7.5 2*{FeNO}7	0.75	5.75	3.13	1.82	0.85	1.24	7.46	6.50	5.88	5.44
MAD( ${\langle S^2\rangle }_{BS}^{WC}$)				2.08	2.51	3.25	3.12	0.75	0.52	0.69	0.92

^aSee also Supporting Information Table S6 for the B3LYP and B3LYP* values using ORCA in combination with a CP(PPP) basis set on Fe and a TZVP basis set on the remaining atoms.

^bFor the mononuclear Fe complexes, the expectation value of S² is for the unrestricted, rather than broken symmetry, state. WC refers to weak-coupling limit.

^cThe OLYP/STO-TZP COSMO geometry is used instead. See Computational Methods section for details.

$${\langle {\widehat{S}}^2\rangle }_{BS}=\left(\frac{N^{\alpha }-N^{\beta }}{2}\right)\left(\frac{N^{\alpha }-N^{\beta }}{2}+1\right)+N^{\beta }-\sum _i^N\sum _j^N{\left|S_{ij}^{\alpha \beta }\right|}^2$$ (3)

$${\langle {\widehat{S}}^2\rangle }_{BS(\mathit{COT})}=\left(\frac{N^{\alpha }-N^{\beta }}{2}\right)\left(\frac{N^{\alpha }-N^{\beta }}{2}+1\right)+N^{\beta }-\sum _i{n}_i^{\alpha }{n}_i^{\beta }{\left|{\stackrel{\sim }{S}}_{ii}^{\alpha \beta }\right|}^2$$ (4)

where N^α and N^β are the number of spin-up and spin-down electrons, respectively, S_ij are is the overlap integrals, and n_i^α and n_i^β are the spin-orbital occupation numbers. Equation (3) is the standard method used to determine expectation values from an unrestricted single-determinant wavefunction,⁸⁰ while Equation (4) pertains to the magnetic orbital pairs (with overlap squared ${\left|S_{ii}^{\alpha \beta }\right|}^2$) obtained via the corresponding orbital transformation (COT).⁸¹ Further, N^α and N^β can be defined as

$$N^{\alpha }=N_W^{\alpha }+N_D{N}^{\beta }=N_W^{\beta }+N_D$$ (5)

where $N_W^{\alpha }$ and $N_W^{\beta }$ are the number of singly-occupied (W for weakly coupled) spin-up and spin-down electrons, respectively, and 2N_D is the total number of electrons in doubly-occupied orbitals. The contributions from the singly- and doubly-occupied orbitals can be written explicitly as

$${\langle {\widehat{S}}^2\rangle }_{BS}=\left(\frac{N^{\alpha }-N^{\beta }}{2}\right)\left(\frac{N^{\alpha }-N^{\beta }}{2}+1\right)+N^{\beta }-\sum _i{n}_{iD}{\left|{\stackrel{\sim }{S}}_{\mathit{iiD}}\right|}^2-\sum _i{n}_{iW}{\left|{\stackrel{\sim }{S}}_{\mathit{iiw}}\right|}^2$$ (6)

where |S̃_iiD|² are the corresponding orbital overlaps squared close to 1 (near double occupancy) and |S̃_iiW|² are the corresponding orbital overlaps squared near 0 (weakly coupled). Substituting equation (5) into (6) gives

$${\langle {\widehat{S}}^2\rangle }_{BS}=\left(\frac{N_W^{\alpha }-N_W^{\beta }}{2}\right)\left(\frac{N_W^{\alpha }-N_W^{\beta }}{2}+1\right)+N_W^{\beta }+\left[N_D-\sum _i{n}_{iD}{({\stackrel{\sim }{S}}_{\mathit{iiD}})}^2\right]-\sum _i{n}_{iW}{({\stackrel{\sim }{S}}_{\mathit{iiW}})}^2$$ (7)

In the weak-coupling limit, the contribution from doubly occupied orbitals in Equation 7 is neglected since the third term (in the square brackets) is small and positive and the fourth term is small and negative. In an analogous way, for a system comprised of spin subsystems A and B that couple antiferromagnetically, we can assume that the sites couple weakly to give the spin expectation value as

$${\langle S^2\rangle }_{BS}^{WC}=S_{max}(S_{max}+1)-4S_A{S}_B=(S_A-S_B)(S_A-S_B+1)+2S_B$$ (8)

where S_max = S_A + S_B and S_A = N_W^α/2, S_B = N_W^β. It is easily seen that Eq. (8) corresponds precisely to the first two terms in Eq. (7). The weak coupling limit approximation and its utility for understanding spin states has been described earlier.^82,83

As can be seen in Table 6, the calculated BS values for different exchange-correlation potentials ( ${\langle S^2\rangle }_{BS}^{XC}$) do not always correspond to the pure spin-state values (〈S²〉_pure) or to the BS values in the weak-coupling limit ( ${\langle S^2\rangle }_{BS}^{WC}$). The three Fe–S mononuclear complexes exhibit good agreement between the calculated and pure spin expectation values. Less agreement is observed, however, between the calculated versus pure, 〈S²〉_pure, or weak-coupling limit spin expectation values, ${\langle S^2\rangle }_{BS}^{WC}$, for the four Fe–NO mononuclear complexes. With respect to ${\langle S^2\rangle }_{BS}^{WC}$, these differences can be attributed to our assumption that the Fe–NO unit is bonded covalently, but that it is comprised of high-spin Fe³⁺ (S = 5/2) coupled antiferromagnetically with NO⁻ (S = 1) to give a site spin for Fe–NO of 3/2. Moreover, in principle, several values of ${\langle S^2\rangle }_{BS}^{WC}$ can be constructed, depending on how the Fe–NO unit is described. One notable aspect of our calculated S² values is the different behaviors of the GGA versus hybrid exchange-correlation functionals. Although all levels of theory underestimate ${\langle S^2\rangle }_{BS}^{WC}$ for the mononuclear Fe complexes, B3LYP and B3LYP* give values closer to the weak-coupling limit. Similarly, B3LYP and B3LYP* predict higher values of S² for the di- and tetranuclear Fe complexes. Structurally, this can be understood in terms of the longer bond lengths obtained with these functionals versus the GGA functionals (see, e.g., Tables 2 to 4). The calculated S² values for the polynuclear Fe–NO complexes demonstrate remarkable variability versus ${\langle S^2\rangle }_{BS}^{WC}$, which highlights their challenging electronic structure. In addition to the strong coupling that we assume in the Fe–NO units, the coupling between the Fe–NO units in the polynuclear complexes is often strong, as observed elsewhere,^11,12 which leads to a breakdown in the weak-coupling limit approximation.

Given the rather poor geometries obtained in the present study with B3LYP and B3LYP*, it is possible that spin-projection techniques would give structures in closer agreement to experiment, as observed elsewhere.^78,79 However, since we find that geometries obtained with OLYP/STO-TZP are in very good agreement with experimental structures (see, e.g., Table 2), we examined the effect of calculating B3LYP and B3LYP* linear correlation fits and calculated Mössbauer properties using OLYP geometries (denoted B3LYP//OLYP and B3LYP*//OLYP, respectively). It is quite possible that similar results would be obtained with Gaussian-type orbitals, subject to OLYP with a GTO basis set providing accurate geometries.

Figure 5 shows the data obtained with B3LYP//OLYP are quite an improvement over the calibration fits acquired using B3LYP geometries (Figure S1). That is, fits derived using the entire test set improve the r² from 0.64 to 0.95 and the MAE decreases from 0.086 to 0.031 mm s⁻¹. Universal fit parameters for B3LYP//OLYP are α = −0.331, C = 0.705, and A = 11823 for when the Fe electron density is calculated on a small sphere surrounding the nucleus (ρ(0)_S), and α = −0.330, C = 0.541, and A = 11880 when the Fe electron density is calculated at the nucleus (ρ(0)_N, Table 4). The largest outlier is for [Fe(SEt)₄]⁻, which possesses a MAE of 0.07 mm s⁻¹. It is interesting to note that the fits derived from B3LYP//OLYP calculations are of superior quality to those obtained with OLYP alone. Indeed, the r² and MAE for B3LYP//OLYP (0.95 and 0.031 mm s⁻¹, respectively) reflect a slightly improved performance over OLYP (0.92 and 0.037 mm s⁻¹).

Figure 5.

Isomer shift fit based on 8 Fe–NO and 12 Fe–S complexes (24 sites) calculated at the B3LYP/STO-TZP//OLYP/STO-TZP COSMO level of theory. The Fe electron density is calculated directly at the nucleus (ρ(0)_N, circles) and on a small sphere around the center of the Fe nucleus (ρ(0)_S, triangles).

Similar findings occur for fits derived from B3LYP*//OLYP calculations compared with those using B3LYP* geometries (Figures 3 and S16). In this case, the r² improves from 0.86 to 0.95 and the MAE decreases from 0.053 mm s⁻¹ to 0.032 mm s⁻¹ when OLYP geometries are used instead of those calculated with B3LYP*. As found for B3LYP//OLYP, the largest outlier is for [Fe(SEt)₄]⁻, which in this case possesses a MAE of 0.08 mm s⁻¹. Table 7 and Figure S16 of the Supporting Information provide the universal fit parameters and plot for this level of theory.

Table 7.

Universal Fit Parameters for the Calculation of ⁵⁷Fe Isomer Shifts^a

Functional	Method to calculate ρ(0)b	α	C	A	r2	MAE (mm s−1)
OLYP	S	−0.324	0.594	11820	0.92	0.037
	N	−0.323	0.428	11877
OPBE	S	−0.287	0.594	11820	0.89	0.041
	N	−0.286	0.447	11877
PW91	S	−0.334	0.703	11827	0.89	0.042
	N	−0.332	0.549	11884
BP86	S	−0.354	0.869	11832	0.91	0.040
	N	−0.353	0.718	11889
B3LYP	S	−0.340	0.633	11823	0.64	0.086
	N	−0.338	0.465	11880
B3LYP//OLYP	S	−0.331	0.705	11823	0.95	0.031
	N	−0.330	0.541	11880
B3LYP*	S	−0.403	0.609	11820	0.86	0.053
	N	−0.401	0.804	11876
B3LYP*//OLYP	S	−0.337	0.633	11820	0.95	0.032
	N	−0.335	0.796	11876
B3LYP*c	N	−0.374	0.489	11815	0.77	0.064
B3LYPc	N	−0.347	0.623	11816	0.69	0.079

^aUsing COSMO in combination with a STO-TZP basis set unless otherwise indicated.

^bThe ‘S’ serves to indicate that the Fe electron density has been calculated on a small sphere around the center of the Fe nucleus, while the ‘N’ indicates the density has been calculated at the Fe nucleus.

^cUsing COSMO in combination with the CP(PPP) basis set for Fe and the TZVP basis set for the remaining elements.

Grouping the test set into non-nitrosyl (Fe–S) and iron-nitrosyl (Fe–NO) complexes gives results similar to what we have seen previously (Table 5). Using OLYP geometries instead of B3LYP improves the r² from 0.80 to 0.92 and decreases the MAE from 0.045 mm s⁻¹ to 0.028 mm s⁻¹ for the Fe–S complexes. For the Fe–NO complexes, the r² improves from 0.91 to 0.97 and the MAE decreases from 0.045 mm s⁻¹ to 0.030 mm s⁻¹. The largest IS outliers for the Fe–S and Fe–NO complexes, each with MAEs of 0.06 mm s⁻¹, correspond to the Fe–SPh site in [Fe₄S₄(SPh)₂Cl₂]²⁻, the {FeNO}^7.5 site in [Fe₄(NO)₄(μ₃-S)₄]⁻, and [Fe₂S₂(OPh-p-CH₃)₄]²⁻.

For the B3LYP*//OLYP calculations of the Fe–S complexes, the r² improves from 0.90 to 0.92 and the MAE decreases from 0.034 mm s⁻¹ to 0.027 mm s⁻¹. The largest outlier in this group is [Fe₂S₂(OPh-p-CH₃)₄]²⁻, which possesses a MAE of 0.07 mm s⁻¹. For the Fe–NO complexes, the r² improves slightly from 0.96 to 0.97 and the MAE decreases from 0.033 mm s⁻¹ to 0.028 mm s⁻¹ with B3LYP*//OLYP. The largest outlier in this case is for the {FeNO}⁷ and {FeNO}^7.5 sites in [Fe₄(NO)₄(μ₃-S)₄]⁻ (MAEs of 0.05 mm s⁻¹).

In Tables 7 and 8 we summarize the linear regression fitting parameters obtained in this study. Table 7 provides universal fit parameters derived from all 20 structures within our test set and Table S3 of the Supporting Information gives the calculated isomer shifts for these complexes using these universal fitting parameters. Overall, the OLYP, OPBE, PW91, and BP86 functionals perform very well, with the hybrid method B3LYP* performing slightly worse, and B3LYP performing worse still. However, the use of OLYP geometries to calculate B3LYP and B3LYP* isomer shift parameters significantly improves the correlation analysis. In addition, the performance of B3LYP and B3LYP* increases substantially when the non-nitrosyl (Fe–S) and iron-nitrosyl (Fe–NO) compounds of our test set are grouped separately (Table 8). Indeed, when separate calibration lines are generated for the non-nitrosyl (Fe–S) and iron-nitrosyl (Fe–NO) complexes very good to excellent performance is observed for all levels of theory. This behavior is reminiscent of earlier observations that different Fe oxidation states yield distinct IS calibration lines.^11,24,26 In the present case, the separate grouping appears to be very important when B3LYP* and B3YLP geometries are used. A defining feature of the separate calibration analysis for all levels of theory is the excellent linear correlation of experimental ISs and the calculated Fe nuclear density for the Fe–NO complexes (r² = 0.91 – 0.98), with slightly worse correlation for the non-nitrosyl Fe–S compounds (r² = 0.80 – 0.92).

Table 8.

Fit Parameters for the Calculation of ⁵⁷Fe Isomer Shifts^a

Functional	Fit Type	Method to calculate ρ(0)b	α	C	A	r2	MAE (mm s−1)
OLYP	Fe–S	S	−0.465	0.652	11820	0.88	0.031
		N	−0.463	0.413	11877
	Fe–NO	S	−0.295	0.572	11820	0.98	0.024
		N	−0.294	0.421	11877
OPBE	Fe–S	S	−0.461	0.670	11820	0.83	0.037
		N	−0.459	0.433	11877
	Fe–NO	S	−0.263	0.577	11820	0.98	0.020
		N	−0.262	0.442	11877
PW91	Fe–S	S	−0.485	0.787	11827	0.84	0.041
		N	−0.482	0.564	11884
	Fe–NO	S	−0.329	0.722	11827	0.98	0.027
		N	−0.328	0.570	11884
BP86	Fe–S	S	−0.495	1.012	11832	0.86	0.038
		N	−0.492	0.800	11889
	Fe–NO	S	−0.343	0.871	11832	0.98	0.027
		N	−0.342	0.725	11889
B3LYP	Fe–S	S	−0.279	0.651	11823	0.80	0.045
		N	−0.278	0.513	11880
	Fe–NO	S	−0.503	0.642	11823	0.91	0.050
		N	−0.501	0.393	11880
B3LYP//OLYP	Fe–S	S	−0.372	0.737	11823	0.92	0.028
		N	−0.370	0.553	11880
	Fe–NO	S	−0.314	0.685	11823	0.97	0.030
		N	−0.313	0.529	11880
B3LYP*	Fe–S	S	−0.346	0.620	11820	0.90	0.034
		N	−0.344	0.787	11876
	Fe–NO	S	−0.441	0.577	11820	0.96	0.033
		N	−0.439	0.791	11876
B3LYP*//OLYP	Fe–S	S	−0.407	0.668	11820	0.92	0.027
		N	−0.405	0.864	11876
	Fe–NO	S	−0.316	0.618	11820	0.97	0.028
		N	−0.315	0.771	11876
B3LYPc	Fe–S	N	−0.285	0.641	11816	0.82	0.044
	Fe–NO		−0.476	0.614		0.93	0.048
B3LYP*c	Fe–S	N	−0.326	0.529	11815	0.84	0.037
	Fe–NO		−0.435	0.428		0.93	0.045

^aUsing COSMO in combination with a STO-TZP basis set unless otherwise indicated.

^bThe ‘S’ serves to indicate that the Fe electron density has been calculated on a small sphere around the center of the Fe nucleus, while the ‘N’ indicates the density has been calculated at the Fe nucleus.

^cUsing COSMO in combination with the CP(PPP) basis set for Fe and the TZVP basis set for the remaining elements.

Good correspondence between the fit parameters determined here and those determined previously by our group has been found. Using an identical test set as the one used here, universal fit parameters for the OLYP functional (with COSMO) were determined to be α = −0.315 and C = 0.432, with an r² of 0.915 and a MAE of 0.039 mm s⁻¹ when the Fe electron density is calculated at the nucleus.¹¹ Fit parameters for Fe–NO complexes only were found to be α = −0.290 and C = 0.426, with an r² of 0.979 and a MAE of 0.029 mm s⁻¹. Both sets of these universal and Fe–NO fit parameters compare extremely well with those determined herein with the OLYP functional (Tables 7 and 8). In addition, earlier Mössbauer isomer fitting procedures on a test set comprised of 19 Fe^{2.5+,3+,3.5+,4+} complexes (with 30 Fe sites) yields fit parameters in good agreement with those determined here.^23,24 For example, fits derived from OLYP calculations give parameters α = −0.307 and C = 0.385 with an r of −0.93, while fits derived from OPBE calculations give α = −0.312 and C = 0.373 (r = −0.94), and fits derived from PW91 calculations give α = −0.393 and C = 0.435 (r = −0.93). All of these earlier calculations determined the Fe electron density directly at the nucleus.

c. Quadrupole Splittings

As noted in the Introduction, quadrupole splitting (QS) arises from the interaction between the electric quadrupole moment of the ⁵⁷Fe nucleus and the electric field gradient at its nucleus. Because very few of the signs of the QSs within our test set have been determined experimentally, we quote only their magnitude. Tables S4 and S5 in the Supporting Information show our calculated values for the QS and η values. When one experimental QS value is quoted for polynuclear complexes, our calculated values were averaged over equivalent Fe centers. Table S4 shows B3LYP*/STO-TZP to yield the lowest mean absolute error (MAE) relative to experiment (0.18 mm s⁻¹) for the calculation of QS parameters, followed by B3LYP*//OLYP (0.20 mm s⁻¹) and B3LYP//OLYP (0.21 mm s⁻¹) with the STO-TZP basis set, B3LYP/STO-TZP (0.26 mm s⁻¹), B3LYP and B3LYP* with the CP(PPP)-TZVP basis set (0.27 mm s⁻¹ each), and OPBE (0.28 mm s⁻¹), OLYP (0.29 mm s⁻¹), BP86 (0.30 mm s⁻¹), and PW91 (0.30 mm s⁻¹) with STO-TZP basis set. These calculated values are prior to any linear fitting. See Table 1 for experimental |QS| values. It is noteworthy that the hybrid DFT functionals tend to perform better to calculate QS parameters than the pure functionals examined here.

Next we examined linear correlations between the calculated and the observed QS absolute values based on the equation:

$$\mid {\text{QS}}_{(exp)}\mid =\alpha \mid {\text{QS}}_{(\text{calc})}\mid +C$$ (3)

Universal fit parameters were obtained by linear regression of our calculated QS parameters of 24 distinct Fe sites in the 20 complexes of our test set (Table 9). As we have done in our IS calibration analysis, we also evaluated fit parameters for test sets including non-nitrosyl (Fe–S) and iron-nitrosyl (Fe–NO) complexes separately. Using r² as measure of the quality of the calibration fit, most of the functionals perform very well, especially BP86. For the universal fitting procedure, OLYP/STO-TZP and B3LYP and B3LYP* with the CP(PPP)-TZVP basis set give fits with the worst r² values (0.82). Interestingly, B3LYP//OLYP and B3LYP*//OLYP yield calibration fits substantially improved over the fit obtained from OLYP (with r² values of 0.91 and 0.92, respectively).

Table 9.

Fit Parameters for the Calculation of ⁵⁷Fe Quadrupole Splittings^a

Functional	Fit Type	α	C	r2
OLYP	Universal	1.095	0.138	0.82
	Fe–S	1.278	−0.030	0.89
	Fe–NO	0.617	0.580	0.80
	Fe–NOc	0.646	0.612	0.92
OPBE	Universal	1.088	0.161	0.83
	Fe–S	1.299	−0.034	0.91
	Fe–NO	0.613	0.593	0.88
	Fe–NOc	0.597	0.645	0.91
PW91	Universal	1.055	0.227	0.94
	Fe–S	1.173	0.084	0.98
	Fe–NO	0.663	0.603	0.89
	Fe–NOc	0.651	0.641	0.92
BP86	Universal	1.051	0.223	0.94
	Fe–S	1.169	0.078	0.99
	Fe–NO	0.664	0.599	0.91
	Fe–NOc	0.646	0.646	0.93
B3LYP	Universal	0.808	0.137	0.89
	Fe–S	0.825	0.074	0.91
	Fe–NO	0.712	0.310	0.74
	Fe–NOc	0.823	0.207	0.90
B3LYP//OLYP	Universal	0.849	0.131	0.91
	Fe–S	0.890	0.076	0.95
	Fe–NO	0.591	0.450	0.66
	Fe–NOc	0.708	0.387	0.91
B3LYP*	Universal	0.875	0.115	0.93
	Fe–S	0.909	0.020	0.96
	Fe–NO	0.705	0.377	0.82
	Fe–NOc	0.814	0.262	0.95
B3LYP*//OLYP	Universal	0.874	0.163	0.92
	Fe–S	0.931	0.078	0.97
	Fe–NO	0.577	0.519	0.69
	Fe–NOc	0.675	0.484	0.92
B3LYPb	Universal	0.846	0.082	0.82
	Fe–S	0.883	−0.031	0.86
	Fe–NO	0.653	0.397	0.57
	Fe–NOc	0.861	0.259	0.92
B3LYP*b	Universal	0.917	0.027	0.82
	Fe–S	0.977	−0.122	0.86
	Fe–NO	0.661	0.413	0.65
	Fe–NOc	0.814	0.341	0.97

^aUsing COSMO in combination with a STO-TZP basis set unless otherwise indicated.

^bUsing COSMO in combination with the CP(PPP) basis set for Fe and the TZVP basis set for the remaining elements.

^cExcluding [Fe₄(NO)₄(μ₃-S)₄]⁻.

The worst fits are obtained from the B3LYP and B3LYP* calculations with the CP(PPP)-TZVP basis set for the Fe–NO complexes, with r² values of 0.57 and 0.65, respectively (Table 9). Though not as severe, the calibration fits for the Fe–NO complexes derived from our B3LYP//OLYP and B3LYP*//OLYP calculations give correlation coefficients of 0.66 and 0.69, respectively. The rather poor performance of B3LYP and B3LYP* is also observed with the STO-TZP basis set (r² values of 0.74 and 0.82, respectively). The largest outlier in these calculations is [Fe₄(NO)₄(μ₃-S)₄]⁻ and its removal gives rather impressive results. For instance, r² improves from 0.57 to 0.92 for B3LYP/CP(PPP)-TZVP, from 0.65 to 0.97 for B3LYP*/CP(PPP)-TZVP, from 0.66 to 0.91 for B3LYP//OLYP, and from 0.69 to 0.92 for B3LYP*//OLYP (Table 9). Indeed, the correlation coefficient is improved for every level of theory when [Fe₄(NO)₄(μ₃-S)₄]⁻ is excluded.

Initially we thought the source of the rather poor results for [Fe₄(NO)₄(μ₃-S)₄]⁻ may be a consequence of poorly calculated geometries. For example, B3LYP and B3LYP* tend to overestimate the average Fe–Fe bond distances by approximately 0.2 Å and the average Fe–N bond distances by approximately 0.1 Å (Table 2). However, such deviations are not observed in the geometries optimized with OLYP, OPBE, PW91, or BP86, yet their calibration fits are also improved upon the exclusion of [Fe₄(NO)₄(μ₃-S)₄]⁻. Therefore, while the geometry may clearly play in role in determining accurate QSs, the inherent nature of the functional used to calculate this property is also of great importance.

Conclusions

Density functional theory calculations have been performed on a test set of 20 compounds including nonheme nitrosyls (Fe–NO) and non-nitrosyl (Fe–S) complexes to calibrate Mössbauer isomer shift (IS) and quadrupole splitting (QS) parameters for general use. Fits to determine accurate ISs were obtained by calculating the Fe electron density on a small sphere surrounding its nucleus and directly at the nucleus using the OLYP, OPBE, PW91, BP86, B3LYP, and B3LYP* functionals. In addition, the latter two functionals were used in conjunction with Slater-type orbitals and Gaussian-type orbitals. We find that the methods of calculating the Fe electron density directly at or on a small sphere surrounding the nucleus yield (near) identical slopes from the linear regression analyses but are shifted with respect to ρ(0) along the x axis.

Universal fit parameters for the calculation of ⁵⁷Fe isomer shifts obtained with the OLYP, OPBE, PW91, and BP86 functionals are found to be of very good quality, while those obtained with B3LYP and B3LYP* do not produce the same level of accuracy. We attribute the inferior performance of B3LYP and B3LYP* to poorly calculated geometries with these functionals. This observation has potentially large consequences since B3LYP, in particular, is used widely. Moreover, we note that the largest discrepancies have been observed for the di- and tetranuclear Fe complexes within our training set. The inclusion of effects due to dispersion via the B3LYP-D functional is found to improve slightly the geometries for some mono- and dinuclear Fe complexes, but this functional performs worse than B3LYP for the tetranuclear Fe complexes. Given these findings, it is uncertain whether previously determined calibration fits for the prediction Mössbauer isomer shifts that have included mostly mononuclear Fe complexes are appropriate for the prediction of isomer shifts in polynuclear Fe complexes.

An examination of spin expectation values reveals B3LYP and B3LYP* approach the weak-coupling limit more closely than the GGA exchange-correlation functionals, which can be understood to arise from the longer bond lengths obtained with these hybrid functionals. The Fe–NO complexes demonstrate large variability in the calculated S² values relative to ${\langle S^2\rangle }_{BS}^{WC}$, which is probably a consequence of assuming that the Fe–NO units are bound covalently though coupled antiferromagnetically. Further, for the polynuclear complexes, the strong coupling between the Fe–NO units can lead to a breakdown in the weak-coupling limit approximation, especially for the GGA functionals.

Interestingly, we find that the use of OLYP geometries for the B3LYP and B3LYP* calculations with an STO-TZP basis set (B3LYP//OLYP and B3LYP*//OLYP, respectively) significantly improves the quality of the calibration fits, providing further evidence that the structures obtained with B3LYP and B3LYP* for the complexes within the test set are not reliable. Indeed, we find B3LYP and B3LYP* to frequently overestimate the Fe–Fe and Fe–S distances in the structures of our test set (Tables 2 and 3).

In addition, we have also determined isomer shift calibration fits for test sets comprised of only Fe–NO or Fe–S complexes. Every functional examined gives fits of very good quality, though those determined for the Fe–S complexes tend to demonstrate poorer correlations. As found with the universal fitting parameters, we find the calibration fits for B3LYP//OLYP and B3LYP*//OLYP are superior to those determined using the B3LYP and B3LYP* geometries. These data suggest that the composition of a given test set can strongly influence the correlation between experimental ISs and calculated Fe electron densities. This appears to be especially true for B3LYP and B3LYP*.

Universal and separate Fe–NO and Fe–S fit parameters obtained to determine QSs are found to be of good to excellent quality for every density functional examined, especially if [Fe₄(NO)₄(μ₃-S)₄]⁻ is removed from the test set.