Three-dimensional surface profiling and optical characterization of liquid microlens using a Shack–Hartmann wave front sensor

Abstract

We demonstrate three-dimensional (3D) surface profiling of the water–oil interface in a tunable liquid microlens using a Shack–Hartmann wave front sensor. The principles and the optical setup for achieving 3D surface measurements are presented and a hydrogel-actuated liquid lens was measured at different focal lengths. The 3D surface profiles are then used to study the optical properties of the liquid lens. Our method of 3D surface profiling could foster the improvement of liquid lens design and fabrication, including surface treatment and aberration reduction.

Liquid-based variable-focus microlenses are emerging as important components in optical imaging due to their compact structure, high transmission and simple fabrication.^{1, 2} Variable-focus liquid microlenses have been demonstrated by different mechanisms, including mechanical-wetting using liquid pressure,³ electrowetting of a liquid droplet^{2, 4} and actuation of stimuli-responsive materials.⁵ The optical properties of a liquid lens depend heavily on its geometric profile which is determined by many fabrication factors, such as surface smoothness and control of surface wetting. Accurate three-dimensional (3D) profiling, therefore, is critical to the optimization of the fabrication process and the optical properties of liquid microlenses. Conventional goniometers are incapable of 3D measurements, and they are not applicable where the surrounding structure has poor optical transparency. Limited by the characteristics of liquids, the liquid-to-liquid interface can hardly be directly measured by laser range finder or mechanical profiler which is normally used for solid microlenses.^{6, 7}

Here, we report on the use of a Shack–Hartmann wave front sensor for performing accurate 3D surface profiling of the liquid–liquid interfaces in liquid microlenses. To demonstrate our method, the example we used was a variable-focus liquid microlens actuated by thermoresponsive hydrogels.^{5, 8, 9} A physical model is presented to calculate the surface profile from the obtained wave front profile through the liquid lens. The hydrogel-actuated liquid microlens was measured at focal lengths of 15.2 mm, 23.0 mm, and 34.7 mm, respectively. The liquid–liquid interface was found to have good spherical shape at the center, but become highly linear near the margin of the aperture. The measured water–oil interface was studied by simulation software and the simulated focal length and aberration coefficients are well matched with experiment results. The spherical aberration of the liquid lens was found to increase with decreasing focal lengths. The 3D surface profiling using Shack–Hartmann wave front sensor accomplishes a comprehensive analysis of the surface and determination of optical properties of liquid microlenses.

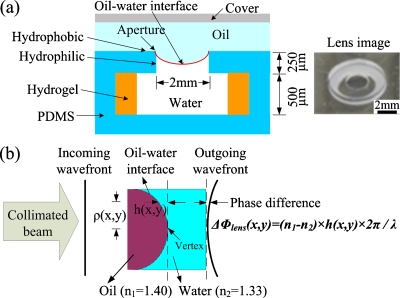
Figure 1a shows the cross section schematic and an image of the tunable liquid microlens actuated by a thermoresponsive hydrogel. The fabrication process was based on liquid phase photopolymerization.⁸ The inner side-wall of the aperture was treated hydrophilic by oxygen plasma, while the top surface of the polydimethylsiloxane (PDMS) structure was naturally hydrophobic. Thus, at the lens aperture, a water-oil meniscus was pinned at the hydrophobic-hydrophilic boundary formed and it functioned as a convergent lens due to the higher refractive index of silicone oil (n₁=1.40) than that of water (n₂=1.33). The lens aperture was 2 mm in diameter. The N-isopropylacrylamide (NIPAAm) hydrogel responded to local temperature variations and exhibited a reversible change in volume, thus tuning the focal length.^{5, 8, 9}

Figure 1.

(a) Schematic cross-section and image of a variable-focus liquid microlens actuated by thermoresponsive hydrogel. The inner side walls of the aperture are treated hydrophilic by oxygen plasma. The oil–water interface is pinned at the hydrophobic–hydrophilic boundary. Responding to temperature variation, NIPAAm hydrogel changes the net volume of water as well as the focal length. The lens aperture is 2 mm in diameter. (b) Schematic of the principles of calculating the surface profile from the wave front profile. On the outgoing wave front, the phase difference Δϕ(x,y) between the vertex and point (x,y) is determined by h(x,y), the difference in the thickness of oil.

The principle of calculating the 3D surface profile from the wave front profile is illustrated in Fig. 1b. The lens is illuminated by a collimated light, and the incoming wave front is a plane wave. The shape of the outgoing wave front depends on the optical path difference (OPD) between the paths going through the liquid lens. Due to the refractive index difference between silicone oil and water, the optical path is determined by the respective thickness of oil and water along the path. The outgoing wave front Δϕ_lens(x,y) through the liquid lens can be calculated as follows:¹⁰

$$\Delta {\varphi }_{lens}\left(x,y\right)=\left(n_1-n_2\right)\times h\left(x,y\right)\times 2\pi ∕\lambda$$ (1)

where n₁ and n₂ are the refractive index of silicone oil and water, respectively; h(x,y) is the difference between the oil thickness at (x,y) and that at the vertex; λ is the wavelength of the light source.

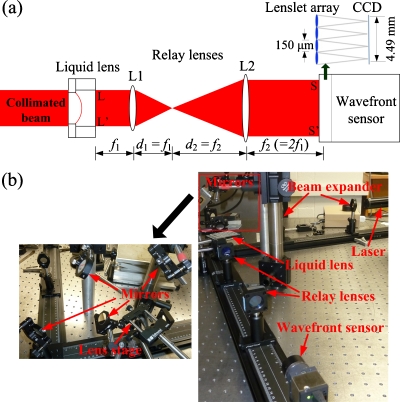
The diagram of the optical setup for measuring the wave front out of the liquid lens is shown in Fig. 2a. A collimated laser beam illuminates the liquid microlens, so that the incoming wave front is a plane wave. The liquid microlens is tested in a transmission mode and relay lenses are used to resize the wave front following the liquid lens.¹¹ The design of the relay optics is constrained by two factors. First, the aperture of the wave front sensor should be filled as much as possible for optimal sampling of the wave front. Second, by conjugating the liquid lens plane with the wave front sensor plane, the relay optics does not change the shape of the wave front through the liquid lens. Thus, the relay optics was set to enlarge the wave front through the microlens by a factor of 2, matching the lens aperture (2 mm) with the dimension of the charge-coupled device (CCD) detector in the wave front sensor (4.49 mm×4.49 mm). Figure 2b is the picture of the experimental setup. The light source was a helium–neon (HeNe) laser (λ=594 nm) and the beam was enlarged to around 2 mm in diameter by a beam expander. The liquid lens was placed on a vertical stage to avoid any possible liquid leakage. Relay lenses and a Shack-Hartmann wave front sensor (WFS150C, Thorlabs Inc., Newton, New Jersey) were fixed on a horizontal optical rail. Several mirrors were used to redirect the beam. The measured wave front profile Δϕ_sensor(x,y) was used to calculate the liquid lens surface profile h(x,y) [defined in Fig. 1b] by Eq. 2 as follows:

$$h\left(x,y\right)=\frac{\lambda \cdot \Delta {\varphi }_{lens}\left(x,y\right)}{2\pi \cdot \left(n_1-n_2\right)}=\frac{\lambda \cdot \Delta {\varphi }_{sensor}\left(2x,2y\right)}{2\pi \cdot \left(n_1-n_2\right)},$$ (2)

where Δϕ_sensor(x,y) is the wave front profile measured by the wave front sensor. Due to the relay optics, the wave front measured by the wave front sensor must be rescaled to obtain the wave front at the liquid lens. The resolution of the measurement is 75 μm, limited by the lenslet array in the wave front sensor. The accuracy of our wave front sensor is λ∕15, or 39.6 nm for λ=594 nm; therefore the theoretical accuracy of the surface measurement is approximately 77 nm, given by 39.6 nm∕(n_glass−n_air).

Figure 2.

(a) Optical setup using the Shack–Hartmann wave front sensor. The wave front sensor is operated in the transmission mode and the liquid microlens is illuminated by a collimated light. Relay lenses are used to conjugate liquid lens plane LL^′ with wave front sensor plane SS^′ and to enlarge the wave front by a factor of 2. (b) Picture of the experiment setup. It consists of a laser source, a beam expander, mirrors, a sample lens on a stage, relay lenses, and a wave front sensor.

To test the reliability and accuracy of the physical model and the optical setup, a commercial planoconvex glass lens (NT47–381, Edmund Optics, Barrington, NJ) was measured and the obtained surface profile was compared with the specifications reported by the manufacturer. The manufacturer-reported radius of curvature (RoC) was 24.81 mm while the measured RoC was 24.57 mm, resulting in a relative error of 0.97%. The root mean square (rms) of the difference between the reported profile and the experiment result was 105.2 nm, only slightly larger than the theoretical accuracy of the measurement, 77 nm. Therefore, this method is proved to be reliable and accurate by the comparison between the manufacturer-reported profile of the glass lens and its measured surface profile.

The tunable liquid microlens in Fig. 1a was tested within a wide range of focal lengths f. It was fixed on a microscope slide before measurements to keep the PDMS substrate flat. Figure 3a illustrates the surface profile at f=15.2 mm. The lens was also measured at f=34.7 mm and f=23.0 mm. The liquid lens had a larger curvature at a shorter f. As f decreased from 34.7 to 15.2 mm, the water–oil interface bent further downward and the peak-to-valley (PV) of the interface increased from 312.0 μm to 799.9 μm. The lens surface was asymmetric due to the nonuniform surface hydrophilicity at the aperture, which in turn resulted from the surface treatment during the fabrication process. Figure 3b shows the scatter plot of surface height h(x,y) [defined in Fig. 1b] versus the distance from point (x,y) to the vertex at f=15.2 mm. The geometric profile shows slight asymmetry. At the center of the lens, the surface has a smooth spherical shape; near the margins of the aperture, the profile gradually evolves to a linear pattern. The surface profile transition can be intuitively explained by the fact that the water–oil interface is pinned at the hydrophobic–hydrophilic boundary. Closer to the aperture edges, the water surface bends further downward toward the hydrophilic side wall, becoming more linear rather than spherical. This phenomenon was also observed at other focal lengths tested.

Figure 3.

(a) Measured 3D surface profile of the water–oil interface at f=15.2 nm. (b) Scatter plot of surface height h(x,y) vs ρ(x,y) at f=15.2 mm. ρ(x,y) is the distance between point (x,y) and the vertex, as defined in Fig. 1b. When ρ(x,y) is relatively small, i.e., within the area near the center, the surface is approximately spherical in shape; near the boundary, the shape of the surface becomes much more linear.

For quantitative geometric analysis of the water–oil interface, the measured surface profiles are fitted to a conical surface defined by

$$z-z_0=\frac{c\cdot \left[{\left(x-x_0\right)}^2+{\left(y-y_0\right)}^2\right]}{1+\sqrt{1-c^2\left(1+k\right)\left[{\left(x-x_0\right)}^2+{\left(y-y_0\right)}^2\right]}},$$ (3)

where c is the reciprocal of the radius, k is conic constant, and (x,y,z) is the vertex of the surface. The conic constant k is less than −1 for hyperbolas. All five coefficients were obtained by a custom surface fit program written in MATLAB and the results are summarized in Table 1. The negative conic constant indicates that the surface is in hyperbolic shape. This result matches well with the observation that the liquid surface is spherical at the center but is stretched into a linear shape near the edges. The contact angles at the boundary are also calculated based on the conical surface fit, as shown in Table 1.

Table 1.

Coefficients of conical surface fit. The surface profiles are fitted to Eq. 3. StDev stands for standard deviation. The last column is the contact angle at the lens aperture based on conical surface interpolation.

Conical surface fit
Focal length (mm)	c (mm−1)	k	StDev (μm)	Contact angle (deg)
34.7	0.41	−5.03	25.0	20.8
23.0	0.62	−2.52	43.2	29.5
15.2	0.94	−1.99	65.8	40.6

The optical properties of the liquid microlens were studied by the software Zemax (Zemax Development Corporation, Bellevue, WA). The surface profile data was imported into Zemax to define the lens surface and to calculate the aberration. The primary aberration of this liquid lens was spherical aberration which is described by the 11th Zernike standard coefficient (Z₁₁). The simulation results are summarized in Table 2. The simulated focal length matches very well with the experiment results. The Zernike coefficients obtained from both methods are also close. The error is mostly due to the assumption that the measured wave front is right following the water–oil interface, while the setup measures the wave front following the PDMS substrate. The liquid microlens has higher spherical aberration at shorter focal length. The relatively large rms error indicates that the lens aberration can be severe when the water–oil interface has a large curvature.

Table 2.

Comparison of measured optical properties vs Zemax simulation results. Spherical aberration is represented by Z₁₁, the 11th Zernike standard coefficient. rms error describes the overall aberrations of a lens.

Comparison between measured results and Zemax simulation
Focal length (mm)	Measured Z11 (wave)	Simulated focal length (mm)	Simulated Z11 (wave)	rms error (wave)
34.7	−1.40	33.33	−1.73	0.22
23.0	−2.46	24.12	−2.07	0.28
15.2	−3.19	15.29	−2.43	0.44

In summary, we demonstrated a method for measuring the 3D surface profile of the liquid-to-liquid interface in a liquid microlens using a Shack–Hartmann wave front sensor. A physical model was presented to calculate the surface profile from the measured wave front. A hydrogel-actuated variable-focus liquid microlens was measured within a wide focal length range and its oil–water interface was found to be hyperbolically shaped. The software-simulated optical properties matched well with the measurements. In the future, this 3D surface profiling technique will be used to improve the design, fabrication process and optimization of the liquid microlenses, e.g., improving the surface wettability and reducing the lens aberrations. In addition, this method could potentially be applied to more general interfacial characterization in microfluidics.