Abstract
The large amplitude oscillatory shear behavior of metallo-supramolecular polymer networks formed by adding bis-Pd(II) cross-linkers to poly(4-vinylpyridine) (PVP) in dimethyl sulfoxide (DMSO) solution is reported. The influence of scanning frequency, dissociation rate of cross-linkers, concentration of cross-linkers, and concentration of PVP solution on the large amplitude oscillatory shear behavior is explored. In semidilute unentangled PVP solutions, above a critical scanning frequency, strain hardening of both storage moduli and loss moduli is observed. In the semidilute entangled regime of PVP solution, however, strain softening is observed for samples with faster cross-linkers (kd ∼ 1450 s−1), whereas strain hardening is observed for samples with slower cross-linkers (kd ∼ 17 s−1). The mechanism of strain hardening is attributed primarily to a strain-induced increase in the number of elastically active chains, with possible contributions from non-Gaussian stretching of polymer chains at strains approaching network fracture. The divergent strain softening of samples with faster cross-linkers in semidilute entangled PVP solutions, relative to the strain hardening of samples with slower cross-linkers, is consistent with observed shear thinning/shear thickening behavior reported previously and is attributed to the fact that the average time that a cross-linker remains detached is too short to permit the local relaxation of polymer chain segments that is necessary for a net conversion of elastically inactive to elastically active cross-linkers. These and other observations paint a picture in which strain softening and shear thinning arise from the same set of molecular mechanisms, conceptually uniting the two nonlinear responses for this system.
Introduction
Associative polymers have rich rheological behavior that fuels their use in a wide range of applications and motivates interest in the mechanisms that determine their behavior.1–6 Their rheological properties can be categorized into two classes of viscoelastic response:7 linear viscoelasticity, as normally measured by small amplitude oscillatory shear, and nonlinear viscoelasticity such as that which occurs under high steady shear rate and large amplitude oscillatory shear.7 In contrast to their linear rheological properties, the mechanisms underlying the nonlinear rheological properties of associative polymers vary from one system to another and are often unclear. As a result, extensive experimental and theoretical research has been devoted to the molecular origin of shear thickening and strain hardening of associative polymers. 8–18
At the core of the visoelastic response of associative polymers is the reversible association itself, and our group has previously demonstrated a useful method of probing the contributions of molecular reversibility to the macroscopic rheological properties of supramolecular polymer networks.18–21 The method takes advantage of steric effects at the N-alkyl positions of N,C,N-pincer Pd(II) and Pt(II) complexes,17 through which the dissociation rate of the cross-linkers can be changed by orders of magnitude independently of the association constant.22 Recently, the steady shear behavior of the metallo-supramolecular polymer networks formed by these bis-Pd(II) cross-linkers and poly(4-vinylpyridine) (PVP) was reported (Figure 1). 18,21,23 The mechanism of shear thickening of samples in the semi-dilute unentangled regime and divergent shear thinning versus shear thickening of samples with identical structure but different cross-linker kinetics in the semidilute entangled regime were explored.18,21,23 We found that shear thickening was dominated by a conversion of intrachain to interchain bound cross-linkers, but that the competition between re-association of dissociated cross-linkers and polymer chain diffusion contributed to the efficiency of the conversion process. 18,21,23 In this paper, the large amplitude oscillatory shear (LAOS) behavior of the same metallo-supramolecular polymer networks is examined. The LAOS experiments allow us to probe the strain hardening and/or strain softening behavior of the networks,7,24,25 classes of nonlinear responses that are central to the behavior of materials under high-strain conditions, but for which a detailed physical picture is often difficult to realize.26 In analogy with the steady shear behavior, depending on the sample, strain hardening and/or strain softening are observed. The mechanisms underlying the LAOS response are explored, and the behavior is compared to the steady shear behavior previously reported.
Figure 1.
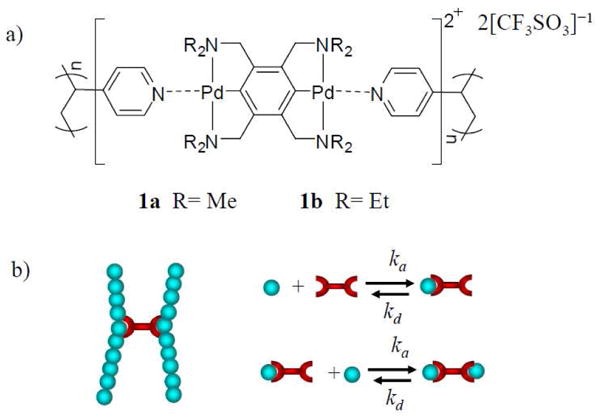
(a) Schematic picture of networks formed from poly(4-vinylpyridine) (PVP) chains and bis-Pd(II) cross-linkers (1a or 1b); (b) Schematic picture of the kinetic parameters of the supramolecular interaction underlying network formation. Each pyridine unit in the PVP chain is represented by a bead.27 Reproduced from Macromolecules 2011, 44, 5465-5472, with permission (Copyright © 2011 American Chemical Society).
Experimental Section
Materials
The bis-Pd(II) cross-linkers [2,3,5,6-tetrakis{(dimethylamino)methyl}phenylene-1,4-bis(palladiumtrifluoromethanesulfonate)] (1a) and [2,3,5,6-tetrakis{(diethylamino)methyl}phenylene-1,4-bis(palladiumtrifluoromethanesulfonate)] (1b) were synthesized as reported elsewhere.22 The binding thermodynamics and exchange kinetics of the metal–pyridine interactions have been characterized previously.20 The equilibrium association constants (Keq) and dissociation rate constants (kd) for 1a·pyridine in DMSO at 25 °C are 29 M−1 and 1450 s−1, respectively. Keq and kd for 1b·pyridine in DMSO at 25 °C are 33 M−1 and 17 s−1, respectively.20 Dimethyl sulfoxide (DMSO), and poly(4-vinylpyridine) (PVP) with Mw = 60000 as reported by the producer, were used as received from Aldrich. The Mn and Mw of the PVP have been reported previously to be 22000 and 64300 g/mol (polydispersity index (PDI) = 2.92), respectively, in the literature.28 We carried out an independent analysis of the specific PVP used in our experiments and obtained values of Mn = 33000 and Mw = 44500 g/mol (PDI = 1.35).23
Sample Preparation
Samples were prepared by mixing PVP solutions with cross-linker solutions. Details of sample preparation can be found in a previous paper.18 The concentration of cross-linkers in the samples varied from 1% to 5% (ratio of Pd atoms to N atoms in the pyridine units of the PVP), all of which are above the critical concentration to form a gel (shown previously to be approximately 0.8 % for ∼0.10 g/mL PVP/DMSO solutions).29 The concentration of PVP in the samples varies from 0.08 (semidilute unentangled regime) to 0.27 g/mL (semidilute entangled regime). Details about the concentration regimes of PVP/DMSO solution have been characterized previously, and the critical concentration of entanglement at 25 °C is 0.155 g/mL.23 Concentrations are often denoted with a “∼” to reflect the slight variation between samples made with cross-linker 1a vs. 1b; see Supporting Information for details.
Rheological Measurements
Rheological experiments were carried out at 25 °C. Data were obtained by using an AR G2 rheometer (TA Instruments) with cone–plate geometry (diameter of 20 mm, cone angle of 2°, truncation height of 49 μm). Strain sweep experiments were performed at different scanning frequencies. Oscillatory frequency sweeps from 10 to ∼30 rad/s were carried out at strains that spanned from the linear rheological region to the nonlinear rheological region for samples with 1b.
The inertia and torque of the AR-G2 rheometer (stress controlled rheometer) must be calibrated carefully in order to measure the small values of storage modulus (G′) of a low viscosity fluid at high frequency, where the measured torque is the sum of the sample torque and inertial torque.30 Slight deviations in the inertial torque can cause significant variations in the derived sample torque. A useful parameter to monitor the effect of inertia, and one we employ here, is the measured (raw) phase angle (δm). If the inertia shifts the phase angle, δm will be larger than the sample's phase angle (δs). Measurements with a raw phase angle below 170° can be calibrated,30 but to avoid the influence of inertial effects on the non-linear rheological properties of samples in this work, only the data for which δm = δs are used in this paper. This restriction limits the range of available scanning frequencies for the strain sweep experiments, especially for samples with low viscosity.30
Data Treatment
At small strain amplitudes, when the response is linear, the material is commonly characterized by the storage modulus (G′) and loss modulus (G″), as determined from the components of the time dependent stress σ(t) in phase with time dependent strain γ(t) and time dependent strain rate γ̇ (t), respectively:31
| (1) |
| (2) |
| (3) |
where γ0 is the strain amplitude, ω is frequency, t is time, γ0ω is the strain rate amplitude, σ0 is amplitude of the stress, and δ is phase angle.
The strain amplitude γ0 can be increased systematically to enter the nonlinear viscoelastic regime, resulting in a LAOS test. The linear storage moduli (G′) and loss moduli (G″) are not uniquely defined once the material response becomes nonlinear,24 since a nonlinear stress response is not a single-harmonic sinusoid. Nonetheless, apparent values of G′ and G″ have proven useful as a framework upon which to discuss nonlinear rheological properties,14, 32–34 and we adopt that practice here.
If the periodic stress response σ(t) is plotted against γ(t) (Lissajous-Bowditch curves), a linear viscoelastic response appears as an ellipse that contains two mirror planes (the major and minor axes of the ellipse), whereas a nonlinear viscoelastic response is characterized by Lissajous-Bowditch curves that deviate from ellipticity.24 For example, Lissajous-Bowditch curves are not elliptical when secondary flow, wall slip, or non-Gaussian stretching of polymer chains takes place in the samples. 24, 35, 36 The Lissajous-Bowditch curves are used here to further characterize the details of the strain sweep behavior, especially during strain hardening or strain softening, and their use complements analyses based merely on G′ and G″.
Results
1. Strain Sweep Results in the Semidilute Unentangled Regime
Influence of Scanning Frequency
In Figure 2, the influence of scanning frequency on the strain sweep behavior of ∼0.11 g/mL PVP with 5% 1a is shown. When the scanning frequency is 0.3 or 0.5 rad/s, substantial strain softening (modulus decreases with increasing strain, γ) is observed in G′, while G″ remains nearly constant in across the experimentally accessible range of γ. As the scan frequency is increased from 1 rad/s to 5 rad/s, G′ is first constant, then decreases with increasing γ, and then increases at larger γ. G″ is constant at small strain and shows strain hardening (modulus increases with increasing γ) at larger strain. At 3 rad/s and 5 rad/s, a dramatic decrease in modulus at high γ is observed that corresponds to the fracture of the network and/or ejection of the sample from the geometry.18 In this paper, we do not focus on this fracture behavior further. Increasing the scanning frequency to above 10 rad/s causes the raw phase angle to become larger than the sample phase angle, meaning that inertia starts to affect the experimental results,30 and these data are therefore omitted from further consideration.
Figure 2.
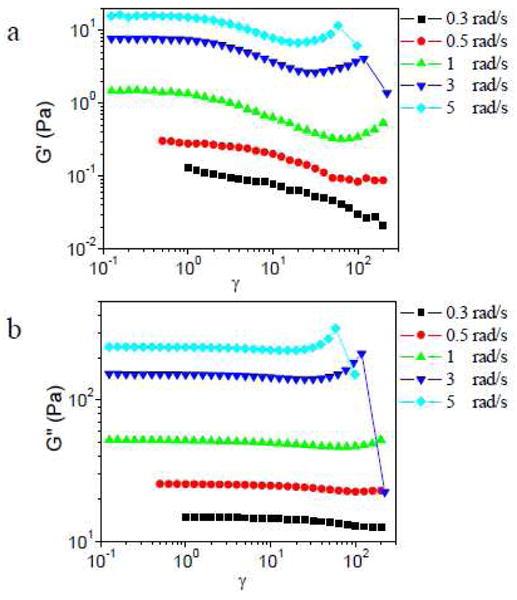
Storage modulus (G′) and loss modulus (G″) versus strain (γ) for sample with 5% 1a in ∼0.11 g/mL PVP during strain sweep experiments at different scanning frequency.
The initial strain softening regime of ∼0.11 g/mL PVP with 5% 1a at low frequency is analyzed further by the raw strain sweep data. Lissajous-Bowditch curves of ∼0.11 g/mL PVP with 5% 1a in the strain softening regime are elliptical (Figure S1 in Supporting Information), indicating a single-harmonic sinusoidal stress response in the strain-softened regime and ruling out substantial non-Gaussian stretching of polymer chains (consistent with expectations for behavior at low strains), for which the Lissajous-Bowditch curves would not be elliptical.24 The mechanism behind the strain softening of G′ at low frequency, during which G″ remains nearly constant, is not further explored in this paper.
Strain sweep results of ∼0.11 g/mL PVP with 5% of the slower cross-linker 1b at different scanning frequencies are shown in Figure 3. Strain hardening of G′ and G″ is observed when the scan frequency is as low as 0.3 rad/s, whereas no strain hardening is observed for the comparable 1a network under those conditions (Figure 2). In Figure 3, ∼0.11 g/mL PVP with 5% 1b also shows some strain softening in G′ prior to strain hardening at 0.3 rad/s, and the Lissajous-Bowditch curves are elliptical in the strain softening regime (Figure S2 in Supporting Information; the Lissajous-Bowditch curves of ∼0.11 g/mL PVP with 5% 1b during strain hardening will be discussed in detail in the next section). During the strain softening of G′, G″ is nearly constant (as seen in the 1a networks), and the phase angle increases. Inertial contributions preclude analysis of data at scanning frequencies above 50 rad/s.
Figure 3.
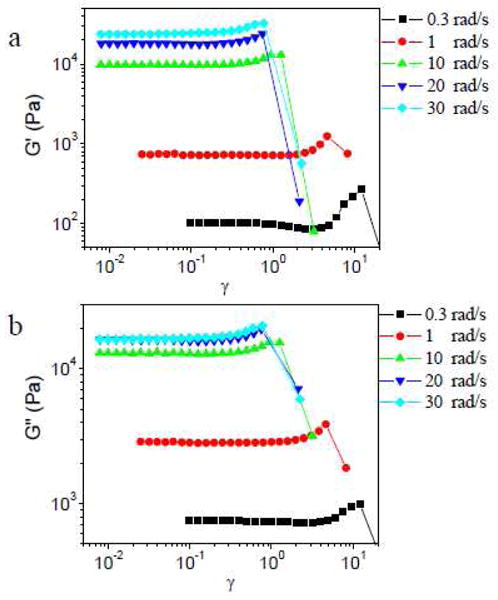
Storage modulus (G′) and loss modulus (G″) versus strain (γ) for sample with 5% 1b in ∼0.11 g/mL PVP during strain sweep experiments at different scanning frequency.
As seen in Figure 2, for samples with 5% 1a, the value of critical strain (γcrit, defined by the onset of strain hardening) or the maximum strain without network fracture during strain hardening (γmax), decreases with increasing scanning frequency from 1 rad/s to 5 rad/s (Figure 2b). For samples with 5% 1b, this trend between γcrit (or γmax) and scanning frequency is also observed with the increase of scanning frequency from 0.3 rad/s to 10 rad/s, but the value of γcrit and γmax during strain hardening are almost the same from 20 rad/s to 30 rad/s (Figure 3). We also notice that, at 1 rad/s, the value of γcrit and γmax for ∼0.11 g/mL PVP with 5% 1a is much bigger than for that with 5% 1b. Because the structure of 1a·PVP and 1b·PVP networks is effectively identical, 18–20 the different trends as a function of scanning frequency are attributed to the different relaxation times (τ) of the networks. The characterization of the apparent relaxation time (τ) of ∼0.11 g/mL PVP with 5% 1a or 5% 1b in the linear regime are shown in Figure S3 in Supporting Information. The apparent relaxation times (τ) of ∼0.11 g/mL PVP with 5% 1a or 5% 1b are determined to be 6.7×10−4 s and 5.7×10−2 s, respectively.
We use the Deborah number (De= ωτ)37 to interpret the strain sweep results in Figure 2 and Figure 3. The relationship of γcrit and γmax to De for ∼0.11 g/mL PVP with 5% 1b (0.1 – 30 rad/s) and for ∼0.11 g/mL PVP with 5% 1a (3 – 5 rad/s) is shown in Figure 4. When De < 1, γcrit and γmax decrease as the scanning frequency is increased. When De > 1, γcrit and γmax remain nearly constant as a function of scanning frequency. From Figure 4, we also see that the values of γcrit and γmax for samples with 1a or 1b fall on the same master curves. This behavior is consistent with scaling relationships reported previously for this system under linear oscillatory frequency sweep and steady shear,18, 20, 27 and verifies that the structures of samples with 1a or 1b are similar.
Figure 4.
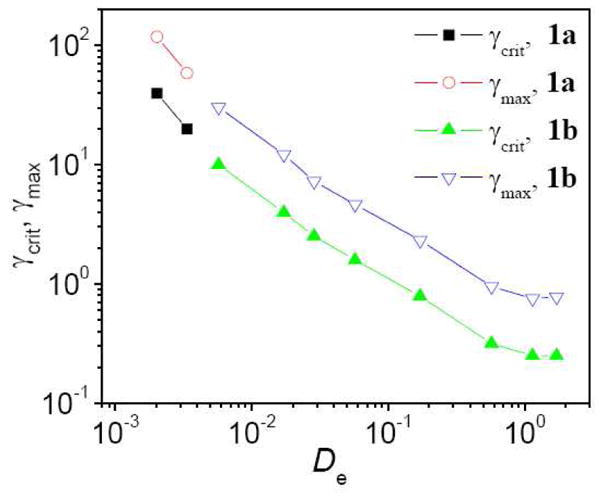
Critical strain (γcrit) and maximum strain (γmax) during strain hardening as a function of the Deborah number (De) for samples with 5% 1a or 5% 1b in ∼0.11 g/mL PVP during strain sweep experiments at different scanning frequency. Lines are provided to guide the eye.
Similar dependencies of γcrit and γmax on De have been reported previously. 24, 33, 34 Tung et al. examined the strain hardening of lecithin/SDC reverse worms, and observed that when De < 1, γcrit and γmax decrease as the scanning frequency is increased.34 Erk et al. observed that when De > 1, the onset of strain hardening in physical networks of triblock copolymers occurs at a similar value of strain.33 The Deborah number measures the amount of elasticity,24, 38 and when the scanning frequency (ω) during strain sweep is smaller than the cross-over frequency (ωc) of G′ and G″ (obtained from frequency sweep measurements), De < 1 and G′ < G″; that is, the fluid is predominantly viscous. When De > 1, G′ < G″, and the fluid is predominantly elastic.38 Ewoldt et al. reported that at low scanning frequency (De < 1), the viscous nonlinearities during strain sweep become apparent near a Weissenberg number (Wi, Wi = γ0ωτ) of close to 1.24 As the strain rate amplitude (γ0ω) is analogous to the shear rate of steady shear experiments, the nonlinearities of a fluid during strain sweep with De < 1 implies a connection to nonlinear steady shear behavior, to which we return later in the manuscript (Figure 5). Similar nonlinear behavior is observed at higher frequency (De > 1) (Figure 5), when the fluid is dominated by elasticity; the nonlinear regime during strain sweep was also found by Ewoldt et al. to be triggered at a critical strain amplitude. 24
Figure 5.
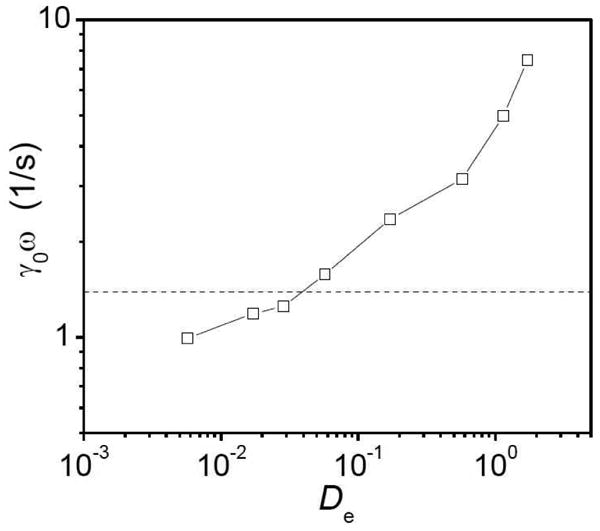
Strain rate amplitude (γ0ω) at the critical strain during strain hardening versus the Deborah number (De) for samples with 5% 1b in ∼0.11 g/mL PVP during strain sweep experiments at different scanning frequencies. The critical shear rate for the shear thickening of 5% 1b in ∼0.11 g/mL PVP is given by the dashed line (γ̇crit = 1.4 s−1).18
We note here that the maximum De number explored in this work is about 2 because of the experimental limitations on the range of scanning frequency. Wang's group reported that the large amplitude oscillatory shear (LAOS) behavior of a polymeric liquid at De ≫ 1 can show more complex behavior such as wall slipping and/or shear banding.39,40 We do not think that the strain hardening and strain softening behavior of interest to us in this work, which occur at De < 3, are related to wall slip and/or shear banding, which generally take place at much higher De.39,40 Mechanistic probes of the behavior, discussed below, support this supposition.
Relationship Between Strain Hardening and Shear Thickening
Bossard et al. have compared the shear thickening effect (shear-induced viscosity enhancement) during steady shear experiments and the strain hardening of G′ during strain sweep experiments in the context of a polyampholyte solution.41 It was reported that the critical strain rate amplitude during strain hardening (∼0.25 s−1) is comparable to the critical shear rate for shear thickening (0.2 s−1) obtained in steady shear flow, and it was reasoned that strain hardening is related to the shear-thickening behavior.41
We therefore compare the critical strain rate amplitude (γ0ω) during the onset of strain hardening, taken at different scanning frequencies for ∼0.11 g/mL PVP with 5% 1b, to the critical shear rate of the samples during steady shear (γ̇crit), previously reported to be 1.4 s−1.18 As shown in Figure 5, the critical strain rate amplitude (γ0ω) is close to the critical shear rate during steady shear when De< 1. This is consistent with Bossard et al.'s work and with our expectation, as stated above. The critical strain rate amplitude (γ0ω), however, is not a constant; the value of γ0ω increases with increasing scanning frequency. The variance may reflect the fact that, during a strain sweep, the strain rate ranges from zero to the strain rate amplitude over each cycle of a dynamic oscillatory measurement.31 This condition differs from the constant shear rate during steady shear experiments,31 and the similarity in values is best taken semi-quantitatively only. As De increases, we observe that the critical strain rate amplitude (γ0ω) increases, until the onset of nonlinearities of the fluid during strain sweep with De > 1 is several times larger than that at low De. Given the aforementioned uncertainty due to a variable strain rate in the oscillatory experiment, we are reluctant to try and interpret this trend. Although the absolute value belies a direct relationship with nonlinear steady shear behavior, the continuity in the trend shown in Figure 5 suggests that even in systems for which the strain sweep and steady shear onsets are substantially different, the two effects might originate from the same dynamics and mechanism.
Influence of Cross-linker Concentration
In Figure 6, the strain sweep data at 1 rad/s are shown for ∼0.11 g/mL PVP with different concentrations of 1b. All of the samples exhibit strain hardening, and the values of γcrit and γmax decrease with increasing concentration of 1b.
Figure 6.
Storage (G′) and loss (G″) moduli versus strain (γ) for sample with different concentration of 1b in ∼ 0.11 g/mL PVP solution. Scanning frequency is 1 rad/s.
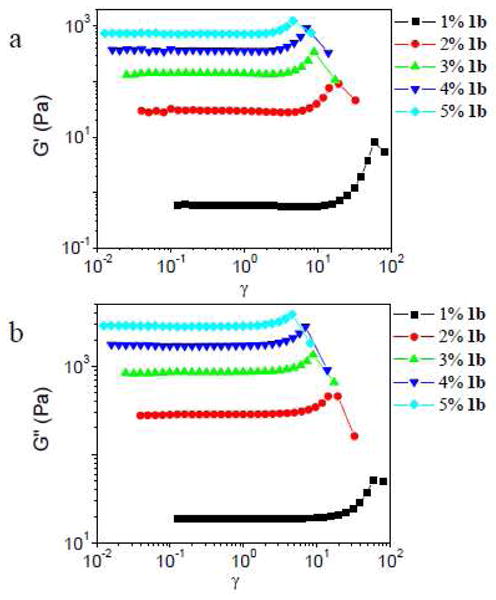
The degree of strain hardening is defined as the ratio between the maximum value of a modulus (either G′max or G″max) during strain hardening and the constant value of that modulus in the linear regime (G′Lin and G″Lin). In Figure 7, the degree of strain hardening (for both G′ and G″) for different concentrations of 1b is shown as a function of scanning frequency. The degree of strain hardening for both G′ and G″ is greatest for the sample with 1% 1b, whereas the degree of strain hardening is relatively independent of the concentration of 1b from 2% to 5%. As seen in Figure 7, G′max/G′Lin is larger than G″max/G″Lin. This phenomenon is connected to the change of phase angle during strain hardening, as discussed further below.
Figure 7.
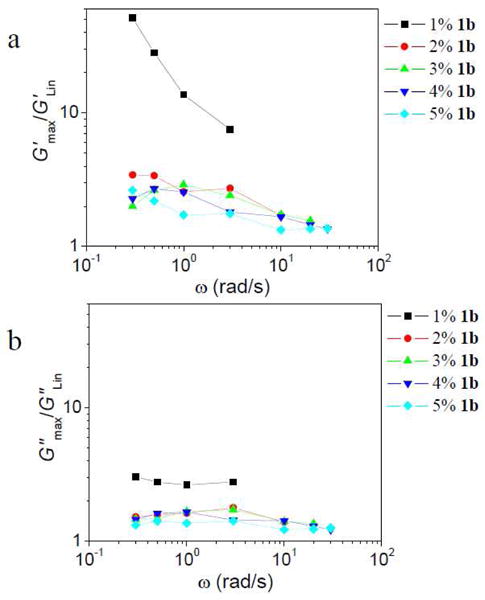
Degree of strain hardening in G′ (a) and G″ (b) versus the scanning frequency (ω) for ∼0.11 g/mL PVP with different concentrations of 1b during strain sweep experiments at different scanning frequencies.
In Figure 8, strain sweep data for the 1a·PVP networks (∼0.11 g/mL PVP, 1 rad/s) with different concentrations of 1a are shown. For samples with concentrations of 1a from 1% to 3%, strain softening but no strain hardening in G′ is observed across the range of strains accessed, whereas G″ is essentially constant; no strain hardening is observed across the experimentally accessible range. For samples with concentrations of 1a of 4% or 5%, strain hardening is observed in G′ and G″. The trends in γcrit (or γmax) as a function of concentration of 1a are more complex than those for samples made with 1b (Figure 6).
Figure 8.
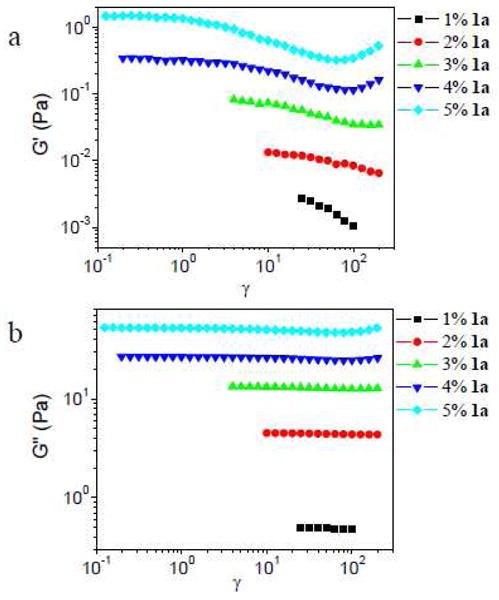
Storage modulus (G′) and loss modulus (G″) versus strain (γ) for samples with different concentrations of 1a in ∼ 0.11 g/mL PVP solution. Scanning frequency is 1 rad/s.
2. Influence of PVP Concentration on Strain Sweep Results
In Figures 9 and 10, strain sweep results in different concentrations of PVP solution are shown (scanning frequency is 1 rad/s) for samples with 5% 1a or 5% 1b, respectively. When the PVP concentration is below the critical concentration of entanglement (∼0.155 g/mL),23 strain hardening in both G′ and G″ is observed for samples with both 1a or 1b. When the PVP concentration is above the critical entanglement concentration, however, samples with 5% 1a show only strain softening in both G′ and G″ (and, accordingly, in the complex modulus ) (Figure 9).31 This behavior contrasts with that of samples made with 5% 1b, for which strain hardening in G′ is observed from 0.159 g/mL to 0.190 g/mL PVP (Figure 10a), and strain hardening in G″ is observed at all concentrations examined (Figure 10b). All samples with 5% 1b in the semidilute entangled regime show strain hardening in |G*|.
Figure 9.
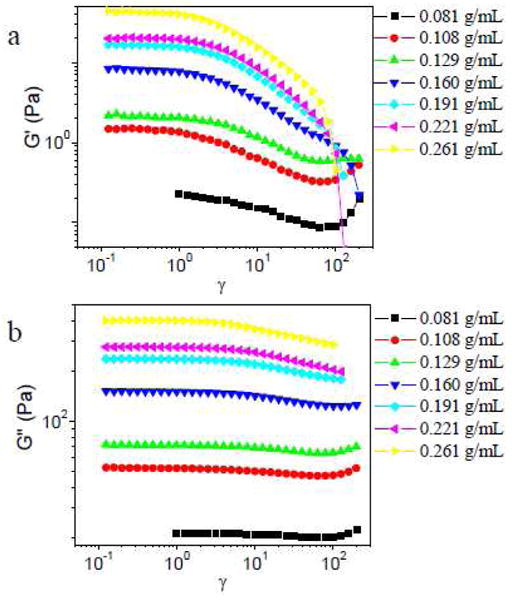
Storage (G′) and loss (G″) moduli versus strain (γ) for samples with 5% 1a in different concentrations of PVP solution. Scanning frequency is 1 rad/s.
Figure 10.
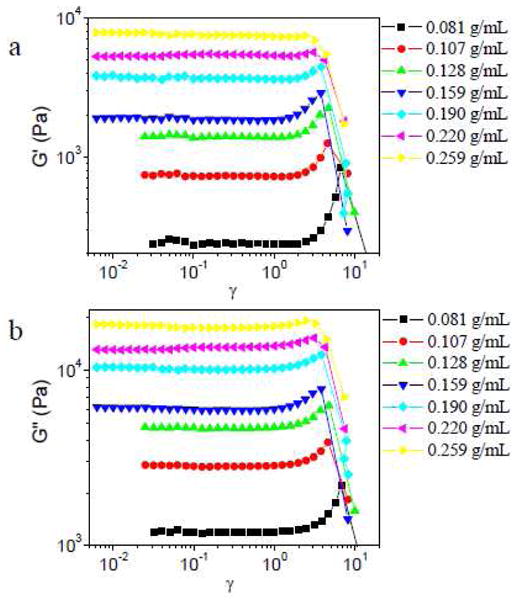
Storage (G′) and loss (G″) moduli versus strain (γ) for samples with 5% 1b in different concentrations of PVP solution. Scanning frequency is 1 rad/s.
These results are reminiscent of the divergent shear thinning/shear thickening behavior of the entangled 1·PVP solutions reported previously,21,23 suggesting that physical entanglement of PVP chains has an influence on the LAOS behavior. This observation motivates an examination of the strain sweep properties in the semidilute entangled regime.
3. Strain Sweep Results in the Semidilute Entangled Regime
Influence of Scanning Frequency
In Figure 11, the strain sweep data of 0.261 g/mL PVP with 5% 1a at different scanning frequencies are shown. As the scanning frequency is increased from 0.3 rad/s to 5 rad/s, 0.261 g/mL PVP with 5% 1a always shows strain softening. These results contrast with that of the ∼0.11 g/mL PVP (semidilute unentangled regime) with 5% 1a (Figure 2), for which strain hardening in G′ and G″ is observed above 1 rad/s. Lissajous-Bowditch curves of 0.261 g/mL PVP with 5% 1a in the strain softening regime appear as ellipses at scanning frequencies of from 0.3 rad/s to 5 rad/s (Figure S4-S5 in Supporting Information), again ruling out a substantial amount of non-Gaussian stretching of polymer chains.24
Figure 11.
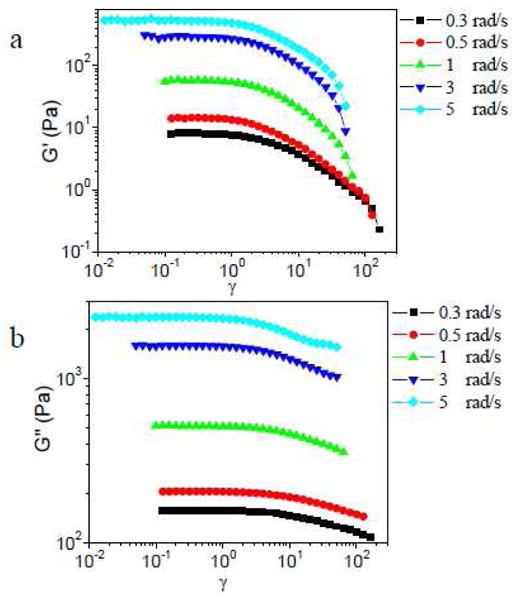
Storage (G′) and loss (G″) moduli versus strain (γ) for samples with 5% 1a in 0.261 g/mL PVP during strain sweep experiments at different scanning frequency.
Shown in Figure 12 are the strain sweep data for 0.259 g/mL PVP with 5% 1b at different scanning frequencies. As scanning frequency is increased from 0.3 rad/s to 1 rad/s, no strain hardening in G′ is observed, in contrast to the strain hardening of G′ for ∼0.11 g/mL PVP (semidilute unentangled regime) with 5% 1b. For 0.259 g/mL PVP with 5% 1b from 0.3 rad/s to 1 rad/s, strain hardening in G″ is still observed, and the complex moduli (|G*|) still show strain hardening with the increasing of strain. The value of G″max/G″Lin and are around 1.1. Under 0.3 rad/s and 1 rad/s, the phase angle increases with strain in the nonlinear regime. With a further increase of scanning frequency to values of from 10 to 30 rad/s, 0.259 g/mL PVP with 5% 1b shows strain hardening in G′ and G″, and the phase angle decreases with strain during strain hardening. Although the degree of strain hardening in G′ is a little larger than the degree of strain hardening in G″, the values of G′max/ G′Lin and G″max/G″Lin are both around 1.1.
Figure 12.
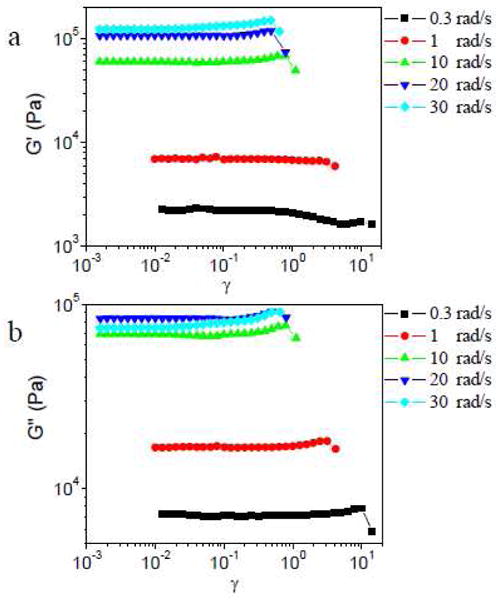
Storage (G′) and loss (G″) moduli versus strain (γ) for samples with 5% 1b in 0.259 g/mL PVP during strain sweep experiments at different scanning frequency.
Influence of Cross-linker Concentration
In Figure 13, the strain sweep data of ∼0.27 g/mL PVP with different concentration of 1a at 1 rad/s are shown. As the concentration of 1a increases from 1% to 5%, strain softening is observed in G′ and G″. The concentration of 1a does not have much influence on the strain softening of ∼0.27 g/mL PVP.
Figure 13.
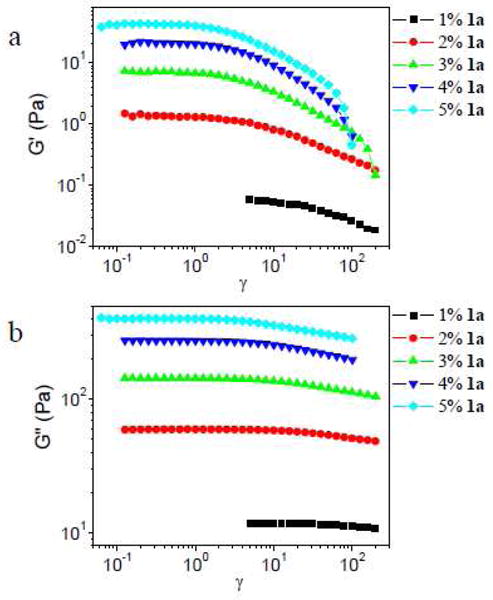
Storage (G′) and loss (G″) moduli versus strain (γ) for samples with different concentrations of 1a in ∼0.27 g/mL PVP solution. Scanning frequency is 1 rad/s.
The strain sweep data for ∼0.26 g/mL PVP with different concentrations of 1b at 1 rad/s are shown in Figure 14. Strain hardening is observed in G′ for samples with 1% and 2% 1b, and the phase angle decreases during strain hardening. For samples with concentrations of 1b from 3% to 5%, no strain hardening in G′ is observed in the experimental range, the phase angle increases with strain in the nonlinear regime, and strain hardening in G″ (and |G*|) is observed for all samples with 1b.
Figure 14.
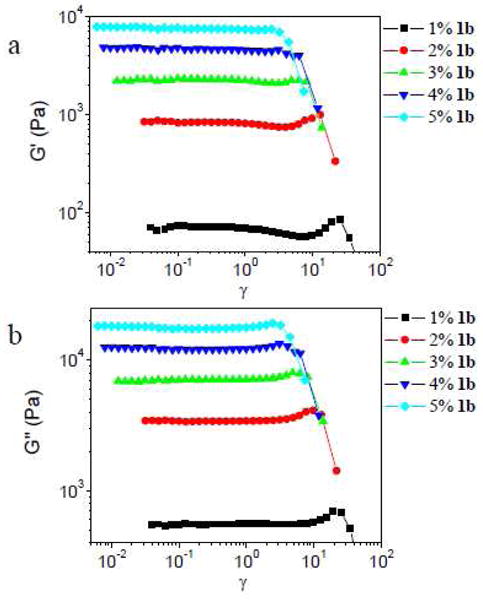
Storage (G′) and loss (G″) moduli versus strain (γ) for samples with different concentrations of 1b in ∼ 0.26 g/mL PVP solution. Scanning frequency is 1 rad/s.
Comparing the data in Figure 10 to that in Figure 14, we see that the concentration of PVP solution and concentration of 1b both affect the strain sweep results in the semidilute entangled regime. The fraction of elastically active chains increases with concentration of PVP and concentration of 1b,23 and the results here suggest that the fraction of elastically active chains influences the strain sweep behavior in a manner similar to that observed previously in the steady shear behavior.23
Discussion
Mechanism of Strain Hardening
Proposed mechanisms of strain hardening for polymer networks fall into either of two main categories: one is strain-induced nonlinear high tension along chains that are stretched beyond the Gaussian range,2, 14,15, 32, 33 and the other is the strain-induced transformation of intrachain cross-linking to interchain cross-linking.12,34,41 Regardless of the strain hardening mechanism, the degree of strain hardening of storage moduli (G′max/G′Lin) and loss moduli (G″max/G″Lin) can be expressed as31
| (4) |
| (5) |
where and are the complex moduli and δLin and δmax are the phase angle in the linear regime and at the maximum strain during strain hardening, respectively. From equation 4 and 5, we get
| (6) |
Since a non-Gaussian stretching stress response is not a single-harmonic sinusoid, the periodic stress response σ(t) versus γ(t) (Lissajous-Bowditch curves) will cease to be elliptical in the strain hardening regime if strain hardening is caused by non-Gaussian stretching.24 Another signature of non-Gaussian stretching arises from the partial rupture of the network that generally accompanies overstretching.15 The observable consequence of the rupture is that δmax is generally larger than δLin, as was observed for example in work reported by Ma et al.42 As , the fact that δmax > δLin means that G″ will always show strain hardening under conditions of non-Gaussian overstretching, according to equation 5. On the other hand, G′ (eq 4) may exhibit either strain hardening or softening, depending on the difference between δmax and δLin.42 When G′ also strain hardens, however, the degree of strain hardening in G″ is larger than the degree of strain hardening of G′, according to equation 6. These relative strain hardening behaviors of G′ and G″ have been reported previously for polymer networks,32,33 and tied to the non-Gaussian stretching of polymer chains in the strain hardening regime.33 Under this mechanism of strain hardening, the relaxation time of the network (τ) is expected to decrease because of the partial break of the network under non-Gaussian stretching, as observed in Serero et al's experimental work.15
In contrast, if strain hardening results from an increase in the number of elastically active chains, more energy is stored relative to that dissipated, and so δmax should be smaller than δLin. According to equation 4 and 5, then, δmax < δLin means that G′ will always show strain hardening and G″ might show strain hardening or softening, depending on the difference between δmax and δLin. Furthermore, if G″ strain hardens, δmax < δLin implies that the degree of strain hardening in G″ is smaller than the degree of strain hardening in G′ (eq 6). Under this mechanism, the relaxation time of the network (τ) should increase because of the larger number of elastically active chains.18 The relationship between τ during strain hardening and the degree of strain hardening in G′ and G″ are discussed in the context of a single Maxwell model in the Supporting Information,20 but, briefly, τ is expected to increase if G′max / G′Lin is larger than G″max/ G″Lin. This consequence is consistent with the decreasing of phase angle during strain hardening, as discussed above. Finally, the time dependent stress response should still be a single-harmonic sinusoid during strain hardening; i.e., the Lissajous-Bowditch curves are still elliptical.24
The mechanism of strain hardening (non-Gaussian stretching vs. increase in elastically active chains) can be distinguished by: (1) the change in τ during strain hardening; (2) the change in phase angle during strain hardening; and, (3) the shape of Lissajous-Bowditch curves. We consider the change in τ, shown in Figure 15 as a function of applied strain for ∼0.11 g/mL PVP with concentrations of 1b from 2–5 % (the 1% 1b sample is clouded by inertial effects and not considered here). The apparent relaxation time (τ) of the samples with 1b at different strains were obtained from the cross-over frequency (ωc) of G′ and G″ during oscillatory frequency sweep from 10 to 30 rad/s at three different applied strains (τ=1/ωc) (Figure S6-S9 in Supporting Information).18 In the linear regime, τ is constant, while in the strain hardening regime τ increases with strain. The increasing τ during strain hardening is consistent with the observed decrease in phase angle, supporting a mechanism of increasing number of elastically active chains.18
Figure 15.
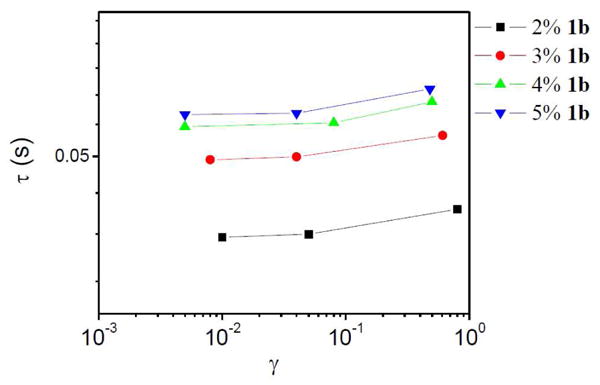
Apparent relaxation time (τ) of ∼0.11 g/mL 1b·PVP versus applied strain (γ) during oscillatory frequency sweep from 10 to 30 rad/s.
In Figure 16, Lissajous-Bowditch curves from the critical strain (γcrit) to maximum strain (γmax) during strain hardening of ∼0.11 g/mL PVP with 1% 1b are shown (scanning frequency is 1 rad/s). In Figure 16, we notice that, for γ > γcrit, the phase angle decreases with increasing strain. At and just beyond the onset of strain hardening (Figure 16a and Figure 16b), the Lissajous-Bowditch curves are elliptical. With further increases in strain (Figure 16c-e), the phase angle continues to decrease, but the Lissajous-Bowditch curves deviate increasingly from a clean ellipse. In comparison, Lissajous-Bowditch curves for a similar sample but with 5% 1b deviate substantially from ellipticity only at the maximum strain (Figure 17), and similar behavior is observed for the sample with 2% – 4% 1b (Figure S10-S12 in Supporting Information), as is the case for the 5% 1b sample at 30 rad/s (Figure S13 in Supporting Information).
Figure 16.
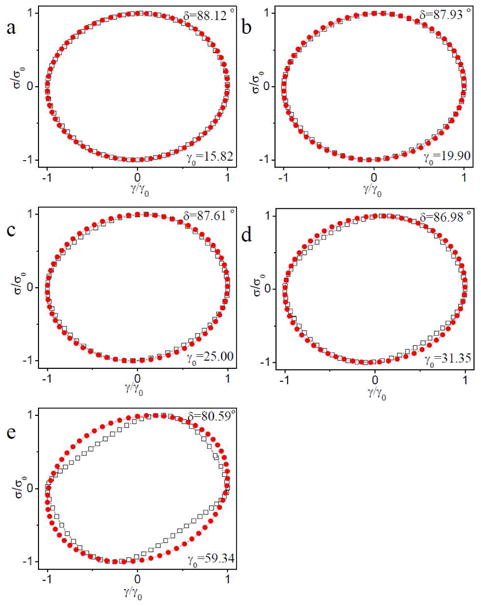
Normalized stress versus strain (Lissajous-Bowditch curves) for the raw data of ∼ 0.11 g/mL PVP with 1% 1b during strain sweep from the critical strain (γcrit) to maximum strain (γmax) associated with strain hardening. The phase angle (δ) at different strains (γ0) is shown. Unfilled square symbol represent the raw data. Filled cycle symbols represent fits to data assuming that time-dependent strain and stress are both single-harmonic sinusoids. The raw phase angle from the experiments is used in the fits. Scanning frequency is 1 rad/s.
Figure 17.
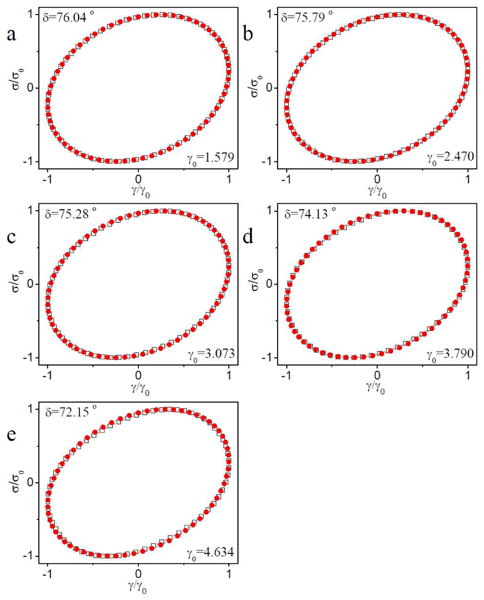
Normalized stress versus strain (Lissajous-Bowditch curves) for the raw data of ∼ 0.11 g/mL PVP with 5% 1b during strain sweep from the critical strain (γcrit) to maximum strain (γmax) associated with strain hardening. The phase angle (δ) at different strains (γ0) is shown. Unfilled square symbol represent the raw data. Filled cycle symbols represent fits to data assuming that time-dependent strain and stress are both single-harmonic sinusoids. The raw phase angle from the experiments is used in the fits. Scanning frequency is 1 rad/s.
From the above data, an increase in τ and a decrease in phase angle during strain hardening is observed, and we can infer that the primary mechanism underlying strain hardening is a strain-induced increase in the number of elastically active chains. At sufficiently large strains (i.e., just prior to network rupture), however, non-ellipticity in the Lissajous-Bowditch curves is often observed. The apparent non-ellipticity means that non-Gaussian stretching of polymer chains might also contribute to the strain hardening. Because non-ellipticity of Lissajous-Bowditch curves can also arise from other effects, including for example secondary flow or wall slip,24, 35, 36 the loss of ellipticity alone cannot be taken as conclusive evidence for non-Gaussian stretching of polymer chains. As polymer chains will be stretched when the Weissenberg number (Wi = γ0ωτ) is larger than 1,37 the value of the Weissenberg number at the maximum strain (γmax) during strain hardening is also used to evaluate the contribution of non-Gaussian stretching of polymer chains on strain hardening. The characterization of the apparent relaxation time (τ) of ∼0.11 g/mL PVP with 1% 1b is shown in Figure S14 in Supporting Information. The apparent relaxation time (τ) of ∼0.11 g/mL PVP with 1% 1b in the linear regime is determined to be 1.1×10−2 s. From the data in Figure 15, we can see that the apparent relaxation times (τ) of samples in the strain hardening regime are on the same order as that in the linear regime. We therefore assume that the value of τ of ∼0.11 g/mL PVP with 1% 1b in the linear regime is close to the value of apparent relaxation times (τ) of ∼0.11 g/mL PVP with 1% 1b in the strain hardening regime, and use this value to calculate the Weissenberg number (Wi = γ0ωτ). For the strain sweep of ∼0.11 g/mL PVP with 1% 1b at 1 rad/s, Wi is about 0.6 at the maximum strain (γmax) during strain hardening (Figure 16e). This number is somewhat ambiguous, given the uncertainty in τ and the heterogeneous relaxation dynamics of these systems,18 but because Wi < 1, non-Gaussian stretching of polymer chains is not obvious here,37 and it is possible that the non-ellipticity of the Lissajous-Bowditch curves is caused by other factors.24, 35, 36 A similar picture emerges from an examination of the strain sweep behavior of ∼0.11 g/mL PVP with 5% 1b. The data in Figure 4 reveal that Wi at γmax ranges from 0.2 to 0.5 when De < 1 (scanning frequency ranges from 0.1 to 10 rad/s), while Wi at γmax ranges from 0.9 to 1.3 when De > 1 (scanning frequency ranges from 20 to 30 rad/s). As Wi at γmax during strain hardening is close to 1, and larger than 1 in some cases, contributions from non-Gaussian stretching of polymer chains certainly cannot be excluded,18, 37 but quantifying the impact of any such effects is difficult.
For samples with 1% 1b in the semidilute entangled PVP solution ([PVP] from 0.164 g/mL to 0.272 g/mL), τ is found to increase with strain during strain hardening (Figure S15 in Supporting Information), consistent with the observed decease in phase angle, and the Lissajous-Bowditch curves of raw data are not elliptical only near γmax (Figures S16-S19 in Supporting Information). The same is true for samples with higher concentration of cross-linkers; for 0.259 g/mL PVP with 5% 1b, τ increases (Figures S20-S23 in Supporting Information) and the phase angle decreases during strain hardening. We infer that the primary mechanism of strain hardening in semidilute entangled solutions is the same increasing number of elastically active chain as in semidilute unentangled solutions.18,23
Absence of Strain Hardening in Semidilute Entangled Networks with Cross-linker 1a
The purely strain softening behavior of G′ and G″ for networks formed with cross-linker 1a in the semidilute entangled regime, as opposed to the strain hardening observed for analogous samples formed with 1b (Figure 9 and 10), implicates the contribution of a process whose dynamics are not strictly proportional to the lifetime of the cross-linkers. This behavior is reminiscent of the steady shear behavior reported previously for these networks, which similarly diverge.23 The divergent behavior under steady shear was interpreted on the basis of a competition between two time scales—the average time that a cross-linker remains open (τ1) and the local relaxation time of a polymer chain segment (τsegment).23 For PVP networks with 1a in DMSO at 25 °C, τ1 is smaller than τsegment,23 and entangled polymer strands do not have enough time to disentangle and then orient prior to reassociation. As a result, there is not a net conversion of intrachain cross-linkers into elastically active interchain cross-linkers, and no shear thickening is observed.23 The correspondence between shear thickening/thinning and strain hardening/softening in these networks as a function of the combination of cross-linker kinetics and PVP concentration, coupled to the predominance of shear- and strain-induced generation of elastically active subchains as the underlying mechanism for the observed shear thickening/strain hardening, strongly suggests that the same dynamic processes are operative in the divergent strain hardening/softening behavior reported here. We therefore infer that the absence of strain hardening in 1a·PVP networks in the semidilute entangled regime is due to the fact that the average time that cross-linker 1a remains open is too short to permit the local relaxation of polymer chain segments that is necessary for a net conversion of elastically inactive to elastically active cross-linkers.23
Absence of Strain Hardening in the Storage Moduli of 1b·PVP Networks in the Semidilute Entangled Regime
During steady shear, we previously observed shear thickening for 1b·PVP in DMSO at 25 °C (τ1 > τsegment),23 and in most cases we observe analogous strain hardening in G′ and G″ here. The strain sweep data for 0.259 g/mL PVP with 5% 1b at 0.3 rad/s to 1 rad/s, however, reveals no strain hardening in G′, although strain hardening is observed in G″ and |G*| (Figure 12). We interpret the absence of strain hardening in G′ on the basis of equations 4 and 5, which establish that, even within the same molecular mechanism, G′ can fail to strain harden as a result of an increase in phase angle (and associated decrease in cos(δ)) that is sufficient to counteract the increase due to complex modulus. Alternatively (or in addition), the strain hardening in G″ and |G*| could be attributed to non-Gaussian stretching. In Figures S24-S25 (Supporting Information), however, there is at most only small deviation from ellipticity in the relevant Lissajous-Bowditch curves for 0.259 g/mL PVP with 5% 1b at 0.3 rad/s to 1 rad/s, and Wi is only about 0.3 before the break of network. As the non-Gaussian stretching of polymer chains is not apparent here,37 we cannot confirm that non-Gaussian stretching is the mechanism of strain hardening in G″ and |G*|. The mechanism behind no strain hardening in G′ and strain hardening in G″ and |G*| for 0.259 g/mL PVP with 5% 1b at 0.3 rad/s to 1 rad/s is still an open question.
Conclusions
Strain hardening is observed under large amplitude oscillatory shear (LAOS) of a family of metallo-supramolecular polymer networks. Based on accompanying variations of phase angle and relaxation time, the strain hardening is attributed primarily to an increase in the number of elastically active chains, as opposed to non-Gaussian stretching of polymer chains. Evidence for non-Gaussian stretching becomes apparent only at strains that are near that of network fracture, which must involve high degrees of polymer stretching in order to generate the forces necessary for rupture. These results present a unified picture of LAOS and steady shear behavior, as shear thickening in these networks has previously been associated with the same mechanism.
In the semidilute entangled regime of PVP solution, samples with rapid cross-linker dissociation (kd = 1450 s−1) exhibit only strain softening (no strain hardening) for both the storage and loss moduli, in contrast to networks of identical equilibrium structure but slower cross-linkers (kd = 17 s−1). The strain softening of samples with faster cross-linkers is ascribed to the same mechanism previously reported for the pure shear thinning of networks with faster cross-linkers in the semidilute entangled regime: the average time that a cross-linker remains open (τ1) is too short to permit the local relaxation of polymer chain segments (τsegment) that is necessary for a net conversion of elastically inactive to elastically active cross-linkers. Looking ahead, the mechanistic understanding of the nonlinear viscoelastic response of these networks provides a foundation for further work in which the LAOS behavior might be controlled through the rational molecular-scale design of supramolecular polymer networks. For example, one can envision optimizing the composition of these and related networks so that they strain harden to the maximum extent achievable for a given strain and strain rate.
Supplementary Material
Acknowledgments
S.L.C. thanks the financial support by NSF (CHE-0646670) and NIH (EB-001037).
Footnotes
Supporting Information Available: Lissajous-Bowditch curves of samples during strain hardening or strain softening; relaxation time (τ) of samples; relationship between strain hardening and the relaxation time of the network; variation in relaxation time during strain hardening. This material is available free of charge via the Internet at http://pubs.acs.org.
References and Notes
- 1.Berret JF, Calvet D, Collet A, Viguier M. Curr Opin Colloid Interface Sci. 2003;8:296–306. [Google Scholar]
- 2.Pellens L, Corrales RG, Mewis J. J Rheol. 2004;48:379–393. [Google Scholar]
- 3.Marrucci G, Bhargava S, Cooper SL. Macromolecules. 1993;26:6483–6488. [Google Scholar]
- 4.Indei T. J Non-Newtonian Fluid Mech. 2007;141:18–42. [Google Scholar]
- 5.Wang SQ. Macromolecules. 1992;25:7003–7010. [Google Scholar]
- 6.Witten TA, Jr, Cohen MH. Macromolecules. 1985;18:1915–1918. [Google Scholar]
- 7.Hyun K, Kim SH, Ahn KH, Lee SJ. J Non-Newtonian Fluid Mech. 2002;107:51–65. [Google Scholar]
- 8.Klucker R, Candau F, Schosseler F. Macromolecules. 1995;28:6416–6422. [Google Scholar]
- 9.Ma SX, Cooper SL. Macromolecules. 2001;34:3294–3301. [Google Scholar]
- 10.Tripathi A, Tam KC, McKinley GH. Macromolecules. 2006;39:1981–1999. [Google Scholar]
- 11.Regalado EJ, Selb J, Candau F. Macromolecules. 1999;32:8580–8588. [Google Scholar]
- 12.Tirtaatmadja V, Tam KC, Jenkins RD. Macromolecules. 1997;30:1426–1433. [Google Scholar]
- 13.English RJ, Gulati HS, Jenkins RD, Khan SA. J Rheol. 1997;41:427–444. [Google Scholar]
- 14.Mewis J, Kaffashi B, Vermant J, Butera RJ. Macromolecules. 2001;34:1376–1383. [Google Scholar]
- 15.Séréro Y, Jacobsen V, Berret JF, May R. Macromolecules. 2000;33:1841–1847. [Google Scholar]
- 16.Tan H, Tam KC, Jenkins RD. Langmuir. 2000;16:5600–5606. [Google Scholar]
- 17.Albrecht M, van Koten G. Angew Chem Int Ed. 2001;40:3750–3781. doi: 10.1002/1521-3773(20011015)40:20<3750::AID-ANIE3750>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- 18.Xu D, Hawk J, Loveless DM, Jeon SL, Craig SL. Macromolecules. 2010;43:3556–3565. doi: 10.1021/ma100093b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Loveless DM, Jeon SL, Craig SL. Macromolecules. 2005;38:10171–10177. [Google Scholar]
- 20.Yount WC, Loveless DM, Craig SL. J Am Chem Soc. 2005;127:14488–14496. doi: 10.1021/ja054298a. [DOI] [PubMed] [Google Scholar]
- 21.Xu D, Craig SL. J Phys Chem Lett. 2010;1:1683–1686. doi: 10.1021/jz1004818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jeon SL, Loveless DM, Yount WC, Craig SL. Inorg Chem. 2006;45:11060–11068. doi: 10.1021/ic061188b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Xu D, Liu CY, Craig SL. Macromolecules. 2011;44:2343–2353. doi: 10.1021/ma2000916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ewoldt RH, Hosoi AE, McKinley GH. J Rheol. 2008;52:1427–1458. [Google Scholar]
- 25.Ewoldt RH, McKinley GH. Rheol Acta. 2010;49:213–219. [Google Scholar]
- 26.Hoy RS. J Polym Sci Part B: Polym Phys. 2011;49:979–984. [Google Scholar]
- 27.Xu D, Craig SL. Macromolecules. 2011;44:5465–5472. doi: 10.1021/ma200096s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chen D, Handa H, Wan L, Mao G. Macromol Rapid Commun. 2007;28:1619–1623. [Google Scholar]
- 29.Loveless DM, Jeon SL, Craig SL. J Mater Chem. 2007;17:56–61. [Google Scholar]
- 30.Franck AJ. Understanding Instrument Inertia Corrections in Oscillation. TA Instrument; 2005. [Google Scholar]
- 31.Ferry JD. Viscoelastic Properties of Polymers. John Wiley& Sons, Inc; 1980. [Google Scholar]
- 32.Orakdogen N, Erman B, Okay O. Macromolecules. 2010;43:1530–1538. [Google Scholar]
- 33.Erk KA, Henderson KJ, Shull KR. Biomacromolecules. 2010;11:1358–1363. doi: 10.1021/bm100136y. [DOI] [PubMed] [Google Scholar]
- 34.Tung SH, Raghavan SR. Langmuir. 2008;24:8405–8408. doi: 10.1021/la704045t. [DOI] [PubMed] [Google Scholar]
- 35.Atalik K, Keunings R. J Non-Newtonian Fluid Mech. 2004;122:107–116. [Google Scholar]
- 36.Graham MD. J Rheol. 1995;39:697–712. [Google Scholar]
- 37.Larson RG. The Structure and Rheology of Complex Fluids. Oxford University Press; 1999. [Google Scholar]
- 38.Yosick JA, Giacomin AJ. J Non-Newtonian Fluid Mech. 1996;66:193–212. [Google Scholar]
- 39.Tapadia P, Ravindranath S, Wang SQ. Phys Rev Lett. 2006;96:196001. doi: 10.1103/PhysRevLett.96.196001. [DOI] [PubMed] [Google Scholar]
- 40.Li X, Wang SQ, Wang XR. J Rheol. 2009;53:1255–1274. [Google Scholar]
- 41.Bossard F, Sfika V, Tsitsilianis C. Macromolecules. 2004;37:3899–3904. [Google Scholar]
- 42.Ma L, Yamada S, Wirtz D, Coulombe PA. Nature Cell Biol. 2001;3:503–506. doi: 10.1038/35074576. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


