Abstract
The distribution of atherosclerotic lesions within the rabbit vasculature, particularly within the descending thoracic aorta, has been mapped in numerous studies. The patchy nature of such lesions has been attributed to local variation in the pattern of blood flow. However, there have been few attempts to model and characterize the flow. In this study, a high-order continuous Galerkin finite-element method was used to simulate blood flow within a realistic representation of the rabbit aortic arch and descending thoracic aorta. The geometry, which was obtained from computed tomography of a resin corrosion cast, included all vessels originating from the aortic arch (followed to at least their second generation) and five pairs of intercostal arteries originating from the proximal descending thoracic aorta. The simulations showed that small geometrical undulations associated with the ductus arteriosus scar cause significant deviations in wall shear stress (WSS). This finding highlights the importance of geometrical accuracy when analysing WSS or related metrics. It was also observed that two Dean-type vortices form in the aortic arch and propagate down the descending thoracic aorta (along with an associated skewed axial velocity profile). This leads to the occurrence of axial streaks in WSS, similar in nature to the axial streaks of lipid deposition found in the descending aorta of cholesterol-fed rabbits. Finally, it was observed that WSS patterns within the vicinity of intercostal branch ostia depend not only on local flow features caused by the branches themselves, but also on larger-scale flow features within the descending aorta, which vary between branches at different locations. This result implies that disease and WSS patterns in the vicinity of intercostal ostia are best compared on a branch-by-branch basis.
Keywords: atherosclerosis, blood flow, wall shear stress, continuous Galerkin
1. Introduction
The prevalence of atherosclerosis varies within the mammalian vasculature, particularly in regions of arterial branching and curvature. Since these regions are associated with complex blood flow patterns, it has been postulated that blood flow may play an important role in regulating atherogenesis. Fry [1] inferred from studies of hypercholesterolaemic animals that lesions develop in regions of high wall shear stress (WSS), hypothesizing that high WSS damaged the arterial endothelium, and hence increased lipoprotein influx into the intima. However, Caro et al. [2,3], who studied human post-mortem material, suggested that lesions develop in regions of low wall shear rate (WSR), owing to a decreased efflux of material made or modified within the arterial wall.
The low WSR theory of Caro et al. is widely accepted today (although the original mechanism is contradicted by evidence that lesion prevalence depends on plasma low-density lipoprotein (LDL) concentrations). However, the existence of a direct correlation between disease patterns and WSR/WSS magnitude may be too simplistic. More complex relationships have been suggested, including the proposal that a combination of low and temporally oscillating WSR/WSS predisposes to disease [4–6]. A better understanding of arterial haemodynamics is required before definitive correlations between flow and disease can be established. In recent years, understanding has been enhanced by numerous computational studies [7–12]. Such studies circumvent technical limitations associated with measuring flow in vivo and facilitate the analysis of derived metrics such as WSR/WSS. However, despite numerous experimental studies of disease location in the rabbit vasculature, there have been few computational studies of blood flow in this species and the corresponding flow therefore remains largely uncharacterized.
In the present study, a high-order continuous Galerkin finite-element method was used to model blood flow within a realistic representation of the rabbit aortic arch and descending thoracic aorta. The geometry was obtained from high-resolution computed tomography (CT) of a vascular cast. It included all vessels originating from the aortic arch (followed to at least their second generation) and five pairs of intercostal arteries originating from the proximal descending thoracic aorta. Steady-state flow of a Newtonian fluid was modelled within the geometry, which was assumed to have rigid and stationary walls. These assumptions, which considerably simplified calculations, clearly represent a significant approximation of in vivo conditions. However, they permitted understanding of the underlying steady-state fluid dynamics, and did not prevent important new information being gained owing to the unprecedented detail and extent of the geometrical definition.
2. Method: obtaining a geometrical definition of the rabbit aorta
2.1. Overview
The following section details the process of obtaining a realistic geometrical definition and volume mesh of the rabbit aortic arch and descending thoracic aorta. The process consists of four stages: casting the rabbit vasculature, CT imaging of the resulting cast, computational reconstruction of the CT data and computational generation of a curved element volume mesh from the surface definition. Similar approaches have been employed in various previous studies [7,11]. However, to the authors' knowledge, no previous studies have obtained geometrical definitions with the combined detail and extent of the one presented here.
2.2. Casting procedure
A male New Zealand white rabbit aged 18 months and weighing 3.25 kg received heparin (2000 USP units, IV) and was then euthanized with an overdose of sodium pentobarbitone (Euthatal, 160 mg kg−1, IV). A cannula was inserted and secured into the cardiac left ventricle. It was used to flush the arterial system with saline and then to infuse Batsons No. 17 casting material (Polysciences, Inc.) at a pressure of 95–100 mm Hg. This pressure, which is physiologically realistic for the rabbit [13], was maintained until the casting material hardened and could no longer be injected (at which point approx. 70 ml had been used). During the initial exothermic stage of the curing process, cold water was trickled through the chest and abdominal cavities to dissipate heat. The casting material was then left overnight to cure fully.
The following day, the rabbit carcass was submerged in a potassium hydroxide solution (approx. 30% w/v). After two weeks, the solution was renewed and left for a further 24 h. The second potassium hydroxide solution was then replaced with a detergent solution and left for another 24 h. Finally, the cast was removed from the detergent and gently washed with warm water. Images of the cast are shown in figure 1. As an indication of scale, the aortic root has a diameter of approximately 6 mm.
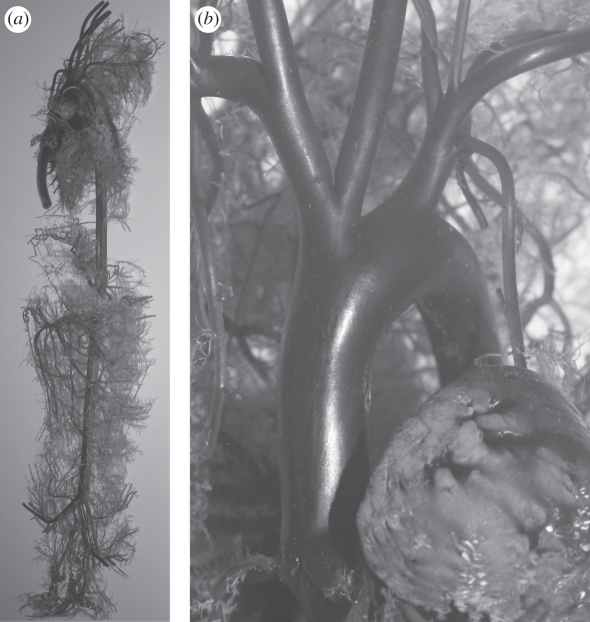
Figure 1.
(a) A ventral–dorsal view of the entire resin cast prepared for the CT scanner. Vessels of the front and rear legs, as well as vessels of the head and the kidneys, have been removed. (b) An enlarged image of the aortic arch. As an indication of scale, the aortic root has a diameter of approximately 6 mm.
2.3. Imaging procedure
The cast was imaged using a Metris X-Tek HMX-ST Micro-CT Scanner at the Natural History Museum, London, UK. A 2000 × 2000 × 2000 voxel cube of DICOM data (approx. 9.2 GB) was obtained, with a voxel size of 55.2 µm. Over 100 voxels spanned the 6 mm diameter of the aortic root.
2.4. Obtaining a surface definition
An intensity isosurface was extracted from the DICOM data using Amira v. 5.2.0 (Visage Imaging, Inc.) The surface was cropped using the Vascular Modelling Tool Kit (VMTK) to remove unwanted arteries. Flow extensions terminating with a circular cross section were then extruded from each outflow vessel using VMTK, to facilitate the application of boundary conditions. Finally, the surface was smoothed using VMTK. The degree of smoothing was highly limited in order to avoid loss of small-scale geometrical features. Images of the final surface definition, including flow extensions, are shown in figure 2. A VTP file of the final surface definition is available online as electronic supplementary material.
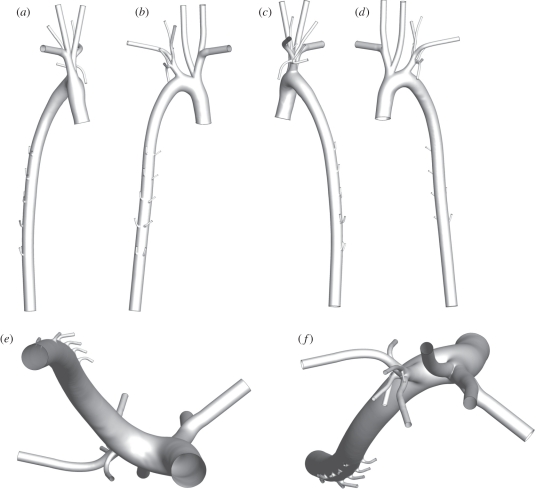
Figure 2.
The reconstructed aortic geometry (including flow extensions) viewed (a) right–left, (b) dorsal–ventral, (c) left–right, (d) ventral–dorsal, (e) posterior–anterior, and (e) anterior–posterior. Note that branches from the aortic arch are reconstructed to at least their second generation, and five pairs of intercostal arteries are included. In terms of combined detail and extent, the geometry represents a significant advance cf. geometries used in previous studies. A VTP file of the surface definition is available online as electronic supplementary material.
2.5. Obtaining a volume mesh
Use of a high-order continuous Galerkin finite-element method requires that the computational domain is subdivided into a mesh of elements, within which the solution is represented by a high-order polynomial expansion. Since each element holds multiple degrees of freedom, the volume mesh can be coarse compared with a typical low-order finite element or finite volume mesh. In this study, a volume mesh of 79 847 tetrahedral elements and 25 498 prismatic elements was constructed using Gambit v. 2.4.6 and Tgrid v. 4.0.24 (ANSYS, Inc.). The size of the elements was based on the local curvature of the surface definition. The prismatic elements were placed adjacent to the luminal surface of the arterial wall in order to improve resolution of any momentum boundary layers that formed. External faces of prismatic boundary elements were curved using SPHERIGON patches [14], following the approach of Grinberg et al. [15], so that they accurately approximated the surface definition despite their large size. Sections of the resulting volume mesh are shown in figure 3.
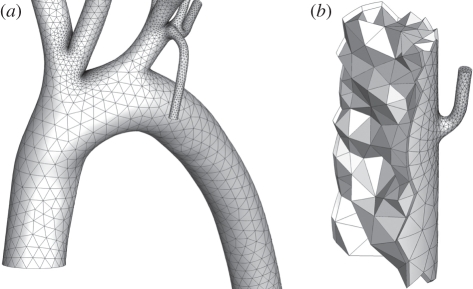
Figure 3.
Images of the high-order curved element volume mesh. (a) The aortic arch. Note that smaller elements are localized in regions of high curvature. (b) A cut-away of a mesh section in the descending thoracic aorta near an intercostal branch. One can see the triangular faces of the internal high-order tetrahedral elements, as well as the quadrangular faces of the prismatic elements placed adjacent to the arterial wall surface.
3. Method: simulating blood flow within the rabbit aorta
3.1. Governing equations
In the present study, blood was treated as an incompressible Newtonian fluid. Also, time-dependent dynamics were ignored, and only steady-state simulation were performed. Specifically, blood flow was modelled using the incompressible steady-state Navier–Stokes equations for a Newtonian fluid, which can be written as
| 3.1 |
and
| 3.2 |
where μ is the viscosity of rabbit blood, ρ is the density of rabbit blood, u is the three-dimensional velocity vector field within the rabbit aorta and p is the pressure field within the rabbit aorta. Such an approach has been adopted in numerous previous studies [10,12].
There are various reasons why steady-state simulations were performed, as opposed to fully time-dependent studies. Primarily, the results of steady-state simulations can be analysed with relative ease; giving insight that will facilitate interpretation of future (more complex) unsteady results, and focus the remit of future (more costly) unsteady studies. Additionally, it was felt that insufficient experimental data existed to reliably parameterize time-dependent conditions at each of the 22 open boundaries (1 inlet and 21 outlets). In reality, however, blood flow is pulsatile. Consequently, there are disadvantages associated with steady-state simulations. In particular, they preclude calculation and analysis of potentially important metrics such as oscillatory shear index (OSI) [4,16]. Also, they cannot capture truly unsteady flow phenomena (but only quasi-steady dynamics). The potential effect of pulsatility on the main findings of the present study will be discussed towards the end of the paper in §5.
3.2. Boundary conditions
A spatially uniform inflow velocity profile was prescribed at the aortic root. Applying such a profile is an approximation, since flow from the left ventricle is likely to be skewed and possess an in-plane component. Parabolic (fully developed) outflow profiles were prescribed perpendicular to all other boundaries, apart from the main outflow of the descending thoracic aorta, where a zero velocity gradient condition was prescribed perpendicular to the outflow plane. At the arterial wall, which was assumed to be rigid and stationary, a no-slip boundary condition was applied (i.e. all components of the velocity were set to zero).
3.3. Parameter values
3.3.1. Reynolds numbers
For any viscous flow, one can define a Reynolds number (Re), which quantifies the ratio of inertial to viscous forces acting within the fluid. In this study, Re is defined as
| 3.3 |
where D0 is the hydraulic diameter of the aortic root inflow plane (the diameter of a circle with the same area as the aortic root inflow plane), and V0 is the spatially constant magnitude of the inflow velocity at the aortic root.
The average flow rate into the rabbit ascending thoracic aorta has been measured by Avolio et al. [13] to be 3.3 ml s−1. These measurements were made using an electromagnetic probe with an internal diameter of 5 mm that caused ‘minimal constriction’ of the ascending aorta. Assuming that the arterial wall thickness was 7 per cent of the vessel diameter (this is constant across many species and vessels [17]), then the inflow area was approximately 15 mm2 and the measured inflow rate corresponds to an inflow velocity magnitude of approximately 0.22 m s−1. The peak inflow velocity magnitude measured by Avolio et al. [13] was 0.927 m s−1. In the present study, three values of inflow velocity magnitude V0 were considered. Specifically, V0 = 0.0332 m s−1 (an arbitrary low value), V0 = 0.199 m s−1 (based on the mean flow rate measurements of Avolio et al. [13]) and V0 = 0.862 m s−1 (based on the peak flow rate measurements of Avolio et al. [13]). Assuming that ρ = 1.044 × 103 kg m−3 [18], μ = 4.043 × 10−3 kg m−1 s−1 [19] and D0 = 5.838 × 10−3 m (measured from the geometry), these values of V0 lead to round values Re = 50, Re = 300 and Re = 1300, respectively.
3.3.2. Flow splits
Flow splits into the innominate artery and the left subclavian artery were based on the measurements of Barakat et al. [20]. Specifically, 14.7 per cent of the inflow at the aortic root went into the innominate artery and 7.1 per cent into the left subclavian artery. Flow splits for all subsequent branches of these arteries were determined using Murray's law [21], which states that the flow in a vessel is proportional to the diameter of the vessel cubed. It was assumed that on average, each intercostal branch received 0.2 per cent of the flow entering the descending thoracic aorta. This value sits within the range considered by Kazakidi et al. [22] but is otherwise arbitrary. The 10 intercostal branches, therefore, received between them a total of 2 per cent of the flow entering the descending thoracic aorta (which is equivalent to 1.56% of the flow entering at the aortic root). The exact split of this aggregate flow between the individual intercostal branches was once again determined using Murray's law.
3.4. Numerical method
The incompressible steady-state Navier–Stokes equations were solved within the arterial geometry using a high-order continuous Galerkin method. This approach combines the superior accuracy of spectral methods with the geometrical flexibility of low-order finite element or finite volume schemes. For further details of the method, see papers by Sherwin & Ainsworth [23] and Sherwin & Karniadakis [24], the textbook by Karniadakis & Sherwin [25] and references therein.
Convergence of the solution was verified by performing simulations at Re = 300 using third-, fifth- and seventh-order polynomial expansions to represent the solution within each element. Since the computational domain contains 79 847 tetrahedral elements and 25 498 prismatic elements, use of these expansions results in a total of approximately 3.07 × 106, 1.37 × 107 and 3.71 × 107 degrees of freedom, respectively (accounting for vertex, edge and face multiplicity, and counting each of the velocity components and the pressure as separate degrees of freedom). When switching from third-order to fifth-order solution polynomials, the total wall force changed by 0.019 per cent, and when switching from fifth-order to seventh-order solution polynomials, the total wall force changed by 0.0040 per cent. The solution was, therefore, deemed to have converged when using fifth-order polynomials within each element, and thus all presented results were obtained using this order. For comparison with a more standard low-order calculation, this corresponds (in terms of degrees of freedom) to using a mesh of approximately 2.05 × 107 linear tetrahedral elements. However, such as scheme will only be second-order accurate in space, whereas the scheme employed here is nominally sixth-order accurate.
4. Results and analysis
4.1. Flow in the aortic arch
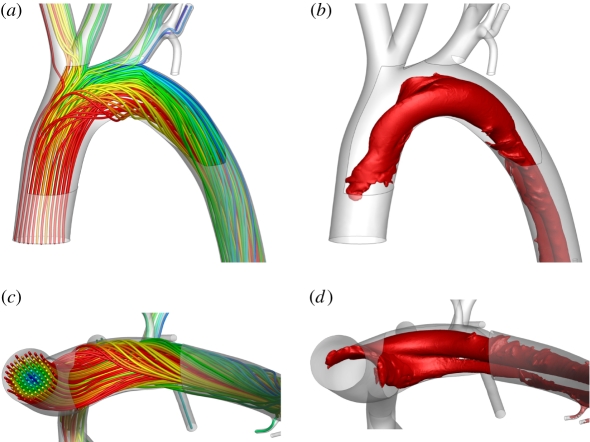
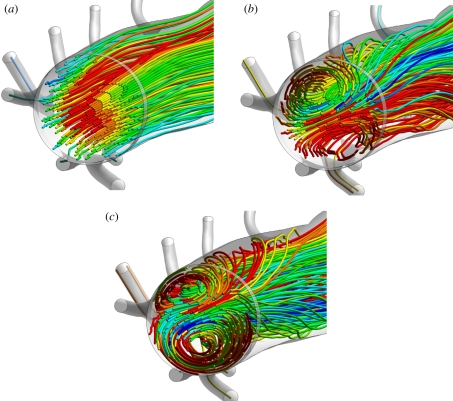
Figure 4a,c shows streamlines in the aortic arch when Re = 300. Significant secondary flow was observed. The streamlines are qualitatively comparable with those obtained by Barakat et al. [26] using microcinematographic methods in excised rabbit aortas. Figure 4b,d shows coherent vortical structures in the aortic arch when Re = 300. The structures were defined by isosurfaces of the widely used metric λ2 [27], which accurately identifies vortices at low Reynolds numbers (unlike minimum-pressure criteria). Two Dean-type vortices [28] of unequal magnitude formed. This is consistent with literature on flow in curved pipes [29,30], and with studies of flow in the aortic arch of mice [11] and human subjects [12]. However, to the knowledge of the authors, formation of such vortices has not previously been demonstrated numerically within the aortic arch of rabbits. Results for Re = 1300 (not shown) were qualitatively similar. However, at Re = 50 (results not shown), there was minimal secondary flow within the arch and no significant Dean vortices developed. In all cases, a Dean number De defined as
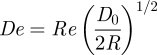 |
4.1 |
can be associated with the vortical structures in the aortic arch, where R is the radius of curvature of the aortic arch. Measurements made using VMTK suggest R ≈ 2D0, and hence De ≈ 0.5Re. Therefore, the Reynolds numbers of Re = 50, Re = 300 and Re = 1300 correspond to Dean numbers of De = 25, De = 150 and De = 650, respectively.
Figure 4.
Streamlines of blood flow in the aortic arch viewed (a) ventral–dorsal and (c) posterior–anterior, along with λ2 isosurfaces defining vortical structures, also viewed (b) ventral–dorsal and (d) posterior–anterior. In all cases, Re = 300. The widely used metric λ2 accurately identifies vortices at low Reynolds numbers (unlike minimum-pressure criteria). For further details of the metric λ2 see the paper of Jeong & Hussain [27].
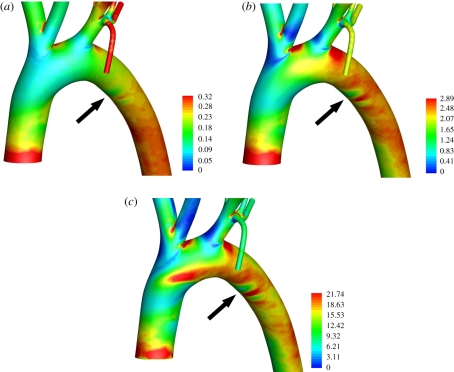
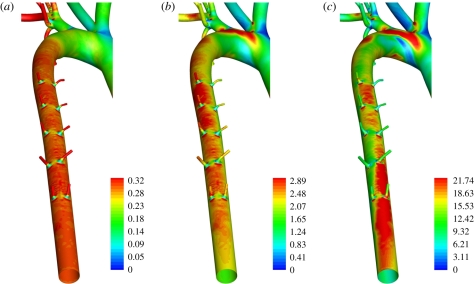
Figures 5 and 6 show maps of WSS within the aortic arch for all three values of Re considered. The patterns are complex and become increasingly heterogeneous as Re is increased. Two important observations can be made. The first is that, owing to the complexity of the patterns, it would be incorrect to characterize the inner curvature of the arch as a ‘low shear region’ and the outer curvature as a ‘high shear region’ (as is common when interpreting experimental data). The second is that small surface undulations associated with the ductus arteriosus scar, while having a negligible effect on flow, induce significant deviations in WSS, comparable to those caused by vascular scale flow features. The deviations are marked with arrows in figures 5 and 6. This observation highlights the critical importance of geometrical accuracy when calculating and analysing WSS or related metrics. Interestingly, Duff [31] suggests that the ductus arteriosus scar is a site of atherosclerotic disease in humans.
Figure 5.
Colour maps of WSS (Pa) in the aortic arch when (a) Re = 50, (b) Re = 300, and (c) Re = 1300. All views are ventral–dorsal. The arrows indicate the location of the ductus arteriosus scar.
Figure 6.
Colour maps of WSS (Pa) in the aortic arch when (a) Re = 50, (b) Re = 300, and (c) Re = 1300. All views are posterior–anterior. The arrows indicate the location of the ductus arteriosus scar.
4.2. Flow in the proximal descending thoracic aorta
Figure 7 shows plots of axial velocity and vorticity magnitude within the descending thoracic aorta when Re = 300. The axial velocity profile is skewed to one side, and the two Dean-type vortices emerging from the aortic arch continue to propagate down the descending thoracic aorta. Figure 8 shows streamlines in the descending thoracic aorta for all three values of Re considered. The results were obtained using the particle-tracking approach of Copella et al. [32], which was devised specifically for post-processing the results of unstructured high-order finite-element simulations. When Re = 50, there is almost no secondary flow within the descending thoracic aorta, since significant Dean-type vortices do not form in the aortic arch. However, when Re = 300 and Re = 1300, vortices are clearly present. Also, it is apparent from figure 8 that the streamline colours, which were uniformly distributed at the aortic root, become increasingly mixed as Re is increased. Hence, raising Re increases the degree of stirring to which the blood is subjected as it travels through the aortic arch and down the descending thoracic aorta.
Figure 7.
Colour maps of (a) blood velocity (m s−1) and (b) vorticity (s−1) perpendicular to four planes within the descending aorta. All planes are themselves perpendicular to the centre-line of the geometry. In both cases, Re = 300, and the views shown are ventral–dorsal.
Figure 8.
Streamlines of blood flow in the descending thoracic aorta viewed posterior–anterior when (a) Re = 50, (b) Re = 300, and (c) Re = 1300.
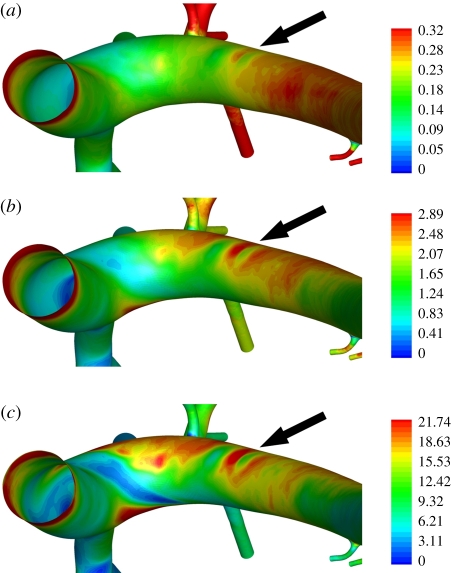
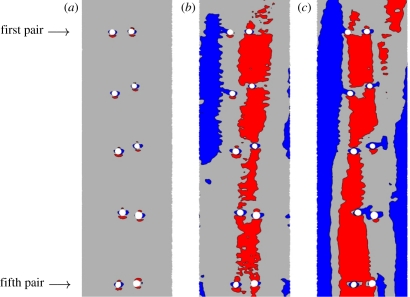
Figure 9 shows maps of WSS in the descending thoracic aorta for all three values of Re considered. When Re = 300 and Re = 1300, the WSS patterns exhibit streaks owing to the presence of a skewed axial velocity profile. Figure 10 shows en face flattened three-colour maps of WSS in the descending thoracic aorta. In all cases, the aorta was unwrapped via a ‘computational incision’ along the ventral aortic wall, and the colour maps are presented with the luminal surface facing upwards. The patterns of WSS in figure 10 can be compared with the patterns of lipid deposition observed in the descending aorta of cholesterol-fed rabbits (figure 11). While detailed quantitative comparisons between figures 10 and 11 are unwarranted at this stage (owing to the small sample sizes), it is clear that distinctive axial streaks of both WSS and lipid deposition are present, indicating that a relationship between WSS and disease may exist. Systematic comparison of several computational and experimental results is necessary to ascertain in more detail the nature of any such relationship.
Figure 9.
Colour maps of WSS (Pa) in the descending thoracic aorta, viewed dorsal–ventral, when (a) Re = 50, (b) Re = 300, and (c) Re = 1300.
Figure 10.
En face three-colour maps of WSS in electronically ‘excised and unwrapped’ sections of the descending thoracic aorta when (a) Re = 50, (b) Re = 300, and (c) Re = 1300. Blue shading denotes areas in which WSS is <75% of the average in each excised region, and red shading denotes areas in which WSS is >125% of the average in each excised region. Specifically, when Re = 50, blue denotes a WSS <0.218 Pa and red denotes a WSS >0.364 Pa, when Re = 300, blue denotes a WSS <1.53 Pa and red denotes a WSS >2.56 Pa, and when Re = 1300, blue denotes a WSS <9.40 Pa and red denotes a WSS >15.7 Pa. In all cases, the descending aorta was unwrapped via a ‘computational incision’ along the ventral aortic wall, and the colour maps are presented with the luminal surface facing upwards. The first and fifth intercostal branch pairs are marked as reference points. Flow is from top to bottom.
Figure 11.
En face views of sections from the descending aorta of mature cholesterol-fed New Zealand white rabbits stained with oil red O dye to identify fatty deposits (early stage atherosclerotic lesions). In all cases, the descending aorta was unwrapped via a incision along the ventral aortic wall, and the sections are shown with the endothelial surface facing upwards. Images (a–c) are each from a different rabbit. The upper segment in each image contains the first and second pairs of intercostal branches (although note that the first ‘pair’ in image (a) has only a single branch). The lower segment contains the fourth and fifth pairs of intercostal branches. The third pair of intercostal branches was excised from each dataset for a different study. The first and fifth intercostal branch pairs are marked as reference points. Flow is from top to bottom. Distinctive axial streaks of lipid deposition are present in the aorta of each rabbit. However, the specific form of the streaks varies between the three specimens. All data are from the study of Cremers et al. [37].
4.3. Flow into the intercostal arteries
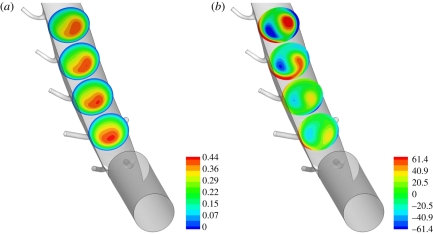
Figure 12 shows plots of WSS in the vicinity of various intercostal branch ostia for all three values of Re considered. The patterns reflect a superposition of both ‘local’ and ‘global’ contributions. The local contributions are caused by the deflection of aortic flow into the branches themselves. Such contributions were studied in detail by Kazakidi et al. [22] within idealized geometries, and are expected to be approximately independent of branch location. The global contributions result from bulk flow within the descending thoracic aorta. When Re = 300 and Re = 1300, these global contributions exhibit streaks of high and low WSS, as discussed above.
Figure 12.
Colour maps of WSS (Pa) when Re = 50 in the vicinity of the (a) second, (b) third and (c) fourth pair of intercostal branches, when Re = 300 in the vicinity of the (d) second, (e) third and (f) the fourth pair of intercostal branches, and when Re = 1300 in the vicinity of the (g) second, (h) third and (i) fourth pair of intercostal branches. Re is constant across each row, and branch location is constant down each column. The WSS legends on the right are for the colour maps in the corresponding row. Flow is from top to bottom.
When Re = 50, the WSS patterns within the vicinity of each branch are approximately independent of the branch location. This is because local contributions to the WSS are approximately independent of branch location and there is minimal spatial variation in the global contribution. However, when Re = 300 and Re = 1300, the WSS patterns within the vicinity of each branch become highly dependent on branch location, since the global contribution now varies spatially. Note that as well as varying between branch pairs, the global contributions to WSS also vary on the scale of the branch pairs themselves. This can be seen by comparing figure 12d and figure 12f which show the second and fourth pair of intercostal branches, respectively, when Re = 300. In figure 12d, one of the branches sits in a streak of high WSS, whereas the other sits on the edge of a low WSS streak. However, in figure 12f, a streak of high WSS runs across the entrance to both branches.
These findings are significant for three reasons. Firstly, they challenge the accuracy of results obtained using models that do not include the spatially varying, large-scale aortic flow field [22]. Secondly, they may explain why disease patterns in the vicinity of intercostal branch entrances vary between different branch locations. Thirdly, they call into question the process of combining disease patterns from intercostal branches in different locations to obtain average maps [33]. It may be more appropriate to analyse disease patterns, and compare them with predicted WSS patterns, on a branch-by-branch basis.
4.4. Summary
The main findings of the present study can be summarized as follows:
Small surface undulations associated with physiologically realistic features such as the ductus arteriosus scar (which was only resolved owing to the unprecedented detail of the geometrical definition) induce deviations in WSS comparable to those caused by vascular scale flow features. Hence, geometrical accuracy is critically important when calculating and analysing WSS or related metrics.
Dean-type vortices form in the aortic arch of rabbits. This phenomenon is consistent with studies of flow in curved pipes [29,30], and with studies of flow in the aortic arch of mice [11] and human subjects [12]. However, to the knowledge of the authors, formation of such vortices has not previously been demonstrated numerically within the aortic arch of rabbits. It is observed that these Dean vortices (along with an associated skewed axial velocity profile) propagate down the descending thoracic aorta, consequently leading to the formation of axial streaks in WSS, which are similar in nature to the streaks of lipid deposition observed in the descending aorta of cholesterol-fed rabbits.
WSS patterns within the vicinity of intercostal branch ostia depend not only on local flow features caused by the branches themselves but also on larger-scale flow features within the descending aorta, which vary between branches at different locations. This result (which was only obtained owing to the combined detail and extent of the geometrical definition) implies that patterns of WSS and disease near intercostal ostia are best compared on a branch-by-branch basis.
5. The effect of pulsatility
The importance of pulsatile dynamics within the rabbit aorta can be assessed by calculating a Womersley number α, defined as
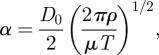 |
5.1 |
where T is a period associated with the rabbit cardiac cycle. The magnitude of α represents the ratio of temporally varying inertial forces to viscous forces within the flow. If α < 1, it can be assumed that the flow is quasi-steady i.e. steady-state results will faithfully represent flow patterns at various points in the cardiac cycle. However, if α > 1, the flow may not be entirely quasi-steady. Barakat et al. [20] suggest that the rabbit heart rate is typically 250–300 beats per minute (making reference to the studies of Borkowski et al. [34], Wyatt et al. [35], and also the textbook of Weisbroth et al. [36]). Also, Avolio et al. [13] measured heart rates of 210 beats per minute in anaesthetized rabbits, and 288 beats per minute in unanaesthetized rabbits. Assuming a heart rate of 275 beats per minute (with all other parameter values as detailed above), a Womersley number of α ≈ 8 is obtained. Consequently, flow in the rabbit aorta is unlikely to be entirely quasi-steady.
Having established α ≈ 8, it is pertinent to consider how pulsatility (which was ignored in the present study) will affect the main findings detailed in §4.4. Finding (1) is a statement about the sensitivity of WSS to geometry, and can reasonably be considered independent of whether WSS varies in time (even if blood flow is not entirely quasi-steady). Consequently, pulsatility is unlikely to affect finding (1). The results of Pitt [30] can be used to estimate how pulsatility will likely affect finding (2). Pitt studied steady state and pulsatile flow in a double bend configuration at a Reynolds number of 250. In his steady-state study, Pitt observed the formation of Dean vortices, which evolved in a quasi-steady fashion when the flow pulsated with a Womersley number of four. However, when the flow pulsated with a Womersley number of eight, the vortices, while not entirely destroyed, were no longer quasi-steady. These results suggest that pulsatility may modify the Dean vortices described in finding (2), but it is unlikely to preclude their formation altogether. Additionally, in the double bend configuration described above, Pitt found that the steady-state WSS pattern was similar to the time-averaged WSS patterns for the pulsatile cases. This suggests that the streaks of WSS described in finding (2) will also occur (in a time-averaged sense at least) if the flow is pulsatile. Finally, it is reasonable to suppose that local and global WSS patterns will superimpose in the vicinity of intercostal ostia, irrespective of whether or not the flow is pulsatile. Therefore, since pulsatility is unlikely to homogenize WSS in the descending thoracic aorta, it can be concluded that pulsatility is unlikely to affect finding (3).
The analysis presented above suggests that the findings of the present study will not be significantly affected by pulsatility. However, future time-dependent studies are required to confirm this is the case. In addition, such time-dependent studies would allow characterization of the potentially non-quasi-steady Dean vortex dynamics in the descending aorta, as well as the distribution of potentially important time-dependent flow metrics such as OSI [4,16].
6. Conclusions
A high-order continuous Galerkin finite-element method was used to simulate blood flow within a realistic representation of the rabbit aortic arch and descending thoracic aorta. Steady-state flow of a Newtonian fluid was modelled within the geometry, which was assumed to have rigid and stationary walls. These assumptions clearly represent a significant simplification of in vivo conditions. Nevertheless, the detail and the extent of the geometrical definition allowed new and interesting results to be obtained. Firstly, small geometrical undulations associated with the ductus arteriosus scar caused significant deviations in WSS, highlighting the importance of geometrical accuracy when analysing WSS or related metrics. Secondly, two Dean-type vortices form in the aortic arch and (along with an associated skewed axial velocity profile) propagate down the descending thoracic aorta. This leads to the formation of axial streaks in WSS, which are similar in nature to the streaks of early-stage atherosclerosis observed to form in the descending aorta of cholesterol-fed rabbits. Thirdly, WSS patterns within the vicinity of intercostal ostia depend not only on local flow features (caused by the branches themselves), but also on larger-scale global flow features within the descending aorta (which vary between ostia at different locations). This finding has several implications. It challenges the accuracy of results obtained using models that do not include the spatially varying large-scale aortic flow field [22]. It may also explain why disease patterns in the vicinity of intercostal ostia vary between branch locations. Finally, it calls into question the process of combining disease patterns from branches at different locations in order to obtain average maps [33]; it may be more appropriate to analyse disease patterns, and compare them with predicted WSS patterns, on a branch-by-branch basis.
Future studies should build on the work presented in this paper to develop a detailed and holistic understanding of blood flow within the rabbit aortic arch and descending thoracic aorta. Such an understanding is required before definitive correlations between blood flow patterns and atherosclerosis can be established with certainty. In particular, future studies should investigate the effect of varying flow splits between the aorta and its daughter vessels, the effect of using a more realistic inflow velocity profile at the aortic root, the effect of anatomical variation between animals and the effect of including more complex physical phenomena, such as pulsatile flow, deformable walls, non-Newtonian rheology and the transport of dissolved solutes.
Acknowledgements
All procedures complied with the UK Animals (Scientific Procedures) Act 1986 and were approved by the Imperial College London local ethical review panel.
This study was funded by the Engineering and Physical Sciences Research Council, the Biotechnology and Biological Sciences Research Council, Fundación Caja Madrid and a British Heart Foundation Research Excellence Award. The authors would like to thank Dr Richie Abel and Dr Stig Walsh for imaging the cast, Dr Donal Taylor and Dr Leopold Grinberg for assistance obtaining the high-order volume mesh, Miss Véronique Peiffer for assistance obtaining the unwrapped shear map images, Dr Stephanie Cremers for providing the disease images, Prof. Kim Parker for useful discussions, and the high-performance computing staff at Imperial College London for useful advice. Finally, the authors would like to thank the Barcelona Supercomputing Centre (HPC-EUROPA2 project number 228398), and Prof. George Karniadakis, for use of their facilities.
References
- 1.Fry D. L. 1968. Acute vascular endothelial changes associated with increased blood velocity gradients. Circ. Res. 22, 165. [DOI] [PubMed] [Google Scholar]
- 2.Caro C. G., Fitz-Gerald J. M., Schroter R. C. 1969. Arterial wall shear and distribution of early atheroma in man. Nature 223, 1159–1161 10.1038/2231159a0 (doi:10.1038/2231159a0) [DOI] [PubMed] [Google Scholar]
- 3.Caro C. G., Fitz-Gerald J. M., Schroter R. C. 1971. Atheroma and arterial wall shear. Observation, correlation and proposal of a shear dependent mass transfer mechanism for atherogenesis. Proc. R. Soc. Lond. B 177, 109–133 10.1098/rspb.1971.0019 (doi:10.1098/rspb.1971.0019) [DOI] [PubMed] [Google Scholar]
- 4.Ku D. N., Giddens D. P., Zarins C. K., Glagov S. 1985. Pulsatile flow and atherosclerosis in the human carotid bifurcation. Positive correlation between plaque location and low oscillating shear stress. Arteriosclerosis 5, 293–302 [DOI] [PubMed] [Google Scholar]
- 5.Shaaban A. M., Duerinckx A. J. 2000. Wall shear stress and early atherosclerosis: a review. AJR Am. J. Roentgenol. 174, 1657–1665 [DOI] [PubMed] [Google Scholar]
- 6.Cheng C., et al. 2004. The role of shear stress in atherosclerosis: action through gene expression and inflammation. Cell Biochem. Biophys. 41, 279–294 10.1385/CBB:41:2:279 (doi:10.1385/CBB:41:2:279) [DOI] [PubMed] [Google Scholar]
- 7.Suo J., Ferrara D. E., Sorescu D., Guldberg R. E., Taylor W. R., Giddens D. P. 2007. Hemodynamic shear stresses in mouse aortas: implications for atherogenesis. Arterioscl. Throm. Vas. 27, 346–351 10.1161/01.ATV.0000253492.45717.46 (doi:10.1161/01.ATV.0000253492.45717.46) [DOI] [PubMed] [Google Scholar]
- 8.Huo Y., Guo X., Kassab G. S. 2008. The flow field along the entire length of mouse aorta and primary branches. Ann. Biomed. Eng. 36, 685–699 10.1007/s10439-008-9473-4 (doi:10.1007/s10439-008-9473-4) [DOI] [PubMed] [Google Scholar]
- 9.Shahcheraghi N., Dwyer H. A., Cheer A. Y., Barakat A. I., Rutaganira T. 2002. Unsteady and three-dimensional simulation of blood flow in the human aortic arch. J. Biomech. Eng. 124, 378. 10.1115/1.1487357 (doi:10.1115/1.1487357) [DOI] [PubMed] [Google Scholar]
- 10.Liu X., Fan Y., Deng X. 2010. Effect of spiral flow on the transport of oxygen in the aorta: a numerical study. Ann. Biomed. Eng. 38, 917–926 10.1007/s10439-009-9878-8 (doi:10.1007/s10439-009-9878-8) [DOI] [PubMed] [Google Scholar]
- 11.Feintuch A., et al. 2007. Hemodynamics in the mouse aortic arch as assessed by MRI, ultrasound, and numerical modeling. Am. J. Physiol. Heart C 292, H884–H892 10.1152/ajpheart.00796.2006 (doi:10.1152/ajpheart.00796.2006) [DOI] [PubMed] [Google Scholar]
- 12.Liu X., Pu F., Fan Y., Deng X., Li D., Li S. 2009. A numerical study on the flow of blood and the transport of LDL in the human aorta: the physiological significance of the helical flow in the aortic arch. Am. J .Physiol. Heart C 297, H163–H170 10.1152/ajpheart.00266.2009 (doi:10.1152/ajpheart.00266.2009) [DOI] [PubMed] [Google Scholar]
- 13.Avolio A. P., O'rourke M. F., Mang K., Bason P. T., Gow B. S. 1976. A comparative study of pulsatile arterial hemodynamics in rabbits and guinea pigs. Am. J. Physiol. 230, 868. [DOI] [PubMed] [Google Scholar]
- 14.Volino P., Magnenat-Thalmann N. 1998. The Spherigon: a simple polygon patch for smoothing quickly your polygonal meshes. In Proc. of Computer Animation 1998, (CA'98), (ed. Werner B.), 8–10 June, Philadelphia, PA, USA, pp. 72–78. Los Alamitos, CA: IEEE Computer Society. [Google Scholar]
- 15.Grinberg L., Anor T., Madsen J. R., Yakhot A., Karniadakis G. 2009. Large-scale simulation of the human arterial tree. Clin. Exp. Pharmacol. Physiol. 36, 194–205 10.1111/j.1440-1681.2008.05010.x (doi:10.1111/j.1440-1681.2008.05010.x) [DOI] [PubMed] [Google Scholar]
- 16.He X., Ku D. N. 1996. Pulsatile flow in the human left coronary artery bifurcation: average conditions. J. Biomech. Eng. 118, 74. 10.1115/1.2795948 (doi:10.1115/1.2795948) [DOI] [PubMed] [Google Scholar]
- 17.Caro C. G., Pedley T. J., Schroter R. C., Seed W. A. 1978. The mechanics of the circulation. Oxford, UK: Oxford University Press [Google Scholar]
- 18.Kenner T., Leopold H., Hinghofer-Szalkay H. 1977. The continuous high-precision measurement of the density of flowing blood. Pflugers Arch. 370, 25–29 10.1007/BF00707941 (doi:10.1007/BF00707941) [DOI] [PubMed] [Google Scholar]
- 19.Windberger U., Bartholovitsch A., Plasenzotti R., Korak K. J., Heinze G. 2003. Whole blood viscosity, plasma viscosity and erythrocyte aggregation in nine mammalian species: reference values and comparison of data. Exp. Physiol. 88, 431–440 10.1113/eph8802496 (doi:10.1113/eph8802496) [DOI] [PubMed] [Google Scholar]
- 20.Barakat A. I., Marini R. P., Colton C. K. 1997. Measurement of flow rates through aortic branches in the anesthetized rabbit. Lab. Anim. Sci. 47, 184. [PubMed] [Google Scholar]
- 21.Murray C. D. 1926. The physiological principle of minimum work. I. The vascular system and the cost of blood volume. Proc. Natl Acad. Sci. USA 12, 207–214 10.1073/pnas.12.3.207 (doi:10.1073/pnas.12.3.207) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kazakidi A., Sherwin S. J., Weinberg P. D. 2009. Effect of Reynolds number and flow division on patterns of haemodynamic wall shear stress near branch points in the descending thoracic aorta. J. R. Soc. Interface 6, 539–548 10.1098/rsif.2008.0323 (doi:10.1098/rsif.2008.0323) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sherwin S. J., Ainsworth M. 2000. Unsteady Navier–Stokes solvers using hybrid spectral/hp element methods. Appl. Numer. Math. 33, 357–363 10.1016/S0168-9274(99)00102-6 (doi:10.1016/S0168-9274(99)00102-6) [DOI] [Google Scholar]
- 24.Sherwin S. J., Karniadakis G. E. 1995. A new triangular and tetrahedral basis for high-order (hp) finite element methods. Int. J. Numer. Methods Eng. 38, 3775–3802 10.1002/nme.1620382204 (doi:10.1002/nme.1620382204) [DOI] [Google Scholar]
- 25.Karniadakis G. E., Sherwin S. J. 2005. Spectral/hp element methods for computational fluid dynamics, 2nd edn Oxford, UK: Oxford Scientific Publications; 10.1093/acprof:oso/9780198528692.001.0001 (doi:10.1093/acprof:oso/9780198528692.001.0001) [DOI] [Google Scholar]
- 26.Barakat A. I., Karino T., Colton C. K. 1997. Microcinematographic studies of flow patterns in the excised rabbit aorta and its major branches. Biorheology 34, 195–221 10.1016/S0006-355X(97)00025-5 (doi:10.1016/S0006-355X(97)00025-5) [DOI] [PubMed] [Google Scholar]
- 27.Jeong J., Hussain F. 2006. On the identification of a vortex. J. Fluid Mech. 285, 69–94 10.1017/S0022112095000462 (doi:10.1017/S0022112095000462) [DOI] [Google Scholar]
- 28.Dean W. R. 1927. Note on the motion of fluid in a curved pipe. Philos. Mag. 20, 208–223 [Google Scholar]
- 29.Lee K. E., Parker K. H., Caro C. G., Sherwin S. J. 2008. The spectral/hp element modelling of steady flow in non-planar double bends. Int. J. Numer. Methods Fluids 57, 519–529 10.1002/fld.1500 (doi:10.1002/fld.1500) [DOI] [Google Scholar]
- 30.Pitt R. 2005. Numerical simulation of fluid mechanical phenomena in idealised physiological geometries: stenosis and double bend. PhD thesis, Imperial College London, London, UK [Google Scholar]
- 31.Duff G. L. 1954. Functional anatomy of the blood vessel wall; adaptive changes. In Symp. on Atherosclerosis, pp. 33–40 Washington, DC: National Academy of Sciences-National Research Council [Google Scholar]
- 32.Coppola G., Sherwin S. J., Peiro J. 2001. Nonlinear particle tracking for high-order elements. J. Comput. Phys. 172, 356–386 10.1006/jcph.2001.6829 (doi:10.1006/jcph.2001.6829) [DOI] [Google Scholar]
- 33.Barnes S. E., Weinberg P. D. 1998. Contrasting patterns of spontaneous aortic disease in young and old rabbits. Arterioscl. Throm. Vas. Biol. 18, 300–308 [DOI] [PubMed] [Google Scholar]
- 34.Borkowski G. L., Danneman P. J., Russell G. B., Lang C. M. 1990. An evaluation of three intravenous anesthetic regimens in New Zealand rabbits. Lab. Anim. Sci. 40, 270–276 [PubMed] [Google Scholar]
- 35.Wyatt J. D., Scott R. A., Richardson M. E. 1989. The effects of prolonged ketamine-xylazine intravenous infusion on arterial blood pH. blood gases, mean arterial blood pressure, heart and respiratory rates, rectal temperature and reflexes in the rabbit. Lab. Anim. Sci. 39, 411–416 [PubMed] [Google Scholar]
- 36.Weisbroth S. H., Flatt R. E., Kraus A. L. 1974. The biology of the laboratory rabbit. New York, NY: Academic Press [Google Scholar]
- 37.Cremers S. G., Wolffram S. J., Weinberg P. D. 2011. Atheroprotective effects of dietary L-arginine increase with age in cholesterol-fed rabbits. Br. J. Nutr. 105, 1439–1447 10.1017/S0007114510005234 (doi:10.1017/S0007114510005234) [DOI] [PubMed] [Google Scholar]