Health safety nets can break cycles of poverty and disease: a stochastic ecological model

Abstract

The persistence of extreme poverty is increasingly attributed to dynamic interactions between biophysical processes and economics, though there remains a dearth of integrated theoretical frameworks that can inform policy. Here, we present a stochastic model of disease-driven poverty traps. Whereas deterministic models can result in poverty traps that can only be broken by substantial external changes to the initial conditions, in the stochastic model there is always some probability that a population will leave or enter a poverty trap. We show that a ‘safety net’, defined as an externally enforced minimum level of health or economic conditions, can guarantee ultimate escape from a poverty trap, even if the safety net is set within the basin of attraction of the poverty trap, and even if the safety net is only in the form of a public health measure. Whereas the deterministic model implies that small improvements in initial conditions near the poverty-trap equilibrium are futile, the stochastic model suggests that the impact of changes in the location of the safety net on the rate of development may be strongest near the poverty-trap equilibrium.

1. Introduction

One-sixth of the world lives in extreme poverty [1]. The extremely poor, by definition, live on the margin of survival and often comprise populations that have never experienced sustained economic growth. The persistence of extreme poverty is increasingly attributed to poverty traps. In canonical economic models, poverty traps arise from nonlinearities between income (or productivity) and inputs into the production process, such as capital, such that threshold levels are necessary for growth [2–4]. Recently, however, there has been increasing interest in the possibility that poverty traps are formed by feedbacks between income and biophysical processes, such as agricultural productivity, environmental degradation and human health [5–9]. The sources of these nonlinearities are important: in the former, it is the mechanics of the production process; in the latter, it is often ecological. Our focus here is on the role of infectious diseases in economic development. Can healthcare break cycles of poverty and disease?

At the individual level, the evidence is overwhelming that health and nutrition are essential for cognitive and physical development, especially at early stages of life, when children acquire the education and training that are ultimately necessary for income generation [10–16]. Diseases also directly inhibit labour productivity and cause early deaths, which are known to influence the economic behaviour through a range of channels that have long-term negative consequences, such as through lower private investment and larger family size [17,18].

At the macro-scale, there is a large body of evidence that suggests that health and longevity have significant direct impacts on economic growth, but there is also a robust counter literature that suggests that these effects are insignificant or only indirect [18–23]. One challenge for this research is a dearth of theoretical structure that can inform the analysis of health and economic data.

Although human health has been considered in economic models for decades, it has generally been incorporated as a simple factor of production (i.e. labour and ‘human capital’). However, the leading cause of death of the poor is infectious diseases, which are ecological agents. A preponderance of theory and evidence in the science literature indicate that the dynamics of infectious diseases are generally nonlinear and have had significant and systematic impacts on the population dynamics of their hosts in the natural world as well as in laboratory settings [24,25]. Modelling the effect of human health on economic growth, therefore, may require ecological feedbacks to be explicitly incorporated.

Recently, Bonds et al. [9] put forth a theory of poverty traps based on an ecological model of infectious diseases. The value of this framework is that: (i) it produces specific conditions for the existence of disease-driven poverty traps, and (ii) because it is based on an established model in population ecology, it is amenable to methods of analysis developed in the natural sciences [26–28]. However, the model also has significant shortcomings. Because it is deterministic, the initial conditions determine whether the population is permanently stuck in a trap of poverty or permanently enjoys economic development.

Such deterministic poverty traps are based on intrinsic functional relationships between state variables (e.g. income, health) and are therefore considered examples of ‘structural poverty’ [29,30]. Alternatively, disease-induced poverty can be stochastic. ‘Stochastic poverty’ is the consequence of external shocks, such as those associated with employment, prices, food productivity, natural disasters or health [29,31]. Though stochastic poverty is often thought of as transitory, its long-term effects on economic development may be more subtle. For example, a household may be ‘trapped’ in poverty despite structural economic growth trajectories because of frequent setbacks due to external shocks. This has been shown, for example, for livestock production by pastoralists in the Horn of Africa who suffer from catastrophic weather-related losses [32]. Stochastic forces could also move a household from a state of structural economic growth to a deterministic poverty trap by changing the initial conditions.

These distinctions have important implications for policy. Whereas breaking out of a structural poverty trap may depend critically on the level of the state variables relative to a threshold, breaking stochastic poverty traps in the context of structural growth requires reducing volatility. Thus, the former requires substantial temporary externally driven positive shocks, whereas the latter requires the prevention of negative shocks. It is for this reason that the literature on stochastic poverty has placed special attention on the importance of ‘safety nets’, designed to prevent negative downturns in economic status [31,33,34]. Unlike structural poverty, stochastic poverty can theoretically be reduced by internally funded risk-management schemes such as insurance.

The difference between stochastic and structural poverty, although only a specialized topic in economics, is analogous to one of the most formative debates in population ecology: that of whether biological populations are ‘regulated’ (i.e. determined by intrinsic factors) or driven by stochastic variation [35–37]. Indeed, a substantial amount of empirical work, from laboratory studies of marine microorganisms to field studies of large mammals, has contributed to a growing consensus that stochastic processes are often as important as their underlying deterministic structure in explaining the dynamics of biological populations [38–43]. Among the systems that have received particular attention are infectious diseases of humans, such as measles, whooping cough, cholera and dengue fever, where stochastic models were essential for explaining the temporal behaviour of the disease [44–48].

The current study is thus motivated by the following findings developed from disparate literatures: (i) health, which is largely determined by disease ecology, can influence economic productivity, (ii) the effectiveness of policy is sensitive to the nature of poverty dynamics, and (iii) the dynamics of income and disease have both deterministic and stochastic components.

Specifically, we compare deterministic and stochastic simulations of income and infectious diseases in the context of structural poverty traps. In the deterministic model, interventions that do not cross a critical threshold have no long-term benefits. However, we find that in the stochastic model there is always some probability that a population will leave or enter a poverty trap, with the probabilities varying according to the location in the state space. In some regions, the most efficient path to development is through improving health, whereas for others it is income. We show that a ‘safety net’, defined as an externally enforced minimum level of health or economic conditions, can guarantee ultimate escape from a poverty trap, even if it is set within the basin of attraction of the poverty trap, and even if the safety net is only in the form of a health intervention. If a population is near the poverty-trap equilibrium, the benefits of a safety net in the deterministic system are lowest, whereas for the stochastic model they are highest.

This model serves as an example of how ecological theory can inform our understanding of poverty dynamics, both structurally and stochastically, and of the potential effects of policy interventions.

2. General model framework

The extremely poor routinely suffer from a broad range of infectious and parasitic diseases. Although it is the cumulative effect of the total disease burden that is most important, a few diseases have individually received special attention for their economic impacts: HIV/AIDS, tuberculosis, malaria and hookworm. Although these infections each have very different properties, they all cause high rates of morbidity or mortality, and they have all been modelled as simple compartmentalized systems represented by differential equations [27,28].

In order to better understand how healthcare policies may break cycles of poverty and disease, it is not necessary to model the full community ecology of economically important infections. Instead, for simplicity, our model is a one-disease S-I-S (susceptible–infected/infectious–susceptible) compartmentalized system. This framework corresponds to the general class of diseases that can serially re-infect their hosts such as bacterial diseases, sexually transmitted diseases and many vector-borne diseases, such as malaria [20,49–56].

We denote the proportions of infected and susceptible individuals as I and S respectively, and the respective numbers of infected and susceptible individuals as and 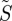. Individuals are born into the susceptible class at rate α; become infected at rate 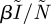, where β is the transmission rate and 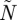is the total population; and then re-enter the susceptible class at the recovery rate γ. Individuals die naturally at rate μ and at an additional rate ν as a result of infection. A schematic of the general framework is presented in figure 1, which corresponds to a set of differential equations for the deterministic analysis and to a computational algorithm for the stochastic simulations.

Figure 1.

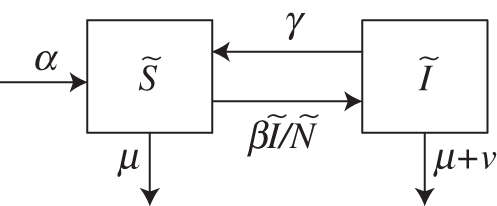
Schematic of the S-I-S model system. This corresponds to a set of differential equations for the deterministic analysis. For the stochastic analysis, it is simulated via the Gillespie algorithm.

Because the basis of a disease-driven poverty trap is a positive feedback between income and disease, we follow Bonds et al. [9] by explicitly modelling transmission (β) and recovery (γ) rates as functions of per capita income of the population (M):

2.1

and

2.2

where β₁ represents the maximum transmission rate that occurs when income is 0 and γ₁ is the maximum recovery rate, which decreases with lower income. Thus, as income rises, the transmission rate asymptotically approaches 0 and the recovery rate asymptotically approaches its maximum.

Based on this general model framework, we explore the deterministic structure of this system in §3, and then stochastically simulate the same system in §4. In §5, we investigate specific policy scenarios and implications of the different model structures.

3. Deterministic analysis

The deterministic model is represented by a set of differential equations, where the state variables represent proportions of susceptible, 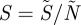, and infected/infectious, :

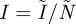3.1

3.2

3.3

where τ represents dimensionless time. (See the electronic supplementary material for an explanation of the process of non-dimensionalization with respect to time.) Whereas previous work has modelled the equilibrium per capita income as a function of the equilibrium disease prevalence [9,54,57], here we explicitly model income, M, as a state variable that is a simple direct function of the disease. The parameter M₀ represents the maximum income that would be earned in the absence of the disease. Equation (3.3) is meant to serve as a simple way to depict the process of income converging to its maximum over time. This logic has an analogue in economic growth theory, where canonical models suggest that, in the absence of multiple equilibria, low-income countries should grow faster than high-income countries until their growth paths converge to an equilibrium rate [58–60].

Figure 2a illustrates the structure of this deterministic system by presenting the partial equilibrium value of income for all values of disease prevalence, dM/dτ = 0, and the partial equilibrium value of disease prevalence for all values of income, dI/dτ = 0 (for a more complete analysis of the equilibria of this system, see the electronic supplementary material). The equilibria, E₁^*, E₂^* and E₃^*, of the system are located at the intersection of these curves, which is where dM/dτ = 0 and dI/dτ = 0 simultaneously. To better understand the behaviour of this system, we numerically integrate the model over the full range of initial income and disease prevalence. For illustrative purposes, figure 2a presents the path over M and I space for two different initial conditions, one which is in the basin of attraction of the low-income high-disease equilibrium (i.e. the poverty trap) and the other which is in the basin of attraction of the high-income low-disease equilibrium, which we define as ‘development’. Notice that E^*_M0 and E₃^* are stable, whereas E₂^* is unstable. Therefore, trajectories originating close to E₂^* converge to either E^*_M0 or E₃^*. A phase plot that represents the equilibrium outcome for all initial conditions is presented in figure 2b.

Figure 2.

(a) Simulation results for the deterministic model, showing the paths taken by two typical trajectories that start at different initial points to arrive at either the development stable equilibrium solution, E^*_M0, or the poverty trap, E₃^*. Dashed line, dS/dτ = 0; dashed-dotted line, dI/dτ = 0; black solid line, path 1; grey solid line, path 2. (b) Phase plot illustrating the effect of initial conditions on determining the stable equilibrium point to which the system relaxes in the long time limit (grey shaded region, development; unshaded region, poverty trap). α = 0.06, ν = 0.02, r = 0.05, β₁ = 40, ɛ = 15, δ = 0.15, ρ = 90, κ = 100, M₀ = 100.

There are important shortcomings of modelling a poverty-trap system deterministically. For a given set of parameters, determinism implies that a country is permanently stuck in a trap of poverty and disease if its initial epidemiological and economic conditions fall within the basin of attraction of the poverty-trap equilibrium. Escaping the poverty trap would therefore require either a ‘big push’ to move the state variables (i.e. the ‘initial conditions’) beyond the basin of attraction of the poverty trap or a change in the parameters that alter the existence or location of equilibria in the state space. This offers an unnecessarily restrictive set of potential policy recommendations that are biased towards large external interventions. It also provides a limited set of criteria for detecting poverty traps empirically.

4. Stochastic analysis

For infectious disease dynamics, stochasticity is most often modelled as ‘demographic’, i.e. through inherently random movement between discrete states. The disease process here is accordingly simulated using the Gillespie algorithm, where the rates of transition between states of birth, death, infection and recovery are determined by the same parameters as those in the deterministic model (for details, see the electronic supplementary material; figure 3).

Figure 3.

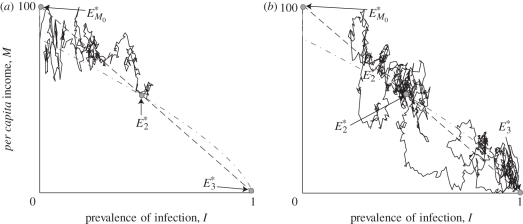
Stochastic simulations. In contrast to the deterministic case, it is possible to attain either of the two stable equilibria with the same initial conditions, (I,M) = (0.5,50). α = 0.06, ν = 0.02, r = 0.05, β₁ = 40, ɛ = 15, δ = 0.15, ρ = 90, κ = 100, M₀ = 100, σ = 3. (a,b) Dashed line, M^*(I); dashed-dotted line, I^* (M); solid line, path.

For income, we model the stochastic process as ‘environmental’, through a Weiner process that includes the addition of an exogenous stochastic component. This is a standard method in economics and finance that applies naturally to poverty dynamics where incomes are often generated from highly variable agricultural productivity or through volatile earnings associated with the informal economy [34,61]. Because income is a continuous variable, it is modelled here as a simple differential equation:

4.1

Here, dW_t is a random variable (with mean 0) generated by a Weiner process and g(M) is the average growth rate of per capita income (equation (3.3)). The parameter σ is the volatility of per capita income. Constant volatility implies that the poor are more vulnerable to fluctuations in income.

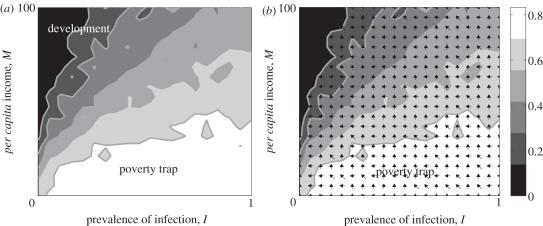
Running the simulation multiple times from different initial conditions allows us to quantify the probability of ending up in either a steady state of development or a poverty trap. Figure 4 presents the stochastic analogue to figure 2b. In figure 4, we see that, instead of initial conditions corresponding deterministically to only three possible outcomes, the initial conditions instead correspond to a probability of reaching one of the two stable equilibria. Each solid line in figure 4 represents a cline of a single probability of reaching either the development or poverty-trap equilibrium. Although the area nearest the poverty-trap equilibrium corresponds to near-predetermined fates, there is considerable uncertainty of the ultimate outcome in much of the state space. Each arrow in figure 4a is pointed in the direction of the neighbouring point with the highest probability of ending up in the development equilibrium. By following the arrows from the bottom right of the plot to the top left corner of the plot (figure 4b), one can trace the highest probability path that a population can take to leave the poverty trap.

Figure 4.

(a) Phase plot illustrating probabilities that an initial condition will lead to development or a poverty trap. Each solid line corresponds to a single probability of reaching either the development or poverty-trap equilibrium. (b) The arrows indicate the quickest path to the development equilibrium. Note that this path depends on the status of the level of income and disease. α = 0.06, ν = 0.02, r = 0.05, β₁ = 40, ɛ = 15, δ = 0.15, ρ = 90, κ = 100, M₀ = 100, σ = 3.

5. Policy interpretations

Stochastic dynamics gives meaning to a qualitatively different set of interventions than would be considered from deterministic models. From figure 4b, we see that the highest probability strategy for escaping a poverty trap depends on the specific status of the income and disease conditions. Assuming equal costs of intervention, in the areas of the state space where the arrow is pointed up, the most efficient intervention, in terms of the highest probability of leading to development, would be to increase income. In areas where the arrow is pointed to the left, the most efficient intervention would be to lower the disease prevalence. And in other areas where the arrow is faced diagonally up and to the left, the most efficient intervention would occur from doing both simultaneously. Such policies would always be futile in a deterministic system where small interventions could only change the rate at which the system approaches its pre-destined stable equilibrium outcome.

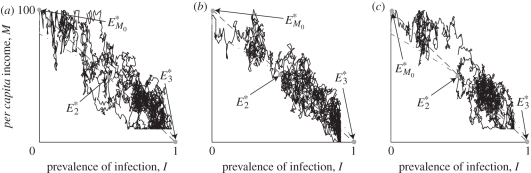
In addition to policies that are designed to directly change the status of the state variables, another set of interventions that have meaningful theoretical implications for this system are safety nets. ‘Safety nets’ generally refer to a range of potential systems that help households or populations offset the risk of significant negative harm related to downturns in economic status [33,34]. In this context, a safety net is defined as a minimum level of income or public health below which the population is prevented from falling. Figure 5 demonstrates the development process for populations with (a) an income safety net, (b) a health safety net and (c) a safety net for both health and income. Notice that, in each case, the system eventually reaches the development equilibrium even though the safety net is set within the basin of the attraction of the poverty trap. Although a simultaneous health and income safety net results in a shorter time period to the development equilibrium, a health safety net alone, without an explicit economic intervention, could be enough to lead to economic development even if it is not established in the basin of attraction of the development equilibrium.

Figure 5.

Stochastic simulation where the initial state is reinforced by a safety net. (a) Income safety net, M = 10; (b) health safety net, I = 0.90; and (c) income and health safety net, (I,M) = (0.90,10) (dashed line, M^* (I); dashed-dotted line, I^* (M); solid line, path). The safety net ensures that the system is driven towards the development equilibrium even though it is set in the basin of attraction of the poverty trap. α = 0.06, ν = 0.02, r = 0.05, β₁ = 40, ɛ = 15, δ = 0.15, ρ = 90, κ = 100, M₀ = 100, σ = 3.

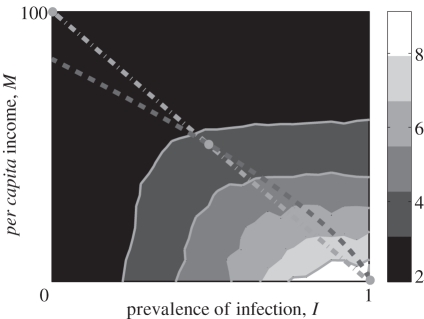
The location of the safety net is important in determining the expected time of this process. Figure 6 presents the expected (i.e. mean) time it takes to reach the development equilibrium (which we define here as the ‘rate of development’) for the full range of initial conditions, when reinforced by safety nets in both health and income (for details, see the electronic supplementary material). The slope of the contour lines in figure 6 indicate the relative sensitivity of this rate of development to safety nets at different levels of income and disease. For example, if the slope of the contour lines in figure 6 is greater than 1, then changes in the disease safety net will have a larger impact on the rate of development than changes in the income safety net. At the extreme, a vertical contour line (slope =∞) would indicate that the development process was limited only by disease, and therefore changes in a safety net in income would have no effect on the rate of development. Likewise, horizontal contours (slope = 0) would signify that the rate of development is limited only by income. The proximity of the contour lines on the bottom right corner of figure 6 indicates that the rate of development is most sensitive to changes in the location of the safety net closest to the poverty-trap equilibrium.

Figure 6.

Phase plot illustrating the average time in years required to attain the development equilibrium from initial conditions that are reinforced by safety nets. α = 0.06, ν = 0.02, r = 0.05, β₁ = 40, ɛ = 15, δ = 0.15, ρ = 90, κ = 100, M₀ = 100, σ = 3.

6. Discussion

The majority of the extremely poor are subsistence farmers whose economic welfare may be less vulnerable to changes in traditional market forces than to their biophysical environment. Extreme poverty, by definition, also implies a lack of buffers from external shocks such as disease and natural disasters [29,61]. These are important reasons for theories in development and macroeconomics to be integrated into the natural sciences. For poor populations in general, physical health is a fundamentally important component of economic productivity because the poor rely almost exclusively on their physical labour [34]. Development economists are therefore paying increasing attention to the biological foundation of economic performance among the poor [6,10,30,62,63].

Despite the significant interest in the role of health in economic development across the biological and economic sciences, there remains a dearth of integrated theoretical frameworks for understanding poverty and health dynamics at the population level. This has created substantial confusion over the interpretation of data. The model presented here addresses some basic questions on the feedback between income and disease using a general framework that has been heavily explored in the biological sciences. Accordingly, these poverty traps are generated not by nonlinear structural relationships in the production process, but by explicit ecological feedbacks.

In addition to deterministic structure, stochasticity is especially important in the context of disease-driven poverty traps. The economics literature generally treats stochasticity as a negative influence that can undermine structural growth, either through catastrophic setbacks or by inducing structural poverty through changes in the initial conditions. The analysis here relies on the possibility that the inverse can occur: stochastic growth in the context of structural poverty. We show that steering such random processes can be done through policies.

Whereas breaking disease-driven poverty traps in the deterministic model requires changing the initial conditions beyond a threshold, the stochastic model shows how external interventions in the form of safety nets can significantly improve the development trajectory no matter where it is in the state space. Not only can development result from safety nets that are set within the basin of attraction of the poverty trap, but the rate of development is most sensitive to changes to safety nets near the poverty-trap equilibrium, where marginal improvements in population health are also likely to be the least expensive. In the deterministic model, in contrast, small interventions near the poverty-trap equilibrium are futile.

There are limitations of this analysis that span theoretical, empirical and practical considerations. On empirical grounds, some have questioned the existence of poverty traps based on the rates of turnover of populations identified as extremely poor [64], and others have pointed to some low estimates of influences of health on the income in the literature [23]. Many economists have pointed at the potential negative indirect consequences of safety nets in the form of ‘moral hazard’ that would be expected from rational human responses to such policies [33]. In addition, the model's one-disease S-I-S structure errs on the side of simplicity; it does not consider many details that would be necessary to parametrize a model empirically, such as seasonality, population age-structure or vector dynamics. And it does not directly model the complex relationships between multiple diseases that have significant impacts on the income through their cumulative effects.

However, despite the model's simplicity, the conclusions about safety nets and stochasticity in the context of poverty traps are generalizable. What is most important is the presence, and stochasticity, of feedbacks between income and disease. The model shows that the existence of poverty traps can be highly consistent with volatility in income and disease, and they can exist even if the direct effects of health on income are small, if the effects of income on health are large enough. Indeed, stochastically driven volatility confers particular advantages to safety nets. Future work could consider different kinds of epidemiological systems, such as HIV, TB and childhood diseases, and could directly integrate dynamic optimizing human behaviour. Of particular interest would be to consider multiple pathogens and explicitly incorporate relationships with malnutrition. Perhaps most urgently, we need a broader range of theories that provide insights into dynamic feedbacks between population-level economic processes and ecology. Our model here is an example of how such theoretical frameworks can be explicitly linked to basic policy questions and suggests that health safety nets can break cycles of poverty and disease.