Modelling platelet–blood flow interaction using the subcellular element Langevin method

Abstract

In this paper, a new three-dimensional modelling approach is described for studying fluid–viscoelastic cell interaction, the subcellular element Langevin (SCEL) method, with cells modelled by subcellular elements (SCEs) and SCE cells coupled with fluid flow and substrate models by using the Langevin equation. It is demonstrated that: (i) the new method is computationally efficient, scaling as 𝒪(N) for N SCEs; (ii) cell geometry, stiffness and adhesivity can be modelled by directly relating parameters to experimentally measured values; (iii) modelling the fluid–platelet interface as a surface leads to a very good correlation with experimentally observed platelet flow interactions. Using this method, the three-dimensional motion of a viscoelastic platelet in a shear blood flow was simulated and compared with experiments on tracking platelets in a blood chamber. It is shown that the complex platelet-flipping dynamics under linear shear flows can be accurately recovered with the SCEL model when compared with the experiments. All experimental details and electronic supplementary material are archived at http://biomath.math.nd.edu/scelsupplementaryinformation/.

1. Introduction

Damage or inflammation of the blood vessel wall can lead to the development of an intravascular clot or thrombus. Venous thromboembolic disease is a significant biomedical problem, with the annual incidence in the USA being estimated as high as 900 000 cases per year leading to 300 000 deaths [1,2]. Understanding the processes involved in the formation and development of a thrombus is of significant biomedical importance.

The recruitment of platelets flowing freely in blood to sites of injury is a key step in the formation of a thrombus. Before contacting the vessel wall, free-flowing platelets near the surface exhibit shear-dependent flipping. The flipping of free-flowing platelets affects the orientation of platelets when first contacting the surface of the vessel. After contact, the platelet receptor component GPIbα of the GPIb-V-IX complex forms transient bonds with the von Willebrand factor (vWF) exposed at the injury site. The rapid association and dissociation kinetics of the GPIbα–vWF results in transient tethering and subsequent flipping (or rolling) of platelets on the vessel surface [3,4]. Interestingly, the formation of the GPIbα–vWF bond is influenced by the orientation of the platelet when contacting the surface. This GPIbα–vWF binding is critical for supporting the initial attachment (tethering) and subsequent translocation of platelets in flow [5]. The initial attachment permits other platelet receptors to interact with the ligands in the vessel wall and blood (GPIV–collagen, GPIaIIb with collagen and vWF) that in addition to contributing to adhesion also activate intracellular signalling pathways leading to platelet morphological changes and activation of another platelet receptor, GPIIb–IIIa, which is necessary for binding to fibrin(ogen), vWF and vitronectin. These latter interactions are necessary for firm irreversible adhesion and the formation of stable platelet aggregates.

Therefore, several computational models have been developed to characterize platelet motion quantitatively and to study platelet–blood vessel wall adhesion dynamics. Image analysis of platelet motion in flow-chamber experiments was used in Mody et al. [6] to identify motion of platelets before, during and after contact with surface coated with the vWF for a range of fluid shear stresses (0.2–0.8 dyn cm⁻²). An analytical two-dimensional model was also introduced in Mody et al. [6] to characterize the flipping of tethered platelets. A three-dimensional computational model was presented in Mody & King [7–9] for simulating motion of platelet-shaped cells in a flow near a wall to elucidate GPIbα–vWF-mediated platelet and substrate binding that leads to shear-induced platelet aggregation. The adhesion model, introduced in King & Hammer [10], was combined in Mody & King [7–9] with the completed double-layer boundary integral equation method for solving the Stokes hydrodynamics equation. Effects of hydrodynamics, the shape of platelets and proximity of a plane wall on cell–cell collisions and on two unactivated platelets bridged by GPIbα–vWF–GPIbα at high shear rates were investigated.

A number of methods modelling cells, cellular interactions and cell–flow interactions have been developed previously. The subcellular element (SCE) model introduced in Sandersius & Newman [11] and Newman [12] represents each cell by a collection of elastically coupled SCEs, interacting with each other via short-range potentials, and being dynamically updated using Langevin dynamics. Using a large number of SCEs, cells yield viscoelastic properties consistent with those measured experimentally. The cell–cell adhesion is modelled as a modified Morse PP. However, the SCE model in Sandersius & Newman [11] and Newman [12] does not couple the cell dynamics to that of the fluid. A parallel implementation of the SCE method for individual cells residing in a lattice-free spatial environment is described in Christley et al. [13] (without coupling to a flow).

The immersed boundary (IB) method [14,15] has been widely used for modelling flexible structures immersed in a fluid. For instance, it was applied to the study of blood flow around heart valves [16]. The IB method of Jadhav et al. [17] represents a cell (leucocyte) as a massless elastic membrane enclosing an incompressible fluid. The continuity between the fluid and the cell is achieved by the interpolation of the velocities from the fluid and the distribution of the forces from the elastic membrane. An adhesion model employed in Jadhav et al. [17] represents individual receptor–ligand (P-selectin and P-selectin glycoprotein ligand-1 pair) interactions as harmonic springs that form or break according to probabilities depending on the values of forward and reverse rate constants obtained from the literature [18]. The immersed finite-element method (IFEM) [19] is similar to the IB method. However, the IFEM models a cell as an elastic solid with mass. A Lagrangian solid mesh for cells moves on top of a fixed Eulerian fluid mesh that covers the entire computational domain. Solutions in both the solid and the fluid subdomains are computed by the finite-element method and the continuity between the fluid and solid subdomains is also enforced by the interpolation of the velocities and the distribution of the forces with the reproducing Kernel particle method delta function. Cell–cell and cell–vessel adhesion in Liu et al. [19] is modelled as a modified Morse pairwise potential (PP). In the papers by Fogelson & Guy [20,21], an IB-based method in which individual platelets were modelled as a massless elastic fibre was used to simulate the formation of platelet aggregates.

The dissipative particle dynamics (DPD) method [22,23] is based on the idea of introducing discrete ‘soft’ fluid particles to replace the continuum flow description. In addition to the soft particles, random perturbations are introduced to model the fluid atoms interacting with the immersed cellular structures, which are also modelled as collections of particles. Many fine-grained features of the fluid dynamics and immersed structures within the fluid are often not resolved in detail. Additionally, the DPD method generally requires many DPD particles in relation to the number of cells, which increases computational cost. However, the work in Pivkin & Karniadakis [23] reveals the potential to develop DPD-based models with low computational cost for simulating fluid and blood cell interactions.

Several models of thrombus formation have also been introduced, which take the recruitment of free-flowing blood cells and initial contact between blood cells and blood vessel walls into account. For example, models [20,21] used the IB approach to study the formation of platelet thrombi in coronary-artery-sized blood vessels. Pivkin et al. [24] developed a platelet thrombi model using the force-coupling method. In recent papers [25–29], a multiscale model of venous thrombosis was introduced that combined continuum submodels for the blood flow and the chemical cascade, induced by tissue factors at injuries, and discrete stochastic cellular Potts models (CPMs) for simulating cell–cell and cell–injury interactions. The CPM has proved to be efficient in implementing simulations of thousands of cells but has limited abilities in describing in detail cell properties such as elasticity and shape.

In this paper, we develop a new method for three-dimensional flow–cell interaction simulations—the subcellular element Langevin (SCEL) method. This method uses SCEs to simulate cell motion and deformation and the SCE cell is coupled to the plasma flow by a novel variation of the Langevin equation [30]. The SCEL method allows one to model the mechanical properties of cells accurately, while retaining the 𝒪(N) computational scaling of Langevin solvers with short-range interactions. It also confers greatly reduced computational cost. Our approach confers ‘forward’ coupling between the flow field and the SCE.

We ran experiments on the tracking motion of platelets in a blood flow chamber. Human platelets were introduced into a plasma flow passing through a rectangular capillary tube. Images were captured at a rate of 30 fps, and individual platelets were tracked for analysis. Flipping of the platelets was detected by measuring the minor and major axes of the platelets in each frame, since the shape of a platelet is approximately elliptical in cross section with the ratio of minor and major axes being 0.5 and the diameter of the platelet being 4 mm. The angle of the platelet then was deduced and the time to complete a flip was calculated.

It is demonstrated in this paper that: (i) the new SCEL method is computationally efficient, scaling as 𝒪(N) for N SCEs; (ii) cell geometry, stiffness and adhesivity can be modelled by directly relating parameters to experimentally measured values; (iii) modelling the fluid–platelet interface as a surface leads to a good correlation with experimentally observed platelet–flow interactions. Using this method, the three-dimensional motion of a viscoelastic platelet in a shear blood flow was simulated and compared with experiments on tracking platelets in a blood chamber. It is shown that the complex platelet-flipping dynamics under linear shear flows can be accurately recovered with the SCEL model when compared with the experiments.

The paper is organized as follows. Section 2 describes in detail SCE cell-based model coupled to the flow by using a novel variation to the Langevin equation. Section 3 describes simulations of flipping platelets moving in a linear shear flow and refines the choice of parameter values used in simulations. Section 4 includes conclusions and discussion of the future work. Electronic supplementary material §B.1 discusses the numerical schemes to solve model equations. Biological background section in the electronic supplementary material provides biological details about the platelet and blood interaction.

2. Model description

In what follows, we describe a new method for three-dimensional flow–cell wall interaction simulations, the SCEL method. This method uses SCEs to model the cells and the Langevin equation is employed to couple the SCE to the plasma flow.

This coupling idea is similar to the DPD extension in that the microscopic fluid–SCE interactions can be modelled (as random forces) and that the fluid acts as a heat bath. We extend the Langevin equation to allow the coupling of the coarser flow structure using a Stokes–Langevin approach [30]. Perturbations in the flow field at the cellular scale are assumed to couple to SCEs using Stokes' Law, with the force being proportional to the fluid velocity.

2.1. Model assumptions

We assume that the plasma–cell mixture is homogeneous up to cells attached to the injury site or rolling on the substrate surface. We assume that in a free-flowing environment, the cells will eventually achieve the same velocity as the underlying fluid, and moving cells do not affect the flow as we only consider the ‘forward coupling’ in the present paper. The fluctuation–dissipation theorem assumes that the random forces can be positive or negative with equal probability [31], an assumption that may be violated by the introduction of a biased flow. To reduce such errors, we subtract the average flow velocity from the system (combined plasma and SCEs) velocity for the propagation of the SCE and assume, since the flow is considered incompressible, that the resulting flow field is unbiased.

2.2. Subcellular elements and forces

Our coarse-grained approach is based on modelling the platelets and blood cells using SCEs and treating the solvent (plasma) as removed degrees of freedom (d.f.) that are introduced stochastically as velocity damping and random fluctuations.

2.2.1. Subcellular element model of cells and schematic of problems being modelled

Sandersius & Newman [11] and Newman [12] introduced the SCE model to compute the dynamics of a large number of three-dimensional deformable cells in multicellular systems. In the SCE model framework, each cell is represented by a collection of elastically linked SCEs, interacting with one another via short-range potentials. Figure 1b shows the SCE representation of a platelet in our model. In our cell representation, a cell comprises an SCE at the cell centre and a set of SCEs discretizing the proximity of surface of the cell (discussed in §2.2.2). The position of an SCE changes according to three processes (or forces): (i) a stochastic component simulating cellular fluctuation, (ii) an elastic force by intracellular interactions, (iii) a hydrodynamic force by fluid–cell interaction. To this end, a modified Langevin equation including these three processes is used to update the position of an SCE. Using this model, we simulate the platelet motion by placing the platelet in a linear shear flow field within a rectangular channel.

Figure 1.

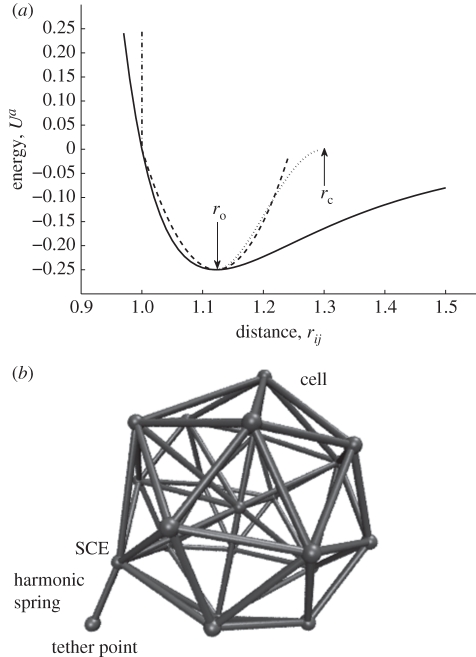
Cell–substrate interaction potential energy. (a) Potential energy U^a changes with inter-SCE distance r_ij showing switch-on point r_o and switch cut-off r_c. Solid line, Lennard Jones; dashed lines, harmonic spring; dashed-dotted line, hard wall; dotted line, switched LJ. (b) SCE representation of a platelet with Harmonic tether.

2.2.2. Cell mechanical properties

Each cell consists of a number of surface nodes (or SCEs) and a central node (or a central SCE). The surface nodes represent points close to the cell surface (defined below) and the central node represents a point close to the cell nucleus. The mechanical properties and geometry of a cell are modelled by connecting each surface node to both its immediate neighbours and the central node, by harmonic ‘spring’ forces of given rest length. The associated potential energy function for bodies i and j are

2.1

where l_ij is the rest length, r_ij = x_j − x_i the position vector difference for bodies i and j, respectively, and k_ij the coefficient that defines the spring ‘stiffness’. The corresponding force vector acting on body i by body j is

2.2

here 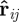is a unit vector defined by .

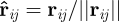We note that the effective surface of an SCE cell is defined by the intersection of the spheres of radius σ around each node. σ is dependent on the SCE geometry and should be chosen to give a continuous platelet surface, i.e. its diameter should be greater than the distance between adjacent SCEs. A detailed description of the choice of σ can be found in §3.2.1.

2.2.3. Cell–vessel wall interaction

Previous attempts to resolve SCE cell–substrate interactions have used a simplistic pairwise interaction based on the Morse potential [11,12]. We have extended the SCE model to prevent cellular-vessel overlap and also to allow accurate representations of cell rolling dynamics. This has been accomplished by using the idea of bonds, representing ligand–receptor (GPIbα–vWF in our case) pairs, that break beyond a given extension [9,17,32]. Since the number of SCEs representing a cell is generally much less than the number of platelet receptor sites, the statistics of modelling many ligand–receptor pairs per SCE is well defined.

The ligand–receptor adhesion modelling component in our model is an extension of the original SCE Morse PP [12]. Namely, we integrate an adhesion submodel from Krasik et al. [32] into the SCE model. (We note that similar adhesion models were used in Jadhav et al. [17] and Mody & King [9] for the study of selectin-mediated leucocyte rolling and platelet–platelet bridging by forming GPIbα–vWF–GPIbα bonds, respectively. However, in those works, the bond force is calculated directly.) In the work of Krasik et al. [33], the adhesion model was developed to study the mechanisms of the neutrophil arrest. Here the probabilities of breakage and formation of bonds are calculated using the Bell model [33].

Our approach to modelling platelet adhesivity is to introduce forces representing the observed receptor–ligand interactions averaged over the individual SCE surfaces, and to model their stochastic behaviour via the Langevin equation. We introduce individual linear springs between each of the SCE and the vessel wall to mimic the receptor–ligand interactions. Parameters in the cell–wall interaction model are determined by the mechanical properties of the receptor–ligand bond, the number of such bonds that are likely to form, given cell contact surface area and the probability of the bonds breaking beyond a given length [9,17,32]. Each SCE/vessel wall interaction is represented by a potential energy function, which is a quadratic function truncated at the maximum and minimum length of the spring (bond) (figure 1a, dashed line). To prevent the SCE surface and the vessel wall from overlapping, a ‘hard wall’ interaction term is added [34] (figure 1a, vertical (dashed-dotted) line).

Since forces in our model are defined as the negative of the gradient of the potential energy, we have to modify this function so that it is continuous, i.e. the spring (bond) cannot break instantaneously. Our approach is illustrated in figure 1a. The ideal force that combines harmonic spring force and hard wall force prevents overlap between the SCE (on the cell surface) and the substrate. We approximate this force with a PP of the Lennard–Jones type [35,36] that emulates the ‘hard wall’ and the first section of the spring potential well. Since the PP force has a long ‘tail’, we truncate this by using a ‘switch’ that turns off the PP force over a short distance and prevents instantaneous energy changes.

The result is a nonlinear spring with a known region of breakage coupled to the defined surfaces that cannot overlap.

The potential energy function between the SCE i and the substrate point j is

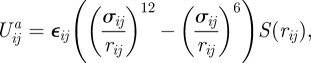2.3

where r_ij = x_j − x_i is the SCE-substrate vector and r_ij = ‖r_ij‖. ε_ij and σ_ij define the adhesion level and distance, respectively. The switch S is defined as

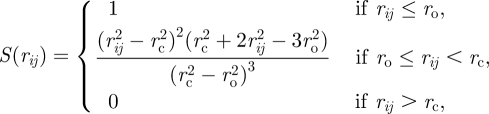2.4

where r_o is the switch-on value and r_c is the cut-off value.

The corresponding vector acting on the SCE i is

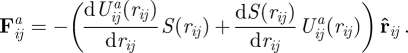2.5

Having defined the form of the potential energy, we now need to determine the position of the substrate point j. We assume that the substrate surface consists of discrete contact points with a known ‘granularity’. The point nearest to the SCE i on the substrate is calculated (using the normal to the substrate surface) and the nearest discrete point, in a direction opposite to the SCE velocity, is selected. Specifically, given a unit vector normal to a plane tangential to the substrate (blood vessel wall) 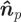and point on this plane x_p, we find the distance to the plane as follows: 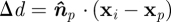. We then find the ‘anchor’ point

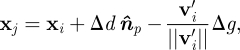2.6

for granularity Δg and vector v′_i, the ith SCEs velocity projected onto the plane. The granularity Δg represents the average distance between receptor–ligand on the substrate.

To parametrize equations (2.3) and (2.4), we need to find the spring constant associated with extending the combined microvillus and receptor–ligand k_s, the rest length (un-forced) d_rest and breaking length d_rest + δd of the combined microvillus and receptor–ligand. The parameters σ_ij, ε_ij are then derived from these. Given the required spring constant k_s, receptor–ligand rest length d_rest and breaking extension δd, we can calculate the variables ε_ij, σ_ij, switch on distance r_o and switch cut-off r_c from equations (2.3) and (2.4)

2.7

2.8

2.9

2.10

Since there is no experiential data for the platelet GPIbα receptor and the wall immobilized vWF ligand binding bonds, we assume that the mechanical properties of the platelet–wall binding bonds are similar to those of the leucocyte selectin–ligand bonds. Therefore, spring constants, receptor–ligand rest length and breaking extension distances are taken from Jadhav et al. [17].

A discussion of the parametrization can be found in §3. The SCEL simulation work flow can be seen in figure 2. The platelet geometry and force parameters for the simulation are generated using the SCE factory written in Python. The resulting simulation files are input to the SCEL simulation engine to produce the relevant trajectory files. The platelet angles are then extracted from the trajectory files using Matlab scripts that are available on the electronic supplementary material website.

Figure 2.

Cell–substrate interaction potential energy.

2.2.4. Brownian dynamics

The simplest fluid–SCE interaction can be modelled as Brownian dynamics. Consider a body with mass m and radius r moving with velocity v in a fluid with viscosity η. The fluid effectively applies a force f to the body in the opposite direction to its movement, which we typically approximate with f = −γv for friction coefficient γ. We can calculate γ from Stokes' Law γ = 6πηr. The simplistic equation of motion is then

2.11

with solution

2.12

Clearly, the velocity would go to zero as time increases, which is not what we observe in reality. We can improve the model by simulating the, assumed random, collisions of the fluid particles with the body. The equation of motion now becomes

2.13

for the random force δR(t). We make the following assumptions about δR(t) by considering that the sum effect of the collisions must be unbiased and that the force of the impacts varies extremely rapidly in any infinitesimal time interval

2.14

for S being the strength of the random force.

Assuming that the fluid acts as a constant-temperature ‘heat bath’, we have

2.15

for N being the d.f., k the Boltzmann coefficient and T the temperature.

From equations (2.14) and (2.15), we can show that δR(t) is satisfied by a random variable with a Gaussian distribution, zero mean and variance of 2γkT. Before we discuss our approach to modelling fluid–SCE interaction, we would like to point out that the Brownian motion of a platelet in the creeping flow regime near a surface has been studied in Mody & King [37], indicating that Brownian motion played an insignificant role in influencing platelet motion.

2.2.5. The Langevin equation

The more complex scenarios of the fluid–SCE interaction can be modelled by using the Langevin equation, allowing the introduction of systematic forces related to SCEs. Given a system of N bodies with a potential energy U(x) as a function of position vector x, then the conservative force vector is given by the gradient F(x) = −∇U(x) and our equation of the motion becomes

2.16

where Z is a vector of normally distributed random variables and M is the diagonal matrix of particle masses.

More rigorous analysis of the method can be made by considering Mori–Zwanzig formalism, and making the appropriate model-dependent approximations. This is the basis for many coarse-grained methods; generally a new set of variables is chosen to model ‘important’ aspects of the system (usually slow d.f.) and the remaining d.f. (usually fast and in our case the fluid) are modelled by their effects on the chosen variables.

Given the large-scale separation of the model, we require a numerical propagation method that gives the correct solutions for a large time step Δt and damping coefficient γ. Appropriate methods that give the correct solution for γΔt ≫ 1 [38] are discussed in numerical methods section in the electronic supplementary material.

2.2.6. Coupling technique

Our problem is to model the interactions of a flowing fluid with bodies representing the blood cellular constituents. This is an extension to the general idea of a non-equilibrium system, which is generally close to equilibrium in some sense. For instance, the expected value of the kinetic energy per degree of freedom is now not equal to kT/2.

The flow is calculated on a three-dimensional grid where the distance between the grid points, Δd, is similar to the platelet dimensions of 2–4 mm. The grid is defined on a domain with x ∈ [0,X], y ∈ [0,Y], z ∈ [0,Z]. We define the fluid velocity vector at grid point i,j,k to be v_ijk^g with corresponding position g_ijk = {iΔd − Δd/2, jΔd − Δd/2, kΔd − Δd/2}, with the indices bounded by I = X/Δd, J = Y/Δd, K = Z/Δd for i, j and k, respectively. The flow is incompressible, so is divergence free. Hence, for a given constant inlet velocity, we have a well-defined average three-dimensional velocity vector

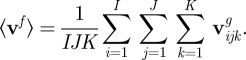2.17

We define the flow velocity at SCE m as

2.18

The system flow velocity vector for inclusion in the modified Langevin framework is then v^f = [v₁^f, … ,v_N^f]^T.

We consider the dynamics to be in a reference frame having velocity 〈v^f〉. We then need to consider the interaction between the underlying flow perturbation vector δv^f = v^f − 〈v^f〉 with the bodies of interest. The additional force vector f^f on the bodies can again be modelled by using Stokes' Law, which gives f^f = γδv^f.

Then, we have

2.19

Note that we need to add the average velocities to those resulting from these equations to get the observed velocities v_o, i.e.

2.20

and add the average movement of the reference frame to get the observed positions x_o

2.21

2.2.7. Surface interface modification

Equation (2.19) does not take account of the cellular surface; each SCE is treated as if it is immersed in the fluid. A more realistic interaction can be achieved by scaling the damping factor γ along the vector connecting the surface SCE to the SCE at the cell centre. We denote this ‘surface interface’ modification as SIM. The centre SCE should see no effect from the flow. The damping applied to SCE i given local damping factor γ_i is

2.22

where Φ is the set of SCEs not on the cell surface, and

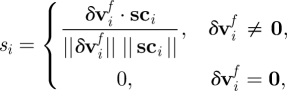2.23

here sc_i = x_i −x_c, and x_c is the position of the SCE at the centre of the cell associated with SCE i.

The updated equation is

2.24

where Γ is now a matrix containing the γ_i.

3. Results

We tested whether our model provides accurate fluid mechanical solutions that can be applied to microscopic spherical and ellipsoidal cells in a bounded fluid. We note that any shapes of cells can be represented by the model. To validate our method, we compare with both theoretical studies and actual experiments of platelet flipping in the plasma flowing through a capillary tube. We separate the results into comparisons with theoretical and experimental results, respectively. All experimental details and electronic supplementary material are archived at http://biomath.math.nd.edu/scelsupplementaryinformation/.

Figure 5 (below) shows the snapshots of the platelet during the flipping process in our simulations.

Figure 5.

Figure showing the flipping of the platelet owing to interaction with high shear rate flow.

3.1. Comparison with experimental data

Here, we compare the experimental results of flipping platelets conducted in vitro with the simulation results. We show that we have achieved good agreement between experiments and simulations.

3.1.1. Experimental and simulation conditions

Flipping of the platelets is detected by measuring the minor and major axes of the platelets in each frame, since the shape of a platelet is approximately elliptical in cross section with λ = 0.5, with the diameter of the platelet being 4 mm. The angle of the platelet can then be deduced and the time to complete a flip can be calculated.

The motion of platelets in different experiments was measured in a platelet-rich plasma prepared from ACD anticoagulated blood from the same healthy donor after informed consent on different days. The platelet counts in the blood samples were in the normal range 2.2–2.5 × 10⁵ ml⁻¹.

Two separate sets of experiments were carried out, differing in the flow rate of 4 or 10 ml min⁻¹ and also the date on which the platelets were obtained (from the same subject). Platelet-rich plasma was drawn through a 0.2 × 2.0 mm rectangular capillary tube (Vitricon, NJ, USA) at 4 or 10 ml min⁻¹. The motion of flowing platelets was recorded by videomicroscopy at 30 fps. Each experiment enabled one to follow multiple different platelets. In the first experiment, the average flow velocity through the capillary was 0.1667 mm s⁻¹ and the maximum platelet velocity was estimated to be 0.4 mm s⁻¹. In the second experiment, the average flow velocity through the capillary was 0.4168 mm s⁻¹ and the maximum velocity was estimated to be 0.7 mm s⁻¹.

To estimate the shear, we assume that the velocity profile is parabolic with zero velocity at the wall of the capillary tube, and the maximum platelet velocity is estimated by finding the platelet with the highest velocity. The shear rate ζ for a platelet can then be readily calculated and, with the observed flipping time t, the product tζ can be found (see also experimental results section for these estimated values).

In the first experiment ten platelets, with velocities ranging from 0.08–0.13 mm s⁻¹ were measured and the upper and lower bounds were found for the flipping time-shear rate products.

In the second experiment, a further 12 platelets, with velocities ranging from 0.08 to 0.39 mm s⁻¹ were measured, and again the upper and lower bounds were found for the flipping time-shear rate products.

The simulations were repeated with a platelet of diameter of 4 mm and λ = 0.5 (cf. 2 mm and λ = 0.25 in the theoretical experiments above).

3.1.2. Experimental results

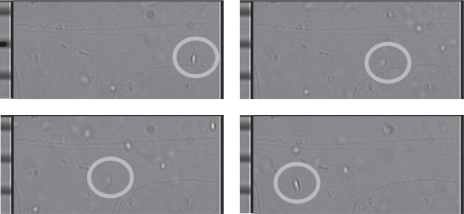
Frames from the first set of experiments for one flipping platelet can be seen in figure 3. Frames 8, 11, 13 and 16 from the file ‘Grabbed Frames from 7-8-2010 4ul-min 2mm cap PRP+Ca.ppt' in the electronic supplementary material and the calibration grid (for converting pixel measurements from the camera frames to physical measurements) has graduations of 10 mm. The platelet can be seen to transition from an elliptical cross section in frame 1 to circular in frame 3 and back to elliptical in frame 4. This represents a half flip (through 180°) in seven frames (233 ms at 30 fps), which has a velocity of 0.17 mm s⁻¹ and a shear rate (from the parabolic profile assumption) of 6.7 s⁻¹. The time-shear rate product is 1.58 (unit-less). We would like to remark that this shear rate is quite low compared with physiological values in the circulation or in previous platelet studies [6], by two orders of magnitude. The microfluidic experimental system used in the study required low flow rates in order to capture high-resolution images of flipping platelets. However, this value of shear rate does not invalidate any of the analysis conducted in the paper.

Figure 3.

Experimentally observed flipping of a human platelet travelling from right to left. The calibration grid shown on the left-hand side of each image has graduations of 10 mm. Snapshots are taken from frames 8, 11, 13 and 14 from the file ‘Grabbed Frames from 7-8-2010 4ul-min 2 mm cap PRP+Ca.ppt' in the electronic supplementary material.

The results for the two sets of experiments can be found in table 1. The average tζ product for each experiment is close in value; we note that the standard deviation (s.d.) for tζ is larger at the higher velocity. Complete tabular data for these experiments can be found in the electronic supplementary material.

Table 1.

Platelet-flipping results.

experiment set	flow (ml min−1)	average tζ	s.d. tζ
1	4	1.6556	0.0814
2	10	1.6972	0.3553
simulation	—	1.81	—

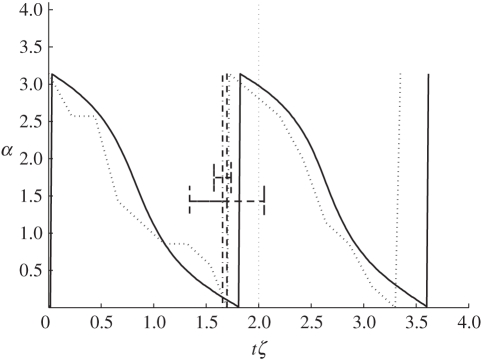
The average time-shear rate product for each experiment set, plotted with the simulation results in figure 4, shows good correlation. Here, the solid curve represents the simulation results and the dotted lines show the mean and 1 s.d. for each of the experiment sets, showing a small error in the simulation. The simulation method reproduces the flow interacting with the human platelets with an observed maximum error (difference in the flipping time of experiment and simulation normalized by the simulation flipping time) of less than 2 s.d. for the first experimental set and less than 1 s.d. for the second experimental set.

Figure 4.

Comparison of the simulated platelet-flipping dynamics with the experiment results for human platelets. The solid curve represents the simulation and the dark-dashed curves represent the results from experiment sets 1 and 2 with error bars at 1 s.d, both showing good correlation with the simulated flipping times. The light-dotted curve represents the actual measured angle of the representative platelet. The variation in angle α to the platelet major axis is plotted against the unit-less time, shear-rate product tζ. Solid line, simulation with γ = 250; dotted line, sample experiment data; dashed–dotted line, experiment 1, tζ; dashed line, experiment 2, tζ.

3.2. Comparison to theoretical studies

We compare, in what follows, our simulation results with the results of Mody et al. [6], which describe theoretical solutions obtained using the Jeffery orbit theory [39] and provide predictions obtained using the analytical platelet-flipping model.

Specifically, we compared our simulation predictions of the effect of the wall on the rotational motion of a platelet, where the ratios of major and minor axes are λ = 0.25 and λ = 0.5 with the analytical solutions for a circular disc computed by Kim et al. [40]. The platelet or circular disk was oriented with its major axis parallel to the surface so that its axis of symmetry lay at right angles to the surface (figure 5). These results are verified using the analytical solutions of Jeffery [39] for the rotational trajectory of an oblate spheroid flowing in the linear shear flow in an unbounded fluid.

In addition to the basic Langevin–Stokes (LS) coupling, we have introduced the ‘surface interaction modification’ (SIM) method in §2.2.7 as an extension to the LS idea. We illustrate the effects of this modification in the tests as well.

3.2.1. Modelling parameters

For modelling the platelet dynamics, we use a set of units based on distance in mm, mass in pg and time in ms.

The flow velocity in the x-direction is given by the following equation

3.1

where ζ is the shear rate and y is the y-coordinate of the SCE. In our simulations, we set ζ = 10⁻³ ms⁻¹, with offset velocity of v₀ = 1.25 ×10⁻⁵ mm ms⁻¹. These parameters were obtained from Mody & King [7].

In our simulations, the relative platelet height H of the platelet from the vessel wall is selected as H >20, where the units are multiples of the platelet radius r. Again this parameter is taken from Mody & King [7].

For the platelet parameters, we use inter-SCE spring constant κ_SCE = 2.4 fJ mm⁻² with all SCEs connected to their nearest neighbours and the central SCE. This parameter is chosen from Jadhav et al. [17], where the cell membrane elasticity is 0.3–3.0 fJ mm⁻².

The mass of each SCE is 0.08 pg by calculating the volume of the spheroid and assuming that the platelet has the same density as water. The platelet is constructed from the SCE on the circumference of five circles stacked in the z-plane. We denote the central (largest) circle as type ‘circle 1’, the adjacent two circles (above and below) as type ‘circle 2’ and the remaining two (smallest) circles type ‘circle 3’.

The effective radius of the SCE is 0.3 mm for circle 3, 0.2 mm for circle 2 and 0.1 mm for circle 1 (the circle with largest radius) to provide a connecting surface map. We use a total of 53 SCEs with platelet λ = 0.25 (ratio of minor to major axis) as depicted in figure 6.

Figure 6.

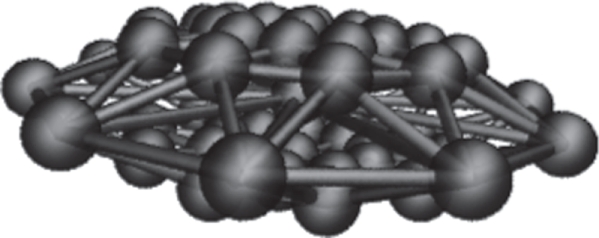
Platelet constructed from 53 SCEs.

To estimate the damping coefficient γ, we consider the force from Stokes' equation weighted by the mass; for a sphere, it is

3.2

where η is the viscosity of the fluid, set to η = 1.2 nNms m s⁻², r is the radius of the cell and m_i is the SCE mass. This yields an approximate figure of 283 m s⁻¹; however, the actual figure should be less since λ < 1.

We incorporate the adhesivity submodel described in §2.2.3 (including the repulsive force) to constrain platelets within the simulated blood vessel and to account for the platelet–vessel wall interactions. We note that we do not provide simulations that specifically test this part of the model, but for completeness, we use the estimated parameters from the literature. For the vessel wall, we select the effective surface distance σ = 0.45 mm from Jadhav et al. [17], which is the combined receptor–ligand length. An estimate for cell–vessel adhesion coefficient can be made from Jadhav et al. [17] as follows. If we consider that the rest length of the receptor–ligand is 0.45 mm and calculate the forward rate constants near to equilibrium, we have k_r ≈ 10⁻³ ms⁻¹. The probability of bond rupture is P_r = 1 − exp(−k_rδt) for time δt; so by choosing a significant probability, say 0.5, we find that the bond lifetime is of the order of 1 ms. If we further assume that the velocity of the cell is approximately equal to that of the liquid at a height of 3r, then the ligand–receptor extension is 2 × 10⁻³ mm. From §2.2.3, this gives adhesion coefficient ε = 8 ×10⁻⁶ fJ per receptor–ligand. From Jadhav et al. [17] if we assume that there are of the order of 250 receptors per cell and two SCEs contact the vessel, then we potentially have six bonds, equating to a combined adhesion coefficient ε_TOT = 5 × 10⁻⁵ fJ. Note that the coefficients are combined as 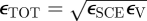for the SCE and vessel coefficients, respectively.

Note that all of the parameters used in the model are estimated from measurements from physical systems—there are no free parameters (table 2).

Table 2.

Model parameters.

parameter	value	units	reference
shear rate ζ	10−3	µs−1	[7]
κSCE	2.4	fJ µm−2	[17]
SCE mass	0.08	pg	water density
SCE radius	0.1–0.3	µm	[7]
SCE number	53
λ	0.25	ratio	[7]
εTOT	5 ×10−5	fJ	[17]
γ	283	µs−1

3.2.2. Platelet surface interaction with flow modification

As discussed in §2.2.7, the LS coupling does not take account of the cellular surface. Instead, each SCE is treated as if it is immersed in the fluid. We find that a more realistic description of the interaction can be achieved by treating the damping factor γ as if scaled along the vector connecting the surface SCE to the SCE at the platelet centre. This effectively allows each SCE to ‘shield’ other SCEs from the fluid flow field, as which would occur in a real-flow scenario. In addition to this modification, the centre SCE should see no effect from the flow. In the following text, we refer to this as the surface interaction modification (SIM) method.

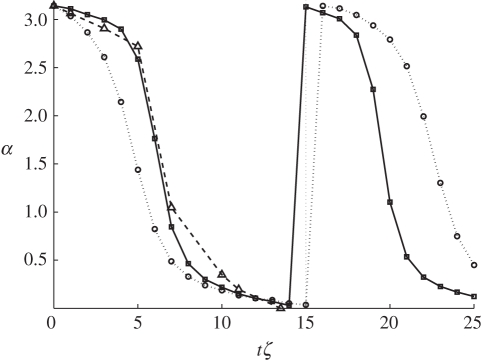
In the first set of simulations, for the platelet flipping, we employed both the basic LS coupling and the SIM method, where we effectively apply a local damping factor to each SCE. All simulation results are compared with the modified Jeffery orbit from Mody et al. [6]. In the LS model, we expect the rate of initial rotation of the platelet to be larger since the flow interacts with all of the SCEs equally. With the SIM method, the flow only acts on the surface SCEs facing the up-stream flow, which slows the initial rotation. These results are illustrated in figure 7, where the advantages of using the SIM approach can be clearly seen. The initial flow/platelet interaction follows the theoretical curve closely, in contrast to the basic LS approach.

Figure 7.

Comparison of the SIM and LS methods on the platelet-flipping dynamics. The surface interaction method SIM shows flipping rates closer to the theoretical Jeffery orbit. The variation in angle α to the platelet major axis is plotted against the unit-less time, shear-rate product tζ. Solid lines with squares, SIM method; dotted line with circles, LS method; dashed line with triangles, Jeffery orbit.

3.2.3. The effect of the damping factor γ

In general, the damping factor 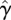is chosen to model the viscosity of the fluid from Stokes' Law

3.3

where η is the viscosity of the fluid and r is the radius of the spherical body. For our LS approach, where we require that the fluid also acts as heat bath for our platelets, the actual value is divided by the mass of the SCE to give γ for our Langevin equation (3.2) in the electronic supplementary material, §B.1. In addition, the use of the SIM method means that the final value will be dependent on the geometry chosen for the platelet.

To determine the correct value, we simulated the flipping platelet with a range of damping factors 25 ≤ γ ≤ 500. The effect of changing this parameter can be seen in figure 8, in which we also compared with the results of Jeffery [39]. Optimal results occur at γ = 250 m s⁻¹, which is close to our estimated value of 283 m s⁻¹ for a spherical cell.

Figure 8.

Effect of varying damping factor γ on the platelet-flipping dynamics. The predicted value of γ = 250 shows flipping rates close to the theoretical Jeffery orbit. The variation in angle α to the platelet major axis is plotted against the unit-less time, shear-rate product tζ.

3.3. Stiffness of platelet

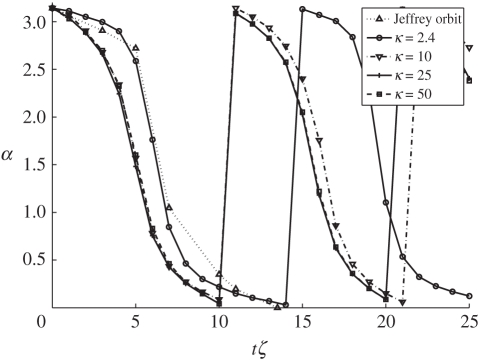
Elasticity of the platelet is defined by the spring constant κ_SCE between pairs of SCEs in a cell. In our model, κ_SCE is not a free parameter as discussed above. Instead it is determined from experimental results (table 2). In this subsection, we demonstrate how the values of κ_SCE affect flipping dynamics of the platelet. The results can be seen in figure 9. Here, we ran simulations with κ = 2.4, 10, 25, 50, respectively. In each of these simulations, we used γ = 250 m s⁻¹. It is evident that if the cell is less elastic, it flips faster under the influence of shear flow. Clearly, if the cell is more elastic, it can absorb more of the stress owing to the flow.

Figure 9.

Effect of varying κ_SCE on the platelet-flipping dynamics. As the stiffness of the platelets κ_SCE is increased the flipping rates become faster than the theoretical Jeffery orbit. The variation in angle α to the platelet major axis is plotted against the unit-less time, shear-rate product tζ.

In Mody et al. [6], simulations were used to characterize trajectories of the freely flowing platelets. It was shown that platelets consistently attach to an adhesive surface only during the first-half of their rotation. Namely, angular orientations of platelets result in compression along the length of the platelet by the hydrodynamic flow forces. Our results suggest that the patterns of platelet flipping are also influenced by the mechanical properties of the platelet itself, which can subsequently affect the platelet binding to an adhesive surface. Conceivably, with a less elastic cell that flips faster, the time it remains in an orientation relative to the surface that permits binding may be shorter than the time required for bond formation. On the other hand, a more elastic cell could stay in the orientation, which allows forming the binding bond for a longer period of time once the cell makes the contact with the surface. Since experimental measurements of the effects of elasticity on platelet dynamics are not available at this time, we use simulations to predict the effects of the elasticity on platelet flipping in the flow. The study of the effect of platelet elasticity on binding to the surface will be the focus of the future work.

4. Discussion

The formation of intravascular thrombi can impair blood flow leading to ischaemic damage to tissues in the vascular field of the vessel. A critical process in the formation or growth of a thrombus is the binding of resting platelets in the flowing blood with the injury site or developing thrombus surface. The binding of platelets is a multistep process involving the establishment of rapidly forming but transient interactions that slow the platelet and cause it to flip. The flipping on the thrombus or injury surface allows for the establishment of slower forming but stable adhesive bonds. To understand the recruitment of resting platelets, it is necessary to understand the initial interactions that are governed by the blood flow, the orientation of the resting platelet flowing in blood and the mechanical properties of platelets.

The main focus of this paper is to describe and to demonstrate a new SCEL method that couples continuum blood flow field, either fixed or modelled using an incompressible Navier–Stokes fluid solver, and the discreet SCE model of a platelet using an innovative Langevin coupling approach. This is a forward coupling where the SCE dynamics are coupled to the flow field, but the flow calculations are not influenced by the SCE positions and velocities (see also figure 10). It is shown that such coupling gives good agreement between simulation results and experimental data provided that the flow rate is not very high. In addition, a SIM is introduced that more accurately models the fluid/platelet interface by considering the interaction to occur at the platelet surface. Moreover, since we use potentials to represent interactions among SCEs, we have further refined the basic adhesion models of Sandersius & Newman [11] and Newman [12] that use potential energy to model adhesion, to both prevent cellular overlap and allow accurate representations of ‘flipping’ dynamics of platelets. We would also like to point out that the stochastic approach to model adhesion is better [9,17,32], and we will incorporate this approach in the future.

Figure 10.

Forward flow coupling.

The extension of the SCE method [12] described in this paper allows modelling of the platelet with realistic shape, elasticity and adhesivity coupled to the flow that is essential to the delivery mechanism in thrombus development in a blood vessel.

Using the SCEL, the three-dimensional motion of a viscoelastic platelet in a shear blood flow was simulated and compared with experiments on tracking platelets in a blood flow chamber under conditions similar to those found in veins in terms of flow velocity and geometry. It has been shown that the complex platelet-flipping dynamics under linear shear flows could be accurately recovered with the SCEL model when compared with the experiments. Simulation results in Mody et al. [6], in which platelets are represented as rigid ellipsoids, suggest that the patterns of platelet binding to and releasing from an adhesive surface are determined by hydrodynamic forces exerted on platelets. Because of this, binding bonds form only in specific platelet orientations where a hydrodynamic compressive force pushes the platelet against the surface. Our study suggests that platelet flipping is also influenced by the mechanical properties of platelets. We show that a softer cell has a longer period of flipping in a blood flow. How cell elasticity affects platelet binding to the adhesive surface will be the subject of the future study.