Volumetric imaging of shark tail hydrodynamics reveals a three-dimensional dual-ring vortex wake structure

Abstract

Understanding how moving organisms generate locomotor forces is fundamental to the analysis of aerodynamic and hydrodynamic flow patterns that are generated during body and appendage oscillation. In the past, this has been accomplished using two-dimensional planar techniques that require reconstruction of three-dimensional flow patterns. We have applied a new, fully three-dimensional, volumetric imaging technique that allows instantaneous capture of wake flow patterns, to a classic problem in functional vertebrate biology: the function of the asymmetrical (heterocercal) tail of swimming sharks to capture the vorticity field within the volume swept by the tail. These data were used to test a previous three-dimensional reconstruction of the shark vortex wake estimated from two-dimensional flow analyses, and show that the volumetric approach reveals a different vortex wake not previously reconstructed from two-dimensional slices. The hydrodynamic wake consists of one set of dual-linked vortex rings produced per half tail beat. In addition, we use a simple passive shark-tail model under robotic control to show that the three-dimensional wake flows of the robotic tail differ from the active tail motion of a live shark, suggesting that active control of kinematics and tail stiffness plays a substantial role in the production of wake vortical patterns.

1. Introduction

Fundamental to understanding how moving organisms generate locomotor forces is the analysis of aerodynamic and hydrodynamic flow patterns that are generated during body and appendage oscillation. Previous work on flying birds [1–4], bats [5,6], swimming fishes [7–9] and jellyfish [10,11] using two-dimensional flow visualization techniques has shown how animals generate wake flow patterns, and has allowed calculation of average lift and thrust forces produced by untethered moving animals. Such two-dimensional visualizations, known as particle image velocimetry (PIV), are accomplished by seeding the air or water with small particles, and using a sheet of laser light to illuminate flow patterns that are then imaged at rates varying from 3 to 1000 Hz. These two-dimensional slices are then used to reconstruct an estimated three-dimensional flow model [1,2,6–8,12,13]. However, building up a three-dimensional pattern of flow vorticity from separate two-dimensional slices is extremely challenging, owing to the need to estimate out-of-plane fluid motion and the requirement of phase-averaging intrinsically unsteady animal movements to derive an average flow pattern [14].

We have applied a new, fully three-dimensional, volumetric imaging technique that allows instantaneous capture of wake flow patterns, to a classic problem in functional vertebrate biology: the function of the asymmetrical (heterocercal) tail of swimming sharks. We use these data to test a previous three-dimensional reconstruction of the shark vortex wake estimated from two-dimensional flow analyses, and show that the volumetric approach reveals a different vortex wake not previously reconstructed from two-dimensional slices. In addition, we use a simple passive shark-tail model under robotic control to show that the three-dimensional wake flows of the robotic tail differ from the active tail motion of a live shark, despite similarities in tail shape.

Sharks, unlike most bony fishes, lack a buoyant swim bladder, and their ability to produce lift while swimming has long been a subject of research and debate in the field of vertebrate locomotion [12,13,15–19]. The shark tail has a dorsal lobe that is larger and extends further posteriorly than the ventral lobe (hence, the shark tail is termed heterocercal), and previous research has suggested that the vortex wake behind swimming sharks differs from that generated by swimming fishes with symmetrical (homocercal) tails [20] because of differences in tail shape: dorsal and ventral lobe asymmetry in heterocercal tails is believed to cause distortions of the vortex wake relative to an externally symmetrical tail shape, as is the case in the engineering example of the effect of inclined trailing edge geometry on vortex ring structure [8,13,21–23].

2. Material and methods

Using an instantaneous volumetric PIV system [21,24,25], we were able to capture series of complete three-dimensional snapshots of the wake structure produced by the heterocercal tails of freely swimming sharks. Four live sharks (mean total length = 24.6 cm), two each of two species, spiny dogfish (Squalus acanthias; see electronic supplementary material) and chain dogfish (Scyliorhinus retifer) with trailing edge spans of 5–6.5 cm and tail beat amplitudes of 6.5–7.5 cm swam at 0.5, 0.75 and 1.0 body lengths per second in a recirculating flow tank equipped with a volumetric PIV system that captured volumes of 14 × 14 × 10 cm³ (x, y, z) at 7.25 Hz (TSI Inc., Shoreview, MN, USA). All wake structures analysed were located completely in the sampling volume and multiple volumes were not combined for wake reconstruction. In addition, a robotic flapping heterocercal plastic foil made of a 22.6 cm long (total length to tip, with a trailing edge span of 6.85 cm) piece of 0.19 mm thick plastic was actuated in ±1.0 cm heave at 2 Hz at the leading edge to swim in the flow tank at its self-propelled speed, 18.8 cm s⁻¹ (see electronic supplementary material) [26]. We measured the flexural stiffness of this flexible foil material to be 3.1 × 10⁻⁴ N m², which is equivalent to the flexural stiffnesses measured for the middle of a fish body [27]. These tail foils are thus good representations of the passive body properties of swimming fishes.

Assuming that the inclined angle of the heterocercal tail was responsible for the structure of the wake vortices as has been previously suggested [13,28], it was hypothesized that the shape of vortices produced by the robotic flapping foil and live sharks should be similar.

Spiny dogfish (Squalus acanthias) were obtained from the Woods Hole Marine Resource Center (Woods Hole, MA, USA). Chain dogfish (Scyliorhinus retifer) were borrowed from the New England Aquarium (Boston, MA, USA) for these experiments. Sharks were kept in two 1140 l circular tanks of 16°C saltwater with 12 L : 12 D cycles and fed three times weekly until satiation. For data capture, sharks were placed into a 160 l recirculating flow tank with an 80 × 20 × 20 cm working area, and trained to swim in the centre of flow, away from the walls. All animals were handled ethically according to Harvard University and New England Aquarium Animal Care and Use protocols. A total of 39 sequences of spiny dogfish and 25 sequences of chain catsharks were analysed, with 10–15 fluid volumes captured per sequence.

For the robotic shark tails, flexible foil material cut into the general shape of a heterocercal shark tail with an inclined trailing edge (as seen in figures 1a and 4) was mounted on a rod and attached to a carriage, which is able to move freely on air-bearings with very little friction [26]. Five extended sequences of the robotic heterocercal foil and three extended sequences of the more ‘shark-like’ robotic foil (as seen in figure 4) were analysed with 15–20 fluid volumes captured per sequence. Fewer sequences were necessary with the robot as there was no variation among settings or sequences.

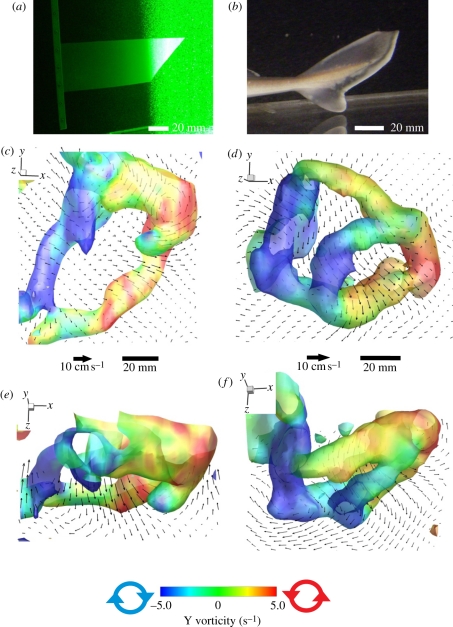
Figure 1.

Three-dimensional wakes from the robotic heterocercal plastic foil (left) and spiny dogfish (right). (a) Robotic heterocercal plastic foil swimming (self-propelled) in laser volume. (b) Tail fin of the spiny dogfish. Lateral (c,d) and dorsal (e, f) views of the wake structure isosurfaced by absolute vorticity and then colour-coded by Y vorticity (±5.0 s⁻¹) of the wake produced by the robotic foil (c,e; actuated at 2.0 Hz) and spiny dogfish (d,f; swimming at 0.5 l s⁻¹, or 0.63 Hz), respectively. Lateral isosurface views include a vertical slice (XY plane) with velocity vectors; dorsal isosurface views include a horizontal slice (XZ plane) with velocity vectors. Every third velocity vector is shown for clarity.

Figure 4.

Shark tail-shaped plastic robotic flapping foil (left) and lateral view of Y vorticity isosurface (3.5 s⁻¹; right) of vortex produced when swimming at 2.0 Hz, recorded with volumetric imaging. Velocity vectors are shown for two horizontal (XZ plane) slices, one through each the dorsal and ventral rings. The isosurface is shown as a mirror-image to the original recording, to have same upstream orientation as other figures. These results demonstrate that the inclined trailing edge of a passive foil actuated only in heave at the leading edge can generate a ring-within-a-ring vortex structure. Only every third velocity vector is shown for clarity.

The volume of interest (14 × 14 × 10 cm) downstream of the swimming shark or robot was illuminated by a 120 mJ dual-head pulse laser [24]. The laser was pulsed at a frequency of 14.5 Hz, which was synchronized with recording capture by the volumetric 3-component velocimetry (V3V) volumetric flow imaging tripod camera probe (TSI Incorporated, Shoreview, MN, USA). The flow tank was seeded with 50 µm plastic particles that were suspended in flow. Particle position and displacements were calculated between laser pulses using V3V software as detailed in Troolin & Longmire [21] and Pereira et al. [25]. In brief, the three lens and charge-coupled device (CCD) arrays (2048 × 2048) were calibrated by traversing a known target across the transverse (Z) plane of the flow tank where the fish were to swim. Groups of image pairs (one pair per camera—3 pairs in total) were captured at 7.25 Hz with a time of 3.5 ms in between each image pair, at 12 bit resolution. The volume imaged was 14 × 14 × 10 cm, and for each image pair approximately 70 000 particles were identified in all three images, and from these approximately 35 000 triplets representing three views of the same particle were identified and tracked between laser pulses. These particles were gridded to give a final volumetric matrix of 57 × 57 × 33 vectors (=107 217 total vectors within the volume). As a control, particle images were captured while the flow tank was running with no fish or robot inside. Under control conditions, mean vorticity magnitude was 0.74 ± 0.11 s⁻¹ (mean ± s.e.; X vorticity = −0.10 ± 0.09 s⁻¹, Y vorticity = −0.20 ± 0.19 s⁻¹, Z vorticity = −0.037 ± 0.079 s⁻¹).

A detailed sensitivity analysis of the V3V technique can be found in Graff & Gharib [29]. Uncertainty of the V3V measurement derives from two primary sources: uncertainty in the time separation between laser pulses and uncertainty in measuring the three-dimensional spatial location of the particles. The firing of the laser pulses is controlled by the timing electronics of the system, and the timing uncertainty is 1 ns, resulting in a negligible effect on velocity. The uncertainty in the measured particle positions has been determined using a planar grid of dots with known spacing placed at various locations within the measurement volume. Measurement of the dot positions showed an uncertainty of 20 µm in the x- and y-directions, and 80 µm in the z-direction. The time between laser pulses is set such that the particle displacement between two successive image frames is approximately 2 mm in the area of interest. Thus, the inherent uncertainty in the velocity measurement is approximately 1 per cent in x- and y-directions and 4 per cent in the z-direction.

3. Results

Freely swimming sharks and robotic models swam at Reynolds numbers of 29 000–62 500 and 42 500, respectively (based on body and foil length), and at Strouhal numbers of 0.36–0.41 and 0.21, respectively (table 1), with the trailing edge of the tail or foil located within the laser light volume within the recirculating flow tank. By definition, self-propelled speed of the foil occurred only at the single speed where position was maintained when driven at a given oscillation frequency [26], and speed of the swimming foil was not altered experimentally from this self-propelled condition. Because of this and the fact that the oscillation frequency was matched to that of the swimming shark, there was no variation possible in Strouhal number. Flexible foil shark tails nonetheless swam at Strouhal numbers in the range observed for swimming fishes [30,31]. The wakes of both the robotic flapping foil and the sharks consisted of linked vortex rings, and in both cases the vortex ring structure induced a substantial downwash at an angle of −32° to −50° to the horizontal, indicating that considerable lift forces were generated by both propulsive surfaces (figure 1 and table 2: jet angle in XY plane). However, the shark vortex wake three-dimensional structure consisted of dual-linked rings of roughly equal size and vorticity (mean vorticity of 6.6–8.2 s⁻¹; table 2) produced during each half beat of the tail, while the robotic flapping shark tail-like foil (figure 1) with the inclined trailing edge produced one large ring (mean vorticity of 11.6–12.5 s⁻¹; table 2) with a much weaker inner vortex ring (mean vorticity of 1.8 s⁻¹; table 2). This smaller inner ring from the flapping foil was of a different size, orientation and significantly lower vorticity (p < 0.0001) than the vortex rings produced by the live shark, and is only visible when lower vorticity thresholds are chosen for the three-dimensional isosurface (e.g. figure 2f, below). This smaller ring in the robotic foil vortex wake was not seen in the volumetric flow data from freely swimming sharks.

Table 1.

Reynolds (Re) and Strouhal (St) numbers of robotic flapping heterocercal foil swimming at its self-propelled speed and spiny dogfish swimming at 0.5, 0.75 and 1.0 l s⁻¹.

		spiny dogfish
	robotic foil	0.5 l s−1	0.75 l s−1	1.0 l s−1
flow tank speed (cm s–1)	18.8	11.4	18.6	25.0
Re	42 500	29 000	45 700	62 500
St	0.21	0.41	0.38	0.36

Table 2.

Dimensions and orientations of wake structures, imaged volumetrically, produced by swimming robotic flapping heterocercal foil (22.6 cm length) and by a 31 cm spiny dogfish (mean and standard error (s.e.), n = 5–7 swimming sequences for each). Jet angle is measured relative to free-stream flow. DS and US refer to the downstream and upstream portions of the large vortex rings, respectively.

	robotic flapper		spiny dogfish
	mean	s.e.	mean	s.e.
long axis of small ring (mm)	45.6	2.6	50.1	3.3
short axis of small ring (mm)	33.1	2.3	40.9	2.7
long axis of large ring (mm)	84.4	3.6	74.3	0.7
short axis of large ring (mm)	43.4	1.6	56.5	2.3
small ring angle relative to XY plane (°)	17.3	2.9	60.5	2.9
small ring angle relative to YZ plane (°)	95.5	3.4	90.5	6.1
small ring angle relative to XZ plane (°)	99.7	2.4	116.6	2.0
large ring angle relative to XY plane (°)	6.9	1.4	40.9	3.2
large ring angle relative to YZ plane (°)	31.2	2.6	92.7	3.0
large ring angle relative to XZ plane (°)	87.7	3.2	117.2	4.8
jet angle in XY plane (°)	−32.7	3.8	−50.7	2.8
jet angle in XZ plane (°)	72.1	1.9	63.5	4.4
maximum vorticity of small ring (s−1)	1.8	0.2	7.1	0.4
maximum vorticity of large ring (s−1); DS	12.5	0.6	8.2	0.5
maximum vorticity of large ring (s−1); US	11.6	1.0	6.6	0.3

Figure 2.

Instantaneously captured three-dimensional vorticity patterns in the wake produced by a robotic heterocercal plastic foil swimming (self-propelled) actuated at the leading edge at a frequency of 2.0 Hz. (a) Lateral view of vorticity magnitude isosurface (6.5 s⁻¹) of linked vortex rings produced by a steadily swimming robotic foil. (b) Top, (c) middle and (d) bottom horizontal (XZ plane) slices from sequence shown in (a) coloured by Y vorticity (±5.0 s⁻¹) to demonstrate the separated and connected portions of the rings (e.g. blue areas of vorticity). The strongest jets are produced in the dorsal portion of the ring, as illustrated by the vectors in (b). (e) Dorsal view of (a) in which the laterally displaced linkage of the rings is apparent. (f) Same structures as (a) at a vorticity magnitude isosurface of 4.0 s⁻¹. The small ring in the dorsal region is of lower vorticity less than or equal to 4.5 s⁻¹.

The double vortex ring structure behind swimming sharks had one ring facing downstream behind the shark and the other projecting laterally to the point of maximum lateral excursion of the shark tail beat. While the dimensions of the large vortex structures were similar between the robotic flapper and the live shark (table 2), the angle of the small ring relative to the XY plane was greater for the live shark than the flapper (p < 0.001) indicating that the shark vortices were oriented more downstream while the flapping foil produced vortices that were oriented laterally (table 2). The long-axis of the large ring produced by the shark was oriented at greater angles with respect to the XY (p < 0.001), YZ (p < 0.001) and XZ planes (p = 0.001), indicating production of a jet oriented more posteriorly and ventrally, and therefore producing more thrust and lift than that of the robotic flapping foil.

Continuous tail beats by both sharks and the robotic flapper produced a chain of linked rings facing in alternating left and right directions. Rings produced by the robotic heterocercal flapping foil (figure 2a–e) were linked at their horizontal midlines and separated more dorsally and ventrally (figure 2b–d) than shark vortex rings. The highest velocity jets within the ring structure were produced in the area of the small ring (figure 2b,c) whereas weaker jets were observed in the large ring (figure 2d). The small rings produced by the robotic flapping heterocercal foil, which resembled the structure proposed by Wilga & Lauder [13], were of a lower vorticity than the large rings (4.0 s⁻¹ or less, figure 2f).

Analysis of the time course of three-dimensional vortex formation from the shark tail shows that the smaller ring forms first, and is then shed as the tail passes behind the midline of the shark (figure 3). The larger, more laterally directed ring within the vortex is then shed as the tail reaches maximum lateral excursion, producing a dual-linked ring vortex structure.

Figure 3.

Sequential time series of vortices being shed from the tail of a swimming shark (0.5 l s⁻¹, or 0.63 Hz) in lateral (XY plane, (a)) and ventral (XZ plane, (b)) views. Isosurfaces and slices are contoured by Y vorticity. White asterisks denote the downstream edge of the forming vortex through the time series. The grey-dashed line at t = 0.133 s in (a) represents the location of the slices shown in panel (b). In (b), high-speed video of the same shark that produced the vortex in this figure, swimming at approximately the same frequency, was matched to each time frame by comparison with the silhouette of the tail visible in the upstream edge of the three-dimensional isosurface reconstruction to show tail position.

To examine the effect of the narrow region of the shark body just anterior to the tail (the caudal peduncle), which was not a component of the heterocercal foil shown in figure 1, a second foil with a more ‘shark-like’ shape and narrower peduncle was constructed and swam in the flow tank, flapping at 2.0 Hz at its self-propelled speed (figure 4). There was no effect of the resulting increased range of lateral excursion of the dorsal lobe on the shape or orientation of vortices produced when compared with the heterocercal robotic flapping foil. Like the heterocercal foil, the small ring produced by the shark-like robotic foil was of relatively low vorticity (less than or equal to 4.5 s⁻¹).

4. Discussion

Just as the use of three-dimensional kinematics was imperative to determine the position of the shark tail during locomotion and for rejecting models of tail function based on two-dimensional views [16], it is now apparent that volumetric study of hydrodynamics is necessary for a complete, instantaneous view of wake structures [24]. The vertically oriented ring-within-a-ring vortex ring structure proposed by Wilga & Lauder [13] using two-dimensional methods was a sensible interpretation of the planar view PIV, but the single two-dimensional slice did not give enough information for a correct interpretation in three dimensions (figure 5). A more lateral slice of the same orientation would have shown that the two areas of clockwise rotation vorticity (shown in blue) merge together as two points of the same section of the vortex ring, and these volumetric data allow reconstruction of previous two-dimensional slices and show how difficult reconstruction of a complex three-dimensional wake is from planar two-dimensional slices.

Figure 5.

(a) Two-dimensional (XY plane) PIV reanalysis of swimming dogfish data from Wilga & Lauder [13,28] with high-vorticity regions used to produce hypothetical vortex ring structure circled in white. The Wilga & Lauder [13,28] data were from planar PIV only, and were used to infer the vortex structure described in that paper. The volumetric data presented here show the same vorticity patterns when sliced appropriately in the vertical plane, but further demonstrate that the previously reconstructed vortex wake is inaccurate. (b) Vorticity magnitude isosurface (grey) of three-dimensional vortex ring structure produced by swimming dogfish recorded with volumetric imaging, along with corresponding XY plane showing similar vorticity patterns to (a). Dorsal (c) and posterior (d) views of the volumetric isosurface and XY plane in (b) with vortex rings coloured by vorticity. Only every third velocity vector is shown for clarity.

It is now evident that the inclined angle of the shark heterocercal tail is not the determinant factor in vortex ring formation, as previously reported [12,13]; live swimming sharks produce a wake structure very different from that of the classical engineering model of the inclined vortex generator and the inclined flapping foil used here. Other factors, such as stiffness of the tail, swimming frequency and Strouhal number may be responsible for differences in wake structure [32,33].

As suggested by previous research [12,13], the angle of the trailing edge of the tail is reflected in the angle of the vortex ring structure and jet direction (table 2). This effect was seen in chain dogfish, the second shark species studied, which has a tail angled more towards the horizontal than does the spiny dogfish, resulting in more ventrally facing vortex rings (figure 6). Also, the chain dogfish tail is shorter in the dorso-ventral orientation than the spiny dogfish, which may explain the compressed ring structure that we observed relative to the vortex rings produced by spiny dogfish. This compressed, ventrally oriented ring structure of the chain dogfish suggests a relatively smaller jet that may generate less thrust than produced by the spiny dogfish tail.

Figure 6.

(a) Wake vortices created by steady swimming chain dogfish (Scyliorhinus retifer) in the lateral, (b) dorso-lateral, (c) posterior or downstream and (d) ventral views, produced with volumetric imaging. The major vortex loop is shown as a vorticity isosurface which is then coloured by Y vorticity. Also shown is a vertical (XY) planar vector field through the centre of the vortex ring. Note the strong side jet flows in panel (c) and the downwash through the centre of the ring in (b). Only every third velocity vector is shown for clarity.

However, the dissimilarity of the vortex shape produced by swimming sharks with respect to that produced by the flapper indicates that the angle of the trailing edge of the heterocercal tail is not the only determinant of wake structure. Kinematics of the tail probably play a large role producing the orientation of the jet and vortex, as has been demonstrated in sturgeon, mackerel and bluegill sunfish [20,34,35]. Furthermore, in contrast to the robotic flapping foil, live sharks possess musculature in the tail that can act to modify the tail angle or stiffness of the fin [36]. Such active stiffness modulation would allow sharks to actively alter their vortex wake and manipulate thrust and lift force directions during swimming.

As the shark tail oscillates through a tail beat cycle, the hydrodynamic loading experienced by the tail is expected to be dependent upon tail speed and position. In addition, recent study of freely swimming sharks in which electrical activity in the radialis muscle, an intrinsic shark tail muscle, was recorded during locomotion, has shown that this muscle is capable of actively altering tail stiffness [36]. As the tail crosses the midline, the radialis muscles within the tail are actively stiffening the tail against this increased hydrodynamic loading [36]. And it is precisely at this time of maximum expected stiffness and greatest drag that the first vortex is produced (figure 3), resulting in a jet with strong lift and thrust components (table 2). The remaining vorticity is shed as the tail is cupped slightly and continues laterally until it changes direction at maximum lateral excursion [36]. Experimental fluid dynamical analysis of live fishes swimming has shown that vortices are released from the trailing edge of a swimming object at points of maximum lateral excursion [37–39]; however, the data presented here illustrate that the shark sheds the first vortex during the lateral pass of the tail (figure 3), perhaps as a result of the highly flexible tail and shedding that occurs as the two lobes move differentially (something not seen in previously studied fishes with symmetrical tails). We speculate that the most likely way to accomplish release of a vortex without a change in the direction of travel is to change the physical properties of the fin—such as its stiffness. Additionally, we hypothesize that the production of two vortices during a single tail pass serves continuously to generate lift and thrust throughout the tail beat, as opposed to more periodic thrust generation during which time the animal would experience a relative reduction in forward momentum and travel.

Our results also highlight the potential importance of active stiffness modulation in the highly deformable propulsive surfaces of fishes [36,40,41], which adds a dimension of control beyond the passively flexible foils often studied as engineering propulsive surfaces and relatively inflexible robotic wing models [42–44]. Fish fins undergo considerable deformation during movement [14] and this deformation is under partial active control and is a key factor in allowing thrust generation throughout the fin or tail beat cycle [45,46]. The approach of comparing the vortex wake produced by a self-propelled highly flexible robotic model of a propulsive surface with that produced by a freely swimming shark demonstrates the utility of simple flexible robotic models as a ‘null hypothesis’ in facilitating identification of the underlying factors responsible for generating a particular wake pattern. We propose that highly flexible robotic foils need to incorporate active stiffness control akin to that available in a shark or bony fish tail if they are to generate biomimetic wakes and demonstrate biomimetic locomotor performance.

Our findings also emphasize two items of concern in the study of biological fluid dynamics. The first is that using repetitive two-dimensional PIV flow field slices to extrapolate three-dimensional vortex wake structures can lead to misinterpretation and erroneous representations of wake hydrodynamics in cases where a complex three-dimensional wake is produced by a flexible flapping surface. Using such methods, it is difficult to ensure that only one possible three-dimensional model of a vortex wake is consistent with two-dimensional data. The difficulty in reconstructing a three-dimensional model from two-dimensional data is certainly not a novel problem, and is a cause for concern in many science fields. Secondly, while a robotic model may replicate the shape and kinematics of a biological propulsor, it often does not possess the inherent ability to modulate shape or stiffness in the way that a live swimming organism does. The lack of ability to control shape and stiffness is apparent in the difference in the wake structures produced by the live swimming shark and the robotic model, and incorporating active stiffness control into swimming robotic platforms is a key future challenge for the field of swimming biorobotics.