Nonlinear acoustic complexity in a fish ‘two-voice’ system

Abstract

Acoustic signals play essential roles in social communication and show a strong selection for novel morphologies leading to increased call complexity in many taxa. Among vertebrates, repeated innovations in the larynges of frogs and mammals and the syrinx of songbirds have enhanced the spectro-temporal content, and hence the diversity of vocalizations. This acoustic diversification includes nonlinear characteristics that expand frequency profiles beyond the traditional categorization of harmonic and broadband calls. Fishes have remained a notable exception to evidence for such acoustic innovations among vertebrates, despite their being the largest group of living vertebrates that also exhibit widespread evolution of sound production. Here, we combine rigorous acoustic and mathematical analyses with experimental silencing of the vocal motor system to show how a novel swim bladder mechanism in a toadfish enables it to generate calls exhibiting nonlinearities like those found among frogs, birds and mammals, including primates. By showing that fishes have evolved nonlinear acoustic signalling like all other major lineages of vocal vertebrates, these results suggest strong selection pressure favouring this mechanism to enrich the spectro-temporal content and complexity of vocal signals.

1. Introduction

Acoustic signals play essential roles in social communication to mediate inter- and intraspecific interactions [1]. Across the diversity of vocal vertebrates—from fishes to frogs, songbirds and mammals—analysis of communication signals from these taxonomic groups suggests a strong selection for increased call complexity [2–7]. Complexity in acoustic signals has traditionally been described by patterns of frequency and/or amplitude modulation, or the sequential combination of harmonic and broadband elements [1,4,7]. However, recent application of chaos theory and nonlinear time-series analysis to animal calls [4,8] has revealed a new metric of acoustic complexity that expands frequency profiles beyond this dichotomous categorization of harmonic and broadband calls in both vertebrate [1,4,7,8] and invertebrate lineages [9–11].

Vertebrates' ability to produce nonlinear acoustic signals is facilitated by specific vocal morphologies, as shown for the larynges of frogs and mammals [4,7] and the syrinx of songbirds [12–14]. Songbirds exhibit biphonation (‘two-voices’), the most thoroughly studied vocal mechanism capable of producing nonlinear signals, which arises from the ability of each side of the syrinx to independently produce temporally overlapping sounds (e.g. [12,14,15]). Bilateral morphological structures appear to facilitate such acoustic innovations in birds, as well as amphibians and mammals [4,7,14].

Fishes have remained a notable exception to a demonstration of such acoustic innovations, despite their being the largest group of living vertebrates with evidence for widespread evolution of sound production [16]. Toadfishes are one of the best-studied groups of vocal fishes, producing several types of advertisement and agonistic calls that play essential roles in mate attraction and territoriality [5,17,18]. The toadfish vocal organ, the swim bladder, is typically a single structure in toadfishes and most other fishes using this sonic mechanism [17,19]. Here, through mathematical modelling of acoustic signals and experimental silencing of the vocal organ, we demonstrate that the bilaterally separated swim bladder in the three-spined toadfish, Batrachomoeus trispinosus, has facilitated a concomitant acoustic innovation resulting in nonlinear acoustic complexity previously only observed in tetrapods. Novel vocal morphologies have thus led to nonlinear acoustic signalling among fishes, convergent with both the morphologies and signals underlying tetrapod communication.

2. Material and methods

Batrachomoeus trispinosus (Günther) were acquired through the aquarium trade and maintained in community aquaria in an environmental control room maintained on a 13 L : 11 D cycle. Main room lights were switched off from 20.00 to 07.00 h, with the lunar cycle replicated by an incandescent moonlight timer [5]. All methods used for animal husbandry and acoustic recording are described fully elsewhere [5].

(a). Experimental acoustic recording

Three different treatment groups of animals were used for experiments. (i) Control animals (n = 6) were housed communally (150 l aquaria) to allow for recording of sounds in social contexts. (ii) Fish in the experimental group to undergo swim bladder nerve transection (n = 4) were housed individually (38 l aquaria) and separately recorded in isolation (76 l aquarium with no gravel or filter to create background noise). (iii) Sham-operated fish (n = 6), to determine whether the experimental surgery limited the fish's ability to produce nonlinear vocalizations, were housed communally (150 l aquaria) to maximize the occurrence of social vocalizations.

For the experimental fish, grunts were elicited from individuals by chasing them by hand. After multiple sounds (more than five) were recorded from each individual, fish had the left (n = 2) or right (n = 2) swim bladder muscle nerve transected. Following recovery, grunts were elicited from these experimental fish to allow for the direct comparison of pre-operative and post-operative sounds, enabling each animal to serve as its own control.

(b). Surgery

Fish were anaesthetized by immersion in 0.025 per cent benzocaine [5] and were randomly assigned to either an experimental group (n = 4) where the vocal motor nerve was transected or a sham-surgery control group (n = 6), where only the body wall was cut, but the vocal motor nerve remained intact. For the experimental group, a small incision was made on the left (n = 2) or right (n = 2) side of the body wall (randomly chosen), and the vocal motor nerve was cut. For the sham operation, only a small incision was made in the left (n = 3) or right (n = 3) side of the body wall (randomly chosen). The surgical site was closed with silk suture, sealed with Vetbond tissue adhesive (3M Corporation, Saint Paul, MN, USA), and the fish was allowed to recover for at least one week before sound recordings. Following deep anaesthetization, all experimental fish were euthanized at the end of the experiments to verify the presence and absence (sham-operated) of transections.

(c). Acoustic analysis

Sounds were recorded as in Rice & Bass [5], and spectrograms were qualitatively analysed using the Raven 1.4 software package [20] (Hann window, FFT size = 2048, 95% overlap). Mean (±s.e.) power levels at each frequency were calculated from power spectra for calls from both intact and transected animals exported from Audacity (http://audacity.sourceforge.net). Nonlinear features were quantitatively analysed with the TSTool analysis package for MatLab [21], a nonlinear time-series analysis program. For calls analysed with TSTool, all calls were down-sampled to the same sampling frequency of 22.05 kHz. Incidental ambient noise (such as aquarium filters or sounds generated by fish movement) was filtered out of the recordings (using Raven or Audacity); however, filtering of this noise did not substantially change the results of the analysis, as the analysis on different permutations of the sound (e.g. different levels of background noise, different sampling frequencies) was remarkably consistent. We also experimented with the nonlinear analysis of synthetically designed signals in Audacity (100 Hz sine wave, 100 Hz square wave, 75 Hz combined with 105 Hz sine waves to produce biphonation, white noise); those results (not shown) were consistent with our findings of the presence and absence of nonlinear phenomena in natural signals.

(d). Statistical analysis

Calls from intact and transected animals were quantitatively compared using spectrographic cross-correlation (SPCC) followed by principal coordinates analysis (PCO), following Rice & Bass [5] and Cortopassi & Bradbury [22]. SPCC was performed by cross-correlation, based on the peaks of the signals using the batch correlator function in Raven with a Hann window, FFT = 2048 and 95 per cent overlap settings (used for the qualitative spectrographic analysis, as above). All sounds were bandpass filtered from 0 to 3000 Hz to reduce the effects of background noise. A total of 82 sounds (n = 22 intact; n = 60 transected) were included in the SPCC analysis, resulting in a total of 6724 sound comparisons. The resulting similarity matrix generated from the SPCC was converted to a distance matrix (distance = 1 − similarity) and analysed with a PCO using the PCoord script in R [23], following Cortopassi & Bradbury [22]. Eigenvectors from coordinate axes 1–4 (all with eigenvalues greater than 1) from the SPCC–PCO were statistically analysed with a nested MANOVA, in order to examine differences between treatment groups while still accounting for differences between fishes. Any additional statistical analyses were performed in JMP 5.0.1.2 (SAS Institute, Cary, NC, USA).

3. Results and discussion

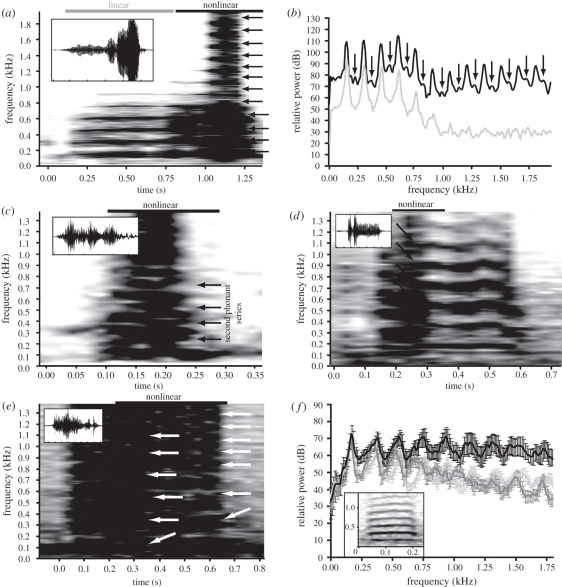
The three-spined toadfish, B. trispinosus, produces two major types of social vocalization: advertisement ‘hoots’ and agonistic ‘grunts’ [5]. Visual analysis of the spectrograms of naturally elicited calls from communally housed fish (n = 6) revealed that 38.0 per cent of hoots (275/723) and 34.1 per cent of grunts (177/519) exhibited at least one form of nonlinearity, including deterministic chaos (267 hoots, 52 grunts; figure 1a), subharmonics (33 hoots, 68 grunts; figure 1a), biphonation (four hoots, 12 grunts; figure 1c), frequency jumps (two hoots, eight grunts; figure 1d) and bifurcation (two hoots, seven grunts; figure 1e). These different classes of nonlinear sounds are readily identifiable through spectrographic analysis [4,24,25]. Deterministic chaos is the combination of a harmonic series coincident with increased levels of broadband energy. Subharmonics are the appearance of frequency bands directly related to some consistent fraction (e.g. a quarter or half) of the frequencies in the original harmonic series. Biphonation is the overlap of two independent (i.e. not-harmonically related) sounds, often referred to as ‘two-voices’; when these two sound series are close in their fundamental frequency, they result in the production of acoustic beats [5,12]. A frequency jump is an abrupt upward shift in all frequency components. Bifurcations are evident when harmonic bands appear to ‘split’ and are often a transition between linear and nonlinear states (usually deterministic chaos).

Figure 1.

Acoustic analysis of linear and nonlinear sounds in the three-spined toadfish. (a) Spectrogram of representative advertisement sound (‘hoot’) of three-spined toadfish (B. trispinosus) showing linear and nonlinear features (with labelled bars above sections), including deterministic chaos and subharmonics (indicated with arrows). Inset shows waveform of this call; here and in (c)–(e), x-axis tick marks represent 0.25 s, for both the oscillogram and the larger spectrogram. (b) Power spectra corresponding to spectrogram in (a), showing the frequency spectra of linear (grey) and nonlinear (black) portions of the call. Arrows indicate subharmonics. (c) Spectrogram of representative agonistic sound (‘grunt’) exhibiting biphonation, with arrows indicating second phonant series. Inset shows the sound's waveform. (d) Spectrogram of a grunt exhibiting a frequency jump, with arrows indicating the occurrence of the jump; the inset shows the sound's waveform. (e) Spectrogram of a grunt exhibiting a bifurcation, with arrows indicating the bifurcating harmonic bands; the inset shows the sound's waveform. (f) Averaged power spectra (±s.e.) of a subset of agonistic sounds of fish from transection experiments with intact swim bladder nerves from four fish (13 representative sounds) with nonlinear (black) and linear (light grey) components, versus sounds from the same four fish with one transected nerve (dark grey, 32 calls). The inset shows the spectrogram of an agonistic grunt from a fish with a transected swim bladder nerve showing only linear harmonic features (for comparison with (c)). The y-axis represents relative power (dB), and the x-axis represents time (s).

We analysed the number of linear versus nonlinear hoots and grunts per two hour time period (see electronic supplementary material, figure S1). Nonlinear hoots became prevalent at 23.00 and increased in number until 5.00. Linear hoots peaked in number during a more restricted time period (23.00–3.00 h) before starting a sharp decline as the occurrence of nonlinear hoots peaked (see electronic supplementary material, figure S1a). Conversely, nonlinear grunts were most frequent between 21.00 and 23.00 h—threefold greater in number than linear grunts, which were most often from 3.00 to 5.00 h (see electronic supplementary material, figure S1b). During the lunar cycle, all nonlinear calls, hoots and grunts predominantly increased in their occurrence around the full moon, whereas linear calls were highest at the waxing half-moon and approaching the new moon (see electronic supplementary material, figure S1c).

Like the chaotic calls from other vertebrates [4,24,25], the spectrograms revealed co-occurrence of harmonic structure and broadband energy (i.e. deterministic chaos) that was independent of harmonics. For example, 40.5 per cent of hoots with deterministic chaos, the predominant nonlinearity, had an initial linear section followed by a chaotic nonlinear section (figure 1a). A statistical analysis of a subset of these calls (n = 9) reveals significantly more amplitude in chaotic portions of the calls for the first four harmonics; the frequency range of these harmonics corresponds to the range of greatest hearing sensitivity in toadfishes [5] (two-tailed paired t-tests followed by Bonferroni correction [26]; F₀: t₈ = −5.92, p < 0.0004; F₁: t₈ = −6.46, p < 0.0002; F₂: t₈ = −7.48, p < 0.0001; F₃: t₈ = −8.43, p < 0.00002; figure 1a,b).

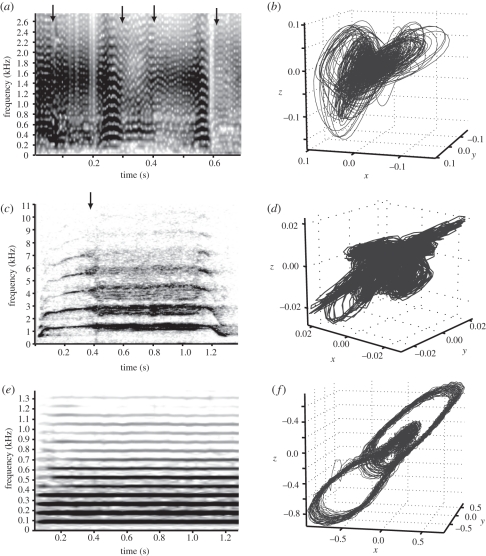
For a more rigorous mathematical analysis to compare nonlinearities in toadfish vocalizations with those reported for tetrapods [4], we employed three analytical tools derived from chaos theory [8,27]: phase-space plots, Poincaré sections and recurrence plots. We chose a chimpanzee (Pan troglodytes) pant-hoot and cockatoo (Cacatua galerita) scream as exemplars of tetrapod calls previously characterized as exhibiting deterministic chaos [4,28]. Like the spectrogram of three-spined toadfish calls (figure 2a, shown on a slower time scale than figure 1a to facilitate comparisons with other species), the chimpanzee (figure 2c) and cockatoo (electronic supplementary material, figure S2q) calls showed transitions from stable harmonics to a combination of harmonic and broadband features indicative of deterministic chaos [4,7,8,27]. The hoot-like calls of two other closely related toadfishes, the plainfin midshipman (Porichthys notatus) and the gulf toadfish (Opsanus beta) [5,29,30], were analysed to demonstrate the evolutionary novelty of nonlinear calls among toadfishes. Unlike three-spined toadfish, chimpanzee and cockatoo, spectrograms from midshipman (figure 2e; electronic supplementary material, figure S2e) and gulf toadfish (electronic supplementary material, figure S2i) showed a stable harmonic stack.

Figure 2.

Spectrographic and phase-space representations of linear and nonlinear fish and mammalian calls. (a) Representative spectrogram of three-spined toadfish advertisement hoot with chaotic features and (b) the corresponding phase-space plot from a nonlinear time-series analysis showing a three-dimensional, periodic structure indicative of deterministic chaos. (c) Representative spectrogram of a pant-hoot from a chimpanzee (P. troglodytes) and (d) its corresponding phase-space plot from nonlinear time-series analysis of the sound, showing a periodic three-dimensional structure. (e) Representative spectrogram of midshipman toadfish (P. notatus) advertisement ‘hum’ [5] and (f) the corresponding phase-space plot from nonlinear time-series analysis of the sound showing only a two-dimensional structure, indicative of linear signals. See electronic supplementary material, figure S2 for more examples.

Phase-space representations show the progression of a signal through time as a function of its first (x), second (y) and third (z) derivatives [4,8,27]. In chaotic nonlinear signals, the phase-space plot has a distinctive three-dimensional, aperiodic structure, whereas linear signals are periodic and often two-dimensional [4,8,27]. The three-spined toadfish advertisement hoot (see figure 2b and electronic supplementary material, figure S2b for animations) was three-dimensional and aperiodic like the chimpanzee pant-hoot (figure 2d; electronic supplementary material, figure S2n) and cockatoo scream (electronic supplementary material, figure S2r). By contrast, the advertisement calls of the plainfin midshipman (figure 2f; electronic supplementary material, figure S2f) and gulf toadfish (electronic supplementary material, figure S2j) were periodic and largely restricted to two dimensions in phase space.

Poincaré sections illustrate the instantaneous cross section through the signal's phase-space plot [8]. A strongly two-dimensional distribution of points in a Poincaré map confirms the internal three-dimensional structure of the phase-space plot, and thus the deterministically chaotic nature of the signal in phase space [4,8]. Additionally, Poincaré sections in which the points ‘mix’ by stretching and folding are the best sign of deterministic chaos [8]. For toadfish and tetrapod calls studied here, animations of Poincaré sections showed the changing nature of these analyses at each point along the signal's progression. The animations suggested that the chaotic calls of three-spined toadfish, chimpanzee and cockatoo had more mixing of points in the sections, further emphasizing their structural similarities (electronic supplementary material, figure S2c,o,s).

Recurrence plots determine whether signals are chaotic by representing the times at which a signal passes through the same position in phase space [27]. In systems with deterministic chaos, signals pass through the same point in phase space irregularly, while linear systems exhibit a clear pattern of recurrence [27]. These distinctions were again visible in the calls of the three-spined toadfish, chimpanzee and cockatoo, but not in the calls of either midshipman or gulf toadfish (electronic supplementary material, figure S2d,h,e,p,t). Together, the use of recurrence plots and the other nonlinear time-series analyses strongly supported nonlinear phenomena (and not stochastic noise) as the cause for the observed spectra of three-spined toadfish calls, as well as those of chimpanzee and cockatoo.

We took advantage of the readily accessible toadfish sonic organ, the swim bladder, to test the proposed role of coupled peripheral oscillators in generating chaotic calls [4,7,12–14]. Like other toadfishes, the three-spined toadfish's swim bladder has a single vocal muscle completely attached to each bladder wall; however, unlike any other known fish species, there are two completely separate bladders, each with one muscle [5]. While three-spined toadfish hoots are only produced in social contexts [5], grunts can be elicited from individually housed/identified fish. Surgical transection of the vocal motor nerve completely eliminated each individual's prior ability to produce grunts with any nonlinear phenomena, leaving them only with linear calls (figure 1f, inset shows spectrogram). SPCC and PCO followed by a nested MANOVA on principal coordinates 1–4 (accounting for 30% of the total variation in the signal) showed significant overall differences in call structure from each fish before and after the transection (F_7,74 = 28.075, p < 0.0001).

From the four transected fish, 28 calls were produced before nerve transection, 18 of which were nonlinear (deterministic chaos: n = 8; biphonation: n = 4; bifurcation: n = 4; subharmonics: n = 2). Following transection, 44 calls were produced, but none exhibited any form of nonlinearity. The lack of nonlinearity was not the result of the operation itself, as our sham-operated fish still retained the ability to produce naturally elicited nonlinear hoots (n = 211) and grunts (n = 90). The spectrograms of calls from transected fish were composed of stable harmonic stacks (figure 1f inset) like those of intact midshipman and gulf toadfish (figure 2e; electronic supplementary material, figure S2e,i). Recurrence plots, which most succinctly reveal differences in phase space between nonlinear and linear calls (compare the electronic supplementary material figures S2d,p,t and S2h,l), were also similar between the calls of transected fish (see inset of electronic supplementary material, figure S2d) and the linear calls of intact midshipman and gulf toadfish (electronic supplementary material, figure S2h,l).

In summary, we show that fish can produce vocalizations exhibiting nonlinear features previously only observed in tetrapods. Using spectrographic analysis and three analytical methods derived from chaos theory, we demonstrated that three-spined toadfish calls display a degree of complexity comparable to the chaotic vocalizations of birds and primates. Additional complexity of sounds with multiple nonlinear features (for example, figure 1a) may depend on the interaction of the contracting muscle (the sound's source) with the resonance created by the swim bladder (the sound's filter), comparable to source–filter interactions in the larynx and syrinx [13]. Loss in power and changes in frequency profile that accompanied the loss of nonlinearities following unilateral vocal nerve transection were consistent with the interaction of the two swim bladders as the source of acoustic complexity.

Some of the nonlinearities shown here for three-spined toadfish may arise from the independent control of each swim bladder, as suggested from behavioural evidence for the closely related Lusitanian toadfish, Halobatrachus didactylus [31]. Neurophysiological evidence shows independent neural control of the two sides of the swim bladder in the more distantly related Northern sea robin (Prionotus carolinus, Scorpaenidae [32]), leading to frequency modulation of natural calls [33]. Nonlinearities may thus be more widespread among fishes, depending on a range of novel peripheral and central neuronal mechanisms [19]. The repeated evolution of nonlinear acoustic signals in vertebrates and insects suggests the existence of broad selection pressures favouring the evolution of these signals. However, since inter-order (or inter-phyla) taxonomic comparisons of acoustic communicatory signals are rare, these broad pressures may not have previously been recognized.

Studies in both vertebrates and invertebrates suggest a range of adaptive advantages of nonlinear acoustic signals. First, the increased amplitude and frequency content afforded by nonlinearities provides for increased propagation distance and detection range in their environment [5,34]; similarly, deterministic chaos has been suggested as a mechanism to increase the propagation distance of the airborne signals of cicadas [11]. Second, deterministic chaos may contribute to a heightened sense of urgency in the receiver, as suggested for meerkat alarm calls [35] and film score music in humans [36]. Third, biphonation may allow for individual recognition, as with penguins [37] or canids [38]. Toadfishes use vocalizations in territorial displays [29,39], with evidence for biphonation contributing to the discrimination of agonistic from advertisement calls. The closely related plainfin midshipman can discriminate acoustic beats, one form of biphonation resembling three-spined toadfish grunts (figure 1c), from signals resembling midshipman advertisement hums and the linear portion of three-spined toadfish hoots (figures 1a, 2e) [40]. Both the central and peripheral auditory systems of midshipman also encode beats [41], providing a physiological basis to support the role of these signals in acoustic recognition tasks.

Further indication of the behavioural context of nonlinear calls in three-spined toadfish comes from the demonstration here of increased prevalence of nonlinear grunts and hoots at different times of day and phases of the lunar cycle. As shown for midshipman that make agonistic grunts and growls that are an amalgam of grunt and hoot-like calls, diel and lunar rhythms in call occurrence probably indicate changing behavioural and hormonal state [29,42,43]. Midshipman growls and repetitive series of grunts (grunt trains) are generated only at night during the breeding season when males in reproductive condition are guarding nests; we predict a similar context of territorial defence for the nonlinear calls of the three-spined toadfish.

The co-occurrence of nonlinear and linear calls during any one time period (see electronic supplementary material, figure S1) may further reflect an ability to rapidly change call types depending on social context. Playback studies with gulf toadfish (O. beta) show that they can rapidly shift the spectro-temporal properties of calls; males guarding nests increase call rate and duration within 5 min in response to playbacks of hoot-like calls that mimic conspecific calls [39]. These rapid alterations in call attributes, similar to diel and seasonal changes in agonistic call type in midshipman (see above), are probably under hormonal control [44,45].

Together, these results provide new experimental and analytical support for the proposed role of other coupled peripheral oscillators, the paired vocal cords of the larynx and the two halves of the syrinx, in producing calls with nonlinearities in non-aquatic vertebrates, including humans [4,7,12–14]. Strong selection for innovation in acoustic signals has apparently led to the evolution of acoustic communication signals exhibiting nonlinearities in all major lineages of vocal bony vertebrates, including fishes.