Querying Pathways in Protein Interaction Networks Based on Hidden Markov Models

Abstract

High-throughput techniques for measuring protein interactions have enabled the systematic study of complex protein networks. Comparing the networks of different organisms and identifying their common substructures can lead to a better understanding of the regulatory mechanisms underlying various cellular functions. To facilitate such comparisons, we present an efficient framework based on hidden Markov models (HMMs) that can be used for finding homologous pathways in a network of interest. Given a query path, our method identifies the top k matching paths in the network, which may contain any number of consecutive insertions and deletions. We demonstrate that our method is able to identify biologically significant pathways in protein interaction networks obtained from the DIP database, and the retrieved paths are closer to the curated pathways in the KEGG database when compared to the results from previous approaches. Unlike most existing algorithms that suffer from exponential time complexity, our algorithm has a polynomial complexity that grows linearly with the query size. This enables the search for very long paths with more than 10 proteins within a few minutes on a desktop computer. A software program implementing the algorithm is available upon request from the authors.

1. Introduction

Recent advances in high-throughput experimental techniques for measuring protein interactions—such as the two-hybrid systems (Ito et al., 2001) and co-immunoprecipitation assays (Mann et al., 2001; Uetz et al., 2004), have enabled the systematic study of biological interactions on a global scale for an increasing number of organisms (von Mering et al., 2002). These complex interaction networks can be represented by graphs, in which the nodes represent biological entities in a given network and the edges indicate interactions between them. Comparing the networks of different organisms and identifying their common substructures, such as signaling pathways and protein complexes, can lead to a better understanding of the regulatory mechanisms underlying various cellular processes. For this reason, there have been growing efforts to find conserved interaction patterns in protein interaction networks (Dost et al., 2008; Kelley et al., 2003; Koyutürk et al., 2004; Scott et al., 2006; Sharan et al., 2005; Shlomi et al., 2006; Singh et al., 2008; Yang and Sze, 2007), metabolic networks (Koyutürk et al., 2004; Pinter et al., 2005; Yang and Sze, 2007), gene regulatory networks (Akutsu et al., 1998), and signal transduction networks (Steffen et al., 2002). It has been demonstrated that searching for conserved interaction patterns can detect many well-known pathways and can also make statistically significant predictions of novel interaction pathways.

Despite the initial success of existing methods, there still exist a number of problems that limit the applicability of these methods. For example, many of these methods suffer from high computational complexity that makes it difficult to use them to search for long query paths. The number of consecutive insertions and deletions are often restricted in these methods, which may prevent the detection of distant homologous pathways, and many of them rely on heuristics or randomized algorithms that may not necessarily yield optimal results.

In this paper, we focus on the problem of finding conserved pathways in a protein interaction network that are homologous to a known linear pathway. We formulate the problem as a pathway alignment problem, in which the goal is to find the path in a given protein network that is most similar to a given query. Based on hidden Markov models (HMMs), we propose a general probabilistic framework for scoring pathway alignments and present an efficient search algorithm that overcomes the aforementioned limitations of previous algorithms. Given a query path, our method identifies the top k matching paths in a network of interest, where the detected paths may contain any number of consecutive insertions and deletions. Since the search algorithm has a very low computational complexity that is linear in the query size as well as in the number of edges in the network, our method can be used to effectively search for long query paths in remotely related organisms. Although HMMs have been widely used in sequence homology search, we believe that this is their first application to homology search in pathways.

2. Methods

In this section, we present an algorithm for solving the following pathway alignment problem: Given a linear query path p and a protein interaction network 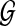, find the optimal path q in the network 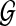that is closest to the query.

2.1. Pathway alignment

Let 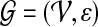be an undirected graph representing a protein interaction network. We assume that 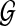has a set 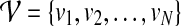of N nodes, representing the proteins in the network, and a set ɛ = {e_ij} of M edges, representing the interactions between proteins v_i and v_j. As the network 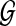is an undirected graph, we assume that if there exists an interaction between v_i and v_j, both e_ij and e_ji are present in the set ɛ. For a protein pair (v_i, v_j) with 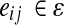, we define their interaction reliability as w(v_i, v_j). Given a query path 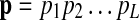that consists of L proteins, we define the sequence similarity score between p_i and v_j as h(p_i, v_j). Our goal is to find the best matching path 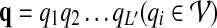in the protein interaction network that maximizes a predefined pathway alignment score S(p, q).

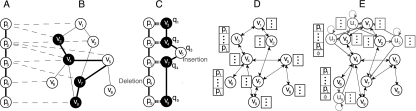
To obtain meaningful pathway alignments, the alignment score S(p, q) should be defined in such a way that combines the similarity score h(p_i, q_j) between the aligned proteins p_i and q_j, the interaction reliability score w(q_j, q_j+1) between the proteins q_j and q_j+i (1 ≤ j ≤ L′ − 1), and the penalty for insertion (q_j that does not have a matching protein in the query path p) and deletion (p_i that does not have a matching protein in the retrieved path q). Figure 1C illustrates an example of a query path p (Fig. 1A) that is aligned to the best matching path q in the network 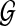(Fig. 1B). A dashed line between p_i and v_j or between p_i and q_j indicates that they have significant sequence similarity. In this example, the optimal alignment that maximizes the alignment score S(p, q) has one insertion (node q₃ in the retrieved path) and one deletion (node p₄ in the query).

FIG. 1.

(A) Query path p. (B) Protein interaction network 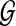. (C) An example of a pathway alignment with the best matching path q in the network 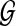. (D) Ungapped hidden Markov model (HMM) for finding the optimal pathway alignment. The dots next to the hidden states represent all possible symbols that can be emitted. (E) Modified HMM that allows insertions and deletions. The hidden states can emit a gap symbol φ in this modified model. For simplicity, changes to the HMM are shown only for the nodes v₁, v₂, v₃ and v₆.

2.2. Network representation using HMM

To define the alignment score S(p, q), we adopt the HMM formalism. For simplicity, we start with an HMM that does not allow insertions or deletions in the pathway alignment. We construct the HMM based on the network graph 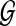so that each node 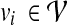in the graph corresponds to a hidden state in the HMM. For convenience, we represent this hidden state using the same notation v_i and the HMM has an identical structure as the network graph 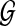. The resulting HMM can be viewed as a generative model that produces (or “emits”) an interesting substructure of the original network, such as a signaling pathway. From this point of view, we regard the query path 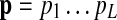as an observation sequence generated by the constructed HMM. Figure 1D illustrates the HMM where the emittable symbols are shown next to the hidden states.

Based on this representation, the interaction reliability score and the sequence similarity score can be integrated naturally into the probabilistic framework. We define a mapping f : w(v_m, v_n) ↦ t(v_n|v_m) that converts the interaction reliability w(v_m, v_n) between two proteins to the following transition probability

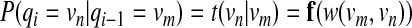(1)

between the corresponding hidden states in the HMM. The mapping f is defined so that (i) t(v_n | v_m) = 0 for 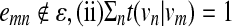for all m, and (iii) t(v_n1 | v_m) > t(v_n2 | vm) for w(v_m, v_nl) > w(v_m, v_n2). We define another mapping g : h(p_i, v_m) ↦ e(p_i | v_m) that converts the sequence similarity score h(p_i, v_m) to the following emission probability

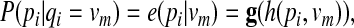(2)

where q_j = v_m is a hidden state in the HMM (representing a protein in the network 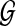) and p_i is an emitted symbol (representing a protein in the query p that is aligned to q_j). The mapping g is defined so that (i) 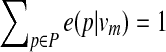for all m, where P is the set of distinct proteins in the query path 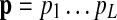, and (ii) e(p_i1 | v_m) > e(p_i2 | v_m) for h(p_i1, v_m) > h(p_i2, v_m).

2.3. Ungapped pathway alignment

Based on the HMM framework, the problem of finding the best matching path is transformed into the problem of finding the optimal state sequence in the HMM that maximizes the observation probability of the given query path. In an ungapped pathway alignment, the matching path 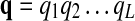has the same length as the query path 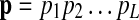, hence q_i will be the underlying state for the “observed symbol” p_i.

To find the best matching path, a dynamic programming algorithm, called the Viterbi algorithm, can be used to solve the problem in polynomial time. We define γ(t, j) as the log-probability of the most probable path for the sub-query 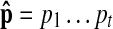of length t(≤ L), where the underlying state of p_t is q_t = v_j. We compute γ(t, j) recursively as follows:

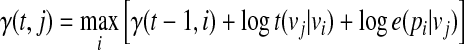(3)

We repeat the above iterations until t = L. We then obtain the maximum log-probability of the query p as follows:

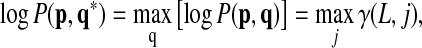(4)

where q* = arg max_q [log P(p, q)] is the best matching path for p in the network. Once we have log P(p, q*), it is straightforward to find q* by tracing the recursive equations that led to the maximum log-probability log P(p, q*). Although the above algorithm only finds the optimal path, we can extend the algorithm to find the top k paths simply by replacing the max operator by an operator that finds the k largest scores.

Note that S(p, q) = log P(p, q) can serve as a good alignment score for the paths p and q that effectively combines sequence similarity and interaction reliability. In principle, we can also use non-stochastic emission scores s_em(p_t | v_j) and transition scores s_tr(v_j | v_i) in place of the log-probabilities log e(p_t | v_j) and log t(v_j | v_i), respectively, in the recursive equation, Equation (3). This will yield a non-stochastic alignment score instead of an observation probability.

2.4. Pathway alignment with gaps

To accommodate insertions and deletions, we modify the HMM as follows. To model deletions, we add an accompanying state u_m for every state v_m in the HMM. We add an outgoing edge from v_m to u_m and add outgoing edges from u_m to all of the neighboring states of v_m in the network 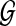. To be more precise, u_m will have an outgoing edge to every 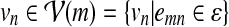. By varying the transition probability t(u_m | v_m), we can control the probability (hence, the penalty) of having deletions. We adjust the outgoing transition probabilities from v_m so that 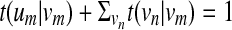. We control the probability of having consecutive deletions by adjusting the probability t(u_m | u_m) for making self-transitions at u_m. The outgoing transition probabilities t(v_n | u_m) from an accompanying state u_m are chosen so that they are proportional to t(v_n |v_m) and satisfy 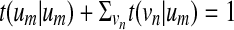. To model insertions, we allow the original states 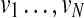in the HMM to emit a gap symbol φ in addition to the proteins in the query path p. The gap emission probability e(φ|v_m) can be used to control the probability (hence, the penalty) of having insertions. The structure of the modified HMM is depicted in Figure 1E. Note that the matching path 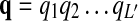might have different length L′ from the length L of the query path 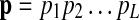when there are insertions or deletions in the pathway alignment. Hence we may have j ≠ i for the underlying state q_j of the “observed symbol” p_i.

To find the optimal path that may include one or more gaps, we modify our dynamic programming algorithm correspondingly. We define γ(t, d, j) as the log-probability of the most probable path for 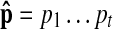that contains d insertions and ends at v_j (1 ≤ j ≤ 2N), where we use v_m+N = u_m for convenience. The value of γ(t, d, j) is computed recursively as follows:

(5)

We repeat the above iterations until we reach t = L and d = D, where D is the maximum number of allowed insertions. Note that there is no explicit limit for the number of deletions. We then compute the log-probability of the optimal path as follows:

(6)

The path q* = arg max_q [log P(p, q)] is the closest match to the query p, and it may contain some number of insertions and deletions. As before, we can replace the max operator by an operator that finds the k largest scores if we want to find the top k matching paths instead of a single top-scoring path.

The computational complexity of the above algorithm is O(kLDM) for finding the top k matching paths, where L is the length of the query, D is the maximum number of allowed insertions, and M is the number of edges in the network 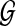. Note that the complexity is linear with respect to the query size, the number of edges in the network, the maximum number of insertions, and the number of best matching paths we want to retrieve.

2.5. Statistical significance

We estimate the statistical significance of a retrieved path using a similar approach as the one proposed in Kelley et al. (2003). We first generate a large number of random graphs by permuting the protein locations in the original network 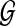. Therefore, all random graphs will be comprised of the same set of proteins and retain a similar structure as the original network. For each random graph, we construct an HMM and compute the best pathway alignment score for the query p. It is well known that the Gumbel distribution provides a good approximation for the extreme value distribution (EVD) of various random variables, and it has been widely used in sequence homology search to assess the significance of predicted results (Durbin et al., 1998; Karlin and Altschul, 1990). As we are interested in evaluating the statistical significance of the maximum pathway alignment score obtained from the original network, the Gumbel distribution provides a better approximation when compared to the widely used Gaussian distribution. The two unknown parameters α and β in the Gumbel distribution function 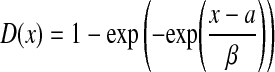can be estimated using simple least squares regression based on the alignment scores obtained from the random graphs. Once we have estimated α and β, we can compute the p-value of the best pathway alignment score in the original network based on the estimated distribution.

3. Results

3.1. HMM parameterization

We tested our algorithm using several protein interaction networks in the Database of Interacting Proteins (DIP) (Xenarios et al., 2002). We adopted a simple non-stochastic scoring scheme for parameterizing the HMMs.

We set the transition scores s_tr (v_n | v_m) based on the presence of interaction between the corresponding proteins. If there exists an interaction between the two nodes v_m and v_n in the network 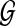, we set the transition score to s_tr (v_n | v_m) = 0 (and also s_tr (v_m | v_n) = 0). Otherwise, we set the score to s_tr (v_n | v_m) = −∞ (and also s_tr (v_m | v_n) = −∞). This keeps the state v_m in the HMM from making a direct transition to a non-relevant state v_n, and vice versa, thereby preventing the inclusion of any irrelevant protein interactions with no biological support in the retrieved path q. The score for making a transition into an accompanying state u_m was set to s_tr (u_m | v_m) = 0, and we set the self-transition score to s_tr (u_m | u_m) = 0 to allow consecutive deletions. 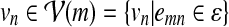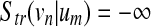The score for making a transition from u_m back to a regular state v_n was set to s_tr (v_n | u_m) = 0 for and for .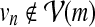

We set the emission score s_em(p_t | v_m) based on the sequence similarity of the proteins p_t and v_m. We assume that every state in the HMM (including the accompanying states) can emit any protein p_t in the query path p. The emission score was made larger for more similar proteins so that it is more likely that a hidden state v_m will emit a protein p_t that is closer to its corresponding protein. For all protein pairs (p_t, v_m) between a protein p_t in the query and a protein v_m in the network , we computed their E-values using the PRSS routine in the FASTA package (Pearson and Lipman, 1988). PRSS (Pearson, 1996) computes accurate E-values using the Smith-Waterman algorithm with sophisticated shuffling methods, and it is believed to be better than BLASTP in detecting significant matches (Pagni and Jongeneel, 2001). We regarded a protein pair (p_t, v_m) as a “match” if its E-value E_v(p_t, v_m) was below some predefined threshold λ_th. Otherwise, we viewed (p_t, v_m) as a “mismatch,” which implies that the two proteins do not contain significant similarity. Based on this criterion, we set the emission score s_em(p_t | v_m) as follows:

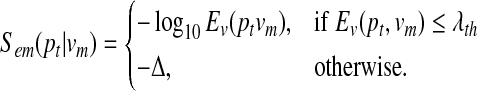(7)

The value Δ can be viewed as the mismatch penalty, and is selected so that −Δ ≪ −log₁₀ λ_th. We set the insertion penalty to s_em(φ |v_m) = −Δ_i and the deletion penalty to s_em(p_t|u_m) = −Δ_d. Note that the accompanying state u_m cannot emit a gap, hence s_em(φ |u_m) = −∞. Finally, we set the maximum number of insertions to be the same as the length of the query (D = L).

3.2. Querying yeast pathways in various organisms

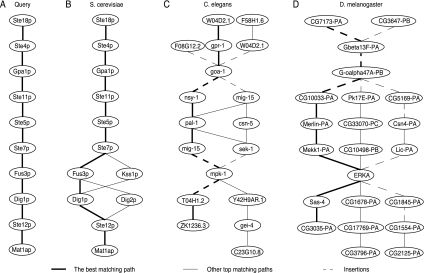
To verify the capability of our method for identifying relevant pathways in different organisms, we obtained the protein interaction networks of S. cerevisiae, C. elegans, D. melanogaster, and E. coli from DIP. We took a mating-pheromone response pathway of S. cerevisiae with 10 proteins as our query path, which contains the mitogen-activated protein (MAP) kinase cascade Ste11p–Ste7p–Fus3p (Fig. 2A). The same pathway has been used by other existing algorithms for performance evaluation (Scott et al., 2006; Yang and Sze, 2007). We searched for similar paths in the S. cerevisiae network with 17,579 interactions among 4969 proteins, the C. elegans network with 4037 interactions among 2647 proteins, and the D. melanogaster network with 22,840 interactions among 7476 proteins. We set λ_th = 0.5 and Δ = Δ_i = Δ_d = 12.

FIG. 2.

Query results in different networks. (A) The S. cerevisiae query path. (B) Matching paths in the S. cerevisiae network. (C) Matching paths in the C. elegans network. (D) Matching paths in the D. melanogaster network.

As we would expect, the best matching path in S. cerevisiae network was identical to the query path. This is shown in Figure 2B, where other top matches are shown with the best matching path. The retrieved paths in the C. elegans network and the D. melanogaster network are shown in Figures 2C and 2D. It is interesting to note that many proteins in the retrieved paths share similar functions with the corresponding proteins in the query path. The proteins Ste11p, nsy-1, mig-15, CG10033-PA, Pk17E-PA, and CG5169-PA, which are aligned to each other, all belong to the serine/threonine protein kinase family. Similarly, Ste7p, mig-15, sek-1, Mekk1-PA, CG10498-PB, and Lic-PA, also belong to the serine/threonine protein kinase family, with sek-1, Mekk1-PA, and Lic-PA being MAPK kinases. All the proteins Fus3p, Kss1p, mpk-1, and ERKA, which are aligned to each other in Figure 2, are MAP kinases (Flybase Consortium, 1996; Gustin et al., 1998; Stein et al., 2001). These results clearly indicate that our method is able to effectively identify similar pathways that are biologically meaningful.

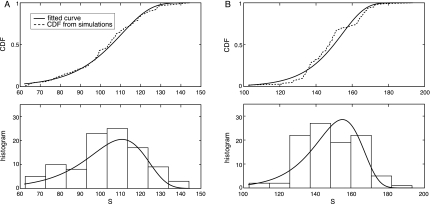
In order to estimate the statistical significance of the predicted results, we computed the p-values for the best matching paths in the respective networks. The p-values have been computed as described in Section 2.5 using 100 random networks. Figures 3A and 3B show the resulting cumulative distribution functions (CDFs) and histograms of the maximum alignment scores in the random networks of C. elegans and D. melanogaster, respectively. The fitted Gumbel distributions are also shown in the figure. The p-value of the optimal path in the original C. elegans network was p = 0.014, while the p-value of the optimal path in the D. melanogaster network was p = 0.069. For both organisms, the optimal alignment scores in the original networks ranked among the top scores, indicating that the retrieved results are statistically significant. One point to note is that using a shorter query path typically leads to a smaller p-value, as it becomes more likely to detect good matches that contain less insertions and deletions. For example, if we take a small portion (Ste11p–Ste5p–Ste7p–Fus3p) of the original query shown in Figure 2A and search the C. elegans network, the algorithm retrieves the corresponding part in Figure 2C, with a smaller p-value p = 2.6 × 10⁻³. Similarly, if we use the same short query to search the D. melanogaster network, the corresponding portion in Figure 2D is retrieved, where the p-value of the optimal path is only p = 3.6 × 10⁻⁹.

FIG. 3.

The cumulative distribution functions (CDFs) and histograms of the maximum alignment scores S computed from the random networks. The estimated extreme value distribution (EVD) curves are shown together. (A) C. elegans. (B) D. melanogaster.

In addition to the D. melanogaster, C. elegans, and S. cerevisiae networks, we used the same mating-pheromone response pathway in Figure 2A to find relevant paths in the E. coli protein interaction network, which contains 6976 interactions among 1850 proteins. We reduced the mismatch and indel penalties to Δ = Δ_i = Δ_d = 2 so that the retrieved paths may contain more indels and mismatches. The p-value of the optimal path was p = 0.66 and its alignment score was among the lowest when compared to the alignment scores obtained from the random networks. Similarly, the p-value of the retrieved path was also high (p = 0.59) for the short query. This implies that the search results are statistically insignificant, which is consistent with the fact that there are no known MAP kinase pathways in bacteria (Chang and Stewart, 1998). This is a good indication that our method is very useful in identifying conserved pathways that are biologically meaningful.

3.3. Querying human pathways in fly

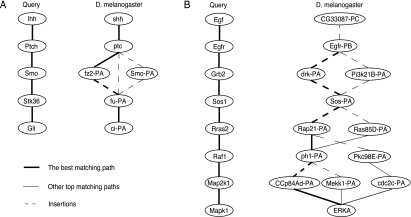
We further applied our algorithm to search the D. melanogaster network for matching paths that are similar to known human signaling pathways. We used the same parameters as before: λ_th = 0.5 and Δ = Δ_i = Δ_d = 12. Figure 4A shows the retrieved paths for the human hedgehog signaling pathway and Figure 4B shows the retrieved paths for the human MAP kinase pathway. In both cases, the top matching paths agreed well with the query paths, according to the known functional annotations of D. melanogaster. In Figure 4A, ptc is a receptor of the hedgehog pathway located at the plasma membrane (Lum and Beachy, 2004), and it has been shown that ci-PA plays an important role in the hedgehog pathway that regulates cell growth in many tissues (Lum and Beachy, 2004). For the MAP kinase query (Fig. 4B), Egfr-PB is a putative growth factor receptor; drk-PA is downstream of the receptor kinase; Rap21-PA and Ras85D-PA have putative GTPase activity; ph1-PA, Pkc98E-PA, Mekk1-PA, and cdc2c-PA all belong to the serine/threonine protein kinase family; and ERKA is an annotated nuclear MAP kinase which likely activates specific transcription factors (Flybase Consortium, 1996; Gustin et al., 1998).

FIG. 4.

Human queries and their best matching paths in the D. melanogaster network. (A) Human hedgehog pathway and the matching paths. (B) Human MAP kinase pathway and the matching paths.

Figures 4A and 4B contain the putative homologous pathways in D. melanogaster reported in the KEGG database (Kanehisa and Goto, 2000): one of the top matching paths in Figure 4A (shh–ptc–Smo–fu–ci) is the core of the D. melanogaster hedgehog signaling pathway given in Kanehisa and Goto (2000), and Egfr–drk–Sos–Ras85D–ph1–Mekk1–ERKA (Fig. 4B) is part of the putative MAP kinase pathway for D. melanogaster in Kanehisa and Goto (2000). By comparing the retrieved pathways with the corresponding putative pathways of D. melanogaster in the KEGG database (Kanehisa and Goto, 2000), we found that our algorithm was able to retrieve the identical core segment with five proteins in the putative hedgehog signaling pathway.¹ For the MAP kinase query, the retrieved pathway included seven proteins that exactly matched the proteins in the putative D. melanogaster MAP kinase pathway.² These results compare favorably to the previously reported results (Shlomi et al., 2006), which found two and five matched proteins for the respective pathways, indicating that our algorithm can make biologically meaningful predictions with better accuracy. As before, we also computed the p-values for the top matching paths using 100 random networks. The p-value of the optimal path for the human hedgehog signaling pathway was p = 7.0 × 10⁻²³ and the p-value of the top retrieved path for the human MAP kinase pathway was p = 2.6 × 10⁻⁴, which show the statistical significance of the predictions.

3.4. Running time

Our method has a very low computational complexity that is linear with respect to the length of the query as well as the number of interactions in the network. Unlike most existing methods whose utility is limited to relatively short queries with 3–10 proteins, our method can search for very long query paths in large protein interaction networks. Table 1 summarizes the running time of our method with different parameters. We searched for queries with six to 20 proteins in the S. cerevisiae network that consists of 4969 proteins and 17,579 interactions. The running time has been measured on a desktop computer with 2.13-GHz CPU and 2-GB memory. From Table 1, we see that it takes only about three minutes to find the top path for a query of length 20, where the retrieved path may contain any number of deletions and mismatches but no insertions. We see clearly in Table 1 that the running time grows linearly with the query length. If we search for the top five paths using the same query (of length 20), and allow up to five insertions and any number of deletions and mismatches, it still takes only about 80 minutes. Note that this is about 25 (= D × k) times larger compared to the previous running time (3 min.), which confirms that the computational complexity is also linear in the maximum number of insertions D and the number of paths k we want to retrieve.

Table 1.

Running Time of Our Algorithm with Different Parameters (Time Measured in Seconds)

		Query path length
Maximum no. of insertions	No. of paths	6	8	10	12	14	16	18	20
D = 0	k = 1	47.9	67.5	85.8	105.4	122.6	144.0	163.6	179.2
D = 5	k = 5	1373.4	1878.3	2382.4	2881.5	3384.4	3894.5	4387.5	4817.5

3.5. Accuracy and robustness

To evaluate the accuracy and the robustness of our HMM-based algorithm, we performed the following experiments.

We first estimated the accuracy of our algorithm in retrieving homologous pathways by using synthetic query paths. For this purpose, we followed a similar procedure used in Dost et al. (2008). To obtain a reasonable set of query paths, we randomly extracted 10 paths from the S. cerevisiae network, whose lengths range from L = 6 to L = 10. Each of these paths was perturbed by inserting, deleting, and replacing one or more nodes. We also applied point mutations to the protein sequences in the query paths with different mutation rates of up to 80%. For each path, we used our algorithm to retrieve the top matching path in the S. cerevisiae network. As in the previous experiments, we used λ_th = 0.5 and Δ = Δ_i = Δ_d = 12. The retrieved results have been compared to the original unperturbed paths that were used to obtain the query paths. We computed the edit distance between each retrieved path and the original path to evaluate the prediction accuracy. As a comparison, we also tried to find the best matching proteins based on sequence similarity alone. For each node in the query paths, we reported the node in the S. cerevisiae network with the highest alignment score using the PRSS routine (Pearson, 1996) as the “matching node” and counted the number of nodes that were correctly predicted. The prediction results are summarized in Table 2. We can see from this table that the predictions made by our HMM-based algorithm are far more accurate than those based on the best PRSS scores. For HMM-based predictions, the average distance between the retrieved optimal paths and the original paths was less than one for all types of perturbations with up to 70% point mutations. The advantage of our algorithm over the sequence-based approach becomes more pronounced for higher mutation rates. These results clearly show that the HMM-based algorithm can make accurate predictions by integrating sequence similarity and the interaction network in a sensible manner.

Table 2.

Average Edit Distances of the Retrieved Paths and the Original Query Paths for Different Types of Node Perturbations and Different Levels of Point Mutations

	Point mutation rate
	0%		50%		60%		70%		80%
Note perturbation	PRSS	HMM	PRSS	HMM	PRSS	HMM	PRSS	HMM	PRSS	HMM
None	0	0	0	0	0.2	0	0.9	0.3	3.9	0.9
1 replacement	1	0.2	1	0.2	1.2	0.2	1.9	0.8	4.9	1.5
2 replacements	2	0.5	2	0.5	2.2	0.5	2.9	0.8	5.9	2.2
1 insertion and 1 deletion	1.8	0.3	1.8	0.3	2.0	0.3	2.7	0.7	5.7	2.3
2 insertions and 2 deletions	3.3	0.6	3.3	0.6	3.5	0.6	4.2	0.7	7.2	3.8

The results obtained by our algorithm are denoted as “HMM,” and the results obtained based on the best PRSS hits are denoted as “PRSS.”

We also measured the sensitivity of our algorithm with respect to parameter changes. For this purpose, we used the human hedgehog signaling pathway shown in Figure 4A to query the D. melanogaster network using different sets of parameters. For each parameter setting, we compared the proteins in the top 10 retrieved paths with the proteins included in the top 10 paths based on the original setting (λ_th = 0.5 and Δ = Δ_I = Δ_d = 12) that was used to obtain the results in Section 3.3. To estimate the relative changes of the retrieved proteins, we computed the following values:

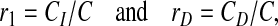where C is the number of proteins in the top retrieved paths based on the original setting, C_I is the number of proteins that were added as a result of the parameter change, and C_D is the number of proteins that were removed from the top paths due to the change.

Table 3 shows the relative number of added proteins and that of removed proteins for different sets of parameters. As we can see, the retrieved results are not significantly affected by parameter changes. For large ranges of λ_th (from 0.05 to 1.0) and Δ = Δ_i = Δ_d (from 6 to 18), the set of top 10 retrieved paths stayed the same. Even for larger values of λ_th (= 5.0) and Δ = Δ_i = Δ_d (= 26), the changes in the retrieved results were relatively small. In addition to measuring the relative changes in the predicted results, we computed the p-values of the top paths based on 100 random networks. In all cases, the p-values ranged between 1.1 × 10⁻²⁶ and 6.2 × 10⁻¹⁸, showing that the predictions made by our HMM-based method are statistically significant. This explains why the retrieved paths were so close to each other. As we can see from these results, our HMM-based algorithm performs robustly for a considerably large range of parameter values, especially when the retrieved paths are biologically meaningful. The predicted results may have larger variations when the retrieved paths are not statistically significant, as in the case of querying the E. coli network using the yeast MAP kinase pathway, described in Section 3.2.

Table 3.

Relative Changes in the Top 10 Retrieved Paths

	Δ = Δi = Δd
	6		12		18		26
λth	rI	rD	rI	rD	rI	rD	rI	rD
0.05	0	0	0	0	0	0	0.07	0.03
0.25	0	0	0	0	0	0	0.07	0.03
0.5	0	0	0	0	0	0	0.07	0.03
1.0	0	0	0	0	0	0	0.07	0.03
5.0	0.02	0.02	0.02	0.02	0.02	0.02	0.09	0.05

We computed the relative number of proteins that were added to or removed from the predicted results due to the parameter changes. The changes have been measured by comparing the predicted results to the results obtained using the original parameters (λ_th = 0.5 and Δ = Δ_i = Δ_d = 12) employed in Section 3.3. The relative number of added proteins is denoted by r_I , and the relative number of removed proteins is denoted by r_D.

4. Discussion

There exist a number of algorithms that can be applied to pathway search (Kelley et al., 2003; Pinter et al., 2005; Scott et al., 2006; Shlomi et al., 2006; Yang and Sze, 2007). Among these algorithms, PathBLAST (Kelley et al., 2003) focuses on finding conserved pathways by comparing two networks, and this reduces to a pathway search problem if one of the networks is a specific pathway. However, PathBLAST does not allow consecutive deletions of proteins in the query path nor consecutive insertions of proteins in the matching path, limiting its applicability to closely matching pathways. Furthermore, its computational complexity contains factorial factors in the query length, making it impractical for long paths that contain more than six to seven proteins.

To solve these problems, two algorithms have been proposed based on the color coding technique (Scott et al., 2006; Shlomi et al., 2006) that can search for simple paths of length around 10. Although these algorithms have significantly reduced the running time, the algorithmic complexity is still exponential in the query length. Hence they quickly become infeasible for slightly longer queries. In addition, the use of randomized algorithms does not guarantee the optimality of the query result.

A more recent algorithm called PathMatch (Yang and Sze, 2007) reduces the pathway search problem to the problem of finding the longest weighted path in a directed acyclic graph by relaxing the constraint for finding simple paths. This allows top matching paths to be found in polynomial time and obviates the need for randomized algorithms. However, PathMatch has a limited flexibility in the choice of the scoring scheme since mismatches and indels are treated in an identical manner and it is difficult to use different penalties for different mismatches or indels.

When compared to the existing methods, our HMM-based method has a significantly lower computational complexity that is linear with respect to the query length and the number of edges in the network, and it can search for query paths with more than 10 proteins in a network with thousands of nodes and tens of thousands of interactions within a few minutes. An important advantage of the HMM-based framework is that it is very flexible in the choice of the scoring scheme. We can use different penalties for mismatches, insertions, and deletions, and it is also possible to assign different penalties to different types of mismatches. Furthermore, our algorithm allows the matching paths to contain any number of consecutive deletions and insertions. We can also use an affine gap penalty model for scoring consecutive deletions, where gap openings and gap extensions are treated differently.

Similar to the PathMatch algorithm (Yang and Sze, 2007), we may in principle have a repeated occurrence of a network node v_j in the retrieved path. Such repeated occurrences are not frequently observed in practice unless all the proteins in the query p are very similar to each other. As mentioned in Yang and Sze (2007), these limited occurrences of repeats can be biologically useful in identifying proteins that have multiple roles in a signaling pathway, and there exist many known examples of such multi-functional proteins (Teichmann et al., 2001). We did not observe many repeated occurrences of the same protein in our retrieved paths.

In our tests, we have used relatively simple non-stochastic scores for parameterizing the HMMs. We have shown that, even with this simple scoring scheme, our retrieved paths are closer to the putative homologous D. melanogaster pathways in KEGG than the paths reported in Shlomi et al. (2006). Considering the flexibility of the proposed framework, it would be beneficial to use a more elaborate scoring scheme in the future. For example, we may incorporate additional information, such as gene ontology (GO) annotations and gene expression data (Sharan et al., 2005; Shlomi et al., 2006), for more reliable estimations of the HMM parameters. We may also incorporate methods for evaluating the reliabilities of protein interactions (Bader et al., 2004; Sharan et al., 2005; von Mering et al., 2002) to obtain more robust transition scores for the HMMs. Although the pathway alignment score S(p, q) used in this paper incorporates only the interaction reliability of the protein network, we can easily incorporate the interaction reliability of the query as well. This can be achieved by adding an additional term for the reliability of the interaction between p_{t − 1} and p_t in the recursive equations, Equations (3) and (5). As a final remark, the HMM-based method proposed in this paper is currently limited to linear queries, and we are investigating the possibility of extending the framework to support more general queries such as trees.

Acknowledgments

This work was supported in part by the National Cancer Institute (grant 2-R25CA090301-06 to X.Q.) and the National Science Foundation (grant DBI-0624077 to S.S.).

Disclosure Statement

No conflicting financial interests exist.