Skip to main content
PMC home page
Journal of Computational Biology logoLink to Journal of Computational Biology
. 2010 Jun;17(6):853–868. doi: 10.1089/cmb.2008.0023

Discretization of Time Series Data

Elena S Dimitrova 1,✉, M Paola Vera Licona 2,,3,,4, John McGee 5, Reinhard Laubenbacher 6
PMCID: PMC3203514  PMID: 20583929

Abstract

An increasing number of algorithms for biochemical network inference from experimental data require discrete data as input. For example, dynamic Bayesian network methods and methods that use the framework of finite dynamical systems, such as Boolean networks, all take discrete input. Experimental data, however, are typically continuous and represented by computer floating point numbers. The translation from continuous to discrete data is crucial in preserving the variable dependencies and thus has a significant impact on the performance of the network inference algorithms. We compare the performance of two such algorithms that use discrete data using several different discretization algorithms. One of the inference methods uses a dynamic Bayesian network framework, the other—a time-and state-discrete dynamical system framework. The discretization algorithms are quantile, interval discretization, and a new algorithm introduced in this article, SSD. SSD is especially designed for short time series data and is capable of determining the optimal number of discretization states. The experiments show that both inference methods perform better with SSD than with the other methods. In addition, SSD is demonstrated to preserve the dynamic features of the time series, as well as to be robust to noise in the experimental data. A C++ implementation of SSD is available from the authors at http://polymath.vbi.vt.edu/discretization.

Key words: gene networks, genetic algorithms, linear algebra, reverse engineering, time discrete dynamical systems

1. Introduction

The development of algorithms to infer biochemical networks from system-level data, such as DNA microarray or 2D-gel data, is a central problem of computational systems biology. Several such algorithms have been proposed in recent years, using tools from a variety of fields. Many of these methods are statistical in nature, resulting in a “dependency graph” for the network. Depending on the method used, the edges represent either a statistical correlation of two variables (de la Fuente, 2004) or a causal relationship (Friedman, 2000). One commonly used modeling framework is that of dynamic Bayesian networks (Pournara, 2004; Yu, 2004; Beal, 2005; Nariai, 2005; Zou, 2005; Dojer, 2006). Toward the other end of the spectrum one finds methods that use a dynamical systems modeling framework, such as systems of differential equations (Gardner, 2003; Andrec, 2005; Kim, 2007), Boolean networks (Liang, 1998; Akutsu, 2000; Mehra, 2004; Martin, 2007), or multi-state discrete models (Laubenbacher, 2004; Jarrah, 2005). The different methods have different data requirements.

We focus here on methods that require discretized data as input, that is, experimental data that have been discretized into a finite number of discrete states. This is a requirement for almost all Bayesian network methods, as well as discrete multi-state model-based methods, such as Boolean networks. Relatively little systematic work has been done on discretization methods for this purpose (Di Camillo, 2005; Ernst, 2006), and such work assumes larger data sets than those available in reality and/or knowledge of the data distribution also rarely available. Di Camillo et al. (2005), for instance, require knowledge of the distribution of the error (x(t) − xb), where x(t) is the measurement and xb is its basal value, and suggest using experimental replicates for finding it. Such a requirement makes their method inapplicable when no such experiments are possible due to their prohibitive cost or the particular experimental design. There is also a large selection of discretization methods which cluster data points but many of them are not directly applicable in the network inference context or are not suitable. One important limitation is typically that the number of available data points is very small, e.g., DNA microarray measurements. Also, methods that provide as output a dynamic model rely on appropriate methods for the discretization of time series data.

We argue in this paper that appropriate data discretization is crucial for the optimal performance of network inference algorithms and deserves to be studied more extensively. To this aim we present the results of a comparison of different discretization methods. We compare the performance of two different network inference methods on the same data set using several different discretization algorithms. The two inference methods are the dynamic Bayesian network algorithm (Bernard, 2005) using the software BANJO (Hartemink, 2006) and the polynomial dynamical system method developed in Jarrah (2005). We apply both methods with the discretization algorithms available in BANJO, namely interval, as well as quantile discretization into 2, 3, 4, and 5 states. Similarly, we evaluate the performance of both inference methods using a new discretization algorithm described in this paper. It has been developed specifically for short time course data, with the goal of obtaining dynamic network models. In order to assess the effect of the different discretization algorithms on network inference accurately we use data from a synthetic gene regulatory network, whose structure is known. We emphasize that our purpose is to compare the performance of discretization methods and not inference methods.

2. Data Discretization

Discretization of real data into a typically small number of finite values is often required by machine learning algorithms (Dougherty, 1995), data mining (Han, 2000), discrete dynamic Bayesian network applications (Berlo, 2003), and any modeling algorithm using discrete-state models. Binary discretizations are the simplest way of discretizing data, used, for instance, for the construction of Boolean network models for gene regulatory networks (Kauffman, 1969; Albert, 2003). The expression data are discretized into only two qualitative states as either present or absent. An obvious drawback of binary discretization is that labeling the real-valued data according to a present/absent scheme generally causes the loss of a large amount of information. Discrete models and modeling techniques allowing multiple states have been developed and studied previously (Laubenbacher, 2004; Thieffry, 1998). In order to place the further discussion in a general context we give a definition of discretization (Hartemink, 2001).

Definition 2.1.

A discretization of a real-valued vector 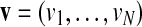Inline graphic is an integer-valued vector 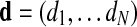Inline graphic with the following properties:

  • 1. Each element of d is in the set 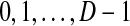Inline graphic for some (usually small) positive integer D, called the degree of the discretization.

  • 2. For all 1 ≤ i, j ≤ N, we have di ≤ dj if and only if vi ≤ vj.

Without loss of generality, assume that v is sorted, i.e., for all i < j, vi ≤ vj. Spanning discretizations of degree D are a special case that we focus on in this paper. They are defined in Hartemink (2001) as discretizations that satisfy the additional property that the smallest element of d is equal to 0 and that the largest element of d is equal to D − 1. Given 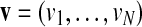Inline graphic, there is a large variety of schemes to obtain a discretization that is consistent with the above definition. Here we present two simple ways that are often used as a starting point in more complicated methods.

Interval discretizations divide the interval [v1, vN] into k equal sized bins, where k is user-defined. Another simple method is quantile discretization which places N/k (possibly duplicated) values in each bin (Dougherty, 1995). Any method based on those two approaches would suffer from problems that make it inapplicable to the type of biological data we consider. Interval discretizations are very sensitive to outliers and may produce a strongly skewed range (Catlett, 1991). In addition, some discretization levels may not be represented at all which may cause difficulties with their interpretation as part of the state space of a discrete model. In fact, for the method that we propose, we assume that for each integer a with 0 ≤ a ≤ D − 1, there is an entry di of d such that a = di.

On the other hand, quantile discretizations depend only on the ordering of the observed values of v and not on the relative spacing values. Since distance between the data points is often the only information that comes with short time series, losing it is very undesirable. A shortcoming, common for both interval and quantile, as well as for most other discretization methods, is that they require the number of discrete states, k, to be user-provided. We discuss later why this is impractical.

A number of entropy-based discretization methods deserve attention. An example of those is Hartemink's Information-preserving Discretization (IPD). It relies on minimizing the loss of pairwise mutual information between each two real-valued vectors (variables). The mutual information between two random variables X and Y with joint distribution p(X, Y) and marginal distributions p(x) and p(y) is defined as

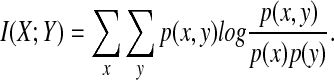graphic file with name M5.gif

Note that if X and Y are independent, by definition of independence p(x, y) = p(x)p(y), so I(X; Y) = 0. When modeling regulatory networks and having as variables, for instance, mRNA, protein, and metabolite concentrations, the joint distribution function is rarely known and it is often hard to determine whether two variables are independent or not. In fact, finding dependencies is a primary objective of regulatory network inference. Therefore, computing mutual information and basing discretization on its pairwise minimization is inapplicable.

As pointed out earlier, a major challenge of discretizing biological data is the small number of data points. For example, about 80% of microarray time series experiments are short: 3-8 time points (Ernst, 2006). For the case of such small samples of data, many statistical methods for discretization, such as Peer (2001), are not applicable due to the insufficient amount of data. For example, the sample size may be insufficient to estimate distributions.

Another common discretization technique is based on clustering (Jain, 1988). One of the most often used clustering algorithms is k-means developed in MacQueen (1967). It is a non-hierarchical clustering procedure whose goal is to minimize dissimilarity in the elements within each cluster while maximizing this value between elements in different clusters. Many applications of k-means clustering, such as the Multi-Experiment Viewer (Saeed, 2003), start by taking a random partition of the elements into k clusters and computing their centroids. As a consequence, a different clustering may be obtained every time the algorithm is run. Another inconvenience is that the number k of clusters to be formed has to be specified in advance. Although there are methods for choosing “the best k”, such as the one described in Crescenzi (2001), they rely on some knowledge of the data properties that may not be available.

Another method is single-link clustering (SLC) with the Euclidean distance function. SLC is a divisive (top-down) hierarchical clustering that defines the distance between two clusters as the minimal distance of any two objects belonging to different clusters ( Jain, 1988). In the context of discretization, these objects will be the real-valued entries of the vector to be discretized, and the distance function that measures the distance between two vector entries v and w will be the one-dimensional Euclidean distance |v − w|. Top-down clustering algorithms start from the entire data set and iteratively split it until either the degree of similarity reaches a certain threshold or every group consists of one object only. For the purpose of data analysis, it is impractical to let the clustering algorithm produce too many clusters containing only one real value. The iteration at which the algorithm is terminated is crucial since it determines the degree of the discretization. SLC with the Euclidean distance function satisfies one of our major requirements: very little starting information is needed—only distances between points. In addition, being a hierarchical clustering procedure, it lends itself to adjustment in case that clusters need to be split or merged. It may result, however, in a discretization where most of the points are clustered into a single partition if they happen to be relatively close to one another. Another problem with SLC is that its direct implementation takes D, the desired number of discrete states, as an input. However, we would like to choose D as small as possible, without losing information about the system dynamics and the correlation between the variables, so that an essentially arbitrary choice is unsatisfactory.

This brief discussion of commonly used discretization methods and the issues that arise when applying them to data from short time course measurements is intended to demonstrate that data discretization for the purpose of inferring properties of biochemical networks has to be approached with care.

3. New Discretization Method: SSD (Short Series Discretization)

We introduce a new method for discretization of time series of experimental data into a finite number of states. While of interest for other purposes, this method is designed specifically for the discretization of short multivariate time series, such as those used for the construction of discrete models of biochemical networks built from time series of experimental data. An important characteristic of such time series that we kept in mind is the relatively small number of data points—typically no more than ten. We employ a graph-theoretic clustering method to perform the discretization and an information-theoretic technique to minimize loss of information content. One of the most useful features of our method is the determination of an optimal number of discrete states that is most appropriate for the data. Our C++ program takes as input one or more vectors of real data and discretizes their entries into a number of states that is most suitable for the data. Our main objective was to construct a method that is capable of preserving information about the network dynamics inherent in the time series as well as performing well in the presence of noise in the experimental data. While in the current paper we use the method only for reconstructing the network interactions, we have evidence that it can be used for the reverse-engineering of the network dynamics as the following example shows.

The current paper acknowledges the problem of having to deal with very small data sizes and presents a method that is specifically designed to work with a small number of data points and does not make ungrounded assumptions about their statistical properties. Some existing discretization techniques assume that the number of discrete classes to be obtained is given (Friedman, 2000). While this number is extremely important, it is not clear how to properly select it in many cases. Also, in these cases it is rarely known what the appropriate discretization thresholds for each gene might be. These two issues were addressed by modifying the SLC algorithm: our method begins by discretizing a vector in the same way as SLC but instead of providing D as part of the input, the algorithm contains termination criteria which determine the appropriate number D. After that each discrete state is checked for information content and if it is determined that this content can be considerably increased by further discretization, then the state is separated into two states in a way that may not be consistent with SLC. We point out that although the discretization method we propose uses clustering as a tool to distribute the data points among the different states, it is not the same as data clustering and pursues different objectives. The details of the SSD algorithm follow next.

3.1. Discretization of one vector

Even if more than one vector is to be discretized, SSD begins by discretizing each vector independently and for some applications this may be sufficient. The example of such a vector to keep in mind is a time series of expression values for a single gene. If the vector contains m distinct entries, a complete weighted graph on m vertices is constructed, where a vertex represents an entry and an edge weight is the Euclidean distance between its endpoints. The discretization process starts by deleting the edge(s) of highest weight until the graph gets disconnected. If there is more than one edge labeled with the current highest weight, then all of the edges with this weight are deleted. The order in which the edges are removed leads to components, in which the distance between any two vertices is smaller than the distance between any two components, a requirement of SLC. We define the distance between two components G and H to be min 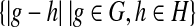Inline graphic. The output of the algorithm is a discretization of the vector, in which each cluster corresponds to a discrete state and the vector entries that belong to one component are discretized into the same state.

3.2. Example

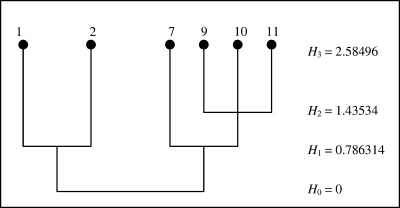
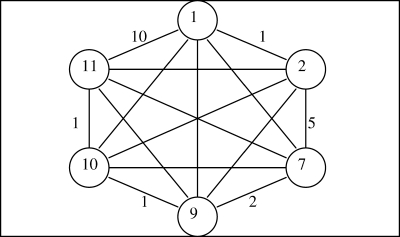
Suppose that vector v = (1, 2, 7, 9, 10, 11) is to be discretized. The corresponding SLC dendrogram that would be obtained by SLC algorithms such as the Johnson's algorithm (Johnson, 1967) is given in Figure 1. We start with constructing the complete weighted graph based on v which corresponds to iteration 0 of the dendrogram (Fig. 2). Eight edges with weights 10, 9, 9, 8, 8, 7, 6, and 5, respectively, have to be deleted to disconnect the graph into two components: one containing vertices 1 and 2 and another having vertices 7, 9, 10, and 11; this is the first iteration. Having disconnected the graph, the next task is to determine if the obtained degree of discretization is sufficient; if not, the components need to be further disconnected in a similar manner to obtain a finer discretization. See the following summary for details.

FIG. 1.

FIG. 1.

Open in a new tab

Dentrogram representing the SLC algorithm applied to the data of Example 3.2. The column on the right gives the corresponding Shannon's entropy increasing at each consecutive level.

FIG. 2.

FIG. 2.

Open in a new tab

The complete weighted graph constructed from vector entries 1, 2, 7, 9, 10, and 11. Only the edge weights of the outer edges are given.

3.3. Algorithm summary

An implementation of the algorithm is available from the authors at polymath.vbi.vt.edu/discretization.

Input: set 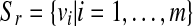Inline graphic where each 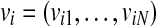Inline graphic is a real-valued vector of length N to be discretized.

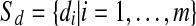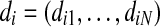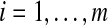Output: set Inline graphic where each Inline graphic is the discretization of vi for all Inline graphic.

  • 1. For each 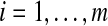Inline graphic, construct a complete weighted graph Gi where each vertex represents a distinct vij and the weight of each edge is the Euclidean distance between the incident vertices.

  • 2. Remove the edge(s) of highest weight.

  • 3. If Gi is disconnected into components 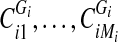Inline graphic, go to 4. Else, go to 2.

  • 4. For each 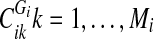Inline graphic, apply “disconnect further” criteria 1–3. If any of the three criteria holds, set 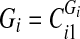Inline graphic and go to 2. Else, go to 5.

  • 5. Apply DF criteria (see below). If this criterion is satisfied, go to 6. Else, go to 7.

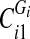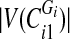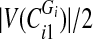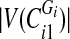  • 6. Sort the vertex values of Inline graphic and split them into two sets: if Inline graphic is even, split the first Inline graphic sorted vertex values of Inline graphic into one set and the rest—into another. If Inline graphic is odd, split the first 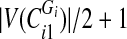Inline graphic sorted vertex values of 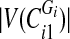Inline graphic into one set and the rest—into another.

  • 7. Sort the components 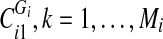Inline graphic, by the smallest vertex value in each 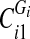Inline graphic and enumerate them 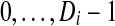Inline graphic, where Di is the number of components into which Gi got disconnected. For each 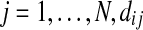Inline graphic is equal to the label of the component in which vij is a vertex.

Disconnect Further (DF) Criteria. A component is further disconnected if and only if both (1) and (2) hold:

  • 1. The minimum vertex degree of the component is less than the number of its vertices minus 1. The contrary implies that the component is a complete graph by itself, i.e., the distance between any two of its vertices is smaller than the distance between the component and any other component.

  • 2. One of the following three conditions is satisfied:

  • (a) The average edge weight of the component is greater than half the average edge weight of the complete graph.

  • (b) The largest distance between two vertices is greater than or equal to half this distance in the complete graph. For the complete graph, the distance is the graph's highest weight.

  • (c) Finally, if the above two conditions (a) and (b) fail, a third one is applied: disconnect the component if it leads to a substantial increase in the information content carried by the discretized vector (see Section 3.4.)

3.4. Information measure criterion

Discretizing the entries of a real-valued vector into a finite number of states inevitably reduces the information carried by the discrete vector in the sense defined in Shannon (1948). Shannon developed a measure of how much information is produced by a discrete source. The measure is known as entropy or Shannon entropy. Suppose there is a set of n possible events whose probabilities of occurrence are known to be 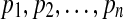Inline graphic. Shannon proposed a measure of how much choice is involved in the selection of the event or how certain one can be of the outcome, which is given by

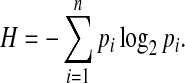graphic file with name M28.gif

The base 2 of the logarithm is chosen so that the resulting units may be called bits. In our context the Shannon entropy of a vector discretized into n states is given by

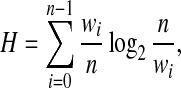graphic file with name M29.gif

where wi is the number of entries discretized into state i. An increase in the number of states implies an increase in entropy, with an upper bound of log2n. However, we want the number of states to be small, so it is important to notice that H increases by a different amount depending on which state is split and the size of the resulting new states. For example, if a state containing the most entries is split into two new states of equal size, H will increase more than if a state of fewer entries is split or if we split the larger state into two states of different sizes. Splitting a state into two states of equal size maximizes the entropy increase. For that reason, if a component fails the other conditions, we consider splitting it further only if doing so would provide a very significant increase of the entropy, i.e., if the component corresponds to a “large” collection of entries. In our implementation a component gets disconnected further only if it contains at least half of the vector entries.

3.5. Algorithm complexity

Given M variables, with N time points each, we compute N(N − 1)/2 distances to construct the distance matrix so the complexity of this step is 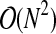Inline graphic. The distance matrix is used to create the edge and vertex sets of the complete distance graph, containing N(N − 1)/2 edges. This can also be accomplished in 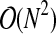Inline graphic time. These edges are then sorted into decreasing order, so that the largest edges are removed first. A standard sorting algorithm, such as merge sort, has complexity 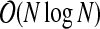Inline graphic (Knuth, 1998). As each edge is removed, the check for graph disconnection involves testing for the existence of a path between the two vertices of the edge. This test for graph disconnection can be accomplished with a breadth-first search, which has order 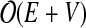Inline graphic (Pemmaraju, 2003), with E the number of edges and V the number of vertices in the component. In our case this translates to complexity 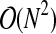Inline graphic. Edge removal is typically performed for a large percentage of the N(N − 1)/2 edges, so this step has overall complexity 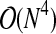Inline graphic. The edge removal step dominates the complexity so that the overall complexity is 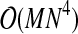Inline graphic to discretize all M variables. While this is the theoretical worst-case performance, because of the heuristics we have added the typical performance is significantly better.

3.6. Requirements on the number of states

While for some applications any number of discretization states is acceptable, there are some cases when there are limitations on this number. For example, if the purpose of discretizing the data is to build a model of polynomials over a finite field, as in Laubenbacher (2004), then the number of states must be a power of a prime since every finite field has cardinality pn, where p is prime and n is a positive integer. SSD deals with this problem in the following way. Suppose that a vector has been discretized into m states in the way described above. The next step is to find the smallest integer k = pn such that m ≤ k. This value for k gives the number of states that needs to be obtained. Since SSD yielded m clusters, the remaining k − m can be constructed by sorting the entries in each cluster and splitting the one that contains the two most distant entries with respect to Euclidean distance. The splitting should take place between these entries. This is repeated until k clusters are obtained. This approach has a potential problem. For instance, if a vector got discretized into 14 states and the total number of distinct entries of the vector is 15, then k = 16 cannot be reached. In this case the two closest states could be merged together to obtain 13 states. In general it may not be desirable to reduce the number of states because this results in loss of information. We would rather increase the number of states unless it is impossible as in the above example.

3.7. Discretization of several vectors

Some applications may require that all vectors in a data set be discretized into the same number of states. For example, the approach adopted by Laubenbacher (2004) imposes such a requirement on the discretization. The way we deal with this is by first discretizing all vectors separately. Suppose that for N vectors, SSD discretized each into 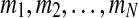Inline graphic states, respectively. Let 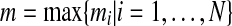Inline graphic Now find the least possible k = pn such that m ≤ k. Finally, discretize all variables into k states in the same way that was described for the discretization of a single vector into the required number of states.

3.8. Preservation of correlation

While any discretization inevitably results in information loss, a good multivariate discretization should preserve some important features of the data such as correlation between the variables. To demonstrate that SSD has this property, we use the temporal map of fluctuations in mRNA expression of a set of genes related to rat central nervous system development presented in Wen (1998). This paper focuses on the cervical spinal cord and the genes included in their study are from families that are believed to be important for spinal cord development. They used an RT-PCR protocol to measure the expression of 112 genes in central nervous system development. The data consist of nine expression measurements for each gene: cervical spinal cord tissue was dissected from animals in embryonic days 11, 13, 15, 18, and 21 and in postnatal days 0, 7, 14, and 90.

We calculated the Spearman rank correlation coefficient between each gene's analog time series and discretized time series according to Walpole (1998). Then we identified each coefficient value as representing a “significant” or “not significant” correlation based on a critical value of 0.683, which corresponds to a significance level of 0.025 for a time series of nine points. This means that the probability that the correlation coefficient for a pair of uncorrelated time series of length 9 will be greater than or equal to 0.683 is 0.025. The result is that 71 out of 112 genes were found to be significantly correlated to their discrete version, which is 63.39% of the total number of genes. By changing the level of significance to 0.05, this percentage increases to 76.79%. We also calculated the Spearman rank correlation coefficient for each pair of genes before and after discretizing the data, considering only the genes that discretized into exactly three states (56 of them). For the original data given in Wen (1998), out of the 1540 gene pairs, 234 pairs were identified as significantly correlated at significance level 0.025. Based on the discretized data, 132 pairs were correctly identified as significantly correlated and 1181 pairs were correctly recognized as not significantly correlated. That is, 1313, or more than 85%, of the correlations were correctly classified after discretization. These results suggest that SSD can be successfully applied to cases when preserving the correlation among the variables in a system is important.

We performed more correlation analysis to compare SSD to quantile and interval discretization (see Section 4.5).

3.9. SSD algorithm validation

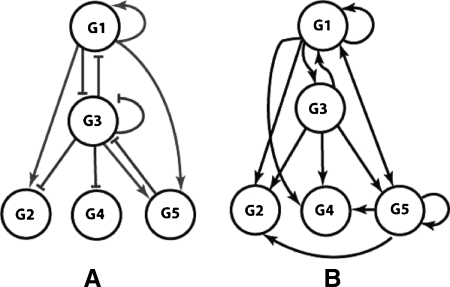
We now demonstrate how SSD can be used for reconstruction of a gene network. Due to limited knowledge of the dynamic features of real biochemical networks, the validation of our method is best done with a simulated network. In order to extract information about the network topology and dynamics from the discretized data, we use the network reconstruction method in Laubenbacher (2004). The goal of this validation is to show that the discretized data preserved the information about the network that was contained in the corresponding continuous data generated from the network. We used the A-Biochem software system developed by Mendes (2003) to generate the simulated network. A-Biochem automatically generates artificial gene networks with particular topological and kinetic properties. These networks are embodied in kinetic models, which are used by the biochemical-network simulator Gepasi (Mendes, 1993, 1997) to produce simulated gene expression data. We generated an artificial gene network with five genes and ten total input connections using the Albert-Barabási algorithm (Albert, 2000). In Figure 3A, the arrows represent gene activation in the arrow's direction and the segments stand for inhibition.

FIG. 3.

FIG. 3.

Open in a new tab

(A) Dependency graph of the A-Biochem-generated artificial gene network on five genes Gi. (B) Dependency graph of the reverse-engineered system.

Gepasi uses a continuous representation of biochemical reactions, based on ordinary differential equations (ODE). With the parameters we specified, Gepasi generated an ODE system that represents the network. Analyzing the dynamics of the ODE system, one finds that it has two stable steady states. As Laubenbacher (2004) demonstrated, the performance of their algorithm dramatically improves if knockout time series for genes are incorporated. For this reason, we supplied seven time series of 11 points each: two wild-type time series and five knockout time series, one for each gene. The wild-type time series are generated by solving the ODE system numerically for two different initial conditions. One can simulate a gene knockout by setting the corresponding variable and initial condition to zero. The time points from each of the seven time series constitute the input vectors. The discretization algorithm chose a state set X of cardinality 5 and, based on the discrete data, the reverse-engineering method generated five polynomials describing the discrete model. That is, the discrete model is given by a time-discrete dynamical system

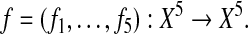graphic file with name M39.gif

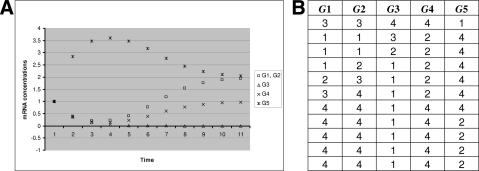
Now we compare the dynamics of the two models. First, the discretization maps the ODE's stable steady states to fixed points of the discrete model. To illustrate the matching dynamics of the two models, notice how the discrete model's trajectory in Figure 4B can be superimposed over the continuous trajectory in Figure 4A, both ending at a fixed point/steady state. The same can be observed for the second steady-state.

FIG. 4.

FIG. 4.

Open in a new tab

(A) Wild-type time series generated by solving numerically the ODE system. (B) Corresponding discrete point time series.

Further evidence of the ability of SSD to retain information is the fact that the reverse-engineering method in Laubenbacher (2004) was able to extract most of the information about the dependency graph of the network. This can be seen by comparing the inferred diagram in Figure 3B to the diagram of the actual direct interactions in Figure 3A.

3.10. Discretization in the presence of noise

Noise is naturally present in biological data and in microarray data in particular (Hassibi, 2005). Although there are various techniques which increase the accuracy of the microarray measurements, the data inevitably contain errors due to the probabilistic characteristics of the detection process, from sample extraction and mRNA purification to hybridization and imaging. Consequently, it is crucial to study how the proposed discretization algorithm performs in the presence of typical levels of noise in the experimental data.

To study the effect of noise, we considered two types of data. We used the earlier mentioned gene expression measurements generated for a study of rat cervical central nervous system development (Wen, 1998). We selected 18 genes whose nine-point time series have statistical variance of more than 1. Although the data likely contain some noise, here we assume that the measurements are perfect and we add noise of known proportion and distribution assuming it is the only noise in the data. The purpose is to work with data which have the properties of real microarray time series. The second data set is an artificial ten-point time series on 30 “genes.” The values are randomly generated real numbers in the range [0, 20] with statistical variance greater than 10.

Two types of noise are added to the data at the same time: overall and point-specific (Hatzimanikatis, 1999). The overall noise is added by sampling from a normal distribution with zero mean and a standard deviation equal to 12.5% of the standard deviation of each gene. The point-specific noise is simulated by adding noise to each time point sampling from a different normal distribution with zero mean and standard deviation equal to 12.5% of the standard deviation of the particular time point value. Thus, the total proportion of added noise amounts to 25%. For each gene 100 noise containing replicates were generated and discretized.

For each gene, we compare the way the original noiseless time series was discretized to the discretization of the noise-containing replicates. We count the number of noise-containing replicates that got discretized exactly the same as the original noiseless time series. For the gene expression data from Wen (1998), 78.72% of all the 18 × 100 noise-containing replicates were discretized exactly as their corresponding noiseless originals. This number is significantly higher for the randomly generated data of variance 10 or higher: 93.8% of all the 30 × 100 noise-containing replicates were discretized exactly as their corresponding noiseless originals. The big difference between the two results can be explained by the different statistical variance of the original data in the two cases. Only 5 out of the 18 genes in the expression measurements time series in Wen (1998) have variance greater than 10 while the “genes” in the simulated time series had variance of at least 10 with average variance of 34.5. Since the higher the variance of a time series, the better the chance of more distinct and easier to detect discrete states, the discretization of the data with higher variance not surprisingly showed more robustness in the presence of noise.

4. Comparison of Discretization Methods

We now compare the performance of SSD to two other common discretization algorithms: quantile and interval. We point out that data discretization is a crucial step for modeling methods not based on reverse engineering and such methods can also benefit from SSD. To enable the comparison, we use these algorithms to provide discrete data for two reverse-engineering methods: dynamic Bayesian networks (Yu, 2002) and discrete polynomial dynamical systems (Jarrah, 2005). The particular implementations used for the study are outlined next. In 4.1, we describe the in silico gene regulatory networks that produced the input data and our comparison metrics are given in 4.4. The data sets used for the comparison are available at http://polymath.vbi.vt.edu/discretization/DiscretizationComparison/.

4.1. In silico gene regulatory networks

To evaluate the performance of the different discretization methods as part of a network inference algorithm, we use data from four different artificial gene regulatory networks generated using the software package of Mendes (2003). In these networks the interactions between genes are phenomenological and represent the result of the effect of transcription and translation on the regulation of the genes in the network, implemented as a system of ODEs in Copasi (Hoops, 2006).

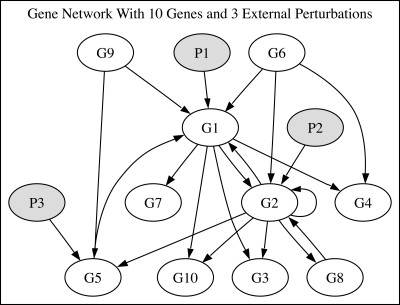
The first network shown in Figure 5, referred to subsequently as “Network 1,” consists of 13 species: ten genes and three different environmental perturbations. The perturbations affect the transcription rate of the gene on which they act directly (through inhibition or activation) and their effect is further propagated through the network by the interactions between the genes. The data used consist of six short time series corresponding to different concentration values for the environmental perturbations, with a total of 144 time steps; this network has been previously used in Camacho (2007).

FIG. 5.

FIG. 5.

Open in a new tab

Network 1: 10 genes and three environmental perturbations. In this network, the three environmental perturbations P1, P2, and P3 directly affect the expression rate of genes G1, G2, and G5, respectively.

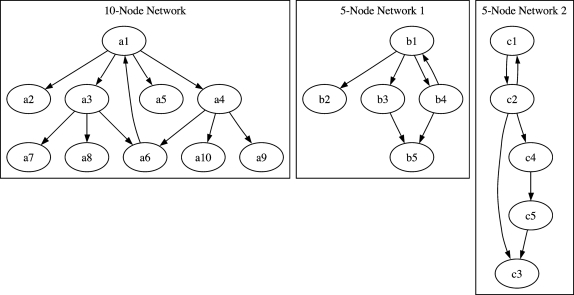
The second and third networks, “Network 2” and “Network 3,” respectively, consist of five genes that interact with each other through inhibition or activation; the data generated consist of seven short time series, with a total of 77 time steps. Similarly, the fourth in silico network, “Network 4,” consists of ten genes; the data generated consist of seven short time series corresponding to the different given initial conditions, with a total of 147 time steps. The three networks are shown in Figure 6.

FIG. 6.

FIG. 6.

Open in a new tab

Three in silico networks. The first network consists of 10 genes and the second and third networks consist of 5 genes. In these three networks, the interactions between genes are phenomenological and represent the result of the effect of transcription and translation on the regulation of the genes in the network.

4.2. Dynamic Bayesian networks

A Bayesian network is a graphical model that describes the causal relationships between variables. Such relationships are represented by a family of joint probability distributions consistent with the independence assertions embedded in the graph (Hartemink, 2002). A dynamic Bayesian network (DBN) (Friedman, 1998) extends the notion of a Bayesian network to model the stochastic evolution of a set of random variables over time. The structure of a DBN thus describes the qualitative nature of the dependencies that exist between variables in a temporal process (Bernard, 2005).

The software Bayesian Network Inference with Java Objects (BANJO) (Hartemink, 2006) is an implementation of a DBN inference method. The type of data required for this method is in the form of temporal response of the system to a perturbation. BANJO also requires as input a set of parameters, such as search method, time lag (how far back in time each variable depends on the others), type of discretization, etc. The core algorithms in BANJO assume discrete variables, and BANJO provides a discretization functionality using either quantile or interval discretization algorithms with a default upper bound of five states per variable.

The data discretization is handled as follows:

  • I. SDD Discretization of Data. The SDD method returned variables discretized into 5 and 11 states for Network 1 and Network 4, respectively. Similarly, the SSD method returned variables discretized into 7 states for both Network 2 and 3. BANJO handles networks with discretized variables up to 5 states, allowing us to use directly the data from Network 1; in order to use our discretization method for the networks with 5 genes, we extracted the time step measurements that return variables discretized into more than 5 states, to reduced the data to approximately 70 time steps in each data set. Due to the 11 state discretization values return by SDD we were unable to use Network 4, but were able to use it with the discrete polynomial dynamical system reverse-engineering method.

  • II. Interval and Quantile Discretization of Data. BANJO provides a discretization functionality using either quantile or interval discretization algorithms with a default upper bound of five states per variable. Assuming no prior information about the ideal type or number of discretization states, we explore all of the possible discretization methods available in BANJO: quantile and interval into 2, 3, 4 and 5 states to find the highest scored inferred DBN.

Per each one of these different discretized data sets, we infer a DBN considering two important aspects:

  • 1. As commonly needed for optimization based methods as BANJO, a set of input parameters should be specified in order to infer a DBN (approximately 13 different parameter values), thus we need to explore different combinations of parameter sets for each of the discretized data sets. A set of parameter values is selected based on BANJO's scoring method.

  • 2. Unless we assume an instantaneous time lag (i.e., time lag value 0), it is necessary to build a consensus DBN from the DBNs inferred from each one of the 6 or 7 different input time courses of a given network; this is done in order to avoid having to consider the state values of the first time step of a given time series to depend on the last time step(s) of the previous time course.

Hence, for a given discretization type we first select the combination of sets of parameters that provide a highest score. Then, in order to build a consensus sparse network (i.e., to avoid a high rate of false positives) from the different DBNs obtained from each time series, we select edges that appear in at least two of the output networks.

4.3. Discrete polynomial dynamical systems

We used the reverse-engineering algorithm of Jarrah (2005) together with their (S1, T1) scoring method1 for which only the network model(s) with the highest score is generated. In this method, the only input needed for the algorithm is the discretized time series (i.e., unlike BANJO, there are no parameter values to explore).

We compare the network models obtained from the method of Jarrah (2005) when using the following discretizations:

  • 1. SSD: As mentioned in section 4.2, the SDD method returned variables discretized into 5 and 11 states for Networks 1 and 4, respectively. Similarly, the SSD method returned variables discretized into 7 states for both networks of five genes (Network 2 and Network 3).

  • 2. Quantile and Interval discretization into 5,11 and 7 states to allow a direct comparison with SSD.

4.4. Metrics for method performance

For an unbiased evaluation of the performance of each reverse-engineering algorithms with the different discretization methods, we quantify:

  • (a) Correct interactions inferred (true positives, TP)

  • (b) Incorrect interactions inferred (false positives, FP)

  • (c) Correct non-interactions inferred (true negatives, TN)

  • (d) Incorrect non-interactions inferred (false negatives FN)

The values of TPs, TNs, FPs, and FNs are calculated to build a confusion matrix. The confusion matrix is a matrix that provides an assessment of the classification procedure, or how “confused” the algorithm might be, by simply counting the interactions discovered. From the confusion matrix we compute the Recall or True Positive Rate TPR = TP/(TP + FN), the False Positive Rate FPR = FP/(FP + TN), Accuracy ACC = (TP + TN)/TotI and Precision or Positive Predictive Value PPV = TP/(TP + FP). It is important to mention that coordinate points (FPR, TPR) represent coordinate points within the Receiver Operator Characteristic (ROC) curves, whereas (TPR, PPV) represent coordinate points within the Recall Precision Curve; both of these curves are commonly used for the evaluation of reverse-engineering methods. Since we are presenting here pairs of coordinate points in both curves, we decided to compare results in both metrics as well as to add the Accuracy (ACC) score for a broader view of the effect of each discretization method. In particular, it is worth to comment how ROC points can be characterized: a perfect reverse engineering method will ideally have score (FPR, TPR) = (0, 1), whereas the worst possible network will have coordinates (FPR, TPR) = (1, 0) and methods with scores below the identity line (or diagonal) are those that perform no better than a random guess.

The best scored consensus DBNs from BANJO are presented in Table 1. Notice that with respect to any of the four metrics—TPR, FPR, ACC, or PPV—our discretization method performs best. The results for the polynomial dynamical systems method are summarized in Table 2. We observe that using any metric, we obtained the best results with SSD. From our analysis, we see that with both reverse-engineering algorithms, the SSD performs consistently better, independently of the metric employed.

Table 1.

Dynamic Bayesian Network Approach

  TP FP TN FN TPR FPR ACC PPV
SSD Net1 7 9 138 15 .318 .0612 .858 .438
BANJO Net1 2 5 142 20 .091 .0340 .852 .286
SSD Net2 4 2 17 2 .666 .105 .84 .666
BANJO Net2 2 4 15 4 .333 .210 .68 .333
SSD Net3 3 2 17 3 .5 .105 .80 .6
BANJO Net3 2 2 17 4 .333 .105 .76 .5
Open in a new tab

Best results for the DBNs obtained in BANJO. The first four columns are the four entries in the confusion matrix.

Table 2.

Polynomial Dynamical Systems Approach

  TP FP TN FN TPR FPR ACC PPV
SSD Net1 12 34 113 10 .5454 .231 .7396 .261
Quantile, 5 states Net1 9 49 98 13 .4090 .333 .6331 .155
Interval, 5 states Net1 7 46 101 15 .3181 .313 .6390 .132
SSD Net2 3 5 14 3 .5 .263 .68 .375
Quantile, 7 states Net2 5 13 6 1 .83 .684 .44 .277
Interval, 7 states Net2 4 11 8 2 .66 .579 .48 .266
SSD Net3 4 7 12 2 .66 .368 .64 .364
Quantile, 7 states Net3 5 13 6 1 .83 .684 .44 .277
Interval, 7 states Net3 5 12 7 1 .83 .632 .48 .294
SSD Net4 7 20 69 4 .63 .225 .76 .259
Quantile, 11 states Net4 10 49 40 1 .90 .551 .50 .169
Interval, 11 states Net4 6 34 55 5 .54 .382 .61 .15
Open in a new tab

The first four columns are the four entries in the confusion matrix.

4.5. Correlation preservation comparison

We calculated the Spearman rank correlation coefficient between each gene's continuous time series and its time series discretized with SSD, interval, and quantile discretizations. 82% of the genes had SSD discretizations that are either more strongly or as strongly correlated to the continuous data as interval and quantile discretizations. Moreover, at level of significance 0.05, the correlation coefficient is large enough to conclude that there is evidence that the continuous time series are strongly correlated to their SSD discretizations.

5. Conclusions

Discretization of continuous experimental data into finitely many discrete states is important in several contexts, in particular in systems biology when inferring biochemical networks from experimental data such as time series data of DNA microarrays. Almost all methods using dynamic Bayesian networks as well as other discrete methods rely on data discretization as a preprocessing step. A particular characteristic of time series data sets is that they are still quite small, typically consisting of less than 10 time points. It is natural to look at one of the many available clustering methods for this purpose. Upon closer study, however, it becomes clear that discretization of this particular data type with standard clustering methods is problematic. This has led us to develop the new method, SSD, described here. The main result of the paper is a comparison to other commonly used discretization methods by means of their application to two very different network inference methods, both of which give as output a most likely dependency. The comparison shows that network inference using either of these methods results in better predictions with SSD as compared to the other commonly used methods.

It has been our experience that, while SSD performs well in many cases, its output can often be improved with human intervention. This would most likely be the case with any discretization method. Furthermore, there are certain types of data that SSD does not handle well. We do not recommend using SSD whenever long time series are available. In this case, a statistical method, such as Peer (2001), that can take advantage of the statistical properties of the data may be more appropriate. Our method assumes no knowledge of these properties and therefore cannot utilize this information. Another situation when virtually any discretization technique may not produce useful results is in the case when one or several of the system variables change much more rapidly than the rest. In order to avoid inconsistencies in the discretized data, one may need a very large number of discrete states which may be a disadvantage for the modeling process. The authors also acknowledge that discretization possibly introduces spurious dynamic phenomena, such as artificial periodic behavior, due to different time scales in the network. This has been well documented in the literature (Hatzimanikatis, 1999). As a result, the output of any discretization algorithm needs to be carefully examined in light of the original data.

Another problem that is specific for polynomial dynamical systems modeling is that discretization sometimes results in a data set that is inconsistent, in the sense that it cannot be produced by a deterministic dynamical system because a given state that appears more than once in the time series might transition to two different subsequent states. While one can devise ad hoc solutions to this problem, a more systematic way of dealing with this problem remains to be found.

Data discretization represents the transition from the continuous to the discrete data world and therefore plays a crucial role in the construction of discrete models. If this transition is not done well, all subsequent steps are flawed.

Footnotes

1

For a Macaulay2 implementation of the (S1, T1) scoring method, contact R. Laubenbacher at reinhard@vbi.vt.edu.

Acknowledgments

We thank A. Jarrah, A. de la Fuente, P. Mendes, and B. Stigler for contributing insights and help with editing, and D. Camacho, I. Hoeschele, and W. Sha for helpful discussions. We are particularly grateful to Pedro Mendes and Diogo Camacho for permitting the use of the simulated gene regulatory networks employed here and that have been constructed by them. The first, second, and fourth authors have been partially supported by the NIH (grant RO1GM068947-01).

Disclosure Statement

No competing financial interests exist.

References

  1. Akutsu T. Miyano S. Inferring qualitative relations in genetic networks and metabolic pathways. Bioinformatics. 2000;16:727–734. doi: 10.1093/bioinformatics/16.8.727. [DOI] [PubMed] [Google Scholar]
  2. Albert R. Barabási A. Topology of evolving networks: local events and universality. Phys. Rev. Lett. 2000;85:5234–5237. doi: 10.1103/PhysRevLett.85.5234. [DOI] [PubMed] [Google Scholar]
  3. Albert R. Othmer H. The topology of the regulatory interactions predict the expression pattern of the segment polarity genes in Drosophila melanogaster. J. Theor. Biol. 2003;223:1–18. doi: 10.1016/s0022-5193(03)00035-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Andrec M. Kholodenko B.N. Inference of signaling and gene regulatory networks by steady-state perturbation experiments: structure and accuracy. J. Theor. Biol. 2005;232:427. doi: 10.1016/j.jtbi.2004.08.022. [DOI] [PubMed] [Google Scholar]
  5. Beal M.J. Falciani F. A Bayesian approach to reconstructing genetic regulatory networks with hidden factors. Bioinformatics. 2005;21:349–356. doi: 10.1093/bioinformatics/bti014. [DOI] [PubMed] [Google Scholar]
  6. van Berlo R. van Someren E. Reinders M. Studying the conditions for learning dynamic Bayesian networks to discover genetic regulatory networks. Simulation. 2003;79:689–702. [Google Scholar]
  7. Bernard A. Hartemink A. Informative structure priors: joint learning of dynamic regulatory networks from multiple types of data. Pac. Symp. Biocomput. 2005 [PubMed] [Google Scholar]
  8. Camacho D. Vera-Licona P. Mendes P., et al. Comparison of reverse-engineering methods using an in silico network. Ann. N. Y. Acad. Sci. 2007;1115:73–89. doi: 10.1196/annals.1407.006. [DOI] [PubMed] [Google Scholar]
  9. Catlett J. Megainduction: machine learning on very large databases [Ph.D. dissertation] University of Sydney; Australia: 1991. [Google Scholar]
  10. Crescenzi M. Giuliani A. The main biological determinants of tumor line taxonomy elucidated by of principal component analysis of microarray data. FEBS Lett. 2001;507:114–118. doi: 10.1016/s0014-5793(01)02973-8. [DOI] [PubMed] [Google Scholar]
  11. de la Fuente A. Bing N. Discovery of meaningful associations in genomic data using partial correlation coefficients. Bioinformatics. 2004;20:3565–3574. doi: 10.1093/bioinformatics/bth445. [DOI] [PubMed] [Google Scholar]
  12. Di Camillo B. Sanchez-Cabo F. A quantization method based on threshold optimization for microarray short time series. BMC Bioinform. 2005;6(Suppl):S11. doi: 10.1186/1471-2105-6-S4-S11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Dojer N. Gambin A. Applying dynamic Bayesian networks to perturbed gene expression data. BMC Bioinform. 2006;7:249. doi: 10.1186/1471-2105-7-249. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Dougherty J. Kohavi R. Sahami M. Supervised and unsupervised discretization of continuous features; Mach. Learn. Proc. 12th Int. Conf.1995. [Google Scholar]
  15. Ernst J. Bar-Joseph Z. STEM: a tool for the analysis of short time series gene expression data. BMC Bioinform. 2006;7:191. doi: 10.1186/1471-2105-7-191. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Friedman N. Murphy K. Russell S. Learning the structure of dynamic proabilist networks; 14th Conf. Uncertainty Artif. Intell..1998. [Google Scholar]
  17. Friedman N. Linial M. Nachman I., et al. Using Bayesian networks to analyze expression data. J. Comput. Biol. 2000;7:601–620. doi: 10.1089/106652700750050961. [DOI] [PubMed] [Google Scholar]
  18. Gardner T.S. Bernardo D. Inferring genetic networks and identifying compound mode of action via expression profiling. Science. 2003;301:102–105. doi: 10.1126/science.1081900. [DOI] [PubMed] [Google Scholar]
  19. Han J. Kamber M. Data Mining: Concepts and Techniques. Academic Press; San Diego: 2000. [Google Scholar]
  20. Hartemink A. Principled computational methods for the validation and discovery of genetic regulatory networks [Ph.D. dissertation] Massachusetts Institute of Technology; Cambridge, MA: 2001. [Google Scholar]
  21. Hartemink A. Gifford D. Jaakkola T., et al. Bayesian methods for elucidating genetic regulatory networks. IEEE Intell. Syst. 2002;17:37–43. [Google Scholar]
  22. Hartemink A. BANJO: Bayesian Network Inference with Java Objects. 2006. www.cs.duke.edu/amink/software/banjo/ [Dec 1;2009 ]. www.cs.duke.edu/amink/software/banjo/
  23. Hatzimanikatis V. Lee K.H. Dynamical analysis of gene networks requires both mRNA and protein expression information. Metab. Eng. 1999;1:275–281. doi: 10.1006/mben.1999.0115. [DOI] [PubMed] [Google Scholar]
  24. Hassibi A. Vikalo H. Probabilistic modeling and estimation of gene expression levels in microarray. Proc. IEEE Workshop GENSIPS 2005 [Google Scholar]
  25. Hoops S. Sahle S. COPASI—a COmplex PAthway SImulator. Bioinformatics. 2006;22:3067–3074. doi: 10.1093/bioinformatics/btl485. [DOI] [PubMed] [Google Scholar]
  26. Jain A. Dubes R. Algorithms for Clustering Data. Prentice Hall; Englewood Cliffs, NJ: 1988. [Google Scholar]
  27. Jarrah A. Laubenbacher R. Stigler B., et al. Reverse-engineering of polynomial dynamical systems. Adv. Appl. Math. 2007;39:477–489. [Google Scholar]
  28. Johnson S.C. Hierarchical clustering schemes. Psychometrika. 1967;32:241–254. doi: 10.1007/BF02289588. [DOI] [PubMed] [Google Scholar]
  29. Kauffman S.A. Metabolic stability and epigenesist in randomly constructed genetic nets. J. Theor. Biol. 1969;22:437–467. doi: 10.1016/0022-5193(69)90015-0. [DOI] [PubMed] [Google Scholar]
  30. Kim J. Bates D. Least-squares methods for identifying biochemical regulatory networks from noisy measurements. BMC Bioinform. 2007;8:8. doi: 10.1186/1471-2105-8-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Knuth D.E. The Art of Computer Programming 3: Sorting and Searching. 2nd. Addison-Wesley; Reading, MA: 1998. [Google Scholar]
  32. Laubenbacher R. Stigler B. A computational algebra approach to the reverse engineering of gene regulatory networks. J. Theor. Biol. 2004;229:523–537. doi: 10.1016/j.jtbi.2004.04.037. [DOI] [PubMed] [Google Scholar]
  33. Liang S. Fuhrman S. Reveal, a general reverse engineering algorithm for inference of genetic network architectures. Pac. Symp. Biocomput. 1998:18–29. [PubMed] [Google Scholar]
  34. MacQueen J. Some methods for classification and analysis of multivariate observations. Proc. 5th Berkeley Symp. Math. Statist. Probabil. 1967:281–297. [Google Scholar]
  35. Martin S. Zhang Z. Boolean dynamics of genetic regulatory networks inferred from microarray time series data. Bioinformatics. 2007 doi: 10.1093/bioinformatics/btm021. [DOI] [PubMed] [Google Scholar]
  36. Mehra S. Hu W-S. A Boolean algorithm for reconstructing the structure of regulatory networks. Metab. Eng. 2004;6:326. doi: 10.1016/j.ymben.2004.05.002. [DOI] [PubMed] [Google Scholar]
  37. Mendes P. GEPASI: a software package for modeling the dynamics, steady states and control of biochemical and other systems. Comput. Appl. Biosci. 1993;9:563–571. doi: 10.1093/bioinformatics/9.5.563. [DOI] [PubMed] [Google Scholar]
  38. Mendes P. Biochemistry by numbers: simulation of biochemical pathways with Gepasi 3. Trends Biochem. Sci. 1997;22:361–363. doi: 10.1016/s0968-0004(97)01103-1. [DOI] [PubMed] [Google Scholar]
  39. Mendes P. Sha W. Ye K. Artificial gene networks for objective comparison of analysis algorithms. Bioinformatics. 2003;19:ii122–ii129. doi: 10.1093/bioinformatics/btg1069. [DOI] [PubMed] [Google Scholar]
  40. Nariai N. Tamada Y. Estimating gene regulatory networks and protein-protein interactions of Saccharomyces cerevisiae from multiple genome-wide data. Bioinformatics. 2005;21(Suppl):ii206–ii212. doi: 10.1093/bioinformatics/bti1133. [DOI] [PubMed] [Google Scholar]
  41. Pe'er D. Regev A. Elidan G., et al. Inferring subnetworks from perturbed expression profiles. Bioinformatics. 2001;17:S215–S224. doi: 10.1093/bioinformatics/17.suppl_1.s215. [DOI] [PubMed] [Google Scholar]
  42. Pemmaraju S. Skiena S. Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Cambridge University Press; New York: 2003. [Google Scholar]
  43. Pournara I. Wernisch L. Reconstruction of gene networks using Bayesian learning and manipulation experiments. Bioinformatics. 2004;20:2934–2942. doi: 10.1093/bioinformatics/bth337. [DOI] [PubMed] [Google Scholar]
  44. Saeed A. Sharov V. White J., et al. TM4: a free, open-source system for microarray data management and analysis. BioTechniques. 2003;34:374–378. doi: 10.2144/03342mt01. [DOI] [PubMed] [Google Scholar]
  45. Shannon C. A mathematical theory of communication. Bell Syst. Technical J. 1948;27:379–423. 623–656. [Google Scholar]
  46. Thieffry D. Thomas R. Qualitative analysis of gene networks. Proc. Pac. Symp. Biocomput. 1998:77–88. [PubMed] [Google Scholar]
  47. Walpole R. Myers R. Myers S. Probability and Statistics for Engineers and Scientists. 6th. Prentice Hall; Englewood Cliffs, NJ: 1998. [Google Scholar]
  48. Wen X. Fuhrman S. Michaelis G., et al. Large-scale temporal gene expression mapping of central nervous system development. Proc. Natl. Acad. Sci. USA. 1998;95:334–339. doi: 10.1073/pnas.95.1.334. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Yu J. Smith V. Wang P., et al. Using Bayesian network inference algorithms to recover molecular genetic regulatory networks. Int. Conf. Syst. Biol. 2002 [Google Scholar]
  50. Yu J. Smith V.A. Advances to Bayesian network inference for generating causal networks from observational biological data. Bioinformatics. 2004;20:3594–3603. doi: 10.1093/bioinformatics/bth448. [DOI] [PubMed] [Google Scholar]
  51. Zou M. Conzen S.D. A new dynamic Bayesian network (DBN) approach for identifying gene regulatory networks from time course microarray data. Bioinformatics. 2005;21:71–79. doi: 10.1093/bioinformatics/bth463. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Computational Biology are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES