A Probabilistic and Continuous Model of Protein Conformational Space for Template-Free Modeling

Abstract

One of the major challenges with protein template-free modeling is an efficient sampling algorithm that can explore a huge conformation space quickly. The popular fragment assembly method constructs a conformation by stringing together short fragments extracted from the Protein Data Base (PDB). The discrete nature of this method may limit generated conformations to a subspace in which the native fold does not belong. Another worry is that a protein with really new fold may contain some fragments not in the PDB. This article presents a probabilistic model of protein conformational space to overcome the above two limitations. This probabilistic model employs directional statistics to model the distribution of backbone angles and 2^nd-order Conditional Random Fields (CRFs) to describe sequence-angle relationship. Using this probabilistic model, we can sample protein conformations in a continuous space, as opposed to the widely used fragment assembly and lattice model methods that work in a discrete space. We show that when coupled with a simple energy function, this probabilistic method compares favorably with the fragment assembly method in the blind CASP8 evaluation, especially on alpha or small beta proteins. To our knowledge, this is the first probabilistic method that can search conformations in a continuous space and achieves favorable performance. Our method also generated three-dimensional (3D) models better than template-based methods for a couple of CASP8 hard targets. The method described in this article can also be applied to protein loop modeling, model refinement, and even RNA tertiary structure prediction.

1. Introduction

To fully understand the biological functions of a protein, the knowledge of its three-dimensional (3D) structures is essential. Many computational methods have been developed to predict the structure of a protein from its primary sequence. These methods can be roughly classified into two categories: template-based and template-free modeling. Despite significant progress in recent years, template-free modeling is still one of the most challenging problems in computational structural biology. Template-free modeling based on fragment assembly (Bowie and Eisenberg, 1994; Claessens et al., 1989; Jones and Thirup, 1986; Levitt, 1992; Simon et al., 1991; Sippl, 1993; Unger et al., 1989; Wendoloski and Salemme, 1992) and lattice-models (Kihara et al., 2001; Xia et al., 2000; Zhang et al., 2003) has been extensively studied. These two popular methods and their combination for template-free modeling have achieved great success in CASP (Critical Assessment of Structure Prediction) competitions (Moult, 2005; Moult et al., 2003, 2005, 2007). For example, the widely used fragment assembly program Robetta (Misura et al., 2006; Simons et al., 1997) is one of the most successful template-free modeling programs. The TASSER program (Zhang and Skolnick, 2005a) and its derivative Zhang-Server (Wu et al., 2007) have achieved outstanding performance in both CASP7 and CASP8 by combining lattice model and threading-generated fragments and distance restraints.

Although existing template-free modeling methods demonstrate exciting performance, several important issues have not yet been addressed. First, due to the limited number of experimental protein structures in the PDB, it is still very difficult to have a library of even moderate-sized fragments that can cover all the possible local conformations of a protein, especially in loop regions. In fact, a new fold may be composed of rarely occurring super-secondary structure motif (A. Fisher, presentation at CASP8). Second, the conformation space defined by a fragment library or a lattice model is discrete in nature. This discrete nature may exclude the native fold from the conformational space to be searched since even a slight change in backbone angles can result in a totally different fold. Fragment-HMM (Li et al., 2008), a variant of Robetta, can sample conformations from a continuous space, but still has the coverage problem since the Hidden Markov model (HMM) used in this method is built from 9-mer fragments. The lattice model used in the TOUCHSTONE programs (Kihara et al., 2001; Zhang et al., 2003) does not have the coverage problem, but it samples protein conformations from a 3D lattice with finite resolution. More importantly, the sampled conformations may not have a protein-like local structure because the TOUCHSTONE programs do not sample a conformation based upon the primary sequence of a protein. Instead, the TOUCHSTONE programs use a few short-range statistical potentials in its energy function to guide the formation of protein-like local structure.

There are also a few methods that attempt to sample protein conformations in a continuous space by probability. The probability of a conformation approximately reflects its stability and is estimated from sequence information. Feldman and Hogue (2002) developed a program FOLDTRAJ, which implements a probabilistic all-atom conformation sampling algorithm. Tested on three small proteins 1VII, 1ENH, and 1PMC, FOLDTRAJ can obtain the best structural models with RMSD from native being 3.95, 5.12, and 5.95 Å, respectively, out of 100,000 decoys for each protein. However, neither sequence profile nor the nearest neighbor effects is used in FOLDTRAJ to model local sequence-structure relationship. Therefore, FOLDTRAJ cannot generate models with quality comparable with the popular fragment assembly method Rosetta. Recently, Hamelryck and colleagues have developed two HMM models (Boomsma et al., 2008; Hamelryck et al., 2006), which not only capture the relationship between backbone angles and primary sequence, but also consider the angle-dependency between two adjacent residues. They demonstrated that their Torus-HMM model can generate local conformations as accurately as the fragment assembly method (Boomsma et al., 2008). However, these HMM models do not consider angle-dependency among more than two residues. It is also very difficult for these HMM models to make use of enriched sequence information such as PSI-BLAST sequence profile or threading-generated restraints to further improve sampling efficiency. Furthermore, these HMM models have not been applied to real-world template-free modeling yet.

Recently, we have proposed a protein conformation sampling algorithm based on the 1^st-order conditional random fields (CRF) (Zhao et al., 2008a) and directional statistics. The CRF model is a generalization of the HMM models and is much more powerful. Our CRF model can accurately describe the complex sequence-angle relationship and estimate the probability of a conformation, by incorporating various sequence and structure features and directly taking into consideration the nearest neighbor effects. We have shown that by using the 1^st-order CRF model, we can sample conformations with better quality than Hamelryck et al.'s FB5-HMM (Zhao et al., 2008a). All these studies have demonstrated that it is promising to do template-free modeling without using discrete representations of protein conformational space.

This article presents the first template-free modeling method that can search conformations in a continuous space and at the same time achieves performance comparable to the popular fragment assembly methods. This article differs from our previous work (Zhao et al., 2008a) and FB5-HMM (Hamelryck et al., 2006) in that the latter two only describe a method for conformation sampling in a continuous space, but did not demonstrate that this sampling technique actually lead to a template-free modeling method with comparable performance as the fragment assembly method. By contrast, here we describe a 2^nd-order CRF model of protein conformational space and show that with a simple energy function, the 2^nd-order CRF model works well for template-free modeling. We will show that it is necessary to use the 2^nd-order model instead of the 1^st-order model described in our previous work since the former can dramatically improve sampling efficiency over the latter, which makes the 2^nd-order model feasible for real-world template-free modeling. Blindly tested in the CASP8 evaluation, our CRF method compares favorably with the Robetta server (Misura et al., 2006; Simons et al., 1997), especially on alpha and small beta proteins. Our method also generated 3D models better than template-based methods for a couple of CAP8 hard targets.

2. Results

A 2^nd-order CRF model of protein conformation space

We have described a 1^st-order CRF model for protein conformation sampling in Zhao et al. (2008b). Here we extend our 1^st-order CRF model to a 2^nd-order model to more accurately capture local sequence-angle relationship. Table 1 lists some mathematical symbols used in our CRF model. In the context of CRF, the primary sequence (or sequence profile) and predicted secondary structure are viewed as observations; the backbone angles and their FB5 distributions are treated as hidden states or labels.

Table 1.

Some Mathematical Symbols Used in the CRF Models

Symbols	Annotations
X	The PSIPRED-predicted secondary structure likelihood scores. A matrix with 3×N elements where N is the number of residues in a protein.
Xi	The predicted likelihood of three secondary structure types at position i. It is a vector of three values, indicating the likelihood of helix, beta and loop, respectively.
Xi(x)	The predicted likelihood of secondary structure type x at position i.
M	The position-specific frequency matrix with 20×N entries, each being the occurring frequency of one amino acid at a given position.
Mi	A vector of 20 elements, denoting the occurring frequency of 20 amino acids at position i.
Mi(aa)	The occurring frequency of amino acid aa at position i.
H	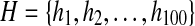, the set of 100 backbone angle states, each representing an FB5 distribution (see Methods for its detailed description).

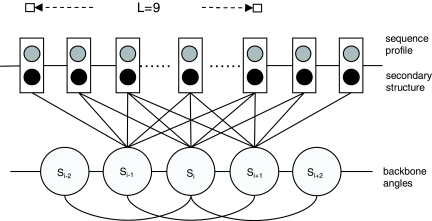
Given a protein with solved structure, we can calculate its backbone angles at each position and determine one of the 100 groups (i.e., states or labels) in which the angles at each position belong. Each group is described by an FB5 distribution. Let denote such a sequence of states/labels (i.e., FB5 distributions) for this protein. We also denote the sequence profile of this protein as M and its secondary structure as X. As shown in Figure 1, our CRF model defines the conditional probability of S given M and X as follows.

(1)

FIG. 1.

A second-order Conditional Random Fields (CRF) model of protein conformation space. Each backbone angle state depends on a window (size 9) of sequence profiles and secondary structure and also the states in its local neighborhood.

where is the model parameter and 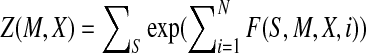is a normalization factor summing over all the possible labels for the given M and X. F(S, M, X, i) consists of two edge features and two label features at position i. It is given by

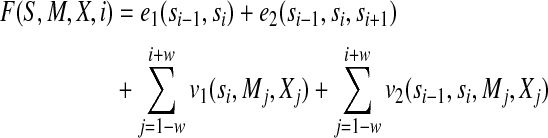(2)

Where e₁(s_i−1, s_i) and e₂(s_i−1, s_i, s_i+1) are the 1^st-order and 2^nd-order edge feature functions, respectively. v₁(s_i, M_j, X_j) and v₂(s_i−1, s_i, M_j, X_j) are the 1^st-order and 2^nd-order label feature functions, respectively. If we remove e₂(s_i−1, s_i, s_i+1) and v₂(s_i−1, s_i, M_j, X_j), then we can get a 1^st-order CRF model.

The two edge functions model local conformation dependency, given by

(3)

(4)

Meanwhile, [s_i = h] is an indicator function, which is equal to 1 if the state at position i is 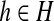, otherwise 0; λ (h′, h″) is a model parameter identified by two states h′ and h″; and λ (h′, h′, h″′) is a model parameter identified by three states. The two label feature functions are given by

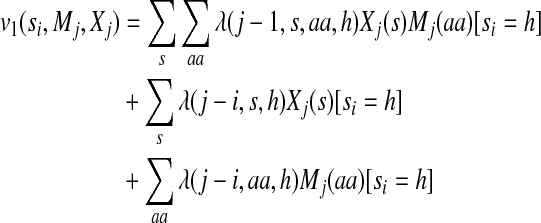(5)

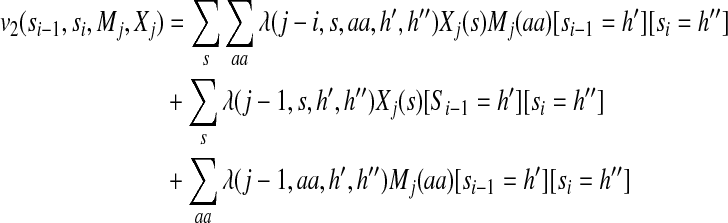(6)

The label feature functions model the dependency of backbone angles on protein sequence profiles and predicted secondary structure. Equations (5) and (6) indicate that not only the state (i.e., angle distribution) itself but also the state transition depend on sequence profiles and predicted secondary structure. As shown in the third and fourth items in the right hand side of Equation (2), the state (or state transition) at one position depends on sequence profile and secondary structure in a window of width 2w + 1 where w is set to 4 in our experiments. It will slightly improve sampling performance by setting the window size larger. Since secondary structure is predicted from sequence profiles, the former is not independent of the latter. Therefore, we need to consider the correlation between sequence profiles and predicted secondary structure, as shown in the first items of the right hand sides of Equations (5) and (6). The model parameters for the label features are identified by one or two states, secondary structure type, amino acid identity, and the relative position of the observations.

The 2^nd-order CRF model has millions of features, each of which corresponds to a model parameter to be trained. Once this model is trained, we can use it to sample protein conformations in a continuous space. Coupled with an energy function and a folding simulation method, we can also use it for template-free modeling.

The 2^nd-order CRF model is much better than the 1^st-order model

We compare our 2^nd-order CRF model with the 1^st-order model in Zhao et al. (2008a) to see how much improvement we can achieve by considering the interdependency among three adjacent residues. To exclude the impact of an energy function in this comparison, we guide conformation search using only compactness and self-avoiding constraints but not an energy function (for more details, see Zhao et al., 2008a). In total, we tested our models on a set of 22 proteins with different structure properties. We generated ∼20,000 decoys for each test protein using each CRF model and then calculated the percentage of decoys with RMSD smaller than a given threshold, as shown in Table 2.

Table 2.

Quality Comparison of the Decoys Generated by the 1^st-Order and 2^ND-Order CRF Models

	Size	C		Best	≤6Å	≤7Å	≤8Å	≤9Å	≤10Å	≤11Å	≤12Å
1aa2	108	α	O1	7.34	0	0	0.0350	0.245	1.05	4.27	13.5
			O2	7.31	0	0	0.0145	0.116	0.97	4.99	17.7
1beo	98	α	O1	6.42	0	0.0200	0.200	0.990	3.27	9.70	23.0
			O2	5.84	0.00963	0.0481	0.385	1.37	4.50	12.5	29.3
1ctfA	68	αβ	O1	3.70	2.41	7.18	16.2	31.4	51.7	77.2	95.9
			O2	3.67	6.62	22.3	47.1	64.7	78.9	94.8	99.5
1dktA	72	β	O1	6.15	0	0.100	0.870	3.81	12.5	33.4	62.8
			O2	5.07	0.121	1.48	5.94	16.2	34.3	59.3	82.6
1enhA	54	α	O1	2.32	22.4	32.4	44.7	61.2	85.4	98.5	100
			O2	2.21	69.3	72.0	77.7	87.1	97.4	99.9	100
1fc2C	43	α	O1	1.94	49.1	64.1	85.0	97.6	99.7	100	100
			O2	2.28	85.4	91.7	97.3	99.8	100	100	100
1fca	55	β	O1	4.99	0.145	1.3	6.00	19.9	49.7	85.5	99.3
			O2	4.96	0.207	2.65	13.5	36.3	68.2	94.0	99.8
1fgp	67	β	O1	7.40	0	0	0.035	0.46	4.21	20.2	54.2
			O2	5.94	0.00481	0.0433	0.582	4.25	18.2	48.2	81.8
1jer	110	β	O1	9.64	0	0	0	0	0.0050	0.120	0.910
			O2	10.2	0	0	0	0	0	0.185	1.11
1nkl	78	α	O1	3.64	5.91	14.1	25.1	45.2	66.6	86.8	97.7
			O2	3.06	20.3	30.1	44.2	65.3	84.0	96.7	99.8
1pgb	56	αβ	O1	3.15	22.3	45.0	65.1	81.0	93.0	98.6	99.9
			O2	2.60	63.2	85.8	93.9	97.7	99.5	99.9	100
1sro	76	β	O1	6.22	0	0.0700	0.525	2.75	10.0	27.1	54.7
			O2	5.39	0.0193	0.289	1.54	5.09	14.5	32.9	60.0
1trlA	62	α	O1	3.53	13.5	25.3	38.5	57.4	85.1	99.1	99.9
			O2	3.72	34.1	45.3	53.5	68.0	94.8	100	100
2croA	65	α	O1	2.80	16.8	31.4	47.9	63.3	79.9	93.0	99.6
			O2	2.58	35.4	52.9	67.4	79.3	88.9	95.6	99.9
2gb1A	56	β	O1	2.91	23.3	45.6	65.8	81.8	93.2	98.8	99.9
			O2	2.04	65.2	86.1	93.8	97.8	99.5	100	100
4icbA	76	α	O1	4.63	0.515	2.65	7.64	16.8	33.6	59.1	84.3
			O2	4.40	0.125	0.600	2.85	12.3	31.0	58.9	88.5
T052	98	β	O1	7.58	0	0	0.0100	0.0350	0.135	0.800	3.52
			O2	8.37	0	0	0	0.0251	0.296	1.78	6.58
T056	114	α	O1	7.78	0	0	0.0198	0.0842	0.510	2.26	7.07
			O2	7.57	0	0	0.00497	0.0944	1.07	3.83	8.38
T059	71	β	O1	6.30	0	0.0100	0.135	1.14	7.20	26.8	61.1
			O2	6.21	0	0.0245	0.421	3.85	17.4	45.1	77.3
T061	76	α	O1	5.36	0.01	0.37	2.89	10.7	27.0	50.9	77.6
			O2	6.04	0	0.282	4.73	19.9	40.5	62.7	82.6
T064	103	α	O1	7.23	0	0	0.035	0.2	0.91	2.79	7.30
			O2	7.47	0	0	0.0320	0.412	1.53	3.62	9.05
T074	98	α	O1	4.86	0.0150	0.235	1.23	4.00	10.4	22.0	41.0
			O2	4.22	0.0980	0.835	3.56	9.62	18.7	30.4	49.3

Columns 1–3 list the PDB code, protein size and the type of the test proteins. Columns “best” list the RMSD (Å) of the best decoys; the other columns list the percentage of decoys with RMSD smaller than a given threshold. “O1” and “O2” denote the 1^st-order and the 2^nd-order CRF models, respectively. In total, ∼20,000 decoys are generated for each protein without an energy function.

In terms of the best decoys, the 2^nd-order model is better on 13 out of 22 test proteins and worse on seven proteins. The best decoys may be generated by chance, so they cannot be reliably used to evaluate the performance of the two CRF models. We further examine their difference in terms of the percentage of decoys with RMSD smaller than a given threshold. A general trend we observed is that when the proteins under consideration are not big (<100 residues), the 2^nd-order model generally outperforms the 1^st-order model by a large margin. The only exception is 4icbA. The performance difference between these two CRF models is small on relatively large proteins such as 1aa2, 1jer, and T056. This may be because a large protein tends to have a large conformation space and neither CRF model can search a very large conformation space efficiently. The reason that the 2^nd-order model performs worse on 4icb is because there is a cis-proline in 4icb, and the length of the virtual C_α-bond ending at this proline is approximately 3.2Å instead of our assumption 3.8Å. Therefore, the more accurately can our CRF models predict the backbone angles, the more the decoys deviate from the native structure of 4icb. It is not very difficult to resolve this issue since from PSI-BLAST sequence profile we can predict with accuracy 92% if a residue is a cis-proline or not (data not shown). This comparison result indicates that we can dramatically improve sampling efficiency by using the 2^nd-order CRF model.

Comparison with FB5-HMM and fragment assembly

We further compare our two CRF models with the FB5-HMM model in Hamelryck et al. (2006), as shown in Table 3. Here we compare FB5-HMM and our CRF models using PSIPRED-predicted secondary structure and sequence information as their input. For each test protein, FB5-HMM generates 100,000 decoys, and we generated only ∼20,000 decoys. As shown in Table 3, our CRF models can generate decoys with significantly better quality than FB5-HMM on five out of six proteins tested in the FB5-HMM article. The only exception is 4icb, which has been explained in the above section. The result of FB5-HMM in Table 3 is taken from Hamelryck et al. (2006). The significant improvement of the 2^nd-order CRF models over the FB5-HMM model lies in that in estimating the probability of the angles at one residue, the 2^nd-order CRF model can directly take into consideration the effects of its neighbor residues. Our 2^nd-order CRF also models the relationship among three adjacent residues. By contrast, FB5-HMM only takes into consideration the relationship between two adjacent residues. Furthermore, FB5-HMM does not consider the effects of the neighbor residues when estimate the probability of angles at one residue.

Table 3.

Quality Comparison of the Decoys Generated by FB5-HMM, the 1^st-Order CRF, the 2^nd-Order CRF, and Rosetta

Test proteins			FB5-HMM		1st-order CRF		2nd-order CRF		Rosetta
PDB	L	α, β	Good	Best	Good	Best	Good	Best	Good	Best
1FC2	43	2,0	17.1	2.6	49.1	1.94	85.4	2.28	36.5	2.72
1ENH	54	2,0	12.2	3.8	22.4	2.32	69.3	2.21	44.8	1.23
2GB1	56	1,4	0.0	5.9	23.3	2.91	65.2	2.04	5.82	2.26
2CRO	65	5,0	1.1	4.1	16.8	2.79	35.4	2.58	17.2	2.38
1CTF	68	3,1	0.35	4.1	2.4	3.70	6.62	3.67	2.35	1.30
4ICB	76	4,0	0.38	4.5	0.51	4.63	0.125	4.40	4.51	3.90

For each protein, 100,000 decoys are generated by FB5-HMM, while only ∼20,000 decoys by each CRF model and Rosetta. No energy function is used in this comparison. Columns 1–3 list name and PDB code, size and number of α-helices, and β-strands of the test proteins. Columns “Good” and “Best” list the percentage of good decoys (with RMSD ≤ 6 Å) and the RMSD of the best decoys, respectively.

We also compare our 2^nd-order CRF model with the fragment assembly method without using energy function. We revised the Rosetta code to do conformation optimization using the compactness and self-avoiding constraints instead of the Rosetta energy function. As shown in Table 3, the advantage of our 1^st-order CRF model over Rosetta is not obvious. However, our 2^nd-order model can generate a much larger percentage of good decoys than Rosetta for five out of six proteins. The protein 4icb is an exception, which has been explained in previous sections. This comparison result further indicates that it is essential to use the 2^nd-order model instead of the 1^st-order model for template-free modeling. In terms of the quality of the best decoys, Rosetta is slightly better. One of the major differences between these two methods is that our CRF model uses a more simplified representation of protein conformation than Rosetta. That is, we use the pseudo backbone angles to represent a protein conformation while Rosetta uses the true backbone angles (i.e., phi/psi). The phi/psi representation has almost twice the degree of freedom as that of the pseudo backbone angle representation. This may explain why our method tends to generate more decoys with RMSD smaller than 6 Å and the best decoys generated by Rosetta tend to have smaller RMSD.

Comparison with lattice model

By combining a simple energy function and our 2^nd-order CRF model, we build a program, denoted as CRFFolder, for template-free modeling. We compare CRFFolder with TOUCHSTONE-II, a representative lattice model method developed by Skolnick group. TOUCHSTONE-II is an excellent template-free modeling program, and its two derivatives TASSER (Zhang and Skolnick, 2005a) and I-TASSER (Wu et al., 2007) perform very well in both CASP7 and CASP8. We do not compare CRFFolder with the two derivatives because both TASSER and I-TASSER use threading-generated constraints to guide conformation search, while CRFFolder does not. Due to the limitations of computational power, we tested CRFFolder on a set of 15 test proteins with various structure properties, which were also tested by TOUCHSTONE-II. These test proteins have very different secondary structures and sizes ranging from 47 to 157. We generated approximately 3000 decoys for each alpha protein, 7000 decoys for each alpha-beta protein, and 10,000 decoys for each beta protein. By contrast, TOUCHSTONE-II used a complex energy function consisting of 21 items and generated 24,000 decoys for each test protein (Zhang et al., 2003). As shown in Table 4, CRFFolder performs much better than TOUCHSTONE-II on all the alpha proteins except one. CRFFolder also has comparable performance on beta and alpha-beta proteins. On larger proteins, CRFFolder is slightly worse than TOUCHSTONE-II. This may be because the replica exchange Monte Carlo algorithm used by TOUCHSTONE-II for energy minimization is better than the simulated annealing algorithm used in CRFFolder. Note that since two programs use very different clustering methods, it is not easy to compare these two programs fairly. TOUCHSTONE-II used a program SCAR to do decoy clustering while we use MaxCluster¹. For the purpose of comparison, we also show the RMSD of the best decoys and the average RMSDs of the top 1% and 2% decoys generated by CRFFolder.

Table 4.

Performance Comparison between Our CRFFolder and Skolnick's TOUCHSTONE-II

			TOUCHSTONE	CRFFolder
Target	Size	Class	BestCluster	BestCluster	Best	1%	2%
1bw6A	56	α	4.79 (2/3)	3.82 (3/3)	2.75	3.38	3.54
1lea	72	α	5.69 (5/5)	4.10 (5/7)	3.41	4.19	4.48
2af8	86	α	11.07 (5/6)	8.9 (12/19)	7.07	8.53	8.97
256bA	106	α	3.61 (2/3)	2.75 (6/11)	2.50	3.45	3.70
1sra	151	α	10.71 (3/12)	13.95 (17/25)	10.82	13.76	14.24
1gpt	47	α β	6.30 (1/25)	5.55 (42/67)	4.34	5.20	5.47
1kp6A	79	α β	10.01 (8/14)	7.99 (1/7)	6.29	7.51	7.81
1poh	85	α β	9.10 (5/9)	8.84 (5/10)	7.49	8.70	9.04
1npsA	88	α β	6.89 (33/34)	9.91 (41/57)	7.87	9.19	9.66
1t1dA	100	α β	8.96 (7/13)	9.22 (10/13)	6.51	9.51	9.94
1msi	66	β	7.72 (19/28)	7.77 (12/15)	6.24	7.55	7.89
1hoe	74	β	9.39 (5/13)	9.87 (16/35)	7.96	10.00	10.37
1ezgA	82	β	11.03 (40/44)	10.42 (42/66)	9.66	10.35	10.62
1sfp	111	β	7.48 (2/18)	11.07 (5/11)	9.32	11.09	11.59
1b2pA	119	β	12.52 (31/56)	10.01 (18/25)	8.76	10.89	11.32

Columns 1–3 list the PDB code, size, and type of the test proteins. Column “Best Cluster” lists the RMSDs of the representative decoys of the best clusters. In this column, the first number in parentheses denotes the rank of the best cluster and the second number is the total number of clusters. Column “best” lists the RMSDs of the best decoys. Columns “1%” and “2%” list the average RMSDs of the top 1% and 2% decoys, respectively. The results of TOUCHSTONE-II are from Zhang et al. (2003).

Performance in the blind CASP8 evaluation

We tested the performance of our method by participating in the blind CASP8 evaluation. Our 2nd-order CRF model was trained before CASP8 started (in May 2008), so it is unlikely for us to overfit our model for the CASP8 targets.

Comparison with Robetta

We first examine the performance of our method by comparing it with Baker's Robetta server on some CASP8 hard targets, on which both Robetta and CRFFolder did template-free modeling before their experimental structures were released. These hard targets have no good templates in the PDB. It is unclear how many decoys Robetta generated for each target, but the top five models generated by Robetta for each target are available at the Robetta web site². Using our template-free modeling program CRFFolder, we generated ∼7000 decoys for each target and then chose the top five models. Note that the first models chosen by CRFFolder are not exactly the same as our CASP8 submissions since we submitted template-based models for some of these targets.

Table 5 compares CRFFolder and Robetta in terms of the quality of the first-ranked models. The model quality is evaluated by a program TM-score (Zhang and Skolnick, 2005b), which generates a real number between 0 and 1 to indicate the quality of a structure model. Roughly, the higher the TM-score is, the better the model quality. Note that in this table the domain definition of T0510_D3 is from Zhang's CASP8 assessment page, while others are from Robetta CASP8 web site. As shown in Table 5, overall CRFFolder is better than Robetta by ∼8%. Compared to the Robetta server, our method performs very well on mainly alpha proteins, e.g., T0460, T0496_D1 and T0496_D2. This could be expected since our CRF model can capture well the local sequence-structure relationship and alpha helices are stabilized by local interactions between neighbor residues. Our method also works well on small, mainly beta proteins. For example, our method is better than Robetta on two small beta proteins T0480³ and T0510_D3. However, our method does not fare well on a relatively large protein (>100 residues) with a few beta strands, e.g., T0482 and T0513_D2. This is probably because our CRF method can only model local sequence-structure relationship while a beta sheet is stabilized by non-local hydrogen bonding. For a small beta protein, our method can search more thoroughly the conformation space by sampling in a continuous space and potentially do better. However, for a large beta-containing protein, the search space is too big to be explored in a continuous space. Another possible reason is that our energy function is not as good as the Robetta energy function in guiding the formation of beta-sheets.

Table 5.

Performance Comparison between CRFFolder and Robetta on Some CASP8 Hard Targets

Target	Size	Class	Robetta	CRFFolder
T0397_D1	70	αβ	0.25	0.258
T0460	111	αβ	0.262	0.308
T0465	157	αβ	0.243	0.253
T0466	128	β	0.326	0.217
T0467	97	β	0.303	0.364
T0468	109	αβ	0.253	0.308
T0476	108	αβ	0.279	0.250
T0480	55	β	0.208	0.307
T0482	120	αβ	0.352	0.223
T0484	62	α	0.253	0.249
T0495_D2	65	αβ	0.312	0.436
T0496_D1	110	αβ	0.235	0.293
T0496_D2	68	α	0.291	0.500
T0510_D3	43	αβ	0.147	0.352
T0513_D2	77	αβ	0.581	0.367
T0514	145	αβ	0.283	0.277
Average			0.286	0.310

It is also worth noting that compared to Robetta, our method did better on the first domain of T0496, a mainly-alpha protein with120 residues. According to the study in Shi et al. (2009), this domain target is one of the only two CASP8 targets with really new folds. Our method did as well as Robetta on another target with new fold (i.e., T0397_D1).

Comparison with template-based methods

Our program CRFFolder can also generate 3D models better than template-based methods for a couple of hard CASP8 targets. According to the CASP8 official assessment, if only the first-ranked models are evaluated, CRFFolder produced the best model among all the CASP8 human and server groups for T0510_D3, a small alpha/beta protein with 43 residues⁴. T0510_D3 is treated as a free-modeling target by CASP8 while Grishin et al. classified it as a fold recognition target (Shi et al., 2009). We also examined all the template-based models generated by our threading methods in CASP8 for this target. The best template-based model has TM-score of 0.339.

CRFFolder also produced one of the best models for T0496_D1, better than other template-based models. Both CASP8 and Grishin et al. classified T0496_D1 as a free-modeling target (Shi et al., 2009). In fact, the first-ranked model we submitted for T0496_D1 is much worse than the best decoy we generated for this target. Among the ∼7000 decoys we generated, there are around 18% decoys with TM-score better than the first-ranked model. The best decoy has TM-score 0.475 and RMSD to native 6.592Å. By contrast, the first-ranked template-free model has TM-score 0.293 and RMSD 11.457Å. The best template-based model generated by our threading methods in CASP8 for this has TM-score 0.251, and RMSD 15.372Å.

We also examined all the template-based models generated by our threading methods in CASP8 for T0397_D1, another target with really new fold (Shi et al. 2009). There are only six template-based models with TM-score higher than the first-ranked template-free models generated by CRFFolder. The best template-based model generated by us in CASP8 has a TM-score of 0.338. while the best template-free model generated by CRFFolder has a TM-score of 0.364. There are 6.6% decoys generated by CRFFolder have have a TM-score better than our first-ranked template-free model.

3. Conclusion

This article has presented a probabilistic and continuous model of protein conformational space for template-free modeling. By using the 2^nd-order CRF model and directional statistics, we can accurately describe protein sequence-angle relationship and explore a continuous conformation space by probability, without worrying about that the native fold is excluded from our conformation space. This method overcomes the following limitations of the fragment assembly method: (1) fragment assembly samples conformations in a discrete space; and (2) fragment assembly is not really template free since it still uses short fragments (e.g., 9-mer) extracted from the PDB. Both restrictions may cause loss of prediction accuracy.

Even though we use a simple energy function to guide conformation search, our probabilistic model enables us to do template-free modeling as well as two well-developed programs TOUCHSTONE-II and Robetta. Both of them have been developed for many years and have well-tuned and sophisticated energy functions. Our template-free modeling is much better than TOUCHSTONE-II on alpha proteins and has similar performance on mainly beta proteins. Blindly tested on some CASP8 hard targets, our method is also better than the Robetta server on quite a few (mainly alpha and small beta) proteins but worse on some relatively large beta-containing proteins. Finally, our method also generated the 3D models for a couple of CASP8 targets (i.e., one mainly-alpha target T0496_D1 and one small alpha/beta target T0510_D3) better than template-based methods. The good performance on alpha proteins indicates that our 2^nd-order CRF model can capture well the local sequence-structure relationship for alpha proteins. The good performance on small beta proteins indicates that by sampling in a continuous space we can explore the conformational space of small beta proteins more thoroughly. To improve the performance of our template-free modeling on relatively large beta-containing proteins, we need to further improve our probabilistic model of beta regions and develop a better hydrogen-bonding energy item for the formation of beta sheets.

A direct application of the method described in this paper is to refine template-based models. By extracting distance constraints from template-based models, the conformational space of a target is dramatically reduced and thus we can afford to search this reduced space using our continuous-model-based sampling method, which may search conformational space more thoroughly and lead to better prediction accuracy. The method described in this article potentially can also be applied to protein loop modeling, model refinement, and even RNA tertiary structure prediction.

4. Methods

Continuous representation of protein conformations

It is time-consuming to evaluate a full-atom energy function, but a residue-level energy function usually is not as accurate as an atom-level energy function. Here we use a simplified and continuous representation of a protein model. In particular, we only consider the main chain and C_β atoms in folding simulation.

C_α-trace representation

The length of the virtual bond between two adjacent C_α atoms can be approximated as a constant (i.e., 3.8Å), so we can represent the C_α-trace of a protein using a set of pseudo backbone angles (θ, τ). Given a residue at position i, its θ is defined as the pseudo bond angle formed by the C_α atoms at positions i−1, i and i+1; τ is a pseudo dihedral angle around virtual bond between i−1 and i and can be calculated from the C_α atoms at positions i−2, i−1, I, and Given the C_α atoms at positions i−2, i−1, and i, we can build the C_α atom at position i+1 using (θ, τ) at position i. Therefore, given the first three C_α positions and N −2 pairs of (θ, τ), we can build the C_α trace of N residues. The relative positions of the first three C_α atoms are given by θ at the second residue.

Distribution of bond angles

The preferred conformations of a residue in the protein backbone can be described as a probabilistic distribution of (θ, τ). Each (θ, τ) corresponds to a unit vector in the 3D space (i.e., a point on a unit sphere surface). We can use the 5-parameter Fisher-Bingham (FB5) distribution to model the probability distributions over unit vectors (Kent, 1982). FB5 is the analogue on the unit sphere of the bivariate normal distribution with an unconstrained covariance matrix. The probability density function of the FB5 distribution is given by

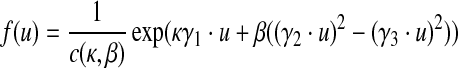where u is a unit vector variable and c(κ, β) is a normalizing constant. The parameters κ and β determine the concentration of the distribution and the ellipticity of the contours of equal probability, respectively. The higher κ and β are, the more concentrated and elliptical the distribution is, respectively. The three vectors γ₁, γ₂, and γ₃ are the mean direction, and the major and minor axes, respectively. The latter two vectors determine the orientation of the equal probability contours on the sphere, while the first vector determines the common center of the contours.

We cluster the whole space of (θ, τ) into 100 groups, each of which can be described by an FB5 distribution. We calculate the (θ, τ) distribution for each group from a set of ∼3000 non-redundant proteins with high-resolution x-ray structures using KentEstimator (Hamelryck et al., 2006). For a detailed description of how to calculate the FB5 distributions, Zhao et al. (2008a). Once we know the distribution of (θ, τ) at one residue, we can sample a pair of real-valued (θ, τ) angles in a probabilistic way and thus, explore protein conformations in a continuous space.

Building backbone atoms

Using (θ, τ) representation, only the coordinates of the C_α atoms can be built. To use an atom-level energy function, we also need to build the coordinates of other atoms. Given a C_α trace, there are many methods that can build the coordinates for the main chain and C_β atoms (Gront et al., 2007; Holm and Sander, 1991; Maupetit et al., 2000). To save computing time, we want a method that is both accurate and efficient. We choose to use a method similar to BBQ (Gront et al., 2007). The original BBQ method can only build coordinates for the backbone N, C, and O atoms. We extend the method to build coordinates for the C_β atom. Experimental results (data not shown) indicate that RMSD of this method is approximately 0.5 Å supposing the native C_α-trace is available. This level of accuracy is good enough for our folding simulation.

To employ the KMB hydrogen-bonding energy (Morozov et al., 2004) for β-containing proteins, we also need to build the backbone hydrogen atoms. We use a quick and dirty method to build coordinates for the hydrogen atom HN (Branden and Tooze, 1999). Let N_i denote the position of the main chain N atom in the same residue as the HN atom. Let N_i C_i−1 denote the normalized bond vector from the N atom to the C atom in the previous residue. Let N_i C_α denote the normalized bond vector from the N atom to the C_α atom in the same residue. Then the position of the hydrogen atom HN can be estimated by . The average RMSD of this method is approximately 0.2Å (data not shown) supposing the native coordinates of other main chain atoms are available.

Model parameter training

Given a set of m proteins with sequence profile Mⁱ, predicted secondary structure Xⁱ and corresponding backbone angles , our CRF model trains its parameter by maximizing the conditional log-likelihood L of the data:

(7)

The second item in Equation (7) is a regularization factor to deal with the sparsity in the training data. When the complexity of the model is high (i.e., the model has many features and parameters) and the training data is sparse, overfitting may occur, and it is possible that many models can fit the training data. Our 2^nd-order CRF model has around one million of parameters;, we place a Gaussian prior exp(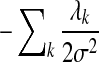) on the model parameter to choose the model with a “small” parameter in order to avoid overfitting. This regularization can improve the generalization capability of the model in both theory and practice (Vapnik, 1998). This kind of training is also called discriminative training or conditional training. Different from the generative training in the FB5-HMM model, discriminative training directly optimizes the predictive ability of the model while ignoring the generative probability of the observation.

The objective function in Equation (7) is convex and hence theoretically a globally optimal solution can be found using any efficient gradient-based optimization technique. There is no analytical solution to the above equation for a real-world application. Quasi-Newton methods such as L-BFGS (Liu and Nocedal, 1989) can be used to solve the above equation and usually can converge to a good solution within a couple of hundred iterations. For a detailed description of how to train a CRF model, see elsewhere (Lafferty et al., 2001; Sha and Pereira, 2003) We revised the FlexCRFs program (Phan et al., 2005) to train our CRF model, and it takes approximately 24 hours to train a single model on a cluster of 150 2GHz CPUs.

We used a set of ∼3000 non-redundant proteins to train the parameters in our CRF model. Any two proteins in the training set share no more than 30% sequence identity, and the resolution of a training protein is at least 2.0Å. To avoid overlap between the training data and the test proteins (i.e., the proteins in Tables 2–4), we removed the following proteins from our training set: (1) the proteins sharing at least 25% sequence identity with our test proteins; (2) the proteins in the same fold class as our test proteins according to the SCOP classification; and (3) the proteins having a TM-score 0.5 with our test proteins in case some recently released proteins do not have a SCOP ID. If the TM-score of two protein structures is smaller than 0.5, then a threading program such as PROSPECTOR_3 cannot identify their similarity relationship with high confidence.

The training set is randomly divided into five sets of same size and then used for five-fold cross validation. We trained our CRF model using three different regularization factors (i.e., σ² in Equation (7)): 25, 125, and 625, and chose the one with the best F1-value. F1-value is a widely used measurement of the prediction capability of a machine learning model. F1-value is an even combination of precision p and recall r and calculated as 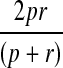. The higher the F1-value is, the better the CRF model. The average F1-values for regularization factors 25, 125, and 625 are 21.73%, 21.55%, and 22.03%, respectively. In terms of F1-value, the difference among these regularization factors is small. Therefore, we choose a small regularization factor 25 to control the model complexity since a model with lower complexity usually generalizes better to the test data. The regularization factor is the only parameter that we need to tune manually. All the other model parameters (i.e., weights for features) can be estimated automatically in the training process.

Conformation sampling and resampling

Initial conformation sampling

Once the CRF model is trained, we can sample a protein conformation or resample the local conformation of a segment by probability using a forward-backward algorithm. We first sample labels (i.e., angle distribution) by probability estimated from our CRF model and then sample real-valued angles from the labels. Let V(i, s_i, s_i+1) denote the sum of all the edge features associated with edge (s_i, s_i+1) and all the label features associated with labels s_t, s_i+1 and (s_i, s_i+1). Let G(i, s_t, s_i+1) denote the marginal probability of a label pair (s_i, s_i+1). We can recursively calculate G(i, s_t, s_i+1) from N-terminal to C-terminal as follows.

where λ (s_i−1, s_i, s_i+1) can be interpreted as state transition log-likelihood. Once G(N−1, s_{N− 1}, s_N) is calculated where N is the protein size, we can sample a conformation from C-terminal to N-terminal. First, we sample a label pair (s_N−1, s_N) for the last two positions by probability 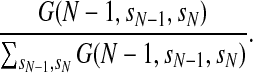. Then we sample the label s_i for position i by probability , supposing that the sampled labels at position i+1 and i+2 are s_i+1 and s_i+2, respectively.

Conformation resampling

The algorithm for resampling the local conformation of a randomly chosen segment is similar. We first randomly determine a segment for which we are going to resample backbone angles. Then we resample the angles for this segment using a forward-backward algorithm similar to the initial conformation sampling algorithm. The major difference is that in this scenario we calculate G(i, s_i, s_i+1) for a segment conditioning on the labels of the two residues flanking this segment at the left and when do resampling we also have to consider the two residues flanking this segment at the right.

Biased sampling

Our sampling method works well in alpha regions but not in beta regions. We decided that we should do more frequent sampling in beta and loop regions than in alpha regions. This is because both beta and loop regions are more varied than alpha regions. By sampling in the beta and loop regions more frequently, we can generate decoys with better quality. We achieve this goal by empirically assigning different weights to each position depending on its predicted secondary structure type. The weights for alpha, beta and loop regions are 1, 5, and 3 respectively. These weights are empirically determined using a simple enumeration method on the test proteins in Table 2. To determine which segment with angles to be resampled, we first uniformly sample the segment length l between 1 and 15. Then we sample the starting position of this segment using biased sampling. We calculate the weight of a segment as the sum of the weights of all the positions in this segment. Then we randomly sample a segment with the length l by probability proportional to the weight of this segment.

Biased sampling is employed only when we do folding simulations using the energy function described in this paper. In the case that the energy function is not used, we still use uniform sampling.

Energy function

The energy function we used for folding simulation consists of three items: DOPE, KMBhbond, and ESP. The weight factors combining these three energy items are trained on the proteins in Table 2 using grid search in a progressive way. First, we fix the weight factor of DOPE to 1 and determine the weight factor for ESP by minimizing the average RMSDs of generated decoys. Then we fix the weight factors of both DOPE and ESP and determine the weight factor for KMBhbond using the same way.

DOPE

DOPE is a full-atom, distance-dependent pairwise statistical potential originally designed by Shen and Sali and then improved by the Sosnick group (Fitzgerald et al., 2007; Shen and Sali, 2006). DOPE performs as well or better than many other statistical potentials and force fields in differentiating a native structure from decoys. The statistical potential in DOPE distinguishes the amino acid identity and atomic identity of two interacting particles. In our folding simulation, we only build coordinates for main chain and C_β atoms, so only the statistical potentials related to main-chain and C_β atoms are used to calculate the energy of a conformation. We denote this revised DOPE as DOPE-C_β. According to Fitzgerald et al. (2007), DOPE-C_β is highly correlated with the full-atom DOPE. DOPE-C_β also performs favorably in applications to intra-basin protein folding (Colubri et al., 2006).

Hydrogen bonding

KMBhbond is a statistical potential for hydrogen bonding developed by the Baker group (Morozov et al., 2004). It depends on the distance between the geometric centers of the N–H bond vector and the C=O bond vector, the bond angle between the N–H bond vector and the hydrogen bond, the bond angle between the C=O bond vector and the hydrogen bond, and the dihedral angle about the acceptor-acceptor base bond. The three angles describe the relative orientation of the bond vectors in the hydrogen bond.

ESP

ESP is an approximation to the Ooi-Scheraga solvent-accessible surface area (SASA) potential (Ooi et al., 1987). Since our conformation representation does not contain side-chain atoms, which are necessary for the calculation of the solvent-accessible surface area potential, we employ a simple ESP that assigns each residue with an environmental energy score. ESP is a function of the protein size and the number of C_α atoms contained within an 8.5-Å sphere centered on the residue's C_α atom (Fernández et al., 2002). Explicitly, the ESP statistical potential has the form given by

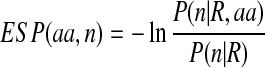where n is the number of C_α atoms in an 8.5-Å sphere centered on the C_α atom of the residue, R is the radius of gyration of the protein, aa is the amino acid identity of the residue, P(n|R) is the number of C_α atoms in an 8.5-Å sphere for a given protein radius regardless of amino acid identity, and P(n|R,aa) is the number of C_α atoms in an 8.5-Å sphere for a given protein radius and amino acid identity. We calculate ESP(aa, n) from a set of ∼3000 non-redundant experimental structures chosen by the PISCES server (Wang and Dunbrack, 2003). Each protein in this set has resolution at least 2.0 Å, R factor no bigger than 0.25, and at least 30 residues. Any two proteins in this set share no more than 30% sequence identity.

To parameterize the ESP potential, we need to discretize the radius of gyration R, which ranges from 7Å to 39Å in our training set. We tested the following three discretization schemes: (1) R is discretized into 65 bins with equal width 0.5Å; (2) R is discretized into 33 bins with equal width 1Å; and (3) R is first discretized into 33 bins with equal width 1Å. Then we merge [7, 9), [34, 36) and [37, 39] into a single bin, respectively, to guarantee sufficient statistics for these intervals. We calculated the Pearson correlation coefficient between the resultant ESP energys and TM-score of the decoys. The third scheme yields the best correlation and thus is used in our energy function.

Energy minimization

We employ a simulated annealing (SA) algorithm to minimize the energy function for a given protein. The SA routine is based on the algorithm proposed by Aarts and Korst (1991). We start with sampling an initial conformation and then search for a better one by minimizing the energy function. Given a conformation, we propose a new conformation by resampling the local conformation of a randomly-chosen small segment using the CRF model. The new conformation is rejected if there are serious steric clashes among atoms; otherwise, it is accepted with probability min (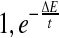) where ΔE is the energy increment and t is the annealing temperature.

The initial annealing temperature is chosen so that at the beginning of the annealing process an energy increase is accepted with a given probability p₀(=0.8). The initial temperature t₀ is determined by where ΔE is the average energy increase. To determine ΔE, we first conduct a series of trial conformation samplings and accept all the generated conformations. Then we estimate ΔE by calculating the average energy increase observed in our trial samplings.

During the folding simulation process, we decrease the annealing temperature gradually using an exponential cooling schedule. The temperature is updated by t_k+1 = 0.9t_k. At each annealing temperature, the number of sampled conformations is set to (100+N) where N is the number of residues in the protein. This number is set to achieve thermal equilibrium. The termination of the SA process is triggered when any of the following two conditions is satisfied: (1) either the temperature is low enough such that almost no energy increase is accepted and the annealing process is trapped at local minima; or (2) or the number of conformations generated in a single simulation process reaches a threshold (say 10,000).

Acknowledgments

We are grateful to Dr. Ming Li, Dr. Ian Foster, Dr. John McGee and Mats Rynge for their help with computational resources. This work was supported by the internal research funding of TTI-C and NIH (grant R01GM081642-01). This work was made possible by the facilities of the Shared Hierarchical Academic Research Computing Network (SHARCNET: www.sharcnet.ca), the Open Science Grid Engagement VO, and the University of Chicago Computation Institute.

Author Contributions

J.X. designed and performed research and wrote the paper; J.P. performed research; F.Z. performed research and analyzed data; and J.D., K.F., and T.S. helped with energy function.

Disclosure Statement

No competing financial interests exist.