Is Reasoning in Rats Really Unreasonable? Revisiting Recent Associative Accounts

Introduction

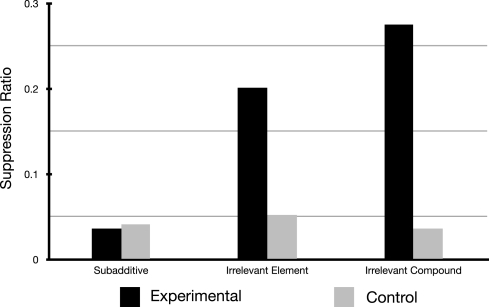
Beckers et al. (2006) published intriguing results, obtained in the rat fear conditioning paradigm, challenging classical associativist theories of learning. One of the main findings of Beckers et al. (2006) is that what they called subadditive pretraining abolished the expression of blocking (see Table 1; Figure 1), an effect that Beckers et al. (2005) had previously demonstrated in Human subjects. Beckers et al. (2006) contended that it was difficult to see how an associative account of this interesting phenomenon could be put forward. Recently, Haselgrove (2010) has put forward an associative account of this phenomenon based on the Rescorla-Wagner model (Rescorla and Wagner, 1972). This associative account is based on the idea of a common element (p) shared by the cues A, B, C, D, E, and X resulting in the presentation of compound trials for each elemental cue presentation i.e., ap, bp, cp, dp, ep, xp, and cdp¹ for the compound CD (where a, b, c, d, e, and x represent the element that distinguished the cues used). This assumption was based on the fact that five of the six cues used were drawn from the same auditory modality, and the purported failure by Beckers et al. (2006) to demonstrate that “the cues used in pretraining and those used for blocking were represented by the rats as entirely different stimuli.”

Table 1.

Experimental design of Experiment 1 Beckers et al. (2006).

Conditions	Groups	Pretraining	Phase 1	Phase 2	Test
EXPERIMENT 1
Subadditive	Experimental	4C+, 4D+, 4CD+	12A+	4AX+	X
	Control	4C+, 4D+, 4CD+	12B+	4AX+	X
Irrelevant element	Experimental	4C+, 4D+, 4E+	12A+	4AX+	X
	Control	4C+, 4D+, 4E+	12B+	4AX+	X
Irrelevant compound	Experimental	4C+, 4C+, 4DE+	12A+	4AX+	X
	Control	4C+, 4C+, 4DE+	12B+	4AX+	X

+ Indicates reinforcement. A, B, C, D, E, X are audiovisuals cues, numbers indicate the total number of trials of a given type per phase.

Figure 1.

Results of Experiment 1 redrawn from Beckers et al. (2006).

The rationale for Beckers et al. (2006) experiments is based on an “inferential” explanation of blocking. Beckers et al. (2006) put it this way:

[if p then q] If potential causes A and X are both effective causes of a particular outcome, then the outcome should be stronger when both are present than when only one is present.

[not q] The outcome is not stronger when A and X are both present than when only A is present.

[therefore, not p] Thus, A and X are not both effective causes of the outcome.

In other words, consider a classical conditioning procedure to demonstrate blocking, with the experimental group receiving A+ in phase 1 and AX+ in phase 2, and the control group receiving B+ in phase 1 and AX+ in phase 2 (+ symbolizing reinforcement). If the compound AX is followed by the same outcome intensity as A, then X cannot be an effective cause of the outcome and therefore X will not predict the outcome in the experimental condition. However, in the control position blocking will be observed, since neither A nor X was paired with the outcome alone.

Beckers et al. (2006) make three main predictions based on this explanation of blocking. The first, addressed in Experiment 1, is that if we demonstrate that the outcome of two effective causes of an outcome (here footshock) is not additive we should be able to abolish blocking. The second, addressed in Experiment 2, is that if we put ourselves in conditions that are normally not conducive to the expression of blocking we should be able to restore blocking by demonstrating outcome additivity during pretraining. The third, addressed in Experiment 3, asserts that exposure during pretraining to the possibility of a larger shock than used in blocking training will restore blocking (using a procedure conducive to weak blocking at best), whereas no restoration of blocking will be observed in the group exposed to the stronger shock during blocking training and pretraining.

Haselgrove (2010) proposed an explanation, based on the well known Rescorla-Wagner Model (Rescorla and Wagner, 1972), using the following assumptions: (1) The model reaches its asymptote (i.e., the model stabilizes) after each learning phase (that is pretraining, phase 1 and phase 2, see Table 1); (2) there exists an element p which the physical stimuli A, B, C, D, E, and X have in common; (3) each physical pairing of CS and US may result in more that one iteration of the model. We will demonstrate here that the account offered by Haselgrove (2010) is contradictory to the basic assumptions of the Rescorla-Wagner Model in its implementation and, crucially, once corrected in order to not contradict the most basic assumption of the Rescorla-Wagner model, does not yield an associative explanation of Experiment 1.

The Rescorla-Wagner Model

In the Rescorla-Wagner Model the variation of the associative strength of a cue I after each trial is given by the equation:

$$\Delta V_I={\alpha }_{{\rm I}}\beta \left(\lambda -\Sigma V\right),$$ (1)

where λ is the learning asymptote, α_I (with 0 ≤ α ≤ 1) is the learning rate of the given cue or stimuli, β (with 0 ≤ β ≤ 1) is the parameter associated with the given reinforcer, and ΣV is the sum over the associative strengths of all relevant cues present during the trial. Furthermore, in the case of a compound AB, the associative strength of the compound is the sum of the associative strength of its elements. So after an AB+ trial:

$$\Delta V_A={\alpha }_A\beta \left(\lambda -\sum V_{AB}\right);$$ (2)

$$\Delta V_B={\alpha }_B\beta \left(\lambda -\sum V_{AB}\right);$$ (3)

$$V_{AB}=V_A+V_B,$$ (4)

where ΣV is the sum of the associative strengths of all cues present at a given trial, in this case ΣV = V_A + V_B. It may be important to point out here that the associative strength of a given cue changes only if it is present in a given trial. This point is, as we shall see, critical to the ability of the model to account for the result obtained by Beckers et al. (2006).

Methods

Simulations

In order to run our simulations of the Rescorla-Wagner model we used Scilab 5.3 a Gnu Public License (GPL) tool for mathematical computation available for download at http://www.scilab.org. In Haselgrove (2010) it is indicated that the simulations assumed that each learning phase reached asymptotic conditions (model stabilization) and that pairing of the CS–US presentation resulted in more than one iteration of the Rescorla-Wagner Model. In order to reproduce the simulations presented by Haselgrove (2010) we performed three types of simulation: (i) simulations where each iteration of the Rescorla-Wagner Model was equal to one physical trial and learning phases proceeded as in Beckers et al. (2006) constituting a direct simulation of the published Rescorla-Wagner Model (Rescorla and Wagner, 1972); (ii) simulations where multiple iterations of the model resulted from each physical trial until stabilization of the model at the phase level; (iii) simulations where each phase (i.e., pretraining, phase 1 and phase 2) was repeated multiple times until the model stabilized.

Simulation of experiment 1

For all our simulations we used the same order of events as described in Beckers et al. (2006). Namely, during pretraining in the Subadditive condition the physical stimuli C, D, and CD were presented in the following order: C, D, CD, C, CD, D with the whole sequence repeated twice. In the Irrelevant Element condition the physical stimuli C, D, and E were presented in the following order: C, D, E, C, E, D the whole sequence being repeated twice. In the Irrelevant Compound condition the physical stimuli C, and DE were presented in the following order: C, C, DE, C, DE, C. Once again this sequence was repeated twice (the experimental design of Beckers et al. (2006) Experiment 1 is presented Table 1). In simulations of type (iii) the whole phase was iterated multiple times until stabilization of the model, whereas in simulations of type (ii) each individual physical trial resulted in multiple iterations of the Rescorla-Wagner model. For instance, in a type (ii) simulation, a C+ trial followed by a D+ trial would have resulted in n iterations of ΔV_cp followed by n iterations of ΔV_dp (assuming the common element p), whereas in a type (iii) simulation a C+ trial followed by a D+ trial would have resulted in n iterations of the tandem ΔV_cp, ΔV_dp until model stabilization.

Parameters and constraints of the simulations

The learning parameters α (the learning rate for each cue), β (reinforcer parameter), and λ (the learning asymptote) were set as put forward by Haselgrove (2010) and it was assumed that all associative strengths were null at the start of learning. For the simulations of type (ii) and (iii) the additional constraint that for each phase the number of iterations of the model was at least equal to the number of physical trials experienced by the animal was imposed. For example even if V_axp ≈ λ ± δ with δ = 10⁻⁹ after trial 1 of phase 2 (where δ is the criterion for asymptotic performance), the simulation will nevertheless perform four iterations of the model.

Subadditive Pretraining Prevents Blocking

Experiment 1 of Beckers et al. (2006) is arguably the most challenging for classical associativist theories. Nevertheless the main claim of Haselgrove (2010) is that the Rescorla-Wagner model (Rescorla and Wagner, 1972), taken together with the assumption of a common element p, can predict the subadditive pretraining effect on blocking, given two additional assumptions: (i) that each phase of training reaches its asymptote and (ii) that each pairing of the cue and the unconditioned stimulus results in more than one iteration of the Rescorla-Wagner model². The claim in Haselgrove (2010) which we consider here, is based on the idea that after subadditive training, that is C+, D+, CD+, the associative strength of p has reached its asymptote (λ). Haselgrove (2010) put it as follows:

However, blocking was not present in the subadditive condition. Here the associative strength of xp was essentially at asymptote for both the experimental and control group. The reason why the Rescorla-Wagner model makes this final prediction is because the pretraining given to the groups in the subadditive condition should endow the element common to all the stimuli (p) with asymptotic associative strength. It is fairly straightforward to see why this is the case, following the pretraining phase:

$$\begin{array}{l}{V}_c+V_p=V_d+V_p=V_c+V_d+V_p=\lambda \\ \therefore V_c+V_d+2V_p=2\lambda .\end{array}$$

Furthermore

$$\begin{array}{l}(V_c+V_d+2V_p)-(V_c+V_d+V_p)=\lambda \\ \therefore V_p=\lambda .\end{array}$$

We note that not every instance of “=” above occurs between equal quantities. The manner in which these equations were derived is not made entirely clear, but it appears they result from a notational abuse which obscures the fact that the values of V_c, V_d, and V_p change throughout the pretraining.

Results

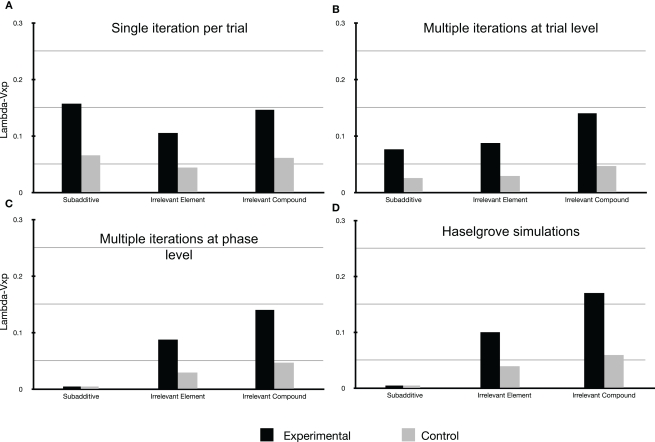
Figure 2 presents the results of our three types of simulation for α_i = 0.2, where i belongs to {a, b, c, d, e, x, p} and β = λ = 0.7.

Figure 2.

For all simulations presented here α_i = 0. 2, where i stands for any of the cues used (i.e., the learning rate for each cue is identical) and β = λ = 0.7 as per Haselgrove (2010). (A) Straight forward simulation of the Rescorla-Wagner model assuming a common element p. (B) Simulation of the Rescorla-Wagner model assuming a common element p and that each learning phase reached its asymptote (by multiple iterations of the model per discrete trial). (C) Simulation of the Rescorla-Wagner model assuming a common element p and that each learning phase reached its asymptote (by multiple iterations of the model at the learning phase level). (D) Simulation redrawn from Haselgrove (2010). Please note that in the case of (C,D), and for the subadditive group, the value of Lambda − V_xp is indeed equal to zero.

First of all Figure 2A demonstrates that a straight forward account using the Rescorla-Wagner Model assuming a common element p is not possible using the parameter values offered by Haselgrove (2010). Classically the model can be made to stabilize more rapidly (i.e., reach the learning asymptote) by setting the parameter β to 1 (the model specifications impose that 0 ≤ β ≤ 1). However doing so, even allowing the common element p to be 100 times more salient than the element distinguishing the physical cues used, give rise to simulations that are very different from the experimental results obtained in Experiment 1 of Beckers et al. (2006). It is therefore clear that additional assumptions are necessary in order to simulate the results reported by Beckers et al. (2006).

Figure 2C reproduces the results of simulations integrating one possible implementation of the additional assumption used by Haselgrove (2010), namely that learning was assumed to have reached its asymptotic value at the conclusion of each learning phase (Pretraining, Phase 1, and Phase 2). This assumption was implemented by multiple iterations of each phase. Figure 2C is clearly a good fit for the experimental results presented by Beckers et al. (2006; compare Figures 1 and 2B) and are a close match to the simulation presented by Haselgrove (2010; see Figure 2C); no blocking is predicted for the subadditive group whereas blocking is predicted in the two remaining groups. The simulation also reasonably models the relative amount of blocking observed in these two remaining groups. To accomplish this the simulation consisted of 148 iterations of the whole pretraining phase for the subadditive group, 23 iterations for the Irrelevant Element and 11 iterations for the Irrelevant Compound group (the model had comfortably reached asymptotic values for all remaining phases after 12 iterations (Phase 1) and 4 iterations (Phase 2).

Figure 2B shows the results of our simulation when, in order to implement the assumption that all phases reached model stabilization, multiple iterations of the model resulted from one discrete trial. Blocking is again predicted in the Irrelevant Element and Irrelevant Compound groups in a similar fashion to the previous simulation. However, this time blocking is also predicted for the subadditive group in clear contrast with the experimental results presented by Beckers et al. (2006; see Figure 1). In this simulation, for the subadditive group, each trial resulted in 53 iterations of the Rescorla-Wagner equation in the pretraining phase, 53 in phase 1, 31 in the control group, and 4 in the experimental group during phase 2. (Up to100,000 iterations per physical trial were attempted for the pretraining phase yielding no change in V_p at the end of this phase as compared to the results presented here.) In the Irrelevant Element group 43 iterations of the model per physical trial were necessary for the pretraining phase, 53 in phase 1, and respectively for the control group and the experimental group, 31 and 4 in phase 2. For the Irrelevant Compound group 36 iterations of the model per physical trial were necessary in the pretraining phase, 55 in phase 1, and 32 and 4 respectively for the control and experimental group in phase 2.

Discussion

The results of these simulations show that it is only if each phase, and not each physical trial, is repeated numerous times (148 times in the case of the subadditive group) that simulations resembling the results obtained by Beckers et al. (2006) can be realized. Phase repetition is not necessarily equivalent to trial repetition unless, for example, only one trial type is presented during each learning phase (i.e., as in Phase 1 and 2). The simulations show clearly for the subadditive group that these approaches are not equivalent in the pretraining phase where 3 different types of trial are presented together with the assumption of a common element p. The fundamental question here is to what extent the type of simulation called herein type (iii) is compatible with the Rescorla-Wagner model.

Haselgrove's simulations using the Rescorla-Wagner model are able to predict the absence of blocking in the subadditive group of Beckers et al. (2006) Experiment 1 only because Haselgrove (2010) is allowing multiple iterations of the model at the phase level (that is iterations of the model while the cue is physically absent) until model stabilization. Under these conditions the associative strength (V_p) of the postulated common element p is able to stably reach the maximum possible value (V_p = λ = 0.7) after the pretraining phase in the subadditive group. Thus the associative strength of each other element is equal to zero (V_a,b,c,d,e,x = 0). In the remaining conditions the associative strength of the unique elements remain positive at model stabilization (V_a,b,c,d,e,x > 0) thus predicting blocking. In essence, the argument here is that the rats learn only about the common element p and nothing about each unique cue a, b, c, d, and x in the subadditive group but not in the other experimental groups. This argument could be easily tested and should be. The whole prediction rests on the assumption that the asymptotic value for V_p is maximal (V_p = λ = 0.7) at the end of the pretraining phase of the subadditive group whereas the associative strength of p after the pretraining phase in the remaining two groups should be substantially less. Therefore testing X just after the pretraining phase should at least allow the observation of greater fear of the test stimulus X in the subadditive groups than in the irrelevant element or compound groups without any training involving X. Indeed, Haselgrove's associative account rests solely on the existence of the hypothetical common element p shared by, at a minimum, the physical stimuli C, D, and X, together with the claim that the associative strength of p reaches its maximal possible value only after the subadditive pretraining and not after the Irrelevant Element or Irrelevant compound pretraining. A negative result, produced while conserving the subadditive effect reported by Beckers et al. (2006), would give a strong refutation of Haselgrove's assumption (Haselgrove, 2010) whereas a positive result would provide a strong justification for the major modification of the Rescorla-Wagner model necessitated by the account put forward by Haselgrove (2010).

In the Rescorla-Wagner model the associative strength of a cue is updated only if this cue is present at a given trial. From a formal point of view the choice of whether to consider the asymptotic behavior of the model after multiple iterations at the trial or the learning phase level may seem rather arbitrary. However, from the point of view of the model, there is a clear distinction between these choices. For example in the case of Beckers et al. (2006) the pretraining phase took place over 4 days; in keeping with the model requirement that a stimulus be present at a given trial for its associative strength to be updated it is not entirely unreasonable to admit multiple iterations of the model during a given physical trial [as in the type (ii) simulation]. However, imagining multiple iterations of the model at the phase level is far less reasonable. Indeed the first iteration would need 4 days to be achieved (the pretraining phase occurred across 4 days), and only after the whole phase had been experienced once could new iterations of the model occur, seemingly in absence of any physical trial. This would be a clear violation of the model's assumptions³ [as in the type (iii) simulation].

To accept this proposition one should at least expect a strong rationale as to how such an assumption is compatible with the Rescorla-Wagner model. Even if such a rationale were convincing, there still remains the issue of what is the compelling reason to repeat at the phase level and not at the level of the whole experiment, or at the experimental day level, and not to simply allow multiple iterations per physical trial? Such an assumption would need to be formalized rather than to appear as an ad hoc explanation of a very challenging phenomenon for classical associative theories of learning. Surprisingly, such rationales are absent from Haselgrove paper (Haselgrove, 2010), and we can offer none; given the experimental setup a simulation via phase repetition is in violation of the assumptions of the Rescorla-Wagner model. Therefore we believe that this assumption is invalid and thus are led to challenge the associative account offered by Haselgrove (2010) of Experiment 1 of Beckers et al. (2006).

Although not presented here, we were able to simulate the results of Experiment 2 and 3 reported by Beckers et al. (2006) using the assumptions put forward by Haselgrove (2010) with the parameter β within the range allowed by the Rescorla-Wagner model [0 ≤ β ≤ 1, as opposed to some simulations put forward by Haselgrove (2010) with 0 ≤ β ≤ 1.4]. But it was evident that the simulations, without the additional assumptions of asymptotic performance at the end of each learning phase and multiple iterations of the model per physical trial, agreed with the experimental results with the same degree of fitness as the simulations presented in Haselgrove (2010). Therefore, we concur that the Rescorla-Wagner model can accommodate some of the results obtained by Beckers et al. (2006) in Experiment 2 and 3, but certainly not all of them. Nonetheless, these simulations also indicate that the assumption of asymptotic learning at the end of each phase (regardless of its implementation) is not necessary in these cases.

Conclusion

We have demonstrated unambiguously that the associative account offered by Haselgrove (2010) is either flawed or necessitates not only major modifications to the model but also a strong rationale or experimental support for making such modifications. Furthermore it is important to remember that, computationally, multiple iterations of the learning phase are not always equivalent to multiple iterations of the model per physical trial (the latter assumption may be compatible with the Rescorla-Wagner model). This is the error that appears to be at the origin of the main claim of Haselgrove (2010).

It seems that the Rescorla-Wagner model, and probably numerous other associative models, cannot accommodate the main results of Beckers et al. (2006) reported in Experiment 1: that blocking is abolished by the so called subadditive pretraining. Other experimental results as presented in Beckers et al. (2005) and in Beckers et al. (2006) also seem to be problematic for associative models. However, it may be, as suggested by Schmajuk and Larrauri (2008), that these experimental results are within the explanatory power of their associative model Schmajuk et al. (1996; see also Schmajuk and Larrauri, 2006), although this still needs to be formally demonstrated. Nevertheless, the effects put forward by Beckers et al. (2005, 2006) demonstrate the influence of prior learning on subsequent learning about unrelated cues, and should not be dismissed lightly.