Decision-Making Based on Emotional Images

Abstract

The emotional outcome of a choice affects subsequent decision making. While the relationship between decision making and emotion has attracted attention, studies on emotion and decision making have been independently developed. In this study, we investigated how the emotional valence of pictures, which was stochastically contingent on participants’ choices, influenced subsequent decision making. In contrast to traditional value-based decision-making studies that used money or food as a reward, the “reward value” of the decision outcome, which guided the update of value for each choice, is unknown beforehand. To estimate the reward value of emotional pictures from participants’ choice data, we used reinforcement learning models that have successfully been used in previous studies for modeling value-based decision making. Consequently, we found that the estimated reward value was asymmetric between positive and negative pictures. The negative reward value of negative pictures (relative to neutral pictures) was larger in magnitude than the positive reward value of positive pictures. This asymmetry was not observed in valence for an individual picture, which was rated by the participants regarding the emotion experienced upon viewing it. These results suggest that there may be a difference between experienced emotion and the effect of the experienced emotion on subsequent behavior. Our experimental and computational paradigm provides a novel way for quantifying how and what aspects of emotional events affect human behavior. The present study is a first step toward relating a large amount of knowledge in emotion science and in taking computational approaches to value-based decision making.

1. Introduction

The role of emotion in decision making has attracted the interest of many researchers (Damasio, 1994; Loewenstein and Lerner, 2003; Cohen, 2005; Shiv et al., 2005; Seymour and Dolan, 2008). The emotional state of a decision maker and the emotional outcome of decision-making affect decision making. From this perspective, emotion science (or affective science) and decision science should have a close relationship. However, studies on emotions and decision making have been independently developed. Studies on decision making have been developed in many fields, such as behavioral economics, neuroscience, and the fusion of these disciplines, neuroeconomics. While emotion science attempts to study a broad range of topics in emotion (De Gelder, 2010), researchers in behavioral economics have mapped many factors in decision making onto a single variable: value.

Studies on decision making (including those that address the effect of emotion) have mainly used primary or secondary reinforcers (i.e., food for animals and money for humans) to form values for the actions in decision makers. These reinforcers are useful for manipulating values in a uniform way and reducing individual variability. For humans, however, what affects decision making is not only food or monetary rewards. Specifically, several aspects of an outcome, including the emotional content, affect decision making. The emotional content is often difficult to quantify and exhibits a great deal of individual variability. For example, the values of a movie or music are difficult to measure and can show large individual variability, as music inducing happiness in some people could be just noise to others.

One goal of the present study was to propose a paradigm for measuring the effect of an emotional event on human behavior by inferring the “reward value” of a general emotional event from choice data. One of the influential models of emotion is a two-dimensional model consisting of valence (positive–negative) and arousal (arousal–sleepiness; Russell, 1980; Russell and Bullock, 1985; but see Fontaine et al., 2007). In the present study, we focused on the former factor, valence, which is a primary component of emotion. Thus, we investigate how the valence of decision-making outcomes is mapped onto reward values in decision makers, thereby affecting subsequent behavior. To achieve this, we use emotional images instead of monetary rewards in a conventional stochastic reinforcement learning task. We hypothesized that positive/negative reward values would be associated with approaching/avoidance behaviors that would increase/decrease the probability of actions upon which these reward values are contingent. From this hypothesis, we can measure the “reward value” of emotional stimuli from participants’ choice behaviors. To evaluate the reward values from choice data, we employed a computational model, which is a reinforcement learning model that has successfully been applied to value-based decision-making behavior in both human and animal studies (for reviews, Daw and Doya, 2006; Corrado and Doya, 2007; O’Doherty et al., 2007). Our participants rated the subjective valence of how they experienced the valence of the picture. Our specific goal was to investigate the relationship between the rated valence for emotional pictures and the reward value of the pictures estimated from the choice data. Possible results were (1) the distance between the rated subjective valence from the neutral pictures was preserved in reward value, (2) the distance was amplified for either positive or negative pictures or (3) only positive or negative pictures have non-zero reward value (compared to neutral pictures). We construct the reinforcement learning models that correspond to each possibility and compare them by using the goodness of fit to the participants’ choice data.

We used pictures adopted from the International Affective Picture System (IAPS; Lang et al., 1999), which have been commonly used in emotion studies as the emotional images (e.g., Lang, 1995; Bradley et al., 2001; Hariri et al., 2002; Cahill et al., 2003; Scherer et al., 2006). In previous studies, the IAPS has primarily been used for measuring reactions to emotional stimuli in behavioral, physiological, and neural responses rather than for investigating the influence of emotional stimuli on subsequent behavior, as we do in the present study. Thus, the present study is a first step toward linking the computational approach to value-based decision making with emotion science that explores the emotional reactions to emotional stimuli. As in previous reward-based decision-making studies (e.g., Sugrue et al., 2004; Corrado et al., 2005; Lau and Glimcher, 2005), we also examined how the past history of emotional images influences current choices by using linear filter (regression) analysis.

2. Materials and Methods

Participants and procedure

The participants were 22 healthy volunteers (10 females and 12 males) recruited at the Wako campus of RIKEN (Saitama, Japan). All participants were native Japanese speakers and had normal or corrected-to-normal vision. Three participants were excluded from the analysis because they forget or misunderstood the instruction that pictures were contingent on previous choices. Two additional participants were excluded because the mean valence rating for the positive/negative pictures did not sufficiently differ from the neutral rating (the departure from neutral was less than 1, where the maximum was 4). Thus, the pictures used were deemed to be ineffective positive and/or negative stimuli for these individuals. The 17 remaining participants (8 females and 9 males) had an average age of 36.5 years old (SD = 8.0, range: 28–51). The study was approved by the Ethics Committee of the Japan Science and Technology Agency (JST). Participants were given detailed information and provided written consent.

Task description

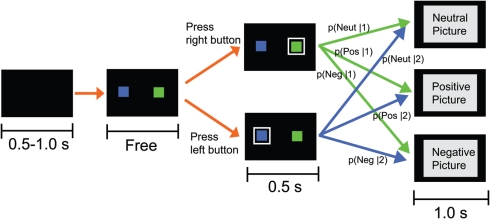
The task consisted of 600 trials with short breaks after every 200 trials. Figure 1 outlines the flow for one trial. Each trial began with a black screen, the duration of which was sampled from a uniform distribution between 0.5 and 1.0 s. Next, two colored (green and blue) squares were presented, and participants were required to choose one square using a button box. We referred to the green box as target 1 and the blue box as target 2. These two colors were chosen following a previous experiment on human decision making (Behrens et al., 2007). Target colors were not counterbalanced across participants, following Behrens et al. (2007). No time limits for responses were imposed so that participants could not use a simple strategy where they made no responses to avoid seeing negative pictures. The positions of the targets (left or right) were randomized. After a white frame indicating the choice had been presented for 0.5 s, a picture was presented for 1.0 s. The picture category (negative, neutral, or positive) was related to the choice through conditional probabilities p(valance|choice). The probabilities were changed between blocks according to the pre-determined schedule described in Table 1. The number of trials included in one block ranged from 50 trials to 120 trials. There were 7 blocks in total. We introduced breaks within blocks rather than between blocks to avoid providing the participants with a signal of the change of the probability, which might be an artifact in examining the effect of learning. The same schedule was used for all participants. We employed a common schedule for three reasons: (1) to examine various combinations of choice-picture contingencies with a restricted numbers of trials; (2) to avoid situations where the change in contingency was too difficult to detect, which could occur if similar contingencies followed (this was likely to occur if we randomized the order of blocks); and (3) to make it possible to directly compare the time courses for the choices and the goodness of fit of models between participants. Each valence group contained ten pictures taken from IAPS. Their normative valence/arousal ratings were (mean ± SD): 4.995 ± 0.160/2.372 ± 0.450 for the neutral group, 7.743 ± 0.482/5.278 ± 0.618 for the positive group, and 2.735 ± 0.475/5.378 ± 0.553 for the negative group. The negative and positive pictures were selected to be equidistant from the neutral pictures in terms of valence and arousal. After the valence category was determined depending on choice, a picture was randomly selected with the constraint that the same picture was not shown in consecutive trials. The picture numbers that we used are presented in Section “Appendix A.”

Figure 1.

Schematic of one trial in the experiment. After the presentation of a blank screen whose duration was drawn from a uniform distribution between 0.5 and 1.0 s, a green square (target 1) and a blue square (target 2) were presented for 1.0 s. Each participant chose one target and indicated his/her choice by pressing a corresponding key. After a white frame surrounding the chosen target was presented for 0.5 s, a picture whose valence (neutral, positive, or negative) depended on the choice was presented for 1.0 s. The picture valence was related to the choice through conditional probabilities p(valence|choice), which are described in Table 1.

Table 1.

Schedule of picture assignment probability and the participants’ choice preferences for each block.

Trial	Target 1	Target 2	No. of participants choosing target 1	No. of participants choosing target 2	Preference across participants
	Neut:Pos:Neg	Neut:Pos:Neg	(p < 0.05)	(p < 0.05)
1–50	0.7:0.2:0.1	0.7:0.1:0.2	5	0	1**
51–130	0.1:0.0:0.9	0.1:0.9:0.0	0	17	2**
131–210	0.1:0.7:0.2	0.2:0.7:0.1	0	15	2**
211–330	0.2:0.4:0.4	1.0:0.0:0.0	7	10	2**
331–420	0.2:0.0:0.8	0.0:0.2:0.8	6	10	n.s.
421–480	0.0:1.0:0.0	1.0:0.0:0.0	9	1	1**
481–600	0.7:0.1:0.2	0.7:0.2:0.1	6	11	n.s.

Each row represents one block. From the left column: trial range for each block, the probabilities for picture category for target 1 (second column) and target 2 (third column), the number of participants showing a significant preference to target 1 (fourth column) and target 2 (fifth column) over 17 participants, and the preferred target across all participants. Neut: neutral, Pos: positive, and Neg: negative pictures. **p < 0.01.

Participants were told that various pictures would be presented depending on the box they chose, and that there was some relationship between their choice and the picture. They were instructed to carefully look at the picture to answer questions about the scenes and people in the picture after the entire experimental session had finished (not conducted). They were not given instructions on more specific task structures or the goals of the experiment. The stimuli were presented with a program written using Presentation ver.14.1 (Neurobehavioral Systems, Inc.). After the entire experiment had been completed, participants rated all pictures for valence on a scale from 1 (most unpleasant) to 9 (most pleasant) in a paper-based questionnaire. They were asked to rate how the images made them feel during the decision-making experiment. The scale was converted for convenience from −4 (most unpleasant) to 4 (most pleasant) in the analysis. Participants sat comfortably in front of a monitor that presented stimuli, and they used a button pad to indicate their choices.

We administered the Japanese version of the Positive and Negative Affect Schedule (PANAS; Sato and Yasuda, 2001) to examine whether mood states influenced choice behavior. Participants completed the PANAS twice before starting the experiment and immediately after they had completed it. Participants were instructed to “please indicate your emotion right now.”

Model-free analyses

Choice preferences

To test whether there were significant choice preferences during each block, we submitted the number of choices for each target and participant to the Pearson’s chi-square test (discarding the first 10 trials of each block).

Dependence of choice behavior on history

To measure how the valences of previous pictures affected the next choice, we computed empirical probability p(stay(t)|valance(t −1)) or the probability of choosing the same target at trial t as at the previous trial t − 1, given the picture valence at trial t − 1. The effects of the picture valences were tested with ANOVA.

We also examined how more than one past picture affected choice. Computing the conditional probability given more than one previous picture involved the problem of sample size due to the exponential growth of combinations. Therefore, we used a linear regression analysis (filter analysis), following Sugrue et al. (2004), Corrado et al. (2005), and assumed that the current choice was influenced by a linear combination of recent choices and their outcomes. With the index of valence j = Neut, Pos, Neg, we define the picture history by r_j(t) such that r_j(t) takes 1 (−1) if a participant chose target 1 (2) on trial t, and the resulting picture is valence j, but r_j(t) takes 0 if the resulting picture is not valence j. Choice history is also defined by c(t) such that c(t) = 1 if a participant chooses target 1, and c(t) = −1 if a participant chooses target 2 on trial t. With these quantities, the linear regression model is given by

$$L_j\left(t\right)={\displaystyle \sum _{i=1}^M}{k}_j\left(i\right)r_j\left(t-i\right)+{\displaystyle \sum _{i=1}^M}h\left(i\right)c\left(t-i\right),$$ (1)

where k_j(i) and h(i) correspond to the regression coefficients for ith trials before for the picture history of valence j and for the choice history. M is the length of choice-picture history (from the current trial to the past trials) and we used M = 7. We optimized the coefficients, k_j(i) and h(i), so that they minimized the sum of squared errors between L_j(t) and the choices made by participants:

$$E_j={\displaystyle \sum _t}{\left\{L_j\left(t\right)-c\left(t\right)\right\}}^2.$$ (2)

Model-based analyses

Q-learning models

To model the participants’ choice behaviors, we employed the Q-learning model, which is a standard reinforcement learning model (Watkins and Dayan, 1992; Sutton and Barto, 1998). The Q-learning model represents the estimated “value” of each action (selecting one target) as Q-values. Let Q_i(t) denote the Q-value for target i (i = 1,2) on trial t. The Q-values are updated according to the action and the resulting outcome (the outcome in this study corresponded to a picture valence). Let a(t) ∈ {1,2} denote the target the participant chooses on trial t. If a(t) = i, then the Q-value corresponding to the selected target is updated as

$$Q_i\left(t+1\right)=Q_i\left(t\right)+\alpha \left(v\left(t\right)-Q_i\left(t\right)\right),$$ (3)

while the Q-value corresponding to the unselected target does not change. Here, α is the learning rate that determines the degree of the update, and v(t) is the “reward value” for the picture presented during trial t, which is specified below. Given a Q-value set, a choice is made according to the probability of choosing target 1, which is given by a soft-max function:

$$P\left(a\left(t\right)=1\right)=\frac{exp\left(Q_1\left(t\right)\right)}{exp\left(Q_1\left(t\right)\right)+exp\left(Q_2\left(t\right)\right)},$$ (4)

with P(a(t) = 2) = 1 − P(a(t) = 1). Let us consider six variants of the Q-learning models (models 1–6) and compare them based on how well they fit the participants’ choice behaviors. The models are divided into category- and rating-based models. The former uses pre-determined valence categories (neutral, positive, and negative) to compute value v(t), whereas the latter uses the participants’ valence ratings.

The category-based models (models 1–4) set v(t) to v(t) = κ_P if the picture valence on trial t is positive, v(t) = 0 if the picture valence is neutral, and v(t) = κ_N if the picture valence is negative. We set the value of the neutral picture to zero because the relative values of these three categories are most important. Because we did not know the subjective value of each valence beforehand, κ_P and κ_N are free parameters that should be adjusted based on participants’ choice data. To examine the asymmetric effect of positive and negative valence, we included a model with symmetric value parameters (κ_P = −κ_N, model 1) and a model that allows the value parameters to be asymmetric (model 2). Where there was asymmetry in the picture values, the next question was whether both values for positive and negative valences influence choice behavior or only one parameter of positive or negative valences influences choice behavior. To answer this, we included a model in which only negative pictures have an effect on choice behavior (κ_P = 0, model 3), and a model in which only a positive value have an effect (κ_N = 0, model 4).

The rate-based models (models 5–6) use each participant’s valence rating for individual pictures to compute v(t). Denoting the rating for the picture presented at trial t as rating(t) = [−4(most negative),…, 0 (neutral),…, 4 (most positive))], we divide the rating value into negative and positive parts as rating(t) = rating⁺(t) + rating⁻(t). Again, we considered the symmetric value-weighting (v(t) = m·rating(t); model 5) and asymmetric value-weighting (v(t) = m⁺·rating⁺(t) + m⁻·rating⁻(t); model 6), where m, m⁺ and m⁻ are free parameters. To examine how well our models fit participants’ choice behaviors, we also employed a biased random choice model (null model) that constantly produces the same probability of choosing two targets with the biases of the actual participants’ choices. The list of free parameters and the number of parameters for all models are shown in Table 2.

Table 2.

List of model parameters.

Model	Learning rate	Reward value of pictures	No. of parameters (k)
1	α	pos: κ, neut: 0, neg: −κ	2
2	α	pos: κP, neut: 0, neg: κN	3
3	α	pos: 0, neut: 0, neg: κN	2
4	α	pos: κP, neut: 0, neg: 0	2
5	α	m·rating	2
6	α	m+·rating+, m−·rating−	3
Null model	–	–	1 (bias)

Models 1–4 are picture category-based models, which use valence category to compute the reward value of pictures. Models 5–6 are rating-based models, which use the participants’ valence ratings. Null models have only one parameter for choice bias. The entire set of models, except for the null model, has learning rate, α, as a free parameter that determines the degree of update of the Q-values. To compute the reward value of pictures, the category-based models have κs for positive and/or negative pictures. The rating-based models have ms as a multiplicative factor for participants’ valence ratings. The number of free parameters in each model is listed in the far right column.

Parameter fitting

We adopted the maximum-likelihood approach to fit the model parameters to participants’ choice behaviors. If the participant’s actual choice for the tth trial is a(t) = i, the likelihood is given by P(a(t) = i), which is computed from the soft-max function given above. The log-likelihood for the entire trial is given by

$$L={\displaystyle \sum _{t=1}^T}\text{ln}P\left(a\left(t\right)\right),$$ (5)

where T denotes the total number of trials, which was 600 in our experiment. We computed this log-likelihood by initializing the Q-values at zero and updating the Q-values based on the actual participants’ choice data.

We performed a grid search to find the best parameter set, in which we varied the parameters systematically in discrete steps, and selected the parameter set that produced the highest log-likelihood. We varied learning rate α within the range [0.05 1.5] in increments of 0.05, value parameters κ, κ_P, and κ_N within the range [−10 10] in increments of 0.2, and value-weighting parameters m, m+, and m− within the range [−10 10] in increments of 0.2. To compare the goodness of fit of the seven models with the best-fit parameters, we computed Akaike’s information criterion (AIC) given by

$$\text{AIC}=-2L+2k,$$ (6)

where k is the number of free parameters. Smaller AIC values indicate better fits. We computed another model selection criterion, the Bayesian information criterion (BIC), but we did not find quantitative differences (in relative values among models) from the results with AIC. Thus, we only report the results with AIC.

3. Results

We first report the results of the model-free analysis, or the direct analysis of the choice data and valence rating data for the stimulus pictures. We then present the results obtained from the model-based analysis.

Valence rating

We first examined the valence rating data to verify our valence categories for the pictures used, where those scaled to −4 were the most negative, those scaled to 0 were neutral, and those scaled to 4 were the most positive. The valence rating for the neutral group (mean ± SD over ten pictures) was −0.19 ± 0.38, which did not significantly differ from zero (p = 0.15, Wilcoxon’s signed-rank test). The valence rating for the positive group was 2.66 ± 0.76, and the valence rating for the negative group was −2.41 ± 0.74, both of which significantly differed from zero (p < 0.01). These results indicate that the picture categories assigned to each picture were valid. The absolute values for rating the positive and negative groups did not significantly differ (p = 0.30, paired-sample Wilcoxon’s signed-rank test), implying the valence symmetry of our picture set. This symmetry is important when interpreting the asymmetry in choice behavior in response to positive/negative pictures, which will be discussed later.

Choice preferences

The participants’ choice preferences for each block are listed in the right three columns of Table 1. Overall, the participants preferred positive pictures over neutral pictures and neutral pictures over negative pictures. For example, 5 participants indicated a significant preference for target 1, while no participants reported a preference for target 2 in the first block (trials 1–50), where the probability for positive/negative pictures was slightly larger/smaller for target 1. In the second block (trials 51–130), all participants indicated a significant preference for target 2, in which positive pictures appeared with a probability of 0.9, while target 1 evoked negative pictures with a probability of 0.9. There were blocks in which preferences across participants were split, and no significant preferences across participants were observed (trials 331–420 and 481–600). This is possibly due to the combined effects of the persistence of preferences for a previous block (carry-over effect) and individual differences between the relative “reward values” of three valences. In either case, this can be interpreted as participants choosing hypothetical values, with positive > neutral > negative pictures. We intend to strengthen this view with the model-based analysis discussed later.

Dependence on history

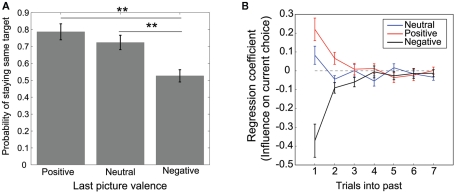
We examined how the valence of a previous picture affected subsequent choices. Figure 2A shows the probability of repeating (staying) an action conditioned on previous picture valences. An ANOVA revealed that the main effect of the valence category was significant (F(2,32) = 23.97, p < 0.01). The probability of staying was significantly smaller after a negative picture than after a neutral or positive picture, indicating that participants tended to switch when negative pictures were presented compared with when positive or neutral pictures were presented (p(stay|negative) vs. p(stay|positive) and p(stay|negative) vs. p(stay|neutral); HSD = 0.123, α = 0.01, Tukey’s honestly significant difference test). The mean stay probability did not fall below 0.5, even after a negative picture, implying that the participants did not undertake the strategy of switching their choice immediately after viewing a negative picture. This may be due to the effects of positive or neutral pictures presented more than one trial before.

Figure 2.

Dependencies of choice behavior on history. (A) Empirical probability of repeating an action (staying) given the valence of previous pictures. (B) Mean regression coefficients for the history of each picture valence. The larger the absolute value of the coefficient, the larger the influence of the picture valence of the past trial on the current choice. Error bars indicate standard error.

We performed linear filter (regression) analysis to analyze the influence of pictures presented more than one trial before. We measured the extent of this influence by using fitted regression coefficients. Figure 2B plots the regression coefficients (k_j(i)) averaged over all participants. The larger the absolute value of the coefficient, the larger the influence of the past trial’s picture valence on the current choice. For positive and negative valences, the coefficients appeared to decrease exponentially from one trial before to older trials. This tendency was consistent with reward-based choice behaviors observed in monkey experiments (Sugrue et al., 2004; Lau and Glimcher, 2005). This decay pattern suggests that what affected the participants’ choices was not only pictures presented in the immediate past but also pictures presented a few trials prior. Because there was large variability in the estimated regression coefficients due to small trial size (600 trials), we cannot state more quantitative properties, such as how far back previous trials influence current choice or whether the histories of negative pictures and positive pictures are different in the decay time constants. A more thorough experiment using a larger number of trials is required to clarify these points. The following model-based analysis describes the mechanism responsible for the decay pattern in history dependencies.

Model-based analysis of choice behavior

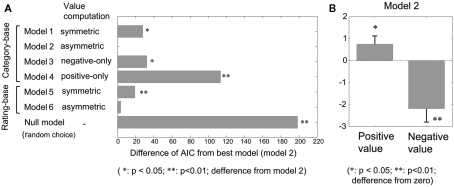
Of particular interest in the present study was the “reward value” of emotional pictures in terms of action selection. To measure the value solely from choice data, we applied reinforcement learning models, which are established models for human and animal learning in decision making (Daw and Doya, 2006; Corrado and Doya, 2007). We compared six versions of the model under various assumptions. We used the Akaike information criterion (AIC) to measure goodness of fit, which includes a penalty that increases as a function of the number of adjustable parameters. The adjustable parameters for models 1–6 were learning rate, which determines the degree of update of the value function for the selected target, and the value parameters for the positive and negative valences (Table 2). Figure 3A shows the difference in AIC relative to the best model (model 2), which was a full model that allowed the value parameters for positive and negative pictures to be asymmetric. Model 2 yielded a significantly better fit than model 1 (p < 0.05, paired-sample Wilcoxon’s signed-rank test), in which the value parameters were symmetric, indicating that the reward values for positive and negative pictures were asymmetric. Model 2 was also significantly better than model 3 (p < 0.05), in which the positive value was zero, and model 4 (p < 0.01), in which the negative value was zero. These results suggest that both the valences of positive and negative pictures affected choice behavior, while the effect was larger for negative pictures, which can be confirmed by checking the estimated value parameters for model 2 (Figure 3B).

Figure 3.

Results of the model-fitting using various Q-learning models. (A) Goodnesses-of-fit of various Q-learning models. Differences in AIC from the best model (model 2) are plotted. **p < 0.01; *p < 0.05; difference from the best model (model 2), Wilcoxon’s signed-rank test. (B) Estimated values for the value parameters of the positive/negative pictures for model 2. *p < 0.05; **p < 0.01; difference from zero.

Rating-based models (models 5 and 6) directly use participants’ ratings for the valences of individual pictures to compute their reward values. If the variability of subjective valences for individual pictures is large and if the variable valence is directly related to the action value, then the rating-based model would show a better fit than models based on pre-determined valence categories (models 1–4). However, even if the weights for positive and negative ratings could have been asymmetric (model 6), no significantly better model fit was obtained (p = 0.093) and the mean of AIC was even larger. This suggests that the effect of picture valence variability within the same category on choice behavior was not significant.

To examine how well the models fit participants’ choice behavior, we also calculated an AIC for the biased random choice model (null model) that constantly produced the same probability of two targets being chosen with biases of the actual participants’ choices. The AIC of the null model was significantly larger (worse) than that for all six models (p < 0.05 for model 4; ps < 0.01 for models 1, 2, 3, 5, and 6).

Next, we checked the learning process of the Q-learning model and examined how close the model was to that of the participants. Figure 4A shows a sample run of a simulation of model 2 with the mean parameters over fits for all participants. The model chose targets based on the probability of targets being chosen, computed from two Q-values, which were updated depending on the resulting pictures. The valences of pictures given were dependent upon the same schedule as those in the experiment (although only 80 trials at the beginning are plotted). As seen in the top panel of Figure 4A, the probability of choosing target 1, p(a = 1), moved, increasing the probability of choosing a target from which a positive picture (represented by a red bar) appeared, decreasing the probability of choosing a target from which a negative picture (represented by a black bar) appeared (top panel). This was accomplished by the updates of Q-values.

Figure 4.

Simulation of the experiment with the Q-learning model (model 2). (A) An example of single run from trials 1 to 80. Parameters were set to the mean of the fitted parameters (α = 0.62, κ_P = 0.75, κ_N = −2.19). (B) Mean regression coefficients obtained from a simulation of 50 runs of model 2 with a parameter set fitted to each participant.

We applied choice-picture history regression analysis to the choice data obtained from the simulation (Figure 4B) in the same manner as the real data (Figure 2B). The simulations were conducted 50 times for each parameter set and were fitted to one participant. As seen when comparing Figures 2B and 4B, although the coefficients differ quantitatively from the results of the experiment, the qualitative properties (i.e., the exponential decay for positive and negative pictures) were reproduced in the simulation. The mechanism for Q-learning to produce exponential decay in the coefficients can be explained as follows: if the value of a picture after a target is chosen is larger than the current Q-value of the target, the Q-value increases and the probability of choosing the target increases. Thus, if the current Q-value is below zero, the probability of choosing the target increases, even if the value of the picture is zero (as was the case for the neutral picture in the current model setting). In contrast, the probability of choosing the target decreases if the value of the picture is smaller than the current Q-value. Suppose a positive picture appearing after target 1 was chosen m-trial before. This would increase the probability of target 1 being chosen again and thus would increase the regression coefficient for the m-trial before. The effect on the current Q-value decreases by a factor that is proportional to 1-(learning rate) as we go back one trial (m + 1-trial before; see Appendix B for more details). The similarity between the dependence on history of the experimental results (Figure 2B) and simulation with the Q-learning model (Figure 4B) implies that similar mechanisms for history dependence with the Q-learning model underlie participants’ choice behavior.

Mood effects

To evaluate the effects of participants’ moods prior to and following the experiment, we examined the positive and negative scores calculated from the PANAS that were completed by the participants before and immediately after the experiment. The positive score significantly decreased from the pre-experiment to the post-experiment (pre: 24.47 ± 6.00, post: 19.53 ± 5.69; t(16) = 4.90, p < 0.01), while the negative scores exhibited a tendency to increase (pre: 14.59 ± 6.89, post: 17.29 ± 5.85; t(16) = 2.01, p = 0.061). The correlation coefficients of mood scores (pre-experiment, post-experiment, and their differences) and the estimated parameters in the best model (model 2) are summarized in Table 3. Although no significant correlations were found, the positive mood score (post-experiment) tended to negatively correlate with the value of positive pictures, κ_P (r = −0.43, p = 0.082). In addition, the change in the negative mood score also tended to positively correlate with the value of positive pictures (r = 0.42, p = 0.091). These tendencies may imply that either the participants who feel the positive pictures more positively tend to show a change toward negative mood when exposed to negative pictures, or they show that changing to a negative mood causes the participants to seek positive pictures, thus increasing the estimated reward value of positive pictures. We should note that the sensitivity to detect a correlation was relatively low due to the relatively small number of participants (n = 17; for p ≤ 0.05 and df = 15, the correlation coefficient must be r ≥ 0.482). A replication of our results with a larger number of participants is needed in the future.

Table 3.

Correlation coefficients between estimated model parameters (for model 2) and mood scores (pre-experiment, post-experiment, and differences of them).

Model parameter	Positive mood score			Negative mood score
	Pre	Post	Post-pre	Pre	Post	Post-pre
Learning rate, α	0.14	0.13	−0.03	−0.28	−0.32	0.01
Positive picture value, κP	−0.21	−0.43 (0.082)	−0.29	−0.16	0.21	0.42 (0.091)
Negative picture value, κN	−0.32	−0.15	0.26	0.04	−0.21	−0.28

All of the correlations were non-significant (all p > 0.05). Only p-values where p < 0.1 are shown in parentheses.

4. Discussion

Using a stochastic two-alternative choice task paradigm, we investigated how the valence of emotional pictures was mapped onto reward values that determined the tendency toward subsequent choices. The results from analyzing the block-wise preferences and fitting the value parameters in reinforcement learning models suggest that reward values increase from negative to neutral to positive pictures. The estimated values for the positive pictures were significantly positive relative to that of neutral pictures, and the values for negative pictures were significantly more negative than neutral pictures. These results suggests that positive pictures act as approaching stimuli, and that negative pictures act as aversive stimuli. The participants were only instructed to look at the pictures to answer questions about portrayed scenes or people after the experiment, and no instructions were given concerning avoidance of negative pictures or attempting to maximize the time they observed the positive pictures. In addition, unlike decision-making tasks in many previous studies, task performance was not related to actual rewards for participating in the experiment. All participants were volunteers unpaid for participating in the experiment. In light of this, our findings suggest that emotional pictures themselves can be “internal rewards” that have value for humans. Furthermore, the same picture was presented many times in our experiment (each picture was presented 20 times on average.) Although the time course of values was not examined in this study, significant preferences across the entire experiment implied the values of pictures were resistant to repetition. This property is reminiscent of experiments demonstrating that the relative magnitudes of the startle reflex to emotional pictures were relatively uninfluenced by repetitive presentations compared with other physiological measures (Bradley et al., 1993).

Participants in free-viewing experiments using emotional pictures tended to spend as much time looking at negative as positive pictures, which was more time than spent on neutral pictures (Hamm et al., 1997). This indicates that negative pictures were not aversive stimuli in the free-viewing task. This seemingly contradictory difference from our results can be explained as follows: a crucial difference is that negative pictures were already presented to participants before they took action in the free-viewing experiment, while in our experiment, the pictures were presented depending on actions preceding the presentation. After a negative event has already happened, an adaptive strategy in a natural environment is to investigate what happened and to consider how one should act next. Thus, people may take considerable time looking at negative pictures. This may account for the results from free-viewing tasks. In contrast, when the probability of occurrence of negative events can be reduced if one takes some action, an adaptive strategy is to take such action. This corresponds with our experiment.

We found that the models assuming value asymmetry (models 2 and 6) between positive and negative pictures fit the choice data better than the value-symmetric models (models 1 and 5). The magnitude of the estimated value parameters was larger for negative pictures than for those that were positive. It is worth noting that the normative valence ratings for picture sets used were symmetrical between the positive and negative categories. In addition, no significant asymmetry was found in the valence ratings by our participants. It is notable that they were asked to rate the valence of how the images made them feel in the experiment rather than the valence depicted in the images. This implies that the positive and negative pictures had equivalent values in terms of absolute valence and what was experienced by participants. Nonetheless, the estimated value yielded from the choice behavior results indicated that avoiding negative events was more relevant than approaching positive events. This tendency may be adaptive in natural environments. Specifically, when both a negative and a positive event are likely to occur, avoiding negative events likely yields better consequences for survival than approaching positive events. This kind of asymmetry is known in the economic literature to be asymmetry between gain and loss, which has been explained by prospect theory (Kahneman and Tversky, 1979). Although this may only be a superficial similarity, it would provide an opportunity to enable the commonality and difference in mechanisms underlying emotional event-based and economic choices to be studied.

For the calculation methods of the reward value of pictures, we compared the category-based models that used pre-determined valence categories and the rating-based models that used the individual valence ratings. We observed that the category-based model (model 2) yielded better performance than the rating-based model (model 6), although the difference did not reach significance (p = 0.092). This is perhaps a counterintuitive result, given that the rating-based model can include the between-subject and within-subject variability of how participants feel for individual pictures. A possible reason for this is that the variability of picture valences within categories is small, and the variability of the rated valence serves as noise rather than a signal that indicates the model of the true reward value of the pictures. When the experienced valences were relatively uniform within the same category, a bias toward distributing the rating more than the true subjective valences might occur in the participants. However, we cannot exclude the possibility that it was some other feature that differed between categories that predicted choice behavior, not picture valence.

Because we focused on the valence of pictures, our picture sets were not distributed along another other emotional dimensions, such as:, i.e., arousal. Thus, our experiment did not allow us to analyze what effect the arousal level of the stimuli had on decision making. The arousal level of stimuli has been reported to affect cognition in memory and attention, possibly through the amygdala function of amygdala (Kensinger and Corkin, 2004; Anderson et al., 2006). Thus, the arousal of stimuli probably affects learning in decision-making tasks. It would be interesting future work to incorporate the effect of arousal into the reinforcement learning model. One possible effect is to modulate the learning rate, which was assumed to be constant in our model.

The computational processes involved in our experimental paradigm and the models used were relatively simple in the context of economic decision making. The two important computational processes are the habitual and goal-directed mechanisms (Daw et al., 2005). The habitual mechanism represents action-value association and is described by “model-free” reinforcement learning methods. Here, “model-free” refers to the assumption that the model does not include a state transition in the environment, which should not be confused with the “model-free analysis” conducted in the present study. The goal-directed mechanism represents action-outcome and outcome-value associations and is described by the model-based reinforcement learning methods, which explicitly represent the action-outcome transitions. In our experiment, because the trials were mutually independent in our task paradigm (i.e., the past choice does not affect future outcomes), the habitual mechanism is sufficient. In fact, all the models used in the present study belong to the model-free reinforcement learning method class. Investigating how emotional events affect goal-directed controllers would be a beneficial avenue for future research. In this direction, Pezzulo and Rigoli (2011) recently proposed a novel model that includes a prospection ability for anticipating future motivational and emotional states in utility assignments (i.e., the model considers what emotion will be experienced after a specific choice). It would be interesting to generalize our paradigm using emotional pictures to a paradigm which needs such prospection ability and to examine how Pezzulo and Rigoli’s model predicts choice behavior. Motivation is another important component in decision making, especially in assigning specific utilities to outcomes (e.g., if a decision-maker is hungry, he will assign high utility to food, whereas if he is thirsty, he will assign high utility to drink). Because our model does not include the motivational state, it may be interesting to see how motivational state influences the valuation of emotional pictures. For example, we may expect neutral pictures to have high utility in the context of negative pictures frequently appearing, which tend to disgust participants.

We observed that the reinforcement learning model reproduced the participants’ actual behavior with regards to the influence that choice-picture history had on current choices (Figure 4B). This result suggests that human choice behavior based on emotional pictures may use similar computational principles with the reinforcement learning model; the action value (Q-value) for each target is updated based on “reward-prediction error” (i.e., the actual reward value minus the expected reward). In the present study, the reward corresponds to the reward value of emotional pictures and the expected reward corresponds to the action value. Functional magnetic imaging (fMRI) studies using monetary rewards have suggested that several distinct brain regions encode reward-prediction error or action values (for a review, see O’Doherty et al., 2007). Also, the reward-prediction error is reflected in an event-related potential (ERP) measured by electroencephalogram (EEG; Holroyd and Coles, 2002; Ichikawa et al., 2010). By measuring the brain response using fMRI or EEG during emotional picture tasks, as in the present study, one could find the similarities and differences in processing of emotional pictures and monetary reward. In addition, it would be interesting to observe how prediction error or action values in the reinforcement learning model co-vary with peripheral physiological measurements, including skin conductance, heart rate, facial electromyographs (EMG), and blink magnitude, which have been used for measuring reactions to emotional stimuli (e.g., Lang, 1995; Bradley et al., 2001). The relationship between peripheral autonomic activities and decision-making based on monetary rewards has recently been investigated (Ohira et al., 2010). One interesting future direction would be to examine whether responses to emotional content in choice outcomes facilitate or interfere with autonomic activities in decision-making processes. These kinds of studies would link a great deal of knowledge from emotion science with decision-making theory and research.

One remaining question is what aspect of emotion drives the results reported in the present study. Is it the emotion experienced by the participants upon viewing the images, or is it the emotional valence of the images perceived? As we did not instruct the participants to respond to the emotional content, the emotion experienced by participants after viewing the images likely drives our findings. Measuring peripheral autonomic activities in our framework will also help clarify this point.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Appendix

Appendix A

The IAPS slide numbers we used were 2411, 5740, 7004, 7217, 7491, 2840, 7010, 7175, 7500, and 7950 for the neutral group; 1440, 2156, 5199, 5910, 8190, 1710, 2347, 4614, 5833, and 7502 for the positive group; and 1301, 3230, 9041, 9295, 9419, 1271, 6231, 9421, 9530, and 9610 for the negative group.

Appendix B

Here, we discuss how the influences of past positive/negative pictures on current choice decay for the Q-learning model. We consider the situation where the model chooses target i for both the m-trial before and m + 1-trial before from trial t. From the update rule of the Q-value (equation 3), Q_i is updated from trial t − (m + 1) to t − m as

$$Q_i\left(t-m\right)=\left(1-\alpha \right)Q_i\left(t-\left(m+1\right)\right)+\alpha v\left(t-\left(m+1\right)\right).$$

Then, the update from t − m to t − m + 1 is computed as

$$\begin{array}{rcll}{Q}_i\left(t-m+1\right)& =\left(1-\alpha \right)Q_i\left(t-m\right)+\alpha v\left(t-m\right)& & \\ & =\left(1-\alpha \right)\left[\left(1-\alpha \right)Q_i\left(t-\left(m-1\right)\right)+\alpha v\left(t-\left(m+1\right)\right)\right]+\alpha v\left(t-m\right)& & \\ & ={\left(1-\alpha \right)}^2{Q}_i\left(t-\left(m-1\right)\right)+\left(1-\alpha \right)\alpha v\left(t-\left(m+1\right)\right)+\alpha v\left(t-m\right).& & \end{array}$$

We find from the last equation that the effect of the picture value at trial t − (m + 1) is smaller than that at trial t − m by a factor of 1 − α. In addition, there is another case where the model chooses another target at trial t − m. For this, the effect of value v(t − (m + 1)) remains without being diminished. Because the regression coefficient for m + 1 trials before includes both cases, the decay factor in the regression coefficient is larger than 1 − α.