Prediction of Native State Hydrogen Exchange from Perfectly Funneled Energy Landscapes

Abstract

Simulations based on perfectly funneled energy landscapes often capture many of the kinetic features of protein folding. We examined whether simulations based on funneled energy functions can also describe fluctuations in native state protein ensembles. We quantitatively compared the site-specific local stability determined from structure-based folding simulations, with HX protection factors measured experimentally for ubiquitin, CI2, and Staphylococcal nuclease. Different structural definitions for the open and closed states based on the number of native contacts for each residue, as well as the hydrogen bonding state or a combination of both criteria were evaluated. The predicted exchange patterns agree with the experiments under native conditions indicating that protein topology indeed has a dominant effect on the exchange kinetics. Insights into the simplest mechanistic interpretation of the amide exchange process were thus obtained.

Introduction

The energy landscape theory of protein folding and the minimum frustration principle establish a powerful framework for understanding the dynamic behavior of macromolecules and the processes in which they are involved^1,2. Simulations based on perfectly funneled landscapes using coarse grained models (often referred to as Gō models) have been able to capture many of the fundamental aspects of the folding process^3-6. The structures of transition state ensembles ^7-9, folding intermediates ^7,10, and the mechanisms of dimerization ^11,12 and domain swapping ¹³ have all been well predicted by models where frustration has been entirely removed and topological information about the native state is the sole input. Although these results validate the global accuracy of funneled landscapes, it remains unclear whether such simple models can capture the finer details of dynamic motions in proteins. One test of such a simple landscape description is provided by the quantitative comparison between simulation results and detailed experimental parameters measured at the single residue level. Phi value analysis and hydrogen exchange measurements are some of the experimental data that provide this type of information at different depths on the folding funnel.

Hydrogen/deuterium exchange of backbone amides (HX) is well known to depend on both the structural and dynamic properties of proteins. Amide protons of the polypeptide backbone that are involved in hydrogen-bonds and/or are sequestered within the protein structure have solvent exchange rates that are orders of magnitude slower than exchange rates in an unfolded polypeptide^14-16. By analyzing the HX rate of individual amide protons, detailed structural and dynamic information can be obtained for many locations along the polypeptide chain. In the local unfolding model of HX, the amides alternate between closed (exchange incompetent) and open (exchange competent) states depending on fluctuations of their local environment ^17-19.

$$[\text{Closed}–\text{H}]\underset{k_{\mathit{\text{cl}}}}{\overset{k_{\mathit{\text{op}}}}{\rightleftarrows }}[\text{Open}–\text{H}]\stackrel{k_{\mathit{\text{ch}}}}{\to }[\text{Open}–\text{D}]$$ (1)

According to this model, under steady state conditions (k_cl ≫ k_op and/or k_cl ≫ k_ch) the experimentally observable H/D exchange rate (k_ex) is expressed as a function of the opening, and closing rates (k_op and k_cl, respectively), and the intrinsic rate of exchange (k_ch) of the amide when it is unprotected in an ideal standard unfolded and thus solvent exposed state²⁰

$$k_{\mathit{\text{ex}}}=\frac{k_{\mathit{\text{op}}}.k_{\mathit{\text{ch}}}}{k_{\mathit{\text{op}}}+k_{\mathit{\text{cl}}}+k_{\mathit{\text{ch}}}}$$ (2)

The protection factor (Pf) is the ratio k_ch/k_ex and is a measurement of the decrease in the exchange rate of a residue in the protein structure compared to its intrinsic rate in an unfolded state. By rearrangement of Eq. 2 we obtain:

$$\mathit{\text{Pf}}=1+\frac{k_{\mathit{\text{ch}}}+k_{\mathit{\text{cl}}}}{k_{\mathit{\text{op}}}}$$ (3)

In the EX1 limit (high pH, high temperature, or low stability) k_cl ≪ k_ch, and Eq. 3 reduces to:

$$\mathit{\text{Pf}}=1+\frac{k_{\mathit{\text{ch}}}}{k_{\mathit{\text{op}}}}$$ (4)

While in the EX2 limit (low pH and temperature) k_cl ≫ k_ch and then:

$$\mathit{\text{Pf}}=1+\frac{k_{\mathit{\text{cl}}}}{k_{\mathit{\text{op}}}}$$ (5)

In particular, when stable conformations are analyzed and k_op ≪ k_cl, Eq. 4 and 5 are further reduced to Eq. 6 and 7 for the EX1 and EX2 limits, respectively:

$$k_{\mathit{\text{ex}}}=k_{\mathit{\text{op}}}$$ (6)

$$\mathit{\text{Pf}}=\frac{k_{\mathit{\text{cl}}}}{k_{\mathit{\text{op}}}}=\frac{1}{K_{\mathit{\text{op}}}}$$ (7)

Assuming an EX2 mechanism and a stable conformation, protection factors directly scale with the inverse of the equilibrium constant of the unfolding transition required for exchange to occur ^15,21, providing therefore information about the free energy change associated with this process.

$$\Delta G_{HX}=–k_{B}T\text{ln}{K}_{\mathit{\text{op}}}=k_{B}T\ln \mathit{\text{Pf}}$$

The size of the structural fluctuations for the opening reaction range between local, subglobal and global unfolding transitions. Protection factors less than those predicted from the global stability arise from partial unfolding or local fluctuations of the backbone ^15,21. In principle, all possible states are accessible at any experimental condition, but the relative populations, given by the Boltzmann distribution, depend on the free energy of each state.

In the past, there have been attempts to correlate the hydrogen exchange protection factors with the fluctuations observed in molecular dynamic simulations²². However, most of these analyses used full atomistic models that are limited to the analysis of small fluctuations around the native state. In such analyses, little or no information is obtained about large scale unfolding transitions to partially or totally unfolded states associated with the exchange process preventing a thorough evaluation of the structural features of the open states. The use of coarse grain structure based models simulations represents an advantage over all atom molecular mechanics simulations since they allow an intensive sampling of the full range of conformational fluctuations.

In this work we compare the conformational dynamics of protein structures simulated using perfectly funneled structure-based models, and the HX protection factors of the backbone amide hydrogens measured under native conditions giving insights into the structure of the open (exchange competent) state at the residue level in whole proteins.

Results and Discussion

Analysis of the protection factor from simulations

With the aim of obtaining a detailed interpretation of the backbone amide HX process measured under native conditions, we carried out simulations of a set of three proteins for which NMR-based HX data are available both for fast and slowly exchanging amides (human ubiquitin, chymotrypsin inhibitor 2 (CI2), and Staphylococcal nuclease (SN)). The simulations used a coarse grained structure-based model with a perfectly funneled landscape based on a homogeneous contact potential and a moderate amount of non additivity (for more details see Methods). We first focused on ubiquitin to develop the analysis. Ubiquitin is a small cytoplasmic protein (76 residues, MW: 8565 Da) that has been extensively studied by HX under native conditions both by D₂O dilution experiments followed by HSQC at pH 3.5²³, 5.8²⁴, and 6.2²⁵ (that measures rates of the slowly exchanging amide protons) and phase-modulated clean chemical exchange (CLEANEX-PM) in the 5.5-10.0 pH range²⁶ (that measures rates of the rapidly exchanging amides). These data were combined as described in the Methods section.

An initial short simulation was carried out to determine the folding temperature (Tf) at which the free energy of the folded and unfolded state basins are equivalent. Then a longer simulation with umbrella sampling at the Tf (0.90 in reduced temperature units (T̃)) was used to obtain a good sampling of the configurational space. The weighted histogram analysis method (WHAM)²⁷ was used to obtain the proper Boltzmann distribution and free energy of all the sampled states as a function of temperature. Figure 1 shows the temperature dependence of the free energy of ubiquitin as a function of the global order parameter Qw which describes the foldedness of the protein structure and ranges between 0 for the totally unfolded state and 1 for the reference model structure. For an accurate comparison of the simulations and the experimental data, the simulations were extrapolated to a temperature somewhat less than the folding temperature at which the simulated global stability matched the experimental one. Based on a measured stability of 11-12 k_BT reported for ubiqutin in conditions similar to those used in the HX measurements (11 k_BT at pH 5²⁸, and 12 k_BT at pH 7²⁹), we extrapolated the simulations to the temperature 0.868 T̃ at which the difference in free energy between the native and unfolded state basins best matches the experimental conditions.

Figure 1.

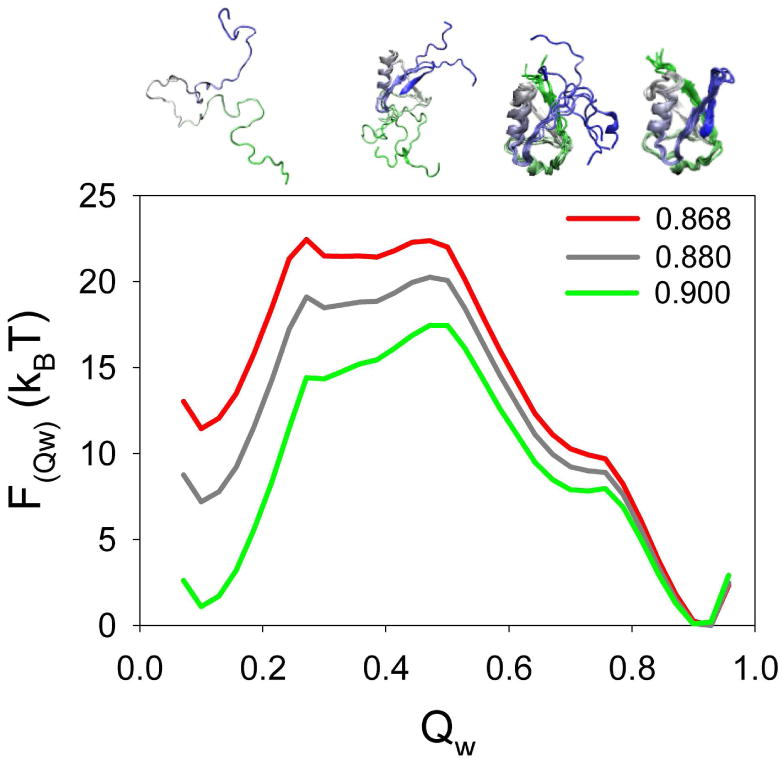
Temperature dependence of the free energy profile of ubiquitin as a function of the global reaction coordinate Qw. Simulations were carried out at the Tf (reduced temperature: 0.9, green line) and extrapolated to different temperatures. The curve in red color is the one in which the difference in Free energy between the folded (Q_w∼0.90) and unfolded (Q_w∼0.10) states basins (∼11.5 k_BT) equals the global stability of the protein under the conditions used in the HX experiments. The structures at the top illustrate the configuration of the protein ensemble at different values of Qw (from left to right correspond to one representative structure at Qw 0.10, three structures at Qw 0.45, six structures at Qw 0.70 and six structures at Qw 0.90). The structures are colored blue to green from the N-terminal to the C-terminal.

After this temperature calibration, the protection factors were obtained from the simulations by evaluation of the probabilities of the open and closed conformations for each residue assuming an EX2 mechanism (see Methods) using a variety of structural definitions of local order.

Criteria for defining the open and closed conformations

The simulations provided a large ensemble of structures for evaluation of local order parameters. Presently, there is no consensus about the appropriate definition of the open or closed state, nevertheless it is clear that the accessibility of residues in the protein structure and their H-bonding state are most important. We therefore used these parameters to structurally define the exchange competent and incompetent states. The accessibility of each residue was assessed by the number of native contacts (Qi), and the H-bonded state was evaluated by assessing the increase in the distance between H-bonded residues in the native state compared to the distance in each structure in the ensemble. The ability of these criteria, either singly or jointly, to reproduce experimental data was evaluated.

The accessibility criterion was defined using a cut-off of 6.5 Å between Cβ atoms for a native contact, and simulations were evaluated using a definition of the exchange competent state as having 0, or less than 1, 2, 3, or 4 remaining native contacts per residue. We then evaluated how well each of these accessibility criteria could recapitulate the experimental results (Figure 2). The protection predicted for each residue increased as the criteria used to define the open state got more stringent. The comparison between predicted and experimental data was assessed both by the correlation coefficient (Figure 2B) as well as by the sum of the residuals (Figure 2C). For ubiquitin, the best agreement was obtained when either 0 or at most 1 contact remained in the open state. This result suggests that significant local destabilization has to occur by moving the Cβ of practically all the locally interacting residues more than 6.5 Å away to allow exchange of the amide proton. The fact that similar results were then obtained for the other proteins (see below) suggested that this criterion was robust for evaluation of different proteins.

Figure 2.

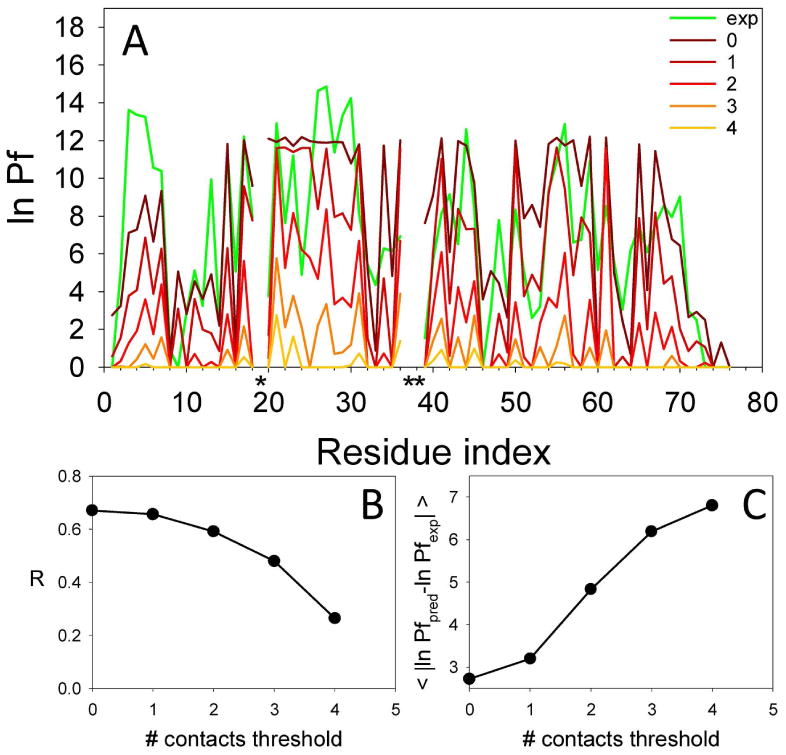
Comparison between the experimental and predicted protection factors for ubiquitin (accessibility criteria). Panel A shows the experimental ln Pf (green line) and the predicted ln Pf (red range lines) calculated allowing an increasing number of contacts from 0 to 4 in the open state. Proline residues are labeled with a black asterisk. Panel B shows the correlation coefficient of the experimental and predicted values as a function of the number of contacts in the open state. Panel C shows the average residuals of all residues.

For completeness, we also evaluated other threshold rules for discriminating between open and closed conformations. Specifically, we evaluated rules in which the open state was defined as having less than half of the total native contacts, or more than a single native contact lost, or a number of native contacts lower than that of the most probable contact-state. However, the performance of each of these criteria was worse than the optimum definitions discussed above.

We next developed a criterion for whether a residue was H-bonded. Given the limitation of the coarsegrained model, residues H-bonded in the native structure were considered as having preserved their H-bond along the simulations if the pairwise distance between the Cβs at each snapshot did not increase more than a specified amount. Figure 3 shows the comparison between the experimental and predicted HX patterns of ubiquitin calculated using different H-bonding criteria, defined as the amount of Cβ displacement, for structurally defining the open state.

Figure 3.

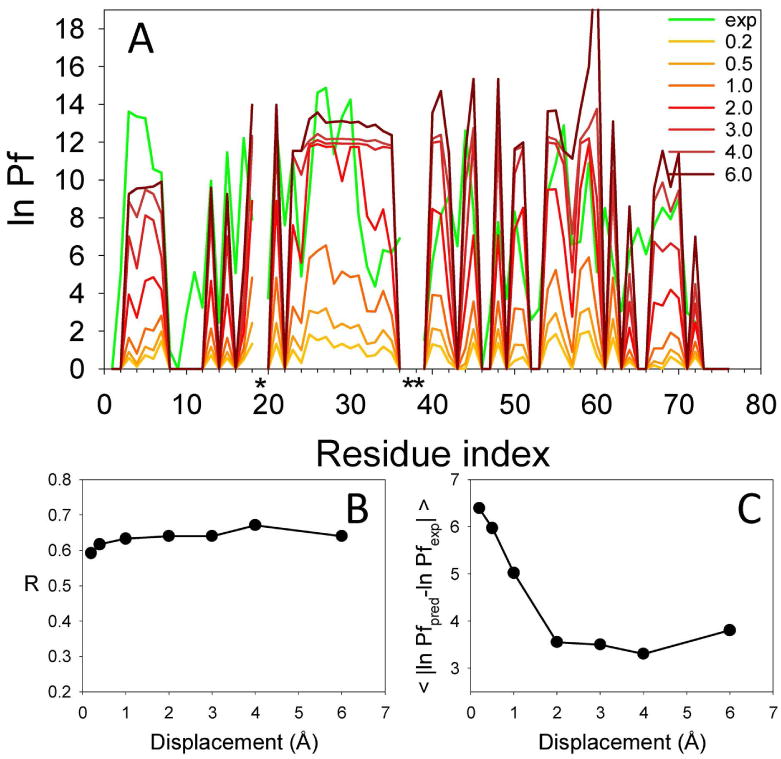
Comparison between the experimental and predicted protection factors for ubiquitin (H-bonding criteria). Panel A shows the experimental ln Pf (green line) and the predicted ln Pf (red range lines) calculated for increasing displacements from the native distance (0.2 to 6 Å). Proline residues are labeled with a black asterisk. Panel B shows the correlation coefficient between the experimental and predicted values as a function of the displacement used to define the open state. Panel C shows the average residuals of all residues.

The magnitude of the predicted protection factor varied significantly with increasing distance from the native Cβ-Cβ distance. The optimal H-bonding criterion was defined as an increase of > 2.0 Å from the Cβ distance between the H-bonded interacting pairs. This result agrees with previous studies that estimated that the distance between H-bonded residues must increase by 2-3 Å for a successful exchange event ^30,31.

Comparison of the predicted and experimental protection factors for Ubiquitin, CI2, and SN

Two other proteins for which NMR-based HX data are available both for slow and fast exchanging backbone amide H (CI2^26,32, and SN^33,34) were analyzed using the optimum accessibility and H-bonding definitions established for ubiquitin. The optimal accessibility criterion allowed up to 1 contact in the open state, and the criterion for a broken H-bond was a Cβ−Cβ displacement of > 2.0 Å from the distance in the native state. In addition, we also evaluated the combined criteria in which the residues were considered to be in the closed state in a particular conformation if they had either more than 1 native contact or maintained an H-bond according to the above criterion and otherwise they were considered to be in the open state. The comparative performance of the different predictions was evaluated by the average of the residuals between predicted and experimental ln Pf values (Figure 4). In general the performance of predictions using individually the accessibility and H-bonding criteria was similar for each protein. However, in all cases the combined criteria performed somewhat better (Figure 4). This parameter ranged between 2 and 3 k_BT for the three proteins. These results buttress the idea that both the accessibility and H-bonding properties are important in determining the exchange kinetics^30,35-39.

Figure 4.

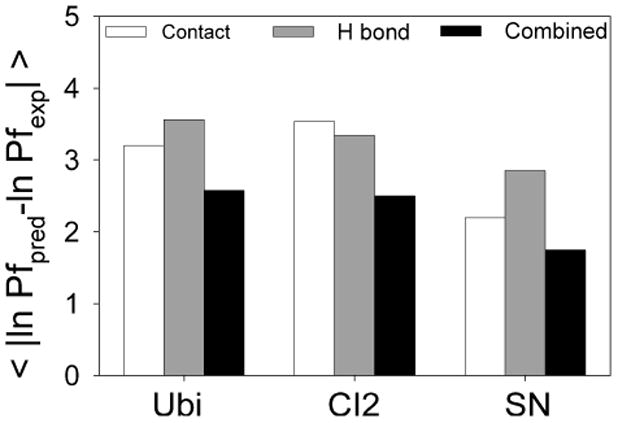
Performance of criteria used to predict the protection factors for ubiquitin, CI2, and SN. The evaluation was carried out based on the average of the residual between the experimental and predicted ln Pf for all residues within each protein. The figures show the comparison between the predictions using solely the accessibility criteria (open state: <= 1 native contact, white bars) or the H-bonding criteria (open state: displacement > 2.0 Å, grey bars), and the combined criteria that uses both properties (black bars).

Figure 5 shows the comparison between the experimental and predicted ln Pf patterns for the three proteins, calculated at the experimental temperature using the combined criteria.

Figure 5.

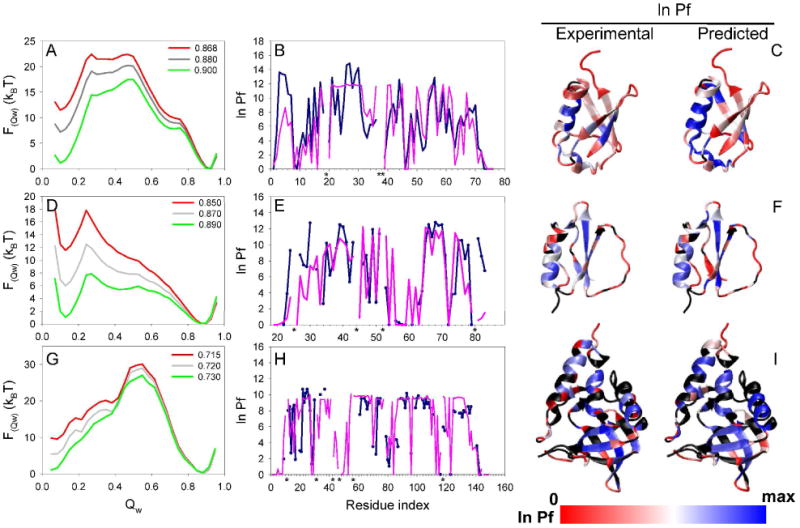
Simulated and experimental properties of ubiquitin (panels A-C), CI2 (panels D-E), and SN (panels G-I). The first column shows the free energy as a function of the global reaction coordinate Qw derived from the simulations of each protein at the Tf and extrapolated to different temperatures (green line is the sampling temperature whereas the red line represents the extrapolated experimental temperature). The plots in the second column show the comparison of the experimental (blue line) and predicted (purple line) HX patterns for each protein at the experimental temperature. Proline residues are labeled with a black asterisk. The third column shows the structure of each protein colored by the value of the experimental and predicted ln Pf (blue: high protection, white: medium protection, red: low or no protection. The residues colored in black represents the ones with not reported experimental Pf. Sampling was carried out at or near the Tf, and the results were extrapolated to the experimental temperature (Simulation temperature|Extrapolated temperature in reduced units: 0.900|0.868, 0.890|0.850, and 0.730|0.715, for ubiquitin, CI2, and SN, respectively). Calculation of the predicted protection factor was done as described in Methods using the combined accessibility and H-bonding criteria. The analysis corresponds to the same simulations as the ones presented in Figure 4.

The agreement between the predicted and experimental ln Pf was good for the three proteins, in spite of the simplicity of the model used. The model was able to predict the distribution of highly and poorly protected regions along the structure of the proteins studied, as evidenced in Figure 5. We were able to properly discriminate ∼80% of the residues with ln Pf higher and lower than 5 k_BT. The correlation coefficient (R) between the predicted and experimental parameters was ∼0.7 for all proteins (Figure 6). To evaluate the quality of these correlations, we compared the three ubiquitin experimental data sets to each other to determine the variability of the experimental measurements. This analysis gave correlation coefficients (R) that ranged between 0.86 and 0.96.

Figure 6.

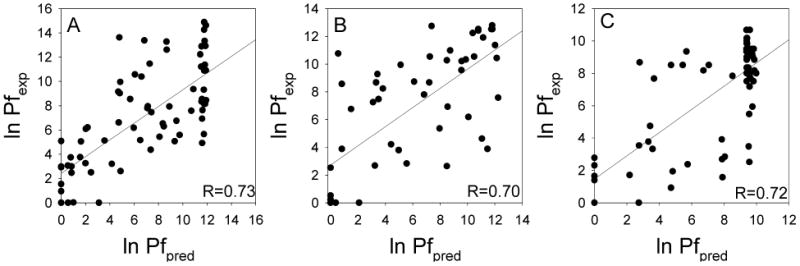
Linear correlation analysis between the experimental and predicted protection factors of ubiquitin (panel A), CI2 (panel B), and SN (panel C). The data correspond to the one used in Figure 5. Only residues with reported experimental Pf were used for the analysis.

We expect that the performance of the predictions will depend to some extent on the level of description i.e. coarse graining used in the models. In principle, all atom models could allow the analysis of solvent accessibility and H bonding parameters in a more precise manner than our coarse grained model. These improvements, however, would be obtained at the expenses of simulation time and sampling completeness.

In the simulations, WHAM was used to obtain the proper Boltzmann distribution of all the sampled states as a function of temperature. The highest ln Pf predicted for most residues at a given temperature was lower or equal to the global stability of each protein at the same temperature. For example, compare the free energy difference between the native and unfolded state basins of ubiquitin at the experimental temperature (red curve in Figure 5A), with the predicted ln Pf pattern of the protein at the same temperature (magenta curve in Figure 5B). This result, that all residues become open in the unfolded state, sets an upper limit for the free energy difference between the open and closed states⁴⁰.

Structural properties of residues correctly versus not correctly predicted

In spite of the similarity between the experimental and predicted Pf patterns of the three proteins, we observed some quantitative differences in particular regions. In order to evaluate the reasons for these anomalies, we divided the residues in categories depending on the difference between their experimental and predicted protection factor, and compared structural properties between each category. Residues were classified as anomalous (∼20%) if their predicted ln Pf varied by more than 4 k_BT from the experimental value, and further subdivided in two groups depending on whether the protection factor was under or overestimated (colored in red and yellow, respectively, in Figure 7). The well-predicted residues (∼80%) were also subdivided into two groups; those with an experimental ln Pf below 5 k_BT, and those with an experimental ln Pf above 5k_BT (colored in cyan and blue, respectively, in Figure 7).

Figure 7.

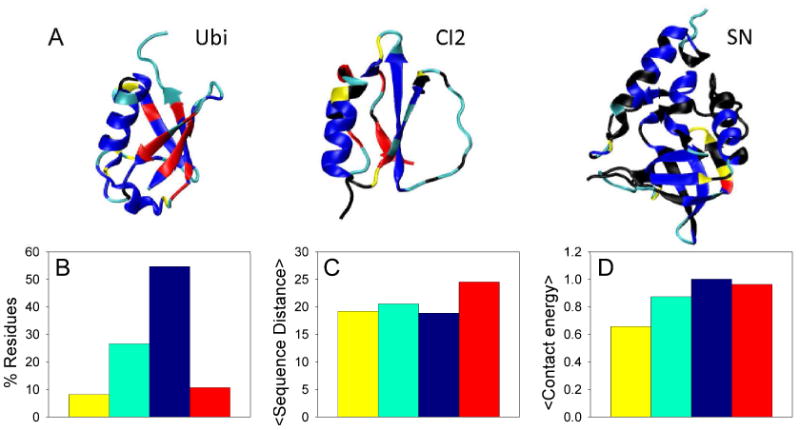
Structure of Ubi, CI2, and SN colored by categories defined based on the difference between predicted and experimental protection factors (panel a). Residues were classified as non-anomalous if their predicted ln Pf was within 4 k_BT of the experimental value, and anomalous otherwise. The non-anomalous residues were subdivided in two groups corresponding to low/none protection (cyan) and moderate/high protection (blue), depending on whether the experimental ln Pf was lower or higher than 5 k_BT. The anomalous category was subdivided in two groups depending if the predicted ln Pf was below (red) or above (yellow) 4 k_BT from the experimental value. The predicted values correspond to the ones obtained from the analysis using the combined accessibility and H-bonding criteria (same as Figure 5). Residues colored in black correspond to residues with no reported protection factor. A variety of structural properties measured for the residues corresponding to each category are evaluated in panels B, C, and D. The bars are colored depending on the color used for each category in panel A. The Figure shows the % of residues in each category (panel B), the average sequence distance between contacting residues (panel C), and the average contact energy corresponding to the AMW potential (panel D). The contact energy of each category is expressed relative to the energy of the blue category. Higher energy means more stable.

The average structural properties of the residues in each category were analyzed (Figure 7). This analysis revealed that the residues for which the protection factor was under predicted (red category) have a high contact order compared to the other groups (Figure 7C). These residues, found mainly in β-sheet regions in ubiquitin, and CI2 (Figure 7A), seem to be more stable than our simulations indicate. The reason for this behavior might be a relative penalization of long range over short range interactions produced as a consequence of an increased backbone flexibility in the model used.

On the other hand, residues with over estimated protection factors showed some heterogeneity and uneven distribution of contact energies along the protein structure. In this regard, it has to be noted that the Hamiltonian used in the predictions had a homogeneous contact potential such that all the native contacts were assigned the same strength. This kind of model was chosen to evaluate the contribution of the topology to the dynamics of the protein structure. To assess the contribution of relative contact energy, we evaluated the average strength of the contacts within each group using the AMW interaction parameters, based on a statistical contact potential optimized by maximization of the energy gap between native and molten globule like configurations of a set of training proteins⁴¹. This analysis indicated that the residues with over predicted protection (shown in yellow in Figure 7A) correspond to residues with a contact energy lower than the average (Figure 7D). The stability as well as the predicted protection factor of many of these residues, found in loops and irregular backbone configurations that are most likely dynamic, would decrease if heterogeneity was taken into account.

The analysis presented above illustrates how the comparison between the predicted and experimental protection factors could guide improvements and tuning of the energy functions and parameters used in the simulations.

Conclusions

In this work we examined a simple model to connect the structural fluctuations observed in molecular dynamics simulations of perfectly funneled energy landscapes and experimental data of the dynamics for HX. Coarse grained structure-based model simulations allow an extensive and fast sampling of the conformational space. Using these models we were able to simulate entire folding trajectories from fully unfolded configurations to the native state. This sampling advantage over full atomistic and frustrated models was even further exploited by using the umbrella sampling technique. The results allow a direct assessment of the free energy cost for local unfolding events connected both to small and large conformational fluctuations, and the calculation of protection factors based on a probabilistic analysis of the exchange competent and incompetent states of each residue assuming an EX2 mechanism.

We were able to predict the general features of the HX pattern under highly native conditions of ubiquitin, CI2, and SN. The agreement between the predicted and experimental results was striking despite the simplicity of the model in which only a homogenous contact potential was used. Only native interactions were considered whereas non-native interactions were not allowed, preventing local energy traps. Therefore, the folding mechanism as well as the global and local fluctuations only depend on topological factors. The results of the predictions presented in this work suggest that the protein topology plays a dominant role in determining the local stability of proteins. This seems to be a consequence of the minimal energetic frustration of the overall energy landscape.

A variety of computational approaches have been developed that use HX data to help the modeling of protein ensembles ^37,42-45. Others have predicted protection factors based on structural properties ^46,47 and have attempted to correlate the fluctuations observed in molecular dynamics simulations with HX data ^48,49. In our work, we have attempted to predict HX protection factors based on the evaluation of the probability of the open and closed states of each residue in simulations that use an extremely simple energy function. Vendruscolo and colleagues took an inverse approach and used the experimental protection factors as restraints to guide Monte Carlo³⁷ and molecular dynamics simulations⁴³ for the characterization of structural intermediates, based on an empirical correlation between the protection factors and the number of contacts along with H-bonds of native proteins. Similarly, Dixon, Dokholyan and colleagues used hydrogen exchange data to tune the strength of the interaction parameters of the focal adhesion targeting domain on a structure-based model simulation⁴⁵. In both of these approaches, the predicted protection factors were calculated based on average structural properties of each residue along the simulations (i.e. the number of contacts and H-bonds or the energy of the interactions). In our approach we calculate the probability of open and closed states directly from simple structure-based models that allow sampling of rare opening events. The approach presented in this paper also differs from that described by Hilser using COREX⁴⁷ in the sampling procedure and the method used to evaluate the probability of the states. Hilser and colleagues used a combinatorial algorithm to systematically generate a large ensemble of conformational states, and an empirical parameterization of free energy to evaluate the probability of each microstate. By contrast, the method presented in this paper uses a coarse grained purely structure-based simulation to sample the conformational space on a funneled and totally unfrustrated landscape. Our analysis allows a direct evaluation of the probability of open and closed states from the trajectories using WHAM to obtain the Boltzmann distributions.

The results from simulations using different criteria based on the accessibility (approximated by the number of contacts of each residue) and the distance increase between H-bonded residues clearly show that a significant distortion of the local environment of the residues must occur to generate the exchange-competent state. Indeed, the Cβ of almost all neighboring residues must move more than 6.5 Å apart, and the distance between the Cβs of residues H-bonded in the native state must increase more than 2 Å. In spite of the well documented effect of hydrogen bonding, it is important to note that we were able to accurately predict the general features of the protection pattern without any explicit consideration of H-bond energy or geometry. This result suggests that the structural change needed for the H-bonded residues to become exchange-competent depends much more on the stability of the local environment than it does on the detailed energetic and microscopic fluctuations of the H-bonded interaction per se. Our analysis supports the idea that the environment has the dominant role in determining the stability of the H-bond. This approach may allow a deeper understanding of the HX process that goes beyond structural categorization yielding new information about the kinetics of formation of the open (exchange-competent) state and the size of the associated fluctuations.

Methods

HX experimental data

Ubiquitin has been extensively studied by HX under native conditions both by D₂O dilution experiments followed by HSQC at pH 3.5²³, 5.8²⁴, and 6.2²⁵ (measuring rates for the slowly exchanging amide protons) and phase-modulated clean chemical exchange (CLEANEX-PM) in the 5.5-10.0 pH range²⁶ (measuring rates for the rapidly exchanging amides). For comparison with our simulations, all the experimental results at different pHs were scaled to pH 5.8 to account for the different experimental conditions. We then averaged the ln Pf of the three sets and included the values obtained from CLEANEX-PM experiments in the 5.5-10.0 pH range. For SN and CI2 we also combined results for slow and fast exchanging amide protons. We supplemented the information obtained from HSQC proton-deuterium exchange experiments (measured at pH 5.5 for SN³³, and pH 5.3-6.8 for CI2³²) with WEX II-FHSQC (pH 6.03-7.03 for SN³⁴) and CLEANEX-PM measurements (pH 5.5-10.0 for CI2²⁶), assuming no significant change in the local stability of the proteins in the pH range used. In SN, residues 33, 77, 98, 113, 115, and 120 were discarded from the analysis because of possible contribution of alternative magnetization transfer pathways. The global stability of the proteins used in our analysis was based on the global stability reported for each protein at the conditions of the HSQC D₂O dilution experiments or similar (Ubiquitin: 11-12 k_BT ^28,29, SN: 10 k_bT ³³, and CI2: 11.5 k_BT ³².

Model - AMH-Gō Hamiltonian

The Gō-style Hamiltonian that we used for the simulations has been described previously^50,51. It has two energy terms that evaluate the geometry of the backbone and the contacts between residues.

$$H=H_{\mathit{\text{backbone}}}+H_{\mathit{\text{na}}}$$

This energy function applies to a reduced set of coordinates of the heavy atoms of the backbone, Cα, Cβ, and O. In this reduced description, the position of the N and C' carbons can be calculated assuming ideal protein backbone geometry.

The backbone potential described in detail previously⁵⁰ includes many terms that ensure that the backbone adopts physically allowable conformations.

The H_na energy depends on Gaussian interaction terms for native contact pairs, and is given by

$$H_{\mathit{\text{na}}}=–\frac{1}{2}\sum _i{\left|E_i\right|}^p$$

where

$$E_i={\sum _j{\epsilon }_{\mathit{\text{ij}}}\left(r_{\mathit{\text{ij}}}\right)=–\sum _j\left|\frac{\epsilon }{a}\right|}^{1/p}\theta \left(r_c–r_{\mathit{\text{ij}}}^N\right){\gamma }_{\mathit{\text{ij}}}\times \text{exp}\left(–\frac{{\left(r_{\mathit{\text{ij}}}–r_{\mathit{\text{ij}}}^N\right)}^2}{2{\sigma }_{\mathit{\text{ij}}}^2}\right)$$

The indices i and j run over Cα and Cβ atoms, and r_ij is the distance between atoms i and j. The parameter p is the power of nonadditivity. Increasing p tends to more extensively many body interactions, resulting in additional cooperativity and an increased barrier of the folding transition. In our simulations we used a moderate value for the non additivity parameter which was previously shown to increase the correlation of simulations with experimental measurement of kinetics⁵². We used p=2.5 for all proteins. The r_c, cut-off parameter, ensures via a step-function, $\theta \left(r_c-r_{\mathit{\text{ij}}}^N\right)$, that there are only interactions between sites closer than this distance in the native structure (we used r_c = 8 Å). The well width, σ_ij = |i − j|^0.15 Å, was set to give slightly broader wells for interactions between sites separated in sequence. In the homogenous model used in this work all interaction weights γ_ij where set to 1. The unit of energy is denoted ε, and is defined in terms of the native state energy excluding backbone contributions via: ε= H_na/4N, where N is the number of residues. This last equivalence is ensured if the normalization constant a is defined as

$$a=\frac{1}{8N}\sum _i{\left|\sum _j{\gamma }_{\mathit{\text{ij}}}\theta \left(r_c‐r_{\mathit{\text{ij}}}^N\right)\right|}^p$$

Temperatures are quoted in terms of the reduced temperature T̃ = k_BT/ε. Distances are in units of angstroms.

The simulations were based on the PDB IDs 1UBQ⁵³ chain A (human ubiquitin), 2CI2⁵⁴ chain I (chymotrypsin inhibitor 2 from barley seeds), 1SNP⁵⁵ chain A (Staphylococcal nuclease) including missing residues 45-50 repaired with Jackal⁵⁶.

Sampling

To analyze the local stability of proteins and compare this property with HX data, we performed molecular dynamics simulations and analyzed the probability and free energy of microstates using the multiple histogram technique^27,57. For an efficient sampling of the phase space of the protein conformations, we performed umbrella sampling by setting up of a series of runs using different biasing potentials added to the Hamiltonian, each acting to constrain the protein to a chosen region of the conformational space.

$$H_s=H+V_s\left(\mathit{\text{Qw}}\right)$$

The functions V_s(Qw) are well-shaped potentials centered on different values of the order parameter Qw to give a good sampling of phase space along the reaction coordinate of interest, with care taken that “adjacent” simulations have overlap in the regions sampled. We used V_s(Qw)=5×10⁴ ε (Qw-Q₀)⁴, with Q₀=0.05, 0.10, …, 1.00. The reaction coordinate used, Qw, involves a sum over all pairs (except nearest-neighbors) of Cα atoms, and ranges between 0 (completely unfolded) and 1 (native reference model). Note that in many cases the intermediate values of Qw are slightly lower (∼0.1 unit) than the frequently used global order parameter Q that represents the fraction of native contacts.

$$\mathit{\text{Qw}}=\frac{2}{\left(N‐1\right)\left(N‐2\right)}\sum _{i<j–1}\text{exp}\left(–\frac{{\left(r_{\mathit{\text{ij}}}–r_{\mathit{\text{ij}}}^N\right)}^2}{2{\sigma }_{\mathit{\text{ij}}}^2}\right)$$

The simulations centered on values of Q₀ between 0.05 and 0.50 were started from extended conformations, whereas the ones centered on values of Q₀ above 0.50 were started from the native structure. Typically, a set of simulations included 20 runs centered at different values of Q₀.

In a first stage of the analysis a set of short simulations of 10000 time steps were carried out at different temperatures (0.80, 0.85, 0.90, 0.95, 1.00 T̃), to approximately locate the folding temperature, Tf. Then, at the putative Tf, 10 sets of simulations of 20000 time steps were performed. The biasing energy applied was taken into account in the free energy calculations (see below) and unbiased probabilities were thus obtained.

Free energy calculations

We used the WHAM analysis²⁷. During each simulation N_s^obs sample structures were taken at regular time intervals (50 time steps). For each simulation a total of 400 samples were taken. The first 40 samples of each simulation run were discarded to help ensure that the system reached the equilibrium before samples were entered into the free energy calculation. Given that each set of umbrella sampling included 20 simulations centered at different values of Q, over 7200 independent samples were measured per set. A histogram N_s(H,Q) of all simulations was created, and the density of states n(H,Q) of the system was calculated from the histograms

$$n\left(H,Q\right)=\sum _s{w}_s\left(H,Q\right)\frac{N_s\left(H,Q\right)}{N_s^{\mathit{\text{obs}}}}{Z}_s\left({\beta }_s\right)\text{exp}\left({\beta }_s\left(V_s\left(Q\right)+H\right)\right)$$

Here s labels the simulation, β_s = 1/k_BT_s is the inverse of the simulation temperature, and W_s represents a weighting function defined as

$$\begin{array}{ll}{w}_s=\frac{A_s^{–2}}{\sum _m{A}_m^{–2}}\hfill & A_s^{–2}=\frac{n\left(H,Q\right)}{N_s^{\mathit{\text{obs}}}}{Z}_s\left({\beta }_s\right)\text{exp}\left({\beta }_s\left(V_s\left(Q\right)+H\right)\right)\end{array}$$

In this function m runs over all simulations. The density of states and the weighting function are functions of the partition function Zs. The partition function, on the other hand, is also a function of the density of states,

$$Z_s\left({\beta }_s\right)=\sum _{H,Q}n\left(H,Q\right)\text{exp}\left(–{\beta }_s\left(V_s\left(Q\right)+H\right)\right)$$

This set of equations for n(H,Q)and Zs self consistently determine n(H,Q) to within a multiplicative constant, and hence the free energy to within an additive constant.

$$F\left(Q,T\right)=–k_{B}T\text{log}\left(\sum _{H,Q}n\left(H,Q\right)\text{exp}\left(–\frac{H}{k_{B}T}\right)\right)$$

Evaluation of the open and closed conformations

For the evaluation of the open and closed conformations of each residue along the simulations we evaluated both the number of native contacts (as an approximation of the accessibility of residues) and the distance between residues H-bonded in the native state (as an approximation of the H-bond fluctuations). These criteria were applied independently or in combination.

1. Accessibility criteria

Residues were evaluated for accessibility at each snapshot during the simulations as approximated by the calculation of their total number of native contacts (Q_i). This parameter is inversely related to the global accessibility of the residues.

$$\begin{array}{c}{Q}_i=\sum _j{q}_{\mathit{\text{ij}}}\\ q_{\mathit{\text{ij}}}=0.5\left(1+\text{tanh}\left(5\left(r_{\mathit{\text{cutoff}}}-r_{\mathit{\text{ij}}}\right)\right)\right)\end{array}$$

The total number of native contacts for residue i in any given conformation corresponds to the sum of the pairwise contacts (q_ij), evaluated for all residues j in contact with residue i in the native structure. The q_ij value was calculated using a tanh function that switches between 0 and 1 in a very steep manner depending if the pairwise distance between the Cβ of the interacting residues is lower than a certain cut-off established as a threshold. In the case of Gly residues the q_ij contact was evaluated from their Cα. The evaluation was done solely for native interactions defined by the analysis of the corresponding structure using a cut-off distance of 6.5 Å.

The analysis of Q_i along the simulations allowed the calculation of the probability of native contacts for every residue. The different structural criteria used to discriminate open and closed conformations (from 0 to 4 native contacts allowed in the open state) were applied homogenously to all residues.

In our model, only native interactions are favorable, non native interactions do not contribute any stabilizing energy so residues that are not making contacts in the native state collide with each other but do not remain bound by any force. Therefore non native contacts are very improbable, and are not expected to significantly contribute to the predicted protection factors in case they were considered.

2. H-bonding criteria

For the evaluation of the H-bond fluctuations we first identified the backbone amide H-bonds in the native structure of the protein using the program, Chimera ⁵⁸. For each snapshot, the distance between the Cβ of the interacting pair was compared to their distance in the native structure. For Gly residues the distance was evaluated from their Cα. The “displacement” was defined as the increase or decrease in the H-bond distance from the native state.

$$\mathit{\text{displacement}}=r_{\mathit{\text{ij}}}–r_{\mathit{\text{ij}}}^N$$

The analysis of the displacement along the simulations allowed the calculation of the probability of the residues to be in the open or closed state. When the displacement was higher than a certain amount, the H-bonded interaction was assumed to be broken and the residue to be in the open state, and in the closed state otherwise. A variety of different displacements from 0.2 to 6 Å were evaluated for their performance.

3. Combination of H-bonding and accessibility criteria

Residues were considered to be in the closed state either when they correspond to an H-bonded pair when the Cβ-Cβ distance had not increased more than 2Å, or if they retained more than one native contact.

Calculation of the predicted protection factor

For evaluation of the probability of the open and closed states for each residue we carried out a two dimensional WHAM over Qw and the local order parameters L_i (Q_i or displacementi). The joint probabilities P(Qw,L_i) thus obtained were then integrated over the global reaction coordinate and the regions of the local order parameter corresponding to the open or closed states (defined by the structural criteria chosen) obtaining the probability of the residue to be in the open or closed conformation. Then, the predicted protection factor was calculated by

$$\text{ln}{\mathit{\text{Pf}}}_{\mathit{\text{pred}}}=\text{ln}\left(1+\frac{P_{\mathit{\text{cl}}}}{P_{\mathit{\text{op}}}}\right)$$

This equation is valid under the steady state approximation (k_cl>k_ch and/or k_cl>k_op) and EX2 (k_cl>k_ch) conditions. This is a good assumption for native proteins below or near neutral pH where k_cl > k_ch for most residues. However, care should be taken in the analysis of unstable regions where this assumption is uncertain.

Average sequence distance

The average sequence distance per contact⁵⁹ for regions along the structure of Ubi, CI2 and SN was calculated by:

$$<\text{Sequence Distance}{>}_n=\frac{1}{c}\stackrel{c}{\sum \Delta }{S}_{i,j}$$

where c is the total number of contacts of region n, and ΔS_i,j is the sequence separation, in residues, for all contacting residues i and j. The analysis was based on the 6.5 Å radial distribution of Cβ-Cβ contacts in the native structure. The contacts for glycine residues were calculated from the Cα atom.

Abbreviations

HX

Hydrogen exchange

Pf

protection factor

NMR

nuclear magnetic resonance

CI2

chymotrypsin inhibitor 2 from barley seeds

SN

Staphylococcal nuclease

Tf

folding temperature

WHAM

weighted histogram analysis method

AMH

Associative Memory Hamiltonian

AMW

AMH with water mediated contacts

Qi

number of native contacts per residue