Locating an extracellular K⁺-dependent interaction site that modulates betaine-binding of the Na⁺-coupled betaine symporter BetP

Abstract

BetP, a trimeric Na⁺-coupled betaine symporter, senses hyperosmotic stress via its cytoplasmic C-terminal domain and regulates transport activity in dependence of the cytoplasmic K⁺-concentration. This transport regulation of BetP depends on a sophisticated interaction network. Using single-molecule force spectroscopy we structurally localize and quantify these interactions changing on K⁺-dependent transport activation and substrate-binding. K⁺ significantly strengthened all interactions, modulated lifetimes of functionally important structural regions, and increased the mechanical rigidity of the symporter. Substrate-binding could modulate, but not establish most of these K⁺-dependent interactions. A pronounced effect triggered by K⁺ was observed at the periplasmic helical loop EH2. Tryptophan quenching experiments revealed that elevated K⁺-concentrations akin to those BetP encounters during hyperosmotic stress trigger the formation of a periplasmic second betaine-binding (S2) site, which was found to be at a similar position reported previously for the BetP homologue CaiT. In BetP, the presence of the S2 site strengthened the interaction between EH2, transmembrane α-helix 12 and the K⁺-sensing C-terminal domain resulting in a K⁺-dependent cooperative betaine-binding.

The Na⁺-coupled betaine symporter BetP from Corynebacterium glutamicum, a member of the betaine-carnitine-choline transporter (BCCT)-family, regulates its transport rate according to the external osmolality (1). Together with OpuA, an ABC-transporter from Lactococcus lactis (2) and the H⁺-solute symporter ProP from Eschericha coli (3), BetP became a paradigm for regulated osmolyte transport. All three transporters have been studied in detail by biochemical, biophysical, and genetic approaches to understand their osmoregulatory function (4, 5). However, BetP holds a special position within the group of these intensively studied osmolyte solute transport systems because its structure has been solved (1, 6). BetP responds to hyperosmotic osmotic stress with instant regulation of its transport activity. Thereby two types of stimuli trigger activity regulation: (i) an increased cytoplasmic K⁺-concentration raising above a threshold of 100 mM, which is usually achieved in elevated medium osmolality (7, 8), and (ii) a change in membrane properties, e.g., the surface charge density as well as the fatty acid composition of the membrane (9). The C-terminal domain of BetP facing the cytoplasm consists of 55 amino acids (aa) and is involved in sensing and regulation upon hyperosmotic stress as shown by stepwise truncation and amino acid scanning mutagenesis (10). Truncating the C-terminal domain by 45 aa resulted in BetP deregulation and truncation of the N-terminal domain shifted the activation profile to higher osmolalities (11). The C-terminal domain functionally interacts also with particular loops at the cytoplasmic side of BetP. The crystal structure of BetP (12) presents the C-terminal domain as a long α-helix that reaches towards the adjacent protomer within the BetP trimer, where it interacts with cytoplasmic loops 2 and 8. These interactions within the trimer might play a crucial role in transport regulation of BetP allowing adjacent protomers to influence their functional state (12, 13). BetP exhibits the LeuT-overall fold of two inverted structurally related repeat domains of 5 transmembrane α-helices each, which was first reported for the leucine transporter LeuT (14). The two domains are tightly intertwined and residues from both contribute to the coupled transport of the substrate and cosubstrate (15). Structural insights of BetP provide different transporter conformations without and in complex with the substrate (12, 13). However, these insights were obtained in the absence of the activating K⁺ and therefore might represent only a snapshot of the not fully activated BetP trimer. To understand the molecular mechanisms of regulation we need to know how K⁺-binding establishes diverse interactions that modulate the functional states of BetP.

In the past, single-molecule force spectroscopy (SMFS) was applied successfully to several transmembrane α-helical and β-barrel membrane proteins to quantify their molecular interactions and locate these onto the primary, secondary, and tertiary structure (16–24). Dynamic SMFS (DFS) probes these interactions at different force-loading rates and reveals their kinetic parameters (25, 26). Using both techniques we quantified how the interactions, transition state, lifetime, free energy difference, and the mechanical properties of structural regions of BetP change upon Na⁺-, K⁺-, and betaine-binding. Surprisingly our data indicate the formation of a periplasmic second substrate-binding (S2) site that is involved in K⁺-dependent activation of BetP.

Results and Discussion

SMFS Reveals Distinct Interaction Patterns of BetP.

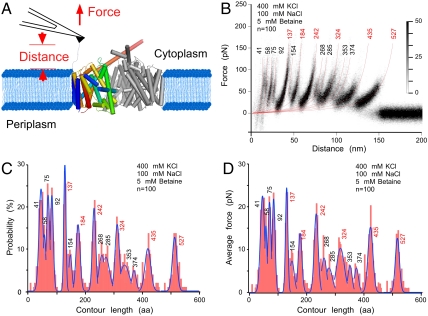
To localize interactions in BetP by SMFS we first probed BetP reconstituted into E. coli lipid liposomes and set into an up-regulated state in the presence of the substrate betaine, of the coupling ion Na⁺ necessary to energize betaine transport and of K⁺ that activates BetP at concentrations above 100 mM. Membrane protein patches were located using atomic force microscopy (AFM) imaging (27). To attach the BetP polypeptide, the AFM stylus was pushed towards the membrane protein at 0.8–1 nN for ≈500 ms (Fig. 1A). Subsequently, the stylus was retracted recording a force-distance (F-D) curve (Fig. S1). This retraction applied an external force that mechanically stressed the polypeptide and induced the unfolding of the symporter (28). We analyzed only F-D curves, whose lengths corresponded to BetP that was attached by the N-terminal domain to the AFM stylus and fully unfolded and stretched (see Materials and Methods, SI Text). The F-D curves showed characteristic saw-tooth like patterns with each force peak characterizing an unfolding event of BetP (Fig. S1). The sequential unfolding process ends after the last structural segment has been unfolded and extracted from the membrane. All F-D curves (see also Materials and Methods) were superimposed to observe their dominant features (Fig. 1B) and six pronounced force peaks (high density peaks labeled with red numbers) became prominent. Fitting every force peak of every F-D curve with the worm-like-chain (WLC) model (red curves in Fig. 1B) revealed average contour lengths of the stretched polypeptide (28, 29). Force peaks (fp) at contour lengths of 41, 58, 75, 92, 137, 154, 184, 242, 268, 285, 324, 353, 374, 435, and 527 aa are clearly visible in the superimposition (Fig. 1B). The probability at which individual fp were detected is shown as histogram (Fig. 1C). Measuring the magnitude of each fp provided the strengths of the interactions that have been established. A second histogram maps the average force over the contour length of BetP (Fig. 1D).

Fig. 1.

Single-molecule force spectroscopy of BetP. (A) One single BetP protomer from the trimer reconstituted into a membrane of native E. coli lipids was nonspecifically attached to the stylus of an AFM cantilever. Increasing the distance between stylus and membrane establishes a force, which induces stepwise unfolding of BetP. (B) Superimposition of force-distance (F–D) curves recorded upon unfolding of individual BetP protomers being set in an up-regulated state in presence of betaine and K⁺ (400 mM KCl, 100 mM NaCl, 5 mM betaine, 50 mM Tris-HCl, pH 7.5). Every reproducibly occurring fp (increased density) was fitted using the WLC model to reveal the contour length of the unfolded and stretched polypeptide. Numbers at the end of each WLC fit give the numbers of amino acids the stretched polypeptide. Major fp occurring at a probability of > 80% were labeled red. At close proximity to the membrane (< 25 nm) four partially overlapping peaks occurring were detected. All F-D curves superimposed (A) were recorded at a pulling velocity of 100 nm/s. Histograms show probability (B) and average forces (C) of fp detected at certain contour lengths. Blue lines represent Gaussian fits of histograms. n gives the number of F-D curves superimposed and analyzed.

Interactions at Structural and Functional Key Roles.

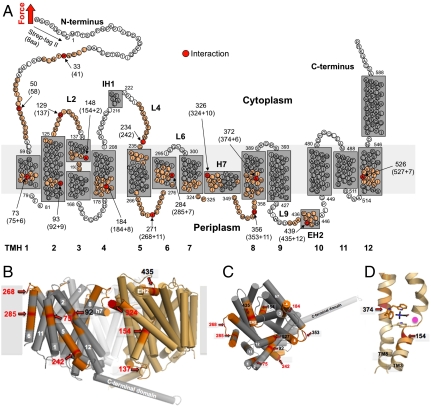
To localize the interaction on the BetP structure we clarified from which terminal end BetP was mechanically pulled and unfolded. SMFS on BetP mutants having either C- or N-terminally truncated ends showed that WT BetP preferably attached via the N-terminal end to the AFM stylus (SI Text, Fig. S2, S3). The contour length of each fp provides the length of the unfolded polypeptide tethered between AFM stylus and a structural unfolding intermediate formed by BetP. This length localizes interactions that stabilized structural regions against unfolding (Fig. 2A) (28). In some cases these interactions had to be assumed to lie in the membrane or at the periplasmic surface located opposite to the pulling AFM stylus. In these cases (indicated by “+” in Fig. 2A) the contour length had to be corrected by the so-called membrane compensation procedure (SI Text) that locates the interaction in the membrane or at the periplasmic surface.

Fig. 2.

Mapping interactions on the secondary structure of BetP. (A) Interactions mapped onto the secondary structure. Red colored aa highlight interactions detected in Fig. 1. aa colored at less intensity approximate the full-width-at-half maximum (FWHM) of the average fp. Numbers at arrows give the structural position of the interaction detected. This structural position corresponds to the N-terminal Strept-tag II (8 aa) subtracted from the average contour length as revealed from the WLC fitting of individual fp (given in brackets). In case the interaction had to be assumed to lie within the membrane or at the opposite of the membrane a certain number of aa were added (indicated by +) to the contour length to structurally locate the interaction. This procedure called “membrane compensation” (16) is described in the SI Text. All 12 transmembrane α-helices (TMHs) of BetP were labeled with bold numerals. The short helices in loop4 and loop9 at the cytoplasmic and periplasmic sides were denoted IH1 and EH2, respectively. The amphiphatic α-helix H7 is thought to face the periplasm and to make contacts with TMH1, TMH2, and TMH9 and H7 of the other two BetP molecules forming the BetP trimer (12). (B) Side view on the BetP trimer (PDB entry code 2WIT) showing two adjacent protomers in cylinder presentation indicating molecular interaction sites detected by SMFS. TMHs are numbered in white and the contour lengths of fp are given in red or black. One protomer is colored in gray with labeled interaction sites in red according to (A). The membrane is shown as gray rectangle. (C) Top view on one protomer from the periplasmic side. (D) Central substrate-binding site of BetP with a betaine molecule in stick presentation colored in black located close to two interaction sites in TMH3 and TMH8.

The majority of interactions detected by SMFS could be assigned to structurally important regions of BetP (Fig. 2 B–D) involved in: (i) hydrophobic interactions with the membrane, (ii) interhelical hydrophobic stabilization of transmembrane α-helices (TMHs), (iii) stabilization of the trimeric interface, and (iv) substrate-binding. Beginning from the N-terminal end we locate interactions around Pro33 (fp41 aa) and Glu50 (fp58 aa) of the N-terminal domain (Fig. 2) that is suggested to interact with the C-terminal domain while up-regulating the BetP transport activity (8, 11). Fp75 aa locates an interaction that stabilizes TMH1. Fp92 aa locates an interaction in TMH2 being close to Trp101, which is together with Asn331 in h7 the crucial residue for trimerization (13). Fp137 aa locates an interaction at loop2 that plays an important role by providing Asp131, the charged residue that interacts with the C-terminal domain of an adjacent protomer. TMH3 (fp154 aa) and TMH8 (fp374 aa), both of which have a key role in transport, establish interactions close to residues involved in substrate and cosubstrate coordination (Fig. 2D). TMH4 (fp184 aa), which establishes an interaction around Thr184, harbors aromatic residues Trp189, Trp194, and Tyr197 that are involved in substrate coordination (12). Fp242 locates interactions around Trp233 of cytoplasmic loop4 and fp268 around Ile270-271 of periplasmic loop5. Both loops connect to the functionally important scaffold helix TMH5. Interactions stabilizing TMH6 are detected by fp285 aa. Fp324 aa locates interactions to h7 that stabilize the BetP trimer interface via Leu330-Trp101 of TMH2 and Pro325-Thr419 of the bundle helix TMH9. Similarly, fp353 aa locates at loop7 an interaction which contributes to contacts (Asp356-Tyr166) between protomers of the BetP trimer (13). Interactions stabilizing the periplasmic helix EH2 are detected by fp435 aa. Fp527 aa locates an interaction halfway across TMH12.

These interactions detected by SMFS may not be considered as a complete picture of all intermolecular interactions established in BetP. The functional structure of BetP is described as inverted repeat topology with two domains, TMH3-TMH7 and TMH8-TMH12, sharing the same structural fold, but being inverted with respect to each other (12, 15). The close intertwining of both structural repeat domains results in a complex interaction network between them. One may assume that after unfolding of the first repeat domain (TMH3-TMH7) the symmetry related interactions established with helices of the second repeat domain are no longer detectable. On the other hand molecular dynamic simulations show that secondary structures do not alter significantly when unfolding a membrane protein (e.g., bacteriorhodopsin) sufficiently fast from the membrane (30, 31). This lack of structural changes is because the secondary structures need time to relax. If we could detect such a relaxation the fp of the F-D curves would change position in time dependent pulling experiments. So far such structural relaxation was not detected (26, 28) (see also following experiments). Nevertheless, the fp detected upon unfolding BetP may reflect only part of all interactions related to substrate- and cosubstrate-binding (Figs. 1 and 2), while stabilizing interactions with the membrane lipids are less affected and independent of the unfolding degree.

Interactions of the Osmosensing C-Terminal Domain.

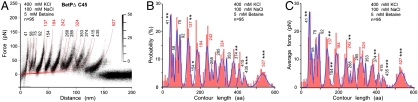
Interactions stabilizing the C-terminal domain can be deduced investigating C-terminally truncated BetP (BetPΔC45, see Materials and Methods) that are functionally deregulated and constitutively active (10). Compared to wild type (WT) BetP (Fig. 1 B–D) F-D curves recorded upon unfolding of BetPΔC45 (Fig. 3) showed interactions changing at various structural regions. Only changes passing significance tests were interpreted. Fp41 aa locating interactions at the N-terminal domain changed significantly. Changes are also observed in loop2 (fp137 aa) and TMH3 (fp154 aa) confirming that these structures are sensitive to interactions with the C-terminal domain as predicted from the X-ray structure (12). A decrease in probability and magnitude of fp242 aa points towards a possible interaction of the C-terminal domain with loop4, which contains a highly conserved, charged cluster found in BCC-transporters (6). A drastic change observed for fp527 aa suggested that truncation of the C-terminal domain changed stability of TMH12. This change is expected because the C-terminal domain stabilizes TMH12 via interaction with loop2 of the adjacent BetP protomer (12). Another drastic change was observed for fp435 aa suggesting that interactions at EH2 depend on the presence of the C-terminal domain. This finding is surprising because EH2 being located at the periplasmic surface cannot establish direct interactions with the C-terminal domain. However, the C-terminal domain affects the stability of TMH12 that establishes a putative interaction between Asp512 in TMH12 and Gly437 in EH2 (12). This link to TMH12 may transfer changes of the C-terminal domain to EH2.

Fig. 3.

SMFS spectra recorded upon unfolding of BetpΔC45 recorded in buffer solution that enables transporter activation and substrate-binding. (A) Superimpositions of 95 F-D curves. Histograms show probability (B) and average forces (C) of fp detected at certain contour lengths. n gives the number of F-D curves superimposed. F-D curves were recorded in buffer condition (400 mM KCl, 100 mM NaCl, 5 mM betaine, 50 mM Tris-HCl, pH 7.5) at a pulling velocity of 100 nm/s. fp were marked with p-values of < 0.1 (*), < 0.05 (**), and < 0.01 (***) from T-student tests that show which of the fp changes compared to WT BetP (Fig. 1) were significant.

These results confirm, that in BetP the C-terminal domain most likely interacts with the N-terminal domain, loop2, loop4, and propose the formation of an interaction between TMH12 and EH2, which depends on the presence of the C-terminal domain. Although other interactions detected by the F-D spectra changed they did not pass significance tests. In the future advanced SMFS techniques may enable to detect more subtle changes.

Interaction Network of BetP Depends on Functional Regulation.

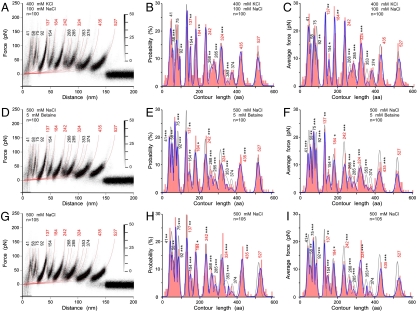
Whereas in Fig. 1 we quantified interactions of functionally up-regulated BetP in the presence of betaine, Na⁺ and K⁺, we characterized to which extent these interactions depend on the presence of K⁺ ions as stimulus regulating the transport activity of BetP. For this, we quantified interactions of up-regulated BetP (presence of 400 mM K⁺) in absence of betaine (Fig. 4 A–C) and of down-regulated BetP (absence of K⁺) and in presence (Fig. 4 D–F) and in absence (Fig. 4 G–I) of betaine. At first view the superimposed F-D spectra recorded of differently regulated BetP revealed no alterations. However, differences became evident when comparing the histograms of probabilities and average forces. Interactions detected of up-regulated BetP in the presence (Fig. 1 C–D) and absence (Fig. 4 B–C) of betaine showed significant changes at the N-terminal domain (fp58 aa), TMH2 (fp92 aa), loop2 (fp137 aa), TMH4 (fp184 aa), loop4 (fp242 aa), loop5 (fp268 aa), TMH6 (fp285 aa), and h7 (fp324 aa). These changes indicate that substrate-binding changes interactions at these structural regions. Comparing interactions of down-regulated BetP in presence of betaine and Na⁺ and in the presence (Fig. 1 C and D) and absence (Fig. 4 E and F) of K⁺ highlights to which extent K⁺ modulates intramolecular interactions. Significant changes of interactions were detected at the N-terminal domain (fp41, fp58, and fp75 aa), TMH2 (fp92 aa), loop2 (fp137 aa), loop4 (fp242 aa), loop5 (fp268 aa), TMH6 (fp285 aa), h7 (fp324 aa), loop8 (fp353 aa), and EH2 (fp435 aa). Removing betaine from the buffer solution changed the interaction probabilities and strengths within down-regulated BetP only slightly (Fig. 4 H and I).

Fig. 4.

Superimposition of F-D curves recorded at buffer conditions setting BetP into different functional states. (A–C) BetP in an up-regulated state in absence of betaine (400 mM KCl, 100 mM NaCl, 50 mM Tris-HCl, pH 7.5), (D–F) BetP in a down-regulated state in presence of betaine and in absence of K⁺ (500 mM NaCl, 5 mM betaine, 50 mM Tris-HCl, pH 7.5), and (G–I) BetP in a down-regulated state in absence of betaine and K⁺ (500 mM NaCl, 50 mM Tris-HCl, pH 7.5). All F-D curves superimposed (A, D, and G) were recorded at a pulling velocity of 100 nm/s. Histograms show probability (B, E, and H) and average forces (C, F, and I) of fp detected at certain contour lengths. Blue lines represent Gaussian fits of histogram and gray lines are Gaussian fits of the reference data shown in Fig. 1. fp were marked with p-values of < 0.1 (*), < 0.05 (**), and < 0.01 (***) from T-student tests that show which of the fp changes compared to BetP characterized in 400 mM KCl, 100 mM NaCl, 5 mM betaine, 50 mM Tris-HCl, at pH 7.5 (Fig. 1 B–D) are significant. Because the comparison of individual fp can vary for certain pulling velocities, the p-values are averages revealed from comparing the fp across all pulling velocities (Tables S1 and S2).

These results show that in presence of betaine, the up-regulation of BetP via K⁺-binding (compare Fig. 1 C and D and 4 E and F) significantly affected almost every interaction. Up-regulating BetP in absence of betaine (compare Fig. 4 B and C and H and I) demonstrated how drastically K⁺ modulates interaction probabilities and strengths. The fact that betaine changes interactions within down-regulated BetP only little (compare Fig. 4 E and F and H–I) indicates that only K⁺ changes interactions at larger scale. It was expected that interactions established at functionally important structures, especially at the cytoplasmic surface, change upon up-regulating BetP, but unexpected that interactions at the periplasmic surface (loop5, loop7, and EH2) changed, too.

In our SMFS experiments we located interactions established in BetP and observed to which extent they change upon functional regulation and substrate-binding. To elucidate to which extent these interactions modulate energetic, kinetic, and mechanical properties of the structural regions in BetP we performed DFS.

Energy Barriers, Lifetimes, and Mechanical Properties of Up-Regulated BetP.

The interaction strength stabilizing a structure against unfolding depends on the force-loading rate applied to overcome the free unfolding energy barrier (25, 32). Quantifying the average interaction strength for a wide variety of loading rates allows estimating the width and the height of the free unfolding energy barriers (Fig. S4), and how they determine the kinetic and mechanical properties of the structural region stabilized (22, 33). To investigate the effect of betaine- and K⁺-binding on the kinetic and mechanical properties of BetP, we unfolded single BetP molecules at pulling velocities of 100, 300, 600, 1,200, 2,400, and 5,000 nm/s (Fig. S5). From this DFS data we determined the most probable force (Fig. S6, S7, S8, S9) of every stable structural region of BetP mapped in Fig. 2.

The DFS spectra of every stable structural region (Fig. S10) could be approximated by one linear regime. According to the Bell-Evans model (25, 34), this indicates that one energy barrier separates the folded from the unfolded state. These energy barriers determined from the DFS data (Materials and Methods) showed ground-to-transition state distances, x_u, ranging between 0.22 to 0.58 nm in the absence of betaine and K⁺ (Table 1), comparable to the range observed for bacteriorhodopsin (35, 36), bovine rhodopsin (33), and the secondary transporters NhaA (37) and SteT (22).

Table 1.

Parameters characterizing the energy barriers (x_u, k₀, and ΔG_u) and spring constants (κ) of stable structural regions of BetP

Peak position / structural region	xu (nm)				k0 (s-1)
	400 mM KCl 100 mM NaCl 5 mM betaine	400 mM KCl 100 mM NaCl no betaine	500 mM NaCl 5 mM betaine	500 mM NaCl	400 mM KCl 100 mM NaCl 5 mM betaine	400 mM KCl 100 mM NaCl no betaine	500 mM NaCl 5 mM betaine	500 mM NaCl
41 aa / N-terminal	0.35 ± 0.08	0.34 ± 0.11	0.55 ± 0.10***	0.47 ± 0.07**	0.03 ± 0.06	0.01 ± 0.04	0.01 ± 0.01	0.01 ± 0.01
58 aa / N-terminal	0.21 ± 0.04	0.29 ± 0.04***	0.33 ± 0.09**	0.30 ± 0.09**	0.46 ± 0.50	0.05 ± 0.05*	0.08 ± 0.17	0.17 ± 0.32
75 aa / TMH1	0.20 ± 0.03	0.21 ± 0.02	0.39 ± 0.03***	0.29 ± 0.04***	0.56 ± 0.42	0.46 ± 0.26	0.06 ± 0.05**	0.37 ± 0.32
92 aa / TMH2	0.14 ± 0.02	0.26 ± 0.10**	0.22 ± 0.04***	0.22 ± 0.04***	3.04 ± 1.29	0.16 ± 0.41***	1.37 ± 1.08**	2.25 ± 1.66
137 aa / Loop2★	0.23 ± 0.02	0.25 ± 0.01**	0.25 ± 0.01**	0.26 ± 0.02**	0.18 ± 0.11	0.08 ± 0.03**	0.27 ± 0.07	0.18 ± 0.10
154 aa / TMH3	0.19 ± 0.03	0.24 ± 0.05*	0.24 ± 0.02**	0.27 ± 0.03***	0.97 ± 0.75	0.15 ± 0.21**	0.79 ± 0.32	0.59 ± 0.34
184 aa / TMH4★	0.27 ± 0.05	0.20 ± 0.01**	0.27 ± 0.06	0.32 ± 0.02*	0.17 ± 0.22	0.76 ± 0.23***	0.71 ± 0.81	0.19 ± 0.07
242 aa / TMH5★	0.23 ± 0.03	0.23 ± 0.02	0.27 ± 0.03**	0.31 ± 0.02***	0.22 ± 0.15	0.22 ± 0.13	0.30 ± 0.22	0.11 ± 0.04
268 aa / Loop5	0.20 ± 0.01	0.22 ± 0.02**	0.26 ± 0.04***	0.34 ± 0.04***	1.30 ± 0.43	0.79 ± 0.31**	1.29 ± 0.90	0.23 ± 0.18***
285 aa / TMH6	0.45 ± 0.02	0.35 ± 0.05***	0.35 ± 0.04***	0.37 ± 0.05***	0.02 ± 0.01	0.12 ± 0.13*	0.19 ± 0.14**	0.16 ± 0.16**
324 aa / H7★	0.23 ± 0.02	0.31 ± 0.02***	0.36 ± 0.03***	0.35 ± 0.04***	0.32 ± 0.16	0.06 ± 0.03***	0.10 ± 0.05***	0.12 ± 0.09**
353 aa / Loop7	0.22 ± 0.03	0.34 ± 0.04***	0.29 ± 0.05**	0.32 ± 0.04***	0.85 ± 0.61	0.04 ± 0.03***	0.22 ± 0.21**	0.11 ± 0.10**
374 aa / TMH8	0.32 ± 0.06	0.34 ± 0.09	0.23 ± 0.02***	0.30 ± 0.08	0.10 ± 0.12	0.04 ± 0.09	1.24 ± 0.37***	0.28 ± 0.44
435 aa / EH2★	0.32 ± 0.02	0.32 ± 0.02	0.67 ± 0.05***	0.56 ± 0.11***	0.13 ± 0.04	0.12 ± 0.04	(1.1 ± 0.8) × 10-3***	(7.0 ± 12.5) × 10-3***
527 aa / TMH12★	0.63 ± 0.10	0.60 ± 0.06	0.65 ± 0.07	0.58 ± 0.04	(1.1 ± 1.9) × 10-3	(1.9 ± 2.1) × 10-3	(3.2 ± 3.5) × 10-3	(8.6 ± 5.3) × 10-3 ***

Peak position / Structural region	ΔG(kBT)				κ (N/m)
	400 mM KCl 100 mM NaCl 5 mM betaine	400 mM KCl 100 mM NaCl no betaine	500 mM NaCl 5 mM betaine	500 mM NaCl	400 mM KCl 100 mM NaCl 5 mM betaine	400 mM KCl 100 mM NaCl no betaine	500 mM NaCl 5 mM betaine	500 mM NaCl
41 aa / N-terminal	24 ± 1.9	25 ± 3.0	26 ± 1.9	26 ± 1.6	1.60 ± 0.86	1.75 ± 1.38	0.71 ± 0.30**	0.94 ± 0.35
58 aa / N-terminal	22 ± 1.1	24 ± 0.9***	23 ± 2.2	22 ± 1.9	4.17 ± 1.92	2.33 ± 0.66*	1.77 ± 1.18**	2.05 ± 1.34*
75 aa / TMH1	21 ± 0.7	22 ± 0.6	24 ± 1.3***	22 ± 0.9	4.52 ± 1.51	4.05 ± 1.00	1.26 ± 0.46***	2.17 ± 0.74***
92 aa / TMH2	20 ± 0.4	23 ± 2.6**	20 ± 0.8*	20 ± 0.7	8.03 ± 2.33	2.69 ± 2.44***	3.39 ± 1.34***	3.41 ± 1.38***
137 aa / Loop2★	22 ± 0.6	23 ± 0.4**	22 ± 0.3	22 ± 0.6	3.60 ± 0.70	3.07 ± 0.37	2.88 ± 0.26**	2.73 ± 0.52**
154 aa / TMH3	21 ± 0.8	22 ± 1.4**	20 ± 0.4	21 ± 0.6	4.61 ± 1.62	3.14 ± 1.49	3.06 ± 0.55*	2.46 ± 0.60**
184 aa / TMH4★	23 ± 1.3	21 ± 0.3**	21 ± 1.1*	22 ± 0.3	2.50 ± 1.10	4.16 ± 0.56***	2.32 ± 1.09	1.80 ± 0.21
242 aa / TMH5★	22 ± 0.7	23 ± 0.6	22 ± 0.7	23 ± 0.4*	3.52 ± 0.90	3.45 ± 0.74	2.46 ± 0.69**	2.04 ± 0.25***
268 aa / Loop5	20 ± 0.3	21 ± 0.4**	20 ± 0.7	22 ± 0.8***	4.36 ± 0.73	3.67 ± 0.61	2.55 ± 0.88***	1.56 ± 0.44***
285 aa / TMH6	25 ± 0.4	23 ± 1.1***	22 ± 0.7***	23 ± 1.0***	1.02 ± 0.11	1.56 ± 0.55**	1.53 ± 0.41**	1.37 ± 0.44*
324 aa / H7★	22 ± 0.5	23 ± 0.5***	23 ± 0.5***	23 ± 0.8**	3.44 ± 0.68	2.09 ± 0.31***	1.46 ± 0.24***	1.58 ± 0.41***
353 aa / Loop7	21 ± 0.7	24 ± 0.9***	22 ± 1.0**	23 ± 0.9***	3.51 ± 1.15	1.69 ± 0.44***	2.20 ± 0.82**	1.89 ± 0.60**
374 aa / TMH8	23 ± 1.3	24 ± 2.1	21 ± 0.3***	22 ± 1.6	1.88 ± 0.76	1.72 ± 1.07	3.13 ± 0.48***	1.99 ± 1.21
435 aa / EH2★	23 ± 0.3	23 ± 0.3	28 ± 0.8***	26 ± 1.8***	1.87 ± 0.22	1.89 ± 0.22	0.51 ± 0.08***	0.68 ± 0.30***
527 aa / TMH12★	28 ± 1.8	27 ± 1.1	26 ± 1.1	25 ± 0.6**	0.57 ± 0.22	0.63 ± 0.15	0.51 ± 0.13	0.63 ± 0.10

Average values are shown for the energy barriers that stabilize structural segments of up-regulated BetP in the presence (400 mM KCl, 100 mM NaCl, 5 mM betaine, 50 mM Tris-HCl, pH 7.5) and absence (400 mM KCl, 100 mM NaCl, 50 mM Tris-HCl, pH 7.5) of substrate, and for down-regulated BetP in the presence (500 mM NaCl, 5 mM betaine, 50 mM Tris-HCl, pH 7.5) and absence (500 mM NaCl, 50 mM Tris-HCl, pH 7.5) of substrate. Table S1 shows the values detected for all conditions probed relative to up-regulated BetP in presence of substrate. Black stars denote major fp that became dominant in superimposed F-D curves. Differences compared to BetP characterized in 400 mM KCl, 100 mM NaCl, 5 mM betaine, 50 mM Tris-HCl, at pH 7.5 were considered being significant when p-values approached < 0.05 (**) and < 0.01 (***) from T-student tests (Table S2) and their changes did not overlap within their standard deviation. Barrier heights, ΔG_u, and spring constants, κ, were calculated as described under Calculation of Transition Barrier Heights and Rigidity. Values that showed a significant difference are highlighted in bold. Errors of x_u and k₀ represent S.D. Errors in ΔG_u were estimated by propagating the errors of k₀. Errors in κ were estimated by propagating the errors of ΔG_u and k₀

Upon exposure to betaine the x_u of most structural regions of BetP showed no significant differences (Table 1). However, in presence of K⁺ this situation changed. The largest change was a reduction in x_u by a factor of 2 for EH2. A reduction in x_u signifies that the energy valley stabilizing a structural region becomes narrow. Consequently, EH2 adopts less conformational substates and decreases structural flexibility in presence of K⁺. Similarly, x_u of the N-terminal domain, TMH2, loop7, and H7 at the trimer interface was reduced by a factor of 1.5. The x_u of all other structural regions remained largely unaffected by K⁺ and betaine. While the N-terminal domain, and the trimer interface are key players in regulation upon K⁺-binding (13), it can be concluded that also EH2 is restrained to a specific conformation, which most likely is related to an active state of BetP.

In the absence of betaine and K⁺, the unfolding rates, k₀, of the stable structural regions varied from ≈0.01 to 2.25 s^-1 (Table 1), which fits well with rates observed for most transmembrane α-helical proteins (22, 33, 35–37). EH2 showed the lowest unfolding rate between 0.001 and 0.007 s^-1 and therefore the highest lifetime ranging between 142 and 1,000 s. In presence of K⁺ the unfolding rate increased to ≈0.13 s^-1 thereby reducing the lifetime of EH2 by a factor of ≈100. This change in lifetime did not depend on the presence of betaine. The unfolding rate of TMH12 was comparably low, but in contrast to EH2 did not change in the presence of K⁺ or betaine. TMH2 showed a 10-fold reduction of lifetime in the presence of K⁺ and loop5 reduced lifetime fivefold. Interestingly, loop7 reduced its lifetime sevenfold only in the presence of substrate and K⁺, which may indicate cooperative effects.

The free unfolding energies, ΔG_u, ranging between 21 to 28 k_BT (Table 1) were similar to those reported in literature (22, 33, 36–38). Most pronounced changes were observed again for EH2 in which the free unfolding energy dropped in the presence of K⁺ by 3–5 k_BT. In contrast, the free unfolding energies of all other structural regions showed much smaller changes, which suggest that they were largely independent of the presence of K⁺ and betaine.

Up-Regulation and Substrate-Binding Regulate Structural Flexibility of BetP.

Mechanical rigidity of a protein can be approached using the energy landscape that describes energy as a function of the conformational entropy of a protein structure (39–41). Accordingly, the width of an energy valley trapping a protein structure defines its conformational entropy and number of conformational states in a catalytic and regulatory cycle (22, 33, 36, 42, 43). This rigidity can be described by the spring constant, κ, which is calculated from the curvature of the potential well that precedes the free unfolding energy barrier, the height of this energy barrier, ΔG_u, and the distance, x_u, separating folded and transition state (Fig. S4) (Eq. 3, Materials and Methods) (Table 1). In absence of K⁺, the stable structural regions of BetP showed spring constants between 0.5 and 3.4 Newton/meter (N/m). In presence of K⁺, the spring constants of the individual structural regions varied strongly from 0.6 to 8.0 N/m indicating that K⁺ significantly increased the mechanical rigidity of every structural region. It is striking that the mechanical rigidity of nearly all functional important structural regions involved in transport and trimerization were affected in the presence of K⁺. Upon K⁺- and substrate-binding the mechanical rigidity of almost every structural region enhanced even further. Among these the largest K⁺-dependent changes in structural flexibility were observed again for EH2, which is neither involved in the coordination of betaine in the central betaine-binding site nor in trimerization. These findings suggests that BetP is structurally more flexible in the down-regulated state, increases rigidity in the functionally up-regulated state, and gains highest structural rigidity in the up-regulated substrate-bound state. The increase in structural rigidity might be closely related to the two inverted structurally related repeat domains, both of which contributing to substrate-binding and -transport. A tight connection between individual residues of both domains allow for an efficient cycling through conformations during the alternating access. Therefore we assume that the presence of K⁺ results in a strengthening of interaction sites that couples both repeat domains. A similar allosteric effect but in opposite direction was recently observed by DFS of the antiporter SteT whose structural flexibility decreased with substrate-binding (22). Here we observed a three-state process by which BetP stepwise decreases structural flexibility.

The Role of EH2 in K⁺-Regulation.

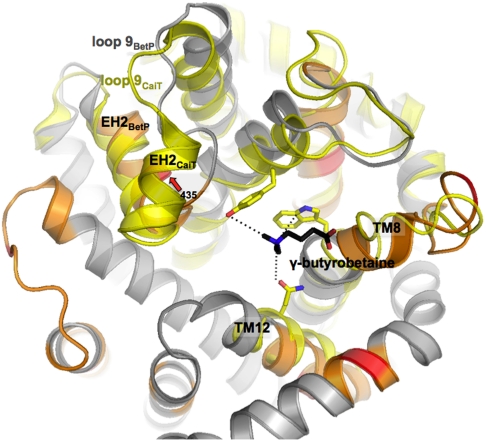
EH2 together with TMH12 show the longest lifetime of all structural regions (Table 1). Both regions also exhibit the highest unfolding free energy and the smallest rigidity indicating that they are the mechanically most flexible, and energetically and kinetically most stable structures. Up-regulating BetP by K⁺ significantly changed mechanical and kinetic stability of EH2 (fp435 aa). The functional role of EH2 in BetP is unknown. In LeuT, a phenylalanine in the corresponding EH2 segment (EL4) was proposed to contribute to the formation of a periplasmic second substrate-binding (S2) site (44). The S2 site is assumed as being transiently occupied during translocation as the substrate moves towards the primary substrate-binding (S1) site (45). Formation of a S2 site in BetP has not been structurally corroborated although a periplasmic S2 site was reported for the homologous antiporter CaiT (46), a nonregulated member of the BCCT-family (6). In CaiT, a γ-butyrobetaine molecule is loosely bound at the periplasmic S2 site (Fig. 5).

Fig. 5.

Superposition of residues coordinating the second substrate-binding site in CaiT (yellow) with the periplasmic side of BetP. BetP is shown in spiral presentation and colored as in Fig. 2. Only TMH3, TMH8, TMH12, and EH2 of CaiT are depicted and colored in yellow (PDB entry code 2WSW). The periplasmic second substrate-binding site in CaiT is shown in stick presentation with individual residues in yellow and the substrate γ-butyrobetaine in black.

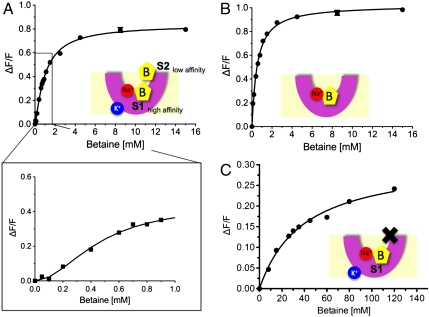
Positive cooperative substrate-binding was deduced for CaiT from tryptophan fluorescence (TF) studies (46). TF studies were also performed for BetP reconstituted in liposomes in the absence and presence of K⁺ (Fig. 6). In the presence of 450 mM K⁺ WT BetP revealed a stronger positive cooperativity with a Hill factor of 1.8 ± 0.3 (Fig. 6A) compared to WT CaiT that showed a Hill factor of 1.4–1.5. Moreover our results indicate a biphasic binding isotherm in which two binding events are discernable (Fig. 6A) with apparent binding constants of K_d1 = 0.49 ± 0.09 mM and K_d2 = 1.01 ± 0.04mM. In the absence of K⁺ a single binding event with a Hill factor of 1.0 ± 0.1 and K_d = 0.52 ± 0.03mM was detected (Fig. 6B). In BetP the residues Trp366 and Gln519 structurally correspond to Trp316 and Gln473 that facilitate substrate-binding to the S2 site in CaiT (46). Replacing Trp366 and Gln519 against alanine drastically affected the apparent substrate-binding constant of BetP to K_d = 39.2 ± 4.3 mM (Fig. 6C). Moreover, the cooperativity in the presence of K⁺ was lost resulting in a Hill factor of 0.9 ± 0.1. Our results suggest that up-regulating K⁺-concentrations promote the formation of a K⁺-dependent S2 site, which is located at a similar position as that observed for the nonregulated BCCT-protein CaiT, and acts as a regulatory site in BetP.

Fig. 6.

Maximum tryptophan fluorescence studies performed for BetP reconstituted in liposomes in the absence and presence of potassium. (A) In the presence of 450 mM K⁺ WT BetP shows a biphasic binding isotherm with apparent binding constants of K_d1 = 0.49 ± 0.09 mM and K_d2 = 1.01 ± 0.04 mM. Inset: Positive cooperativity with a Hill factor of 1.8 ± 0.3. (B) In the absence of K⁺ a single binding event with a Hill factor of 1.0 ± 0.1 and K_d = 0.52 ± 0.03 mM was detected. (C) Tryptophan fluorescence measured for the BetP mutant BetP-W366A/Q519A in proteoliposomes as a function of the external betaine concentration in the presence of 450 mM K⁺. Each data point shows the average of at least three independent experiments. A binding constant of K_d = 39.2 ± 4.3 mM and a Hill factor of 0.9 ± 0.1 show the dramatic effect of the mutation on the periplasmic second betaine-binding (S2) site. S1 and S2 assign primary and secondary substrate-binding sites, respectively. (B) assigns betaine, K⁺ potassium, Na⁺ sodium, and X the mutated and inactivated S2 site.

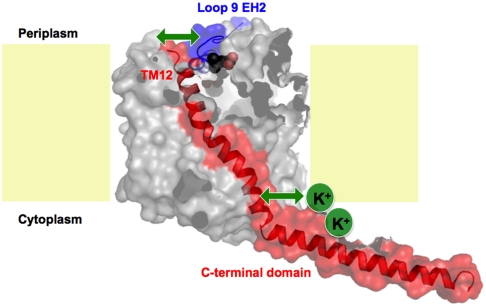
This raises the question as to how the formation of a S2 site is linked to the K⁺-induced stabilization of the interaction between EH2 and TMH12 observed by SMFS. One possible scenario might be that K⁺-binding to the cytoplasmic side of BetP induces conformational changes at the C-terminal domain, which subsequently affects the conformation of TMH12. The SMFS data quantifies that K⁺-binding to BetP significantly decreases the distance from the transition state, increases the mechanical rigidity, and the kinetic stability of EH2. This pronounced change may allow TMH12 to move closer towards EH2 and establish stronger interactions between both segments. Vice versa the interactions changing at EH2 could result in a more stable formation of the S2 site via Gln519. Thereby, EH2 together with TMH12 would play a crucial role in K⁺-dependent transport regulation by transferring the stimulating signal from the cytoplasmic to the periplasmic side in BetP. The nonregulated CaiT lacks the long C-terminal domain and an obvious interaction with TMH12 due to a more rigid loop9 that consists of two helical segments. Therefore, only BetP may provide an interaction network coupling the S2 site to a cytoplasmic osmosensor. A functional and structural investigation of the molecular mechanism of K⁺-stimulated activity regulation in BetP is in progress.

Materials and Methods

Preparation of WT BetP and BetPΔC45.

WT BetP and BetpΔC45 expression, cell membrane preparation, and protein purification were followed as described (47). Purified WT BetP and BetpΔC45 (in concentration of ∼1 mg/mL) was crystallized in presence of E. coli polar lipids (Avanti Polar Lipids.) mixed with 40% of cardiolipin (CL) of bovine heart (Avanti polar lipids), in the presence of native C. glutamicum lipids prepared as described (48). WT Betp and BetpΔN characterized in the control experiments of Fig. S3 were reconstituted into synthetic POPG (Avanti polar lipids). Two-dimensional (2D) crystals were obtained as shown (47). Activity measurements of the reconstituted protein in the proteoliposomes showed that WT BetP remains fully active (49).

Protein Reconstitution into Liposomes.

Functional reconstitution of BetP and its mutants were performed as described (50). Briefly, liposomes (20 mg phospholipid/mL) from E. coli polar lipids (Avanti polar lipids) were prepared by extrusion through polycarbonate filters (100 nm pore-size) and diluted 1∶4 in buffer (250 mM KPi or 250 mM Tris-HCl, pH 7.5). After saturation with Triton X-100, the liposomes were mixed with purified protein at a lipid/protein ratio of 10∶1 (wt/wt). BioBeads at ratios (wt/wt) of 5 (BioBeads/Triton X-100) and 10 (BioBeads/DDM) were added to remove detergent. Finally, the proteoliposomes were centrifuged and washed before being frozen in liquid nitrogen and stored at -80 °C.

Tryptophan Fluorescence-Binding Assay.

Binding assays were performed with 100 μg/mL of purified BetP in proteoliposomes. Betaine concentrations ranged from 0.05 to 15 mM. Tryptophan fluorescence emission between 315 and 370 nm was recorded on a Hitachi F-4500 fluorescence spectrophotometer and averaged over four readings, with the excitation wavelength set to 295 nm and a slit width of 2.5 or 5.0 nm for excitation or emission, respectively, at a constant NaCl concentration of 300 mM. The mean value and standard deviation at the 342 nm emission maximum was plotted for each substrate concentration. Data were fitted using the program GraphPad Prism (version 5.0c for Mac OS X, GraphPad Software Inc.).

SMFS and DFS.

The AFM (Nanowizard II, JPK Instruments) was equipped with 70 μm long (NPS series, Veeco) Si₃N₄ AFM cantilevers having nominal spring constants ≈80 pN/nm at resonance frequencies of 4.8 to 5.5 kHz in buffer solution. Spring constants of individual cantilevers were calibrated in solution using the thermal noise technique (51). 2D crystals of BetP were adsorbed onto freshly cleaved mica in 500 mM NaCl, 50 mM Tris/HCl, pH 7.5. After an adsorption time of ≈15 min, the sample was gently rinsed with the experimental buffer to remove nonadsorbed membranes. Experimental buffer solutions used were either 500 mM NaCl, 50 mM Tris-HCl, pH 7.5, or 500 mM NaCl, 5 mM betaine, 50 mM Tris-HCl, pH 7.5, or 400 mM KCl, 100 mM NaCl, 50 mM Tris-HCl, pH 7.5, or 400 mM KCl, 100 mM NaCl, 5 mM betaine, 50 mM Tris-HCl, pH 7.5. All buffer solutions were made freshly using nano-pure water (18.2 MΩ·cm) and purity grade (≥98.5%) reagents from Sigma/Merck. Upon buffer exchange the AFM setup was thermally equilibrated for ≈30 min. Samples were imaged using contact mode AFM applying a force of ≤ 100 pN to the cantilever. To prevent possible sample perturbations, differences between AFM topographs scanned in trace and retrace directions were minimized by adjusting scanning speed, feedback loop, and applied force. After imaging of the membrane an unperturbed area was selected to perform SMFS. The AFM stylus was pushed onto the membrane at a force of ≈0.8 nN for 0.5 s, which promoted the nonspecific adhesion of the BetP peptide to the AFM stylus. In the following step the stylus was withdrawn from the membrane surface at a given pulling velocity (see figure legends), while detecting the cantilever deflection. The deflection at each separation was used to calculate the interaction force via Hook’s law.

DFS experiments were performed at six pulling velocities (100, 300, 600, 1,200, 2,400, and 5,000 nm/s) using BetP in 500 mM NaCl, in 500 mM NaCl and 5 mM betaine, in 400 mM KCl and 100 mM NaCl, and in 400 mM KCl, 100 mM NaCl and 5 mM betaine. To minimize errors that may occur due to uncertainties in the cantilever spring constant calibration, BetP was unfolded using at least three different cantilevers for each pulling velocity.

Data Analysis.

Attachment of the BetP to the AFM stylus could occur at any region of the polypeptide chain exposed to the solvent. The studied recombinant BetP polypeptide is composed of 603 aa that, if entirely stretched, would extent to 218 nm. The last peak, detected in the F-D curves, usually corresponds to the unfolding of two or one last transmembrane α-helices remaining embedded in the membrane bilayer until they are forced to unfold as well (17, 19, 29). The expected length interval of the fully unfolded BetP (of the last peak for BetP) should lie within 523–554 aa when pulling from N-terminal end, or 516–536 aa when puling from C-terminal end. Fully stretching peptide lengths between 516 and 554 aa corresponds to a pulling distance of ≈185–199 nm. Subtracting the last transmembrane α-helices and terminal ends that would remain embedded in the membrane (≈100–130 aa) indicates that the last fp of a F-D curve would occur at pulling distances ranging ≈130–180 nm. Shorter F-D curves were not included into data analysis. All fp of F-D curves showing a length above ≈143 nm were fitted by the WLC model (52), using a persistence length of 0.4 nm and monomer length of 0.36 nm. Igor Pro software (Wavemetrics Inc.) and home-written macros were used for data analysis.

When pulling BetP from one side of the membrane sometimes the interaction establishing a barrier against unfolding had to be assumed to occur inside the membrane or at the opposite side of the membrane. Lipid membrane thickness (≈4 nm) should be considered and 11 aa (11 × 0.36 nm ≈ 4 nm) be added to the number of aa demonstrated by WLC model in first case, or in the latter case a fraction of the membrane thickness in aa proportional to the length of the stretched membrane embedded polypeptide should be considered (16).

Calculation of x_u and k₀ from DFS Data.

Suggested by the Bell-Evans theory (34), the most probable unfolding force F^∗ plotted vs. 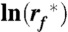describes the most prominent unfolding energy barriers that have been crossed along the force-driven reaction coordinate (53). The interplay between F^∗ and 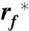can be described by:

[1]

with k_B being the Boltzmann constant, T the absolute temperature, 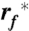the most probable loading rate, x_u the distance between free energy minimum and transition state barrier, and k₀ the unfolding rate at zero force. The force-loading rate was calculated using r_{f_kspacer_v} where v is the pulling velocity. Experimental force-loading rate and force histograms (Figs. S6–S9) were fitted with Gaussian distributions. The resulting F^∗ was semi logarithmically plotted vs. 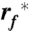. x_u and k₀ were obtained by fitting Eq. 1 using a nonlinear least squares algorithm.

Calculation of Transition Barrier Heights and Rigidity.

The height of the free energy barrier, ΔG_u, that separates the folded and unfolded state was assessed using an Arrhenius equation,

[2]

with τ_D denoting the diffusive relaxation time. Values for τ_D found for proteins are in the order of 10^-7–10^-9 s (54, 55). A τ_D of 10^-9 s has also been used for molecular dynamics simulations of protein unfolding (56, 57). We used τ_D = 10^-9 s throughout all our calculations. Varying τ_D from 10^-7–10^-9 s would change the free energy of activation by ≈15%. Moreover even if τ_D would be different by orders of magnitude, the influence of the error of τ_D would be the same for all conditions and values and hence would not affect the qualitative results. Errors were estimated by propagation of the errors of k₀. In the absence of any information on the energy shape, we assume that a simple parabolic potential and the spring constant κ of the bond can be calculated using ΔG_u and x_u (43, 53).

[3]

Errors in ΔG_u and x_u were propagated for estimation of errors in κ.