Abstract
Brain is one of the most energy demanding organs in mammals, and its total metabolic rate scales with brain volume raised to a power of around 5/6. This value is significantly higher than the more common exponent 3/4 relating whole body resting metabolism with body mass and several other physiological variables in animals and plants. This article investigates the reasons for brain allometric distinction on a level of its microvessels. Based on collected empirical data it is found that regional cerebral blood flow CBF across gray matter scales with cortical volume 
as 
, brain capillary diameter increases as 
, and density of capillary length decreases as 
. It is predicted that velocity of capillary blood is almost invariant (
), capillary transit time scales as 
, capillary length increases as 
, and capillary number as 
, where 
is typically a small correction for medium and large brains, due to blood viscosity dependence on capillary radius. It is shown that the amount of capillary length and blood flow per cortical neuron are essentially conserved across mammals. These results indicate that geometry and dynamics of global neuro-vascular coupling have a proportionate character. Moreover, cerebral metabolic, hemodynamic, and microvascular variables scale with allometric exponents that are simple multiples of 1/6, rather than 1/4, which suggests that brain metabolism is more similar to the metabolism of aerobic than resting body. Relation of these findings to brain functional imaging studies involving the link between cerebral metabolism and blood flow is also discussed.
Introduction
It is well established empirically that whole body metabolism of resting mammals scales with body volume (or mass) with an exponent close to 3/4, which is known as Kleiber's law [1], [2], [3], [4]. The same exponent or its simple derivatives govern the scalings of respiratory and cardiovascular systems in mammals and some other physiological parameters in animals and plants [2], [3], [5]. Because of its almost ubiquitous presence, the quarter power has often been described as a general law governing metabolism and blood circulation, and several formal models explaining its origin have been proposed that still cause controversy [6], [7], [8], [9]. However, as was found by the author [10], the brain metabolism at rest seems to follow another scaling rule. Total brain metabolic rate (both oxygen and glucose) scales with brain volume with an exponent 
, or close to 5/6 [10]. Consequently, the volume-specific cerebral metabolism decreases with brain size with an exponent around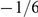 
, and this value is highly homogeneous across many structures of gray matter [10]. The origin of these cerebral exponents has never been explained, although it is interesting why brain metabolism scales different than metabolism of other systems.
The brain, similar to other organs, uses capillaries for delivery of metabolic nutrients (oxygen, glucose, etc.) to its cells [11]. Moreover, numerical density of cerebral capillaries is strongly correlated with brain hemodynamics and metabolism [12], [13]. However, the cerebral microvascular network differs from other non-cerebral networks in two important ways. First, in the brain there exists a unique physical border, called the brain-blood barrier, which severely restricts influx of undesired molecules and ions to the brain tissue. Second, cerebral capillaries exhibit a large degree of physical plasticity, manifested in easy adaptation to abnormal physiological conditions. For instance, during ischemia (insufficient amount of oxygen in the brain) capillaries can substantially modify their diameter to increase blood flow and hence oxygen influx [14], [15], [16]. These two factors, i.e. structural differences and plasticity of microvessels, can in principle modify brain metabolism in such a way to yield different scaling rules in comparison to e.g. lungs or muscles. Another, related factor that may account for the uncommon brain metabolic scaling is the fact that brain is one of the most energy expensive organs in the body [10], [17]. This is usually attributed to the neurons with their extended axons and dendrites, which utilize relatively large amounts of glucose and ATP for synaptic communication [18], [19].
The main purpose of this paper is to determine scaling laws for blood flow and geometry of capillaries in the brain of mammals. Are they different from those found or predicted for cardiovascular and respiratory systems? If so, do these differences account for brain metabolic allometry? How the scalings of blood flow and capillary dimensions relate to the scalings of neural characteristics, such as neural density and axon (or dendrite) length? This study might have implications for expanding of our understanding of mammalian brain evolution, in particular the relationship between brain wiring, metabolism, and its underlying microvasculature [10], [20], [21]. The results can also be relevant for research involving the microvascular basis of brain functional imaging studies, which use relationships between blood flow and metabolism to decipher regional neural activities [22], [23].
Results
The data for brain circulatory system were collected from different sources (see Materials and Methods). They cover several mammals spanning 3–4 orders of magnitude in brain volume, from mouse to human.
1. Empirical scaling data
Cerebral blood flow CBF in different parts of mammalian gray matter decreases systematically with gray matter volume, both in the cortical and subcortical regions (Fig. 1). In the cerebral cortex, the scaling exponent for regional CBF varies from 
for the visual cortex (Fig. 1A),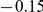 
for the parietal cortex (Fig. 1B), 
for the frontal cortex (Fig. 1C), to 
for the temporal cortex (Fig. 1D). The average cortical exponent is 
. In the subcortical regions, the CBF scaling exponent is 
for hippocampus (Fig. 2A), 
for thalamus (Fig. 2B), and 
for cerebellum (Fig. 2C). The average subcortical exponent is identical with the cortical one, i.e., 
, and both of them are close to 
. It is interesting to note that almost all of the cortical areas (except temporal cortex) have scaling exponents whose 95
confidence intervals do not include a quarter power exponent 
.
Figure 1. Scaling of cerebral blood flow CBF in the cortical gray matter.
(A) Visual cortex: 
(
, 
). 95
confidence interval for the slope CI = (−0.168,−0.086). (B) Parietal cortex: 
(
, 
), slope CI = (−0.222,−0.078). (C) Frontal cortex: 
(
, 
), slope CI = (−0.239,−0.100). (D) Temporal cortex: 
(
, 
), slope CI = (−0.286,−0.096).
Figure 2. Scaling of cerebral blood flow CBF in the subcortical gray matter.
(A) Hippocampus: 
(
, 
), slope CI = (−0.271,0.000). (B) Thalamus: 
(
, 
), slope CI = (−0.272,−0.062). (C) Cerebellum: 
(
, 
), slope CI = (−0.252,−0.102).
The microvessel system delivering energy to the brain consists of capillaries. The capillary diameter increases very weakly but significantly with brain size, with an exponent of 0.08 (Fig. 3A). On the contrary, the volume-density of capillary length decreases with brain size raised to a power of 
(Fig. 3B). Thus, the cerebral capillary network becomes sparser as brain size increases. Despite this, the fraction of gray matter volume taken by capillaries is approximately independent of brain size (Fig. 3C). Another vascular characteristic, the arterial partial oxygen pressure, is also roughly invariant with respect to brain volume (Fig. 3D).
Figure 3. Scaling of brain capillary characteristics against brain size.
(A) Capillary diameter scales against cortical gray matter volume with the exponent 0.075 (
, 
, 
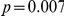), exponent CI = (0.034,0.117). (B) Volume density of capillary length 
scales with the exponent 
(
, 
, 
), exponent CI = (−0.316,−0.008). (C) Fraction of capillary volume 
in gray matter is essentially independent of brain size (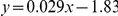
, 
, 
), the same as (D) the arterial partial oxygen pressure (
, 
, 
).
A degree of neurovascular coupling can be characterized by geometric relationships between densities of capillaries and neurons. Scaling of the density of neuron number in the cortical gray matter is not uniform across mammals [24], [25], [26]. In fact, the scaling exponent depends to some extent on mammalian order and the animal sample used [26]. For the sample of mammals used in this study, it is found that cortical neuron density decreases with cortical gray matter volume with an exponent of 
(Fig. 4A). This exponent is close to the exponent for the scaling of capillary length density, which is 
(Fig. 3B). Consistent with that, the ratio of cortical capillary length density to neuron density across mammals is approximately constant and independent of brain size (Fig. 4B). Typically, there is about 10 
m of capillaries per cortical neuron. The scaling dependence between the two densities yields an exponent close to unity (Fig. 4C), which shows a proportionality relation between them.
Figure 4. Neuron density versus capillary length density in the cerebral cortex.
(A) Across our sample of mammals, the cortical neuron number density 
scales against cortical volume with the exponent 
(
, 
, 
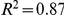), exponent CI = (−0.221,−0.036). (B) The ratio of the density of capillary length 
to the density of neurons 
in the cortex does not correlate with brain size (
, 
, 
), exponent CI = (−0.228,0.161). (C) The log-log dependence of the capillary length density 
on neuron density 
gives the exponent of 1.05 (
, 
, 
).
Cerebral blood flow CBF scales with brain volume the same way as does capillary length density (Figs. 1,2,3B), and thus, CBF should also be related to neural density. Indeed, in the cerebral cortex the ratio of the average CBF to cortical neural density is independent of brain scale (Fig. 5). This means that the average amount of cortical blood flow per neuron is invariant among mammals, and about 
mL/min. Taken together, the findings in Figs. 4 and 5 suggest a tight global correlation between neurons and their energy supporting microvascular network.
Figure 5. Invariance of cerebral blood flow per cortical neuron across mammals.
The ratio of CBF to neuron density 
in the cerebral cortex does not correlate significantly with brain size (log-log plot yields 
, 
, 
). The value of CBF for each species is the arithmetic mean of regional CBF across cerebral cortex.
2. Theoretical scaling rules for cerebral capillaries
Below I derive theoretical predictions for the allometry of brain capillary characteristics, such as: capillary length and radius, capillary number, blood velocity, and time taken by blood to travel through a capillary. I also find relationships connecting cerebral metabolic rate and blood flow with neuron density. The following assumptions are made in the analysis: (i) Oxygen consumption rate in gray matter CMR
scales with cortical gray matter volume 
as 
, in accordance with Ref. [10]; (ii) Capillary volume fraction, 
, is invariant with respect to 
, which follows from the empirical results in Fig. 3C. The symbol 
denotes total capillary number in the gray matter, 
is the length of a single capillary segment, and 
is its radius; (iii) Driving blood pressure 
through capillaries is independent of brain size, which is consistent with a known fact that arterial blood pressure (both systolic and diastolic) of resting mammals is independent of body size [27], [28], [29]; (iv) Partial oxygen pressure 
in capillaries is also invariant, which is consistent with the empirical data in Fig. 3D on the invariance of arterial oxygen pressure; (v) Cerebral blood flow CBF is proportional to oxygen consumption rate CMR
, due to adaptation of capillary diameters to oxygen demand.
The cerebral metabolic rate of oxygen consumption CMR
, according to the modified Krogh model [11], [14], is proportional to the product of oxygen flux through capillary wall and the tissue-capillary gradient of oxygen pressure 
, i.e.
 |
(1) |
where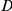 
is the oxygen diffusion constant in the brain. The dependence of CMR
on capillary radius in this model has mainly a logarithmic character, and hence it is neglected as weak. Since oxygen pressure in the brain tissue is very low [30], the pressure gradient 
is essentially equal to the capillary oxygen pressure 
. Consequently, the formula for CMR
simplifies to 
, where 
is the density of capillary length 
.
From the assumptions (i) and (iv) we obtain that capillary length density 
. Additionally, from (ii) we have 
, implying that capillary radius (or diameter) 
scales as 
. Consequently capillary diameter does not increase much with brain magnitude. As an example, a predicted capillary diameter for elephant with its cortical gray matter volume 1379 cm
[31] is 7.2 
m, which does not differ much from those of rat (4.1 
m [15], [32]) or human (6.4 
m [33], [34]), who have corresponding volumes 3450 and 2.4 times smaller.
The blood flow 
through a capillary is governed by a modified Poiseuille's law in which blood viscosity depends on capillary radius [35]:
 |
(2) |
where 
is the axial driving blood pressure along a capillary of length 
, and 
is the capillary radius dependent effective blood viscosity. The latter dependence has a nonmonotonic character, i.e. for small diameters the viscosity 
initially decreases with increasing 
, reaching a minimum at diameters about 
m. For 
m the blood viscosity 
slowly increases with 
approaching its bulk value for diameters 
500 
m. This phenomenon is known as the Fahraeus-Lindqvist effect [36]. In general, blood viscosity in narrow microvessels depends on microvessel thickness because red blood cells tend to deform and place near the center of capillary leaving a cell-free layer near the wall [35], [37]. These two regions have significantly different viscosities, with the cell-free layer having essentially plasma viscosity 
, which is much smaller than the bulk (or center region) viscosity 
. The formula relating the effective blood viscosity 
with capillary radius and both viscosities 
and 
is given by [35]:
 |
(3) |
where 
, and 
is the thickness of cell-free layer.
For capillary radiuses relevant for the brain, i.e. 1.5 
m
3.5 
m (see Suppl. Table S2), the ratio 
increases with increasing 
, which causes a decline in the effective blood viscosity down to its minimal value at 
m (Table 1). Using the data in Table 1 taken from [35], we can approximate the denominator in Eq. (3) for this range of radiuses by a simple, explicit function of 
. The best fit is achieved with a logarithmic function, i.e. 
, where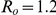 
m (Table 1). As a result, the effective blood viscosity takes a simple form:
 |
(4) |
Table 1. Parameters affecting the effective blood viscosity.
 [ m] |
 [ m] |
|
|
|
| 1.5 | 0.07 | 0.05 | 0.27 | 0.31 |
| 2.0 | 0.30 | 0.15 | 0.54 | 0.54 |
| 2.5 | 0.60 | 0.24 | 0.71 | 0.69 |
| 3.0 | 0.90 | 0.30 | 0.79 | 0.80 |
Data for 
and 
were collected from [35]. The value of 
was taken as 1/8. The last column represents values of the fitting function to the function in the fourth column.
Cerebral blood flow CBF in the brain gray matter is defined as 
, where 
is the total capillary blood flow through all 
capillaries. Thus CBF is given by
 |
(5) |
or
 |
(6) |
We can rewrite the logarithm present in Eq. (6), in an equivalent form, as a power function 
with a variable exponent 
given by (see Appendix S1 in the Supp. Infor.):
 |
(7) |
so that CBF becomes
 |
(8) |
The exponent 
in this equation can be viewed as a correction due to non-constant blood viscosity (Fahraeus-Lindqvist effect [36]). The dependence of 
on the capillary diameter is shown in Table 2. Because in general 
, its presence in Eq. (8) reduces the power of 
. However, this effect is weak for medium and large brains as 
. Even for a small rat brain the relative influence of 
is rather weak, since 
. In contrast, for very small brains, such as mouse, the effect caused by 
is strong (Table 2), which reflects a sharp increase in the effective blood viscosity for the smallest capillaries [35], [37].
Table 2. Exponent 
as a function of capillary diameter.
| Species | mouse | rat | cat | dog | monkey | human |
 [ m] |
3.1 | 4.1 | 5.1 | 4.5 | 5.6 | 6.4 |
|
−3.51 | −0.77 | −0.25 | −0.49 | −0.13 | −0.01 |
Data for 
were taken from Suppl. Inform. Table S2 (references therein).
Now we are in a position to derive scaling rules for the capillary length segment 
, capillary blood velocity 
, and the number of capillaries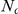 
. From Eq. (8), using the assumptions (i), (iii), and (v), we obtain 
, which implies that 
(viscosity of blood plasma is presumably independent of brain scale [38]). Consequently, 
, i.e. capillary length should weakly increase with brain size. Although there are no reliable data on 
, we can compare our prediction with the measured intercapillary distances, which generally should be positively correlated with 
. Indeed, the mean intercapillary distance in gray matter increases with increasing brain volume, and is 
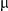m in rat [39], 24 
m in cat [40], and 58 
m in human [33].
Average velocity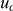 
of blood flow in brain capillaries is given by 
. Using the expressions for 
and 
, we get 
. Since 
above, and using the assumption (iii), we obtain 
. Thus, capillary blood velocity is almost independent of brain size for medium and large brains, as then 
(Table 2). For very small brains, instead, there might be a weak dependence. A related quantity, the blood transit time 
through a capillary, defined as 
, scales as 
, regardless of the brain magnitude. This indicates that 
and CBF are inversely related across different species, 
, because of their scaling properties.
We can find the scaling relation for the total number of capillaries 
from the volume-density of capillary length 
. We obtain 
, i.e. the exponent for 
is close to 2/3 for not too small brains. As an example, the number of capillary segments in the human cortical gray matter should be 123 times greater than that in the rat (cortical volumes of both hemispheres in rat and human are 0.42 cm
[24] and 572.0 cm
[41], respectively).
As was shown above, CMR
must be proportional to the volume density of capillary length 
(Eq. 1). On the other hand, the empirical results in Fig. 4 indicate that 
is roughly proportional to neuron density 
. Thus, we have approximately CMR
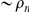across different mammals. This implies that oxygen metabolic energy per neuron in the gray matter should be approximately independent of brain size. Exactly the same conclusion was reached before in a study by Herculano-Houzel [26], based on independent data analysis. Moreover, since cortical CMR
and CBF scale the same way against brain size, we also have 
, which is confirmed by the results in Fig. 5. In other words, both cerebral metabolic rate and blood flow per neuron are scale invariant.
Discussion
1. General discussion
The summary of the scaling results is presented in Table 3. Some of these allometric relations are directly derived from the experimental data (CBF, 
, 
, 
, 
, CBF/
), and others are theoretically deduced (
, 
, 
, 
). The interesting result is that cerebral blood flow CBF in gray matter scales with cortical gray matter volume raised to a power of 
. The similar exponent governs the allometry of cortical metabolic rate CMR [10], which indicates that brain metabolism and blood flow are roughly linearly proportional across different mammals. This conclusion is compatible with several published studies that have shown the proportionality of CMR and CBF on a level of a single animal (rat, human) across different brain regions [12], [42].
Table 3. Summary of scalings for brain capillaries and hemodynamics against cortical gray matter volume 
.
| Parameter | Scaling rule |
Capillary radius, 
|
|
Capillary length density, 
|
|
Capillary volume fraction, 
|
|
Total capillary number, 
|
|
Capillary segment length,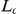 
|
|
Capillary blood velocity, 
|
|
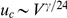
Capillary transit time, 
|
|
Capillary oxygen pressure, 
|
|
Capillary length per neuron, 
|
|
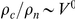
Cerebral blood flow, 
|
|
Blood flow per neuron, 
|
|
Oxygen consumption rate, 
|
|
Oxygen use per neuron, 
|
|
The coupling between CMR and CBF manifests itself also in their relation to the number of neurons. In this respect, the present study extends the recent result of Herculano-Houzel [26] about the constancy of metabolic energy per neuron in the brains of mammals, by showing that also cerebral blood flow and capillary length per neuron are essentially conserved across species. There are approximately 10 
m of capillaries and 
mL/min of blood flow per cortical neuron (Figs. 4 and 5; Supp. Tables S2 and S3). This finding suggests that not only brain metabolism but also its hemodynamics and microvascularization are evolutionarily constrained by the number of neurons. This mutual coupling might be a result of optimization in the design of cerebral energy expenditure and blood circulation.
It should be underlined that both CBF and CMR scale with brain volume with the exponent about 
, which is significantly different from the exponent 
relating whole body resting specific metabolism with body volume [1], [2], [3]. Instead, the cerebral exponent 
is closer to an exponent 
characterizing maximal body specific metabolic rate and specific cardiac output in strenuous exercise [43], [44]. In this sense, the brain metabolism and its hemodynamics resemble more the metabolism and circulation of exercised muscles than other resting organs, which is in line with the empirical evidence that brain is an energy expensive organ [10], [17], [18]. This may also suggest that there exists a common plan for the design of microcirculatory system in different parts of the mammalian body that uses the same optimization principles [45].
The results of this study show that as brain increases in size its capillary network becomes less dense, i.e. the densities of both capillary number and length decrease, respectively as 
and 
(Table 3). Contrary to that, the capillary dimensions increase weakly with brain volume, their radius as 
and their length segment as 
, which are sufficient to make the fraction 
of capillary volume in the gray matter to be scale invariant (Table 3). The correction 
appearing in the scaling exponents for 
and 
reflects the fact that blood viscosity depends on capillary radius (Fahraeus-Lindqvist effect [36]). This correction is however small for sufficiently large brains, generally for brains larger or equal to that of rat, for which typical values of 
are in the range from 
to 
(Table 2). On the contrary, for brains of mouse size or smaller, this correction is substantial, about 
, which implies that for very small brains 
is essentially constant.
Despite the changes in the geometry of microvessels, the velocity of capillary blood 
is almost scale invariant for not too small brains (exponent 
; Table 3). This prediction agrees with direct measurements of velocity in the brains of mouse, rat, and cat, which does not seem to change much, i.e. it is in the range 
mm/sec [40], [46]. Consequently the transit time 
through a capillary increases with brain size as 
, i.e. the scaling exponent is again 
. Another variable that seems to be independent of brain scale is partial oxygen pressure in cerebral capillaries (Table 3), which is consistent with the empirical findings in Fig. 3D on the invariance of oxygen pressure in arteries, as the two circulatory systems are mutually interconnected.
2. Capillary scaling in cerebral and non-cerebral tissue
The above scaling results for the brain can be compared with available analogous scaling rules for pulmonary, cardiovascular, and muscle systems. For these systems, it was proposed (no direct measurements) that partial oxygen pressure in capillaries should decline weakly with whole body volume (or organ volume as lung and heart volumes, 
, scale isometrically with body volume [2]) with an exponent around 
, to account for the whole body specific metabolic exponent 
[47], [48]. In the resting pulmonary system, the capillary radius as well as the density of capillary length scale the same way as they do in the brain, i.e., with the exponents 1/12 and 
, respectively, against system's volume [49]. Also, the capillary blood velocity in cerebral and non-cerebral tissues scale similarly, at least for not too small volumes, i.e. both are scale invariant [2], [3] (Table 3). However, the number of capillaries and capillary length seem to scale slightly different in the resting lungs, i.e. 
and 
[47], although the difference can be very mild. For the resting heart, it was predicted (again, no direct measurements) that 
, and blood transit time through a capillary 
[48], i.e. the exponents are multiples of a quarter power and are slightly larger than those for the brain (Table 3). Interestingly, for muscles and lungs in mammals exercising at their aerobic maxima, the blood transit time scales against body mass with an exponent close to 1/6 [50], which is the same as in the brain (Table 3). This again suggests that brain metabolism is similar to the metabolism of other maximally exercised organs. Overall, the small differences in the capillary characteristics among cerebral and non-cerebral resting tissues might account for the observed differences in the allometries of brain metabolism and whole body resting metabolism. In particular, the prevailing exponent 1/6 found in this study for brain capillaries, instead of 1/4, seems to be a direct cause for the distinctive brain metabolic scaling.
3. Brain microvascular network vs. neural network
The interesting question from an evolutionary perspective is how the allometric scalings for brain capillary dimensions relate to the allometry of neural characteristics. The neural density 
(number of cortical neurons 
per cortical gray matter volume 
) scales with cortical volume with a similar exponent as does the density of capillary length 
(Fig. 4A). Thus, as a coarse-grained global description we have approximately 
(Fig. 4B,C), or 
. The latter relation means that the total number of neurons is roughly proportional to the total length of capillaries, or equivalently, that capillary length per cortical neuron is conserved across different mammals. This cross-species conclusion is also in agreement with the experimental data for a single species. In particular, for mouse cerebral cortex it was found that densities of neural number and microvessel length are correlated globally across cortical areas (but not locally within a single column) [51]. Moreover, since axons and dendrites occupy a constant fraction of cortical gray matter volume (roughly 1/3 each; [52], [53]), we have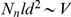 
, where 
and 
are respectively axon (or dendrite) length per neuron and diameter. Furthermore, because the average axon diameter 
(unmyelinated) in the cortical gray matter is approximately invariant against the change of brain scale [52], [54], we obtain the following chain of proportionalities: 
, where the exponent 
. For medium and large brains, 
, implying a nearly proportional dependence of axonal and dendritic lengths on capillary segment length. For very small brains (roughly below the volume of rat brain), 
can be substantially greater than 1, suggesting a non-linear dependence between capillary and neural sizes.
Given that the main exchange of oxygen between blood and brain takes place in the capillaries, these results suggest that metabolic needs of larger brains with greater but numerically sparser neurons must be matched by appropriately longer yet sparser capillaries. This finding reflects a rough, global relationship, which might or might not be related to the fact that during development neural and microvessel wirings share mutual mechanisms [20], [55]. At the cortical microscale, however, things could be more complicated, and a neuro-vascular correlation might be weaker, as both systems are highly plastic even in the adult brain (e.g. [56]). Regardless of its nature and precise dependence, the neuro-vascular coupling might be important for optimization of neural wiring [53], [57], [58]. In fact, neural connectivity in the cerebral cortex is very low, and it decreases with brain size [58], [59], similar to the density of capillary length (Fig. 3B, Table 3). To make the neural connectivity denser, it would require longer axons and consequently longer capillaries. That may in turn increase excessively brain volume and its energy consumption, i.e. the costs of brain maintenance. As a result, the metabolic cost of having more neural connections and synapses for storing memories might outweigh its functional benefit.
The brain metabolism is obviously strictly related to neural activities. In general, higher neural firing rates imply more cerebral energy consumed [18], [19]. It was estimated, based on a theoretical formula relating CMR with firing rate, that the latter should decline with brain size with an exponent around 
[19]. This implies that neurons in larger brain are on average less active than neurons in smaller brains. Such sparse neural representations may be advantageous in terms of saving the metabolic energy [18], [60], [61]. At the same time, what may be related, neural activity is distributed in such a way that both the average energy per neuron and the average blood flow per neuron are approximately invariant with respect to brain size (Fig. 5; Table 3, [26]). Additionally, average firing rate should be inversely proportional to the average blood transit time 
through a capillary, because both of them scale reversely with brain size (Table 3). Thus, it appears that global timing in neural activities should be correlated with the timing of cerebral blood flow. These general considerations suggest that apart from structural neuro-vascular coupling there is probably also a significant dynamic coupling. This conclusion is qualitatively compatible with experimental observations in which enhanced neural activity is invariably accompanied by increase in local blood flow [62].
4. Relationship to brain functional imaging
The interdependencies between brain metabolism, blood flow, and capillary parameters can have practical meaning. Currently existing techniques for non-invasive visualization of brain function, such as PET or fMRI, are associated with measurements of blood flow CBF and oxygen consumption CMR
. It turns out that during stimulation of a specific brain region, CBF increases often, but not always, far more than CMR
[63]. However, both of them increase only by a small fraction in relation to the background activity, even for massive stimulation [62], [63]. This phenomenon was initially interpreted as an uncoupling between blood perfusion and oxidative metabolism [64]. Later, it was shown that this asymmetry between CBF and CMR
can be explained in terms of mechanistic limitations on oxygen delivery to brain tissue through blood flow [65]. We can provide a related, but simpler explanation of these observations that involves physical limitations on the relative changes in capillary oxygen pressure and radius.
During brain stimulation, both CBF and CMR
change by 
and 
, which are according to Eqs. (1) and (8) related to modifications in capillary radius (from 
to 
), and changes in partial oxygen pressure (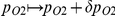
). The density of perfused capillary length 
remains constant for normal neurophysiological conditions. Accordingly, a small fraction of blood flow change is
 |
(9) |
and similarly, a small fractional change in the oxygen metabolic rate is:
 |
(10) |
In general, oxygen pressure increases with increasing capillary radius, in response to increase in blood flow CBF. This relationship can have a complicated character. We simply assume that 
, where the unknown exponent 
contains all the non-linear effects, however complicated they are. Thus, a small fractional change in oxygen pressure can be written as 
. As a result, we obtain
 |
(11) |
If partial oxygen pressure 
depends on capillary radius linearly or sublinearly, i.e., if 
, then the fractional increase in oxygen metabolism is significantly smaller than a corresponding increase in cerebral blood flow. This case corresponds to the experimental reports showing that this ratio is 
, for example, in the visual cortex (
) [66] and in the sensory cortex (
) [64], [67]. If, in turn, 
depends on 
superlinearly, i.e. if 
, then the coefficient 
in Eq. (10) can be of the order of unity. Such cases have been also reported experimentally during cognitive activities [42] or anesthesia [68], [69].
Materials and Methods
The ethics statement does not apply to this study. CBF data were collected from different sources: for mouse [70], rat [71], rabbit [72], cynomolgus monkey [73], rhesus monkey [74], pig [75], and human [76]. Cerebral capillary characteristics were obtained from several sources: for mouse [14], [51], rat [15], [77], [32], cat [40], [78], dog [79], rhesus monkey [80], and human [33], [34]. Data for calculating neuron densities were taken from [24], [25], [41], [52], [81], [82]. Cortical volume data (for 2 hemispheres) are taken from [52], [41], [81]. Their values are: mouse 0.12 cm
, rat 0.42 cm
, rabbit 4.0 cm
, cat 14.0 cm
, cynomolgus monkey 21.0 cm
, dog 35.0 cm
, rhesus monkey 42.9 cm
, pig 45.0 cm
, human 571.8 cm
. All the numerical data are provided in the Supporting Information (Tables S1, S2, and S3).
Supporting Information
(TEX)
Regional cerebral blood flow CBF in mammals.
(TEX)
Cerebral capillary and neural characteristics in mammals.
(TEX)
Arterial partial oxygen pressure and average cortical CBF per neuron.
(TEX)
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: The work was supported by the grant from the Polish Ministry of Science and Education (NN 518 409238), and by the Marie Curie Actions EU grant FP7-PEOPLE-2007-IRG-210538. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Kleiber M. Body size and metabolic rate. Physiol. Rev. 1947;27:511–541. doi: 10.1152/physrev.1947.27.4.511. [DOI] [PubMed] [Google Scholar]
- 2.Schmidt-Nielsen K. Scaling: why is animal size so important? Cambridge: Cambridge Univ. Press; 1984. [Google Scholar]
- 3.Calder WA. Size, function, and life history. Cambridge, , MA: Harvard Univ. Press; 1984. [Google Scholar]
- 4.Dodds PS, Rothman DH, Weitz JS. Re-examination of the ‘3/4-law’ of metabolism. J Theor Biol. 2001;209:9–27. doi: 10.1006/jtbi.2000.2238. [DOI] [PubMed] [Google Scholar]
- 5.Enquist BJ, West GB, Brown JH. Quarter-power allometric scaling in vascular plants: functional basis and ecological consequences. In: Brown JH, West GB, editors. Scaling in biology. Oxford: Oxford Univ. Press; 2000. pp. 113–128. [Google Scholar]
- 6.West GB, Brown JH, Enquist BJ. A general model for the origin of allometric scaling laws in biology. Science. 1997;276:122–126. doi: 10.1126/science.276.5309.122. [DOI] [PubMed] [Google Scholar]
- 8.Darveau C, Suarez R, Andrews R, Hochachka P. Allometric cascade as a unifying principle of body mass effects on metabolism. Nature. 2002;417:166–170. doi: 10.1038/417166a. [DOI] [PubMed] [Google Scholar]
- 9.Savage VM, Deeds EJ, Fontana W. Sizing up allometric scaling theory. PLoS Comput Biol. 2008;4(9):e1000171. doi: 10.1371/journal.pcbi.1000171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Karbowski J. Global and regional brain metabolic scaling and its functional consequences. BMC Biology. 2007;5:18. doi: 10.1186/1741-7007-5-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Krogh A. The anatomy and physiology of capillaries, 2nd ed. New Haven, , CT: Yale Univ. Press; 1929. [Google Scholar]
- 12.Klein B, Kuschinsky W, Schrock H, Vetterlein F. Interdependency of local capillary density, blood flow, and metabolism in rat brain. Am J Physiol. 1986;251:H1333–H1340. doi: 10.1152/ajpheart.1986.251.6.H1333. [DOI] [PubMed] [Google Scholar]
- 13.Borowsky IW, Collins RC. Metabolic anatomy of brain: a comparison of regional capillary density, glucose metabolism, and enzyme activities. J Comp Neurol. 1989;288:401–413. doi: 10.1002/cne.902880304. [DOI] [PubMed] [Google Scholar]
- 14.Boero JA, Ascher J, Arregui A, Rovainen C, Woolsey TA. Increased brain capillaries in chronic hypoxia. J Appl Physiol. 1999;86:1211–1219. doi: 10.1152/jappl.1999.86.4.1211. [DOI] [PubMed] [Google Scholar]
- 15.Hauck EF, Apostel S, Hoffmann JF, Heimann A, Kempski O. Capillary flow and diameter changes during reperfusion after global cerebral ischemia studied by intravital video microscopy. J Cereb Blood Flow Metab. 2004;24:383–391. doi: 10.1097/00004647-200404000-00003. [DOI] [PubMed] [Google Scholar]
- 16.Ito H, Kanno I, Ibaraki M, Hatazawa J, Miura S. Changes in human cerebral blood flow and cerebral blood volume during hypercapnia and hypocapnia measured by positron emission tomography. J Cereb Blood Flow Metab. 2003;23:665–670. doi: 10.1097/01.WCB.0000067721.64998.F5. [DOI] [PubMed] [Google Scholar]
- 17.Aiello LC, Wheeler P. The expensive-tissue hypothesis: The brain and the digestive system in human and primate evolution. Curr Anthropology. 1995;36:199–221. [Google Scholar]
- 18.Attwell D, Laughlin SB. An energy budget for signaling in the gray matter of the brain. J Cereb Blood Flow Metabol. 2001;21:1133–1145. doi: 10.1097/00004647-200110000-00001. [DOI] [PubMed] [Google Scholar]
- 19.Karbowski J. Thermodynamic constraints on neural dimensions, firing rates, brain temperature and size. J Comput Neurosci. 2009;27:415–436. doi: 10.1007/s10827-009-0153-7. [DOI] [PubMed] [Google Scholar]
- 20.Carmeliet P, Tessier-Lavigne M. Common mechanisms of nerve and blood vessel wiring. Nature. 2005;436:193–200. doi: 10.1038/nature03875. [DOI] [PubMed] [Google Scholar]
- 21.Attwell D, Gibb A. Neuroenergetics and the kinetic design of excitatory synapses. Nat Rev Neurosci. 2005;6:841–849. doi: 10.1038/nrn1784. [DOI] [PubMed] [Google Scholar]
- 22.Heeger DJ, Ress D. What does fMRI tell us about neuronal activity? Nat Rev Neurosci. 2002;3:142–151. doi: 10.1038/nrn730. [DOI] [PubMed] [Google Scholar]
- 23.Logothetis NK, Wandell BA. Interpreting the BOLD signal. Annu Rev Physiol. 2004;66:735–769. doi: 10.1146/annurev.physiol.66.082602.092845. [DOI] [PubMed] [Google Scholar]
- 24.Herculano-Houzel S, Mota B, Lent R. Cellular scaling rules for rodent brains. Proc Natl Acad Sci USA. 2006;103:12138–12143. doi: 10.1073/pnas.0604911103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Herculano-Houzel S, Collins CE, Wong P, Kaas JH. Cellular scaling rules for primate brains. Proc Natl Acad Sci USA. 2007;104:3562–3567. doi: 10.1073/pnas.0611396104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Herculano-Houzel S. Scaling of brain metabolism with a fixed energy budget per neuron: Implications for neuronal activity, plasticity, and evolution. PLoS ONE. 2011;6(3):e17514. doi: 10.1371/journal.pone.0017514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Woodbury RA, Hamilton WF. Blood pressure studies in small animals. Am J Physiol. 1937;119:663–674. [Google Scholar]
- 28.Gregg DE, Eckstein RW, Fineberg MH. Pressure pulses and blood pressure values in unanesthetized dogs. Am J Physiol. 1937;118:399–410. [Google Scholar]
- 29.Li JK-J. Scaling and invariants in Cardiovascular biology. In: Brown JH, West GB, editors. Scaling in biology. Oxford: Oxford Univ. Press; 2000. pp. 113–128. [Google Scholar]
- 30.Lenigert-Follert E, Lubbers DW. Behavior of microflow and local PO 2 of the brain cortex during and after electrical stimulation. Pflugers Arch. 1976;366:39–44. doi: 10.1007/BF02486558. [DOI] [PubMed] [Google Scholar]
- 31.Hakeem AY, Hof PR, Sherwood CC, Switzer RC, Rasmussen LEF, Allman JM. Brain of the african elephant (Loxodonta africana): Neuroanatomy from magnetic resonance images. Anat Rec A. 2005;287 A:1117–1127. doi: 10.1002/ar.a.20255. [DOI] [PubMed] [Google Scholar]
- 32.Michaloudi H, Batzios C, Grivas I, Chiotelli M, Papadopoulos GC. Developmental changes in the vascular network of the rat visual areas 17, 18, and 18a. Brain Res. 2006;1103:1–12. doi: 10.1016/j.brainres.2006.05.069. [DOI] [PubMed] [Google Scholar]
- 33.Meier-Ruge W, Hunziker O, Schulz U, Tobler HJ, Schweizer A. Stereological changes in the capillary network and nerve cells of the aging human brain. Mechanisms of Ageing and Development. 1980;14:233–243. doi: 10.1016/0047-6374(80)90123-2. [DOI] [PubMed] [Google Scholar]
- 34.Lauwers F, Cassot F, Lauwers-Cances V, Puwanarajah P, Duvernoy H. Morphometry of the human cerebral cortex microcirculation: General characteristics and space-related profiles. NeuroImage. 2008;39:936–948. doi: 10.1016/j.neuroimage.2007.09.024. [DOI] [PubMed] [Google Scholar]
- 35.Sugihara-Seki M, Fu BM. Blood flow and permeability in microvessels. Fluid Dynamics Research. 2005;37:82–132. [Google Scholar]
- 36.Fahraeus R, Lindqvist T. The viscosity of the blood in narrow capillary tubes. Am J Physiol. 1931;96:562–568. [Google Scholar]
- 37.Pries AR, Secomb TW, Gaehtgens P. Biophysical aspects of blood flow in the microvasculature. Cardiovasc Res. 1996;32:654–667. [PubMed] [Google Scholar]
- 38.Amin TM, Sirs JA. The blood rheology of man and various animal species. Q J Exp Physiol. 1985;70:37–49. doi: 10.1113/expphysiol.1985.sp002895. [DOI] [PubMed] [Google Scholar]
- 39.Schlageter KE, Molnar P, Lapin GD, Groothuis DR. Microvessel organization and structure in experimental brain tumors: microvessel populations with distinctive structural and functional properties. Microvascular Res. 1999;58:312–328. doi: 10.1006/mvre.1999.2188. [DOI] [PubMed] [Google Scholar]
- 40.Pawlik G, Rackl A, Bing RS. Quantitative capillary topography and blood flow in the cerebral cortex of cat: an in vivo microscopic study. Brain Res. 1981;208:35–58. doi: 10.1016/0006-8993(81)90619-3. [DOI] [PubMed] [Google Scholar]
- 41.Herculano-Houzel S, Mota B, Wong P, Kaas JH. Connectivity-driven white matter scaling and folding in primate cerebral cortex. Proc Natl Acad Sci USA. 2010;107:19008–19013. doi: 10.1073/pnas.1012590107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Roland PE, Eriksson L, Stone-Elander S, Widen L. Does mental activity change the oxidative metabolism of the brain? J Neurosci. 1987;7:2373–2389. [PMC free article] [PubMed] [Google Scholar]
- 43.Bishop CM. The maximum oxygen consumption and aerobic scope of birds and mammals: getting to the heart of the matter. Proc R Soc Lond B. 1999;266:2275–2281. doi: 10.1098/rspb.1999.0919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Weibel ER, Hoppeler H. Exercise-induced maximal metabolic rate scales with muscle aerobic capacity. J Exp Biol. 2005;208:1635–1644. doi: 10.1242/jeb.01548. [DOI] [PubMed] [Google Scholar]
- 45.Weibel ER, Taylor CR, Hoppeler H. The concept of symmorphosis: a testable hypothesis of structure-function relationship. Proc Natl Acad Sci USA. 1991;88:10357–10361. doi: 10.1073/pnas.88.22.10357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Unekawa M, Tomita M, Tomita Y, Toriumi H, Miyaki K, Suzuki N. RBC velocities in single capillaries of mouse and rat brains are the same, despite 10-fold difference in body size. Brain Res. 2010;1320:69–73. doi: 10.1016/j.brainres.2010.01.032. [DOI] [PubMed] [Google Scholar]
- 47.Dawson TH. Scaling laws for capillary vessels of mammals at rest and in exercise. Proc R Soc Lond B. 2003;270:755–763. doi: 10.1098/rspb.2002.2304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.West GB, Brown JH, Enquist BJ. The origin of universal scaling laws in biology. In: Brown JH, West GB, editors. Scaling in biology. Oxford: Oxford Univ. Press; 2000. pp. 87–112. [Google Scholar]
- 49.Dawson TH. Modeling the vascular system and its capillary networks. In: Yim PJ, editor. Vascular Hemodynamics: Bioengineering and Clinical Perspectives. New York: Wiley; 2008. [Google Scholar]
- 50.Kayar SR, Hoppeler H, Jones JH, Longworth K, Armstrong RB, et al. Capillary blood transit time in muscles in relation to body size and aerobic capacity. J Exp Biol. 1994;194:69–81. doi: 10.1242/jeb.194.1.69. [DOI] [PubMed] [Google Scholar]
- 51.Tsai PS, Kaufhold JP, Blinder P, Friedman B, Drew PJ, et al. Correlations of neuronal and microvascular densities in murine cortex revealed by direct counting and colocalization of nuclei and vessels. J Neurosci. 2009;29:14553–14570. doi: 10.1523/JNEUROSCI.3287-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Braitenberg V, Schüz A. Cortex: Statistics and Geometry of Neuronal Connectivity. Berlin: Springer; 1998. [Google Scholar]
- 53.Chklovskii DB, Schikorski T, Stevens CF. Wiring optimization in cortical circuits. Neuron. 2002;43:341–347. doi: 10.1016/s0896-6273(02)00679-7. [DOI] [PubMed] [Google Scholar]
- 54.Olivares R, Montiel J, Aboitiz F. Species differences and similarities in the fine structure of the mammalian corpus callosum. Brain Behav Evol. 2001;57:98–105. doi: 10.1159/000047229. [DOI] [PubMed] [Google Scholar]
- 55.Stubbs D, DeProto J, Nie K, Englund C, Mahmud I, et al. Neurovascular congruence during cerebral cortical development. Cereb Cortex. 2009;19:32–41. doi: 10.1093/cercor/bhp040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Chklovskii DB, Mel BW, Svoboda K. Cortical rewiring and information storage. Nature. 2004;431:782–788. doi: 10.1038/nature03012. [DOI] [PubMed] [Google Scholar]
- 57.Mitchison G. Neuronal branching patterns and the economy of cortical wiring. Proc R Soc Lond B. 1992;245:151–158. doi: 10.1098/rspb.1991.0102. [DOI] [PubMed] [Google Scholar]
- 58.Karbowski J. Optimal wiring principle and plateaus in the degree of separation for cortical neurons. Phys Rev Lett. 2001;86:3674–3677. doi: 10.1103/PhysRevLett.86.3674. [DOI] [PubMed] [Google Scholar]
- 59.Karbowski J. How does connectivity between cortical areas depend on brain size? Implications for efficient computation. J Comput Neurosci. 2003;15:347–356. doi: 10.1023/a:1027467911225. [DOI] [PubMed] [Google Scholar]
- 60.Levy WB, Baxter RA. Energy efficient neural codes. Neural Comput. 1996;8:531–543. doi: 10.1162/neco.1996.8.3.531. [DOI] [PubMed] [Google Scholar]
- 61.Laughlin SB, de Ruyter van Steveninck RR, Anderson JC. The metabolic cost of neural information. Nature Neurosci. 1998;1:36–41. doi: 10.1038/236. [DOI] [PubMed] [Google Scholar]
- 62.Moore CI, Cao R. The hemo-neural hypothesis: on the role of blood flow in information processing. J Neurophysiol. 2008;99:2035–2047. doi: 10.1152/jn.01366.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Raichle ME, Mintun MA. Brain work and brain imaging. Annu Rev Neurosci. 2006;29:449–476. doi: 10.1146/annurev.neuro.29.051605.112819. [DOI] [PubMed] [Google Scholar]
- 64.Fox PT, Raichle ME. Focal physiological uncoupling of cerebral blood flow and oxidative metabolism during somatosensory stimulation in human subjects. Proc Natl Acad Sci USA. 1986;83:1140–1144. doi: 10.1073/pnas.83.4.1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Buxton RB, Frank LR. A model of the coupling between cerebral blood flow and oxygen metabolism during neural stimulation. J Cereb Blood Flow Metab. 1997;17:64–72. doi: 10.1097/00004647-199701000-00009. [DOI] [PubMed] [Google Scholar]
- 66.Fox PT, Raichle ME, Mintun MA, Dence C. Nonoxidative glucose consumption during focal physiologic neural activity. Science. 1988;241:462–464. doi: 10.1126/science.3260686. [DOI] [PubMed] [Google Scholar]
- 67.Seitz RJ, Roland PE. Vibratory stimulation increases and decreases the regional cerebral blood flow and oxidative metabolism: a positron emission tomography (PET) study. Acta Neurol Scand. 1992;86:60–67. doi: 10.1111/j.1600-0404.1992.tb08055.x. [DOI] [PubMed] [Google Scholar]
- 68.Nilsson B, Siesjo BK. The effect of phenobarbitone anaesthesia on blood flow and oxygen consumption in the rat brain. Acta Anaesthesiol Scand. 1975;Suppl. 57:18–24. doi: 10.1111/j.1399-6576.1975.tb05408.x. [DOI] [PubMed] [Google Scholar]
- 69.Smith AL, Wollman H. Cerebral blood flow and metabolism. Anesthesiology. 1972;36:378–400. doi: 10.1097/00000542-197204000-00015. [DOI] [PubMed] [Google Scholar]
- 70.Frietsch T, Maurer MH, Vogel J, Gassmann M, Kuschinsky W, et al. Reduced cerebral blood flow but elevated cerebral glucose metabolic rate in erythropoietin overexpressing transgenic mice with excessive erythrocytosis. J Cereb Blood Flow Metab. 2007;27:469–476. doi: 10.1038/sj.jcbfm.9600360. [DOI] [PubMed] [Google Scholar]
- 71.Frietsch T, Krafft P, Piepgras A, Lenz C, Kuschinsky W, et al. Relationship between local cerebral blood flow and metabolism during mild and moderate hypothermia in rats. Anesthesiology. 2000;92:754–763. doi: 10.1097/00000542-200003000-00019. [DOI] [PubMed] [Google Scholar]
- 72.Tuor UI. Local cerebral blood flow in the newborn rabbit: an autoradiographic study of changes during development. Pediatric Res. 1991;29:517–523. doi: 10.1203/00006450-199105010-00020. [DOI] [PubMed] [Google Scholar]
- 73.Orlandi C, Crane PD, Platts SH, Walovitch RC. Regional cerebral blood flow and distribution of [99mTc]Ethyl Cysteinate dimer in nonhuman primates. Stroke. 1990;21:1059–1063. doi: 10.1161/01.str.21.7.1059. [DOI] [PubMed] [Google Scholar]
- 74.Noda A, Ohba H, Kakiuchi T, Futatsubashi M, Tsukada H, et al. Age-related changes in cerebral blood flow and glucose metabolism in conscious rhesus monkeys. Brain Res. 2002;936:76–81. doi: 10.1016/s0006-8993(02)02558-1. [DOI] [PubMed] [Google Scholar]
- 75.Delp MD, Armstrong RB, Godfrey DA, Laughlin MH, Ross CD, et al. Exercise increases blood flow to locomotor, vestibular, cardiorespiratory and visual regions of the brain in miniature swine. J Physiol. 2001;533.3:849–859. doi: 10.1111/j.1469-7793.2001.t01-1-00849.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Bentourkia M, Bol A, Ivanoiu A, Labar D, Sibomana M, et al. Comparison of regional cerebral blood flow and glucose metabolism in the normal brain: effect of aging. J Neurol Sci. 2000;181:19–28. doi: 10.1016/s0022-510x(00)00396-8. [DOI] [PubMed] [Google Scholar]
- 77.Bar TH. The vascular system of the cerebral cortex. Adv Anat Embryol Cell Biol. 1980;59:71–84. doi: 10.1007/978-3-642-67432-7. [DOI] [PubMed] [Google Scholar]
- 78.Tieman SB, Moller S, Tieman DG, White JT. The blood supply of the cat's visual cortex and its postnatal development. Brain Res. 2004;998:100–112. doi: 10.1016/j.brainres.2003.11.023. [DOI] [PubMed] [Google Scholar]
- 79.Luciano MG, Skarupa DJ, Booth AM, Wood AS, Brant CL, et al. Cerebrovascular adaptation in chronic hydrocephalus. J Cereb Blood Flow Metab. 2001;21:285–294. doi: 10.1097/00004647-200103000-00012. [DOI] [PubMed] [Google Scholar]
- 80.Weber B, Keller AL, Reichold J, Logothetis NK. The microvascular system of the striate and extrastriate visual cortex of the macaque. Cereb Cortex. 2008;18:2318–2330. doi: 10.1093/cercor/bhm259. [DOI] [PubMed] [Google Scholar]
- 81.Mayhew TM, Mwamengele GLM, Dantzer V. Stereological and allometric studies on mammalian cerebral cortex with implications for medical brain imaging. J Anat. 1996;189:177–184. [PMC free article] [PubMed] [Google Scholar]
- 82.Haug H. Brain sizes, surfaces, and neuronal sizes of the cortex cerebri: A stereological investigation of Man and his variability and a comparison with some mammals (primates, whales, marsupials, insectivores, and one elephant). Am J Anatomy. 1987;180:126–142. doi: 10.1002/aja.1001800203. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(TEX)
Regional cerebral blood flow CBF in mammals.
(TEX)
Cerebral capillary and neural characteristics in mammals.
(TEX)
Arterial partial oxygen pressure and average cortical CBF per neuron.
(TEX)