Depletion forces drive polymer-like self-assembly in vibrofluidized granular materials

Abstract

Ranging from nano- to granular-scales, control of particle assembly can be achieved by limiting the available free space, for example by increasing the concentration of particles (“crowding”) or through their restriction to 2D environments. It is unclear, however, if self-assembly principles governing thermally-equilibrated molecules can also apply to mechanically-excited macroscopic particles in non-equilibrium steady-state. Here we show that low densities of vibrofluidized steel rods, when crowded by high densities of spheres and confined to quasi-2D planes, can self-assemble into linear polymer-like structures. Our 2D Monte Carlo simulations show similar finite sized aggregates in thermally equilibrated binary mixtures. Using theory and simulations, we demonstrate how depletion interactions create oriented “binding” forces between rigid rods to form these “living polymers.” Unlike rod-sphere mixtures in 3D that can demonstrate well-defined equilibrium phases, our mixtures confined to 2D lack these transitions because lower dimensionality favors the formation of linear aggregates, thus suppressing a true phase transition. The qualitative and quantitative agreement between equilibrium and granular patterning for these mixtures suggests that entropy maximization is the determining driving force for bundling. Furthermore, this study uncovers a previously unknown patterning behavior at both the granular and nanoscales, and may provide insights into the role of crowding at interfaces in molecular assembly.

Introduction

High concentrations of macromolecules, sometimes termed “macromolecular crowding”, can lead to a shift in the equilibrium state of many supra-molecular assemblies. An important driving force behind this effect is the minimization of steric interactions, as determined by the size, shape, and density of the molecules^1-4. Of particular interest are self-assembly processes involving crowding in two-dimensions (2D)^{5, 6}, as in protein aggregation at cellular membranes^{7, 8} or fabrication of nanomaterials at interfaces⁹.

Under certain conditions, high concentrations of macroscopic objects can exhibit collective ordering that is reminiscent of behavior shown by their molecular counterparts. Interestingly, even though vibrofluidized granular materials display a wide variety of driven-dissipative behaviors and usually demonstrate complex non-equilibrium phenomena^10-16, such particles can also spontaneously form equilibriumlike patterns¹¹. A few recent studies have shown similarities between equilibrium, entropy driven, order-disorder type phase transitions and steady-state granular experiments^17-21, even when mechanically-driven granular particles do not possess Gaussian velocity distributions²⁰.

Entropy driven processes in hard classical particles arise only from variations in the number density of particles. For any classical ensemble, the total energy is separable into kinetic energy that depends on momentum, and potential energy that depends on particle positions²². In addition, when only hard core interactions are present, the total system potential energy of an ensemble of particles is the same for every allowed configuration. This implies that, in such systems at thermodynamic equilibrium, the probability for all allowed states is equal and independent of temperature (see “Thermodynamic depletion interaction theory for rod binding” in Material and Methods). Thus, under certain experimental conditions where the granular materials behave as microscopic hard core particles, patterning can be independent of their kinetic energy.

For example, we previously demonstrated that macroscopic rods can exhibit a lyotropic isotropic-to-nematic (I-N) transition¹⁷, which is driven, in simplest form, by increasing density that leads to geometrical “hard core” constraints between particles²³. In this temperature independent (“athermal”) transition, crowding drives the competition between two forms of entropy - rotational and translational - until ultimately one form of entropy “wins” at the expense of another. This suggests that the transitions in these granular experiments, as in their molecular analogues, simply result from maximization of configurational entropy.

To further explore the analogy between driven granular media and thermal equilibrium, we ask if entropy maximization can also determine pattern formation in granular mixtures in terms of molecular self-assembly. We focus on binary mixtures in 2D, where one type of particle is immersed in an excess of another, effectively “solvating” it. Although other experimental factors can influence granular segregation¹¹, evidence exists for entropy driven separations related to particle sizes in bidisperse mixtures of granular spheres that involve “depletion forces”¹⁹. Effective attractive interactions between large spheres result from a competition between large (“solute”) and small (“solvent”) particle entropies. According to Asakura-Oosawa (AO) theory²⁴, originally developed for colloidal suspensions, this “force” arises when the distance between two solute particles is less than the diameter of a solvent particle (Fig. 1).

Fig. 1.

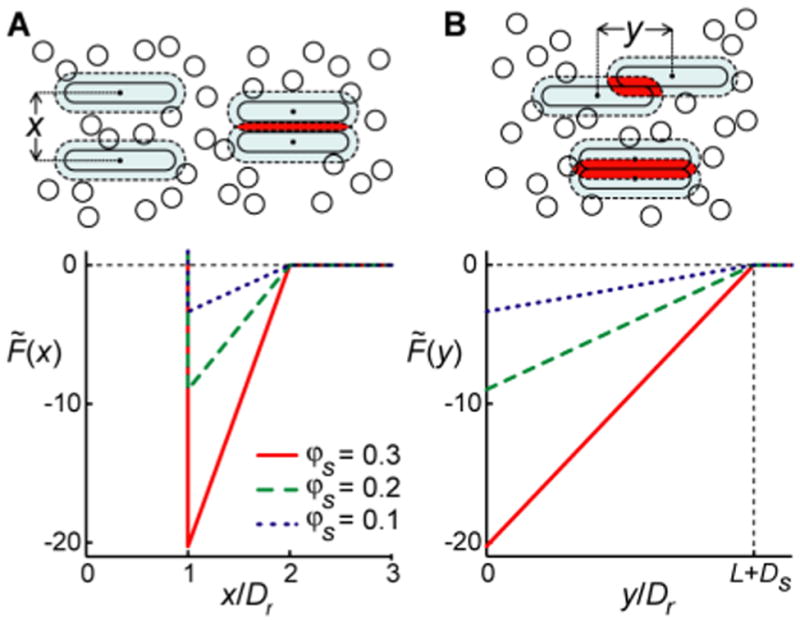
Attractive depletion interactions between hard rods in the presence of sphere crowders favor rod binding and suppress rod slip. Diagrams depict the area that rods exclude from spheres (dashed regions) and excluded area overlap (shaded regions) when two rods are less than one sphere diameter apart, shown for rod “binding” (A) and rod “slip” (B). The amount of excluded area overlap depends on mutual rod positions and adds to the free area of spheres, thereby increasing sphere entropy. With sufficient sphere density, the subsequent gain in sphere entropy can offset the loss in rod translational entropy, causing rod binding. The graphs show the scaled Helmholtz free energy F̃ = F_U/ kT between two hard rods immersed in a sea of hard spheres, as derived from the modified Asakura-Oosawa (AO) depletion interaction theory (see text). The free energy is shown as a function of the relative separation x and mutual “slip” y (as defined in respective diagrams) for various sphere area fractions φ_s, where D_r=D_s=1 and L = 20.

The free energy gain from depletion interactions between molecules or colloids can measure up to several kT ²⁵ (kT is thermal energy), comparable to many additional forces including van der Waals, screened electrostatic, and hydrogen bonding²⁶. While attractive interactions are traditionally deemed necessary for mediating precise binding in self-assembly processes²⁶, here we show how depletion interactions together with particle shape are, in fact, sufficient to induce specifically-oriented binding.

We report on fluidized mixtures of granular rods that self-assemble to form well defined linear stacks in quasi-2D environments with the addition of spheres. By using equilibrium 2D Monte Carlo simulations and a modified AO theory, we find that depletion forces drive the patterning in the granular and the analogous molecular systems, suggesting that these forces can act on many different scales. Unlike the known equilibrium phases for rod-sphere mixtures in 3D^27-33, both 2D simulations and experiments show finite sized linear (1D) aggregates, indicating that lower dimensionality prevents true phase separation.

This manuscript progresses as follows: We begin with a general description of the patterning diagram for granular rod and sphere mixtures, delineating particle arrangements for different densities of both particles. We then discuss the role of kinetic energy on the established granular analogue of the liquid crystal phase transition for vibrofluidized rods, demonstrating that, in some cases, the specifics of granular motion can be irrelevant for pattern formation. For the remainder of the manuscript, we focus on newly found arrangements in the patterning diagram—finite-sized linear rod aggregates. We show that these aggregates can be reproduced via equilibrium Monte Carlo simulations of hard rod and sphere mixtures. Using a simple depletion interaction theory in combination with self-assembly ideas, we then show that it is possible to fully predict the formation of these linear rod aggregates. And, with the same depletion interaction theory, we account for fluctuations of the stacking geometry in the rod aggregate structure. We conclude with a summary.

Results and discussion

Vibrofuidized granular rod-sphere mixtures form distinct patterns

We vertically vibrated stainless steel rods (r) and spheres (s) with equal diameters D_r= D_s, constrained to a container of area A and thickness 20D_r enclosing N_s spheres and N_r rods of length L (L/D_r =40) so that sphere area fraction is ${\phi }_s=\pi D_s^2{N}_s/4A$and rod area fraction is φ_r=L D_r N_r/ A. These binary granular mixtures exhibit rich patterning behavior in (φ_s, φ_r) space that is often visually similar to known liquid-crystalline phases (Fig. 2A-G).

Fig. 2.

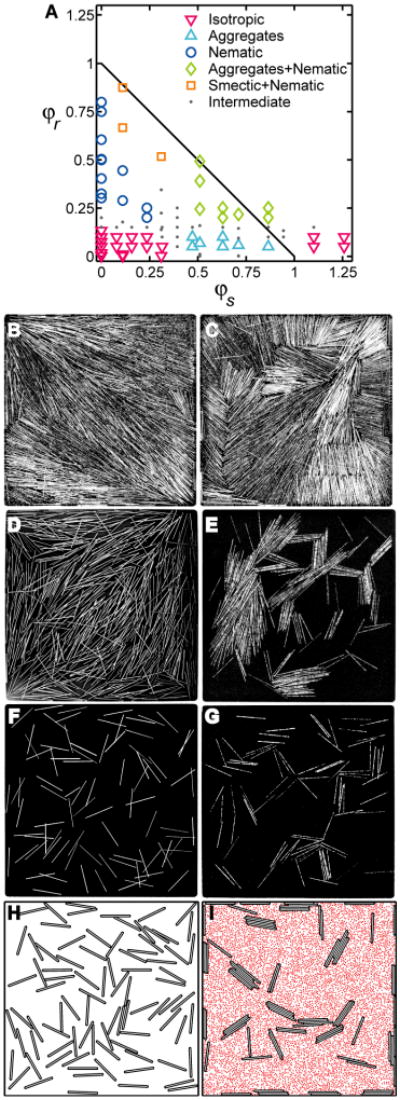
Rods aggregate in the presence of sphere crowders in both granular experiments and Monte Carlo simulations. (A) Diagram indicating the various patterning regimes for rod-sphere mixtures in quasi-2D granular experiments at steady-state, with D_r = D_s and L/D_r = 40. (B-G) Representative enhanced contrast, experimental images from smectic+nematic regimes (B, C, φ_r = 0.87, φ_s = 0.11, panels showing two snapshots of the same experiment at different times), nematic (D, φ_r = 0.40, φ_s = 0), aggregates+nematic (E, φ_r = 0.20, φ_s = 0.87), isotropic (F, φ_r = 0.05, φ_s = 0) and aggregate (G, φ_r = 0.05, φ_s = 0.63) regimes. (F) and (G) highlight sphere-induced rod aggregation at constant rod area fraction φ_r. In (E) and (G), spheres were anodized black to blend with background. (H, I) Strict-2D Monte Carlo simulations of thermally equilibrated rods (H, φ_r = 0.1, φ_s = 0) and rods mixed with spheres (I, φ_r = 0.1, φ_s = 0.3), with L D_r = 20 and with the following parameters matching those of granular experiments: D_r = D_s, N_r, and L -to-container dimensions. For clarity, only sphere midpoints are shown in (I). Strong visual similarities exist between experiments and simulations, both showing sphere-induced rod aggregation into finite sized clusters.

For φ_s = 0, rods exhibit liquid crystal-like behavior with an isotropic-nematic (I-N) transition¹⁷. This patterning appears to exist for low φ_s and low φ_r. As φ_r increases, the spheres induce smectic-like ordering, where rods align and form bundles that are quasi-periodic along the direction of the rod's long axis. However, unlike the stable smectic phase that appears in 3D equilibrium rod-sphere mixtures³⁰, the structure of the vibrofluidized mixtures oscillates in time between “smectic” and nematic patterns (Fig. 2B,C). We attribute this difference to non-equilibrium effects that arise from the details of kinetic energy input and losses in these experiments^10-16.

For high φ_s and low φ_r, we find that the rods coalesce, with their long axes in close proximity (Fig. 2G). This pattern, designated as “aggregates”, has not been previously described in granular mixtures and will be the focus of the remainder of this manuscript. This regime is bounded above on the φ_r -axis of Fig. 2A by the formation of a new pattern that we have called “aggregates+nematic”, which is evidently a non-equilibrium pattern, as discussed later in this manuscript. In addition, the “aggregate” pattern is also bound on the φ_s -axis, so that once φ_s + φ_r > 1, rods “float” on top of a bed of spheres and return to an isotropic configuration, as is also discussed later in the manuscript.

The role of temperature

Before further discussing the patterning diagram, we first address how particle kinetic energy can affect granular spatial arrangements. Due to the relatively large size of particles, thermal temperature does not appreciably move granular materials¹⁰; instead, energy must be supplied externally for particle motion to occur. In addition, energy is dissipated in the form of heat with every particle collision. Many non-equilibrium effects are known to emerge from this driven-dissipative combination of energy flow^10-16. However, for granular materials that behave as hard core particles, we propose that as long as all states are accessible and equally probable, the specifics of particle motion can be neglected. Similar to microscopic hard-core particles, the part of the free energy which dictates pattern formation depends only on the potential energy. For these cases, the potential energy is both separable from kinetic energy and independent of temperature.

Adding to the growing body of work on entropy driven transitions in granular materials that support this idea^17-21, we provide further experimental evidence based on the behavior of granular rods of different aspect ratios, L/D_r = 20, 40, and 60, in containers of various shapes and areas. The rod patterning diagram with respect to dimensionless acceleration, Γ ≡ b(2πf)²/g has previously been reported, where b is the vibration amplitude, f is frequency, and g is gravity³⁴. Here, we focus on the granular I-N transition since this transition has been shown to closely resemble that of microscopic particles¹⁷. In addition, extensive experimental, theoretical, and computational studies on rods at equilibrium in 3D, 2D, and quasi-2D serve as reference points for our results^35-37. For 2D systems, the I-N transition is expected to be continuous, with a critical density ρ^*. Note, though, that our granular experiments are not infinitely sized and, therefore, cannot show a true phase transition^{17, 38}.

By holding Γ constant and varying f, we can alter the peak container velocity v_p = b/2π f and measure the resulting changes in the rod orientational order parameter Σ = 〈cos (2θ_i)〉, where θ_i is the angle of the i th rod with the nematic director. Fig. S1 is a plot of Σ versus the normalized density ρ =φ_rL/D_r that characterizes the I-N transition in 2D. For a given f, the data for all rod aspect ratios and containers collapse to a single curve, within experimental error (Fig. S1).

When f decreases, the critical density, ρ^*, also increases. There are two potential causes for this shift. First, the rods bounce higher with decreasing f, and, therefore, occupy more space in the direction parallel to gravity. Indeed, in equilibrium simulations, increasing the thickness of a quasi-2D sample was found to decrease the 3D critical normalized density³⁶, which, when using the measurement methods employed for these granular experiments, leads to an apparent increase in the 2D ρ*. This shift roughly scales to the thickness of the 3^rd dimension. Second, there may be a kinetic contribution to the I-N transition in granular rods, where, for example, kinetic energy losses from rod collisions cause rod alignment.

We cannot accurately measure the locations of the rods in the direction parallel to gravity, and are thus unable to determine the distribution of rods in this direction. As an alternative control parameter, we have mechanically changed the height of the container. Decreasing the container height-to-rod diameter ratio, H/D_r, from 20 to 14, does not significantly encroach upon the rods, as is confirmed by the similarities in the results for those two heights (Fig. S2). However, a further decrease in the container height results in lower values of ρ*.

We find that a simple and purely geometric scaling of ρ, which accounts only for the variations of the effective rod density due to changes in H/D_r (see Materials and Methods), collapses the data from all f and all container heights to a single curve, within experimental error (Fig. 3). We thus demonstrate that the I-N transition is robust to multiple variations in experimental conditions. While we cannot exclude the possibility that these multiple experimental variations also change the kinetic energy of the particles to yield this simple geometrical scaling, our results suggest that it is mainly the excluded volume that controls patterning in these experiments.

Fig. 3.

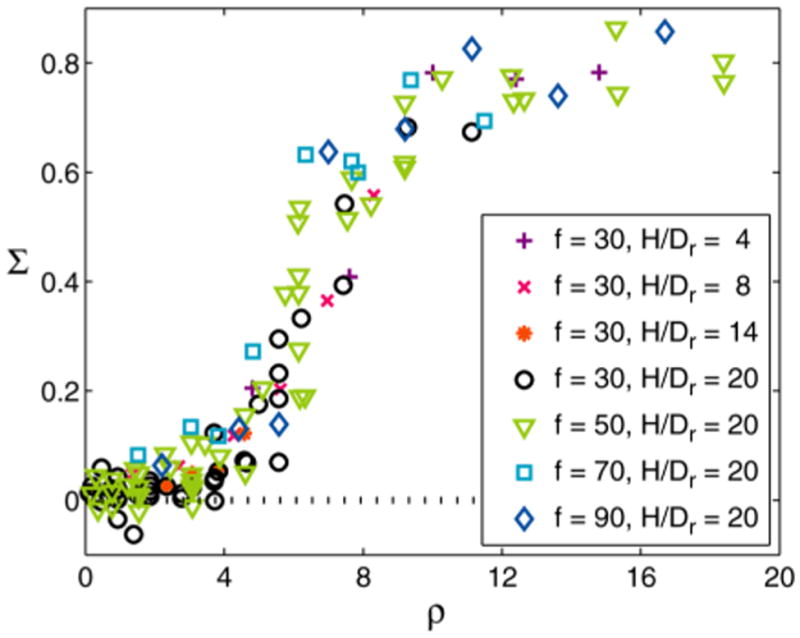
The isotropic-nematic phase transition for granular rods. Plot shows the rod orientational order parameter S versus normalized density ρ. Data from Figs. S1 and S2 collapse to a single curve when the normalized density ρ is rescaled as described in the section on Granular Experiments in Material and Methods.

Vibrofuidized granular rod-sphere mixtures show rod-rod clustering

We now focus on the region in (φ_s, φ_r) space showing linear rod stacking in the presence of spheres (Fig. 2A, designated as “aggregates”, △). As φ_s increases in this regime, we find that rods coalesce, with their long axes in close proximity (Fig. 2F,G). After an initial equilibration period of about 5 to 10 minutes, the size distribution of the aggregates remains constant in time, although individual rods associate and disassociate from groups, and aggregates merge and separate as they move over the container bottom. We find experimentally that aggregate sizes depend on crowding and grow with increasing φ_r (Fig. 4A) and φ_s (Fig 4B, see discussion below). Correspondingly, the rod-rod correlation function in the direction perpendicular to the rod axis reveals an increase in local rod density upon aggregation (Fig. S3A). This discrete aggregation differs from the known behavior of 3D thermally equilibrated molecular or colloidal rod-sphere mixtures, where experiments^{27, 28}, theory^{29, 30} and simulations^{31, 32} show that spheres induce a shift in the I-N transition towards lower rod densities and cause layered-like phases of interlaced rods and spheres and, even, complete separation into rod- and sphere-rich phases. We suggest that the different behavior in 2D occurs because restriction to a plane favors the formation of linear (1D) rod aggregates, for which there cannot be a phase transition^{39, 40}.

Fig. 4.

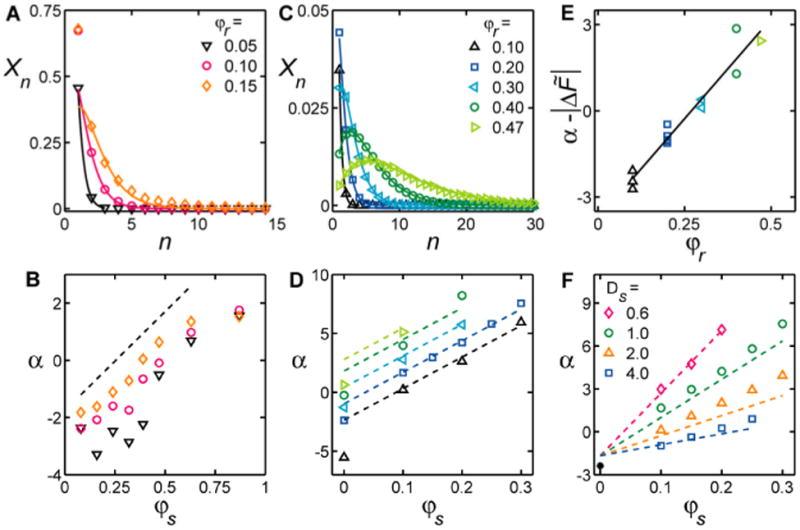
The distribution of rod aggregate sizes n and “rod binding energy” α (see text) depends on crowding. Size distribution of rod aggregates in granular experiments for φ_s = 0.39 (A, symbols) and simulations for φ_s=0.1 (C, symbols). Corresponding lines are fits using eqn [3]. The magnitude of α as determined from the fits for experiments (B, symbols as defined in A) and simulations (D, symbols as defined in C). The line in (B) corresponds to the AO fit with sphere density divided by 7.5, to compensate for a container thickness of 20D_r. The lines in (D) denote the predictions from AO theory, where the offset between α and |ΔF̃| due to changes in φ_r was taken from (E) (symbols as defined in C). Note, that since the entropy gain for spheres drives rod aggregation, the linear relation of rod binding to φ_s is not expected to hold as φ_s approaches zero in (D). Figure F shows variations of α due to D_s based on simulations (symbols) and as predicted from AO theory (lines).

Monte Carlo simulations of mixtures at equilibrium show rod-rod clustering

We performed equilibrium 2D Monte Carlo simulations to test if rod clustering in the granular mixtures could result from sphere-induced depletion interactions. Simulations included mixtures of “rods” (hard rectangles capped by semicircles) and “spheres” (circular disks) in containers with reflecting boundaries. Like our granular experiments, the simulations reveal finite aggregates (Fig. 2H, I) whose average size increases with crowding (Figs. 4C and 4D, see discussion below). Rod-rod correlations exhibit the most dramatic density variations with distance of all measured particle pair correlation functions. Upon increasing φ_s, we find sharp rod-density undulations at distances < L/2, reflecting the formation of highly ordered rod associations (Fig. S3B) and indicating that spheres can induce an effective attractive force between rods in this thermally-equilibrated analogue of our granular system.

Rod “binding” and the formation of 1D rod “polymer” stacks

Approximate relations for the effective strength of these depletion-induced attractive interactions can be derived by extending the classical AO mean-field theory²⁴ to rod-sphere mixtures in 2D (derivation in Materials and Methods). Briefly, the dimensionless Helmholtz free energy associated with the potential energy U for a sea of N_s spheres surrounding two parallel rods (Fig. 1) is F̃ = F_U/k = −Tln Q≈−lnq^N_s, with Q being the total configurational partition function, and q the partition function for a single sphere. Here F̃ is calculated for a particular rod separation x (Fig. 1A) and, as in the original AO theory, we make the approximation that the partition functions of different spheres are independent. For particles interacting though hard core potentials, entropy S fully determines the free energy F̃ = −S/k. The thermodynamic temperature T is therefore irrelevant in this instance and need not correspond to the so called granular temperature¹⁰. Since particles interact only through hard core potentials, q relates to the area accessible to a sphere as determined by the mutual positions of the rods (eqn [10] in Materials and Methods).

The area available to spheres is maximized when the rods are parallel and fully apposed (Fig. 1A). This implies that depletion interactions cause rods to associate with a specific orientation. We first assume this particular (parallel) orientation for rods at all separations x. Therefore, F̃ is infinite for x ≤ D_r, zero for x > D_r + D_s, and negative at intermediate separations with the minimum occurring when the rods touch (Fig. 1A). It can be shown that the modified AO free energy difference ΔF̃ in 2D for a two-rod “dimer” (x = D_r) versus fully separated rods (x = ∞), is (derivation in Materials and Methods)

$$\text{Δ}\stackrel{\sim }{F}=\stackrel{\sim }{F}(x=D_r)-\stackrel{\sim }{F}(x\to \infty )\approx -\frac{N_s{D}_s(L+D_s)}{A}.$$ [1]

Our experiments and simulations, however, not only show dimers but also aggregates composed of multiple rods (Fig. 2G,I). This rod stacking is analogous to a linear self-assembly process where individual rods act as monomers and reversibly bind to form “living polymers” or 1D micelles^{40, 41}. Hence, we next compare the granular experiments and Monte Carlo simulations with self-assembly theory to determine if the size distribution of the observed aggregates can be predicted.

For a system in equilibrium, the chemical potential μ of monomers in all aggregates is necessarily equal, so that

$$\mu ={\mu }_n={\mu }_n^{°}+\frac{kT}{n}1\text{n}\frac{X_n}{n}$$ [2]

where μ_n and ${\mu }_n^{°}$are the chemical potential and standard chemical potential, respectively, per monomer, and X_n is the mole fraction of rods in clusters of size n. Using eqn [2] and assuming αkT is the binding free energy between rods, we find the following size distribution of aggregates (derivation in Materials and Methods),

$$\frac{X_n}{n}=\exp \left[\left(\alpha +\text{ln}{X}_1\right)n-\alpha \right].$$ [3]

The lines for the distributions of aggregate sizes in Fig. 4A,C are fits to eqn [3], obtained by varying the parameters α and X₁. The theory provides excellent predictions for granular experiments at low φ_r, and for simulations at all tested φ_r and φ_s≠ 0. Fig. 4B, D shows how α increases as a function of crowding in both experiments and simulations.

In principle, α is related to |ΔF̃|. Indeed, we find that values of α determined from simulations and values of |ΔF̃| derived using the same parameters (N_s,D_s,L, A) are close in magnitude and have similar slopes with increasing φ_s (Fig. 4D). Unlike α, however, ΔF̃ does not account for all contributions to the changes in free energy upon binding, such as misaligned rod association or “slip” (Fig. 1B), rod rotational entropy, multiple rod interactions, and aggregate entropy. Interestingly, these additional contributions cause α to vary linearly with φ_r, as shown in Fig. 4E, and thus shift α from the predictions of the AO theory by only a constant. Finally, we further tested the predictions of eqn [3] by varying D_s and found the behavior of α and |ΔF̃| comparable (Fig. 4F).

Note that, for the experiments, |ΔF̃| overestimates α. This most likely reflects the fact that our experimental setup is quasi-2D, with a container thickness of 20D_r. Therefore, out-of-plane sphere bouncing in experiments significantly decreases the effective φ_s that causes rod aggregation, as we have similarly shown for rod-only systems. We can empirically account for out-of-plane sphere configurations by dividing the sphere density used in eqn [1] by 7.5. This value roughly agrees with previous estimates indicating that, on average, the centre of mass of a sphere lies between 3 to 7 D_s above the container bottom for our experimental conditions¹⁵.

Rod aggregation occupies a restricted region of the patterning diagram (Fig. 2A). As φ_s approaches 1, rods begin to float on top of a bed of spheres, resulting in isotropic rod patterns. This particle separation by gravity, where larger objects rise to the top, has been shown in other granular mixtures^{11, 12}. Also, as φ_r increases beyond 0.1, large nematic-like rod tactoids transiently appear (“aggregates+nematic”, Fig. 2A,E), which increases the probability of finding larger aggregate sizes than predicted. Two possible explanations can account for these tactoids. First, because nematic phases are observed in 3D rod-sphere mixtures, the presence of tactoids in our quasi-2D experiments may be a residual 3D effect. To test this possibility, we performed quasi-2D simulations with container thickness ranging from 1.5D_r to 4D_r. Unlike the behavior in the experiments, we found that rods phase-separated from spheres onto both planar surfaces of the container, forming isotropic patterns for all φ_r and φ_s tested. This patterning has also been noted in simulations of similar rod-sphere mixtures³³. Second, the nematic-like aggregates may be a consequence of granular cluster formation resulting from kinetic energy loss due to inelastic collisions¹⁴.

Rod “slip” in clusters diminishes with crowding

We also find that rods in aggregates may show a significant amount of “slip” (Fig. 1B), so that the entire cluster appears as a skewed parallelogram rather than a rectangle (Fig. 2G,I). However, experiments and simulations both show that the slip between the long axis of neighboring rods decreases (clusters appear more rectangular) as crowding increases. To analyze the dependence of slip on increasing φ_s and φ_r, we follow changes in Δy, defined as the width at half height of the first peak in the rod-rod correlation function in the direction parallel to the rod axis (Fig. S3C,D). Figures 5A and 5B show that, in both simulations and experiments, Δy decreases with increasing φ_s and φ_r.

Fig. 5.

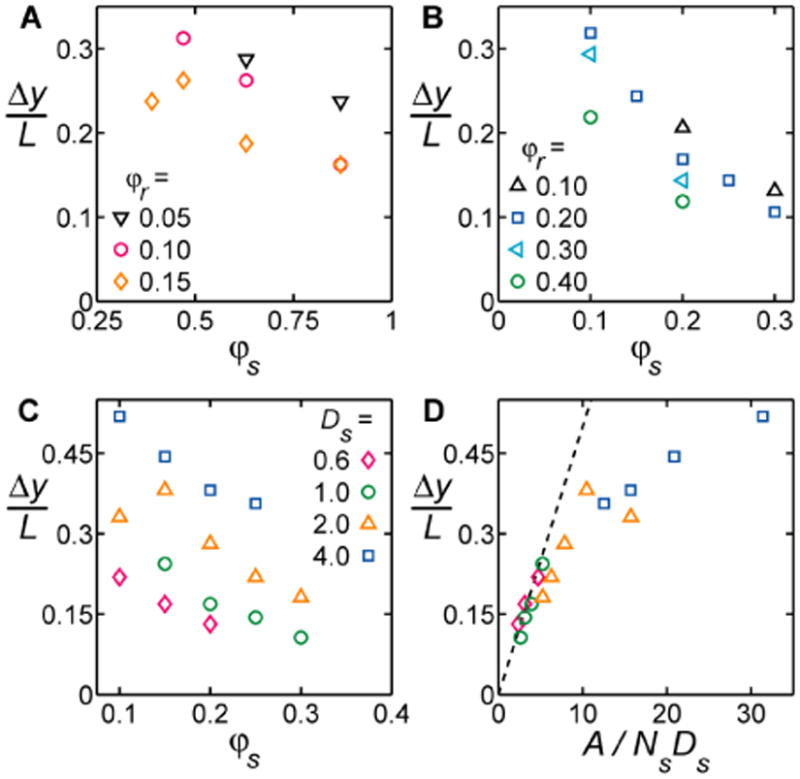
Rod slip decreases with crowding and shows universal scaling behavior. The width at half height of the first peak in the rod-rod correlation function in the direction parallel to the rod axis, Δy, versus sphere density φ_s for experiments (A) and simulations (B) at various φ_r and fixed D_s=1. (C) The dependence of rod slip on several sphere diameters in Monte Carlo simulations. (D) Same data as (C), now collapsed when plotted versus a scaling parameter derived from AO theory (symbols as in C). Dashed line in (D) shows the linear scaling predicted from eqn [4]. The linear region of the data is extended when AO theory incorporates sphere-sphere excluded volume (Fig. S4).

Clearly, maximum excluded volume overlap occurs when the midpoints of two contiguous rods are aligned, as shown in Fig. 1A. In reality, the extent of overlap mismatch is controlled by competition between the translational entropies of spheres and rods. Thus, as crowding increases, the entropic penalty for rod misalignment becomes larger, thereby reducing rod slip. We can quantify this behavior, with the same AO theory, by further considering rods sliding past each other (Fig. 1B). The extent of rod slip that can be accounted for by “thermal” fluctuations are those for which ΔF_U/ kT ≈ 1 (or S/k ≈ 1). Therefore, we can estimate (derivation in Materials and Methods) that the fluctuations in Δy should scale as,

$$\mathrm{\Delta }y\approx \frac{A}{N_s{D}_s}.$$ [4]

To test for scaling behavior, we focus on the dependence of Δy on D_s in the simulations, where we define Δy as the width at half height of the most prominent peak in g_2,r–r(x*,y) (Fig. S3). We find that Δy decreases with increasing D_s (Fig. 5C). Using eqn [4] to plot data from Fig. 5C, we find that all points collapse to a single “universal” curve (Fig. 5D). While the specific linear dependence predicted by eqn [4] holds only for low A/N_sD_s, the inclusion of sphere-sphere excluded volume further extends the range for which the linear regime seems applicable (Fig. S4). We also examined the dependence of sphere size in the granular experiments, but found that larger, heavier spheres rolled on top of rods, rather than mixing in the same plane.

Summary

Energy input (vibration) and losses (friction) make it difficult to predict a priori whether a particular set of granular experimental conditions will result in equilibriumlike behavior. We suggest, however, that as long as the experiments satisfy the requirement that all states are equally probable and properly sampled, similar behavior can be expected for granular materials and their molecular counterparts, irrespective of particle dynamics.

In this study we have shown that low densities of vibrofluidized steel rods, in a “solution” of sphere crowders, self-assemble to form linear polymer-like structures when confined to a quasi-2D plane. Simulations and theory demonstrate how similar aggregates should be expected for the molecular-scale analogue when only depletion-interaction acts to induce rod self-assembly. The qualitative and quantitative analogy that we find between the granular and molecular mixtures suggests that granular materials may behave as their molecular counterparts in this part of the rod-sphere patterning diagram. Moreover, this link between the different length scales also provides insight into molecular patterning, allowing access to conditions that are difficult to probe directly at the nanoscale level. It is surprising to find such close agreement between our granular experiments and equilibrium theory. Additional work will be necessary to determine the depth and generality of this analogy; therefore, the results described in this manuscript are likely to stimulate discussion and further work.

Finally, this work highlights how particle assembly due to crowding in 2D yields fundamentally different behavior than in 3D. Reduced dimensionality, combined with anisotropic particle shape, leads to the formation of linear rod aggregates which, due to their 1D nature, do not undergo an order-disorder transition but instead form finite sized rod stacks. More generally, understanding particle behavior in such confined environments opens the possibility of controlling aggregations by using appropriately shaped particles that will specifically bind, even without the assistance of attractive interactions.

Granular experiments

The methods presented here are similar to those previously described¹⁷. Briefly, we used stainless steel spheres (diameter D_s = 0.08cm) and stainless steel wire (diameter D_r = 0.08cm) cut into rods with aspect ratios of L/D_r = 20, 40, and 60 where L is rod length. The lateral walls of the container were machined into a square (diagonal = 29cm) or circle (radius = 7 or 15cm). Unless otherwise stated, the container chamber was covered by a Plexiglas lid to give a thickness of 20D_r, and the rods were shaken by an Unholtz-Dickie vibration system with a sinusoidal acceleration of 50Hz . All experiments had a constant peak acceleration of 4 times gravity, as measured by an accelerometer. Possible effects of the magnetic field of the shaker were minimized by distancing the chamber from the shaker, and electrostatic forces were reduced by using aluminum components for the chamber and applying an anti-static coating to non-metallic surfaces. To randomize initial conditions, particles were dropped into the containers from above before experiments. In order to better visualize the rods, spheres were anodized black; we found no significant differences between the patterning with or without sphere coating. Images of rods in motion were captured by a high speed digital camera. The position and orientation of each rod were found by an image processing algorithm written in Matlab 6.5.

Because our experiments are not infinitely sized, a true istoropic-nematic phase transition cannot be observed^{17, 38}. We, therefore, approximate ρ* by performing a linear least squares fit of the data in the transition zone^{17, 36}. In order to perform the rescaling for Fig. 3, we set the data from H/D_r = 4 (closest to 2D confinement) as the reference. For each set of experimental conditions, we determined the ratio between the slopes from the least square fits and the reference, and divided ρ by this ratio.

Monte Carlo simulations

We performed two-dimensional (2D) Monte Carlo simulations in the canonical (NVT) ensemble with hard particles⁴²: disks (referred to here as 2D “spheres”) and diskorectangles (rectangles capped by two semi-circles, referred to here as “rods”). Particles were confined to a square area bounded by hard walls, with dimensions similar to those in the granular experiments: diagonal = 9.2L and D_r = D_s = 1. We also performed simulations with L/D_r = 20, 40, and 60. Data presented in this manuscript are from L/D_r = 20. While the majority of simulations with longer rods yielded jammed states, computations for low φ_s and φ_r showed linear rod aggregates with similar scaling behavior as data with L/D_r = 20.

The interaction potential U(d_min) between spheres, rods, and walls was infinity if d_min < d* and zero if d_min ≥ d*, where d_min is the minimum distance between two objects and d* is the distance at which objects overlap. Initial particle positions (and orientations for rods) were selected at random, except for simulations with very high densities where particles were randomly inserted into previously equilibrated runs with lower rod densities. An attempted move involved a change in a particle's midpoint position x, y (and also angle θ for a rod). Attempted step sizes for moving both spheres and rods were equal and were adjusted to give an acceptance ratio for a rod move of ≈ 15%. Simulations were considered equilibrated when parameters that reflect the probability distribution of the rods stabilized: orientational order parameter for runs without spheres, average rod group size for runs with spheres. At a minimum, the first 1×10⁵ cycles were discarded, where one Monte Carlo cycle is counted when all particles undergo an attempted move. Simulations ran for approximately 9×10⁸ to 9×10⁹ cycles, and 1 out of every 10⁴ cycles was saved for analysis.

Thermodynamic depletion interaction theory for rod binding

The partition function and Helmholtz free energy

Consider a 2D classical microscopic system in equilibrium composed of two rigid rods immersed in an infinite bath of rigid spheres. We start with the Hamiltonian ℋ (ν^N_s, ξ^N_S, x) of N_S spheres each with momentum ν, located at ξ and interacting with two (fixed) parallel rods that are separated by a distance x, as depicted in Fig. 1A. At thermal equilibrium, the canonical partition function is defined as²²

$$Q_{N_s}=\frac{1}{N_s!h^{2N_s}}\iint \exp \left[-\beta \mathscr{H}({\nu }^{N_s},{\xi }^{N_s},x)\right]d{\nu }^{N_s}d{\xi }^{N_s}$$ [5]

where h is Planck's constant. In classical statistical mechanics, the total energy is separable into a sum of kinetic K(ν^N_s) and potential energy U(ξ^N_s, x) terms ²², giving,

$$Q_{N_s}=\frac{1}{N_s!h^{2N_s}}\left(\int \exp \left[-K({\nu }^{N_s})/kT\right]d{\nu }^{N_s}\right)Q$$ [6]

where we have defined the configurational integral:

$$Q=\int \exp \left[-U({\xi }^{N_s},x)/kT\right]d{\xi }^{N_s}$$ [7]

and where k is the Boltzmann constant and T is temperature. The partition function is associated with the (Helmholtz) free energy F_Total = −KTlnQ_Ns = F_k + F_U, expressed here as a sum of the kinetic and potential energy contributions, F_K and F_U, respectively In eqn [6], the integral containing K(ν^N_s) can be considered as a scaling factor for Q_Ns and as an additive constant to F_Total. We, therefore, will only consider the configurational partition function Q to determine configurations corresponding to the minimum free energy.

With analogy to the work of Asakura and Oosawa (AO)²⁴, we obtain an approximation of the partition function per sphere q. In AO theory, the spheres are modeled as an ideal gas interacting only with rods through excluded volume; therefore, q is simply related to the free space available to the spheres, which only depends on the mutual positions of the rods. The Helmholtz free energy for a given x is defined as

$$\stackrel{\sim }{F}=F_U/kT=-T\text{ln}Q\approx -\text{ln}{q}^{N_s}$$ [8]

$$q=\underset{A}{\int }\exp \left[-U(\xi ,x)/kT\right]d\xi$$ [9]

where A is the total area of the system. We therefore obtain

$$q=\{\begin{array}{cc}A-2(L+D_s)(D_r+D_s)& \text{if}x\text{≥}{D}_r+D_s\\ A-2(L+D_s)(D_r+D_s)+(L+D_s)(D_r+D_s-x)& \text{if}{D}_r\le x<D_r+D_s\end{array}$$ [10]

In our approximation, (L + D_s)(D_r + D_s) is the excluded area between a rod and a sphere, and (L + D_s)(D_r + D_s–x) is area gained when two rod-sphere excluded areas overlap.

When discussing granular materials, the same derivations can be conducted in a similar fashion as in molecular systems, noting that now kT refers to a granular analogue of thermal excitation, rather than the thermal temperature. Granular materials often show non-Gaussian velocity distributions¹⁶; therefore, the integral over K(ν^N_s) may not be adequately described by the Boltzmann distribution. However, these contributions to the granular analogue of Q_Ns would not affect the configurational integral Q for rigid particles, as long as all accessible states are equally probable.

Free energy difference

Next, we derive the free energy difference between two rods aggregated versus separated, ΔF̃ = F̃ (x = D_r) − F̃ (x → ∞), where x = D_r is the closest distance attainable without rod overlap (Fig. 1A). Using eqns [8] and [10] we obtain,

$$\text{Δ}\stackrel{\sim }{F}=-N_s\text{ln}\left(1+\frac{D_s\left(L+D_s\right)}{A-2(L+D_s)(D_r+D_s)}\right)$$ [11]

Assuming that A ≫ 2(L + D_s)(D_r + D_s) and A ≫ D_s (L + D_s), we find

$$\text{Δ}\stackrel{\sim }{F}\approx -\frac{N_s{D}_s(L+D_s)}{A}.$$ [12]

Self-assembly theory and the chemical potential

We consider rod aggregation in both our experiments and simulations as an equilibrium 1D self-assembly process of particles with analogy to “living polymers” or worm-like micelles^{40, 41}. The chemical potential of all monomers in all aggregate species must be equal, so that

$$\mu ={\mu }_n={\mu }_n^{\circ }+\frac{kT}{n}ln\frac{X_n}{n}$$ [13]

where μ_n is the chemical potential of a rod in an aggregate containing n rods, ${\mu }_n^{°}$ is the standard part of the chemical potential per rod in an aggregate containing n rods, and X_n is the mole fraction of rods in aggregates containing n rods. In particular, for the monomer and aggregate of size n, we find

$${\mu }_n^{\circ }+\frac{\mathit{\text{kT}}}{n}\text{ln}\frac{X_n}{n}={\mu }_1^{\circ }+\mathit{\text{kT}}\ln X_1$$ [14]

Rearranging, we obtain

$$\frac{X_n}{n}={\left[X_1\exp \left(\frac{{\mu }_1^{\circ }-{\mu }_n^{\circ }}{kT}\right)\right]}^n$$ [15]

We now assume that αkT is the free energy for binding two rods. Therefore, the total free energy of rod aggregates containing n rods is⁴¹

$$n{\mu }_n^{\circ }=-\left(n-1\right)\alpha kT$$ [16]

Combining eqns [15] and [16], we find that the size distribution of aggregates is

$$\frac{X_n}{n}=\exp \left[\left(\alpha +\text{ln}{X}_1\right)n-\alpha \right]\text{.}$$ [17]

Thermodynamic depletion interaction theory for rod slip

The partition function and Helmholtz free energy

Again, we consider a 2D system of two rigid rods immersed in a bath of rigid spheres. The Hamiltonian ℋ (ν^N_s, ξ^N_s, y) of N_S spheres now depends on its interaction with two parallel rods that are touching but offset by a distance y (“slip”), as depicted in Fig. 1B. As before, we obtain an approximate expression for q by modeling the spheres as an ideal gas that interacts only with rods via excluded volume. Therefore, q depends only on the rods' mutual position. With the Helmholtz free energy for the potential energy defined as in eqn [8], we now have

$$q=\underset{A}{\int }\exp \left[-U(\xi ,y)/kT\right]d\xi$$ [18]

which results in

$$q=\{\begin{array}{cc}A-2(L+D_s)(D_r+D_s)& \text{if}y\text{≥}L+D_s\\ A-2(L+D_s)(D_r+D_s)+D_s(L+D_s-y)& \text{if}y<L+D_s\end{array}$$ [19]

where D_s (L + D_s –y) is the area gained when two rod-sphere excluded areas overlap.

Fluctuations in slip extent Δy

The maximum entropy gain for the spheres occurs when the two rods are touching and their midpoints are aligned (y = 0); however, such strict rod alignment reduces rod entropy. A balance between these two entropic terms can be obtained when rods are allowed to fluctuate in their mutual alignment. We are interested in small fluctuations (on the order of kT) of y, and derive the free energy difference between two aggregated rods that are perfectly aligned (y = 0) versus offset (y = Δy), so that

$$\text{Δ}{F}_U=F_U\left(\text{Δ}y\right)-F_U\left(0\right)\approx kT.$$ [20]

We will only consider rods whose excluded volumes overlap, i.e., y < L + D_s. Therefore using eqns [8] and [19] we find

$$\text{ln}\left(1-\frac{D_s\text{Δ}y}{A-2\left(L+D_s\right)\left(D_r+D_s\right)+D_{s}L+D_s^2}\right)\approx -\frac{1}{N_s}.$$ [21]

Assuming that $A\gg -2\left(L+D_s\right)\left(D_r+D_s\right)+D_{s}L+D_s^2$and A ≫ D_sΔy, we get

$$\text{Δ}y\approx \frac{A}{N_s{D}_s}.$$ [22]

It is also possible to incorporate sphere-sphere excluded volume on the level of the second virial coefficient. This can be done by modifying eqn [19] to

$$q=\{\begin{array}{cc}\stackrel{\sim }{A}-2(L+D_s)(D_r+D_s)& \text{if}y\ge L+D_s\\ \stackrel{\sim }{A}-2(L+D_s)(D_r+D_s)+D_s(L+D_s-y)& \text{if}y<L+D_s\end{array}$$ [23]

where $\stackrel{\sim }{A}=A-\frac{1}{2}\pi D_s^2{N}_s$. Therefore, eqn [22] becomes

$$\text{Δ}y\approx \frac{\stackrel{\sim }{A}}{N_s{D}_s}.$$ [24]

Supplementary Material

Fig. S1. Liquid crystal-like ordering of granular rods occurs at various vibration frequencies f. The granular isotropic-nematic (I-N) phase transition changes with varying frequency f, at constant dimensionless acceleration, Γ = 4, and constant container height-to-rod-diameter ratio H/D_r = 20, where f = 30Hz (black), 50Hz (red), 70Hz (blue), and 90Hz (green). For circular radius =7 cm container: L/D_r =20 (△), 40(□); circular radius =15cm container: L/D_r =20(▷), 40(×), 60 (○); square container: L/D_r = 20 (▽), 40 (◊). Line show the linear least squares fit of the data in the transition region (see Material and Methods). Bars represent the standard deviation from 3 to 100 experiments.

Fig. S2. The critical normalized density ρ^* for the I-N transition decreases with decreasing H/D_r with constant f = 30Hz and Γ = 4, where H/D_r = 20 (○), 14 (▽), 8 (□), and 4 (◊). Lines show the linear least squares fit of the data in the transition region (see Material and Methods).

Fig. S3. Rod-rod correlation functions g_2,r–r (x, y). The g_2,r–r (x, 0) function from the midpoint of a rod in the direction perpendicular to its long axis for granular experiments with φ_s = 0.47 (A), and Monte Carlo simulations with φ_s = 0.10 (B). The g_2,r–r (x^*, y) function parallel to a rod's long axis for granular experiments with φ_r = 0.10 (C) and Monte Carlo simulations with φ_r = 0.20 (D), where x^* is the maximum in the correlation function from g_2,r–r (x, 0). The smaller peak in (C) (occurring between 0.6<y/L < 1.25) indicates a preference for orthogonal aggregate-aggregate associations in granular experiments. For granular experiments (A and C), data was smoothed by a moving average filter with a span of 3 points. The material presented is as close to a direct comparison as possible between the pair correlations in the experiments and simulations, as is seen by the striking similarity in the plots. Comparisons with exactly the same rod and sphere area fractions are not feasible due to limitations in the granular experiments. Specifically, quasi-2D experiments require a higher concentration of spheres to achieve aggregation in rods (see manuscript). In addition, the appearance of non-equilibrium patterning prevents comparison with higher rod area fractions (see manuscript).

Fig. S4. Rod slip shows universal scaling behavior. Same data as Fig 4C, now collapsed when plotted versus a scaling parameter derived from AO theory by incorporating sphere-sphere excluded volume through the parameter à in eqn [20].