Skip to main content
PMC home page
Molecular Biology of the Cell logoLink to Molecular Biology of the Cell
. 2011 Nov 1;22(21):3995–4003. doi: 10.1091/mbc.E11-03-0278

The SCAR/WAVE complex is necessary for proper regulation of traction stresses during amoeboid motility

Effie Bastounis a,b,c, Ruedi Meili c, Baldomero Alonso-Latorre b, Juan C del Álamo b, Juan C Lasheras a,b,*, Richard A Firtel c,*,†
Editor: Peter Van Haastertd
PMCID: PMC3204062  PMID: 21900496

A combination of traction force and F-actin measurements shows that cells lacking either of the SCAR/WAVE complex proteins SCAR and PIR121 exhibit an altered cell motility cycle and spatiotemporal distribution of tractions stresses, which correlate in magnitude with F-actin levels.

Abstract

Cell migration requires a tightly regulated, spatiotemporal coordination of underlying biochemical pathways. Crucial to cell migration is SCAR/WAVE–mediated dendritic F-actin polymerization at the cell's leading edge. Our goal is to understand the role the SCAR/WAVE complex plays in the mechanics of amoeboid migration. To this aim, we measured and compared the traction stresses exerted by Dictyostelium cells lacking the SCAR/WAVE complex proteins PIR121 (pirA−) and SCAR (scrA−) with those of wild-type cells while they were migrating on flat, elastic substrates. We found that, compared to wild type, both mutant strains exert traction stresses of different strengths that correlate with their F-actin levels. In agreement with previous studies, we found that wild-type cells migrate by repeating a motility cycle in which the cell length and strain energy exerted by the cells on their substrate vary periodically. Our analysis also revealed that scrA− cells display an altered motility cycle with a longer period and a lower migration velocity, whereas pirA− cells migrate in a random manner without implementing a periodic cycle. We present detailed characterization of the traction-stress phenotypes of the various cell lines, providing new insights into the role of F-actin polymerization in regulating cell–substratum interactions and stresses required for motility.

INTRODUCTION

Chemotactic cell migration is essential in a wide range of physiological and pathological processes, including angiogenesis, embryonic development, innate immunity, metastasis of cancer cells, and chronic wounds (Ausprunk and Folkman, 1977; Grabher et al., 2007). Dictyostelium is frequently used as a model organism for studying chemotaxis since the core signaling pathways and mechanical properties are highly conserved (Devreotes and Zigmond, 1988; Chung and Firtel, 2002; Van Haastert and Devreotes, 2004; Stradal and Scita, 2006; Charest and Firtel, 2007). Chemotactic cells integrate the complex signaling networks that regulate their directional migration into a repetitive sequence of shape changes: protrusion of frontal pseudopodia and retraction of the back of the cell (Abercrombie et al., 1970; Lauffenburger and Horwitz, 1996; Webb et al., 2002; Uchida and Yumura, 2004; Lombardi et al., 2007). These shape changes are implemented periodically and in coordination with the traction stresses that drive cell motion, forming the stages of a motility cycle (Uchida and Yumura, 2004; del Álamo et al., 2007; Lombardi et al., 2007; Meili et al., 2010).

F-actin polymerization is known to be a key process in cell migration, in particular in the protrusion of the pseudopodia at the cell's leading edge (Weiner et al., 1999; Borisy and Svitkina, 2000). The spatiotemporal dynamics of the actin cytoskeleton are coordinated by upstream signaling regulators, including F-actin nucleators, and by F-actin cross-linking proteins (Mullins et al., 1998; Pollard, 2002; Pollard and Borisy, 2003). One important mechanism for F-actin growth is actin filament branching (dendritic polymerization), initiated by the Arp2/3 heptameric complex (Cooper et al., 2001; Miller, 2002; Beltzner and Pollard, 2008; Koestler et al., 2008). This complex is, in turn, regulated by F-actin nucleation–promoting factors, including the WASP and SCAR/WAVE protein complexes (Machesky and Insall, 1998; Blagg and Insall, 2004). The highly conserved SCAR/WAVE pentameric complex includes PIR121 (Sra-1/CYFIP/GEX-2), SCAR (WAVE), HSPC300, ABI1, and NAP1 (Hem2/KETTE/GEX-3), which bind and activate Arp2/3 and also bind other signaling factors that activate the SCAR/WAVE complex (Cory and Ridley, 2002; Basu et al., 2004; Ibarra et al., 2006; Davidson and Insall, 2011).

An increasing knowledge of actin polymerization regulation is starting to provide a general, more qualitative picture of how biochemical processes control cell migration. Unlike mammalian cells lacking the SCAR protein, Dictyostelium cells lacking SCAR (scrA− cells) can still move, albeit with reduced chemoattractant-induced F-actin polymerization, presumably by employing other F-actin nucleation–promoting factors such as WASP (Blagg et al., 2003; Ibarra and Insall, 2005). On the other hand, Dictyostelium cells lacking the SCAR/WAVE complex protein PIR121 (pirA− cells) undergo increased F-actin polymerization, enhanced pseudopod activity, and reduced substrate adhesion (Blagg et al., 2003).

However, there are essential aspects of this picture that are less clear. In particular, we do not know whether, or how, the regulation of F-actin polymerization by SCAR/WAVE affects the production of the traction stresses that drive cell movement. With this goal in mind, we used traction force cytometry (TFC) to measure the spatiotemporal distribution of the traction stresses exerted by wild-type cells and two SCAR/WAVE complex mutant strains migrating up a chemoattractant gradient on flat, elastic substrates. The precise characterization of each traction stress phenotype was then used to determine the role that SCAR/WAVE–mediated dendritic F-actin polymerization plays in the modulation of the cellular traction stresses and in the implementation of the motility cycle.

RESULTS

To examine the role that SCAR/WAVE–mediated dendritic F-actin polymerization plays in regulating the generation of traction stresses during amoeboid motility, we acquired time-lapse images of wild-type cells and two mutant strains that lack either the SCAR/WAVE complex component SCAR (scrA−) or PIR121 (pirA−). Cells are placed in a chemoattractant gradient on the surface of a polyacrylamide matrix with known elasticity containing fluorescent carboxymethylated poly­styrene beads (see Materials and Methods). As the cells move up the gradient, they deform the substrate, producing time-dependent displacements of the fluorescent beads. We used TFC and field statistical analysis to quantitatively analyze and compare the mechanical phenotypes of wild-type, scrA−, and pirA− cells.

Polarity and speed of the SCAR/WAVE mutants do not correlate with their F-actin levels

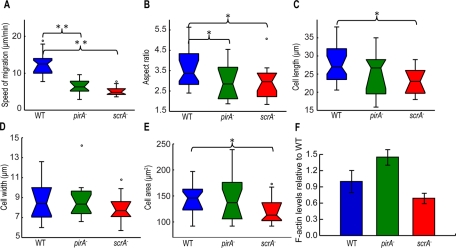
As reported by Blagg et al. (2003), we show that both scrA− and pirA− cells chemotax with less than half the speed of wild-type cells (Figure 1A). In our statistical analysis, we found that both mutants are less polarized than the wild type, and, in addition, scrA− cells have a reduced surface area (Figure 1, B–E). In contrast to Blagg et al. (2003), we did not observe frequent, multiple leading-edge protrusions in pirA− and scrA− cells, possibly due to differences in the experimental conditions (Supplemental Figure S1, A–C). In agreement with previous studies (Blagg et al., 2003; Ibarra et al., 2006), we found that resting pirA− cells contain on average 50% more basal F-actin per cell than wild-type cells, whereas scrA− cells have 30% less basal F-actin per cell than wild-type cells (Figure 1F). In response to the chemoattractant, both mutant strains exhibit proportional, stimulus-induced biphasic F-actin polymerization, as previously reported (Supplemental Figure S1D; Blagg et al., 2003; Ibarra et al., 2006).

FIGURE 1:

FIGURE 1:

Open in a new tab

Boxplots of kinematic parameters of chemotaxing wild-type (blue), pirA− (green), and scrA− (red) cells. (A) Speed of migration (μm/min). (B) Aspect ratio (cell length divided by cell width). (C) Cell length (μm). (D) Cell width (μm). (E) Area (μm2). Open circles represent outliers, and the notched section of the boxplots shows the 95% confidence interval around the median. Asterisks denote significant differences between distributions: *, 0.01 < pd < 0.05; **, pd < 0.01 (Wilcoxon rank sum test for equal medians). (F) Levels of F-actin of unstimulated cells normalized by the corresponding levels of unstimulated wild-type cells (F-actin assay). Error bars, SD from the average.

Disruption of the SCAR/WAVE complex causes the misregulation of the motility cycle

Amoeboid cells migrate by following a series of well-defined steps that result from periodic oscillations of the cell length L(t) and strain energy exerted on the substrate on which they migrate, Us(t) (see later discussion, Eq. 2; Supplemental Figures S2A and S3; Wessels et al., 1994; Fukui, 2002; Uchida and Yumura, 2004; Alonso-Latorre et al., 2009). To assess the importance of the effect of dendritic F-actin polymerization on the periodicity of the motility cycle, we analyzed and compared the temporal evolution of both L(t) and Us(t) time records for wild-type, scrA−, and pirA−cells (Supplemental Figure S2A; see Materials and Methods). The degree of periodicity of the individual records was assessed by fitting the data in a nonlinear, least squares sense with a sine wave and then calculating their cross-correlation (Supplemental Figure S3; see Materials and Methods).

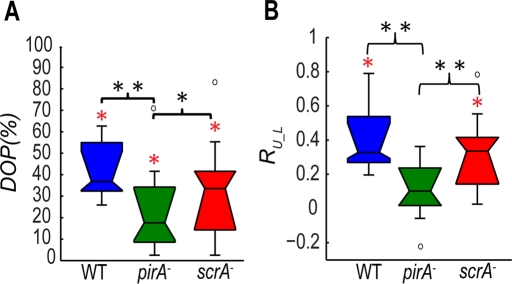
We found that the correlation between the cell length and the best-fitting sine wave (degree of periodicity of the time variation of L [DOP]) for scrA− cells (median of 33%) is similar to that for wild-type cells (median of 37%), whereas that for pirA− cells is significantly lower (median of 18%; Figure 2A). This finding indicates that the time record of the length of the cells in both wild-type and scrA− cells oscillates periodically. However, the time record of the cell length for pirA− cells is not periodic and exhibits more random and uncoordinated oscillations. This lack of periodicity of pirA− cells may be the reason why, despite their high F-actin content, they move less efficiently than scrA− cells, whose F-actin content is much lower. This could indicate that the efficiency of the cell motility depends more on the ability of the cell to perform a periodic cycle of protrusions and retractions rather than its overall F-actin content.

FIGURE 2:

FIGURE 2:

Open in a new tab

(A) Boxplots of the DOP of the time evolution of the cell length L(t). Boxplots refer to wild-type (N = 29, blue), pirA− (N = 18, green), and scrA− (N = 17, red) cells. (B) Boxplots of the correlation coefficients, RL_U, between the time evolution of the strain energy, Us(t), and the cell length, L(t), for each cell line. Boxplots refer to wild-type (N = 18, blue), pirA− (N = 16, green), and scrA− (N = 16, red) cells. Black asterisks, significant differences between distributions: *, 0.01 < pd < 0.05, **, pd < 0.01; red asterisks, a distribution with a median significantly different from zero: *, pz < 0.05 (Wilcoxon signed rank test).

Because the strain energy exerted by the chemotaxing cells on their substrates also exhibits an oscillatory behavior, we explored whether there was any relationship between the cell length and strain energy oscillations. In agreement with previous findings (Alonso-Latorre et al., 2009), we found a positive correlation in wild-type cells, indicating that the cell length oscillates with the same period and is in phase with the strain energy (Figure 2B and Supplemental Figures S2B and S4B). We also obtained a high degree of correlation for scrA− cells, although the cell length was slightly out of phase from the strain energy, suggesting there might be a delay for these cells to generate traction stresses (Figure 2B and Supplemental Figure S2B). In contrast, pirA− cells showed a much lower cross-correlation (Figure 2B).

The frequency of the motility cycle and distance advanced per cycle decrease in cells lacking SCAR

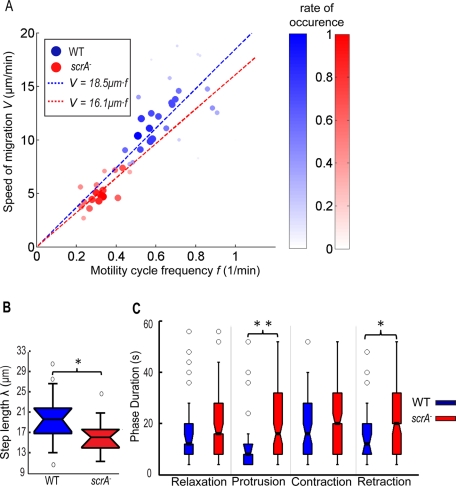
Our previous studies showed that wild-type cells and two strains with contractility deficiencies (Myosin II heavy chain–null cells, Myosin II essential light chain–null cells) migrate with an average speed V linearly proportional to the frequency f of the oscillations in their cell length and strain energy (Meili et al., 2010). This suggests the relation V = f · λ = λ/T, in which λ is a constant equal to the average step length advanced by the cell per cycle. Of interest, we found that this relation holds for scrA− cells, although, compared with the wild-type cells, their velocity–frequency slope is smaller, indicating that they perform, on average, a shorter step length per cycle (Figures 3, A–B, and S4, A and C). Furthermore, we found that the value of λ within the population of scrA− cells does not correlate with the size of the cells (Supplemental Figure S4C). This would suggest that the cause of their reduced step length is, most likely, not due to their smaller cell size. However, we found that for any given cell the step length is always lower than the average length of the cell (Supplemental Figure S4C).

FIGURE 3:

FIGURE 3:

Open in a new tab

(A) Scatter plot of the average speed of migration V versus the frequency f of their motility cycle determined through the time evolution of cell length, L(t) (N = 46). The data points refer to N = 29 wild-type (blue circles) and N = 17 scrA− cells (red circles). The dashed blue and red lines are the least square fits to the data for wild-type and scrA− cells, respectively. V = 18.5f for wild-type and V = 16.1f for scrA− cells, showing that the scrA− cells perform a motility cycle with an average step length of 16.1 μm vs. the 18.5 μm in the wild-type cells. The root mean square errors (RMSEs) when fitting the data linearly were RMSEWT = 3.20 and RMSEscrA = 0.99. The correlation coefficients of the two variables were RWT = 0.364 and RscrA = 0.785. To better visualize the correlation, the f–V plane was divided into rectangular tiles of equal area, and the size and color of each data point were scaled according to the total number of data points that fall on each specific tile (i.e., its rate of occurrence). As a result, darker, larger circles represent those data points that were observed more often in our experiments, and vice versa. (B) Boxplots of the average step length λ advanced per period and (C) time duration of each of the four phases for wild-type (blue) and scrA− cells (red). Asterisks, significant differences between distributions: *, 0.01< pd < 0.05; **, pd < 0.01.

To investigate the cause of the increase in the period for scrA− cells, we dissected the motility cycle into the four phases explained previously (del Álamo et al., 2007; Alonso-Latorre et al., 2009) and compared their time duration with that of wild type (Supplemental Figure S5). We determined that the longer period for scrA− cells was the result of a considerable increase in the time duration of the protrusion phase and, to a lesser extent, an increase in the duration of the retraction phase (Figure 3C).

Strength of traction stresses differs in the SCAR/WAVE mutants and correlates with their altered F-actin levels

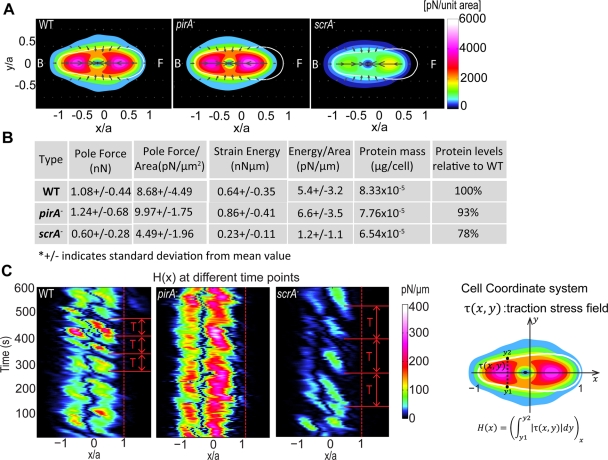
To assess the contribution of F-actin polymerization on the traction stresses generated by the cells during migration, we measured the traction stresses using our traction force cytometry technique (see Materials and Methods) (del Álamo et al., 2007). We then used conditional statistics to calculate the average traction stresses exerted by the cells during each of the four phases of their motility cycle (del Álamo et al., 2007; Meili et al., 2008). We found that for wild-type, pirA−, and scrA− cells, the average stress pattern consists of the localized attachment at the front and back of the cell and the simultaneous contraction of the substrate toward its center, in agreement with our previous studies (Figure 4A and Supplemental Figure S6; Alonso-Latorre et al., 2009). However, whereas the overall stress pattern is conserved in the SCAR/WAVE mutants, the magnitude of the traction stresses is altered. scrA− cells exert ∼50% weaker traction stresses, whereas the traction stresses exerted by pirA− cells are slightly larger than those of wild-type cells (Figure 4A and Supplementary Movies SM1 and SM2). Similar trends are observed for the average strain energy (Eq. 2; Figure 4B). These differences cannot be attributed to the cell size, since all measured mechanical parameters normalized by the cell area confirm that traction stresses are stronger in wild-type and pirA− cells than in scrA− cells (Figure 4B). Of interest, we found that the strength of the traction stresses for all cell lines correlates very well with the specific F-actin level of each cell line (Figures 4A and 1F; Blagg et al., 2003).

FIGURE 4:

FIGURE 4:

Open in a new tab

(A) Average stress distribution pattern for wild-type (N = 14), pirA− (N = 17), and scrA− (N = 14) cells during chemotaxis on elastic polyacrylamide substrate. The contour maps show the average traction stress field, computed in a reference frame rotated to have the x- and y-axes coincide with the instantaneous principal axes of the cells. All dimensions are scaled with the length of their instantaneous major axis, a. Details of how the cell-coordinate system used in these plots is constructed can be found elsewhere (del Álamo et al., 2007; Alonso-Latorre et al., 2009). The colors indicate the magnitude of the stresses in pN/unit area, and the arrows indicate their direction. The white contours show the average shape of the cells in this reference frame. The front (F) of the cell corresponds to x > 0 and the back (B) to x < 0. (B) First five columns: cell type; average values of the pole forces obtained from the integration of the stresses in the front and the back halves of the cells (Fp); average magnitude of the pole forces normalized by the cell area (Fp/Ac); average strain energy (Us); average strain energy normalized by the cell area (Us/Ac). The last two columns show the average protein amount in μg/cell (DC assay) for each cell line and the average protein amounts in the mutants compared with that measured in wild-type cells. (C) Time evolution of the magnitude of the integral of the traction stresses along the width of the cell as a function of the position along the cell length for a representative wild-type, pirA−, and scrA− cell (sketch). Dashed lines indicate the cell front. The adhesion sites of the cell can be clearly seen, as well as the frequency of the formation of frontal adhesions, which coincides with the measured period of the motility cycle (T).

Although the general stress pattern for all cell lines is similar, we found that, unlike the wild type, the leading edge of both SCAR/WAVE mutant strains exerts negligible traction stresses (Figure 4C and Supplemental Figure S7). The location of the maximum in the frontal traction stresses in the mutant cells is shifted toward the center of the cell, away from the leading edge (Figure 4A and Supplemental Figure S7A). By tracking the position of the integral of the traction stresses along the cell width as a function of the position along the cell length during time, we confirmed that the frontal attachments of both mutants are always shifted closer to the cell centroid as compared with the wild type (Figure 4C). Of interest, this specific stress mapping reveals that the frequency of the motility cycle we determined through the analysis of the oscillations in the cell length and strain energy also coincides with the frequency of frontal adhesion formation (Figure 4C).

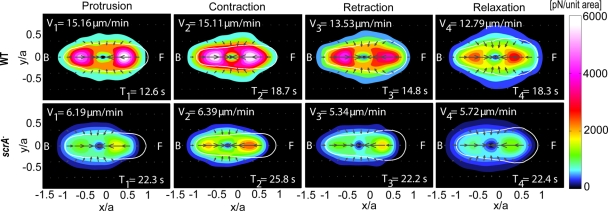
To further compare the mechanics of the cell lines that exhibit a motility cycle (wild-type and scrA− cells), we applied the phase-averaging method and examined the specific stress patterns during each of the four phases of their cycle (Figure 5 and Supplementary Movies SM1 and SM2; del Álamo et al., 2007; Alonso-Latorre et al., 2009). We found that the stress patterns during all phases are similar when comparing the two cell lines. However, for the majority of scrA− cells examined, the position of the maximum in the frontal traction stresses is closer to the cell's centroid for all phases compared the position of the maximum in wild-type cells; however, this difference is only statistically significant during the protrusion phase (Supplemental Figure S7B). The similarities of the phase-averaged stress patterns between the two cell lines not only reconfirm the preservation of the cyclical movement for scrA− cells, but also suggest that the mechanics of migration of scrA− cells are similar to those of wild-type cells, despite their altered F-actin levels and presumed dynamics. A detailed description of the technique used to calculate these phase averaged stress patterns can be found in Meili et al. (2010).

FIGURE 5:

FIGURE 5:

Open in a new tab

Phase-averaged traction stress maps and cell shapes corresponding to the four phases of the motility cycle for wild-type (N = 14) and scrA− (N = 14) cells (for description of the contour maps see Figure 4A). The legends show the average durations, T1,…, T4, and the corresponding average speeds during each phase, V1,…, V4.

F-actin at the cell's front and traction stress strength are highly correlated in wild-type and scrA− cells

We examined the spatiotemporal control of F-actin in vivo during chemotaxis by using the F-actin reporter Lifeact, a peptide derived from the F-actin–binding protein Abp140 fused to green fluorescent protein (GFP; Riedl et al., 2008). Joint analysis of the temporal evolution of the instantaneous maximum fluorescence intensity of Lifeact at the front of the cell, Gmax(t), and the cell length revealed that these quantities are highly correlated and are in phase for wild-type and scrA− cells (Supplemental Figure S8, C and D). However, pirA− cells showed no significant correlation between these two quantities, consistent with our finding that these cells do not undergo a synchronized motility cycle. Nevertheless, the average fluorescence intensity of all three strains is qualitatively similar (Figure 6A).

FIGURE 6:

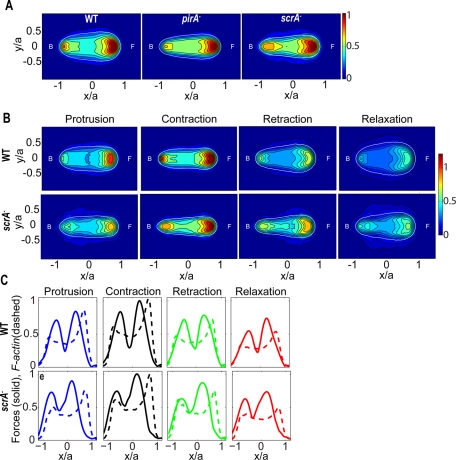
FIGURE 6:

Open in a new tab

(A) Average cell shape and localization of Lifeact, a reporter for F-actin, for wild-type (N = 9), pirA− (N = 8), and scrA− (N = 9) cells. The contour maps show the average fluorescence, computed in the same cell-based normalized reference frame as used in Figure 4A. The colors indicate the intensity of Lifeact. The white contours show the average shape of the cells. The front (F) of the cell corresponds to x > 0 and the back (B) corresponds to x < 0. (B) Phase-averaged cell shape and localization of Lifeact during the four stereotypical phases of the motility cycle for wild-type (N = 9) and scrA− (N = 9) cells. (C) Phase-averaged values of the Lifeact fluorescence intensity (dashed line) and of the traction stresses (solid line) integrated along the width of the cell as a function of the position along the cell length for wild-type (N = 6) and scrA− (N = 4) cells. The intensity and force levels are normalized with their maximum value for each cell.

We further examined the nature of the changes of the F-actin localization throughout the motility cycle for cells expressing the GFP-tagged F-actin reporter Lifeact. We found that the peak of F-actin at the cell front in both wild-type and scrA− cells is localized in a confined area during protrusion and contraction, whereas it is more diffused during retraction and relaxation (Figure 6B). Wild-type cells exhibit moderate frontal F-actin levels during protrusion, which then increase during contraction, decrease during retraction to levels lower than those during protrusion, and become minimal during relaxation (Figure 6B). This temporal pattern of F-actin levels coincides with the temporal pattern of the strength of the traction stresses (Figure 6C and Supplemental Figures S8A and S9). In contrast, scrA− cells show similar frontal F-actin levels during protrusion and retraction, when the strengths of the traction stresses are comparable (Figures 5A and 6, B and C). The locations along the cell's anterior–posterior axis of the frontal peak F-actin and the traction stresses are close to each other in wild-type cells, whereas they are further apart in scrA− cells (Figure 6C). This is consistent with our observation that the front of scrA− cells is elevated off of the substratum. We conclude that, although the localization and intensity modulation of F-actin during the distinct phases exhibit some minor differences, the oscillations of the amplitude of the traction stresses are well correlated with the oscillations of the peak of F-actin at the cell's front for both wild-type and scrA− cells (Figure 6C and Supplemental Figures S8 and S9).

DISCUSSION

We measured and analyzed the time evolution of the cell length, traction stresses, and strain energy exerted by mutants in the SCAR/WAVE complex (pirA− and scrA− cells) and wild-type cells with high spatial and temporal resolution. Although previous studies explored the biochemical role of some of the proteins in the SCAR/WAVE pentameric complex, little is known about their role in the mechanics of directed cell migration (Blagg et al., 2003; Blagg and Insall, 2004). We used TFC techniques and statistical analysis to establish a quantitative comparison of the motility phenotypes of wild-type, pirA−, and scrA− cells. This allowed us to obtain a quantitative insight into the role that these components play in the coordination of the cellular traction stresses that drive directional cell movement.

In our previous work, we showed that wild-type cells and cells with contractility deficiencies chemotax by performing cyclical oscillations of their cell length and strain energy (del Álamo et al., 2007; Meili et al., 2010). In the present study, we first investigated whether the SCAR/WAVE complex proteins PIR121 or SCAR were essential to the existence of a coordinated periodic motility cycle. We found that pirA− cells performed chemotaxis without implementing a periodic cycle, whereas scrA− cells chemotax by performing a well-coordinated periodic cycle of protrusions and retractions, similar to wild-type cells. Nevertheless, both the migration speed and the frequency with which the scrA− cells repeat their motility cycle are much lower than those of wild-type cells, which suggests that scrA− cells need more than twice the time that wild-type cells need to complete a cycle. The lack of a defined motility cycle in pirA− cells could be the reason why they migrate as slowly as scrA− cells even though they contain almost double the amount of F-actin. This suggests that the ability to implement a well-coordinated motility cycle is what determines the efficiency of the cell migration rather than the F-actin content. Moreover, this observation implies that regulated F-actin polymerization at the cell's front plays an essential role in the conservation of the motility cycle. For wild-type and scrA− cells, we found that the cell length and strain energy oscillations are highly correlated, suggesting that the regulation of the cycle depends on the ability of the cell to modulate its length and to generate traction stresses. We confirmed that the average period of the oscillations in the cell length (and strain energy) for wild-type and scrA− cells is inversely proportional to the cell's average migration speed, in agreement with our previous findings for cell movement on gelatin substrates (del Álamo et al., 2007; Meili et al., 2010) and with experimental measurements and theoretical models obtained for crawling keratocytes (Barnhart et al., 2010). This correlation is also consistent with the view that the average speed of migration of the cell is determined by the frequency at which it can perform its motility cycle. Of interest, we found that the step length for scrA− cells is shorter than for wild-type cells. This reduction in the average step length is due not to their smaller size but presumably to their altered F-actin dynamics.

By splitting the motility cycle into four canonical stages (phases), we found that the increase in the period of scrA− cells is mainly due to an increase in the time duration of the protrusion phase and, to a lesser extent, the retraction phase. This finding indicates that misregulating the dendritic F-actin polymerization primarily affects the duration of the phases in which the cell length changes the most, consistent with the key role that F-actin polymerization dynamics plays in the protrusion of the cell's leading edge. The increase in the time duration of protrusion may result from a lack of positive feedback from branching polymerization by Arp2/3. This may also explain why the durations of the contraction and relaxation phases are only slightly prolonged in scrA− cells compared with wild-type cells since they do not require changes in F-actin levels. However, the reason for the observed increase in the time duration of the retraction phase is unclear. One possible explanation is that the coordination of the actomyosin contractile network is affected by the misregulated F-actin dynamics. Contractile stresses are transmitted through the F-actin network, and therefore, structural changes of this network (more or less dendritic) in scrA− cells could also affect the efficiency of phases other than protrusion. Likewise, disruption of Myosin-II contractility or cross-linking has been shown to alter the duration of all the phases of the motility cycle, not only retraction (Meili et al., 2010).

Cells move by attaching and transmitting stresses to the substrate on which they migrate through the formation of adhesion sites whose function is controlled by membrane proteins bound to the cytoskeletal F-actin filaments (Devreotes and Zigmond, 1988). Consistent with this notion, the F-actin content and its cytoskeletal organization should affect the magnitude of the traction stresses. We confirmed this hypothesis by measuring the traction stress field produced by SCAR/WAVE complex mutants during chemotactic migration. Although for wild-type and mutant cells the time-averaged traction stresses show a similar simultaneous front-and-back contractile pattern, we found appreciable differences in the strength of these traction stresses in the different strains. The strength of the stresses is stronger for pirA− cells and weaker for scrA− cells when compared with wild-type cells and correlates with the differences in the levels of F-actin in each strain. This observation indicates that the strength of the traction stresses could be determined by the amount of F-actin present. Nevertheless, one cannot rule out the possibility that this change in magnitude may also be due to the differences in the structural organization of the F-actin networks (more or less dendritic actin) alluded to previously or to other effects associated with the SCAR/WAVE complex. Simultaneous phase average analysis of the traction stresses and F-actin levels using the Lifeact fluorescence reporter showed that the strength of the traction stresses and the maximum fluorescence intensity at the cell's front are both modulated up and down similarly during the different phases of the motility cycle. This provides strong evidence that the level of F-actin is one of the factors that determine the strength of the traction stresses exerted on the substrate.

We found that wild-type, pirA−, and scrA− cells promote F-actin polymerization and display similar localization of the F-actin reporter Lifeact. This suggests that misregulation of the SCAR/WAVE complex does not severely affect F-actin dynamics or its localization (Blagg et al., 2003; Ibarra et al., 2006). However, we found that although frontal F-actin levels and traction stress strength fluctuate considerably during the wild-type motility cycle (increase during protrusion, peak during contraction and decrease significantly in retraction and relaxation), for scrA− cells, F-actin and traction stresses are of similar magnitude in the protrusion and retraction phases, with less F-actin and stresses than wild-type cells during protrusion but more than wild-type cells during retraction. One could consider that, in scrA− cells, the increase in frontal F-actin during retraction and its decrease during protrusion are indicators of a time delay in the actin polymerization relative to the cell's lengthening. This is also consistent with the trend of the maximum frontal F-actin record to precede the cell length record. If actin polymerization is delayed compared with cell lengthening in scrA− cells, it raises the question of what other determinants of cell lengthening, apart from F-actin polymerization, are driving the migration of this strain. Hydrostatic pressure could have an increased effect on scrA− cells compared with wild-type cells, since an impeded dendritic structure of the cortex may result in a weakening of the cortex in the mutant. That could also partially explain the displacement of the frontal peak stresses closer to the cell's centroid and the slight delay of those cells in generating forces. However, we do not observe blebs formed by scrA− cells per se, nor can the short strain energy delay account for our observations. Future studies using a method that allows for better temporal resolution without the current side effects (cell movement altered due to abundant light exposure) will be needed to confirm this hypothesis. If the previous hypothesis does not hold, then the displacement of the frontal peak stresses closer to the cells' centroid observed in pirA− and scrA− cells most likely is due to defects in adhesion that cause the front of the cell to glide constantly. The gliding of the cell's leading edge indicates that misregulation of the SCAR/WAVE complex affects frontal adhesion to the substrate, perhaps due to changes in the F-actin network and/or to pleiotropic effects (i.e., the specific complex may also be involved in pathways controlling adhesion).

In summary, our findings highlight the importance of regulated, anterior F-actin polymerization in the generation of traction stresses and the regulation of the motility cycle of chemotaxing amoeboid cells. We demonstrated that the SCAR/WAVE complex is essential to the preservation of the cell motility cycle and that the strength of the cellular traction stresses is determined by the amount of F-actin in the cell. To fully characterize how the F-actin cytoskeleton regulates the mechanics of cell migration, future studies of actin-related proteins affecting stabilization, cross-linking, and the turnover of F-actin filaments, using the methodologies and techniques discussed here, will be required.

MATERIALS AND METHODS

Dictyostelium cell lines and microscopy

Axenically grown Dictyostelium wild-type and mutant cells were prepared for chemotaxis and seeded onto a flat, elastic polyacrylamide gel as described previously (del Álamo et al., 2007). We used KAx-3 (wild type), scrA−, and pirA− cells obtained from the Dicty Stock Center (DBS0236926 and DBS0236780). An expression plasmid containing the sequence for Lifeact (Abp140-GFP; Riedl et al., 2008), a 17–amino acid peptide that binds F-actin fused to GFP, was constructed using standard molecular biology techniques. The cell lines were transfected with this plasmid to generate Lifeact-expressing cells for fluorescence imaging.

For image acquisition, we used a Nikon TE300 inverted microscope and a PC running Metamorph software (Molecular Devices, Downington, PA), as described previously (del Álamo et al., 2007). For image acquisition of the cells expressing the Lifeact probe, a spinning disk confocal microscope (Leica DMIRE2, Yokogawa CSU10) was used, and a PC running SimplePCI software controlled the specific setup. Images were acquired at 2- and 4-s intervals for the wild-type and mutant cells, respectively. The total acquisition time ranged from 2400 to 4000 s. The time history of the wild-type and mutant cells considered for analysis was at least 320 s (approximately four cycles) and 640 s, respectively.

Polyacrylamide gel fabrication

Polyacrylamide gels of 5% acrylamide and 0.06% bis-acrylamide coated with 0.2 mg/ml collagen were prepared as described (Wang and Pelham, 1998; Engler et al., 2004). The gel consists of two layers: the bottom layer contains no beads, and the upper one contains 4 μl of 2% carboxylate modified yellow latex beads of 0.1 μm diameter (FluoSpheres; Molecular Probes, Eugene, OR). The thickness of the gel is ∼40 μm. The plane of the cells recorded is the same as that of the fluorescent beads. The Poisson ratio of the substrate was assumed to be 0.3, as reported previously (Engler et al., 2004; Frey et al., 2007). Young's modulus of the substrate was ∼1.2 kPa, as determined from measurements of the indentation of a tungsten carbide sphere (Keer, 1964) and also using atomic force microscopy.

Cell contour identification

Differential interference contrast images were acquired using a 40× air objective. A custom algorithm using MATLAB (MathWorks, Natick, MA) identified the contour of the cells (Alonso-Latorre et al., 2009).

Determination of the substrate deformation and calculation of the stresses

The deformation of the substrate was determined from the displacements of the fluorescent beads embedded in the substrate, using image correlation techniques (Willert and Gharib, 1991; Gui and Wereley, 2002). Square windows of 16 pixels with a 50% overlap were used. In each experimental session, the beads were recorded at the plane where their fluorescence intensity is maximum in order to minimize systematic errors caused by any out-of-focus beads. The cellular stress field was calculated using the traction force cytometry method developed by del Álamo et al. (2007), an extension of the method developed by Butler et al. (2002). The method takes into account the finite thickness of the elastic substrate, thus improving the accuracy and resolution of previous ones (Dembo et al., 1996; Butler et al., 2002). The pole forces (pairs of opposing, contractile forces resulting from the integral of the traction stresses at the front and back halves of the cells) exerted on the cell's front, Ff, and back, Fb, were calculated as described in del Álamo et al. (2007):

graphic file with name 3995equ1.jpg

where ξ > 0 indicates the front and ξ < 0 the back of the cell. The strain energy Us (mechanical work) that the cells exert on their substrate was also calculated as shown in del Álamo et al. (2007):

graphic file with name 3995equ2.jpg

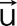where Inline graphic is the measured displacement vector field in the free substrate surface. Further details of our TFC and the various analytical techniques used in the analysis of the traction stresses are provided elsewhere (del Álamo et al., 2007; Alonso-Latorre et al., 2009).

Determination of the periodicity of the cell length and strain energy time records

We applied wave analysis to test whether the measured time records of the cell length and strain energy were periodic (i.e., narrowband spectrum) and to calculate their dominant period. First, we obtained an initial estimate of the main period, T0, of these records from the peaks in their autocorrelation functions. Second, we determined the period of the cycle, T, by fitting the time records to a sinusoidal function of the form 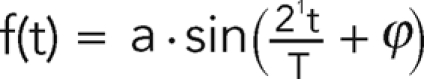Inline graphic in a nonlinear, least squares sense. The signal frequency was estimated as f = 1/T. Because secular fluctuations can shift the detected periods to spurious, long values not related to the changes in cell length associated with the motility cycle, the period T was constrained using the initial estimate between T0/2 and 2T0. We consistently observed that the best fit resulted from a sine function of a frequency similar to the one determined initially through the autocorrelation function. The value of coefficient a was independently set equal to the absolute maximum of the normalized time record, and its value did not affect the estimation of T. The value of the coefficient ϕ was not constrained.

After determining the best-fitted sine waves of the time records of the cell length during motility, we cross-correlated them to determine their degree of periodicity. Thus we were able to quantify the extent to which a sine wave of period T can capture the behavior of the particular cell length time record. We computed the Spearman's correlation coefficients RL_sine and the p values pm for Spearman's RL_sine to test the hypothesis of no correlation. We also defined the parameter degree of periodicity as DOP = RL_sine ·100, so that 0 < DOP < 100.

We applied a similar analysis in order to find the degree of correlation between the time records of the cell length and strain energy. We computed the Spearman's correlation coefficients RL_U to assess how well cross-correlated the cell length and strain energy time records were and the p values pm for Spearman's RL_U to test the hypothesis of no correlation between the time records. We also calculated the time delay between the two time records by locating the maximum of their cross-correlation function. To optimally locate the peak of the correlation function, we applied parabolic-fitting interpolation to the vicinity of the peak point of the cross-correlation function, as described elsewhere (Tamim and Ghani, 2010). We followed a similar technique for the cell lines expressing Lifeact to analyze the correlation between the time records of the maximum Lifeact fluorescence intensity at the cell's front and the cell length.

Phase statistical analysis of the motility cycle

For those cell lines in which we identified the existence of a motility cycle, we obtained the spatiotemporal organization of cell shape and traction stresses during each stage of the motility cycle by using a phase-averaging technique developed previously (del Álamo et al., 2007; Meili et al., 2010). This algorithm uses the time evolution of the cell length or strain energy as a criterion for splitting the motility cycle into four different phases: 1) protrusion, identified as the time during which L and Us are increasing; 2) contraction, the time during which L and Us are near a local maximum; 3) retraction, the time during which L and Us are decreasing; and 4) relaxation, the time during which L and Us are near a local minimum (Supplemental Figure S5).

Supplementary Material

Supplemental Materials
supp_22_21_3995__index.html (2KB, html)

Acknowledgments

We thank Adam Engler for his advice on polyacrylamide gel fabrication and for the characterization of the elasticity of the gels using AFM. We also thank Alexis Lasheras for carefully reading and editing the manuscript. This work was supported by National Institutes of Health Grants USPHS 1R01GM084227 and 3R01GM037830.

Abbreviations used:

DOP

degree of periodicity of the time variation of L

Gmax

maximum fluorescence intensity of F-actin marker at the front of a cell

f

frequency of the motility cycle

L

length of the major moment of inertia of the cell

λ

average distance traveled by a cell during one motility cycle

T

period of the motility cycle

Us

strain energy exerted by a cell on its substrate

V

average speed of a cell

Footnotes

This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E11-03-0278) on September 7, 2011.

REFERENCES

  1. Abercrombie M, Heaysman J, Pegrum S. The locomotion of fibroblasts in culture. I. Movements of the leading edge. Exp Cell Res. 1970;59:393–398. doi: 10.1016/0014-4827(70)90646-4. [DOI] [PubMed] [Google Scholar]
  2. Alonso-Latorre B, Meili R, Bastounis E, Del Alamo JC, Firtel RA, Lasheras JC. Distribution of traction forces and intracellular markers associated with shape changes during amoeboid cell migration; 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN; 2009. pp. 3346–3349. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Ausprunk DH, Folkman J. Migration and proliferation of endothelial cells in preformed and newly formed blood-vessels during tumor angiogenesis. Microvasc Res. 1977;14:53–65. doi: 10.1016/0026-2862(77)90141-8. [DOI] [PubMed] [Google Scholar]
  4. Barnhart EL, Allen GM, Jülicher F, Theriot JA. Bipedal locomotion in crawling cells. Biophys J. 2010;98:933–942. doi: 10.1016/j.bpj.2009.10.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Basu D, El-Assal SED, Le J, Mallery EL, Szymanski DB. Interchangeable functions of Arabidopsis PIROGI and the human WAVE complex subunit SRA1 during leaf epidermal development. Development. 2004;131:4345–4355. doi: 10.1242/dev.01307. [DOI] [PubMed] [Google Scholar]
  6. Beltzner CC, Pollard TD. Pathway of actin filament branch formation by Arp2/3 complex. J Biol Chem. 2008;283:7135–7144. doi: 10.1074/jbc.M705894200. [DOI] [PubMed] [Google Scholar]
  7. Blagg SL, Insall RH. Solving the WAVE function. Nat Cell Biol. 2004;6:279–281. doi: 10.1038/ncb0404-279. [DOI] [PubMed] [Google Scholar]
  8. Blagg SL, Stewart M, Sambles C, Insall RH. PIR121 regulates pseudopod dynamics and SCAR activity in Dictyostelium. Curr Biol. 2003;13:1480–1487. doi: 10.1016/s0960-9822(03)00580-3. [DOI] [PubMed] [Google Scholar]
  9. Borisy GG, Svitkina TM. Actin machinery: pushing the envelope. Curr Opin Cell Biol. 2000;12:104–112. doi: 10.1016/s0955-0674(99)00063-0. [DOI] [PubMed] [Google Scholar]
  10. Butler JP, Tolic-Norrelykke IM, Fabry B, Fredberg JJ. Traction fields, moments, and strain energy that cells exert on their surroundings. Am J Phys Cell Physiol. 2002;282:C595-C605. doi: 10.1152/ajpcell.00270.2001. [DOI] [PubMed] [Google Scholar]
  11. Charest PG, Firtel RA. Big roles for small GTPases in the control of directed cell movement. Biochem J. 2007;401:377–390. doi: 10.1042/BJ20061432. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Chung CY, Firtel RA. Signaling pathways at the leading edge of chemotaxing cells. J Muscle Res Cell Motil. 2002;23:773–779. doi: 10.1023/a:1024479728970. [DOI] [PubMed] [Google Scholar]
  13. Cooper JA, Wear MA, Weaver AM. Arp2/3 complex: advances on the inner workings of a molecular machine. Cell. 2001;107:703–705. doi: 10.1016/s0092-8674(01)00605-5. [DOI] [PubMed] [Google Scholar]
  14. Cory GO, Ridley AJ. Cell motility: braking WAVEs. Nature. 2002;418:732–733. doi: 10.1038/418732a. [DOI] [PubMed] [Google Scholar]
  15. Davidson AJ, Insall RH. Actin-based motility: WAVE regulatory complex structure reopens old SCARs. Curr Biol. 2011;21:R66-R68. doi: 10.1016/j.cub.2010.12.001. [DOI] [PubMed] [Google Scholar]
  16. del Álamo JC, Meili R, Alonso-Latorre B, Rodríguez-Rodríguez J, Aliseda A, Firtel RA, Lasheras JC. Spatio-temporal analysis of eukaryotic cell motility by improved force cytometry. Proc Natl Acad Sci USA. 2007;104:13343–13348. doi: 10.1073/pnas.0705815104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Dembo M, Oliver T, Ishihara A, Jacobson K. Imaging the traction stresses exerted by locomoting cells with the elastic substratum method. Biophys J. 1996;70:2008–2022. doi: 10.1016/S0006-3495(96)79767-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Devreotes PN, Zigmond SH. Chemotaxis in eukaryotic cells—a focus on leukocytes and Dictyostelium. Annu Rev Cell Biol. 1988;4:649–686. doi: 10.1146/annurev.cb.04.110188.003245. [DOI] [PubMed] [Google Scholar]
  19. Engler A, Bacakova L, Newman C, Hategan A, Griffin M, Discher D. Substrate compliance versus ligand density in cell on gel responses. Biophys J. 2004;86:617–628. doi: 10.1016/S0006-3495(04)74140-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Frey MT, Engler AJ, Discher DE, Lee J, Wang YL. Microscopic methods for measuring the elasticity of gel substrates for cell culture: microspheres, microindenters, and atomic force microscopy. Methods Cell Biol. 2007;83:47–65. doi: 10.1016/S0091-679X(07)83003-2. [DOI] [PubMed] [Google Scholar]
  21. Fukui Y. Mechanistics of amoeboid locomotion: signal to forces. Cell Biol Int. 2002;26:933–944. doi: 10.1006/cbir.2002.0959. [DOI] [PubMed] [Google Scholar]
  22. Grabher C, Cliffe A, Miura K, Hayflick J, Pepperkok R, Rørth P, Wittbrodt J. Birth and life of tissue macrophages and their migration in embryogenesis and inflammation in medaka. J Leukoc Biol. 2007;81:263–271. doi: 10.1189/jlb.0806526. [DOI] [PubMed] [Google Scholar]
  23. Gui L, Wereley ST. A correlation-based continuous window-shift technique to reduce the peak-locking effect in digital PIV image evaluation. Exp Fluids. 2002;32:506–517. [Google Scholar]
  24. Ibarra N, Blagg SL, Vazquez F, Insall RH. Nap1 regulates Dictyostelium cell motility and adhesion through SCAR-dependent and -independent pathways. Curr Biol. 2006;16:717–722. doi: 10.1016/j.cub.2006.02.068. [DOI] [PubMed] [Google Scholar]
  25. Ibarra N, Insall RH. Regulation of actin assembly by SCAR/WAVE proteins. Biochem Soc Trans. 2005;33:1243–1246. doi: 10.1042/BST0331243. [DOI] [PubMed] [Google Scholar]
  26. Keer LM. Stress distribution at the edge of an equilibrium crack. J Mech Physics Solids. 1964;12:149–163. [Google Scholar]
  27. Koestler SA, Auinger S, Vinzenz M, Rottner K, Small JV. Differentially oriented populations of actin filaments generated in lamellipodia collaborate in pushing and pausing at the cell front. Nat Cell Biol. 2008;10:306–313. doi: 10.1038/ncb1692. [DOI] [PubMed] [Google Scholar]
  28. Lauffenburger DA, Horwitz AF. Cell migration: a physically integrated molecular process. Cell. 1996;84:359–369. doi: 10.1016/s0092-8674(00)81280-5. [DOI] [PubMed] [Google Scholar]
  29. Lombardi ML, Knecht DA, Dembo M, Lee J. Traction force microscopy in Dictyostelium reveals distinct roles for myosin II motor and actin-crosslinking activity in polarized cell movement. J Cell Sci. 2007;120:1624–1634. doi: 10.1242/jcs.002527. [DOI] [PubMed] [Google Scholar]
  30. Machesky LM, Insall RH. Scar1 and the related Wiskott-Aldrich syndrome protein, WASP, regulate the actin cytoskeleton through the Arp2/3 complex. Curr Biol. 1998;8:1347–1356. doi: 10.1016/s0960-9822(98)00015-3. [DOI] [PubMed] [Google Scholar]
  31. Meili R, Alonso-Latorre B, del Álamo JC,, Firtel RA, Lasheras JC. Myosin II is essential for the spatiotemporal organization of traction forces during cell motility. Mol Biol Cell. 2010;21:405–417. doi: 10.1091/mbc.E09-08-0703. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Meili R, del Alamo JC, Alonso-Latorre B, Lasheras JC, Firtel RA. Mapping the function of myosin II for the spatial and temporal organization of amoeboid cell motility using mutants; Presented at: 2008 Protein Phosphorylation and Cell Signaling Meeting, Salk Institute, La Jolla, CA; 2008. [Google Scholar]
  33. Miller KG. Extending the Arp2/3 complex and its regulation beyond the leading edge. J Cell Biol. 2002;156:591–593. doi: 10.1083/jcb.200201107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Mullins RD, Heuser JA, Pollard TD. The interaction of Arp2/3 complex with actin: nucleation, high affinity pointed end capping, and formation of branching networks of filaments. Proc Natl Acad Sci USA. 1998;95:6181–6186. doi: 10.1073/pnas.95.11.6181. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Pollard TD. Cellular motility powered by actin filament assembly and disassembly. Harvey Lect. 2002;98:1–17. [PubMed] [Google Scholar]
  36. Pollard TD, Borisy GG. Cellular motility driven by assembly and disassembly of actin filaments. Cell. 2003;112:453–465. doi: 10.1016/s0092-8674(03)00120-x. [DOI] [PubMed] [Google Scholar]
  37. Riedl J, et al. Lifeact: a versatile marker to visualize F-actin. Nat Methods. 2008;5:605–607. doi: 10.1038/nmeth.1220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Stradal TEB, Scita G. Protein complexes regulating Arp2/3-mediated actin assembly. Curr Opin Cell Biol. 2006;18:4–10. doi: 10.1016/j.ceb.2005.12.003. [DOI] [PubMed] [Google Scholar]
  39. Tamim NSM, Ghani F. Techniques for optimization in time delay estimation from cross correlation function. Int J Eng Technol. 2010;10:69–75. [Google Scholar]
  40. Uchida KS, Yumura S. Dynamics of novel feet of Dictyostelium cells during migration. J Cell Sci. 2004;117:1443–1455. doi: 10.1242/jcs.01015. [DOI] [PubMed] [Google Scholar]
  41. Van Haastert P, Devreotes P. Chemotaxis: signalling the way forward. Nature Rev. 2004;5:626–634. doi: 10.1038/nrm1435. [DOI] [PubMed] [Google Scholar]
  42. Wang YL, Pelham RLJ. Preparation of a flexible, porous polyacrylamide substrate for mechanical studies of cultured cells. Methods Enzymol. 1998;298:489–496. doi: 10.1016/s0076-6879(98)98041-7. [DOI] [PubMed] [Google Scholar]
  43. Webb DJ, Parsons JT, Horwitz AF. Adhesion assembly, disassembly and turnover in migrating cells—over and over and over again. Nat Cell Biol. 2002;4:E97–E100. doi: 10.1038/ncb0402-e97. [DOI] [PubMed] [Google Scholar]
  44. Weiner O, Servant G, Welch M, Mitchison T, Sedat J, Bourne H. Spatial control of actin polymerization during neutrophil chemotaxis. Nat Cell Biol. 1999;1:75–81. doi: 10.1038/10042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Wessels D, Vawter-Hugart H, Murray J, Soll D. Three-dimensional dynamics of pseudopod formation and the regulation of turning during the motility cycle of Dictyostelium. Cell Motil Cytoskeleton. 1994;27:1–12. doi: 10.1002/cm.970270102. [DOI] [PubMed] [Google Scholar]
  46. Willert CE, Gharib M. Digital particle image velocimetry. Exp Fluids. 1991;10:181–193. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Materials
supp_22_21_3995__index.html (2KB, html)
supp_E11-03-0278_CombinedSupMats.pdf (1.2MB, pdf)
Download video file (1.7MB, mov)
Download video file (3.2MB, mov)

Articles from Molecular Biology of the Cell are provided here courtesy of American Society for Cell Biology

RESOURCES