To bee or not to bee, this is the question…

Abstract

Human inborn numerical competence means our ability to recognize object numbers precisely under circumstances which do not allow sequential counting. This archaic process has been called “subitizing,” from the Latin “subito” = suddenly, immediately, indicating that the objects in question are presented to test persons only for a fraction of a second in order to prevent counting. In contrast, however, sequential counting, an outstanding cultural achievement of mankind, means to count “1, 2, 3, 4, 5, 6, 7, 8…” without a limit. The following essay will explain how the limit of numerical competence, i.e., the recognition of object numbers without counting, has been determined for humans and how this has been achieved for the first time in case of an invertebrate, the honeybee. Finally, a hypothesis explaining the influence of our limited, inborn numerical competence on counting in our times, e.g., in the Russian language, will be presented. Subitizing versus counting by young Down syndrome infants and autistics and the Savant syndrome will be discussed.

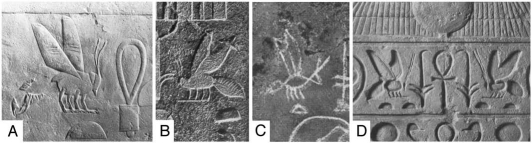
A look back into early history reveals the puzzling fact that in ancient Egypt honeybees, one of the important hieroglyphs (“bjt”) and symbol of Lower Egypt, were represented with four legs (Fig. 1). Moreover, Aristotle (384–322 B.C.) determined that the day-fly has four legs.¹,^† We will never know whether this notion was a consequence of subitizing instead of real counting.

Figure 1.

The “magical number four”: Presentation of honeybees in ancient Egypt. (A) 4^th dynasty (∼2613–2404 B.C.), Roemer-Pelizaeus-Museum, Hildesheim, Germany; (B and C) 5^th dynasty (∼2500–2350 B.C.) and (D) 19^th dynasty (∼1292–1186 B.C.), Egyptian Museum in Berlin-Charlottenburg, Germany, reproduced with permission.

For humans it has been shown already in 1871 that our ability to estimate (“subitize”) object numbers under circumstances where regular, sequential counting is impossible, is rather limited. In his famous experiments, Jevons² estimated the number of black beans thrown into a white box within the fraction of a second, and found that only up to four beans were recognized correctly. Incorrect results started to occur with five and increased with more beans. With other words, our ability to estimate object numbers without sequential counting was limited to four items in this experiment. Details are shown in Table 1 which is modified from Jevons² and gives the number of trials in which each real number was correctly or incorrectly guessed. For example, in 120 cases (of 147 trials) number 6 was correctly guessed, but in 7 cases it was mistaken for 5 and in 20 cases for 7. Another example: 11 beans in the white box were correctly recognized without counting only in 26 of 69 trials and mistaken for 8 in one case, for 9 in 11 cases, for 10 in 19 cases and for 12 in 12 cases. Please note the tendency to over-estimate small numbers and to under-estimate large ones.² These early findings 140 years ago about the “magical number four” have been exhaustively discussed and reconsidered very recently.³

Table 1.

A summary of 1,027 trials to determine the precision of numerical discrimination when sequential counting is prevented (modified from Jevons²)

Estimated Numbers	Actual Numbers
	3	4	5	6	7	8	9	10	11	12	13	14	15
3	23
4		65
5			102	7
6			4	120	18
7			1	20	113	30	2
8					25	76	24	6	1
9						28	76	37	11	1
10						1	18	46	19	4
11							2	16	26	17	7	2
12								2	12	19	11	3	2
13										3	6	3	1
14										1	1	4	6
15											1	2	2t
Totals	23	65	107	147	156	135	122	107	69	45	26	14	11
% correct Numbers	100	100	95.3	81.6	72.4	56.3	62.3	43	37.7	42.2	23	28.6	18.2

Sequential counting is a major cultural achievement of mankind,⁴ whereas the rapid recognition of object numbers without the possibility of counting, also called “subitizing,”⁵ is shared by humans with many non-human vertebrates.⁶ There is convincing evidence that these two abilities have nothing to do with each other. Sequential counting is a rational process. It begins with the help of our 10 fingers and it has to be trained. Quite in contrast, the range of visual attention,⁷ namely the immediate recognition (=subitizing) of object numbers is an archaic, inborn property which can not be improved by training. Interestingly, young Down syndrome infants are unable to subitize but can determine object numbers of 1, 2, 3, 4, 5… only by stepwise counting.⁸ Trisomy 21 (Down syndrome) is the most frequent genetic disorder (∼1 per 800) causing mental retardation. Affected individuals have an additional extra copy of the long arm of chromosome 21 and exhibit cognitive dysfunction thought to be the result of altered expression of chromosome 21 genes. In contrast, patients suffering from autism, a mental condition characterized by a reduced ability to interact or to communicate with the outside world, can often subitize correctly more than 100 objects without counting. In the famous movie “Rain Man” (Barry Levinson, 1988) the autistic Raymond recognizes immediately 246 toothpicks and identifies them as 3 × 82 when a package had dropped and he performed difficult mathematical operations within seconds. Such an extreme talent, which is often restricted to a single skill like calendar calculating, prime number computing, playing many instruments, speaking many languages etc., is called “Savant syndrome”⁹ and is a phenomenon which occurs in up to 10% of the autistic persons. The extraordinary Savant syndrome has been thoroughly discussed and reviewed in reference ¹⁰.

I have recently presented a new hypothesis for the evolution of counting systems in ancient civilizations¹¹ on the basis of our limited inborn numerical competence and provided evidence that even nowadays we avoid the slow process of sequential counting whenever possible and prefer to determine small object numbers by subitizing. Another interesting argument for the notion that even present counting procedures may be influenced by our ability to determine the number of objects up to the “magical number four”³ without counting¹¹ is the way how counting works in Slavic languages. Russians count objects as follows: They use two cases of plural, one (nominative) for small quantities from two up to four objects, but use a second case of plural (genitive) for larger object numbers and count “1 stakan, 2 stakany, 3 stakany, 4 stakany” (1 glass, 2 glasses, 3 glasses, 4 glasses), but continue with “5 stakanov, 6 stakanov …” (5 of the glasses, 6 of the glasses…”). It is a fascinating idea that these two cases of plural reflect the borderline between subitizing (1 to 4) and the need for real counting from five objects upwards.

How can we determine the cognitive capacity and numerical competence of animals? Early experiments along this direction were performed with birds in the fourties of the past century¹² and were later continued with different animals (summarized in ref. 6).

We have recently determined for the first time that even an invertebrate, the honeybee, has almost the same numerical competence as humans,⁶ using the experimental approach of a “delayed match-to-sample” as described in Figure 2.

Figure 2.

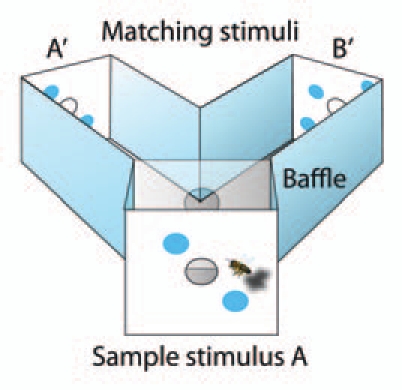
(adapted from Pahl et al.¹³). Delayed match-to-sample (DMTS) setup in a Y-maze. The bee has to memorize the sample stimulus A (two blue dots) and to recall it when deciding for one of the two matching stimuli A' or B' inside the maze. The exit A' leads to a reward (a sugar solution) in this example. The location of the reward was randomized irregularly among A' and B', respectively. During testing, the arrangement of dots differed between the entrance A and the correct exit A'. In order to make the task much more difficult, the dots were arranged in randomized orientations between stimulus A and A'. Finally the dots were replaced by novel objects some of which the bees had never seen before: yellow lemons, green leaves, yellow stars or blue dots in random orientations.⁶ Baffles behind the exits A' and B' prevent the bees from seeing the reward. In this context it is relevant to remember that the duration of the visual working (short term) memory of the honeybee is less than 10 seconds.¹⁴.

The trained bees remembered in about 80% of the assays one, two and three objects correctly in our DMTS test. However, if they are presented four objects at the entrance and at the correct exit A' they still perform their task, but with significant difficulty, indicating that the limit of their numerical abilities has been reached between three and four objects. Such a rigorous proof for the understanding of object numbers is missing in some published experiments with “counting” animals.

We can only speculate about the reasons why some bees take the wrong exit:

1. The worker bee population is heterogeneous. They all have one mother, the queen, but up to 20 different fathers, the drones, and less intelligent drones may have less intelligent offspring with lower numerical capacity.

2. Another reason for bees to take the wrong exit may be their natural curiosity which helps them to find and try new food sources. They may just be interested to find out what is behind the other, wrong exit. Or, depending on their fathers, bees may differ by the degree of their curiosity. At present we are unable to differentiate between these two possibilities. In order to avoid any misunderstanding—we are sure that bees are unable to ”count” in the way we count.

Needless to mention that studies of numerical competence are rather restricted or even impossible with many other insects. Honeybees, which are available almost in unlimited numbers, may in the future possibly play a role as alternative experimental animals instead of mice and rats.¹⁵

The surprising fact that honeybees in our “delayed match-to-sample” experiments⁶ recognize and remember up to three and partially fourt objects correctly even if they see three blue dots at the entrance (Fig. 2) and three yellow lemons at the correct exit A' and two blue dots at the wrong exit B' has an important consequence:

Our results provide convincing evidence that the bees have a real (cardinal) understanding for object numbers, independent of the type of objects and even if they are shown objects which they have never seen before. This will amaze many people and already Cicero (106–43 B.C.) would have been surprised since he argued that domestic animals, including bees, are without any intelligence.¹⁶,^‡

Addendum to: Gross HJ, Pahl M, Si A, Zhu H, Tautz J, Zhang S. Number-based visual generalisation in the honeybee. PLoS One. 2009;4:4263. doi: 10.1371/journal.pone.0004263.