Abstract
The performance of the reaction-field method of electrostatics is tested in molecular dynamics simulations of protein human interleukin-4 and a short DNA fragment in explicit solvent. Two truncation schemes are considered: one based on the position of atomic charges in water molecules and the other on the position of groups of charges. The group-based truncation leads to the melting of the DNA double helix. In contrast, the atom-based truncation maintains the helical structure intact. Similarly for the protein, the group-based truncation leads to an unfolding at pH 2 while the atom-based truncation produces stable trajectories at low and normal pH, in agreement with experiment. Artificial repulsion between charged residues associated with the group-based truncation is identified as the microscopic reason behind unfolding of the protein. Implications of different truncation schemes in reaction-field simulations of biomolecules are discussed.
Keywords: Electrostatic interactions, Reaction-field method, Group-based and atom-based truncation, Simulations of proteins
Introduction
The appropriate treatment of electrostatic interactions is an extremely important consideration in computer simulations of biomolecular systems [1–3]. One common approach is to employ truncation at certain cut-off distance, beyond which the potentials are neglected. This results in a computational speedup as each charge of the simulated system interacts with only a small number of its immediate neighbors. The disadvantage of this is computational accuracy, however. Truncated potentials were seen to cause severe artifacts in simulations of various systems [4–6], indicating that all particles should be included in the electrostatic interactions. Under periodic boundary conditions, this argument leads to the lattice-sum methods, which extend interactions to particles within the central simulation cell as well as the periodic images of the cell replicated throughout the space [7]. While more accurate than the truncation schemes, the lattice-sum methods are also more computationally expensive. Additionally, in simulations of solvated macromolecules, these methods present undesirable periodicity artifacts caused by the interactions of the solute molecule with its own images in the periodic cells [8, 9].
An alternative approach to including interactions beyond cut-offs is based on continuum electrostatics theory [10–13]. It combines the molecular representation of solvent before the cut-off distance with the continuum representation beyond it. The effect of the continuum part is accounted for through the polarization electric field, or reaction field (RF), created by a charged particle in a vacuum cavity embedded in infinite dielectric medium, which for spherical cavities can be found exactly [10, 11]. The resulting reaction-field electrostatics method features only pairwise potential energy summations and thus is fast. Additionally, electrostatic interactions between molecules in neighboring simulation cells are eliminated, thereby diminishing periodicity effects. A serious drawback of this method is that, in theory, only homogeneous systems such as pure water [14, 15] or electrolyte solutions [13, 16] can be treated due to their translational invariance. In practice, however, the reaction field method has been applied to a variety of inhomogeneous systems, including molecular ions [17], nucleic acids [18, 19], lipid membranes [20] and peptides [6, 21, 22]. In some of these systems [6, 18] the method was successful while in others [20, 23] it failed. Currently, the limitations of the RF electrostatics in mixed media are not well understood.
In our earlier work [24], we found that the success of the reaction-field method applied to ions critically depends on how truncation between solutes and solvent is implemented. Truncation schemes based on groups of charges were seen to cause fictitious repulsion between charged solutes, including simple ions and a pair of oppositely charged molecular ions, while atom-based truncation produced results in good agreement with the lattice-sum methods [24]. In this paper, we investigate how different truncation methods affect the structural properties of biomolecules. Our earlier work [24] indicates that the differences between the two truncation schemes are most prominent for charged solutes. We therefore consider in this paper two molecules with high charge density: a protein and a short fragment of DNA double helix. Both the DNA and the protein are found to unfold on the nanosecond time scale when simulated with the group-based truncation scheme. The atom-based truncation, on the other hand, maintains the native state intact, in agreement with the lattice-sum simulations and other experimental and theoretical evidence [23, 25]. For the protein, the unfolding occurs at pH 2, where the charge density is high, and not at pH 6, where the density is low. By computing potentials of mean force for charged contacts involved in the native state, we conclude that the aberrant unfolding is caused by erroneous repulsion induced between charged residues by the group-based truncation. In conclusion, our simulations provide evidence that the artifacts of the group-based truncation may adversely affect simulations of biomolecules with high charge densities.
Methods and models
Different truncation types
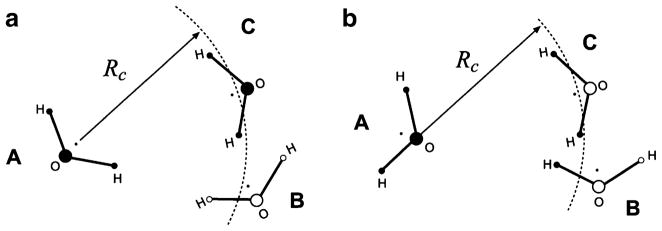
The electrostatic interactions in molecular mechanics force fields are treated with cut-offs whose specific implementation depends on whether charges of the simulated systems are divided into groups or not. Charge groups are typically formed by atoms that belong to an overall neutral entity, such as a water molecule or a side chain of an amino acid residue in proteins. Interactions between charge groups exist only if their mutual separation is equal to or less than certain cut-off distance Rc, as explained in Fig. 1a for the case of water. The separation can be measured between geometrical centers of charge groups (GBT), the locations of certain atoms, or using other definitions. In the atom-based truncation (ABT) method, interactions between two atoms are included if the distance between them is less than or equal to Rc, regardless of what charge groups these atoms belong to. Mathematically, the total electrostatic energy in the two schemes can be written as:
where NAT is the total number of atoms, rij is the distance between atoms i and j, RIJ is the distance between the charge groups to which these atoms belong, and Vij is the interaction between these atoms. The symbols ABT and GBT refer to atom- and group-based truncations, respectively, and H(x) is the Heaviside step function. In the reaction-field method [10–13], the interaction between two charges qi and qj is
Fig. 1.
a–b Explanation of different truncation schemes. In the group-based truncation, a, two molecular – charge groups—interact only if the distance between their centers is Rc or less. By this criterion, molecule A interacts with molecule C but not with molecule B. In the atom-based truncation, b, interactions are computed using the interatomic distances. For instance, the oxygen of molecule A interacts with hydrogens of molecule C but not its oxygen
where ε0 is the dielectric permittivity of the vacuum, ε is the dielectric constant of the simulated medium, and the other quantities are as defined above.
We showed in a previous paper [24] that the difference between effective interactions of ions in water (quantitatively described by the potential of mean force, PMF) simulated by group-based and atom-based approaches can be explained by how the group-based scheme sorts interaction partners. For a centrally located charge q, water molecules separated by a distance r will appear with equal probability in all orientations if r is sufficiently large. These include orientations with the oxygen atom pointing toward q and those with it pointing away from q. The former will be included in interactions with q if the oxygen atom of the water molecule is treated as the center of the charge group, while the latter will be rejected. Since both orientations occur with equal probability, rejecting of one of them results in incomplete cancellation of the charge seen at the site of q. The exact shape of the uncompensated charge varies with the definition of the charge group center. For the oxygen atom, for instance, it is a double-layer made of a negative ring followed by a positive one.
For a single charge q, no net force is applied by the artificial double layer due to the symmetry. For two charges, however, as in the case of the potential-of-mean force calculations, the symmetry of the layer is broken and the net force arises. It is this additional force that leads to the differences in the effective interactions computed by the atom-based and group-based methods for the same pair of ions. The picture with the double layer leads to two conditions under which the group truncation produces artifacts: net charge on solutes and orientational freedom of charge groups. In biomolecules, the first condition is met by ionizable groups of certain amino acids or phosphate groups in nucleic acids. One may expect these groups to be affected by the group-based truncation in simulations of proteins and DNA/RNA. The second condition clearly applies to water and to a much lesser degree to proteins/DNA, whose charge groups are not allowed to take on arbitrary orientations due to the chain connectivity. It therefore makes sense to apply the ABT scheme to the solvent only retaining the GBT scheme for the solute alone. This is the method of truncation we refer to as “atom-based” in this work. We also tested the effect of treating the solute on an atom basis and, as expected, found no differences from the combined ABT/GBT protocol.
Details of the performed simulations
We carried out molecular dynamics (MD) simulations of a DNA tetradecamer with the sequence 5′-(GCATTCT GAGTCAG)-3′:5′-(CTGACTCAGAATGC)-3′ solvated in water. The DNA was placed at the center of a cubic box with measurements 7.2 × 7.2 × 7.2 nm containing 12101 water molecules. To neutralize the system, 26 water molecules were replaced at random with sodium ions. The distribution of ions was monitored along the trajectories to insure sufficient equilibration. Identical pair distribution functions between sodium ions and the phosphate groups of the DNA were observed in the last two consecutive 3 ns segments of each trajectory. Consistent with the earlier study [23], very little DNA-ion binding was seen. Human interleukin-4 (IL-4) was considered as the test protein. It was solvated in a cubic box of size 7.158 × 7.158 × 7.158 nm with 11190 water molecules. Two pH conditions were considered, 2 and 6, with the charge on the ionizable residues was set appropriately. No counterions were added to the system. The conditions of our simulations were chosen to mimic those reported in the earlier simulation studies of these two systems [23, 25].
The GROMACS software package [26] was used to conduct all simulations. The DNA fragment was modeled with the ffG53A6 force field while the ffG45a3 force field was used for the protein. The simple point charge (SPC) water model [27] was used for both molecules. All calculations were performed at a constant temperature of 308 K and a pressure of 1 bar (CPT) with a 2 fs time step and with group- and atom-based truncation complemented by reaction field beyond the cutoff radius. In the group-based truncation, the geometrical centers of the groups were considered as the group centers. Three trajectories of 12 ns were generated for the DNA: two using the group-based and atom-based truncation schemes and one trajectory using smooth particle mesh Ewald (PME) electrostatics [28] for reference. Five trajectories of 4 ns were generated for the protein with each truncation scheme. Two different pH levels were modeled, pH 2 and 6. The chemical bonds in the water molecules were held constant by the SETTLE [29] algorithm. The bonds involving hydrogen atoms in the protein and DNA were constrained according to the LINCS [30] algorithm. In the reaction-field simulations, the twin-cutoff method was employed for the nonbonded van der Waals and electrostatic interactions, with the long and short cut-offs set at 1.4 and 0.8 nm, respectively, and the neighbors were updated every 5 time steps. The dielectric constant was set at ε = 66, which corresponds to the dielectric permittivity of the water model employed under the lattice-sum and atom-based truncations [15, 31, 32]. Other values ranging from 54 [19] to 80 [20] have been used in the literature, but the effect of varying ε in the range between 60 and 70 is negligible [33]. The same setup was used for the van der Waals interactions in the PME simulations.
The initial conformation of the DNA fragment was put into a B-DNA configuration with the help of the 3D-DART server [34]. The initial structure of the protein was downloaded from the protein data bank, PDB ID: 1RCB [35]. Both structures were solvated, minimized and equilibrated with constraints on heavy atoms before conducting productive simulations.
Potentials of mean force between charged residues of the protein
We computed the PMF for different pairs of side chains using an umbrella sampling technique [36]. An umbrella potential with a force constant k = 1000 kJ mol−1 nm−2 was applied along the x axis. We considered twelve windows spaced 0.1 nm from one another and started with an initial separation between residues of 0.3 nm. Neutralizing groups were placed at the N- and C- termini of the amino-acids to avoid interference from the charged groups. The peptides were aligned so that the Cα, Cγ and Cε atoms of one side chain were along the same axis as the analogous atoms of the other chain. Weighted Histogram Analysis Method was employed to obtain unbiased distribution functions [37, 38].
Results and discussion
Group-based truncation disrupts the DNA double helix
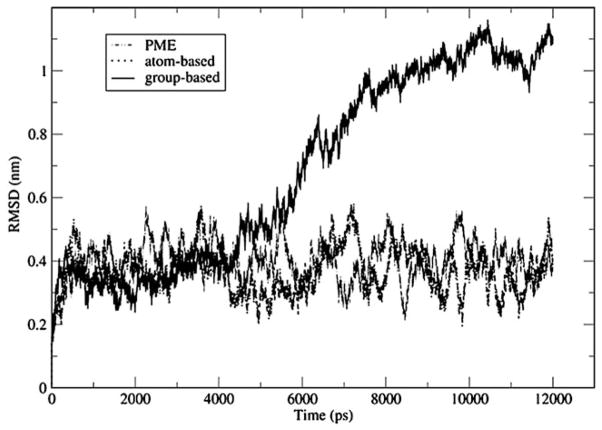
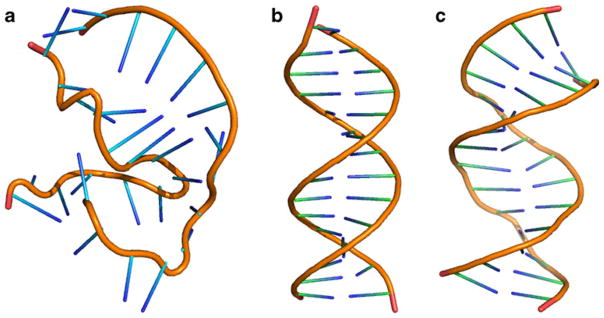
The structure of the DNA helix simulated by the group-based truncation underwent a significant distortion during the course of the simulation. This is evident from the root mean square deviation (RMSD) as a function of time, as shown in Fig. 2, computed over all atoms of residues 3–12 and 17–26. For the first 4 ns, the RMSD fluctuates around 0.4 nm, indicating relative stability of the initial structure. After the 4 ns mark, however, the RMSD begins to rise rapidly, reaching 0.7 nm 6 ns into the simulation. The increase continues thereafter with values as high as 1 nm seen after 10–12 ns of simulation time. These latter RMSDs signal a significant structural change. The extent of the structural transformation is illustrated in Fig. 3a showing the snapshot from the time step at 11 ns. The initial structure, shown in Fig. 3b, is almost completely missing. Base-pair stacking is absent in half of the complex. The structure overall is distinctly non-helical in character.
Fig. 2.
Root mean-square deviation over all atoms of residues 3–12 and 17–26 with respect to the initial structure of B-DNA. Group-based truncation leads to distortion of DNA. Atom-based truncation preserves the DNA’s native configuration, in agreement with the more accurate particle-mesh Ewald method
Fig. 3.
The structures of the DNA complexes simulated by the reaction-field method with a) group-based truncation, b) the initial configuration and c) atom-based truncation. This figure was generated with the help of PyMOL [51]
By contrast, atom-based truncation preserves the initial double-helix structure almost intact. The RMSD observed in that simulation, as shown in Fig. 2, reaches a plateau of ~0.4 nm at 500 ps and stays at that level throughout the remainder of the simulation. A conformation recorded at around 11 ns, and shown in Fig. 3c, confirms that there are no major structural changes. The base-pair stacking and the helical character of the starting conformation are well preserved. The atom-based truncation is in good agreement with the particle mesh Ewald simulation, which is used as reference. The RMSDs generated by the two methods are statistically indistinguishable, as seen in Fig. 2. Visual inspection of the generated conformations does not reveal any noticeable differences either.
Based on the data presented here, we can conclude that the group-based scheme is not adequate for simulations of DNA fragments. It leads to complete disruption of the DNA strand, in sharp contrast to the predictions of the Ewald method. These conclusions agree favorably with the results of Krautler and Hunenberger [23], who also reported that the same DNA fragment denatures when simulated by group-based reaction-field electrostatics, and remains intact in Ewald simulations. Our calculations, however, do not invalidate the reaction-field method in general: the atom-based truncation works as well as the lattice-sum method. We argue therefore that this truncation should be the method of choice in reaction-field simulations of nucleic acids.
Group-based truncation leads to unfolding of IL-4 at pH 2
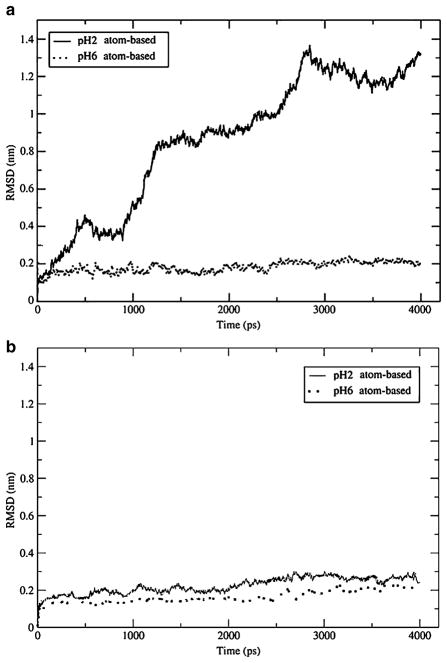
In addition to DNA, proteins constitute an important class of biological molecules. Here we focus on protein IL-4, which was studied in reaction-field simulations previously [25]. The native state of this protein, shown in Fig. 5, has the topology of a 4-helix bundle, as determined experimentally [39]. In the present work, the protein was simulated using group-based truncation at an acidic pH of 2 and a neutral pH of 6. At the neutral pH, its secondary structure remains identical to that determined in X-ray measurements [39]. The stable structure is confirmed by low RMSD values over the Cα atoms, as shown in Fig. 4a, which are less than 0.2 nm throughout the simulation. All simulations reported in this section were repeated 5 times, with different initial velocities, to test their reproducibility. All recorded trajectories were consistent so only one is shown. Visual inspection of the last conformation observed in our representative simulation, shown in Fig. 5a, reveals only small deviations from the initial experimental structure, confirming that the protein remains folded.
Fig. 5.
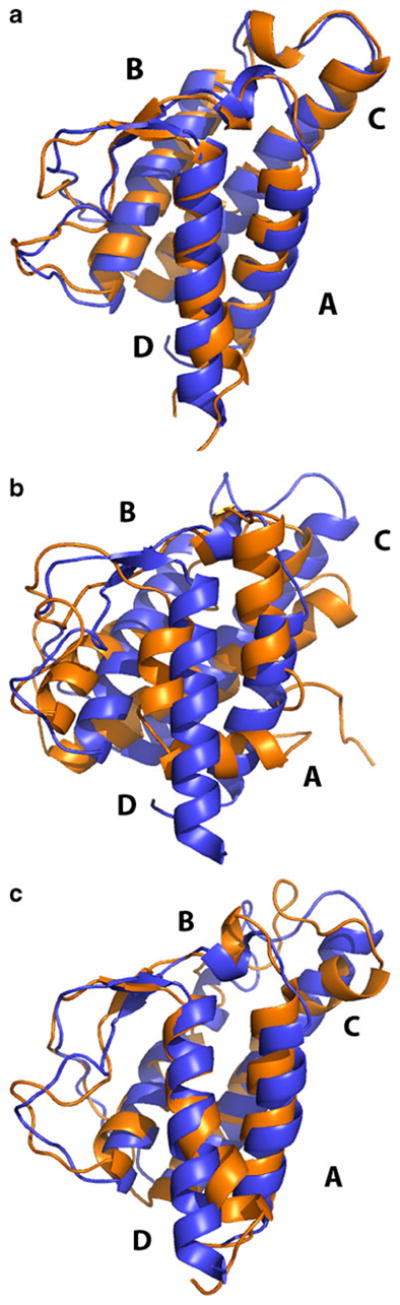
Structure of IL-4 at the end of simulations using group-based truncation at a) pH 6 (RMSD=0.2 nm from the initial structure), b) pH 2 (RMSD=1.3 nm) and c) pH 2 with restrained inter-residue distances (RMSD=0.3 nm). This figure was generated with the help of PyMOL [51]
Fig. 4.
Root mean-square deviation over Cα atoms in IL-4 with respect to the original X-ray structure at pH 6 and 2: a) group-based truncation and b) atom-based truncation. The group-based truncation leads to unfolding at pH 2. The atom-based truncation keeps the protein folded at both normal and low pH
The RMSD of the trajectory at pH 2 is shown in Fig. 4a. It is seen that the deviation is close to 0.4 nm as early as 500 ps into the simulation, signaling major conformational changes. Starting at 1 ns, the protein completely unfolds, reaching RMSD>0.8 nm. Experimentally, IL-4 was seen to undergo partial unfolding, but only in the C helix [39]. The global structure of the protein was determined as highly native-like. Our simulations, therefore, are inconsistent with the experiment. The unfolding of IL-4 at pH 2 was also seen in the group-based reaction-field simulations of Winger et al. [25]. In an effort to explain the discrepancy with the experiment, the authors introduced counterions to compensate for the excessive charge of the protein. Varying the number of added ions helped to reduce the extent of the unfolding somewhat, with RMSDs dropping from 1.5 nm to 0.7–1.0 nm. Nevertheless, even with the maximum of 27 negative ions added, the simulated structure was quite different from the native one.
The final conformation observed in our simulation at pH 2 displays major discrepancies with the native state, as seen in Fig. 5b. Specifically, we noticed that segments corresponding to residues 11–15, 114–118, and 122–129 are completely unfolded. The helices of the protein undergo a substantial rearrangement with respect to each other. While in the initial configuration helices A and D are oriented in parallel with helices B and C, in the final configuration—their mutual orientation is almost perpendicular. Additionally, the C-terminal helix D partially melts, breaking into two parts. The extent of structural distortion varies among all five trajectories we performed. However, all trajectories are consistent in that the protein unfolds.
The RMSDs of the representative trajectories generated for pH 2 and 6 using the atom-based truncation are shown in Fig. 4b. At pH 6, these simulations are consistent with the group-based method and with experiment, producing RMSDs close to 0.2 nm from the native state. Clearly, the atom-based truncation is adequate at neutral pH and does not have any artifacts. At pH 2, this truncation is consistent with experiment in that the protein remains folded. The observed RMSDs are slightly higher—around 0.3 nm—but still far below of what is considered an unfolding. Our simulations for IL-4 therefore show that, like in the DNA fragment, the atom-based truncation is able to efficiently correct the flaws of the group-based reaction-field electrostatics method.
The unfolding at pH 2 is caused by additional repulsion between charged residues associated with the group-based truncation
We showed in our previous work [24] that the group-based truncation produces systematic errors in simulations of charged solutes. Pair of molecular ions modeled by the side chains of LYS and ASP, as well as a pair of sodium chloride ions, were seen to experience unphysical repulsion. Both nucleic acids and proteins have charged groups that could be subject to the aberrant repulsion. In DNA these are phosphate groups; in proteins they are ionizable residues. While the ABT and GBT schemes differ in other aspects, the aberrant repulsion of the latter could be causing unfolding in the studied DNA fragment and the protein. We test this hypothesis for the protein in two steps.
First, we test whether the contacts of charged residues in IL-4 do indeed experience the additional repulsion. There are three types of such contacts at pH 2: LYS-LYS, LYS-ARG and HIS-ARG. Fig. 6 shows the potential-of-mean force we computed for these contacts by reaction-field and lattice sum methods. The curves for all three contacts look qualitatively similar. The effective interactions of the atom-based truncation agree perfectly with those of the lattice-sum method. The two sets of curves almost completely overlap throughout the entire range of distances, up to 1.4 nm. Both sets predict a close contact minimum at separations of around ~0.49 nm, ~0.52 nm, ~0.58 nm for LYS-LYS, HIS-ARG and LYS-ARG pairs respectively, providing stable arrangements of these residues. Other very shallow minima are seen at ~0.7 nm for LYS-LYS, ~0.87 nm for HIS-ARG and 0.75 nm for LYS-ARG that correspond to solvent mediated configurations. The difference in the location of the first minimum in different pairs of residues is associated with the different choices of group centers. The group-based truncation also correctly predicts the location of the first minimum. However, the depth of the minimum is completely wrong. Compared to dissociated conformations with r=0.7–1.3 nm, the close-contact configurations are destabilized by ~2.5, ~1.2 and 2.0 kcal mol−1 for the LYS-LYS, HIS-ARG and LYS-ARG pairs correspondingly. Beginning with 0.6 nm for LYS-LYS and HIS-ARG, and with 0.7 nm for the LYS-ARG pair, the effective interactions calculated with the group-based truncation are purely repulsive, strongly favoring dissociation over association. Thus the repulsion is not specific to the ASP-LYS pair [24] and applies to all charged contacts in the native IL-4. In the case of the oppositely charged residues the repulsion is unphysical. For the pairs of same-charge residues, it enhances the natural repulsion between charges, making it much stronger. In all cases, the repulsion has the potential to destabilize the native state.
Fig. 6.
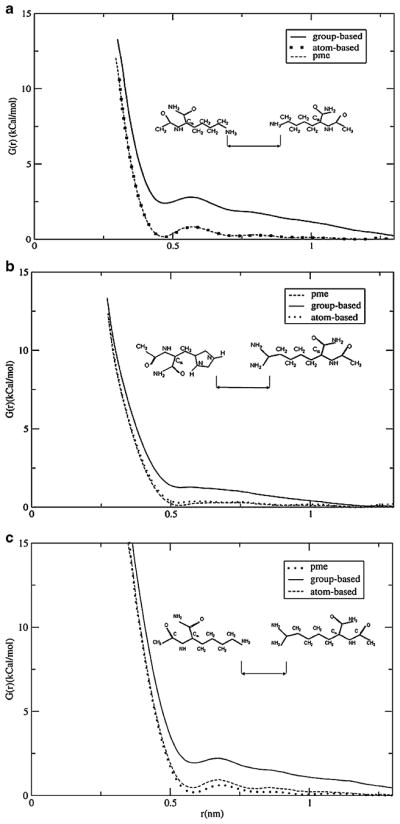
Potentials of mean force calculated for a) LYS-LYS, b) HIS-ARG c) LYS-ARG pairs in water using different electrostatics methods. Group-based RF simulations demonstrate enhanced repulsive interaction between the ions. The atom-based method predicts stable contacts between charged residues and agrees well with the particle-mesh Ewald method
At the second step, we determine if the repulsion causes the unfolding. The group-based and atom-based schemes differ in many respects. It could be that some other aspect of the GBT, as yet undetected, has an even greater effect on the simulations than the repulsion. To test for this possibility, we designed a computational experiment in which the repulsion was cancelled by imposing restraints on charged residues. Contacts with separations of less than 0.8 nm in the native configuration were subjected to a harmonic restraining potential that was applied to the same atoms as in the potential-of-mean force calculations with a force constant of 3.0x103 kJ mol−1 nm−2. The restraints were designed to have the minimum strength required to overcome the artificial repulsion. In total, 11 contacts were affected, Nterm - K42, Nterm - K123, K12 - R85, K21 -K117, K37 - R47, K37 - K102, R53 - K84, H59 - R64, K61 - K77, K61 - R81, and K123 - K126, including the contacts involving the charged N-terminal group. We ran five different restrained simulations, in which no significant unfolding was seen. The RMSD, shown for one trajectory in Fig. 7, is between 0.3 and 0.35 nm, which is comparable to that seen in the pH 6 simulations. All native helices remained well preserved without any obvious deformations. There is a slight re-orientation of A and D helices with respect to B and C helices, as shown in Fig. 5c, but not as severe as in the group-based simulations without restraints.
Fig. 7.
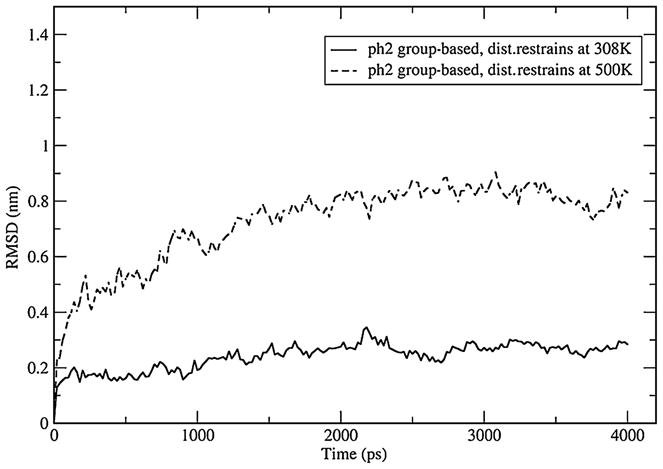
Root mean-square deviation over Cα atoms of IL-4 in simulations with inter-residue restraints at T=308 K and 500 K. The low-temperature trajectory shows that corrected repulsion between charged residues abolishes unfolding. The high-temperature trajectory demonstrates that the protein is not overconstrained and has sufficient conformational freedom to unfold
Finally, there may be two explanations for the restrained protein remaining folded: (a) the major source of unfolding has been removed and (b) the protein is unable to make any conformational changes including unfolding because of too many constraints. To exclude this latter possibility we ran an additional simulation at T=500 K. At this high temperature, the native state is unstable and the protein should denature, unless it is overconstrained. The RMSD of that simulation is shown in Fig. 7. It reaches 0.8 nm after 2 ns of simulation time, indicating that the protein has sufficient conformational freedom. Collectively, these tests demonstrate that the additional repulsion between charged residues in the group-based truncation is the primary source of the observed unfolding.
Conclusions
Computer simulations of biological molecules are faced with a multitude of challenges today [1]. One of the most urgent tasks is to assess the quality of modern force fields designed for proteins and nucleic acids. It is particularly important here to determine the ability of the common molecular representation that assigns one charge to one atom to describe subtle non-covalent interactions such as hydrogen bonds [40] and halogen bonds [41]. However, even within the framework of the fixed-charge model, many challenges remain for successful computer simulations of biomolecules. Key among these is how to treat electrostatic interactions, a subject that attracted considerable research attention recently [6, 23, 42–45]. In particular, much effort went into the investigation of truncated Coulomb potentials in simulations of proteins and nucleic acids (see ref [1] for a recent review), for which various aspects such as the effect of cut-off distances [4], the role of switching/shifting functions [46], and the way in which the truncation is implemented, based on groups or atoms [47], have been discussed at length, sometimes with conflicting conclusions [43]. Significantly less work has been done for the reaction-field electrostatics, with only a handful of papers appearing in the last decade [6, 17, 18]. Yet this method is gaining in popularity among the simulation community [21, 22, 48, 49], especially in massively parallel computing [44]. It is therefore important to study its strengths and limitations in full detail. The present paper is a step toward that goal.
We focused on how group- and atom-based truncations affect reaction-field simulations of proteins and DNA. To the best of our knowledge, this is the first such study. Our main findings are consistent for both molecules and can be summarized as follows. (I) The group-based truncation is able to disrupt native states in short nanosecond simulations. Artificial repulsion between charged groups associated with this truncation appears to play a key role in the forced unfolding. (II) The atom-based truncation generates stable trajectories for both DNA and the protein under a range of pH conditions. For the protein this is consistent with the experiment, while for the DNA it is consistent with more accurate lattice-sum simulations. Our simulations, therefore, expose a limitation in the reaction-field method with the group-based truncation. Applying it to systems with charged residues that form contacts will likely lead to instabilities. It is important that these instabilities are not mistaken for reporting on intrinsic properties of the simulated system. An example of when this may happen is the computational studies of amyloid fibrils where the stability of a short trajectory is used to support or refute a tentative structural model [50].
While we argue that the atom-based truncation is the more accurate method to conduct reaction-field simulations of biomolecules, it is also the more computationally expensive one [24]. Clearly, there are systems for which the group truncation is adequate [6, 18]. In general, such systems will tend to have a low density of charged residues, as is the case with the IL-4 protein at neutral pH investigated in this work. It is difficult, however, to formulate a quantitative criterion for what the critical density should be to warrant the more accurate treatment. It seems reasonable to suggest that the decision over whether to use the group-based or the atom-based truncation should be taken on a case-by-case basis, carefully weighing in all available information about the simulated system. For DNA molecules, the group-based truncation should be avoided, as it will lead to artifacts.
Acknowledgments
This work was supported in part by the National Institutes of Health, grant # R01GM083600-04.
Contributor Information
Boris Ni, Department of Physics and Optical Science, University of North Carolina Charlotte, 9201 University City Blvd, Charlotte, NC 28223, USA.
Andrij Baumketner, Email: abaumket@uncc.edu, Department of Physics and Optical Science, University of North Carolina Charlotte, 9201 University City Blvd, Charlotte, NC 28223, USA. On leave from the Institute for Condensed Matter Physics, NAS of Ukraine, 1 Svientsistsky Str, Lviv 79011, Ukraine.
References
- 1.van Gunsteren WF, Bakowies D, Baron R, Chandrasekhar I, Christen M, Daura X, Gee P, Geerke DP, Glattli A, Hunenberger PH, Kastenholz MA, Ostenbrink C, Schenk M, Trzesniak D, van der Vegt NFA, Yu HB. Biomolecular modeling: Goals, problems, perspectives. Angew Chem Int Ed. 2006;45:4064–4092. doi: 10.1002/anie.200502655. [DOI] [PubMed] [Google Scholar]
- 2.Adcock SA, McCammon JA. Molecular dynamics: Survey of methods for simulating the activity of proteins. Chem Rev. 2006;106:1589–1615. doi: 10.1021/cr040426m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Warshel A, Sharma PK, Kato M, Parson WW. Modeling electrostatic effects in proteins. Biochim et Biophys Acta-Proteins and Proteomics. 2006;1764:1647–1676. doi: 10.1016/j.bbapap.2006.08.007. [DOI] [PubMed] [Google Scholar]
- 4.Schreiber H, Steinhauser O. Cutoff size does strongly influence molecular-dynamics results on solvated polypeptides. Biochemistry. 1992;31:5856–5860. doi: 10.1021/bi00140a022. [DOI] [PubMed] [Google Scholar]
- 5.Monticelli L, Colombo G. The influence of simulation conditions in molecular dynamics investigations of model beta-sheet peptides. Theor Chem Acc. 2004;112:145–157. [Google Scholar]
- 6.Baumketner A, Shea JE. The influence of different treatments of electrostatic interactions on the thermodynamics of folding of peptides. J Phys Chem B. 2005;109:21322–21328. doi: 10.1021/jp051325a. [DOI] [PubMed] [Google Scholar]
- 7.Allen MP, Tildesley DJ. Computer simulations of liquids. Oxford Univ Press; Oxford: 1987. [Google Scholar]
- 8.Hunenberger PH, McCammon JA. Effect of artificial periodicity in simulations of biomolecules under Ewald boundary conditions: a continuum electrostatics study. Biophys Chem. 1999;78:69–88. doi: 10.1016/s0301-4622(99)00007-1. [DOI] [PubMed] [Google Scholar]
- 9.Weber W, Hunenberger PH, McCammon JA. Molecular dynamics simulations of a polyalanine octapeptide under Ewald boundary conditions: Influence of artificial periodicity on peptide conformation. J Phys Chem B. 2000;104:3668–3675. [Google Scholar]
- 10.Barker JA, Watts RO. Monte-Carlo studies of dielectric properties of water-like models. Mol Phys. 1973;26:789–792. [Google Scholar]
- 11.Barker JA. Reaction field, screening, and long-range interactions in simulations of ionic and dipolar systems. Mol Phys. 1994;83:1057–1064. [Google Scholar]
- 12.Hummer G, Soumpasis DM, Neumann M. Pair correlations in an NaCl-SPC water model - Simulations versus extended rism computations. Mol Phys. 1992;77:769–785. [Google Scholar]
- 13.Tironi IG, Sperb R, Smith PE, Vangunsteren WF. A generalized reaction field method for molecular-dynamics simulations. J Chem Phys. 1995;102:5451–5459. [Google Scholar]
- 14.van der Spoel D, van Maaren PJ, Berendsen HJC. A systematic study of water models for molecular simulation: Derivation of water models optimized for use with a reaction field. J Chem Phys. 1998;108:10220–10230. [Google Scholar]
- 15.Hunenberger PH, van Gunsteren WF. Alternative schemes for the inclusion of a reaction-field correction into molecular dynamics simulations: Influence on the simulated energetic, structural, and dielectric properties of liquid water. J Chem Phys. 1998;108:6117–6134. [Google Scholar]
- 16.Hummer G, Soumpasis DM, Neumann M. Computer-simulations do not support Cl-Cl pairing in aqueous NaCl solution. Mol Phys. 1994;81:1155–1163. [Google Scholar]
- 17.Rozanska X, Chipot C. Modeling ion-ion interaction in proteins: A molecular dynamics free energy calculation of the guanidinium-acetate association. J Chem Phys. 2000;112:9691–9694. [Google Scholar]
- 18.Nina M, Simonson T. Molecular dynamics of the tRNA (Ala) acceptor stem: Comparison between continuum reaction field and particle-mesh Ewald electrostatic treatments. J Phys Chem B. 2002;106:3696–3705. [Google Scholar]
- 19.Bonvin AMJJ, Sunnerhagen M, Otting G, van Gunsteren WF. Water molecules in DNA recognition II: A molecular dynamics view of the structure and hydration of the trp operator. J Mol Biol. 1998;282:859–873. doi: 10.1006/jmbi.1998.2034. [DOI] [PubMed] [Google Scholar]
- 20.Patra M, Karttunen M, Hyvonen MT, Falck E, Vattulainen I. Lipid bilayers driven to a wrong lane in molecular dynamics simulations by subtle changes in long-range electrostatic interactions. J Phys Chem B. 2004;108:4485–4494. [Google Scholar]
- 21.Gnanakaran S, Nussinov R, Garcia AE. Atomic-level description of amyloid beta-dimer formation. J Am Chem Soc. 2006;128:2158–2159. doi: 10.1021/ja0548337. [DOI] [PubMed] [Google Scholar]
- 22.Soares T, Christen M, Hu KF, van Gunsteren WF. Alpha-and beta-polypeptides show a different stability of helical secondary structure. Tetrahedron. 2004;60:7775–7780. [Google Scholar]
- 23.Krautler V, Hunenberger PH. Explicit-solvent molecular dynamics simulations of a DNA tetradecanucleotide duplex: lattice-sum versus reaction-field electrostatics. Mol Simul. 2008;34:491–499. [Google Scholar]
- 24.Baumketner A. Removing systematic errors in interionic potentials of mean force computed in molecular simulations using reaction-field-based electrostatics. J Chem Phys. 2009;130:104106.1–104106.10. doi: 10.1063/1.3081138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Winger M, Yu H, Redfield C, Van Gunsteren WF. Molecular dynamics simulation of human interleukin-4: comparison with NMR data and effect of pH, counterions and force field on tertiary structure stability. Mol Simul. 2007;33:1143–1154. [Google Scholar]
- 26.Lindahl E, Hess B, van der Spoel D. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J Mol Model. 2001;7:306–317. [Google Scholar]
- 27.Berendsen HH, Postma J, Van Gunsteren WF, Hermans J. Interaction models for water in relation to protein hydration. Reidel; Dordrecht: 1981. [Google Scholar]
- 28.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. A smooth particle mesh Ewald method. J Chem Phys. 1995;103:8577–8593. [Google Scholar]
- 29.Miyamoto S, Kollman PA. SETTLE - an analytical version of the SHAKE and RATTLE algorythm for rigid water models. J Comput Chem. 1992;13:952–962. [Google Scholar]
- 30.Hess B, Bekker H, Berendsen HJC, Fraaije J. LINCS: A linear constraint solver for molecular simulations. J Comput Chem. 1997;18:1463–1472. [Google Scholar]
- 31.Belhadj M, Alper HE, Levy RM. Molecular-dynamics simulations of water with Ewald summation for the long-range electrostatic interactions. Chem Phys Lett. 1991;179:13–20. [Google Scholar]
- 32.Hochtl P, Boresch S, Bitomsky W, Steinhauser O. Rationalization of the dielectric properties of common three-site water models in terms of their force field parameters. J Chem Phys. 1998;109:4927–4937. [Google Scholar]
- 33.Heinz TN, van Gunsteren WF, Hunenberger PH. Comparison of four methods to compute the dielectric permittivity of liquids from molecular dynamics simulations. J Chem Phys. 2001;115:1125–1136. [Google Scholar]
- 34.van Dijk M, Bonvin A. 3D-DART: a DNA structure modelling server. Nucleic Acids Res. 2009;37:W235–W239. doi: 10.1093/nar/gkp287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wlodaver A, Pavlovsky A, Gustchina A crystal-structure of human recombinant interleukin-4 at 2.25-angstrom resolution. FEBS Lett. 1992;309:59–64. doi: 10.1016/0014-5793(92)80739-4. [DOI] [PubMed] [Google Scholar]
- 36.Torrie GM, Valleau JP. Non-physical sampling distributions in Monte-Carlo free-energy estimation - umbrella sampling. J Comput Phys. 1977;23:187–199. [Google Scholar]
- 37.Ferrenberg AM, Swendsen RH. New Monte-Carlo technique for studying phase-transitions. Phys Rev Lett. 1988;61:2635–2638. doi: 10.1103/PhysRevLett.61.2635. [DOI] [PubMed] [Google Scholar]
- 38.Ferrenberg AM, Swendsen RH. Optimized Monte-Carlo data-analysis. Phys Rev Lett. 1989;63:1195–1198. doi: 10.1103/PhysRevLett.63.1195. [DOI] [PubMed] [Google Scholar]
- 39.Redfield C, Smith LJ, Boyd J, Lawrence GMP, Edwards RG, Gershater CJ, et al. Analysis of the solution structure of human interleukin-4 determined by heteronuclear 3-dimensional nuclear-magnetic-resonance techniques. J Mol Biol. 1994;238:23–41. doi: 10.1006/jmbi.1994.1265. [DOI] [PubMed] [Google Scholar]
- 40.Best RB, Hummer G. Optimized molecular dynamics force fields applied to the helix-coil transition of polypeptides. J Phys Chem B. 2009;113:9004–9015. doi: 10.1021/jp901540t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Politzer P, Murray JS, Clark T. Halogen bonding: an electrostatically-driven highly directional noncovalent interaction. Phys Chem Chem Phys. 2010;12:7748–7757. doi: 10.1039/c004189k. [DOI] [PubMed] [Google Scholar]
- 42.Zuegg J, Gready JE. Molecular dynamics simulations of human prion protein: importance of correct treatment of electrostatic interactions. Biochemistry. 1999;38:13862–13876. doi: 10.1021/bi991469d. [DOI] [PubMed] [Google Scholar]
- 43.Beck DAC, Armen RS, Daggett V. Cutoff size need not strongly influence molecular dynamics results for solvated polypeptides. Biochemistry. 2005;44:609–616. doi: 10.1021/bi0486381. [DOI] [PubMed] [Google Scholar]
- 44.Schulz R, Lindner B, Petridis L, Smith JC. Scaling of multimillion-atom biological molecular dynamics simulation on a petascale supercomputer. J Chem Theor Comput. 2009;5:2798–2808. doi: 10.1021/ct900292r. [DOI] [PubMed] [Google Scholar]
- 45.Miguez JM, Gonzalez-Salgado D, Legido JL, Pineiro MM. Calculation of interfacial properties using molecular simulation with the reaction field method: Results for different water models. J Chem Phys. 2010;132:184102.1–184102.5. [Google Scholar]
- 46.Steinbach PJ, Brooks BR. New spherical-cutoff methods for long-range forces in macromolecular simulation. J Comput Chem. 1994;15:667–683. [Google Scholar]
- 47.Norberg J, Nilsson L. On the truncation of long-range electrostatic interactions in DNA. Biophys J. 2000;79:1537–1553. doi: 10.1016/S0006-3495(00)76405-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Verli H, Calazans A, Brindeiro R, Tanuri A, Guimaraes JA. Molecular dynamics analysis of HIV-1 matrix protein: Clarifying differences between crystallographic and solution structures. J Mol Graph. 2007;26:62–68. doi: 10.1016/j.jmgm.2006.09.009. [DOI] [PubMed] [Google Scholar]
- 49.Mu YG, Nordenskiold L, Tam JP. Folding, misfolding, and amyloid protofibril formation of WW domain FBP28. Biophys J. 2006;90:3983–3992. doi: 10.1529/biophysj.105.076406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Negureanu L, Baumketner A. Microscopic factors that control beta-sheet registry in amyloid fibrils formed by fragment 11–25 of amyloid beta peptide: Insights from computer simulations. J Mol Biol. 2009;389:921–937. doi: 10.1016/j.jmb.2009.04.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Schrödinger LLC. The PyMOL molecular graphics system, Version 1.3r1. 2010. [Google Scholar]