Properties, Solution State Behavior, and Crystal Structures of Chelates of DOTMA

Abstract

The chemistry of polyamino carboxylates and their use as ligands for Ln³⁺ ions is of considerable interest from the point of view of the development of new imaging agents. Of particular interest is the chemistry of the macrocyclic ligand 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetic acid (DOTA) and its derivatives. Herein we report that the tetramethylated DOTA derivative, DOTMA, possess several properties that, from an imaging agent development point of view, are more advantageous than those of the parent DOTA. In particular, the Ln³⁺ chelates of DOTMA exhibit a marked preference for the monocapped twisted square antiprismatic coordination isomer which imparts more rapid water exchange kinetics on the chelates; τ_M²⁹⁸ was determined to be 85 ns for GdDOTMA. Differential analysis of the ¹⁷O R_2ρ temperature profiles of both GdDOTA and GdDOTMA afforded the τ_M²⁹⁸ values for the square (SAP) and twisted square antiprismatic (TSAP) isomers of each chelate that were almost identical: 365 ns (SAP) and 52 ns (TSAP). The origin of this accelerated water exchange in the TSAP isomer appears to be the slightly longer Gd–OH₂ bond distance (2.50 Å) that is observed in the crystal structure of GdDOTMA which crystallizes in the P₂ space group as a TSAP isomer. The Ln³⁺ chelates of DOTMA also exhibit high thermodynamic stabilities ranging from log K_ML = 20.5 for CeDOTMA, 23.5 for EuDOTMA and YbDOTMA comparable to, but a shade lower than, those of DOTA.

INTRODUCTION

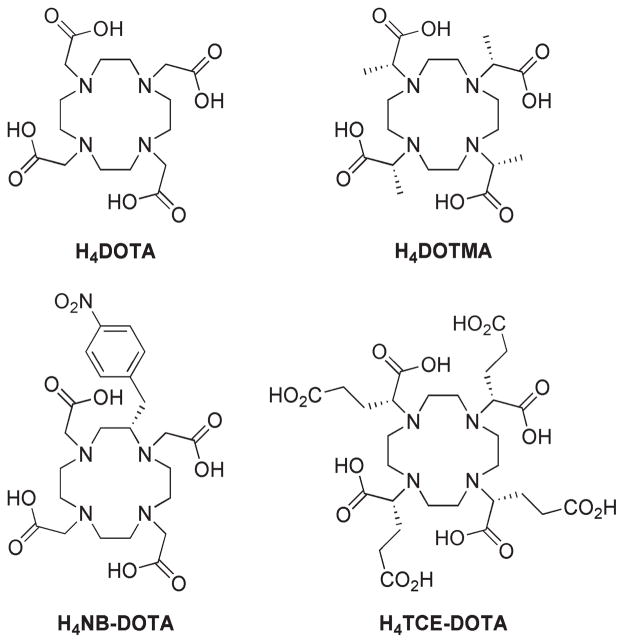
The chelation chemistry of rare earth metal ions with octadentate polyamino carboylate ligands has been widely studied over the past three decades or so. Ligands based upon the azacrown cyclen have received particular interest as a result, in large part, of the application of GdDOTA as an MRI contrast agent. The success of GdDOTA, and other structurally related chelates derived from cyclen, for in vivo applications stems from the high thermodynamic stability and kinetic inertness of these structures.¹ The high stability of these chelates ensures that, when employed in biological systems, there is minimal risk of the Ln³⁺ ion being released. First reported in 1976,² 1,4,7,10-tetraazacyclododecane- 1,4,7,10-tetraacetic acid (DOTA; Chart 1) has since provided the basis for the design of many Ln³⁺ chelates used in nuclear medicine, as luminescent probes, as well as MRI contrast agents. To date, over 1,000 papers have been published examining the chemistry and application to biomedicine of chelates of DOTA. It is a matter of some surprise therefore that DOTMA, the tetra-methylated analogue of DOTA (Chart 1), should have been a primary subject of only 10 original research papers^3–12 since it was first reported in 1984,³ just eight years after DOTA was first reported.

Chart 1.

Formulae of Some Aza-Crown Based Ligands for Ln³⁺ Ions

One reason for the apparent unpopularity of DOTMA may be the introduction of four stereogenic centers. Conventionally the term “DOTMA” is used to refer to the RRRR- enantiomer,³ in part because this is the easiest and least expensive single enantiomer of the ligand to produce. In this paper we will follow this convention; however, three other diastereoisomers are possible. By extension from studies on the related TCE-DOTA chelates,^13–15 each of the diastereoisomeric chelates would be expected to have very different properties. As a result, a stereo-selective synthetic approach is required for the preparation of DOTMA, an additional challenge when compared to the preparation of DOTA. Despite this complication, we have found that in some respects DOTMA exhibits ligating properties that are somewhat more advantageous than those afforded by DOTA. In the developing fields of molecular imaging and targeted therapy, in which metal chelates are to be targeted and bound to specific biological markers thereby increasing their in vivo half-lives, the slow kinetics of chelate formation observed for DOTMA reported herein, and by extension the slow kinetics of dissociation these imply, could be a critical advantage.

EXPERIMENTAL SECTION

General Remarks

All solvents and reagents were purchased from commercial sources and used as received. ¹H NMR spectra were acquired on a Bruker Avance III NMR spectrometer operating at 400.13 MHz. The 1/T₁ nuclear magnetic relaxation dispersion profiles of water protons were measured over a continuum of magnetic field strength from 0.00024 to 0.5 T (corresponding to 0.01–20 MHz proton Larmor frequency) on the fast field-cycling Stelar Spinmaster FFC 2000 relaxometer equipped with a silver magnet. The relaxometer operates under complete computer control with an absolute uncertainty in the 1/T₁ values of ±1%. The typical field sequences were used, such as the NP sequence between 40 and 8 MHz and the PP sequence between 8 and 0.01 MHz. The observation field was set at 13 MHz. Sixteen experiments of 2 scans were used for the T₁ determination for each field. Additional data at higher fields (40–80 MHz) were measured on a Stelar Spinmaster relaxometer equipped with a Bruker magnet operating in the range 20 to 80 MHz. Variable-temperature ¹⁷O NMR measurements were recorded on a JEOL EX-90 (2.1 T) spectrometer, equipped with a 5 mm probe, by using D₂O as external lock. Experimental settings were as follows: spectral width 10,000 Hz, pulse width 7 μs, acquisition time 10 ms, 1000 scans and no sample spinning. Solutions containing 2.6% of ¹⁷O isotope (Yeda, Israel) were used. The observed transverse relaxation rates were calculated from the signal width at half height.

Synthesis

(1R,4R,7R,10R)-α, α′, α″, α‴-Tetramethyl-1,4,7,10-tetraazacyclododecane- 1,4,7,10-tetraacetic Acid Tetrasodium Salt (Na₄DOTMA)

To a solution of cyclen (1.0 g, 5.8mmol) in dry chloroform(30 mL), under an argon atmosphere, was added potassium carbonate (7.41 g, 53.6 mmol). The reaction was then cooled in an ice-bath and, with vigorous stirring, ethyl (S)-2-(trifluoromethylsulfonyloxy)propionate (6.71 g, 26.8 mmol) was added dropwise over the course of 5 min. The reaction was heated to 45 °Cunder an argon atmosphere and stirred for 72 h. After cooling to room temperature, the reaction was quenched by slow addition of water (30 mL), and the organic and aqueous layers divided. The aqueous phase was extracted with chloroform (2 × 70 mL), the extracts combined, dried (Na₂SO₄), and the solvents removed under reduced pressure. The crude reaction product was used without further purification and dissolved in tetrahydrofuran (30 mL) and water (40 mL). Sodium hydroxide (1.52 g, 38.0 mmol) was added, and the resulting biphasic solution heated at 50 °C for 18 h until enough tetrahydrofuran had evaporated to form a monophasic solution and a colorless precipitate had formed. The precipitate was isolated from the solution by centrifugation. The precipitate was dissolved in hot water and filtered while hot, the volume of the filtrate was then reduced to 20 mL by heating at 70 °C. The title compound crystallized as a colorless solid (2.23 g, 70%). All characterization data were consistent with those previously published.^3,4

Crystalline H₄DOTMA · 2HCl · 3H₂O was subsequently obtained by crystallization of the sodium salt from ~5 M HCl.

Na₄[GdDOTMA(H₂O)]₂Cl₂(H₂O)₁₂ Crystals

Toa solution of H₄DOTMA · 2HCl · 3H₂O (100 mg, 17.0 μmol) in H₂O (10 mL) was added Gd₂O₃ (30.9 mg, 8.5 μmol). The resulting suspension was heated to 70 °C with stirring for 3 days. After cooling to room temperature the reaction pH was raised to neutral by addition of a 1Msolution of NaOH. The reaction was then filtered through a 20 μm syringe filter, and solvents were removed from the filtrate by lyophilization. The residue was taken up into H₂O (2 mL), and a layer of EtOH (8 mL) carefully added above the aqueous solution. The vessel was sealed and X-ray quality crystals grown by slow diffusion of EtOH into the aqueous solution.

Crystallography

A crystal, approximately 0.50×0.15×0.05mm³, was placed onto the tip of a 0.1mmdiameter glass capillary and mounted on a Siemens SMART Platform CCD diffractometer for data collection at 173(2) K.¹⁶ A preliminary set of cell constants were calculated from reflections harvested from three sets of 20 frames. These initial sets of frames were oriented such that orthogonal wedges of reciprocal space were surveyed. This produced initial orientation matrices determined from 85 reflections. The data collection was carried out using MoKα radiation (graphite monochromator) with a frame time of 30 s and a detector distance of 4.959 cm. A randomly oriented region of reciprocal space was surveyed to the extent of one sphere and to a resolution of 0.77 Å. Four major sections of frames were collected with 0.30° steps in ω at four different φ settings and a detector position of −28° in 2θ. The intensity data were corrected for absorption and decay (SADABS).¹⁷ Final cell constants were calculated from the xyz centroids of 3658 strong reflections from the actual data collection after integration (SAINT).¹⁸ Please refer to Table 1 and the Supporting Information for additional crystal and refinement information.

Table 1.

Crystallographic Data for Na₄[GdDOTMA(H₂O)]₂Cl₂ · (H₂O)₁₂

empirical formula	C40H86Cl2Gd2N8Na4O30
formula weight	1636.53
temperature (K)	173(2)
wavelength (Å)	0.71073
crystal system	monoclinic
space group	P2
a (Å)	9.6639(12)
b (Å)	9.6379(12)
c (Å)	18.926(2)
α	90°
β	98.266(2)°
γ	90°
volume (Å3)	1744.5(4)
Z	1
density (calculated) (Mg/m3)	1.558
absorption coefficient (mm−1)	2.067
F(000)	828
crystal color, morphology	colorless, block
crystal size (mm3)	0.50 × 0.15 × 0.05
θ range for data collection	2.11 to 27.51°
index ranges	−12 ≤ h ≤ 12, −12 ≤ k ≤ 12, 0 ≤ l ≤ 24
reflections collected	18679
Independent reflections	7882 [R(int) = 0.0352]
observed reflections	7068
completeness to θ =25.05°	99.4%
absorption correction	multiscan
max. and min transmission	0.90 and 0.70
refinement method	full-matrix least-squares on F2
data/restraints/parameters	7882/1/395
goodness-of-fit on F2	0.992
final R indices [I > 2σ(I)]	R1 = 0.0355, wR2 = 0.0813
R indices (all data)	R1 = 0.0426, wR2 = 0.0837
absolute structure parameter	0.000(11)
largest diff. peak and hole	0.783 and −0.877 e Å−3

The structures were solved using Bruker SHELXTL or SHELXS-97¹⁹ and refined using Bruker SHELXTL or SHELXL-97.¹⁹ The space group P2 was determined based on systematic absences and intensity statistics. A direct-methods solution was calculated which provided most non-hydrogen atoms from the E-map. Full-matrix least-squares/difference Fourier cycles were performed which located the remaining non-hydrogen atoms. All non-hydrogen atoms were refined with anisotropic displacement parameters. All hydrogen atoms were placed in ideal positions and refined as riding atoms with relative isotropic displacement parameters. The final full matrix least-squares refinement converged to R1 = 0.0355 and wR2 = 0.0837 (F², all data). The structure of GdDOTMA contains several severely disordered water molecules in a void space which were explored by Platon/Squeeze.²⁰

Potentiometric Measurements

All potentiometric titrations were performed using the conditions and methods reported in our companion paper.²¹ Because of the especially slow rates of chelation of Ln³⁺ ions by DOTMA, the stability constants of these chelates were determined using the “out-of-cell” technique (also known as the batch method). However, unusually long equilibration times were required even by the slow standard of DOTA-type chelates. Sixteen 1.5 mL samples of known DOTMA and Ln³⁺ ion concentrations (approximately 2mMeach using a 100% (Ce³⁺) or 50% (Eu³⁺ and Yb³⁺) excess of ligand to prevent the local hydrolysis during sample prepration) were prepared, and the total acid concentration in the samples was varied. The pH of the samples was adjusted to a range within which chelation was expected to take place (predicted by applying an approximate stability constant estimated from the known value for LnDOTA). Each sample was then sealed under a blanket of N₂ and kept in an incubator at 37 °C for 16 weeks and then at 25 °C for a further 3 months. The minimum time required to reach equilibrium was established by periodically measuring the absorbance of the most and least acidic samples of the Ce³⁺ (λ = 320 nm) and Eu³⁺ (λ = 275nm). Only when no further changes in absorbance were observed were the equilibrium pH values determined. The data were then analyzed as described in our companion paper.²¹

Kinetics of Formation

The rates of EuDOTMA formation were studied at 25 °C and 1.0 M KCl ionic strength using a Varian Cary 300 Bio UV–vis spectrophotometer. Because of the relatively high stability of the H₂GdL⁺ intermediate obtained by direct pH-potentiometric titrations, the complex formation was studied using a 10-fold excess of ligand (1.00 mM Eu³⁺ and 10.0 mM DOTMA). The most suitable ligand concentration (excess) was determined by studying the rates of complex formation versus ligand concentration. It was found that to reach the saturation value (k_obs (s⁻¹) = k_r (s⁻¹)) for EuDOTMA a 5-fold ligand excess would suffice (see Supporting Information for more details). Below pH 5.5 the rates of chelate formation were extremely slow so reaction was followed in the pH range of 5.77–8.61 by spectrophotometry. Samples were buffered using MES (2-(N-morpholino)-ethanesulfonic acid, log K₁^H = 6.06), PIPES (piperazine-N,N′-bis-(2-ethanesulfonic acid), log K₁^H = 6.78) and HEPES (N-(2-hydroxyethyl)- piperazine-N′-3-propanesulfonic acid, log K₁^H = 8.00) at 50 mM).²² Under these conditions excess ligand must be employed to ensure that no hydrolysis and precipitation of Ln³⁺ ions occurs. The rates of formation were studied at pH 8.01 (HEPPS) varying the buffer concentration in the range of 20–60 mM but maintaining constant metal and ligand concentrations, demonstrating a general base catalysis.

The first order rate constants (k_obs of formation) where calculated using eq 1, where A₀, A_e, and A_t are the absorbance values measured at the start of the reaction (t = 0), at equilibrium, and at time t, respectively. Fitting was performed using Scientist (Micromath) using a standard least-squares procedure. The relative error in fitting the absorbance versus time data was less than 1% while the calculated first order rate constants (k_obs) were reproduced to within 0.5–2% error, as determined in three identical experiments.

$$A_{\text{t}}=A_{\text{e}}+(A_0-A_{\text{e}})·{\text{e}}^{(-k_{\text{obs}}·t)}$$ (1)

Stability Determination by Spectrophotometry

Spectrophotometric measurements were carried out on the absorption band of Ce³⁺ in the wavelength range of 310–330 nm. A series of samples (10 samples in total of 1.0 mL volume) were prepared, containing the CeCl₃ at 1.0 mM with the 2.0 mM ligand to prevent local hydrolysis upon base addition during sample preparation. The samples were incubated at 37 °C for about 16 weeks to attain equilibrium. The samples were then allowed to equilibrate at room temperature until no further change in the absorption spectra was observed (3–5 weeks). The molar absorptivity of the colored species was then determined in the concentration range 1.0 to 5.0mM for the Ce³⁺ and 0.25 to 1.0 for the CeDOTMA complex. The stability constants of the complexes were calculated with the program PSEQUAD²³ by fitting equilibrium data measured at 11 wavelengths between 310 and 330 nm (total 110 points were fitted with A = 0.028 fitting parameter).

RESULTS AND DISCUSSION

Synthesis

DOTMA was first prepared by the condensation of sodium S-2-bromopropionate with cyclen in aqueous solution at pH ~9. Subsequent acidification and crystallization afforded enantiomerically pure H₄DOTMA, but the overall yield was relatively poor, just 22%.³ Tweedle and co-workers employed a two step strategy for the synthesis of DOTMA.⁴ Cyclen was first alkylated with the triflate of L-benzyl lactate and the benzyl esters subsequently removed by hydrogenolysis. Although this method was reported to give DOTMA in high purity (>99.9%), and undoubtedly removes the traces of salts inherent in the method of Desreux,³ it does not improve the yield; 20% overall from cyclen.⁴ We have discovered that DOTMA can be prepared as its sodium salt in high purity and good yield by adapting the synthetic method of Tweedle and co-workers.⁴

If cyclen is alkylated with the triflate of L-methyl lactate rather than the benzyl ester then the ester cleavage can be performed by saponification. After the initial alkylation reaction is complete, the reaction mixture is extracted with water. The resulting oil can be subjected to the saponification reaction without need of further purification. The oil is taken up into tetrahydrofuran, to aid solubility, and 1 equiv of sodium hydroxide per ester group is added in aqueous solution. Once the esters are saponified the ligand becomes insoluble and crystallizes from solution affording the ligand in 70% yield overall after isolation and drying. If required, Na₄DOTMA can be further recrystallized from hot water. The DOTMA may also be crystallized as its dihydrochloride salt by dissolving Na₄DOTMA in ~5M HCl and allowing the solvents to slowly evaporate.

Ln³⁺ chelates of DOTMA were prepared by reaction of the acid form of the ligand with the appropriate Ln₂O₃ at 70 °C. This approach to chelate formation, which employs rather acidic conditions, was taken as it was thought it would ensure a highly eniantiomerically pure chelate.¹⁴ The nature of the crystals (blocks versus needles, etc.) grown by diffusion of ethanol into an aqueous solution of LnDOTMA was found to vary considerably according to the nature of the countercation as well as the precise Ln³⁺ ion used in the chelate.

Structural Isomerism of DOTMA Chelates in Solution

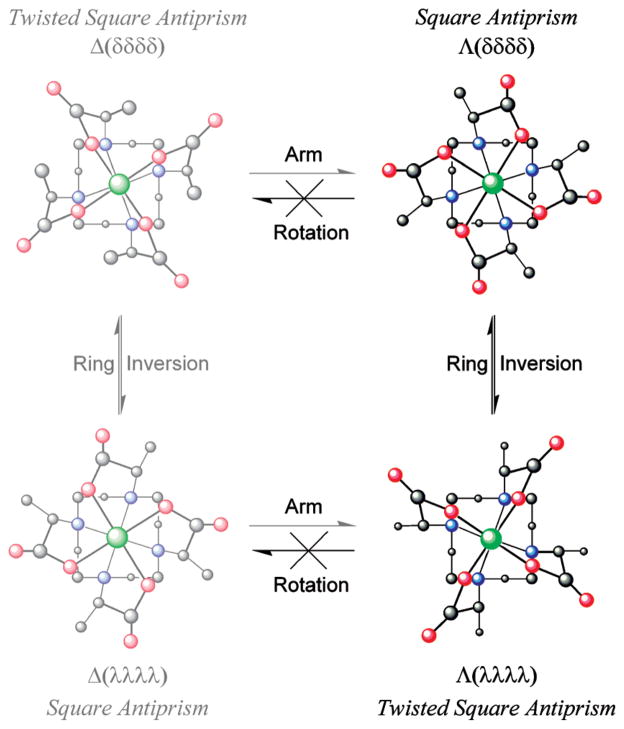
The solution state structure and molecular dynamics of LnDOTA-type chelates are now well understood.^24,25 These chelates can exist in up to four stereoisomeric structures that, in LnDOTA chelates, are related as two enantiomeric pairs. The stereochemistry of each structure is defined by two elements of helicity: the conformation of the macrocyclic ring (either δδδδ or λλλλ) and the orientation of the pendant arms (either Δ or Λ). When the helicity of these two elements is the same then the coordination geometry is defined by a monocapped twisted square antiprism (TSAP), when they are opposed by a monocapped square antiprism (SAP) (Figure 1). These two coordination geometries may interconvert, either by a ring flipping motion (δδδδ ⇌ λλλλ) or reorientation of the pendant arms (Δ ⇌ Λ). The intramolecular conformational exchange processes have rate constants of the order of 10 s⁻¹ and are therefore relatively slow on the NMR-time scale;²⁴ this allows each coordination geometry to be clearly visible in the ¹H NMR spectrum of a chelate.

Figure 1.

Structural isomerism in GdDOTMA chelates. Four stereo-isomeric structures are possible for GdDOTA, but two of these structures are inaccessible to GdDOTMA because the arm rotation motion by which they are accessed is “frozen” out in this chelate. These stereoisomers are represented by the washed out structure on the left.

Substitution of a DOTA chelate has a profound effect upon this situation as it introduces a chiral carbon center into the ligand framework; this in turn renders the four stereoisomeric structures Δ (λλλλ), Δ (δδδδ), Λ (δδδδ), and Λ (λλλλ) diastereoisomers of one another. However, only two species are observed in ¹H NMR spectrum of LnTCE-DOTA,^13,14 LnDOTMA^3,8 and LnNB-DOTA²⁶ chelates indicating that two of the four structures are inaccessible. From crystal structure data acquired on the α-substituted DOTA derivatives TCE-DOTA and NIR-CD data on DOTMA it became clear that the introduction of a substituent onto the pendant arm of aDOTA chelate introduces control over the orientation of that pendant arm.^12–14 The chelate will always seek to place the substituent anti- to the metal ion (looking down the C–N bond),²⁷ thereby lowering torsional strain, and since the arms bind cooperatively, that is, all with the same helicity, wherever possible the chelate will seek to maximize the number of pendant arms that adopt this lower energy conformation.¹⁴ From the crystal data of TCE-DOTA it is apparent that an R- configuration at carbon induces a Λ helicity in the pendant arms and S- Δ.¹⁴ Di Bari and co-workers confirmed that the solution state structure and behavior of LnDOTMA chelates parallels those of RRRR-TCE-DOTA chelates.⁸

In addition to the changes in stereoisomerism discussed above one further difference between α-substituted DOTA chelates and LnDOTA chelates is apparent from the published NMR data;¹⁴ substitution of the pendant arms leads to a marked preference for the TSAP coordination geometry in solution. It has been previously established that for the earlier Ln³⁺ ions DOTA chelates exhibit a preference for the TSAP coordination geometry.^25,28 This has been ascribed to a more “open” coordination cage of the TSAP isomer which more readily accommodates the larger ionic radius of early Ln³⁺ ions. As the ionic radius of the Ln³⁺ ion decreases the SAP coordination geometry becomes increasingly more preferred until a tipping point is reached around Er³⁺. At this point the TSAP geometry is believed to lose its coordinated water molecule, as evidenced by the crystal structure of TmDOTA,²⁹ rendering it increasingly more favorable as the Ln³⁺ ionic radius contracts below the 114 pm of Er³⁺. A comparable trend has been reported for chelates of NB-DOTA.²⁶

The solution state distribution of coordination isomers for LnDOTMA complexes differs radically from those of the 2 acetate appended chelates DOTA and NB-DOTA (Figure 2). For all Ln³⁺ ions there is a marked preference for the TSAP isomer when DOTMA is used as the ligand. This behavior parallels that of LnTCE-DOTA chelates¹⁴ and is strongly indicative of a relationship between coordination geometry preference and α-substitution of the pendant arms. The chelates of DOTMA with early Ln³⁺ ions adopt almost exclusively the TSAP isomer in solution. As with other ligands the SAP isomer becomes increasingly favored as the ionic radius decreases, but this trend reaches a maximum much earlier in the lanthanide series; between Tb³⁺ and Dy³⁺ (~117 pm ionic radius) with never more than ~30% of the chelate as a SAP isomer observed in solution. As the Ln³⁺ ionic radius decreases yet further the TSAP isomer again becomes increasingly favored in a trend reminiscent of those exhibited by other ligands. However, in the case of DOTMA by the time we reach the smallest Ln³⁺ ions Yb³⁺ and Lu³⁺ the TSAP isomer is almost the exclusive isomeric form of the chelate in solution. As with LnDOTA chelates we may suppose that this reversal in the isomeric distribution trend relates to a decrease in the hydration state of the TSAP isomer of LnDOTMA chelates as the ionic radius is decreased beyond ~117 pm.

Figure 2.

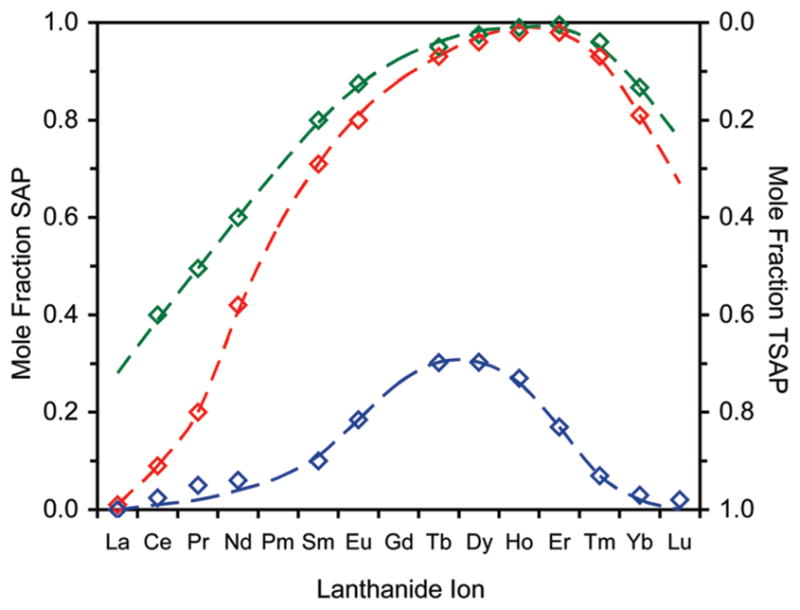
Mole fractions of the SAP (left axis) and TSAP (right axis) isomers of LnDOTMA (blue) chelates as a function of the Ln³⁺ ion. Data for LnDOTA (red)²⁸ and LnNB-DOTA (green)²⁶ chelates are also shown for comparative purposes.

Solid State Structures of DOTMA Chelates

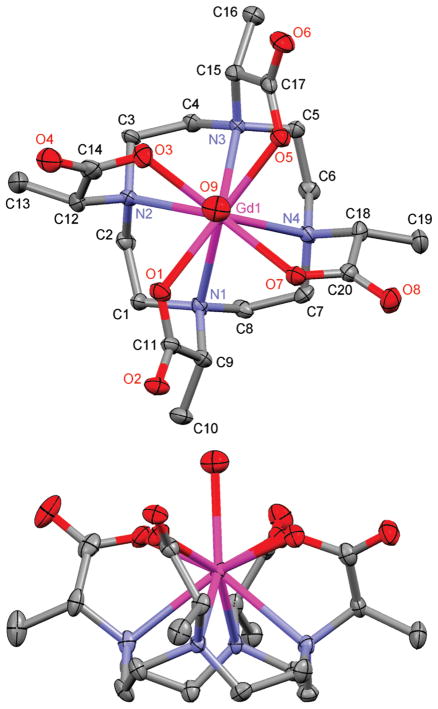
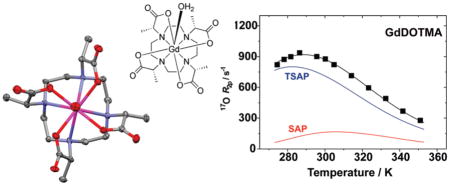
In general it appears that the Gd³⁺ chelates of DOTA and related tetraacetate ligands have a preference for crystallizing in a SAP coordination geometry. The crystal structure of GdDOTA has been determined twice previously^30,31 with a comparable SAP chelate structure observed each time. Perhaps more significantly the crystal structure of the α-substituted SSSS-GdTCE-DOTA also puts the central Gd³⁺ ion in a SAP coordination geometry.¹⁴ This despite the observation that SSSS-GdTCE-DOTA predominates as the TSAP isomer in solution; x^TSAP = 0.8 for Eu³⁺,¹³ cf. EuDOTMA (Figure 2). On this basis one might reasonably expect that the crystal structure of a GdDOTMA chelate would also reveal a SAP coordination geometry. In contrast, when X-ray quality crystals of Na₄[GdDOTMA(H₂O)]₂Cl₂ · (H₂O)₁₂ were grown by slow diffusion of ethanol into an aqueous solution of GdDOTMA the coordination geometry in the structure of the Gd³⁺ chelate was in fact the TSAP isomer. This unusual structure affords a rare opportunity to compare the structures of comparable chelates in both the SAP (GdTCE-DOTA) and the TSAP (GdDOTMA) coordination geometries. One other such rare example is the crystal structure of EuTHP.³²

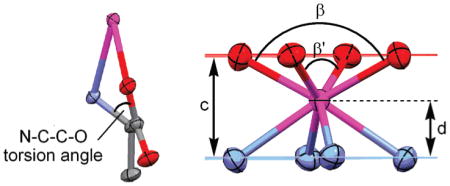
The crystal structure of GdDOTMA is shown in Figure 3. For purposes of comparison selected crystallographic parameters are collected in Table 2, along with those same parameters from the structure of GdTCE-DOTA.¹⁴ Because GdTCE-DOTA was crystallized from a racemic mixture of the homochiral diastereoisomer (RRRR-/SSSS-) and GdDOTMA from an enatiomerically pure sample (RRRR-), the two chelates crystallize in different space groups. Nonetheless, the two chelates share some important characteristics: in each the Gd³⁺ is enna-coordinate with a solvent water molecule occupying the ninth coordination site. The central Gd³⁺ ion is sandwiched between four coplanar nitrogen atoms of the macrocyclic ring and four coplanar carboxylate oxygen atoms. In each chelate the macrocycle adopts a [3333] ring conformation³³ in which each ethylene bridge is an almost ideal gauche conformation. In both chelates the helicity of these ethylene bridges is the same; the negative N–C–C–N torsion angles observed in each structure defining a λλλλ macrocyclic ring conformation. However, at this point similarities between the two structures begin to deviate. To minimize torsional strain in the chelate ring of the pendant arm the orientation of the pendant arms in each chelate is determined by the configuration at the α-carbon^13,14 such that the substituent is positioned anti- to the metal ion.²⁷ Thus, the SSSS-isomer of GdTCE-DOTA has the pendant arms in a Δ orientation (as defined by positive N–C–C–O torsion angles). The opposing helicities of macrocycle and pendant arms in this chelate define a SAP coordination geometry. In contrast, the pendant arms of GdDOTMA (the RRRR- isomer) are in a Λ orientation defining the chelate as a TSAP coordination isomer.

Figure 3.

50% Thermal ellipsoid plot of the crystal structure of Na₄[GdDOTMA(H₂O)]₂Cl₂ · (H₂O)₁₂ showing only the GdDOTMA(H₂O) chelate. Hydrogen atoms, counterions, and water molecules of crystallization have been omitted for clarity.

Table 2.

Comparison of Selected Distances and Angles from the Crystal Structures of RRRR-Na₄[GdDOTMA(H₂O)]₂Cl₂(H₂O)₁₂ and SSSS-H₅[GdTCE-DOTA(H₂O)](H₂O)₃.¹⁴

parameter	GdTCE-DOTAa	GdDOTMA
space group	P1̄	P2
coord. geometry	SAP	TSAP
q	1	1
max N–C–C–N (deg)	−61.41	−60.56
min N–C–C–N (deg)	−58.0	−59.23
max N–C–C–O (deg)	+40.67	−35.39
min N–C–C–O (deg)	+17.53	−13.63
α (deg)b	39.2	26.1
Gd–OH2 (Å)	2.431	2.50
c (Å)	2.326	2.457
d/c(Å)	0.69	0.68
β (deg)	144.87	140.87
β′ (deg)	144.49	140.86

^aTaken from ref 14.

^bα = the N₄–O₄ torsion angle.

Perhaps the most instructive differences between these two chelates are found by comparing the water binding of the two structures. Both structures possess a coordinated water molecule that caps the antiprism; however, the Gd–OH₂ bond distance in GdDOTMA is significantly longer, by almost 0.07 Å. This is consistent with the determination of a longer bond distance for the TSAP isomer of Eu³⁺ chelates in solution.³⁴ In that case the Ln–OH₂ bond distance was elongated by 5% whereas the Gd³⁺ chelates in the crystal exhibit an elongation of just 3%. This water bond elongation has implications for the rate of water exchange in solution vide infra. The origin of this water bond elongation can be seen by considering the relative positions of the N₄ and O₄ planes with that of the Gd³⁺ ion. In the TSAP isomer (GdDOTMA) the N₄ and O₄ planes lie further apart (by 0.131 Å) relative to the SAP isomer (GdTCE-DOTA), a result of the narrowing of the N₄/O₄ torsion angle (α) and the N–C–C–O torsion angles. The consequence of this is that the Gd³⁺ ion lies slightly further from the O₄ plane in the TSAP isomer (GdDOTMA) than it does in the SAP isomer (GdTCE-DOTA). This “buries” the Gd³⁺ ion slightly further within the coordination cage, as evidenced by the slight decrease in the d/c ratio and increase in the O–Gd–O angles β and β′. These parameters have been considered as guides to the steric encumbrance of the water coordination site: at d/c ratios <0.65 and β angles <136° it has been found that water is no longer able to access the apical coordination site on this type of chelate.^35,36 It seems apparent therefore that the reduction in α and N–C–C–O torsion angles necessary to pass from a SAP to a TSAP coordination geometry push the O₄ plane toward the coordinating water molecule, increasing steric encumbrance around its binding site, and pushing the water molecule away from the Gd³⁺ ion thus elongating the water bond distance.

Thermodynamic Stability

Thermodynamic stability constants are a convenient measure of chelate stability and are readily determined by potentiometric titration. The protonation constants of the ligand must first be determined by titrating the ligand in the absence of metal. A constant ionic background must be maintained throughout these titrations, and the nature of the ionic background chosen can have a substantial impact upon the results obtained.³⁷ Metal ions such as Na⁺ form chelates with cyclen based ligands such as DOTA and DOTMA of sufficient stability that their presence influences the protonation constants obtained if present in sufficient quantity. For this reason tetraalkyl ammonium salts are often preferred for this purpose as these cations do not interact with the ligands. However, these salts have their own problems, degrading over time and altering the balance of the sample. To determine the protonation constants of DOTMA we opted to use 1.0 M KCl as the ionic background because of its long-term stability. Although K⁺ does interact with these ligands it does so much more weakly than Na⁺ and introduces only a very small errors into the measurements.³⁷

The protonation constants of DOTMA determined by potentiometric titration are collected in Table 3, along with those of DOTA³⁸ and NB-DOTA²⁶ for comparative purposes. It is apparent that all but the fourth the protonation constant values of DOTMA are comparable with those observed for DOTA. The fourth protonation constant of DOTMA is curious because, unusually, it is actually higher than the third protonation constant. Such an observation is counterintuitive and, although rare, has previously been observed in aza-crown systems.³⁹One way to understand this phenomenon is to consider a ligand that can adopt more than one well-defined conformation. If at high pH the ligand adopts one conformation preferentially but protonation, as the pH drops, results in conformational change then the site of the next protonation event may be rendered more basic due to this conformational change. If this difference is sufficiently large then the pK_a of this site (which will reflect the second conformation) may exceed that of the one preceding it (which will reflect the initial conformation). However, in this case it is believed that a second explanation accounts for the observed inversion of pK_a’s in DOTMA. The protonation constants were determined with KCl as the ionic background, and although it has previously been stated that the K⁺ ion interacts only weakly with these types of ligand systems, it does nonetheless interact. From data presented in a companion paper²¹ it seems likely that K⁺ interacts with the carboxylates of these ligand systems. The third protonation step may well displace K⁺ from the ligand and in so doing render the fourth protonation step easier, in certain cases even easier than the third.

Table 3.

Protonation and Thermodynamic Stability Constants of DOTMA, DOTA and NB-DOTA (I = 1.0MKCl, 25 °C). ^a

log KiH	DOTMA	DOTAb	NB-DOTAc,d	(TCE-DOTAc,e
Protonation Constants
log K1	12.59 (0.02)	12.60	10.93	12.22
log K2H	9.28 (0.02)	9.70	9.14	9.18
log K3H	4.66 (0.05)	4.50	4.44	4.17
log K4H	5.78 (0.02)	4.14	4.19	3.93
log K5H	1.84 (0.02)	2.32	2.33	2.88
log K6H			1.40	n.d.
Σ log KiH	33.43	33.26	32.43	32.38f
Thermodynamic Stability Constants
log KCeL	20.47 (0.09)	23.4g
log KCeLh	20.96 (0.02)
log KEuL	23.52 (0.05)	24.7g
log KGdL	23.6i	24.7g	24.2	24.03
log KYbL	23.56 (0.05)	25.0g
log KLuL			24.5

^aValues in bold highlight instances were the fourth pK_a is higher than the third.

^bData taken from ref 40.

^cI = 0.1 M NMe₄Cl;

^dData taken from ref 26.

^eData taken from ref 15, pK_a’s of peripheral carboxylates are not given herein.

^fi = 1–5 only;

^gData taken from ref 38.

^hDetermined by spectrophotometry.

ⁱData taken from ref 41; n.d. = not accurately determined.

Determining the thermodynamic stability constants of LnDOTMA chelates is made more difficult because of the extremely slow kinetics of formation of these chelates, vide infra. An out-of-cell technique, in which sealed samples of ligand and metal are incubated for prolonged periods prior to measurement, ²⁶ is commonly applied in the determination of the thermodynamic stability constants of DOTA-type chelates owing to the slow kinetics of formation. However, DOTMA chelates are extraordinarily slow to reach equilibrium. In an attempt to circumvent this problem alternative methods of determining the thermodynamic stability of these chelates were trialed. Ligand and metal substitution reaction were trialed to reduce the time necessary for thermodynamic stability determinations to be made without success. More details of these experiments are available in the electronic Supporting Information. Since alternative methods proved unsatisfactory the thermodynamic stability constants of the Ce³⁺, Eu³⁺, and Yb³⁺ chelates of DOTMA were determined using the out-of-cell technique. Although this required substantially longer than usual incubation times this approach did afford useful data that could be used to determine the thermodynamic stability constant of each chelate (Table 3).

The stability constants of the three LnDOTMA chelates are notable for being slightly lower than those observed in other DOTA-type ligand systems (Table 3). However, it should be remembered when comparing these data that the value determined for chelates of TCE-DOTA and NB-DOTA were determined in an ionic background of NMe₄Cl, whereas those of DOTMA and DOTA were determined in KCl. This change in ionic background will tend to lower the values of the thermodynamic stability constants of DOTMA and DOTA relative to those of TCE-DOTA and NB-DOTA.³⁷ With this in mind we can conclude that the stability constants of GdDOTMA and GdTCE-DOTA are approximately equivalent, hardly surprising given the structural similarities of the two chelates. The thermodynamic stability constants determined for LnDOTMA chelates are consistently slightly lower than those of LnDOTA chelates determined in the same ionic background. This is superficially rather surprising since DOTMA is the more basic of the two ligands, and in general more basic ligands form stronger chelates with the same metal ion. Although a similar difference is observed between the Gd³⁺ chelates of the more basic NOTMA and the less basic NOTA, both based on the aza-crown system, 9N₃.^38,42,43

A different trend in stability constant is observed across the lanthanide series for DOTA and DOTMA. The thermodynamic stability constants of LnDOTA chelates increase consistently across the lanthanide series,³⁸ an effect that is generally ascribed to an increase in the electrostatic interaction between ligand and metal as the charge density on the metal ion increases with contraction across the lanthanide series. In contrast the stability constants of LnDOTMA appear to increase on passing from Ce³⁺ to Eu³⁺ and then remain approximately constant across to Yb³⁺. DOTMA is different from DOTA in at least one significant respect here; all its Ln³⁺ chelates, to a greater or lesser extent, exhibit a marked preference for the TSAP isomer in DOTMA chelates (Figure 2). In contrast LnDOTA chelates appear to be free to adopt an equilibrium position determined by the metal ion that reflects a balance of the thermodynamic stabilities of the two coordination geometries.²¹ Thus, the apparent constraint of coordination geometry in LnDOTMA chelates must be considered when examining these stability data. EuDOTA, GdDOTA, and YbDOTA predominate in the SAP coordination geometry, and this is found to be the more thermodynamically stable coordination geometry for these metal ions.²¹ But in DOTMA the TSAP geometry, which is less thermodynamically stable, predominates for these metals, and this may explain why the stability constants of the mid and later Ln³⁺ ions is lower for DOTMA than it is for DOTA.

The stability constant of CeDOTMA is more difficult to understand however. K_CeDOTMA comes in between 10²⁰ and 10²¹, 2 to 3 orders of magnitude less stable than the later Ln³⁺ chelates reported herein (Table 3). This is unexpected since CeDOTA predominates in the TSAP coordination geometry which is approximately 5 orders of magnitude more stable than the SAP geometry²¹ for Ce³⁺ and CeDOTMA exists almost exclusively as the TSAP isomer in solution. Despite the preference and predominance of the TSAP isomer for Ce³⁺, its chelate with DOTMA is less stable than those of Ln³⁺ ions that have a preference for the SAP isomer. That Ce³⁺ is less charge dense than these other Ln³⁺ undoubtedly contributes to this observation but it cannot be the entire explanation for such a large difference in stability.

Chelate Formation

The mechanism by which LnDOTA-type chelates form was elucidated by Brücher and co-workers.⁴⁴ This mechanism invoked the extremely rapid formation of an intermediate chelate H₂LnL⁺, the formation of which was driven by the electrostatic attraction of opposing charges. The involvement of the same intermediate chelate in the formation of LnDOTMA chelates was established by potentiometric titration of DOTMA in the presence of Gd³⁺. A more thorough description of this process is presented in a companion paper;²¹ however, from comparison of the titration curves in the presence and absence of Gd³⁺ (Supporting Information) it is possible, not only to confirm that H₂GdL⁺ is the key intermediate chelate in the formation of LnDOTMA chelates but also to determine the thermodynamic stability constant of this intermediate: log K_H2GdL⁺ = 7.05 (0.01) (25 °C, 1.0 M KCl). Understanding this intermediate is the key, not only to understanding the mechanism of chelate formation, but also to performing the appropriate measurements for determining the kinetics of formation.

Given the highly stable chelates formed by DOTMA with Ln³⁺ ions, the kinetics of formation are of acute interest. Applications that involve chelating radio-nuclides require ligands that form chelates very quickly, many of the most interesting radio-nuclides have very short half-lives, but also form exceedingly stable chelates, to preclude release of the radio-nuclide in vivo prior to excretion or decay. From the thermodynamic stability constant log K_H2GdL⁺ and the potentiometric data in Table 3 it is possible to determine the mole fraction of H₂GdL⁺ as a function of pH.^21,44 This exercise enables us to determine the pH range over which to examine the formation kinetics of LnDOTMA chelates should be performed to ensure that H₂GdL⁺ is the sole starting reactant in solution. Since formation of this chelate is extremely fast, the rate of chelate formation is determined by the second deprotonation-rearrangement step in which the two protons of the macrocyclic ring dissociate allowing the metal ion to drop down into the coordination cage of the ligand.⁴⁴ Using this information it is clear that above pH 4.0 H₂GdDOTMA⁺ is the sole species in solution;^21,44 accordingly kinetic measurements were performed over the range pH 5.77–8.81 by measuring changes in the absorbance of EuDOTMA at 275 nm since the formation of complex results in a significant change in the UV spectrum of Eu³⁺ (between 245 and 290 nm). The data were treated according to the methods set out in a companion paper²¹ to afford a rate constant for the base catalyzed deprotonation-rearrangement, k_OH⁻ of (7.02 ± 0.12) × 10³ M⁻¹s⁻¹ for EuDOTMA. This value is 3 orders of magnitude smaller than that determined for EuDOTA^21,45 but of the same or similar order of magnitude to those determined for other ligands that are substituted on the pendant arms.²¹ This observation is highly indicative of the influence of α-substitution in increasing ligand rigidity in such a way as to slow the kinetics of formation of the Ln³⁺ chelates and by extension, presumably also the kinetics of dissociation, although these have not been directly measured. The slow kinetics of formation observed for DOTMA chelates means that although this ligand system affords the kind of thermodynamic stability that is highly desirable for chelation of radio-nuclides, its kinetics of formation are too slow for such applications.

Relaxometry and Variable Temperature ¹⁷O NMR Studies

The previously stated use of GdDOTA as a contrast agent for MR imaging is one of the major causes for the intense interest in the chemistry of DOTA and its Ln³⁺ chelates. GdDOTA is often considered the gold standard of MRI contrast agents and so it is instructive to compare the effectiveness of GdDOTMA as an MRI contrast agent with GdDOTA. MRI contrast agents, and their effectiveness, are commonly assessed though the use of nuclear magnetic relaxation dispersion (NMRD) profiles. These examine the agent at different magnetic field strengths in terms of its relaxivity, the increase in the longitudinal relaxation rate constant of water per unit concentration of contrast agent. Fitting NMRD curves to theory^1,46–52 is a useful exercise that allows several key parameters that determine relaxivity to be extracted. The NMRD profiles acquired for GdDOTA and GdDOTMA are remarkably similar (Figure 4).

Figure 4.

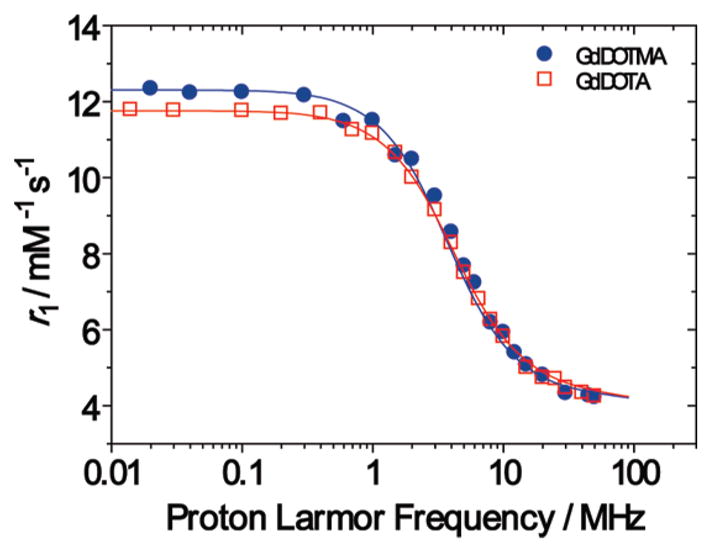
Nuclear Magnetic Resonance Dispersion (NMRD) profiles of GdDOTMA (blue) and GdDOTA (red) at 298 K and pH = 7.2.

Both GdDOTA and GdDOTMA give rise to NMRD profiles that are characteristic of low molecular weight Gd³⁺ chelates. The observed relaxivity at a given field strength is the sum of an outer sphere contribution (arising from diffusion of the water molecules in close proximty to the chelate in solution) and an inner sphere contribution (arising from exchange of the coordinated water molecule with the bulk solvent). Of these, inner sphere relaxivity is the more amenable to manipulation to improve the effectiveness of a contrast agent. Inner sphere relaxivity is predominantly governed by the interplay of three parameters: the residence lifetime of the coordinated water molecule (τ_M), the rotational correlation time of the chelate (τ_R) and electron spin relaxation (T_1e and T_2e). For low molecular weight chelates at higher magnetic field strengths (>10 MHz) τ_R is so short that it limits the inner sphere relaxivity of the chelate, hence GdDOTA and GdDOTMA have almost identical high field relaxivities. Providing that τ_M is not exceptionally slow it does not affect relaxivity at these fields unless the limiting effect of τ_R is lifted, say by conjugating the chelate to a larger molecule with a long τ_R.^1,34 At very low magnetic field strengths (<1 MHz) the inner sphere relaxivity of a Gd³⁺ chelate remains predominantly determined by molecular rotation but is also sizably affected by electron spin relaxation. The characteristics of aGd³⁺ chelate that influence the electron spin relaxation time constants T_1e and T_2e are not understood, but from Figure 4 and the appropriate fitting data in Table 3 it is apparent that both GdDOTA and GdDOTMA have comparable electron spin relaxation time constants. This gives rise to very similar low field relaxivities for the two chelates. This is in spite of the observation that the isomeric distributions of GdDOTA and GdDOTMA are very different (Figure 2); with the former predominating in the SAP geometry and the latter in the TSAP in solution. We have recently shown that both the SAP and the TSAP isomers of Gd³⁺ chelates have almost identical electron spin relaxation characteristics⁵³ consistent with the observed similarity between GdDOTA and GdDOTMA at low fields.

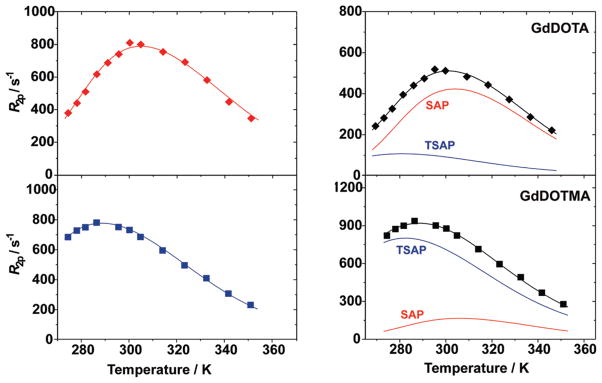
The marked preference of GdDOTMA for a TSAP coordination geometry in solution (Figure 2) also has one further implication: it suggests that the water exchange kinetics of this chelate should be markedly more rapid that those of GdDOTA. It is now well established that the water exchange kinetics in TSAP isomers are as much as a factor of 50 faster than those of a SAP isomer.^14,54–56 The kinetics of water exchange in Gd³⁺ chelates may be probed by the methods of Merbach and co-workers who used the temperature dependence of the solvent water ¹⁷O transverse relaxation rate constant (R₂) to extract the key exchange parameters.⁵⁷ Accordingly the temperature profiles of ¹⁷O R₂ were recorded for GdDOTA and GdDOTMA (Figure 5, left). Characteristic bell shaped curves were obtained in each case, and by inspection it is possible to see that, as expected, GdDOTMA has the more rapid water exchange kinetics of the two as the maximum of the bell shaped curve is shifted to lower temperature. Global fitting of these data and NMRD profiles for single species affords τ_M only as a weighted average value for the two isomers, even so when this is done it is apparent that GdDOTMA has a substantially shorter τ_M value than GdDOTA (Table 4). This observation is readily rationalized by considering the mechanism of exchange in these chelates. In these coordinatively saturated chelates exchange can only occur by dissociation of the coordinated water molecule in a rate determining step. Thus, the weaker the interaction between metal ion and water, the more rapid exchange will inevitably be. We have already seen from the crystal structures of GdDOTMA and GdTCE-DOTA that the O₄ plane pushes the water further from the metal ion in the TSAP isomer, weakening the metal-water interaction, vide supra. To account for this difference in the NMRD fitting procedure, the values of r_Gd–H were fixed to 3.02 and 3.10 for GdDOTA and GdDOTMA, respectively.

Figure 5.

Temperature dependence of the ¹⁷O transverse relaxation rate constant (R_2ρ) of solutions of GdDOTA (35 mM, top) and GdDOTMA (58 mM, bottom) at 2.1 T. The profiles are fitted to a single chelate model (left, data normalized to 50 mM) and to a ratio of SAP (red) and TSAP (blue) isomers based upon the mole fraction of each isomers determined by ¹H NMR of the corresponding Eu³⁺ chelates, Figure 2, (right) to afford the water exchange rates of each isomer.

Table 4.

Fitting Parameters Used in the Global Fitting of the NMRD and ¹⁷O Relaxation Profiles of GdDOTMA and GdDOTA^a

	GdDOTA	GdDOTMA
rGd–H (Å)b	3.02	3.10
τM weighted average (ns)	261 ± 13	85 ± 5
ΔHM (kJ mol−1)	52.6 ± 2.8	44.5 ± 2.2
1019 Δ2 (s−2)	1.6 ± 0.1	1.7 ± 0.1
τV (ps)	7.7 ± 0.3	7.9 ± 0.4
τR (ps)	66 ±3	81 ± 2
ΔHV (kJmol−1)b	1.0	1.0
a (Å)b	4.0	4.0
10−5D (cm2 s−1)b	2.24	2.24
A/ħ (106 rad s−1)	−3.7 ± 0.1	−3.7 ± 0.2

	GdDOTA		GdDOTMA
	SAP	TSAP	SAP	TSAP
Mol. fracn. (298 K)	0.83	0.17	0.19	0.81
τM (ns)	360 ± 15	53 ± 6	370 ± 17	50 ± 4
ΔHM (kJmol−1)	58.1 ± 2.5	41.9 ± 3.1	53.4 ± 2.9	40.3 ± 2.2
τV (ps)	7.8 ± 0.2	8.0 ± 0.3	8.1 ± 0.2	7.8 ± 0.1

^aIn fitting the data to a two chelate model the values of A/h and ΔH_V obtained in the single chelate analysis were employed and the value ofΔ² fixed to 1.6 × 10¹⁹ s⁻².

^bParameter fixed during fitting.

Each ¹⁷Oprofile was fitted to a sum of two species, the SAP and TSAP isomers, the distribution of each being determined from the ¹H NMR spectrum of the corresponding Eu³⁺ chelate (Figure 5, right and Table 4). This fitting procedure afforded τ_M values for both the SAP and TSAP isomers of each chelate. There is strong agreement between the values obtained for each coordination isomer suggesting that the only significant difference between the weighted average τ_M values obtained for each chelate is the distribution of coordination isomers in each chelate. Notably the τ_M values for each isomer extracted in this way are somewhat longer than those obtained for chelates that were constrained into a single coordination geometry: τ_M^TSAP = 51.5 ± 1.5 ns (cf. 6 ns for a constrained isomer);³⁴ τ_M^SAP = 365 ± 5 ns (cf. 70 ns for a constrained isomer).³⁴ This appears to be the result of asymmetric substitution of the macrocycle in NB-cyclen based chelates which seems to accelerate water exchange slightly in all cases^26,34,58

CONCLUSIONS

DOTMA provides a fascinating insight into aspects of the chemistry of tetra-acetate derivatives of cyclen that cannot necessarily be probed by studying the parent ligand DOTA and its chelates. The crystal structure of GdDOTMA demonstrates that the Gd–OH₂ distance is longer in the TSAP isomer than in the SAP. Notably this elongation is not as pronounced in the crystal as in solution, presumably because of the dynamic nature of the solution state measurements. In terms of their use as the basis of MRI contrast agents the elongation of the Gd–OH₂ results in water exchange kinetics that are more favorable for GdDOTMA than GdDOTA. In terms of the effectiveness of each chelate itself as a contrast agent, there is nothing to choose between the two in terms of relaxivity because of the limiting effect of τ_R. GdDOTMA does have one potential advantage over GdDOTA as an MRI contrast agent, especially in the current climate of concern about contrast agent safety in instances where in vivo residence times may be prolonged such as targeted imaging applications or renally compromised patients. The chelates of DOTMA with Ln³⁺ ions are much slower to form than those of DOTA, and while the kinetics of chelate dissociation have not been explicitly measured in this work, it is generally observed that chelates that form slowly also dissociate slowly. Therefore, even though the Ln³⁺ chelates of DOTMA are slightly less thermodynamically stable than those of DOTA (a possible consequence of the isomeric distribution in each system), it seems likely that they are considerably the more kinetically inert chelates. This suggests that DOTMA may be a more suitable choice of ligand in applications where chelate clearance from the body is likely to be slow.