Limitations of beam damage in electron spectroscopic tomography of embedded cells

Summary

Elemental mapping in the energy filtering transmission electron microscope (EFTEM) can be extended into three dimensions (3D) by acquiring a series of two-dimensional (2D) core-edge images from a specimen oriented over a range of tilt angles, and then reconstructing the volume using tomographic methods. EFTEM has been applied to imaging the distribution of biological molecules in 2D, e.g. nucleic acid and protein, in sections of plastic-embedded cells, but no systematic study has been undertaken to assess the extent to which beam damage limits the available information in 3D. To address this question, 2D elemental maps of phosphorus and nitrogen were acquired from unstained sections of plastic-embedded isolated mouse thymocytes. The variation in elemental composition, residual specimen mass and changes in the specimen morphology were measured as a function of electron dose. Whereas 40% of the total specimen mass was lost at doses above 10⁶ e^–/nm², no significant loss of phosphorus or nitrogen was observed for doses as high as 10⁸ e^–/nm². The oxygen content decreased from 25 ± 2 to 9 ± 2 atomic percent at an electron dose of 10⁴ e^–/nm², which accounted for a major component of the total mass loss. The specimen thickness decreased by 50% after a dose of 10⁸ e^–/nm², and a lateral shrinkage of 9.5 ± 2.0% occurred from 2 × 10⁴ to 10⁸ e^–/nm². At doses above 10⁷ e^–/nm², damage could be observed in the bright field as well in the core edge images, which is attributed to further loss of oxygen and carbon atoms. Despite these artefacts, electron tomograms obtained from high-pressure frozen and freeze-substituted sections of C. elegans showed that it is feasible to obtain useful 3D phosphorus and nitrogen maps, and thus to reveal quantitative information about the subcellular distributions of nucleic acids and proteins.

Introduction

Elemental maps from unstained sections of plastic-embedded cells in the energy filtering transmission electron microscope (EFTEM) provide quantitative information about the distributions of different types of biomolecules within subcellular compartments (Ottensmeyer, 1984; Reimer, 1995; Leapman et al., 1997; Leapman & Aronova, 2007). For example, the phosphorus L_2,3-edge signal reveals the distribution of nucleic acids, whereas the nitrogen K-edge signal reveals the distribution of proteins plus nucleic acids (Ottensmeyer & Andrew, 1980; Bazett-Jones et al., 1988; Bazett-Jones & Hendzel, 1999; Bazett-Jones et al., 1999). With recent advances in electron tomography (ET) and automated data collection methods (Frank, 1992, 2006; Kremer et al., 1996; Mastronarde, 1997), it is now possible to obtain three-dimensional (3D) elemental maps using quantitative electron spectroscopic tomography QuEST (Aronova et al., 2007a). This technique enables 3D correlation of biomolecular composition with subcellular structure. The principle of dose fractionation, whereby the electron dose is distributed over all the images in an acquired tomographic tilt series, implies that the signal-to-noise ratio of a particular feature in the 2D projection of a 3D reconstructed object should be the same as the signal-to-noise ratio of that feature acquired at an equivalent total dose in a single 2D image (McEwen et al., 1995). The same principle can be applied to elemental mapping. If a feature is detectable in a 2D elemental map recorded at a particular dose, then we expect it to be detectable in the 3D reconstructed volume from a tomographic tilt series recorded at the same total dose. Moreover,overlappingfeaturesinthe2Dmapwillbeseparated in the 3D reconstruction without any additional dose. The dose fractionation principle is well established in cryo-electron tomography of beam-sensitive frozen hydrated specimens and provides high quality 3D reconstructions from tilt series of images, each recorded at an exposure of a few electrons per pixel and a dose below 10⁴ e^–/nm² for the whole series (Koster et al., 1997; Grimm et al., 1998; Grünewald, 2003; Baumeister, 2004; McIntosh et al., 2005; Subramaniam, 2005; Hsieh et al., 2006). Because the core-edge scattering cross-section is so weak (10^–7–10^–5 nm²/atom) for elements such as phosphorus, calcium and iron, elemental mapping with a pixel size of a few nanometers typically requires very high electron doses in excess of 10⁶ e^–/nm² (Leapman & Rizzo, 1999; Leapman, 2003). Even taking advantage of dose fractionation, we expect that doses of order 10⁷ electrons/nm² will be required to map the 3D distributions of phosphorus and nitrogen in embedded cells, which raises questions about limitations due to electron beam-induced damage. It is known that the specimen structure is degraded at high electron doses (Isaacson, 1977; Braunfeld et al., 1994; Egerton et al., 2004), but the extent to which the damage affects elemental composition in the context of EFTEM is not well documented. Here we will address this question by measuring changes in total specimen mass per unit area, specimen thickness and chemical composition as a function of incident electron dose. We choose unstained sections of plastic-embedded mouse isolated thymocytes as a convenient specimen on which to perform these analyses, since thymocyte morphology is dominated by a nucleus containing densely packed heterochromatin with high levels of phosphorus and nitrogen. In addition, to demonstrate application of QuEST, elemental tomograms are obtained from the organism C. elegans prepared by rapidly freezing and freeze-substitution.

The total mass per unit area is determined from a relative thickness measurement based on the fraction of transmitted electrons that suffers inelastic scattering (Egerton, 1996). If the unfiltered image intensity is I^unfilt and the zero-loss filtered image intensity is I^zero, the relative specimen thickness is given by t/λ = ln(I^unfil/I^zero), where t is the thickness and λ is the inelastic mean free path. Since the total inelastic scattering cross-section per unit mass is nearly constant for organic materials that have approximately the same average atomic number, the relative thickness t/λ is proportional to the mass per unit area (Leapman et al., 1984).

A direct determination of the specimen thickness as a function of dose is obtained by reconstructing bright field tomograms acquired at different electron beam exposures. In these measurements, gold nanoparticles deposited on the sections enable straightforward delineation of the surfaces.

To calculate the loss of specific chemical elements as a function of dose, 2D elemental maps of phosphorus and nitrogen were obtained by recording pre-edge and post-edge intensities. Since major biological elements such as phosphorus are typically present at local concentrations of 1–2 atomic percent or less, the background intensity underlying the core-edge of interest must be subtracted accurately when calculating the elemental signal (Haking, 1999). Furthermore, it is necessary to account for subtle changes in the shape of the electron energy loss spectrum (EELS) due to plural inelastic scattering as a function of specimen thickness by modelling the background intensity (Aronova et al., 2007b).

From these determinations of mass per area, absolute specimen thickness, and elemental composition, we are able to assess the limits for determining the 3D composition in plastic sections of embedded cells and tissues. Then by using QuEST, we demonstrate that it is possible to obtain a quantitative 3D distribution of phosphorus and hence the nucleic acid in the vicinity of the cell nucleus.

Experimental methods

Specimen preparation

To obtain the unstained sections for 2D elemental mapping in EFTEM, freshly isolated wild-type mouse thymocytes were post-fixed in 2.0% glutaraldehyde in PBS solution for 2 h. After extensive washing in PBS, the specimens were dehydrated in ethanol solutions of 30%, 50%, 70%, 90% for 10 min and 100% for 45 min, before being infiltrated with Epon-Araldite (Ted Pella, Redding, CA): 30% Epon-Araldite and ethanol for 2 h, 50% Epon-Araldite and ethanol for 4 h, 75% Epon-Araldite for 12 h and 100% for 1 day. Then the embedded blocks were polymerized at 60°C for 2 days.

The protocol for preparation of unstained sections of C. elegans for 3D elemental mapping is described in Aronova et al., 2007a. The composition of the embedding resin was as follows: 29.4 g of bisphenol A/epichlorohydrin (C₂₁H₂₅ClO₅), a constituent of EMbed-812 and Araldite-502; 12.4 g of 1,4-butanediol diglycidyl ether (C₁₀H₁₈O₄), a constituent of EMbed-812); 2.7 g of dibutyl phthalate (C₁₆H₂₂O₄), a constituent of Araldite-502; 55.0 g of dodecenyl succinic anhydride (C₁₆H₂₆O₃); and 0.5 g of benzyldimethyl amine (C₉H₁₃N). This gave an estimated a net oxygen-to-carbon atomic ratio of 0.23 : 1.

Sections were cut using a Leica EM UC6 Ultramicrotome (Bannockburn, IL) to a thickness of 90–150 nm, and picked up on 400 mesh bare copper finder grids (EM Sciences, Hatfield, PA). To ensure stability of the tomography specimens under the electron beam, 5–10 nm carbon films were evaporated directly onto the copper grids supporting the sections using an Auto 306 evaporator (Edwards Inc., Tewksbury, MA). Gold nanoparticles provided fiducials for tracking drift during acquisition of the tilt series and for aligning the images prior to tomographic reconstruction. The grids were glow-discharged in air for 30 s and 10 nm colloidal gold (SPI Inc., West Chester, PA) was deposited on top and bottom surfaces of the sections. After adsorption for 5 min, the samples were thoroughly washed with de-ionized water to remove excess reagent.

EFTEM imaging

The tomographic tilt series and the 2D projections were obtained using a Tecnai TF30 transmission electron microscope (FEI Inc., Eindhoven, The Netherlands) operating at an accelerating voltage of 300 kV and equipped with a Tridiem post-column imaging filter (Gatan Inc., Pleasanton, CA). To optimize contrast in the unstained plastic embedded sections a 40-μm diameter objective aperture was inserted. Images acquired on the imaging filter's 2048 × 2048 pixel Ultrascan cooled CCD detector were hardware-binned to 512 × 512 pixels to improve the signal-to-noise ratio, resulting in a final pixel size of 2.6 nm.

To study the effects of beam damage, uncoated plastic sections supported on bare grids were exposed to the electron beam, while varying the dosage and the acquisition time. Carbon was not deposited onto these specimens, so that we could directly observe the effects of electron radiation damage on the embedding plastic. The specimens used for elemental tomography were carbon coated in order to stabilize the plastic sections and to help retard the radiation damage. The incident accumulated dose was determined for each experiment and measurements were made for doses from 50 e^–/nm² to 2 × 10⁸ e^–/nm². Five sets of measurements were made in regions of plastic as well as in regions of cells. Deployment of the shutter, i.e. beam deflector, in front of the specimen allowed precise control of the electron exposure. For each measurement, the relative thickness t/λ was obtained from the acquired unfiltered and zero-loss images. At some doses zero-loss (i.e. bright field) tomograms were collected in order to track the thickness changes in nanometres as the specimen continued to damage. To track changes in phosphorus and nitrogen concentrations as a function of dose, we began our measurements with the lowest possible dose of 10⁵ e^–/nm² up to 2 × 10⁸ e^–/nm² by collecting energy-selected images in the vicinity of the P L_2,3 edge and N K edge, respectively. Pre-edge and post-edge energy windows for phosphorus were set at 120 eV and 152 eV. Pre-edge and post-edge energy windows for nitrogen were set at 375 eV and 410 eV, respectively. The energy width of the integration window, determined by the energy selecting slit, was adjusted to 20 eV for each edge (Fig. 1). The integration time for the energy-selected images was selected as 4 or 8 s and each image was summed over 4 or 8 readouts, depending on the electron dose. Electron energy loss spectra that included the P L_2,3, N K and O K edges were also acquired. To calculate the oxygen loss from the specimen, energy windows of 40 eV centered at 305 eV and 552 eV were used to integrate the C K and O K edge signals, respectively.

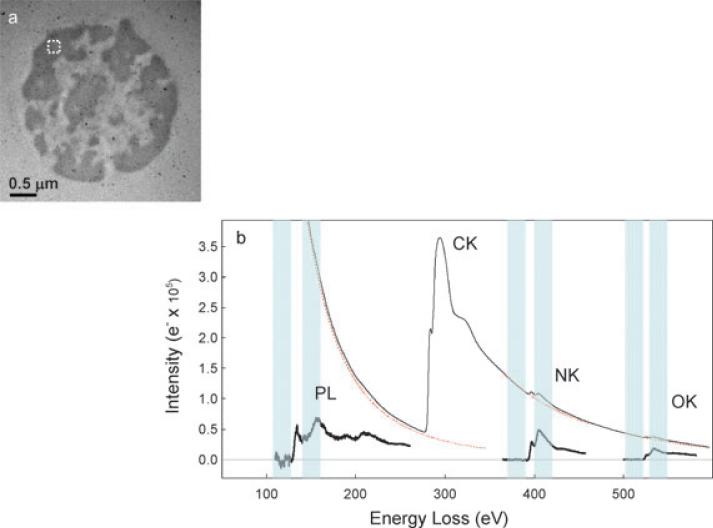
Fig. 1.

(a) Bright field TEM image (I^unfilt) of 100 nm unstained section of Epon embedded mouse thymocyte nucleus. Dark regions correspond to densely packed chromatin, rich in phosphorus and nitrogen. (b) Experimental electron energy loss spectrum (EELS) obtained from an area outlined in (a). The background-subtracted spectrum indicates the presence of phosphorus (P), nitrogen (N) and oxygen (O) in this specimen. The energy of P L_2,3 pre-edge window used for background extrapolation is 120 ± 10 eV, and the P L_2,3 post-edge window is at 152 ± 10 eV. Similarly, the N K pre-edge and post-edge windows are 375 ± 10 eV and 410 ± 10 eV, respectively.

To obtain 3D elemental distributions, the sample was tilted through a tilt range of ±69° using a tomography holder (Fischione Instruments, Inc., Export, PA) with an increment of 3°. The EFTEM tomography acquisition program (Harmon et al., 2005), written as a module in the Digital Micrograph software package (Gatan, Inc., Pleasanton, CA) provided automated data acquisition through control of the spectrum energy offset and width of the energy-selecting slit. A high-speed shutter situated in the imaging filter allowed successive acquisition of four images (zero-loss, unfiltered, pre-edge and post-edge) at each tilt angle without saturating the CCD detector while maintaining the same illumination on the specimen. Cross-correlation of zero-loss images enabled correction for specimen drift, as well as correction for focus change through determination of the image shift induced by tilting the beam. Zero-loss image series were acquired using a 20-eV slit width. Phosphorus L_2,3 edge tomographic tilt series were obtained using the same parameters as above for the damage measurements, i.e. a 20-eV slit width, a 120 eV pre-edge window and a post-edge window at 152 eV (Fig. 1). Each energy-selected image was summed over four readouts of 4 s integration time per readout.

For all the data acquisition, it was critical to subtract the dark current, to correct the CCD gain, and to tune the isochromaticity of the imaging filter to less than 1 eV across the full image field.

Electron tomograms were obtained using the method described previously (Aronova et al., 2007a). Alignment of the images in the tilt series was performed using the IMOD software from the University of Colorado (Mastronarde, 1997), and the reconstruction was calculated using the simultaneous iterative reconstruction technique (SIRT) (Aronova et al., 2007a).

Results and discussions

Unstained thin plastic embedded sections of mouse thymocyte nuclei were used to study the effects of electron irradiation on total specimen mass, specimen thickness and preferential loss of specific chemical elements. Features identified as regions of densely packed chromatin in thymocyte nuclei are evident in the bright field image in Fig. 1(a). Because of the low signal-to-background ratio (a few percent) for the P L_2,3 and N K-edges, energy loss spectra were also recorded from regions of chromatin to confirm the magnitude of the signal and the shape of the background underlying the weak edges (Fig. 1(b)). No anomalous spectral features are evident in the energy loss range from 100 eV to 600 eV due to impurities or contaminants in the specimen. The observed shapes and relative intensities of the P L_2,3, N K and O K core-edges agree with previous measurements (Leapman, 1986; Leapman & Ornberg, 1988; Leapman et al., 2004).

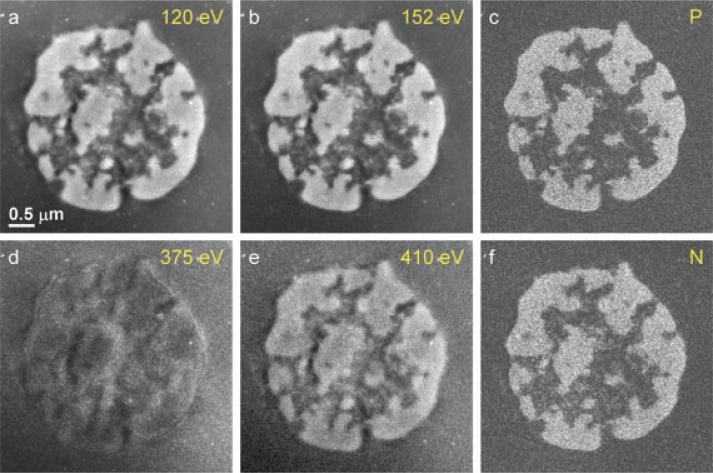
Next, we acquired EFTEM images below and above the P L_2,3 and N K-edges at the four energy windows indicated in Fig. 1(b). The pre-edge and post-edge images are shown in Figs 2(a), (b), (d) and (e), together with the computed phosphorus and nitrogen elemental maps in Figs 2(c) and (f), respectively. Most of the phosphorus and nitrogen is co-localized in regions of chromatin. However, in the open areas of the nucleus containing low phosphorus due to the relative sparseness of the chromatin some nitrogen-rich features are evident, which can be identified as proteins presumably involved in gene regulation.

Fig. 2.

EFTEM elemental mapping of a thymocyte nucleus. Panels (a) and (b) show the PL_2,3 pre-edge image intensity $I_P^{pre}$ at 120 eV and post-edge image intensity $I_P^{post}$ at 152 eV, which are used to calculate the 2D phosphorus map shown in panel (c). Panels (d) and (e) are the N pre-edge image intensity $I_N^{pre}$ at 375 eV and N post-edge image intensity, $I_N^{post}$, at 410 eV, which are used to calculate the 2D nitrogen map shown in (f). The major components of the thymocyte nucleus are densely packed DNA containing phosphorus and nitrogen, and protein containing nitrogen but negligible phosphorus. Nitrogen concentrations attributed to protein structures are visible in regions that contain low levels of chromatin regions that appear dark in the phosphorus map.

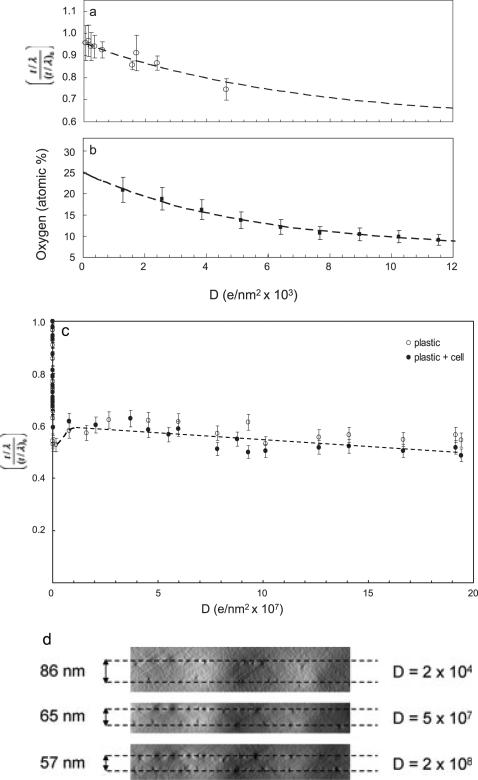
To investigate mass loss as a function of electron dose, t/λ maps were determined from each pair of unfiltered and zero-loss images. Five sets of data were recorded from cellular regions and five sets from the surrounding embedding plastic. Measurements made at similar doses were averaged and errors estimated from the standard deviations. Since cells typically have a water content of ~80%, a large fraction of the embedded cell (~80%) is plastic and only ~20% of the mass can be attributed to proteins, lipids and other cellular components. We therefore expect the damage in the pure plastic to be roughly the same as damage in the embedded cell so we averaged mass-loss measurements from cellular regions and surrounding regions of pure embedding medium. To examine the initial stages of electron beam damage, we plot the changes in t/λ for total exposures up to 1.2 × 10⁴ e^–/nm² (Fig. 3(a)). The y axis scale in Fig. 3(a) was normalized to unity by dividing the measured relative thickness (t/λ) at dose D by the initial relative thickness at very low dose, (t/λ)₀. This removed variations due to changes in the initial thickness across different specimen regions. The mass loss follows an exponential decay that can be fitted to a curve of the form:

$$\left(\frac{t}{\lambda }\right)-{\left(\frac{t}{\lambda }\right)}_{\infty }=\left[{\left(\frac{t}{\lambda }\right)}_0-{\left(\frac{t}{\lambda }\right)}_{\infty }\right]\exp \left(-D∕D_{damage}^{mass}\right),$$

where (t/l)_∞ is the relative thickness at a terminal dose much greater than the damage dose, $D_{damage}^{mass}$, which was found to be 6.8 × 10³ e^–/nm². After the damage dose has been reached the specimen mass has been reduced by approximately 30%, and after an exposure of 10⁶ e^–/nm² nearly 50% of the specimen mass has been lost. We attribute this initial damage to loss of oxygen, hydrogen and some carbon from the embedding medium through radiolysis involving direct breakage of chemical bonds and emission of low molecular weight products. We measured the loss of oxygen from regions of the embedding plastic as a function of electron dose (Fig. 3(b)) by determining the atomic fraction of oxygen relative to carbon based on the intensities of the oxygen K edge at 532 eV and the carbon K edge at 285 eV. The loss of oxygen relative to carbon can be fitted to an exponential decay of the form:

$$f^{oxygen}-f_{\infty }^{oxygen}=\left[f_0^{oxygen}-f_{\infty }^{oxygen}\right]\exp \left(-D∕D_{damage}^{oxygen}\right)$$

where,

$$f^{oxygen}=\left(\frac{I^{oxygen}}{I^{carbon}}\right)\left(\frac{{\sigma }^{carbon}}{{\sigma }^{oxygen}}\right)$$

f^oxygen is the atomic fraction of oxygen to carbon atoms, which is given by the ratio of O K-edge to C K-edge intensities multiplied by the inverse ratio of the O K-edge to C K-edge inelastic cross-sections for the 40 eV integration window. $f_0^{oxygen}$ is the atomic ratio of the oxygen to carbon at very low dose, and $f_{\infty }^{oxygen}$ is the atomic ratio of oxygen to carbon at high dose (>10⁵ e^–/nm²). The damage dose for oxygen loss $D_{damage}^{oxygen}$ estimated from fitting the decay curve to an exponential function is 5.4 × 10³ e^–/nm². The fraction of oxygen to carbon atoms decreases from an initial value of 0.25 in the undamaged specimen to approximately 0.15 after the damage dose $D_{damage}^{oxygen}$ has been reached, i.e. 40% of the oxygen has been removed. At a dose of 10⁴ e^–/nm² the oxygen to carbon ratio falls to approximately 0.10, i.e. 60% of the oxygen has been removed. As expected, it is evident from the fitted decay curves in Figs 3(a) and (b) that the damage dose for total mass loss is similar to the damage dose for oxygen loss. The oxygen to carbon ratio of 0.25 in the undamaged plastic section is consistent with mixture of components used to prepare the embedding medium, which gave a value of 0.23 (see Experimental methods).

Fig. 3.

Mass and oxygen loss measured in regions of Epon plastic and cellular material as a function of electron dose. The relative thickness t/λ measurementin (a) shows that the initial stage of the beam damage follows an exponential decay (dashed line) at electron doses <10⁴ e^–/nm². To avoid the spread in y values due to the disparities in initial specimen thickness (t/λ)₀, the measured t/λ values are divided by (t/λ)₀, thus normalizing the maximum specimen thickness to unity. The damage dose $D_{damage}^{mass}$ obtained by fitting the exponential decay is 6.8 × 10³ e^–/nm², at which the mass loss has reached about 30%. We associate this mass loss with the loss of oxygen atoms from the embedding material, as shown in (b). The atomic percentage of oxygen was calculated from energy loss spectra obtained at different doses, and $D_{damage}^{oxygen}$ obtained from fitting an exponential decay curve was 5.4 × 10³ e^–/nm². At doses above 10⁴ e^–/nm² at least two-thirds of the oxygen has been lost from the specimen. The relative thickness measurement in (c) extends the mass loss measurements up to electron doses of 2 × 10⁸ e^–/nm². Two phenomena are evident: rapid mass loss at doses <10⁵ e^–/nm², which is also shown in (a), and a much slower decay at doses >10⁷ e^–/nm², which appears to follow a simple linear function. A small increase in t/λ at intermediate doses is attributed to lateral shrinkage of the specimen Even for very high doses of 10⁸ e^–/nm² the total mass loss does not exceed approximately 50%. Locations of gold fiducial nanoparticles in y-z tomographic projections in (d) allow measurement of absolute changes in thickness (indicated in nm) as well as the lateral shrinkage.

We also tracked the loss of carbon by measuring the ratio of the carbon K edge intensity to the low-loss intensity as a function of dose. This ratio is proportional to the number of atoms remaining in the specimen, and provides a correction for plural inelastic scattering as the specimen becomes thinner (Egerton, 1996). After an exposure of 10⁴ e^–/nm², 9% of the carbon atoms were found to be lost from the specimen. The relative number of oxygen that remains in the sample is therefore 9% lower than the oxygen to carbon atomic fraction that we measure at a dose of 10⁴ e^–/nm², i.e. 0.09 instead of 0.10. We found there was a further 10% carbon loss at doses of 10⁶ e^–/nm².

The dose dependence of t/λ plotted in Fig. 3(c) reveals two damage processes: the rapid decay with increasing dose below 10⁵ e^–/nm² (also plotted in Fig. 3(a)), which is attributed to radiolysis involving direct breakage of chemical bonds by the electron irradiation, and a much more gradual linear decay at doses far above 10⁶ e^–/nm². After a dose of 10⁵ e^–/nm² the specimen mass per unit area has been reduced to approximately 50%. Then at higher doses, there is evidence for a small increase in t/λ, which is explained by a slight lateral shrinkage of the specimen. The shrinkage is evident from the displacement of gold nanoparticles in the bright-field tomographic reconstructions (Fig. 3(d)). As the irradiation continues to extremely high doses, a gradual linear decrease in mass per unit area is observed, which suggests another damage mechanism. This additional mass loss of approximately 10% at doses of 10⁸ e^–/nm² is likely due to knock-on damage resulting from rare high-angle scattering events. For carbon, the major element remaining in the specimen at these high doses, the knock-on damage cross-section for 300 kV electrons is ~10^–8 nm², assuming that each carbon atom has a net binding energy of 5 eV (Egerton et al., 2006). These knock-on scattering events can result in sputtering of the carbon atoms into the vacuum. However, the rate at which carbon atoms are lost from the plastic section appears to be at least an order of magnitude higher than from amorphous carbon. This might be explained by the plastic being porous after the initial mass loss, so that atoms can be directly ejected from below the surface. In that case, at electron doses of 10⁹ e^–/nm² we would expect holes to be formed in an 80-nm-thick specimen, although we were unable to generate such high doses in our EFTEM images.

Bright field tomograms provide a direct measure of specimen distortion as a function of dose, based on the location of nanoparticles deposited on both top and bottom surfaces. Figure 3(d) shows the y-z tomographic projections of the specimen at three different total doses. The lowest dose at which we could make these measurements was 2 × 10⁴ e^–/nm², which is significantly higher than our measured damage dose for mass loss. Our measurements in the untilted specimen indicate that a lateral shrinkage 9.5 ± 2% occurs from a dose of 2 × 10⁴ e^–/nm² to 5 × 10⁷ e^–/nm², which accounts for the slight increase of 15 to 20% in t/λ at intermediate doses (Fig. 3(c)). Our data indicate that even after the initial mass loss that occurs at low dose, there is a further ~25% reduction in specimen thickness with exposures between 2 × 10⁴ e^–/nm² and 5 × 10⁷ e^–/nm². Most of this change will have occurred during pre-irradiation of the specimen and prior to acquisition of the spectroscopic tomography data.

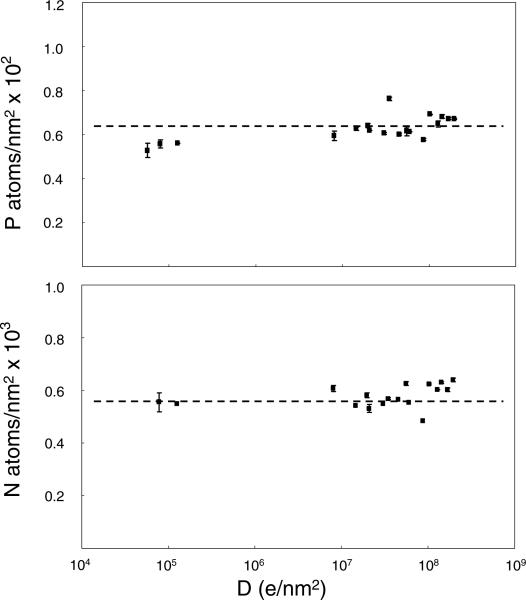
Having determined the effect of electron dose on the overall specimen geometry and morphology in EFTEM tomography, we now consider the effect of damage on the elemental composition. Specifically, we have examined the effects of electron dose on the measured concentrations of phosphorus and nitrogen. The measurements in Fig. 4 indicate that the P and N signals do not decay significantly even when electron doses exceed 10⁷ e^–/nm², i.e. the typical doses necessary to acquire EFTEM tomograms. Although the spatial distributions of elements do not appear to be affected at these higher doses at least on a scale of 10 nm, we do observe qualitative changes in the bright field%as well as in the pre- and post-edge images. Examples of these alterations occurring after a dose of ~10⁸ e^–/nm² are shown in Fig. 5. By comparing bright field images of the undamaged and damaged specimen, it is evident that darker regions, with higher electron density due to chromatin, become lighter in the heavily irradiated specimen. A similar effect is observed in the pre- and post-edge (dark-field) images, except the contrast is reversed. We attribute these changes in morphology to differential mass loss between the plastic embedding material and the biological molecules in the cellular regions. The changes in pre-edge image contrast across boundaries of cellular structure and pure Epon plastic under low dose and high dose conditions indicate that the differential mass loss between the plastic and the cellular regions is probably only about 6%.

Fig. 4.

Measurement of phosphorus and nitrogen distributions (atoms/nm²) in thymocyte nucleus as function of electron dose. Each data point was calculated from a series of four images with intensities I^unfilt (unfiltered), I^zero (zero-loss), I^pre (pre-edge), and I^post (post-edge), for P and N, respectively. Even for doses exceeding 10⁷ e^–/nm², which are typically required for elemental tomography, no significant loss of P and N was observed. It was not feasible to obtain useful compositional maps below a dose of 10⁵ e^–/nm² because the signal-to-noise ratio was too low.

Fig. 5.

Effect of electron dose on distributions of phosphorus and nitrogen in 100-nm plastic sections of thymocytes. Top four images, (a) unfiltered zero-loss, (b) 152-eV post-edge image, (c) net phosphorus, and (d) net nitrogen were acquired when specimen was exposed to low electron dose of 1.3 × 10⁵ e^–/nm². The bottom four images, (e)–(h), were acquired after an exposure of 8 × 10⁷ e^–/nm². Here the bright field and the core edge image exhibit dose effects, with more damage in the biological material. On the other hand, the phosphorus map in (g) and the nitrogen map in (h) not only have similar appearances to the elemental maps from the undamaged material in (c) and (d), respectively, but no significant loss of these elements was observed, as is consistent with Fig. 4. For thinner specimens (images not shown), structural damage was observed at lower electron doses.

Finally, we have applied the QuEST technique to perform 3D elemental mapping of phosphorus in an 80-nm-thick section of a C. elegans cell. Results of these experiments are shown in Fig. 6. The image recorded at a 0° tilt angle in the tomographic tilt series is shown in Fig. 6(a), and the reconstructed phosphorus distribution in Fig. 6(b). A total dose of 8 × 10⁷ e^–/nm² used to record tomographic series did not produce noticeable changes in morphology in the bright field image, which is consistent with the data shown in Fig. 5. It is evident that the signal-to-noise ratio of the phosphorus map at a single projection (0° tilt in Fig. 6(a)) is significantly improved when the reconstructed tomogram (Fig. 6(b)) is re-projected at 0° along the beam direction (Fig. 6(c)), as expected from the much higher accumulated dose. We note that the signal-to-noise ratio for the projected phosphorus distribution shown in Fig. 6(c) could not have been obtained in a single exposure because distortions in the specimen geometry would not have been taken into account, whereas these distortions are corrected in the alignment procedures of the tomographic reconstruction software, e.g. in the IMOD program. The volume-rendered tomographic reconstruction in Fig. 6(b) obtained using the SIRT algorithm shows the two regions of high phosphorus content: cytoplasm containing ribosomes (blue/green) and nucleus (orange/red) containing areas of densely packed chromatin. Bright spherical features in the reconstructed x-z slice shown below the projected tomogram can be identified as ribosomes. Similarly, the nitrogen distribution (not shown) can also be mapped in 3D, which together with phosphorus enables us to distinguish between nucleic acid and other structures that are mainly composed of protein.

Fig. 6.

Demonstration of 3D quantitative elemental tomography used to map the distribution of phosphorus in 80-nm-thick plastic section of a C. elegans cell. Net phosphorus distributions were calculated from four tilt series of unfiltered bright field, I^unfilt, zero-loss, I^zero, P pre-edge, $I_P^{pre}$, and P post-edge, $I_P^{post}$. (a) The net 2D phosphorus distribution at 0° tilt. (b) Volume rendered reconstructed tomogram obtained using the SIRT algorithm, reveals two regions of high phosphorus content: cytoplasm containing ribosomes (blue/green) and nucleus containing areas of densely packed chromatin (orange/red). (c) Projected phosphorus distribution along the z-direction at 0° tilt obtained from the tomogram in (b) shows improved signal-to-noise ratio relative to (a) due to the principle of dose fractionation. An x-z slice extracted from (b) shows the roundness and clarity of ribosomes. The dose used to acquire all the data was 8 × 10⁷ e^–/nm², which did not cause further observable damage to the specimen after initial shrinkage and mass loss.

Conclusions

The application of electron spectroscopic tomography to determine 3D quantitative distributions of specific elements in soft materials and biological structures, in particular, requires a careful assessment of radiation damage effects. We interpret our observations on beam damage in plastic sections following earlier studies by Isaacson (1977), Egerton et al. (2004) and Egerton et al. (2006). At doses in the range 10²–10⁵ e^–/nm², ionization damage is the primary mechanism whereby chemical bonds are broken and volatile products are released from the specimen. These damage processes occur with an exponential decay of a labile fraction of the mass or of a specific element, and a stable fraction remains in the specimen. At intermediate doses of 10⁵–10⁷ e^–/nm², shrinkage occurs, but mass loss essentially ceases. Then at very high doses of order 10⁸ e^–/nm² a gradual linear mass loss is observed, which we attribute to knock-on damage. At an accelerating voltage of 300 kV, atoms are lost at an order of magnitude lower dose than from amorphous carbon, which might be due to differences in the physical properties of the embedding material and pure carbon. Although up to 50% of the specimen mass per area is lost together with a corresponding decrease in specimen thickness, it is found that specific elements are retained in the specimen so that, for example, phosphorus and nitrogen can be imaged in 3D using total electron doses of around 10⁷ e^–/nm². By exploiting the principle of dose fractionation, it is possible to acquire a core-edge tilt series at about the same total dose as required for a single projection of the elemental distribution. However, knock-on damage imposes an ultimate limit on the use of the QuEST technique because higher beam voltages are required to avoid multiple scattering in the tilted specimens, yet knock-on damage cross-sections increase at higher voltages. Despite these limitations, we anticipate that QuEST will prove useful for imaging and quantifying the distribution of nucleic acid in cell nuclei.